Maximum Likelihood Estimation of Ion Channel Kinetics from Macroscopic Currents

Abstract

We describe a maximum likelihood method for direct estimation of rate constants from macroscopic ion channel data for kinetic models of arbitrary size and topology. The number of channels in the preparation, and the mean and standard deviation of the unitary current can be estimated, and a priori constraints can be imposed on rate constants. The method allows for arbitrary stimulation protocols, including stimuli with finite rise time, trains of ligand or voltage steps, and global fitting across different experimental conditions. The initial state occupancies can be optimized from the fit kinetics. Utilizing arbitrary stimulation protocols and using the mean and the variance of the current reduce or eliminate problems of model identifiability (Kienker, 1989). The algorithm is faster than a recent method that uses the full autocovariance matrix (Celentano and Hawkes, 2004), in part due to the analytical calculation of the likelihood gradients. We tested the method with simulated data and with real macroscopic currents from acetylcholine receptors, elicited in response to brief pulses of carbachol. Given appropriate stimulation protocols, our method chose a reasonable model size and topology.

INTRODUCTION

Ion channels control the flow of ions through cell membranes. These molecular gates exist in a continuum of conformations, but in practice these are reducible to a small number of kinetic states that live long enough to be resolved experimentally. Some of the states do not conduct ions (closed), whereas others are partially or fully conducting (open). “Instantaneous” transitions occur between these conformations, with the probability of transition described by a rate constant. The rate constant contains two intrinsic terms that describe the coupling of the rates to driving forces, such as ligand concentration, transmembrane voltage, tension, etc. (Hille, 2001).

The objective of kinetic analysis is to create a model—a hypothesis—with the minimum number of kinetic states and connections that can describe the data. Successful models are wonderful summaries of the data, and in that simplification help us to understand the structure and function of individual ion channels, and their mean behavior in cells. Hodgkin and Huxley provided the earliest prototype of this kind of analysis (Hodgkin and Huxley, 1952). The rate constants quantify the free energy difference between conformational states, providing insight into molecular structure and gating mechanisms. At the cellular level, the differential expression of ion channels, each with specific kinetic and conductance properties and modulation inputs, determine the static and dynamic membrane properties, and ultimately determine the network behavior of excitable cells.

Most properties of ion channels are best studied with single channel data (Neher and Sakmann, 1992), but technical difficulties often restrict recordings to samples containing multiple channels that cannot be resolved into unitary events. The statistical description of single channel data is well developed thanks to the work of many clever scientists (e.g., Ball and Rice, 1992; Ball and Sansom, 1989; Colquhoun and Hawkes, 1982, 1995a; Colquhoun and Sigworth, 1995; Horn and Lange, 1983; Kienker, 1989), and sophisticated analysis techniques based on Markov models have been published (e.g., Colquhoun et al., 1996; Qin et al., 1996, 2000). The statistical properties of macroscopic currents generated by ensembles of ion channels are well known, but the detailed kinetics are blurred by the overlap of many independent channels (Colquhoun and Hawkes, 1977). The time dependence (relaxation) of the current I_t of a model with N_S states, elicited by a step change in experimental conditions, is a sum of N_S − 1 exponentials (unless there are uncommon degenerate solutions), regardless of how states are connected (i.e., regardless of model topology; Colquhoun and Hawkes, 1995b):

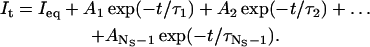(1)

The equilibrium current I_eq, the amplitudes A_i, and the time constants τ_i are not independent quantities because they are all functions of the same rate constants. A traditional method of macroscopic data analysis is to fit exponentials to nonstationary currents, with the main objective of estimating the time constants τ_i. However, the time constants thus obtained are estimated as independent parameters, without imposing the constraints determined by the particular topology of the model, or other constraints, such as loop balance. Hence, the topology of the model remains ambiguous. Rate constants cannot be easily calculated from time constants, and, without molecular rate constants, clues to molecular structure are obscure. Despite these shortcomings, exponential fitting remains the most widely used analytical method; partly for its intuitive feel, partly because of the illusion of model independence, and partly because few procedures for direct estimation of rate constants are available (e.g., d'Alcantara et al., 2002; Celentano and Hawkes, 2004).

A fundamental problem of kinetic modeling is the identifiability of the model, i.e., are there multiple topologies that are equally likely? In a now-classic example (Kienker, 1989), the model C-C-O (Closed-Closed-Open) cannot be distinguished from the model C-O-C, under equilibrium conditions. However, if one or more of the rates is stimulus dependent, they can be distinguished with nonstationary stimuli. Variable stimuli provide higher degrees of model discrimination.

We present here a maximum likelihood method for direct estimation of molecular rate constants from macroscopic ion channel data, using hidden Markov models. The algorithm can estimate the number of channels in the preparation, and the mean and standard deviation of a binary unitary current. The principle is to formulate the nonstationary macroscopic current I_t as a random variable with a Gaussian probability distribution, and to maximize the likelihood of the data with respect to the estimated parameters. For a given model, the mean μ_t and variance V_t of the macroscopic current I_t are functions of the rate constants, channel count, unitary conductance, and experimental protocol. These functions can be complicated, and involve calculation of the exponential of the rate matrix Q, as shown in Theory. The method is “direct” because the a priori assumptions about the topological and other constraints are explicitly specified in the model. We make two key assumptions: i), the ion channels are identical and independent; and ii), the experimental variables (such as ligand concentration, voltage, etc.) are not functions of channel activity. However, environmental variables need not be constant. We approximated continuously changing stimuli with a series of step functions. Although voltage clamp experiments generally satisfy these requirements, concentration and pressure jumps with significant rise time can be well approximated.

The algorithm is quite general, and has a number of features to assist users in model building: i), It works with models of arbitrary size and topology because the structural equations are internally formulated in terms of matrices and vectors. Models can be quantitatively compared, because distinct topologies with different constraints typically have different likelihoods. The modulation of individual state transitions by driving forces can be naturally studied. ii), Constraints can be imposed on rate constants. These constraints may be a priori knowledge of rate values, imposition of identical ligand-binding sites, microscopic reversibility, etc. The constraints reduce the number of free parameters, permitting exploration of larger allosteric models. iii), The current is modeled as a random variable, i.e., both the mean and the variance are used, which tends to reduce the problem of identifiability, and permits a simultaneous estimate of the mean single channel conductance. iv), The algorithm can estimate the number of active channels in the patch, if the single channel amplitude is known or coestimated. v), It works with nonstationary currents elicited in response to arbitrary experimental protocols, allowing for stimuli with finite rise times. A single model with driven rates can be globally fit across multiple data sets, with arbitrary stimulation protocols, and data from the same or from different patches can be combined in a single analysis. vi), The algorithm can analyze a sequence of stimulus steps (e.g., voltage) without assuming that channels reach equilibrium between steps. This reduces the amount of data required to solve the kinetics, and improves identifiability. vii), The starting probabilities (the state occupancies during a conditioning stimulus) are calculated from the fit kinetics and the experimental conditions. Hence, channels need not be assumed to occupy an arbitrary starting state. viii), Finally, the method efficiently calculates the likelihood function. The algorithm is faster than curve fitting using traditional differential equation solvers (d'Alcantara et al., 2002). Because the program utilizes only the diagonal elements of the autocovariance matrix, it is much faster then a recent method that uses the full autocovariance matrix (Celentano and Hawkes, 2004), and hence can handle larger data sets (although with slightly compromised precision). The gradients of the likelihood function are calculated analytically, enabling use of a fast variable metric optimizer (Fletcher and Powell, 1963; Fletcher, 1981; Press et al., 1992), with quadratic convergence.

This article focuses on the algorithm, its basic properties, and the results of extensive testing on simulated data. We concentrated on testing two ligand-dependent models (C-C-O and C-O-C), as the minimum nontrivial kinetic schemes that capture the behavior of more realistic models. As pointed out above, these simple models have identifiability issues: they are not distinguishable with equilibrium data (Kienker, 1989). However, they can be resolved by applying a suitable stimulation protocol.

We evaluated the two most important properties of the algorithm: the accuracy and the precision, and studied the effect of experimental factors, such as the number of channels in the patch, the amount of data, the stimulation protocol, etc. Because the kinetics of ion channels are rarely as simple as our three-state models, and the noise models of experimental data may depart significantly from the Gaussian assumption, we tested the algorithm with actual macroscopic currents from cells expressing acetylcholine receptors (AChRs). The AChR has a relatively complex kinetics, but the equilibrium rates are known in detail from single channel analysis (e.g., Akk and Auerbach, 1999). We showed that our method can choose the “correct” model size and topology based on differences in the goodness of fit. Because some of the time constants of AChR kinetics are quite short relative to the rise time of concentration jumps practically obtained, we explored the effect of finite rise time. In future work, we will apply the method to voltage-gated ion channels. The algorithm was implemented in software and integrated in the QuB electrophysiology suite, available for free at www.qub.buffalo.edu.

THEORY AND ALGORITHM

Kinetic model

We review here some basic results of ion channel kinetics, for an arbitrary Markov model with N_S conformational states. Rate constants are conventionally expressed as an N_S × N_S rate matrix Q (also termed the “generator” matrix; Colquhoun and Hawkes, 1995b). The Q matrix has the properties that each off-diagonal element q_ij is equal to the rate constant of the transition between states i → j, and that each diagonal element q_ii is equal to the negative sum of the off-diagonal elements of row i, so that the sum of each row is zero. When there is no direct transition between states i → j, q_ij = 0. In Eyring-type barrier models, the rate constant q_ij includes a preexponential factor 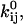multiplied by the concentration C_ij of some ligand, and an exponential factor 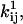multiplied by the magnitude of the driving force V_ij (such as voltage, pressure, etc.; Hille, 2001):

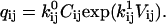(2)

The expression in Eq. 2 is equivalent to the common formulation 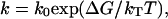where

At any given time, a state probability vector P, of dimension N_S, represents the occupancy of the N_S conformational states. The Kolmogorov differential equation describes the dynamics of a Markov process (Elliott et al., 1995):

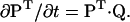(3)

The superscript ^T denotes vector transposition. If P₀ is the state probability vector at time t₀ < t, then P_t is given by the Chapman-Kolmogorov solution:

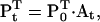(4)

where 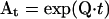is an N_S × N_S matrix, known as the transition probability matrix. Each element a_ij is equal to the conditional probability that the channel is in state j at time t, given that it was in state i at time 0. If the eigenvalues of the Q matrix are all distinct (and most ion channel models have distinct eigenvalues, with one being zero and representing the equilibrium solution, and the others negative), the matrix exponential A_t can be efficiently obtained from Q by spectral decomposition (Moler and Van Loan, 1978) as 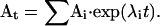The A_i values are the spectral matrices obtained from the eigenvectors of Q, and the λ_i values are the eigenvalues of Q.

Conductance model

To describe the conductance properties of an ensemble of N_C channels, we make the following simplifying assumptions: i), the baseline current (i.e., the current when all channels are closed) is a δ-correlated Gaussian random variable, with mean μ⁰ and variance V⁰; ii), the current passing through a single channel in state i is a δ-correlated random Gaussian variable, with mean μ⁰ + μ_i and variance V⁰ + V_i (Sigworth, 1985). By definition, μ_i = 0 and V_i = 0 for all the closed states. For two channels, one in state i and one in state j, the current is a Gaussian with mean μ⁰ + μ_i + μ_j and variance V⁰ + V_i + V_j. In general, the current given by an ensemble of N_C channels is the sum of Gaussian random variables, which is another Gaussian random variable. Hence, the conditional probability distribution of I_t, for a given probability vector P_t, has the following expression:

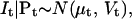(5)

(6,7)

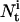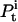is the number of channels occupying state i at time t, and can be formulated as a function of state probabilities: where is the occupancy probability of state i at time t. Let μ and V be vectors of dimension N_S, with elements μ_i and V_i as defined. Equations 6 and 7 can now be written in a more compact, vectorial form, as follows:

(8,9)

Equations 8 and 9 give, respectively, the conditional mean and variance of the current I_t recorded from an ensemble of N_C channels, given a state probability vector P_t. To obtain the unconditional distribution of I_t, we must remember that P_t, as calculated with Eq. 4, is the mean of a probability distribution, and that state occupancies will have fluctuations around this mean. Hence, the recorded current has two sources of variance: i), baseline and intrinsic state noise, and ii), state fluctuations. The state fluctuations theoretically have a multinomial distribution (the extension of the binomial to N_S states), but we will approximate it with a multivariate Gaussian to avoid a complicated convolution of probability distributions. This approximation will introduce a bias for currents arising from small numbers of channels. The covariance matrix of state fluctuations for the ensemble of N_C channels, at time t, is defined as:

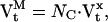(10)

where 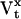is the N_S × N_S state covariance matrix, with elements 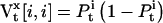and We obtain the unconditional distribution of I_t as follows:

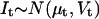(11)

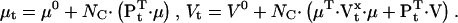(12,13)

The vector product 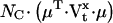represents the linear transformation of the 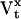state covariance matrix from the N_S × N_S state space into the unidimensional measurement space. To speed the computation, traces recorded in response to the same stimulation protocol can be averaged (assuming stationary kinetics), but to properly exploit the information contained in the sweep-to-sweep fluctuations, the expected variance V_t needs to be divided by the number of averaged traces. The above equations are derived for an arbitrary number of conductance classes. Hence, at least in principle, the method is suitable for models with substates (partially conducting states).

Starting state probabilities

The initial probability vector P₀ can be specified in two ways. One is to let the user assign values from a priori assumptions. This is commonly done with ligand-gated channels, when zero ligand concentration drives channels into an unliganded state, which is assigned a unity starting probability. With voltage gated channels, a conditioning potential is assumed to populate a specific state. However, this approach is not suitable for models with aggregated initial states (e.g., multiple unliganded states). The solution is to calculate the initial state probabilities as the equilibrium probabilities determined by the initial (conditioning) experimental conditions, which are assumed to last long enough for channels to reach equilibrium. 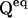The equilibrium assumption requires that P₀ satisfies the condition where is the rate matrix for which the equilibrium conditions hold. One way to calculate P₀ is the following (Colquhoun and Hawkes, 1995b):

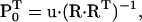(14)

where R is a N_S × (N_S + 1) matrix, formed by adding a column of ones to the right-hand side of 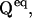and u is a column vector of dimension N_S, with each element u_i = 1.

Likelihood function

We describe here the likelihood function that is to be maximized by the algorithm. The likelihood L is defined as the conditional probability of the macroscopic current trace I, recorded for time t = [0…T], given the model parameters θ:

(15)

We assume that the state probability vector P_t is a function of the initial state probabilities P₀, but does not depend on the state probabilities at any other time. Hence, the distribution of the current at any time t is a function of the initial state probabilities only, which is equivalent to saying that the data have no autocorrelation beyond that contained in the A matrix. Thus, the conditional probability of the entire current trace is equal to the product of the individual conditional probabilities:

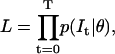(16)

where 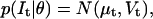with the mean μ_t and the variance V_t as defined in Eqs. 12 and 13. The objective is to find the parameter set θ^ML that maximizes the likelihood L:

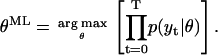(17)

The likelihood may be a very small, or a very large number, because it involves Gaussians, so to reduce numerical errors we actually maximize the logarithm of the likelihood function:

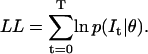(18)

The parameters to be estimated are 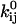and (Eq. 2), and the channel count N_C (in the following, for the sake of clarity, we omit the derivations for conductance parameters). There is no mathematical constraint on the exponential factor but the preexponential factor 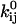and the channel count N_C must be positive numbers, leading to the following useful reparameterization:

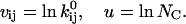(19,20)

The exponential formulation of the rates provides an implicit constraint that the rate constants are all positive, and hence physically realizable.

Parameter constraints

In addition to positivity of the preexponential factors, models may require other constraints. For example, if the two binding sites of the AChR are assumed to be identical and noninteracting, then the rates of the two consecutive binding steps should be constrained in a 2:1 ratio. Without such a constraint, the rates would be different; on the other hand, it is possible to test for independent sites using the likelihood. A priori constraints simplify otherwise complicated models. Each constraint, in addition to incorporating previously known results, reduces the number of free parameters by one. Typical constraints are: i), fix the pre- or exponential factor; ii), scale one pre- or exponential factor proportional to another; iii), enforce microscopic reversibility of cycles (the product of the rate constants going in one direction of a cyclic reaction is equal to the product of the rate constants going the other way). These constraints can be formulated as follows, where ct denotes the constrained value:

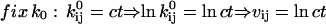(21)

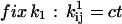(22)

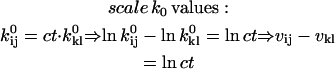(23)

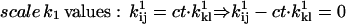(24)

(25)

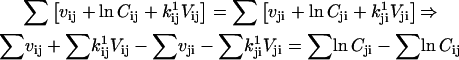The constraint expressions above can be written in matrix form as a set of linear equations (Qin et al., 1996, 2000):

(26)

where r is the vector of dependent (constrained) variables, with entries for and u. M_c is the coefficient matrix and V_c is the constant vector. The dependent variables r can in turn be expressed as a function of the independent variables x (Qin et al., 2000):

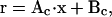(27)

where x is the vector of free parameters. The matrix A_c and the vector B_c can be determined from M_c and V_c using, e.g., the singular value decomposition (Qin et al., 2000). Other, nonlinear constraints could be included as well, by adding penalty terms to the likelihood function.

Computation of the likelihood function and its derivatives

We describe next the details of the computation of the likelihood function and its derivatives. The log likelihood LL of a macroscopic current, recorded for time t = [0…T] under constant experimental conditions, is calculated as follows:

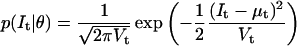(28)

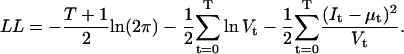(29)

The log-likelihood function in Eq. 29 reduces to the equally weighted (i.e., nonweighted) sum of squares 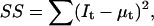if the constant terms and the variance-containing terms are eliminated.

The quantities of interest are the pre- and exponential factors and 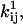and the channel count N_C, but the optimizer maximizes LL with respect to the free parameters x.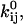 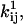and N_C are subsequently obtained from x using Eqs. 19, 20, and 27. The derivative of LL (or SS) with respect to a free parameter x_k can be calculated with the chain rule as follows:

(30)

with and where i and j are indices over the off-diagonal entries in the Q matrix corresponding to nonzero rates in the kinetic model. The partial derivatives of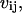 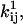and u with respect to x_k are obtained with Eq. 27. Let z denote either q_ij or N_C. Then the partial derivative of LL with respect to z is calculated as follows:

(31)

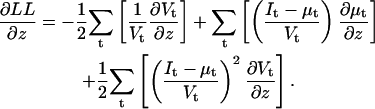(32)

Similarly, The derivatives of μ_t and V_t with respect to z are:

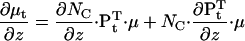(33)

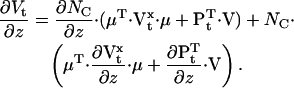(34)

The following results can be immediately derived: 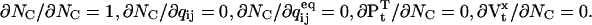The derivative of the 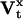matrix with respect to q_ij (and similarly for 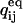) is another matrix with elements:

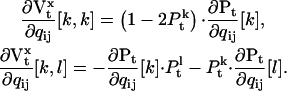(35)

The derivatives of the state probability vector P_t with respect to q_ij and 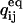are:

(36)

The following results can be immediately derived: The derivative of the initial state probability vector P₀ can be obtained using the following equality:

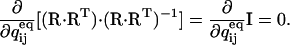(37)

We skip the derivation details and give the final expression:

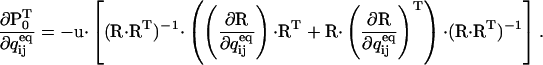(38)

The derivative of the A_t matrix (Ball and Sansom, 1989; Najfeld and Havel, 1995) is:

(39)

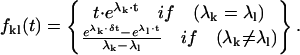(40)

The derivative of Q (and R) with respect to q_ij (and 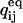) is another matrix Q_ij′, with the properties

Extension to arbitrary stimulation protocols

All the above calculations assume that the experimental conditions (i.e., the stimuli) do not change across the data set. We show next how to extend the method to arbitrary stimulation protocols. We assume that the applied stimulus is approximated by a sequence of S_C steps of constant value and arbitrary duration. Each step s starts and ends at times and 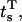respectively. We rewrite the expressions of the log likelihood and its derivative, to show the dependence of μ_t and V_t on the step s, as follows:

(41)

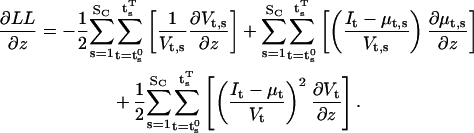(42)

In this case, the log likelihood is a function of multiple Q matrices (in addition to Q^eq), one for each set of experimental conditions that change the ion channel response. Although for each value of the stimulus there is a different Q matrix, the set of free parameters remains the same, as it does not depend on experimental conditions. Accordingly, the derivative of the log-likelihood function LL with respect to a free parameter x_k has the following form:

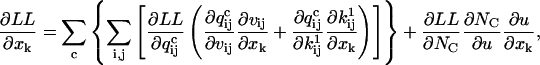(43)

where c is an index over all different experimental conditions, including the initial equilibrium. Let us consider the simpler case when the stimulus changes the kinetics, but not the unitary channel current, e.g., a change of ligand concentration. The expressions of μ_t,s and V_t,s become:

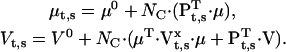(44,45)

For an efficient computation of the state probability vector P_t,s and its derivatives, we derive recursive relations. The state vector at time t, contained in the step s, is calculated as follows:

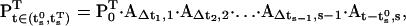(46)

where 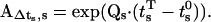By definition, the vector at the start of step s is equal to the vector at the end of step s − 1:

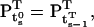(47)

where 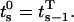Equation 47 can be written recursively and initiated as follows:

(48-50)

The derivative of the state vector can also be calculated recursively and initiated as follows:

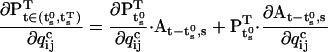(51)

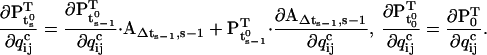(52,53)

The derivative of A_t,s with respect to 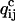is equal to zero when the experimental conditions for step s have an index different than c, thus simplifying the calculations. A similar treatment can be derived for voltage stimuli that change both the kinetics and the unitary current.

Variance of the estimates

Our choice of optimization routine is the Davidon-Fletcher-Powell algorithm (Fletcher and Powell, 1963; Fletcher, 1981), which is a quasi-Newton method with approximate line search, with efficient quadratic convergence. We used the "dfpmin" implementation in Press et al. (1992), with some modifications (Qin et al., 2000). The optimizer provides variance estimates for the optimized, free parameters x. The variance of the pre- and exponential factors 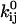and 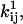and of the channel count N_C can be derived as follows (Qin et al., 2000):

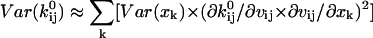(54)

(55)

(56)

MATERIALS AND METHODS

Electrophysiology

The adult mouse muscle-type nicotinic AChRs (α-, β-, δ-, and ɛ-subunits) were transiently expressed in tsA 201 cells using a calcium phosphate-based transfection technique, as described (Akk, 2002). The cells were plated on coverslips in 35-mm dishes. At the time of experiments, one coverslip at a time was transferred into the recording chamber. The electrophysiological recordings were carried out using a piezo-driven liquid filament system to measure the macroscopic responses to 1 mM carbachol on outside-out patches (Heckmann and Pawlu, 2002). The system had a solution exchange time of <50 μs when measured with changes in the liquid junction potential with an open patch electrode, or <100 μs when measured with an electrode containing a patch. The bath solution contained (in mM): 140 NaCl, 5 KCl, 2 CaCl₂, 1 MgCl₂, 10 glucose, and 10 Hepes (pH 7.3). The pipette solution contained (in mM): 140 KCl, 5 MgCl₂, 5 EGTA, 10 glucose, and 10 Hepes (pH 7.3). The agonist was dissolved in the bath saline solution and the membrane potential was held at −40 mV. The experiments were carried out at room temperature. Currents were amplified with an Axopatch 200B amplifier (Axon Instruments, Union City, CA), low-pass filtered at 10 kHz, and digitized at 50 kHz. Traces of 30-ms duration were recorded at intervals of 1 s using the ISO2 software (MFK, Taunusstein, Germany). Averaged currents from 10 to 25 traces were used for kinetic analysis.

Simulation and data analysis

Stochastic and deterministic simulations were generated with the QuB software (www.qub.buffalo.edu), using the ligand-gated kinetic models from Fig. 1, referred to as C-O-C and C-C-O, respectively, and the three stimulation protocols from Fig. 2, referred to as P₁, P₂, and P₃, respectively. We call the parameter values used for simulation true parameters, as opposed to estimated parameters. For each simulation, 10,000 traces were generated. Simulations with other models and protocols are described in the Results. A sampling interval of 10 μs was used for simulations, except in the analysis of experimental data, for which we used 20 μs. The QuB program can generate a stochastic macroscopic simulation as the summation of N_C single-channel stochastic simulations, in conformity with Eqs. 6 and 7. Alternatively, it can make a deterministic macroscopic simulation by calculating the current according to Eq. 8. The starting state probabilities are calculated as the equilibrium probabilities under the conditioning stimuli. For stochastic data, the starting state for each of the N_C channels is chosen randomly, such that the probability of starting in state i is proportional to 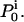The estimation of rate constants and channel count, and the nonweighted exponential fitting were done with QuB.

FIGURE 1.

The models used for simulation. (A) The transitions C₁→O₂ (in model COC) and C₁→C₂ (in model CCO) are ligand-binding steps. (B) An example of single-channel data simulated with the COC model. The single-channel current in either the Closed or the Open state is a random Gaussian variable.

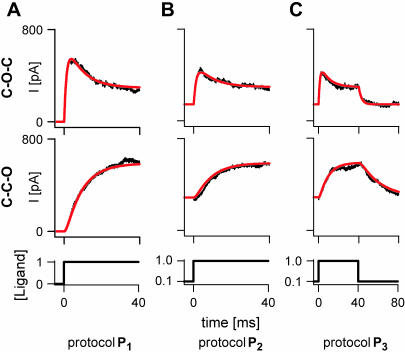
FIGURE 2.

The macroscopic response to different stimulation protocols. Macroscopic traces were simulated deterministically (smooth red lines) and stochastically (noisy traces) with the CCO and COC models, with N_C = 1000. The starting equilibrium probabilities were (1, 0, 0), for protocol P₁, and (0.571, 0.143, 0.286), for protocols P₂ and P₃. The units of the ligand concentration are arbitrary.

RESULTS

Model identifiability

What is a “correct” kinetic model? One first has to answer two identifiability questions: i), for a given stimulation protocol, can two models of the same size but different topology be distinguished? And ii), for a model of given topology and size, and a given stimulation protocol, does the mathematical model have a unique solution with respect to the rate constants and the number of channels, i.e., are there multiple optima?

With respect to the first question, Kienker (1989) showed that two models of different topology cannot be distinguished under equilibrium conditions if their Q matrices are related by a similarity transform. For example, the C-C-O and C-O-C models from Fig. 1 can describe the same equilibrium data with identical likelihood. If some three-state models cannot be distinguished, then we should be wary of more complicated models. However, the use of driving stimuli greatly enhances the ability to differentiate among models. For instance, when started in the leftmost state, the C-C-O model has a second-order latency, whereas the C-O-C has a first-order latency.

Can these two models be distinguished from macroscopic nonstationary data? The answer is yes. We fit the deterministic simulation of the C-O-C model in response to the P₁ stimulation protocol (Fig. 2 A), with the C-C-O model, and vice versa. The results are not shown, but we could not find any set of parameters that could generate the same current as the other model. The two models are therefore mathematically distinguishable with the simplest possible protocol, but how well can they be differentiated from noisy (possibly nonideal) data is a different issue.

With respect to the second question, a model can be classified (Cobelli and DiStefano, 1980) as a priori: i), “uniquely identifiable” if all its parameters have a unique solution; ii), “nonuniquely identifiable” if at least one of its parameters has a multiple but finite number of solutions, and all other parameters have unique solutions; iii) “nonidentifiable” if at least one of its parameters is undetermined, i.e., it has an infinite number of solutions.

We examined the identifiability of the C-C-O and C-O-C models. Macroscopic currents were deterministically simulated in response to the three driving stimuli from Fig. 2, with the rate constants shown in Fig. 1, and the number of channels N_C = 1000. We searched for other values of k₁₂, k₂₁, k₂₃, k₃₂, and N_C that gave the same average current as the true parameters (i.e., other solutions) by fixing one or more parameters and having the algorithm find the others, restarting several times with different initial values. Because the simulated data were noiseless, we minimized the sum of squares. Only the solutions with zero SS (within numerical precision) were accepted.

The results obtained with model C-C-O and protocol P₁ are shown in Fig. 3 A.1. The figure shows that, for a given N_C, for each value of k₂₁ there were two solutions for the other three rates. Hence, with protocol P₁, only two parameters can be uniquely estimated from model C-C-O. When repeated with different values of N_C, the experiment yielded similar results. Interestingly, the admissible domain of k₂₁ had an upper bound (∼341 s⁻¹). With protocol P₂, N_C was varied, and the four rate constants were again estimated (Fig. 3 A.2). For each value of N_C, there were again two solutions for the four rates. Hence, protocol P₂ is more informative, yielding three free parameters. Not surprisingly, the admissible domain of N_C had a lower bound (∼740), determined by the peak current amplitude and the unitary current.

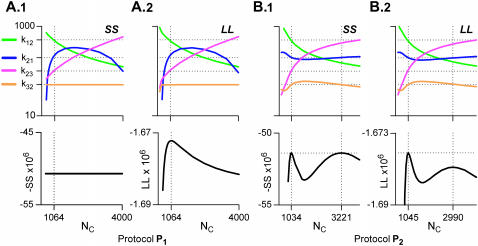
FIGURE 3.

The model identifiability depends on model topology and stimulation protocol. Macroscopic currents of identical mean (but not variance) can be obtained with different sets of the five parameters (four rate constants and N_C). Macroscopic traces were simulated deterministically, as in Fig. 2. The solid and the dashed lines in panels A.1, A.2, and B.1 represent two possible solutions of the estimated parameters, for each value of the varied parameter (k₂₁ and N_C). In panel A.1, N_C was fixed at its true value of 1000 (varying N_C adds an extra dimension to the solution space). In panel B.2, solutions of the four rate constants (solid circles) exist only for two values of N_C (1000 and 3333.333). With protocol P₁, a maximum of two and three parameters could be uniquely estimated for the CCO (A.1) and the COC (B.1) models, respectively. Protocol P₂ increased by one the maximum number of uniquely identifiable parameters (A.2 and B.2), whereas with protocol P₃ all five parameters were uniquely identifiable (results not shown).

The results obtained with model C-O-C and protocol P₁ are shown in Fig. 3 B.1. The rate constant k₂₁ was varied, and N_C and the other three rates were estimated. For each value of k₂₁, there were two solutions for the other four parameters. Therefore, with protocol P₁ three free parameters can be uniquely estimated from model C-O-C. As with the C-C-O model, the admissible domain of k₂₁ had an upper bound. With protocol P₂, N_C was varied, and the four rates were again estimated (Fig. 3 B.2). Only two values of N_C generated a zero SS: 1000, which is also the true solution, and 3333.333. Therefore, with protocol P₂ four free parameters can be uniquely estimated from model C-O-C. It can be argued that the second solution can be dismissed on the basis that N_C should be an integer number. However, this is just a particular case. For example, if the true value of N_C were 3000, then the second solution would have N_C = 10,000.

To summarize, with protocols P₁ and P₂, two and three free parameters can be uniquely estimated for model C-C-O, respectively, and three and four for model C-O-C. With protocol P₃, both models become fully identifiable, with unique solutions for all five parameters (results not shown). In conclusion, model C-C-O is nonidentifiable with protocols P₁ and P₂, and uniquely identifiable with P₃. Model C-O-C is nonidentifiable with P₁, nonuniquely identifiable with P₂, and uniquely identifiable with P₃. Although our search approach was not designed to find all admissible solutions rigorously, it made it clear that even these simple models create identifiability issues, even with nonstationary stimuli. The identifiability can be improved by more complex stimulation protocols. C-C-O is more ambiguous than C-O-C for the same stimulation.

Next, we tested whether including the variance-dependent terms in the likelihood function improves identifiability. Macroscopic currents were stochastically simulated with the C-O-C model, in response to stimulation protocols P₁ and P₂, respectively. The number of channels N_C was fixed at different values and the four rate constants estimated using the nonweighted sum of squares or the log likelihood. The results shown in Fig. 4, A.1 and B.1, essentially restate the conclusion drawn from Fig. 3, i.e., that the parameters of the C-O-C model are not uniquely identifiable with either the P₁ or P₂ protocols. With P₁, the SS corresponding to the best fit is constant for all values of N_C (Fig. 4 A.1), or has two identical minima with P₂ (Fig. 4 B.1). In contrast, the LL function has a global maximum, centered at the true parameter values, with either protocol P₁ (Fig. 4 A.2) or P₂ (Fig. 4 B.2). In conclusion, analyzing the response to more complex stimulation protocols and adding the variance-containing terms to the mathematical model are different ways to increase the number of equations, and hence to improve identifiability.

FIGURE 4.

The model identifiability improves if both the mean and the variance of the macroscopic current are utilized for parameter estimation. Macroscopic currents were stochastically simulated with the COC model, with N_C = 1000, in response to protocols P₁ and P₂ (as in Fig. 2). N_C was varied and the four rate constants were estimated from 100 simulated traces, using either the sum of squares or the log-likelihood method. The SS method uses only the mean, whereas the LL method uses both the mean and the variance. For easier comparison between LL and SS, the graphics show the negative SS.

Including the variance-containing terms also allowed us to calculate the mean and the standard deviation of the unitary current (Fig. 5). Macroscopic currents were stochastically simulated with model C-O-C in response to protocol P₁. The amplitude (Fig. 5 A), or the standard deviation (Fig. 5 B) of the open-state single-channel current was varied, and N_C and the four rate constants were estimated, using the LL method. The figure shows that LL has a global maximum centered at the true parameter values.

FIGURE 5.

Conductance parameters can be estimated from macroscopic currents with the likelihood function. Macroscopic currents were stochastically simulated with the COC model, with N_C = 1000, in response to protocol P₁ (as in Fig. 2). The mean μ_O and the standard deviation σ_O of the single-channel Open current were varied and the four rate constants and N_C were estimated with the LL method.

Statistics of the estimates

In the previous section, we checked the a priori identifiability properties of two simple models, in combination with three stimulation protocols. We found that the two models can be distinguished even with the simplest stimulus (P₁ in Fig. 2), and that for each model, the parameters can be uniquely estimated with the SS method and a suitable protocol (e.g., P₃), or with the LL method. But can the parameters be estimated with sufficient accuracy and precision from noisy data? We explored extensively the statistical properties of our algorithm using stochastic simulations of the same three-state models, but only present results for the C-O-C model, because C-C-O gave similar results.

We started with a qualitative look at the effects of biological variability. The signal/noise ratio (SNR) of a macroscopic current is proportional to 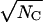and to as follows from Eqs. 12 and 13:

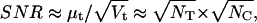(57)

where N_T is the number of averaged traces. The deviation between the fit and the current calculated using the true parameters is inversely proportional to the SNR (Fig. 6). Probabilistically, at low SNR the fit may differ substantially from the deterministically simulated current, but it matches well both the deterministic and the stochastic simulations at high SNR.

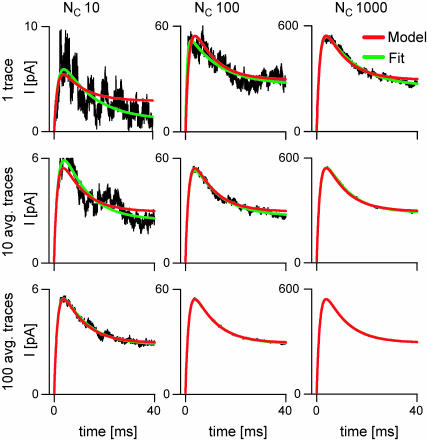
FIGURE 6.

The fit of the stochastic simulation may differ substantially from the deterministic simulation, at low signal/noise ratio. Macroscopic currents were simulated stochastically (noisy traces) and deterministically (red lines) with the COC model, with N_C = 10, 100, or 1000, in response to protocol P₁. The stochastic simulations were fit (green lines) as individual traces or as averages of 10 or 100 traces. The fits are virtually the same for the LL (shown), SS, or exponential fitting.

The accuracy and precision of the estimates are functions of SNR (Fig. 7). Parameter estimates were accurate at high SNR, but the accuracy was poor if <10–20 traces are averaged. The SE of the estimates (defined as the ratio between the standard deviation and the average) shows the expected inverse relationship with the SNR. Our maximum likelihood method and the exponential fitting had the same characteristics. However, fitting individual traces separately yielded results that were biased relative to the true parameter values, and were not symmetrically distributed about the mean (Fig. 8), with either the LL method (Fig. 8 A), or with the exponential fitting (Fig. 8 C). Interestingly, the rate constants estimated from equally short stretches of single-channel data had similar non-Gaussian distributions (Fig. 8 B), probably due to the exponential distribution of dwell times.

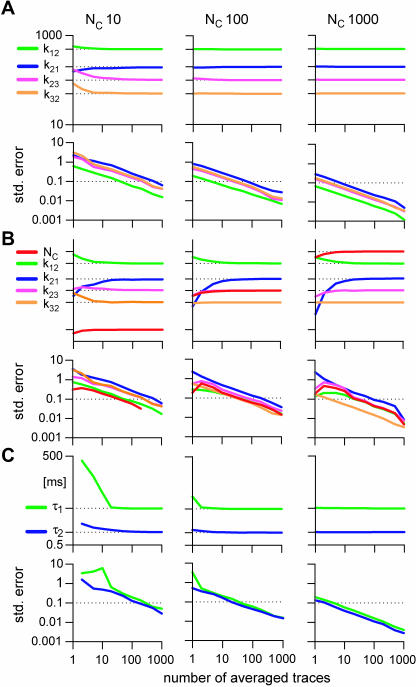
FIGURE 7.

The accuracy and precision of the estimates are functions of the signal/noise ratio. Macroscopic traces were simulated stochastically with the COC model, with N_C = 10, 100, or 1000, in response to protocol P₁. Rate constants (A), or rate constants and channel count (B) were obtained with the LL method, and time constants were obtained with exponential fitting (C). The average and the SE of the estimated parameters were calculated from 1000 fits of single traces or averages of multiple traces. The horizontal dotted lines in the average graphs mark the true parameter values. For easier comparison, the 10% SE is marked with a line in the standard error graphs.

FIGURE 8.

The probability distribution of parameter estimates is not Gaussian. Macroscopic traces with N_C = 10, and single-channel traces were simulated stochastically with the COC model, in response to protocol P₁. Macroscopic traces were fit individually or as averages of 10, and single-channel traces were analyzed individually or in groups of 10. (A) The distribution of rate constants and N_C estimated from macroscopic traces with the LL method. Similar results (not shown) were obtained with N_C fixed. (B) The distributions of rate constants estimated from single-channel traces, using the QuB software (www.qub.buffalo.edu). (C) The distribution of time constants estimated with exponential fitting. In all graphs, the dotted vertical lines mark the true parameter values.

Why is there a bias? One possible explanation is the simplified description of the macroscopic current, as we approximated the multinomial probability distribution of state occupancy with a multivariate Gaussian. This approximation has limits at small numbers of active channels. Fig. 9 A shows the probability distribution of the current, for p_Open = 0.1 and 0.5, respectively. At low p_Open and small N_C, the current distribution shows clearly the discrete peaks of the multinomial component (a high p_Open would give identical results). At p_Open close to 0.5, or for larger N_C, the distribution was well fit by a Gaussian, as indicated by the overlapped red line in the figure. These results are in agreement with the empirical rule, which states that the binomial is well approximated with a Gaussian, if n*p > 30, where n is the number of draws and p is the probability. Fig. 9 B shows that the standard deviation calculated by the algorithm (which includes one copy of the instrumentation noise and N_S copies of the excess state noise, and the gating fluctuations of N_S channels), provides a good representation of the data, as indicated by the red line in the figure.

FIGURE 9.

The probability distribution of macroscopic data can be well approximated with a Gaussian, except for very low (or very high) p_Open and small N_C. Ten-thousand macroscopic traces were simulated stochastically with the COC model, with N_C = 10, 100, or 1000, in response to protocol P₁. (A) Probability distribution of the macroscopic current, calculated from the 10,000 traces, for p_Open = 0.1 and 0.5. Overlapped is the fit with a Gaussian (red lines). (B) Standard deviation of the macroscopic current, measured from the 10,000 traces. Overlapped is the calculated standard deviation (red lines).

Because this approximation does not appear to be the main source of bias, we hypothesized it might be a result of the algorithm ignoring the local time correlation of the data. To test this, we generated data without autocorrelation (Fig. 10). Ten-thousand traces were simulated as in Fig. 7, and the data points at each time were resampled between traces. The resulting traces had the same mean and standard deviation at each time, but lacked the correlation of the original data. The difference between the correlated and the noncorrelated data, and between their respective fit lines is remarkable (Fig. 10 A). The parameter estimates and the mean currents obtained from the noncorrelated traces showed no bias, and higher precision (Fig. 10 B; compare with Fig. 7). The distributions of the estimates were Gaussian, and were statistically centered on the true values (Fig. 10 C; compare with Fig. 8).

FIGURE 10.

The bias of the estimates is caused by autocorrelation. Ten-thousand macroscopic traces were simulated stochastically with the COC model, with N_C = 10, in response to protocol P₁. The traces were further processed, by randomly reshuffling the data across traces, for each data point. The processed traces had the same current probability distribution, but lacked the autocorrelation of the raw data. The rate constants and the channel count were estimated with the LL method, from individual traces or from averages of multiple traces. (A) Examples of a simulated raw trace (top figure) and of a processed trace (bottom figure). Overlapped is the fit (green line), and the deterministic simulation (red line). (B) The average and the SE of the estimates obtained from the processed traces. (C) The distribution of the estimates. The dotted vertical lines mark the true parameter values.

Fig. 11 provides an additional view on bias. Macroscopic traces were simulated stochastically and were fit with three different methods: LL, SS, and exponential fitting. The residuals between the data and the fit line, and between the data and the deterministic simulation were calculated. In all three cases, the residuals obtained from fitting were smaller than the expected values, as if the data were fit “too well” (Fig. 11 A). For each data set, the residuals obtained with the best fit parameters were smaller than the residuals obtained with the true parameters (Fig. 11 B). For all three estimation methods, the fit line follows too closely the local time correlations present in the data, and this consistent “overfitting” leads to biased estimates. We speculate that only a Bayesian filtering algorithm (e.g., Roweis and Ghahramani, 2001) could obtain unbiased estimates from macroscopic data, but this would entail a high computational cost. The magnitude of the bias is hard to generalize for arbitrary models, but in the models tested, the parameters deviated by <10% (provided at least 10 traces were fit together, and N_C ≥ 100), probably much less than the variability introduced by biological heterogeneity and nonideal noise.

FIGURE 11.

Three different estimation methods indicate substantial data overfitting. Macroscopic traces were simulated stochastically with the COC model, with N_C = 10, in response to protocol P₁, and were fit individually or as averages of 10. Rate constants were estimated with the LL and the SS methods, and time constants were estimated with exponential fitting (ExpFit). The sums of squares between the data and the fit line (termed SS_LL, SS_SS, and SS_ExpFit, respectively), and between the data and the deterministic simulation (termed SS_Model) were calculated. (A.1–A.3) The distribution of the SS for the three fitting methods. Overlapped is the distribution of SS_Model (red lines). (B.1–B.3) The correlation between the SS of the three fitting methods and the SS_Model. The graphics indicate that, for each fit, the residuals obtained with the best fit parameters are considerably smaller than the residuals obtained with the true parameters. The estimated parameters are therefore biased.

We examined the cross-correlation between different pairs of parameter estimates, under different conditions of SNR or stimulation protocol (Fig. 12). The estimates of, e.g., k₂₁ and k₃₂ showed bimodal distributions, with protocol P₁ and at low SNR (row A). Correlations were especially strong between k₂₁ and k₁₂, and between k₃₂ and k₂₃. At higher SNR (rows B and C), the width of the distributions was reduced, to the point that with N_C = 1000 they became unimodal (row C). The P₃ protocol likewise narrowed the distribution (row D). As expected, neither a higher SNR (compare rows B and C with row A), nor a more complex protocol (compare row D with row C) could eliminate the correlations between parameters. The implication for fitting is that if one parameter is estimated with bias or with high variance, then its strongly correlated partners will also be biased and imprecise.

FIGURE 12.

The parameter estimates are correlated. Macroscopic traces were simulated stochastically with the COC model, with N_C = 10 or 1000, in response to protocols P₁ or P₃, and were fit individually or as averages of 10. Rate constants were estimated with the LL method. The red solid circles mark the true parameter values. Each graph is a two-dimensional histogram of the estimates for a given pair of two parameters, under a given set of conditions (N_C, protocol, and number of averaged traces). There was strong correlation between, e.g., the k₃₂ and k₂₃ rate constants (row C or D), but little, if any, between, e.g., k₂₃ and k₁₂ (row C). Similar correlations were found between rates and N_C (not shown). The correlations were not eliminated by a higher signal/noise ratio (compare rows B and C with row A), nor by a more complex stimulation protocol (compare row D with row C). Notice the change in scale between the first two and the last two rows of figures.

Model identifiability affects the accuracy and precision of the estimates (Fig. 13). Macroscopic traces were stochastically simulated in response to protocols P₁, P₂, and P₃, and rate constants and channel count, or rate constants, channel count, and unitary current μ_O were obtained with the LL method. The quality of the estimates was improved by a more elaborate stimulation protocol (compare between A, B, and C panels), and it was negatively affected by raising the number of free parameters (compare the left with the right figures in each panel).

FIGURE 13.

The accuracy and precision of the estimates are functions of model identifiability. Macroscopic traces were simulated stochastically with the COC model, with N_C = 1000, in response to protocols P₁, P₂, and P₃ (A, B, and C, respectively). Rate constants and N_C (left-hand side figures of each panel), or rate constants, N_C and the mean of the unitary current μ_O were estimated with the LL method. The average and the SE of the estimated parameters were calculated as in Fig. 7.

Analysis of experimental data

After exploring the statistical properties of our algorithm with simulated data, we determined its performance with experimental data from two patches: the response of AChRs to brief pulses of carbachol. The results obtained with the first patch are presented in Fig. 14. Ten current traces were averaged for analysis (Fig. 14 A). The concentration versus time profile of the experimental carbachol pulse was idealized assuming an instantaneous rise time (Fig. 14 B). The location of the concentration jumps, t_start and t_end, were not precisely known, but were estimated as follows: we tried different combinations of the t_start/t_end pair, searching around the visually selected values, and chose the points that gave the best fit. We used a simplified version of the standard kinetic model of the acetylcholine receptor (Magleby and Stevens, 1972; Colquhoun and Sakmann, 1985), with and without a desensitized state: C-C-C-O-D and C-C-C-O (Fig. 14 C). The ligand binding sites were assumed identical and independent, thus reducing the number of free parameters, as indicated in the figure. Due to contamination with 50 Hz periodic noise and artifacts from the piezoelectric solution exchanger, we analyzed the data with the SS method, because the LL method might have overestimated the variance, and thus N_C. We assumed a unitary current of −3.4 pA. Fits to C-C-C-O and C-C-C-O-D models are shown as the green and the red lines in Fig. 14 A, for which the rate constants and the number of channels were estimated simultaneously. The blue line is the fit with the C-C-C-O-D model, in which all rate constants were fixed to values previously reported in the single channel literature (termed the “reference” rates; e.g., Akk and Auerbach, 1999), and only the channel count was estimated. The rate constants obtained by fitting the C-C-C-O-D model to the data are presented in Fig. 14 D, for comparison with the reference rates. The fits with both the C-C-C-O and the C-C-C-O-D models well matched the data, although the inclusion of a desensitized state provided a better fit in the carbachol wash-in phase. In contrast, the fit using the reference rates clearly deviated from data, during the rise and fall phases.

FIGURE 14.

The kinetics of the acetylcholine receptor can be determined from the macroscopic response to brief pulses of 1 mM carbachol. The experimental procedure is described in Materials and Methods. (A) The average of 10 macroscopic traces. The green and the red lines are the fits with the CCCO and CCCOD models, respectively (C). The rate constants and N_C were estimated from the average trace, using the SS method. For the single-channel amplitude we used the value found in single-channel experiments. The blue line is the fit with the CCCOD model, in which all rate constants were fixed to values previously reported in literature (Akk and Auerbach, 1999; Dilger and Liu, 1992), and only N_C was estimated, using the SS method. (B) The idealization of the carbachol pulse. The exact change points of the ligand concentration (t_start and t_end) were unknown, but were determined as the points corresponding to the best fit (minimum sum of squares). (C) Simplified kinetic models, with two identical and independent ligand binding sites. (D) The rate constants obtained by fitting the CCCOD model versus the reference rates.

Not surprisingly, the rate constants obtained from fitting explained the data better than the reference values. Whole-cell and single-channel recordings are made under different conditions and these deviations have been previously reported (Fahlke and Rudel, 1992). However, if we assume that the reference rates are true, the differences could be attributed to biological variability, to a non-Gaussian distribution of parameters, or to the finite rise time of the concentration jumps. To test the latter hypothesis, we analyzed the errors produced when ligand pulses with finite rise times are approximated by steps. The results are presented in Table 1. Macroscopic data were simulated deterministically with ligand pulses of 0, 70, and 160 μs rise times, and were fit assuming the true ligand concentration, or with step pulses with known or unknown concentration change points. Parameters could be accurately estimated when the true ligand concentration profile was used (Table 1, rows A, B, and E). This was true even though the three fastest time constants of the model in the presence of agonist (167.75, 14.56, and 7.64 μs) were comparable to, or faster then the agonist rise times (70 and 160 μs). In contrast, when a pulse with a finite rise time was idealized with a step, the parameters were estimated with significant errors (proportional to the rise time), whether the concentration change points were correct (Table 1, rows C and F), or were determined by the best fit (Table 1, rows D and G). We conclude that it is worth spending more effort on determining the concentration profile more precisely (including the 50% change points) than on obtaining ultrafast rise times.

TABLE 1.

Ligand pulses with finite but unknown rise time and inaccurate latencies cause estimation errors

	[Ligand] 10–90% rise time [μs]	tstart	tend	ka [M−1s−1]	kd [s−1]	ko [s−1]	kc [s−1]	kD [s−1]	kR [s−1]	SS
A	0	–	–	45,000	20,000	8000	2500	20.0	5.0	0.0
B	70	–	–	45,000	20,000	8000	2500	20.0	5.0	0.0
C	70	–	–	52,000	17,000	6500	2500	21.0	4.5	14.6
D	70	tstart* − dt	tend*	16,000	12,000	16,000	3500	20.5	4.0	8.5
E	160	–	–	45,000	20,000	8000	2500	20.0	5.0	0.0
F	160	–	–	170,000	13,000	3600	2400	25.0	2.8	278.6
G	160	tstart* − 3dt	tend* − 2dt	13,500	3200	4400	4200	30.0	5.3	26.5

Macroscopic currents were simulated deterministically using the rates shown in row A, with N_C = 100. For simulation we used three ligand pulses, similar to that shown in Fig. 14, but with 10–90% rise times of 0, 70, and 160 μs, respectively; t_start* and t_end* denote the concentration change points of the first pulse (0 μs rise time). The two pulses with finite rise times were obtained by low-pass filtering the first pulse with a Gaussian filter with cut-off frequency set at 5 and 2 kHz, respectively. The Gaussian filter preserved the 50% concentration change points. Rate constants and N_C were estimated using the SS method, and the estimated values were rounded to within 1% for display. In rows A, B, and E, parameters were estimated using the true ligand concentration curve of each simulation (with 0, 70, and 160 μs rise time, respectively). As shown, estimates obtained from slow rise time pulses were correct to within the numerical precision, if the ligand concentration profile was known exactly. In rows C and F, the parameters were estimated with the slow rise concentration profile approximated by a square pulse, but with known concentration change points t_start* and t_end*. As shown, the error of the estimates was proportional to the error made in approximating the slow rise time with a step. In rows D and G, parameters were estimated as in C and F, respectively, but the jump points were determined as those giving the best fit (denoted by t_start and t_end in the table). In this case, the fit was better (lower SS), but the parameters and the concentration change points were estimated with large errors; dt denotes the sampling interval.

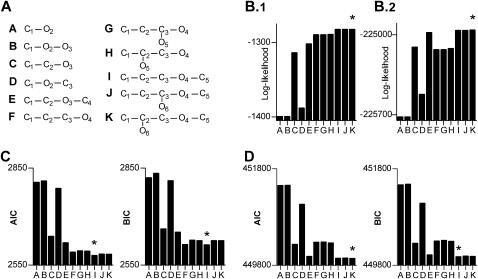
To what extent can the topology and size of a kinetic model be determined from macroscopic data? The experimental data shown in Fig. 14 A, and data simulated stochastically with model K shown in Fig. 15 A were fit with increasingly complex models (Fig. 15 A), with the LL method, using the idealized ligand pulse from Fig. 14 B. Fitting the experimental and the simulated data (Fig. 15, B.1 and B.2, respectively) revealed a similar pattern, with the highest likelihood score assigned to the correct C-C(-O)-C-O-C model (or submodel). We further tested whether the increase in likelihood for larger models is spurious, i.e., simply due to extra fitting parameters. For this, we calculated the Akaike (AIC) (Akaike, 1974) and the Bayesian (BIC) (Schwartz, 1978) information criteria, defined as follows:

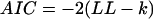(58)

(59)

where k is the number of free parameters, and N is the number of data points. There is a conceptual difference between the two criteria: AIC attempts to find a good approximating model for inference, without assuming a true model actually exists, whereas BIC assumes a true model does exist, and attempts to consistently estimate its dimension (and requires large amounts of data). For our experimental data, both AIC and BIC selected the smaller C-C-C-O-C model (Fig. 15 C). For the simulated data, AIC selected the C-C(-O)-C-O-C model, whereas BIC selected the C-C-C-O-C model (Fig. 15 C). Additional simulations confirmed these results statistically, although for different data sets one model or the other was selected. The experiment showed that the correct topology is statistically favored by LL, AIC, and BIC, but that larger models may be penalized too much by, e.g., BIC. We note that spurious states were often indicated by the optimizer either by virtually zero entry rates, or by very large exit rates (i.e., virtually zero occupancy probability). As with all statistics, the significance level of a given result is largely an aesthetic choice of the experimenter.

FIGURE 15.

The correct kinetic model can be determined from macroscopic currents. The data presented in Fig. 14 A were fit with the kinetic models shown in panel A, using the idealized ligand pulse from Fig. 14 B. For all fits, the change points of the ligand concentration were those determined for model K, as described in Fig. 14. Rate constants and N_C were estimated using the LL method. The same treatment was applied to macroscopic data simulated using rate constants published in the single-channel literature (Akk and Auerbach, 1999; Dilger and Liu, 1992; the rate constants for the C₂→O₆ and O₆→C₂ transitions were 100 s⁻¹ and 3000 s⁻¹, respectively). One-hundred traces were stochastically simulated with model K, and fit with models A–K. The LL values for the real and for the simulated data are presented in panels B.1 and B.2, respectively. The Akaike (AIC) and Bayesian (BIC) information criteria were calculated for the real (C) and for the simulated data (D). The stars in panels B, C, and D mark the best model, selected according to the criterion indicated in the graph.

The analysis of the data from the second patch demonstrates how fitting the whole current trace, as opposed to fitting the rising and the fall phases separately, helps resolve stimulus artifacts (Fig. 16). This patch reveals a long tail current during the wash-out phase (Fig. 16 A). The tail current could presumably be explained in two ways: i), it is an intrinsic property of the patch, or ii) it is caused by residual agonist, probably due to misalignment of the drug application system. To test these two hypotheses, we fit the data using an idealized concentration profile (Fig. 16 B), with the agonist concentration in the wash-out phase denoted by [L]_res. The blue line in panel A is the fit in which all rate constants were fixed to the reference values, and only the channel count was estimated, assuming no residual ligand ([L]_res = 0). The green line is the fit in which both the rate constants and the channel count were estimated, assuming [L]_res = 0. Finally, the red line is the fit in which the rate constants and the channel count were estimated, but allowing for residual ligand. Specifically, the red line is for [L]_res = 0.025 mM carbachol. The rate constants corresponding to the red line fit are presented in panel C. The variation of the estimated parameters and of the goodness of fit (SS) is presented in panel D. The rise and fall phases of the current alone could be well fit using either our method, or the sum of exponentials. However, the trace as a whole could not be fit with the C-C-C-O-D model, unless a nonzero residual ligand concentration was assumed. Hence, we conclude that the hypothesis of residual agonist in the wash-out phase is likely to be correct. Interestingly, the peak in the SS plot versus [L]_res (panel D) indicates that the residual agonist concentration can itself be estimated.

FIGURE 16.

Experimental artifacts can be detected by fitting the macroscopic response to the entire pulse protocol. (A) The average of 25 macroscopic traces. Overlapped are the fits with the CCCOD model (C), using the idealized ligand pulse shown in panel B. The ligand concentration of the pulse's third segment (denoted by [L]_res) was intended experimentally to be zero. The blue line is the fit with [L]_res = 0, with the CCCOD model, in which all rate constants were fixed to reference values, and only N_C was estimated, using the SS method. The green line is the fit with [L]_res = 0, with all rate constants and N_C estimated. The red line is the fit with [L]_res = 0.025 mM, with all rate constants and N_C estimated. (C) The estimated rate constants corresponding to the fit with [L]_res = 0.025 mM. (D) The variation of the estimated rate constants and N_C, and of SS, for different values of [L]_res. For each fit, the change points of the ligand concentration were determined as described in Fig. 14.

Is there an optimal stimulus protocol for resolving a kinetic scheme? In a simple study, we simulated data with the C-C-C-O model, using the AChR reference rate constants, and the ligand pulse from Fig. 16 B. The parameter estimates obtained with zero residual agonist (Fig. 17 A) showed strong bias, unless ∼50 traces were analyzed together. In contrast, the estimates obtained with finite residual agonist (Fig. 17 B) showed virtually no bias and small errors, even with small amounts of data. This is in agreement with the results presented in Fig. 10, from which we have concluded that a more complex protocol (i.e., [L]_res ≠ 0) will give more accurate and more precise estimates. Hence, a stimulation protocol with three different concentration steps, although more difficult to implement, should substantially improve the estimates. Alternatively, one could apply binary protocols, but consisting of several pulses. This agrees with the results of other studies of nonstationary stimuli (Millonas and Hanck, 1998).

FIGURE 17.

The stimulation protocol used in the carbachol experiments is not adequate for accurate and precise estimates. Macroscopic traces were simulated stochastically with the CCCO model, using the reference rates, with N_C = 100, in response to the ligand pulse protocol shown in Fig. 16 B, with [L]_res = 0 (A), or with [L]_res = 0.03 mM (B). Rate constants and N_C were estimated from the averages of 10 or more traces, using the SS method. The average and the SE of the estimated parameters were calculated as in Fig. 7.

The kinetic parameters estimated from the two patches are close to the values reported in the single-channel literature. The SE of the estimates produced by the optimizer (see Figs. 14 D and 16 C) is a measure of how precisely the parameters can be calculated from a given data set, i.e., it quantifies our belief in those values. It does not, however, inform us about the variability between experiments due to the stochastic nature of ion channels, or about biological variability. For example, the k_a in Fig. 16 C is estimated with a small SE ∼3%, whereas Fig. 17 predicts a much higher variability for k_a between experiments, with SE ∼25%.

DISCUSSION

The classic study of nonstationary kinetics is that of Hodgkin and Huxley (1952). With remarkably clever modeling, they were able to describe the complicated kinetics of Na and K channels. By skillful use of constraints (notably independent subunits), they were able to minimize complexity. Most subsequent analyses of macroscopic ion channel data have emulated that paradigm, but many of these studies have ended with a description of the data in terms of time constants rather than molecular rate constants. With the development of molecular biology techniques, there is an increased value of model-based analysis (Cymes et al., 2002). We have previously developed fitting techniques for single-channel kinetics that optimize reaction rates instead of time constants (Qin et al., 1996, 2000). In this article, we extended the analysis to macroscopic currents where individual events cannot be resolved (see www.qub.buffalo.edu). As far as we know, at the time of writing, there is no commercial software available to estimate rate constants from macroscopic currents.

Direct estimation of rate constants and channel count

Rate constants are the primary kinetic quantities, a manifestation of the molecular structure. The mean relaxation kinetics can be simply derived from the rate constants. As explained in the Introduction, fitting with exponentials cannot be used to determine model topology. Only the number of kinetic states N_S can be inferred from the number of exponential components. The 2N_S − 1 parameters of the exponential fitting (see Eq. 1) are generally treated as free parameters, although they are in fact highly correlated functions of the rate constants, and thus are interrelated. In this sense, the direct estimation of rate constants is equivalent to a constrained exponential fitting, where the constraints on the exponential parameters are imposed by a particular topology—only some states are connected to others. Clearly, inverting exponential parameters obtained through nonconstrained fitting into rate constants and channel count for constrained models is difficult. It is much simpler to start with the model itself.

The true rate constants cannot be estimated without knowing, or simultaneously estimating, the number of channels in the preparation. Calculating N_C on the basis of the peak current amplitude is only an approximation, and Fig. 3 showed clearly the potential ambiguity between rate constants and channel count. Our method estimates the number of channels as another free parameter of the optimization.

Model constraints

The algorithm permits constraints on the rate constants. Constraints reduce the number of free parameters, speed computation, and improve identifiability. For example, the experimental data presented in Figs. 14 and 16 were analyzed with a model that assumed two identical and independent ligand binding sites. With all six rates and N_C as free parameters (no constraints imposed), the C-C-C-O model is nonidentifiable using the protocol presented in Fig. 14 B, but the two constraints (k₁₂ = 2k₂₃, and k₃₂ = 2k₂₁) reduced the number of free parameters to five, and made it identifiable. This is not surprising, considering the results of Fig. 3, which state that the C-C-O model, with four rate constants, is uniquely identifiable only with protocol P₃, which has higher complexity than the protocol in Fig. 14 B.

If the model contains cycles, one might want to test for, or to impose microscopic reversibility (Colquhoun and Sakmann, 1985; Rothberg and Magleby, 2001; Song and Magleby, 1994). A loop constraint requires that the product of the rate constants in the clockwise direction is equal to the product in the counterclockwise direction, i.e., no energy is generated (or dissipated) in a traversal of the loop. Special consideration must be given to loops that include driven rate constants. If the cycle contains ligand binding steps, then there must be an equal number of such steps in both directions. If this condition were not satisfied, then the loop balance could not be fulfilled at all ligand concentrations. A similar situation exists for voltage-dependent rates, for which the clockwise charge movement must equal the counterclockwise movement.

We point out that our algorithm does not require the user to initialize the rate constants to satisfy the imposed constraints, which might prove difficult for complex models (Colquhoun et al., 2004). Instead, the singular value decomposition will obtain a consistent set of free parameters from the input values. Nevertheless, practical experience has shown that good approximations of the starting values greatly speed convergence to a global optimum. The simplest way to generate these values is to heavily decimate the data so there may be only a few data points on the most rapid transition, and then to fit one trace or the busiest part on one trace. This will yield approximate rate constants quickly. Then the data set can be sequentially expanded and fit with relative ease.

Calculation of initial probabilities

Exponential fitting does not explicitly involve the initial state probabilities, but our method does. With ligand-gated channels, a zero concentration will drive all the channels to exclusively occupy unliganded states. A simple kinetic scheme, such as the C-C-C-O model in Fig. 14 C, has only one unliganded state (C₁), which, in absence of ligand, can be assigned a unity starting probability. However, this is not suitable for models with initial aggregated states. Moreover, it is not possible to utilize the effects of protocols with conditioning steps of finite concentration, such as the P₂ or P₃ protocols in Fig. 2. According to our results, such protocols are desirable, because they are more likely to discriminate between models, to eliminate parameter ambiguity (Fig. 3), and to provide more accurate estimates (Figs. 12, 13, and 17).

Clearly, without rigorously computing the starting probabilities, it is not possible to create accurate models. Our algorithm calculates them as the equilibrium probabilities determined by the experimental conditions (under the assumption that channels have reached equilibrium during the conditioning phase). Note that the computation of starting probabilities is equally important in nonstationary single-channel analysis (www.qub.buffalo.edu). For example, if stationary single-channel data were simulated with a C-O-C model, analyzing it with C-O-C and C-C-O models will not register identical likelihoods, as it should (Kienker, 1989), unless the initial state occupancies are properly calculated by the optimizer.

Correction for missed events

Unlike single channel analysis programs, such as HJCFIT (Colquhoun et al., 1996), or MIL (Qin et al., 1996), our algorithm does not extract kinetic parameters from dwell time distributions, but from the distribution of the mean current, which is calculated as a function of all state probabilities. Therefore, no correction for missed events is necessary. In this respect, the method is similar to the MPL algorithm for single-channel data (Qin et al., 2000).

Arbitrary stimulation protocols

An important feature of our method is the ability to fit currents elicited by arbitrary protocols. In this sense, the driving stimulus can take any shape, e.g., steps, ramps, or pulses with finite rise times. This is accomplished by approximating the continuous variation of the stimulus with a sequence of steps, and propagating the state probabilities from one step to the next. The derivatives of the state probabilities for each step are calculated efficiently through a recursive formulation. Table 1 has demonstrated that the errors introduced by this approximation are negligible. Rates estimated from data simulated with ligand pulses with finite rise time were correct (within the numerical precision), if the concentration time course was known (rows B and E), but were in serious error if the rise time was assumed instantaneous (rows C, D, F, and G).

Our algorithm supports global fitting, i.e., fitting across different stimuli and different patches. In the second case, the number of channels is estimated as a local parameter, for each patch, whereas the rate constants are estimated globally. An alternative to global fitting is to use complex continuous stimuli. These elaborate stimuli could reduce the required amount of data and, by careful design, reveal model subtleties and data artifacts. A good example is given in Fig. 16. There, any attempt to fit the complete trace with the standard C-C-C-O model failed, as indicated by the fit lines in Fig. 16 A, unless the tail current was explained by a residual concentration of carbachol in the wash-out phase. Moreover, we were actually able to determine the most likely value of that concentration, based on the goodness of fit.

Parameter identifiability

A model should be a priori identifiable to obtain meaningful parameter values, although this condition is not sufficient to guarantee successful parameter estimation from noisy, nonideal data. Testing for a priori identifiability allows one to determine the simplest experimental protocol required to obtain unequivocal parameter values. The identifiability can be improved by adding equations to the model (utilizing both average and variance; using more complex stimulation protocols), or by reducing the number of free parameters (adding constraints).

For example, the P₂ protocol provides more information than P₁ when data simulated with the C-O-C model is analyzed with the SS method (Fig. 3 B). The reason is the following: at zero initial ligand concentration (P₁), all channels occupy state C₁ at equilibrium, because the second-order rate constant k₁₂ is zero. However, this occupancy is determined solely by the lack of ligand, and does not depend on any of the four rate constants. In contrast, the equilibrium occupancy determined by a finite initial ligand concentration (P₂) does depend on all four rate constants, and provides additional information. Whereas parameters obtained with P₁ are nonidentifiable (there is a continuum of solutions), they are nonuniquely identifiable with P₂ (there are only two possible solutions) and uniquely identifiable with P₃. Even when a simpler protocol is adequate for a priori identifiability, a more complex stimulation might give estimates with higher confidence, as evidenced by Fig. 13. We therefore recommend that the minimum stimulation protocol is first determined for the tested model, but that a more complex stimulation is used, whenever possible, for more reliable estimates.

There is no easy way to theoretically determine the parameter identifiability for a given model and a given stimulation protocol. Instead, we propose a simple empirical strategy, based on repeatedly fitting the model, while randomly varying the initial parameters. Existence of different solutions, but of identical goodness of fit, reveals nonunique identifiability, whereas a single solution suggests unique identifiability, with confidence proportional to the number of trial fits and to the extent of the randomly explored parameter space. Even when multiple solutions are found, some may be ruled out due to, e.g., a priori knowledge, or high parameter variance. It is critical, however, that the model is identifiable, albeit nonuniquely. Nonidentifiability can be tested by first finding the optimum parameters. Next, one parameter is slightly modified and fixed with a constraint. Then, if the optimizer can reach another solution with identical likelihood, it means the model is nonidentifiable, and more constraints or a more elaborate stimulation should be tried.

Model selection

As with parameter identification, two models should be a priori identifiable to be separated on the basis of noisy data. Not all models are theoretically distinguishable (e.g., Kienker, 1989), particularly with simple stimulation protocols: the ability to discriminate complex models depends upon the use of complex stimuli. If a priori identifiability is established, models can be separated using the likelihood ratio test, or tests for goodness of fit, using, e.g., the Akaike (Akaike, 1974) and the Bayesian information criteria (Schwartz, 1978). For a detailed discussion and application of different model selection procedures, we refer the reader to Ball and Sansom (1989), Celentano and Hawkes (2004), Horn (1987), Horn and Standen (1983), Song and Magleby (1994), and Wagner and Timmer (2001). With nonnested models, one has to select between kinetic schemes of different connectivity or state composition, according to some criterion. With nested models (i.e., one is a subset of the other), one has to grow a kinetic scheme by adding one state and one connection at a time, until the increase in likelihood becomes insignificant.

Clearly, it is possible to distinguish some groups of models using our algorithm. In Fig. 15, we showed that nonnested models (identical state composition but different connectivity) produced different likelihoods, and the correct model (or submodel) is favored, for both real and simulated data (Fig. 15, B.1 and B.2). The selection of nested models is a more complex issue, as they have a different number of parameters. Both AIC and BIC criteria penalize for a larger number of parameters (i.e., increased model complexity), but BIC also takes into account the number of data points. However, this can be seen as not reliable because adding an infinite number of baseline data points to a transient response has little information content. For our real data, both AIC and BIC selected the simpler model C-C-C-O-C (Fig. 15 C). Although the bigger model C-C(-O)-C-O-C is fit with higher likelihood, the increase in likelihood is overcome by the penalty due to the extra two parameters. For simulated data, statistically AIC selected model C-C(-O)-C-O-C, whereas BIC favored model C-C-C-O-C (Fig. 15 D), even though the data were simulated with the bigger model.

Adding different states to the model may increase the likelihood by different amounts. Thus, the addition of a desensitized state resulted in a relatively large increment (in Fig. 15, B.1 and B.2, compare models E versus C, and I versus F), whereas the addition of a second open state resulted in a considerably smaller increase, although the correct position of this state in the kinetic scheme was recognized (in Fig. 15, B.1 and B.2, compare models G and H versus F, and J and K versus I). The small increase in likelihood brought by the second open state was classified as spurious by AIC and BIC for the real data (Fig. 15 C), and by BIC for the simulated data (Fig. 15 D, right).

Why does the second open state have such a relatively small contribution to the likelihood? The explanation likely resides in the relative weight of the exponential component introduced by the extra state. For example, during the agonist application, the C₅ state in model I adds relative to model F an exponential component with weight A = −143 pA and time constant τ = 81.4 ms (see Eq. 1). In contrast, the O₆ state in model K adds relative to model I an exponential component with A = 0.3 pA and τ = 0.335 ms. Clearly, the extra component of model I weighs two orders of magnitude more than the extra component of model K, which explains the disparity. The small weight of the exponential component is determined by the occupancy probability of O₆ of only 4.6e*5, which requires much more data for reliable estimates. In the same line of argument, we note that spurious extra states (i.e., states with zero occupancy) are generally signaled by the optimizer by practically zero entry rates, and by virtually infinite exit rates. The conclusion is that models with low occupancy states could be rejected by criteria such as AIC and BIC, and new methods are needed to improve model discrimination. One possibility that we are exploring is to use automated stimulus design to generate the simplest stimulus pattern that will provide the maximum difference in LL between the models of interest. In principle, this could be done recursively in real time during an experiment.

Log likelihood versus sum of squares

We implemented our algorithm with two different cost functions: the log likelihood of the data, and the sum of squares. The parameters that make up the likelihood are the rate constants, the channel count, and the mean and variance of the single-channel current in each conductance class. To use the LL method, all these quantities must be available, either as free parameters or as constraints. In principle, the LL method can provide estimates for all these parameters, but in practice one is often forced to guess the properties of the unitary current and estimate only the rate constants and N_C. The additive baseline noise and offset can be estimated from a section of data with no channel activity. The excess variance of the open state, if not known from single-channel experiments, can be considered zero (see Fig. 5 B; Sigworth, 1985).

The results can be affected by the presence of other sources of noise such as power line interference, or by other artifacts. In this case, the LL method should be used carefully, and the SS method might be preferable because SS does not include the variance terms, and some quantities such as the excess variance cannot be estimated. Our implementation of SS inappropriately applies uniform weight to each residual, but this could be corrected to first order by weighting the residuals inversely with the mean because the gating fluctuations are the dominant noise source. For example, the data presented in Figs. 14 and 16 were analyzed with the SS method to minimize the effects of periodic interference and the artifacts caused by the movement of the piezoelectric solution switcher. With simulated data, LL and SS gave virtually identical results. A future improvement to the noise models will be to add a periodic component to remove the effects of power line interference.

Equation 12 formulates the average of the macroscopic current as a function of the product between N_C and the single-channel amplitude vector μ. Hence, N_C and μ cannot be estimated simultaneously from the average alone (i.e., with the SS method), and the single-channel noise vector V cannot be estimated at all. However, μ can be restated as where V_M is the membrane voltage, V_R is the reversal potential, and g is the single-channel conductance vector. Then, a global fit of recordings made at two different V_M values should be sufficient to simultaneously solve for N_C and g, because there would be two current equations for the two unknowns. If the kinetics were voltage dependent, then more than two voltages may be necessary to satisfy identifiability. If both the average and the variance are used, any quantity of the triplet N_C, μ, and V can be estimated, but how many of these can be estimated simultaneously depends on the identifiability of the model, and on the quality of the data.

Our algorithm could be used as a simple calculator of N_C from stationary macroscopic data, without any knowledge of the model. Thus, the k₁₂ rate of a C-O model is fixed (say, at 100 s⁻¹), and k₂₁ and N_C are estimated. The two unknowns, k₂₁ and N_C, will be found such as to explain both the mean current, determined by N_Ck₁₂/k₂₁, and the variance, determined by N_C. For the technique to work without bias, the single-channel amplitude must be known.

Effects of limited bandwidth

Currently, the method does not handle the effects of decreased variance due to low-pass filtering. However, the baseline noise (V⁰) and the state excess noise (V) are wideband components, whereas the spectrum of V^x (channel fluctuations) is bounded by the highest eigenvalue of the Q matrix (it is a sum of Lorentzians). Therefore, the effects of low-pass filtering on V^x, and thus on the estimated kinetics, should be small if the cut-off frequency is above the highest eigenvalue.

Accuracy and precision of the estimates

The results presented in Fig. 7 showed that estimates obtained from macroscopic data have acceptable accuracy (i.e., are unbiased) if at least 10–20 macroscopic traces are averaged for analysis (which is not a restrictive requirement). This is true for rate constants and channel count obtained with our algorithm (Fig. 7, B and C), but also for exponential parameters obtained with exponential fitting (Fig. 7 A), which is a result largely ignored. The estimates have a non-Gaussian distribution (Fig. 8), and are cross-correlated (Fig. 12).

The asymmetric distribution and the bias are not due to the approximate calculation of the variance (Fig. 9; see Eq. 10 and its description in text), but to the local time correlation of the current. Thus, estimates obtained from data that were simulated without time correlation have a Gaussian distribution and are not biased (Fig. 12). Our algorithm assumes that the state probabilities are a stochastic function of the initial probabilities. In reality, macroscopic data are generated by a dynamic process, and should be analyzed with dynamic models, according to which the state probabilities are a stochastic function of the previous (in time) state probabilities. Our assumption allows a much faster computation of the cost function and its gradients, but ignoring the local time correlation of the variance due to the kinetics of gating makes the method somewhat biased. The method of Celentano and Hawkes (2004) takes into account the autocorrelation, but even some of their results suggest a bias in the estimates. However, in the absence of a more detailed study, it remains unclear whether the use of autocorrelation eliminates, or to what extent it reduces the bias. It remains an open question whether all estimates should be intrinsically biased if obtained by any method that is not a Bayesian filtering algorithm (e.g., Roweis and Ghahramani, 2001).

There are several ways to enhance accuracy: i), Record as many traces as possible, but at least 10–20 (Fig. 7). The traces can be recorded in response to the same protocol, in which case they can be averaged for efficiency, or can be elicited by different protocols (e.g., concentration steps), in which case they are fit globally. ii), Design experiments with more channels in the preparation for a higher SNR (Fig. 7). In both cases, a higher SNR will reduce (but not eliminate) the bias, and will improve the precision of the estimates (Fig. 7). iii), Design experiments with more complex stimulation protocols (Fig. 13). We noticed that estimates obtained from single-channel data containing few gating events are also non-Gaussian (Fig. 8 B). Longer stimulation protocols provide more events, and thus tend to result in more Gaussian distributions.

The state occupancy is critical for a reliable estimation of rate constants. For example, the experimental protocol described in Fig. 14 was designed with a short pulse of agonist to minimize the effect of desensitization, yet a model that features a desensitized state considerably improved the fit (compare models F and I in Fig. 15). However, because of the short duration of the record relative to the timescale of desensitization (i.e., relative to the low occupancy of the desensitized state), the estimates of k_D and k_R are less precise than for other parameters (see Fig. 14 D).

For a more complex application of the algorithm see (Akk et al., 2005). That article used a global fit across different ligand concentrations, and 10 free parameters were estimated for a kinetic model describing the response of the AChR to simultaneous pulses of carbachol and choline. The estimated rate constants matched well the rates determined by separate single-channel experiments. Additionally, the fit explained the blocking effect of choline at different concentrations. Globally fitting three data sets with ∼400 data points each, to a state model with nine states and 10 free parameters took ∼10 min on a 1.3-GHz Pentium IV PC, from which we can infer that our program is one or two orders of magnitude faster than that described by Celentano and Hawkes (2004).

We point out that the algorithm is not limited to ion channel macroscopic data, but it can be used to model any Markov process. For instance, it was applied to determine the kinetics of protein-RNA interactions, from surface plasmon resonance data (M. Milescu and P. Golnick, SUNY Buffalo, personal communication).

Performance of the algorithm

In principle, the state probabilities can be advanced in time by a variety of methods such as solving the differential equations (d'Alcantara et al., 2002). The A matrix method we used, despite being more complex, has several advantages: i), it provides an “exact” solution; ii), it allows analytical calculation of the derivatives; iii), it is faster than numerical integration and independent of the timescale. The computational demand grows linearly with the number of data points, but quadratically with the size of the model. Hence, whenever possible, traces should be averaged for analysis for faster computation. More constraints will speed processing, but for large models the computation is dominated by the calculation of the A matrix and its derivatives, which does not depend on the number of free parameters. We are investigating methods to speed calculation, such as a recursive computation of the A matrix, or an adaptive data downsampling (e.g., Celentano and Hawkes, 2004). The algorithm was written in ObjectPascal, using the Borland Delphi 5.0 programming environment (www.borland.com) and integrated in the free QuB electrophysiology software suite (www.qub.buffalo.edu).