Does Water Play a Structural Role in the Folding of Small Nucleic Acids?

Abstract

Nucleic acid structure and dynamics are known to be closely coupled to local environmental conditions and, in particular, to the ionic character of the solvent. Here we consider what role the discrete properties of water and ions play in the collapse and folding of small nucleic acids. We study the folding of an experimentally well-characterized RNA hairpin-loop motif (sequence 5′-GGGC[GCAA]GCCU-3′) via ensemble molecular dynamics simulation and, with nearly 500 μs of aggregate simulation time using an explicit representation of the ionic solvent, report successful ensemble folding simulations with a predicted folding time of 8.8(±2.0) μs, in agreement with experimental measurements of ∼10 μs. Comparing our results to previous folding simulations using the GB/SA continuum solvent model shows that accounting for water-mediated interactions is necessary to accurately characterize the free energy surface and stochastic nature of folding. The formation of the secondary structure appears to be more rapid than the fastest ionic degrees of freedom, and counterions do not participate discretely in observed folding events. We find that hydrophobic collapse follows a predominantly expulsive mechanism in which a diffusion-search of early structural compaction is followed by the final formation of native structure that occurs in tandem with solvent evacuation.

INTRODUCTION

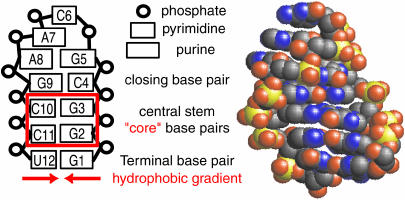
Like proteins, nucleic acid structure consists predominantly of individual structural motifs, the most ubiquitous of which is the hairpin, composed of a basepaired stem and a single-stranded loop region with a sequence and structure independent of the stem (Fig. 1). Although this motif is particularly reminiscent of protein hairpins, the hydrophobic character of individual nucleotides is unlike that of amino acids. Most notably, a hydrophobic gradient is present in nucleotides: located from backbone to side chain are the charged hydrophilic phosphate, the electroneutral, polar and highly soluble sugar ring, and the hydrophobic base unit. Similar to tryptophan and tyrosine side chains, these base units consist of aromatic rings with small hydrophilic substituents. Protein and RNA hairpins thus share a similar backbone topology and side-chain composition. Yet hydrophobic residues are more sparsely located along protein sequences. And, although hydrogen bonding plays a role in stabilizing both RNA and protein hairpins, the structural nature of these hydrogen bonds (on the bases versus on the backbone, respectively) may lead to differences between RNA and proteins as well. It is thus interesting to consider how these intrinsic differences between protein and RNA chemistries impact the nature of how these molecules fold (Sorin et al., 2003).

FIGURE 1.

Schematic and atomic representations of the simulated RNA hairpin with the core region outlined in red.

We have recently reported a computational study of the role of water in the folding mechanism of a 23-residue mini-protein (Rhee et al., 2004). Here we use similar methods to study the roles of water and counterions in RNA hairpin folding. Our previous reports (Sorin et al., 2002, 2003) on the unfolding, collapse, and refolding of a highly stable RNA tetraloop hairpin (sequence 5′-GGGC[GCAA]GCCU-3′) considered solvation effects implicitly using the generalized Born/surface area (GB/SA) model of Qiu et al. (1997). Due to the computational tractability of such continuum solvent models, their use in simulating biomolecular dynamics has become abundant in the literature. However, recent work has emphasized aspects of hydrophobic collapse and folding that may not be observable when using implicit solvation models typically employed in folding simulations. For example, Cheung and co-workers include a solvent-separated minima in their effective protein-protein interaction and find behavior suggesting that water is squeezed from hydrophobic pockets after an initial collapse (Cheung et al., 2002). Another important property of water is the dewetting of hydrophobic surfaces when they come in contact. For example, the simulation of ten Wolde and Chandler indicates that hydrophobic collapse proceeds via an initial formation of hydrophobic contacts followed by the subsequent formation of a dewetting interface in the water degrees of freedom; without the required change in the water degrees of freedom, the hydrophobic elements would not be stabilized and the contact formed would be destroyed (ten Wolde and Chandler, 2002). However, for systems in which the hydrophobic surfaces are relatively small, one would not expect dewetting to occur. Indeed, for a small protein (the 23-residue BBA5 protein), Rhee and co-workers have found, using all-atom simulations in explicit solvation, a concurrent mechanism in which desolvation and core collapse occur simultaneously (Rhee et al., 2004).

Following in the footsteps of the work above for proteins, the central question we ask in this work is, for the case of RNA, whether solvent degrees of freedom are coupled to collapse and folding (ten Wolde and Chandler, 2002) or rather anneal so rapidly as to serve only as equilibrated orthogonal degrees of freedom (Rhee et al., 2004). Why would one expect a difference between proteins and RNA? It is possible that the distinct hydrophobic character of polynucleotides could result in a different mechanism of hydrophobic collapse relative to that observed for small proteins. Additionally, the charged RNA backbone, the presence of counterions, and the interactions between these may or may not play a pivotal role that is not possible for proteins.

Due to limitations in computational methods and resources, such questions could not be addressed previously via simulation. However, our coupling of distributed computing and molecular dynamics (MD) has allowed us to study biomolecular folding at the ensemble level, allowing the sampling of folding events on the microsecond timescale (Pande et al., 2003; Snow et al., 2002; Zagrovic et al., 2001). By further incorporating a highly optimized MD code (Lindahl et al., 2001), ensemble-based MD simulation now offers a convenient method of looking at these issues using a variety of modeling techniques. We thus report below the ensemble folding simulations of small RNAs in all-atom detail using an explicit TIP representation of the solvent (Jorgensen et al., 1983) and counterions, and directly compare these results to previous observations using the GB/SA implicit solvent model to consider the questions posed above.

METHODS

The RNA tetraloop hairpin described above and shown in Fig. 1 was simulated using the AMBER-94 all-atom potential (Cornell et al., 1995) ported to the GROMACS molecular dynamics suite (Lindahl et al., 2001), within Folding@Home (Zagrovic et al., 2001), our distributed computing infrastructure with computational power approximately equivalent to a 150,000 CPU cluster. Simulations were carried out in the TIP3P and TIP4P explicit solvent models (Jorgensen et al., 1983) under constant pressure and temperature conditions (1 atm, 300 K) via independently coupling both the solute and the ionic solvent to an external heat bath with a relaxation time of 0.1 ps (Berendsen et al., 1984). Using the same nucleic acid potential set that was employed in previous simulations of this RNA hairpin in the GB/SA continuum solvent model (Sorin et al., 2003) allows for direct comparison between dynamics in these explicit solvent models and the continuum solvent. A cutoff of 10 Å was used to distinguish short-range and long-range interactions, and long-range electrostatics were treated with the particle-mesh Ewald method (Darden et al., 1995). Nonbonded pair-lists were updated every 10 steps with an integration step size of 2 fs in all simulations, and all bonds were constrained using the LINCS algorithm (Hess et al., 1997).

The native and unfolded starting structures were each centered in 50 Å cubic boxes and neutralized with 11 randomly placed sodium ions with minimum ion-ion and ion-RNA distances of 5 Å, yielding [Na⁺] ∼150 mM. Each system was solvated in ∼3920 TIP3P water molecules, energy-minimized via steepest descent, and annealed for 1 ns of MD with the solute held fixed. The resulting annealed systems were each used as the starting points for 10,000 independent MD trajectories using a fraction of our global network (∼20,000 CPUs).

P_fold calculations (Du et al., 1998; Pande and Rokhsar, 1999) were conducted on 40 conformations taken from the two previously reported folding-unfolding pathways, ranging from fully folded to fully unfolded, as described previously (Sorin et al., 2003). These conformations were then independently neutralized, solvated, and annealed as described above, and used as the starting point for 100 independent MD simulations. Because barrier transitions are fast (nanosecond timescale) relative to waiting times for crossing, P_fold calculations require many short (∼10 ns) trajectories. From those simulations, each conformation is assigned a folding probability (P_fold) based on the fraction of simulations which fold before unfolding in a given time, with the extreme P_fold values of 0 and 1 representing the unfolded and native states, respectively. We operationally define the transition state ensemble as conformations with 0.4 < P_fold < 0.6.

RESULTS AND DISCUSSION

Ensemble simulations

Two simulated ensembles were generated: one set starting from a relaxed native structure (Fig. 1) and the other from a fully unfolded conformation (taken from a 300 K unfolding event in GB/SA), each of which served as the starting point for 10,000 independent MD trajectories, denoted herein as the native and folding ensembles, respectively. The native state ensemble reached an aggregate simulation time of 110.6 μs with a cumulative mean all-atom root-mean squared deviation (RMSD) of 1.81(±0.73) Å, slightly lower than the reported value of 1.89(±0.62) Å using the GB/SA implicit solvent (Sorin et al., 2003). The folding ensemble (starting from the unfolded conformation), totaling 168.1 μs, reached a cumulative mean RMSD of 7.79(±1.97) Å, significantly lower than the 12.35(±1.82) observed in the GB/SA continuum solvent.

Additionally, we probed the conformational free energy landscape in various ionic solvent models via P_fold calculations (Du et al., 1998; Pande and Rokhsar, 1999). To study the effect of ions on folding, P_fold simulations were conducted using Na⁺, Mg²⁺, and an implicit ion model in TIP3P solvent. To test the dependence of our results on the water model chosen, additional P_fold simulations were conducted using TIP4P, as discussed below. In all, these P_fold simulations represent a cumulative sampling time of ∼200 μs, giving a total of over 475 μs of kinetic and thermodynamic sampling in explicit solvent.

Because RMSD alone is not an adequate folding metric (Sorin et al., 2003), and no other single reaction coordinate is easily defined for conformational changes between the native and unfolded states of this small RNA, we define the native character (NC) of the stem as

(1)

where f_nat is the fraction of atomic contacts present in the conformation that are native and f_non is the fraction that are non-native. Native contacts were defined as nonbonded inter-residue atomic pairs separated by 3.0 Å or less at least 25% of the time in a 1 μs simulated ensemble of the native state, thus allowing for conformational flexibility within the native ensemble. For a native contact to be considered to be formed in further simulations, the atomic pair must be within 20% of the mean separation in the native ensemble. This normalized scale of native structure thus ranges from −1 (completely misfolded conformations), to ∼0 (disordered/unfolded conformations), to +1 (conformations in which all contacts are native). Due to the specificity inherent to known RNA basepairing schemes and the limited size of the RNA studied, minimal sampling of conformations with NC significantly below 0.0 might be expected. However, the normalization of NC on this scale allows for observation of such conformations, and the possibility of misfolded states on the free energy surface, without assuming that only the disordered and native states are prevalent in our data. Mean NC values for the 110.6 μs native and 168.1 μs folding ensembles were 0.742(±0.052) and −0.068(±0.097), respectively. We follow additional folding metrics in analyzing our simulations, including RMSD, the all-atom and core-gyration radii (R_g and R_g,core), and the core-solvation number (N_aq), defined as the mean number of waters within 5.0 Å of core atoms.

Stem formation in explicit ionic solvent

Folding events were defined by an RMSD within two standard deviations of the native ensemble mean and having all four basepairs in the stem formed (NC ≥ 0.742, and visual inspection). Within the aggregate 168.1-μs folding ensemble, 19 folding events were observed, with an ensemble minimum RMSD of 2.11 Å. For simple two-state kinetics, the probability of being folded by time t is given by

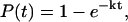(2)

where k is the folding rate. In the limit of t ≪ 1/k, this simplifies to P(t) ≈ kt and the folding rate using a Poisson approximation is given by

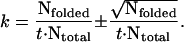(3)

This yields a folding rate of 0.11(±0.03) μs⁻¹, corresponding to a folding time τ = 1/k ≈ 8.8(±2.0) μs, which is in agreement with folding times of ∼10 μs reported for similar sized nucleic acid hairpins (Ansari et al., 2001; Shen et al., 2001).

Our previous report on GNRA tetraloop hairpin folding in the GB/SA continuum solvent distinguished between two mechanisms, denoted as zipping and compaction (Sorin et al., 2003). In the former, the closing basepair (nearest the loop region) forms first, followed by a successive zippering of basepairs toward the termini. The compaction mechanism, dominated by hydrophobic collapse, involves the approach of both strands with the first fully formed basepair occurring in the central stem region, followed by basepair propagation toward both ends of the stem.

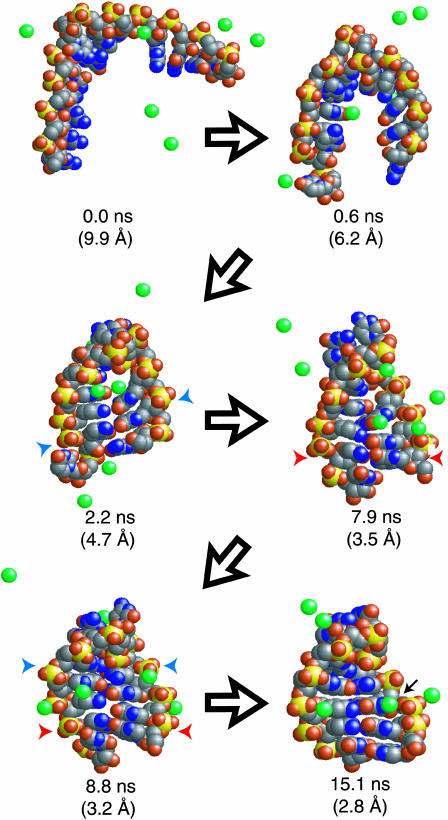
Unlike these distinct mechanisms, the 19 folding events observed in explicit solvent show much greater diversity, with both of the previously mentioned mechanisms simultaneously playing a part to some degree. In essence, collapse drives these folding events (as noted above by the much lower unfolded state RMSD in explicit solvent), resulting in a variety of structures in which the two strands are relatively close (Fig. 2). After this collapse a basepair forms: this nucleation site is native if the strands are aligned properly, and non-native otherwise. Propagation of basepairing follows, also based on the strand alignment, and occurs reversibly (in several trajectories native or non-native basepairs form and subsequently break before proper folding). Several frames from a trajectory that showed significant dynamic basepair sampling are shown in Fig. 2.

FIGURE 2.

An example of the diverse conformational sampling observed in stem formation is shown. Na⁺ ions near the solute are shown in green (due to the two-dimensional image, actual ion distances from the solute are not well represented). Blue and red arrows indicate native and non-native basepairing before proper alignment. Initial collapse is complete within ∼2 ns in this trajectory, yet non-native basepairing is present after 8 ns. At ∼15 ns the stem is fully formed, including one site of significant electrostatic potential binding a hydrated ion (black arrow) that was also observed in simulations of the relaxed native structure.

The differences in the observed mechanism in explicit solvation when compared with the two mechanisms previously reported using GB/SA suggests a potential shortcoming inherent to the implicit solvent. Specifically, as with many common implicit solvent models, the 1997 Still GB/SA assigns a surface area (SA) term to represent hydrophobic effects and treats the electrostatic properties of the solvent as a continuum (such as Generalized Born, i.e., GB, or a distance-dependent dielectric; Ferrara et al., 2002), independent of that hydrophobicity. This distinction between zipping and compaction mechanisms in the implicit solvent represents two extremes of the more general explicit solvation model: in the zipping mechanism, local electrostatic and stacking interactions dominate and stabilize rapid basepairing; in compaction, hydrophobicity dominates (presumably because no random contacts between bases on opposite strands occur) and collapse precedes basepairing. What we see in the explicit solvent is the interplay between these two terms, as well as the introduction of water-mediated interactions, resulting in a spectrum of possible steps during folding that the implicit solvent did not capture and suggesting a rather stochastic conformational-search mechanism of nucleic acid stem formation in which no simple pathway is easily extracted. Interestingly, whereas the GB/SA model is known to overstabilize compact conformations in peptides (Nymeyer and Garcia, 2003), the same model applied to oligonucleotides understabilizes such compact conformations, as seen in the difference in mean RMSD between the explicit and implicit solvents reported above.

A significant difference between the two solvent models used (GB/SA and TIP) is the addition of explicit ions in the TIP simulations. It is generally accepted that monovalent cations are more diffuse than their divalent counterparts, which may become discretely bound. The general effect of monovalent counterions is thus assumed to be the altering of background electrostatic properties of the solvent, thereby stabilizing like-charged phosphate groups in closer proximity than might be expected in a random coil state. Still, it remains to be seen whether these monovalent cations participate directly in stem formation, or only through long-range electrostatic stabilization. To address this question, we considered the interactions between phosphate groups and cations in the solvent, calculating both the distance of closest approach between these groups and the sodium concentration within 5.0 Å of phosphate groups. Pearson correlation coefficients between these two metrics and the structural metrics that describe the folding process (RMSD, R_g, R_g,core, and N_aq) were then calculated, and no significant correlations were observed, revealing that the cations themselves do not play a discrete, structural role in the folding process. We assess the role of explicit ions further below.

Specific and nonspecific collapse in RNA

Based on the significant mechanistic differences between the implicit and explicit solvent models detailed above, we next consider the balance of hydrophobic collapse and desolvation in the folding process. Typical continuum solvation models cannot capture the drying effect (dewetting) and inherently miss the energetic benefits of water-mediated interactions responsible for expulsion, making discrete representation of the solvent a necessary part of evaluating this balance. We consider these two events, collapse and desolvation, by assuming a core (Fig. 1) composed of the hydrophobic base units in the central stem region {G2,G3,C10,C11}, noting that C and G are the least hydrophobic of the natural bases (Shih et al., 1998). To assess whether dewetting or expulsion were dominant in our simulated collapse and folding events the core radius of gyration and the mean core solvation number were monitored.

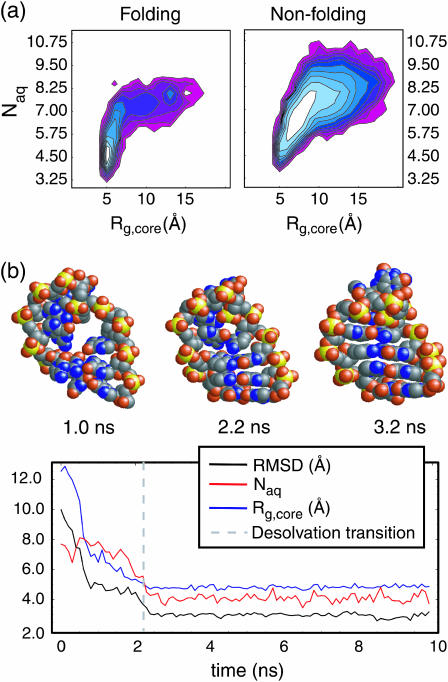
Fig. 3 a shows the log-probabilities of conformations from our trajectories characterized by R_g,core and N_aq for the 19 folding events and for 100 randomly chosen trajectories that collapse to nativelike R_g but do not form significant native structure. The folding trajectories clearly display a trend characterized by early compaction events to nativelike core size, with an apparent (small) barrier along the R_g,core dimension. Final desolvation, in which water is pushed out of the core (as basepairing and stacking interactions are sampled and native structure is formed), then appears to occur as a downhill event (i.e., without barrier crossing) only after formation of the compact core, thus following the expulsion mechanism suggested by Cheung et al. (2002), as shown in Fig. 3 b. Notably, a much broader portion of the accessible phase space is populated by nonfolding collapse events, with no barriers observed.

FIGURE 3.

(a) Log probability distributions are shown for 19 folding and 100 nonfolding collapse events. The apparent barrier for specific collapse trajectories is along the R_g,core degree of freedom, and is crossed early in the collapse event. After collapse to near-native core size, desolvation occurs. In contrast, nonspecific collapse events randomly sample a much greater portion of the conformational space with no apparent bulk trend. (b) Hydrophobic collapse in a single trajectory is shown with the dashed vertical line indicating the midpoint of the desolvation transition. Structures preceding, concurrent with, and after this midpoint are shown above the frame for visual clarification. R_g,core reaches its native value at the desolvation midpoint (∼2.2 ns), but significant exposed base surface area remains to be buried, resulting in an expulsionlike mechanism.

These results represent an intriguing difference between collapse to a nativelike core (specific collapse) and more generic collapse to non-native, compact structure (nonspecific collapse) in nucleic acid basepairing sequences, and show that the expulsion mechanism seen in folding events is not universal in the hydrophobic collapse of such sequences. Indeed, collapse would best be characterized in our explicit solvent simulations as a diffusive search of favorable conformations, with those that allow for basepairing acting as precursors of native structure formation. This observation supports the diffusion-search mechanism suggested by Ansari and co-workers using laser temperature jump spectroscopy (Ansari et al., 2001). As suggested by such a model, a spectrum of collapse mechanisms appears possible that includes expulsionlike behavior at one extreme and concurrent collapse and desolvation at the other, depending on the alignment of basepairing partners during the collapse event, or lack thereof.

We postulate that the expulsion mechanism seen in our folding trajectories results from the previously described hydrophobic gradient inherent to nucleotides and not present in amino acids. That is, concerted collapse of well-aligned RNA strands, which are more likely to undergo proper stem formation, is expected to more readily trap water molecules between hydrophobic bases than weaker or more randomly oriented hydrophobically induced motions. In small proteins, where hydrophobic residues are much more sparsely located along the sequence, collapse is expected to be less cooperative and trapping of waters less likely, as has been observed in our recent folding simulations of BBA5 in explicit solvent (Rhee et al., 2004).

We note here that the concurrent core collapse and desolvation observed for the BBA5 mini-protein may not be generalizable to larger protein structures, as was suggested in that report (Rhee et al., 2004). The Brooks and Onuchic groups have previously used importance sampling and replica exchange methodologies to study the mixed α/β-B1 segment of protein-G (Sheinerman and Brooks, 1998), the all β-SH3 domain (Shea et al., 2002), and the all-α-protein-A three-helix bundle (Garcia and Onuchic, 2003), yielding a variety of protein sizes and secondary structures to which we can compare our results for this small protein and RNA hairpin. In each of these studies, final desolvation appeared to occur in tandem with packing of the hydrophobic core late in the folding process, in qualitative agreement with our observations for BBA5 (Rhee et al., 2004), yet with a stronger tendency for expulsion.

As described above, the trapping of water within hydrophobic regions of small RNAs may be more likely than for BBA5. In this sense, the larger hydrophobic core regions of the more sizable proteins may explain previous observations of expulsionlike behavior during core desolvation. Therefore, it will be intriguing to see whether such a difference in size actually alters the desolvation process. Zhou and co-workers have recently simulated hydrophobic collapse of two domains of the BphC enzyme (Zhou et al., 2004) with a total of 292 residues, demonstrating a dependence of the observed collapse kinetics upon solute-solvent electrostatic interactions. In the case of RNA compaction, the charge-charge interaction between the solute and ionic solvent will be more prevalent than in the case of protein core collapse. Accordingly, studies of RNA folding may offer further insights not observed in peptide systems.

It is interesting to consider how the mechanism found by ten Wolde and Chandler (2002) compares with that of our simulations. We stress that although the dewetting mechanism in general may not apply to the GNRA tetraloop system studied here because of its small size and non-ideal hydrophobicity, it is interesting to apply the prediction of a critical limit of dewetting suggested by Huang and co-workers, who studied the dewetting process between nanoscale plates in explicit solvent MD simulations (Huang et al., 2003). They showed that the critical distance for dewetting between purely hydrophobic plates is linear in (and approximately equal to) the plate facial radius and decreases when atomic dispersion is considered. Although extrapolating this relationship to the facial radii of hydrophobic base units may push dewetting theory beyond its intended regime of applicability, it is interesting to consider what would be predicted.

Upon considering the scale of nucleic acid base units (as well as hydrophobic protein side chains), which fall in the approximate range of 2.5–3.5 Å, we approximate the critical distance for dewetting between two hydrophobic side chains (including atomic dispersion) to be on the order of the size of a single water molecule. At this critical distance, vapor formation consists of removing a single water layer, and the two models (expulsion and dewetting) essentially become equivalent, both representing the same event. This idea is supported by our observation that the predominant conformational changes during folding, after initial core collapse, occur in tandem with the solvent descriptor N_aq. As illustrated in Fig. 3, folding becomes a downhill transition after collapse, and the rearrangement to native local structure and the desolvation process are then simultaneous.

Finally, the ultimate question at hand is whether solvent degrees of freedom are coupled to RNA dynamics. One test of this possible coupling is to examine how commitment probabilities (i.e., probability to fold before unfolding, or P_fold) change when the RNA conformation is held fixed, but the water degrees of freedom are re-equilibrated. One can perform this test in two ways: we can re-equilibrate with the same explicit water model (Rhee et al., 2004) or we can re-equilibrate with another explicit water model. In both cases (see Fig. 4), we find that P_fold is invariant to re-equilibration of the solvent degrees of freedom. This suggests two possibilities. The first is that the water degrees of freedom are not coupled to the RNA conformational degrees of freedom and thus water acts as an important force in RNA folding (e.g., dielectric and hydrophobic properties), but does not play a specific structural role. The second possibility is that the rapid relaxation time of the water degrees of freedom (picosecond timescale) masks the participation of the solvent in folding (nanosecond-to-microsecond timescale) on a structural level. We investigate these possibilities further below.

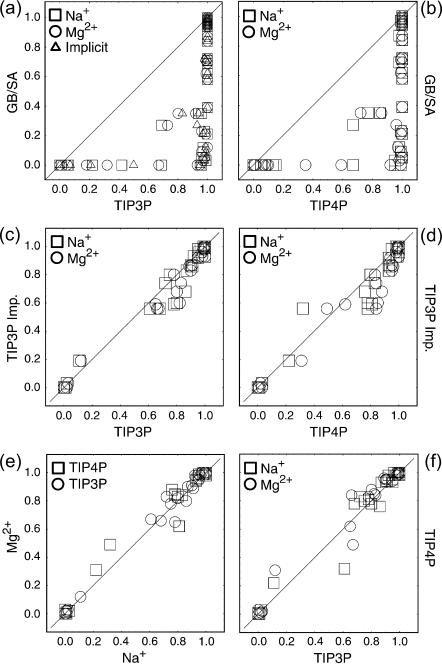
FIGURE 4.

P_fold versus P_fold plots comparing the implicit and explicit solvent and ion models are shown in frames a–d. Each frame combines the P_fold values for both folding pathways previously detected using the GB/SA continuum solvent. Comparisons between TIP3P and TIP4P explicit water models using sodium and magnesium counterions are shown in e and f.

The folding landscape in explicit solvation differs from that of implicit solvation

To better characterize the difference between implicit and explicit solvent models, P_fold simulations for the previously characterized folding-unfolding pathways were conducted in a variety of environments. We note that the use of multiple explicit solvation models with various counterions shows that comparisons to the continuum solvent are not dependent on the explicit solvent model or ions employed.

Fig. 4 a plots GB/SA-derived P_fold values versus TIP3P-derived values using explicit representations of sodium and magnesium, and an analogous comparison is made between GB/SA and TIP4P in Fig. 4 b, with both pathways (40 conformations) contributing to each comparison. These P_fold calculations follow those in our previous study (Sorin et al., 2003), which used RMSD cutoffs of 3 and 9 Å, to define the native and unfolded states, respectively. In both cases, we see an interesting effect: the GB/SA model consistently underestimates the conformational folding probability relative to the explicit solvent representations. The implicit solvent model thus shifts the transition state ensemble (TSE) nearer to the native region of the configurational space, with some conformations that are likely to fold in explicit solvents (TIP P_fold > 0.6) showing no folding behavior in the implicit solvent (GB/SA P_fold ∼ 0).

To verify that these differences were not a result of the addition of explicit ions to the TIP simulations, additional TIP3P P_fold values were calculated using a crude implicit counterion treatment. This treatment is equivalent to smearing a neutralizing countercharge over all space to compensate for the net charge on the solute, as discussed by Hummer et al. (1997). Although this is not a rigorous PME method, it does not alter the forces involved, and allows for direct comparison between TIP/PME and GB/SA without explicit counterion representations. The TIP3P implicit ion P_fold values are compared to the explicit sodium and magnesium values in TIP3P and TIP4P (Fig. 4, c and d). All explicit solvent P_fold comparisons were carried out with more stringent boundaries on the native and unfolded states using both RMSD (native ≤ 3.25 Å; unfolded ≥ 5.82 Å) and NC (native ≥ 0.534; unfolded ≤ 0.126). (Using these more rigid criteria did not qualitatively change the comparison to GB/SA in Fig. 4, a and b, and using the less specific criteria in that comparison maintains consistency with our previously published GB/SA P_fold values.) The results of this explicit solvent/implicit ion treatment are compared to GB/SA values in Fig. 4 a (triangles) and show similar disagreement with GB/SA as observed in explicit ion comparisons. This suggests that the explicit representation of ions is not mandatory for simulating nucleic acid secondary structure dynamics and supports the lack of direct ion participation in the folding process, as described above.

Analogous comparisons between the TIP3P and TIP4P results using both sodium and magnesium counterions are shown in Fig. 4, d and e, and the four permutations show generally good agreement, with no specific differences between the dynamics in TIP3P and TIP4P using Na⁺ or Mg²⁺ counterions being observed. Based on these observations—that explicit ion representations are not necessary and that water models of differing polarity give similar P_fold values—it is interesting to consider whether one can attribute the differences in folding behavior between these models to the discrete representation of water molecules in the TIP simulations.

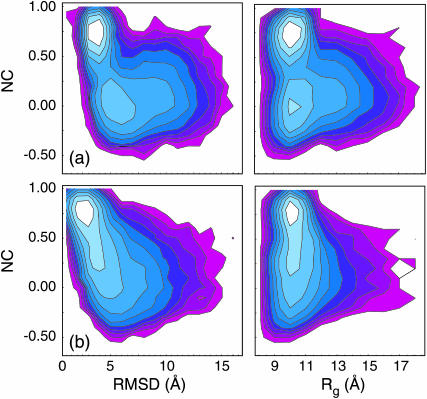
To address this question, we further probed the folding landscape around the two GB/SA 300 K folding/unfolding pathways. Because P_fold calculations are Boltzmann-weighted samplings (as in any MD simulation), and more importantly because these trajectories are started at or near the barrier region, we can use this data to get a qualitative picture of the nature of the free energy landscape near the free energy barrier. We thus calculated free energy landscapes (as projected onto the NC, RMSD, and R_g reaction coordinates) around the two GB/SA-derived pathways using the ∼200 μs of P_fold simulations in varying ionic explicit solvent models. The resulting landscapes around each pathway were qualitatively indistinguishable between varying ion and water models, yet a significant difference between the two pathways is observed (Fig. 5).

FIGURE 5.

Free energy profiles of the two GB/SA folding pathways as sampled in TIP explicit solvent. The compaction pathway in a is two-state, as predicted using the implicit solvent model. In contrast, the zipping pathway in b appears to include diffusive, downhill folding in explicit solvent, whereas GB/SA sampling predicted a two-state landscape. In both cases, the R_g of non-native conformations is predominantly nativelike.

Our previous GB/SA-simulated P_fold ensembles predicted both pathways to occur as two-state events (Sorin et al., 2003). The relevant landscape for the compaction mechanism in explicit solvent is shown in Fig. 5 a and agrees with that two-state prediction. An analogous landscape for the zipping mechanism is shown in Fig. 5 b and, in stark contrast to the previous GB/SA result, the addition of explicit solvent predicts the zipping pathway to be downhill (diffusive) in nature. Thus, conformations on the zipping pathway that were unlikely to fold in GB/SA are much more likely to fold in explicit solvent sampling. Indeed, the transition state for this pathway in GB/SA was characterized by an RMSD ≈ 3 Å, whereas TIP sampling predicts RMSD(TSE) > 6 Å independent of solvent model and ion identity.

In considering the striking difference between the two models, we must consider the sampled conformations that produced the two predictions. The zipping (unzipping) pathway consists of a spectrum of structures in which the strand ends are successively brought closer together (farther apart) during the folding (unfolding) process, with the closing basepair serving as the nucleation center, and zipping (unzipping) of basepairs occurring progressively away from (toward) that nucleus. Structures along this pathway include opposite strands of the hairpin bending away from one another, and the TS for this pathway includes only the initial contact of the closing basepair. In explicit solvent, water-mediated interactions become possible, and larger closing basepair separations do not rule out folding in TIP as was observed in GB/SA. This difference is consistent with the long-lived water-bridged interactions between partially formed basepairs reported by Giudice et al. (2003), as well as the water-mediated stabilization of opened basepairs observed in quantum calculations by Kryachko and Volkov (2001).

From this comparison, it is evident that water does in fact play a structural role in the formation of basepaired regions in terms of mediating solute-solute contacts that cannot be mediated by current implicit solvent models. Why then does the re-equilibration of explicit water degrees of freedom (including mutation to a different TIP potential) not significantly alter commitment probabilities for various conformations along the folding coordinates as we might expect? We suggest that the rapid reorientation of water degrees of freedom, orders-of-magnitude faster that the folding process, allows a single conformation to maintain consistent P_fold values, thus masking the participation of the solvent. Indeed, such water-mediated interactions that appear to be important in the folding process are not solely lock-and-key in nature, as the fit between enzyme and substrate, but instead act as a locksmith, which can fit the key to the lock more rapidly than the lock can undergo significant fluctuation.

These observations support our hypothesis that the discrete representation of water is the predominant factor responsible for the observed folding differences between models, as well as a predominant factor in defining the TSE in real nucleic-acid duplex-forming sequences. Our results thus complement the findings of both Zhou and Garcia, who have reported significant changes when comparing folding landscapes for protein helices and β-hairpins using TIP and GB/SA solvent models with various all-atom force fields (Nymeyer and Garcia, 2003; Zhou, 2003), by extending their comparisons to small nucleic acids.

A recent report on the folding of this same RNA hairpin which employed Monte Carlo sampling of the nucleic acid using a pure heavy-atom Gō potential offers additional insight into this discrepancy (Nivon and Shakhnovich, 2004). Only the zipping pathway, including a loop-folded intermediate state not observed in our all-atom simulations (Sorin et al., 2002, 2003), was observed in that study. As in the case of the implicit GB/SA solvent, the pure Gō potential of Nivon and Shakhnovich (2004) offers no water-mediated interaction effects, which we have observed to be important in describing both the thermodynamics and mechanism of folding. It therefore follows that disordered conformations in which the loop and/or closing basepair are formed would be detected as an intermediate state when employing a Gō-like potential; such conformations offer significant artificial stability over conformations in which the loop is disordered due to the lack of stability gained by the water-mediated interactions described above. We postulate that the addition of a simple, water-mediated interaction term to GB/SA and other continuum-solvent and Gō models, similar to that imposed by Cheung and co-workers in their Gō model SH3 folding simulations (Cheung et al., 2002), may add the necessary continuity to the relevant free energy functions and improve their predictive ability, thus yielding better agreement with both explicit solvent simulations and physical intuition alike.

CONCLUSIONS

We have reported all-atom molecular dynamics folding simulations of a small RNA in all-atom detail using an explicit representation of the ionic solvent with an observed folding rate in good agreement with previous experimental measurements. Folding was observed to occur by hydrophobic collapse via an expulsionlike mechanism of desolvating central hydrophobic regions after initial nucleation of one or more basepairs. The forming of nativelike core size occurs as a diffusive search for favorable conformations, and we attribute this late expulsion of solvent near hydrophobic regions (not observed for a small protein with a hydrophobic core; Rhee et al., 2004) to the random sampling of conformations that are favorable for folding, in which the hydrophobic gradients of opposing strands (not present in peptides) become well aligned for proper basepair formation.

The folding dynamics has been compared to results using the GB/SA continuum representation of the solvent and the mechanism in explicit solvent is a spectrum ranging from the two extreme cases captured by the GB/SA implicit solvent: nucleation points can occur anywhere in the stem, and the zippering of basepairs can occur during or after collapse, making the folding very stochastic in nature and thus offering a qualitative atomistic picture that supports the model proposed by Ansari et al. (2001). In contrast, the implicit solvent model significantly alters the free energy landscape relative to the explicit solvent representation, thus capturing only a portion of the folding dynamics observed in the explicit solvent and shifting the transition state toward the native regime of the conformational space. Indeed, we have shown 1), that the likelihood of folding given a specific separation between nucleating base units is much higher in the explicit solvent; and 2), that this difference derives directly from the discrete nature of water that allows for the occurrence of water-mediated interactions.

Accounting for solvent-mediated interactions in the folding of small nucleic acids thus appears to be vital, both in terms of capturing the correct hydrophobic collapse events and in assessing the nucleation phase of folding that defines the transition state ensemble. In response to these observations, we have suggested the addition of a water-mediated interaction term to contemporary continuum-solvent models. It will be exciting to see such models made capable of implicitly representing the discrete nature of water, and thus making the simulation of larger nucleic acids tractable for future study.

Our results suggest that counterions do not participate directly in the formation of nucleic acid secondary structure, and the explicit representation of counterions is therefore not mandatory in the simulation of small nucleic acids. Interestingly, this further suggests that even the fastest ionic degrees of freedom are not necessary in describing the rapid folding of DNA/RNA stem regions. In contrast, our results demonstrate that water does participate structurally in the folding mechanism of small nucleic acids, such as duplex and hairpin formation.