Sensitivity Analysis of Discrete Stochastic Systems

Abstract

Sensitivity analysis quantifies the dependence of system behavior on the parameters that affect the process dynamics. Classical sensitivity analysis, however, does not directly apply to discrete stochastic dynamical systems, which have recently gained popularity because of its relevance in the simulation of biological processes. In this work, sensitivity analysis for discrete stochastic processes is developed based on density function (distribution) sensitivity, using an analog of the classical sensitivity and the Fisher Information Matrix. There exist many circumstances, such as in systems with multistability, in which the stochastic effects become nontrivial and classical sensitivity analysis on the deterministic representation of a system cannot adequately capture the true system behavior. The proposed analysis is applied to a bistable chemical system—the Schlögl model, and to a synthetic genetic toggle-switch model. Comparisons between the stochastic and deterministic analyses show the significance of explicit consideration of the probabilistic nature in the sensitivity analysis for this class of processes.

INTRODUCTION

Parametric sensitivity is a simple yet powerful tool to elucidate a system's behavior and has found wide application in science and engineering (Varma et al., 1999). In systems biology, sensitivity analysis has been utilized in many applications, e.g., to guide tuning of system parameters to obtain a desired phenotype (Feng et al., 2004), to provide a measure of information through the Fisher Information Matrix for parameter estimation and design of optimal experiments (Zak et al., 2003; Gadkar et al., 2004), and to give insights into the robustness and fragility tradeoff in biological regulatory structures based on the rank-ordering of the sensitivities (Stelling et al., 2004). The sensitivity coefficients describe the change in the system's outputs due to variations in the parameters that affect the system dynamics. A large sensitivity to a parameter suggests that the system's performance (e.g., temperature, reactor yield, periodicity) can drastically change with small variations in the parameter. Vice versa, a small sensitivity suggests little change in the performance. Knowledge of sensitivities can also help to identify the driving mechanisms of a process without having to fully understand the detailed mechanistic interconnections in a large complex system.

Traditionally, the concept of sensitivity applies to continuous deterministic systems, e.g., systems described by differential (or differential-algebraic) equations. The first-order sensitivity coefficients are given by (Varma et al., 1999)

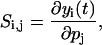(1)

where y_i denotes the i^th output, t time, and p_j the j^th parameter. This equation follows directly from the definition of parametric sensitivity above, and assumes implicitly that the output y_i is continuous with respect to the parameter p_j. Although this concept has wide applicability, it does not directly apply to stochastic/probabilistic systems whose outputs take random values with probability defined by a density function. Nevertheless, sensitivity analysis for stochastic systems has been previously developed in which the stochastic effects enter as additive Gaussian white noise (e.g., Langevin-type problems) (Costanza and Seinfeld, 1981; Dacol and Rabitz, 1984) or as uncertainty in the parameters (Feng et al., 2004).

Discrete stochastic modeling has recently gained popularity because of its relevance in biological processes (McAdams and Arkin, 1997; Arkin et al., 1998) which achieve their functions with low copy numbers of some key chemical species. Unlike the solutions to stochastic differential equations, the states/outputs of discrete stochastic systems evolve according to discrete-jump Markov processes, which naturally lead to a probabilistic description of the system dynamics. The states and outputs are random variables governed by a probability density function which follows a chemical master equation (CME) (Gillespie, 1992a,b). The rate of reaction no longer describes the amount of chemical species being produced or consumed per unit time in a reaction, but rather the likelihood of a certain reaction to occur. Though analytical solution of the CME is rarely available, the density function can be constructed using the stochastic simulation algorithm (Gillespie, 1976).

This work aims to develop parametric sensitivity analysis for discrete stochastic systems described by CMEs. Four sensitivity measures were formulated based on a direct extension of the deterministic sensitivity and on the Fisher Information Matrix (FIM) from information theory (Cover and Thomas, 1991). In addition, the stochastic effects in certain systems can give rise to distinctive density functions, involving multimodality, which necessitate application of the proposed analysis. Here, multimodality relates closely to stochastic systems with multiple attractors operating around a bifurcation point. Such mechanisms are commonly encountered in cellular processes, for example in a cell's decision-making and regulation. The proposed analysis was applied to two representative examples depicting these circumstances: a prototype chemical reaction network—the Schlögl model (Gillespie, 1992b), and a model for a synthetic genetic toggle switch in Escherichia coli (Gardner et al., 2000). The toggle switch consists of two repressor-promoter pairs aligned in a mutually inhibitory network. Comparisons of classical and stochastic sensitivity analysis demonstrate the significance of an explicit treatment of the probabilistic behavior in the analysis of these systems. To the authors' knowledge, this work represents the first sensitivity analysis study for discrete stochastic systems described by chemical master equations.

DISCRETE STOCHASTIC SENSITIVITY MEASURES

In discrete stochastic systems, the states and outputs are random variables characterized by a probability density function. The model parameters affect the outputs indirectly through a chemical master equation which describes the evolution of the corresponding density function. The sensitivity as defined in Eq. 1 requires continuity of the outputs with respect to the parameters and hence does not directly apply to discrete stochastic outputs. However, the notion of sensitivity suitably applies to the density function which characterizes the system outputs. Hence, a direct analog of classical parametric sensitivity in Eq. 1 for a discrete stochastic system is given by (Costanza and Seinfeld, 1981)

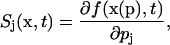(2)

where f is the density function, x denotes the vector of states and outputs, and p denotes the vector of parameters. The aforementioned sensitivity yields a sensitivity measure for discrete stochastic systems:

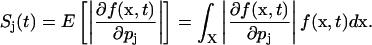(3)

As the states and outputs are described by a single probability density function, the sensitivity coefficient of a single output with respect to a parameter as in Eq. 1 does not exist in this circumstance. The dependence of the states x with respect to the parameters is implicitly assumed. If the outputs assume integer values, then the integral is replaced by a sum. For the purpose of this article, the sensitivity coefficient is concerned only with the magnitude of changes in the density function and hence the absolute operator in Eq. 3.

The differences between the original development of Eq. 2 (Costanza and Seinfeld, 1981) and its use in this work as sensitivity coefficient warrant further remarks. The sensitivity coefficient in Eq. 2 was first introduced to determine the uncertainty of the states x due to the uncertainty of the parameters. In other words, the probabilistic nature of the states arises from the uncertainty in the parameters. In contrast, the chemical master equation gives rise to random values of the states as a result of internal stochastic effects, due to the low copy number of molecules involved in the reactions. Consequently, the computation of the coefficients in Eq. 2 differs between the two approaches. In the original development, such coefficients were derived and solved using a Fokker-Planck equation (Costanza and Seinfeld, 1981). On the other hand, direct derivation of these coefficients using the CME yields a highly complex equation, which motivates our use of a finite difference approach (see Sensitivity Analysis of Chemical Master Equations, below).

The stochastic sensitivity as defined above is closely related to the score function in information theory (Cover and Thomas, 1991):

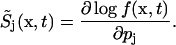(4)

The score function gives the gradient of the log-likelihood function (Beck and Arnold, 1977) and has a strong relevance in parameter estimation problems, as its variance J describes the (maximum) information that can be extracted from (random) measurements to estimate the corresponding parameter values p (note that the expected value of the score function equals to zero):

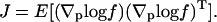(5)

The variance, known as the Fisher Information Matrix, defines the lower bound on the uncertainty in the parameter estimates according to the Cramer-Rao inequality (Cover and Thomas, 1991)

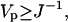(6)

where V_p denotes the covariance of unbiased parameter estimates.

This work adopts the Fisher Information Matrix as a measure of the sensitivities of a discrete stochastic system, based on new interpretations of the FIM (see below). Without loss of generality, the remainder of this section assumes that the density function follows a Gaussian distribution

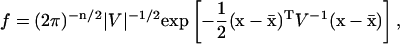(7)

where n denotes the number of parameters and 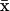is the mean. Under this assumption, the FIM reduces to

(8)

where S denotes the sensitivity matrix as defined in Eq. 1 and V⁻¹ denotes the measurement covariance (measurement error) (Beck and Arnold, 1977). Thus, aside from its conventional use as a measure of information content, Eq. 8 motivates a new utility of the FIM as a consolidation of (weighted) sensitivities. In general, the FIM captures the sensitivity of the (log) distribution with respect to the parameters as shown in Eq. 5. The simplified FIM of Eq. 8 provides the basis of recently-developed hybrid sensitivity analysis schemes, where the sensitivity matrix S is computed deterministically and the covariance V is obtained from stochastic simulations (Bagheri et al., 2003).

The use of the FIM as a sensitivity measure requires novel interpretations of the properties of this matrix. The FIM captures not only the first-order sensitivities of the system, but also the effects of parametric interactions (second-order sensitivities). Three sensitivity measures can be derived based on the FIM—the diagonal elements, the eigenvalues, and the inverse of standard deviations (i.e., the inverse of the diagonals of V_p). The diagonal elements of the FIM represent the magnitudes of the sensitivities with respect to each individual parameter. Under the Gaussian assumption, these elements are equal to the weighted norms of the first-order sensitivities:

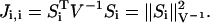(9)

The eigenvalues of the FIM represent the magnitudes of the sensitivities with respect to simultaneous parameter variations whose relative magnitudes and directions are given by the corresponding eigenvectors. The product of the eigenvalues presents an index of the information content for use in the design of optimal experiments, known as D-optimality (Emery and Nenarokomov, 1998). Here, each eigenvalue is assigned as the sensitivity measure with respect to the parameter that corresponds to the element of the eigenvector with the largest magnitude. Thus, a parameter may have more than one sensitivity measure, whereas others may not have an assigned measure (i.e., there may not be a one-to-one correspondence between the eigenvalues and the parameters). Finally, the diagonal elements of the matrix V_p are the square of the standard deviations of the parameters, and their sum is used in the design of optimal experiments as another index of information content known as A-optimality (Emery and Nenarokomov, 1998). Based on Eq. 6, the standard deviations inversely correlate with the sensitivity of the system. As with the eigenvalue measures, the standard deviations incorporate the parametric interactions, but without the problematic one-to-one correspondence. The computation of standard deviation, however, is more prone to numerical inaccuracy in matrix inversion. These new interpretations of the diagonal elements, eigenvalues, and standard deviations of FIM provide sensitivity measures with different attributes, and thus should be utilized and compared accordingly.

SENSITIVITY ANALYSIS OF CHEMICAL MASTER EQUATIONS

The discrete stochastic system of interest is described by a chemical master equation (Gillespie, 1977)

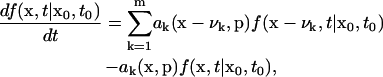(10)

where f(x, t|x₀, t₀) is the conditional probability of the system to be at state x and time t, given the initial condition x₀ at time t₀. Here, a_k denotes the propensity functions, ν_k denotes the stoichiometric change in x when the k^th reaction occurs, and m is the total number of reactions. The propensity function a_k(x, p)dt gives the probability of the k^th reaction to occur between time t and t + dt, given the parameters p. As the state values are typically unbounded, the CME essentially consists of an infinite number of ODEs, whose analytical solution is rarely available except for a few simple problems. The stochastic simulation algorithm (SSA) provides an efficient numerical algorithm for constructing the density function (Gillespie, 1976). The algorithm follows a Monte Carlo approach based on the joint probability for the time to and the index of the next reaction, which is a function of the propensities. The SSA indirectly simulates the CME by generating many realizations of the states (typically in the order of 10⁴) at a specified time t, given the initial condition and model parameters, from which the distribution f(x, t|x₀, t₀) can be constructed as discussed next.

The evolution of sensitivity coefficients in Eq. 3, as well as the score function, can be derived from the CME by taking the derivative with respect to the parameters

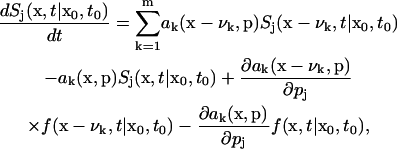(11)

where S_j is the stochastic sensitivity coefficient with respect to the j^th parameter. Such an equation should be solved simultaneously with the CME. As with the CME, the infinite dimensionality of the coupled sensitivity-CME differential equation makes its analytical solution difficult to construct. Moreover, the SSA cannot be directly applied to solve the sensitivity equation without loss of rigorous physical basis (Gillespie, 1992a). These reasons motivate application of a black-box approach, such as finite difference, to estimate the sensitivity coefficients below.

The probability density function approximation begins with the construction of a cumulative distribution function from the SSA realizations. The cumulative distribution function is given by

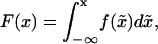(12)

which gives the density function f(x) as the derivative of F(x), i.e.,

(13)

The above equations assume that x is one-dimensional. Extension to multidimensional x is straightforward. The stochastic sensitivity in Eq. 2 and the FIM were estimated using centered difference approximation (finite difference method) such that the density function sensitivity was computed according to

(14)

The perturbation Δp_j should be small enough to minimize truncation error, but large enough to avoid sensitivity to simulation error. The deterministic sensitivity coefficients were computed using the direct method derived from the ordinary differential equations (Varma et al., 1999).

STOCHASTIC VERSUS DETERMINISTIC ANALYSIS

Before proceeding to the application of the proposed sensitivity analysis, it is prudent to identify the stochastic circumstances under which the sensitivity analysis of deterministic models can potentially fail and thus necessitate the use of discrete stochastic analysis. The fundamental difference between the deterministic and stochastic analysis is in the type of system behavior changes that are measured in each analysis. The deterministic analysis considers changes in the underlying distribution that lead to proportional modulations in the lumped variables such as the mean or mode of the distribution. On the other hand, the stochastic sensitivity analysis directly measures the overall changes in the density function. As different distributions can have the same lumped representation, the use of lone lumped variables limits the applicability of the deterministic analysis to general discrete stochastic systems.

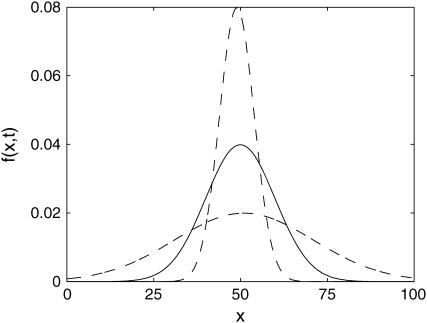
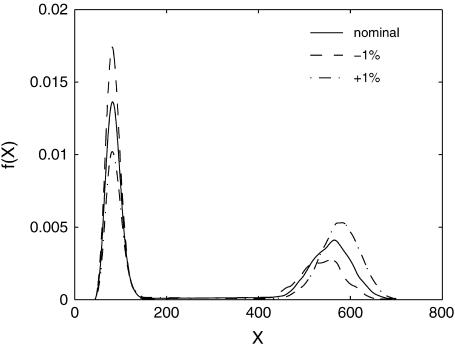
The simplest example of such circumstances is shown in Fig. 1. Here, the parameter perturbation induces large changes in the distribution entropy (uncertainty) (Cover and Thomas, 1991) without an appreciable shift of the mean (mode). Assuming that the deterministic model represents the mean (mode) of the distribution, classical sensitivity analysis will incorrectly suggest that the system is insensitive to the parameter perturbation, because the mean (mode) of the distribution changes very little. The conclusion will be different when the variations of the full distribution, rather than only the mean or mode, are accounted for in the analysis. The stochastic analysis of this example will correctly suggest a strong sensitivity with respect to this parameter.

FIGURE 1.

An example of a sensitive distribution with insensitive mean value. The nominal distribution is shown in solid representation and the perturbed distributions are shown in dashed representation.

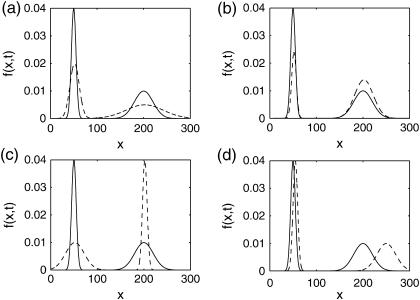
Much richer variations in these circumstances can arise from a form of nonlinear dynamics, namely multistability. A deterministic multistable system occurs when there exists more than one attractor, for which small variations in the bifurcating variable will lead to very different steady states. However, the existence of multiple attractors has much less pronounced effects on the density functions, which will assume multimodal distributions of the states (see next section). When the modes of the distribution are close enough, the stochastic dynamics may exhibit flip-flops between the two attractors. Such mechanisms are believed to play an important role in biological systems, acting for example as dynamical switches (Arkin et al., 1998). Again, the deterministic model can provide only a lumped representation of this distribution; typically the mean or mode of one of the modalities. In this case, the differences between the deterministic and stochastic analysis can arise in multiple situations such as shown in Fig. 2. The example process in Fig. 2 a displays the same behavior as in Fig. 1, but manifested in a bimodal distribution (large change in distribution entropy with small change in mean/mode of each modality). However, in the case of multimodal distribution, other circumstances can arise such that the density function perturbations keep the distribution entropy and means/modes of modalities approximately the same. For example, the parameter perturbation can induce a shift in the weights (area under the density function) between the two modalities such as shown in Fig. 2 b, or cause opposite distribution entropy changes (see Fig. 2 c). In addition, another example can arise from the difference in the sensitivities of the attractors (see Fig. 2 d). In all of the aforementioned behaviors, the deterministic analysis may arrive at incorrect results because the true sensitivity of the density function is not reflected in the sensitivity of the lumped variable.

FIGURE 2.

A bistable system with different sensitivities between the two modalities. The nominal distribution is shown in solid representation and the perturbed distribution in dashed representation. Here, the parameter perturbation causes: (a) small change in the mean/mode of each modality but large change in distribution entropy, (b) a shift in the weights of the modalities (area under the density function), (c) opposite changes in distribution entropies of the two modalities, and (d) unequal sensitivities in the means/modes of the modalities.

EXAMPLES

Schlögl model

The Schlögl model describes a prototype chemical reaction network (Gillespie, 1992b),

(15a)

(15b)

where the concentrations A and B are kept constant (buffered) and the reaction rate constants k_j are the model parameters. The propensity functions for these reactions are

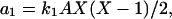(16a)

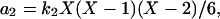(16b)

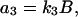(16c)

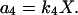(16d)

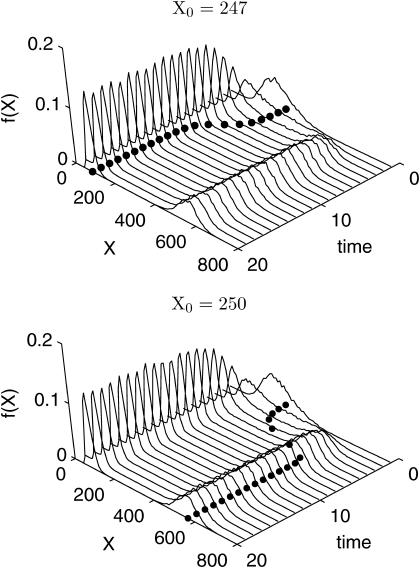
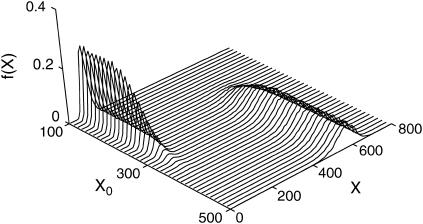
This system possesses two stable steady states for the parameter values in Table 1. Fig. 3 shows the deterministic and SSA simulations of the Schlögl model for the two initial states X₀ = 247 and X₀ = 250. The deterministic simulation with smaller initial value converged to the left mode, and vice versa, the one with larger initial value to the right mode of the distribution. The bifurcation at approximate initial condition X₀ ≈ 247 was apparent from the deterministic simulations, but the density functions from the stochastic simulations differed very little. In fact, the stochastic effects blur the bifurcation point as shown in Fig. 4, where the transition from lower stable steady state at low X₀ to higher steady state at high X₀ in the stochastic simulations proceeded more smoothly than in the deterministic counterpart. Around the bifurcation point, the density functions become bimodal representing the existence of two attractors.

TABLE 1.

Schlögl parameter values

Parameters	Values
k1A	3 × 10−2
k2	10−4
k3B	2 × 102
k4	3.5

FIGURE 3.

Deterministic and SSA simulations of the bistable Schlögl model for the initial conditions X₀ = 247 (top) and X₀ = 250 (bottom). The solid circles represent the deterministic trajectories. Each distribution is constructed from 10,000 realizations of the state X.

FIGURE 4.

Steady-state density functions of the Schlögl model (t = 20) around the bifurcation point. Stochastic effects produced diffused transition from low to high X attractor.

The stochastic sensitivity analysis was first applied to the Schlögl model with initial condition slightly lower than the bifurcation point X₀ = 247. A representation of distribution changes due to variations in a parameter is shown in Fig. 5. Since the deterministic and stochastic sensitivity coefficients have different units, the comparisons between the two analyses focus on the relative ordering of the parametric sensitivity magnitudes. The ordering of the sensitivities also provides information on the robustness of the system with respect to parameter uncertainties (Stelling et al., 2004). The parameters with larger (relative) sensitivities represent the fragilities of the system. The sensitivities were normalized to the parameter values, i.e.,

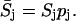(17)

FIGURE 5.

Density function changes arising from 1% perturbations of the parameter k₁A.

In deterministic analysis, the sensitivity coefficients were also normalized with respect to the nominal output values, i.e.,

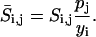(18)

The sensitivities in Eq. 17 require no normalization to the output values because the density functions integrate to 1:

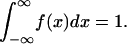(19)

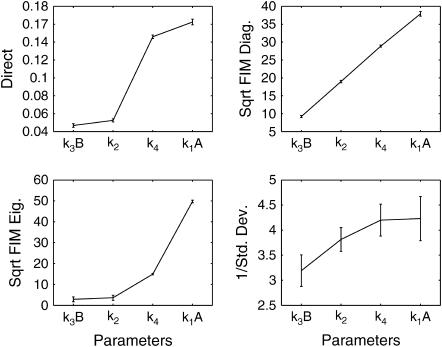
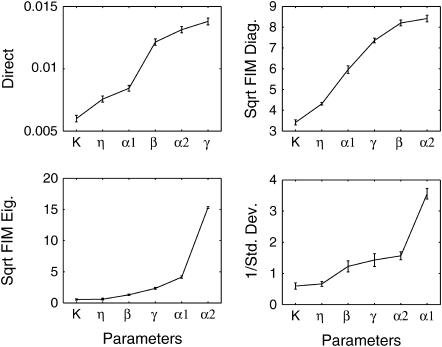
The notation 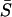is used for both deterministic and stochastic sensitivity, but the differences should be clear from the subscript. Fig. 6 b shows the deterministic sensitivity ordering, whereas the corresponding stochastic sensitivities are shown in Fig. 7 at steady state (t = 20). The first stochastic sensitivity measure (direct in Fig. 7) corresponds to Eq. 3, whereas the remaining three represent the FIM-based sensitivity measures. Since the FIM correlates with the square of sensitivities, the square-roots of the FIM diagonals and eigenvalues give the proportional measures for comparison with the deterministic analysis. Among the four stochastic sensitivity measures, the direct and FIM diagonals are the closest analog of the classical sensitivity because they represent the sensitivity with respect to independent parameter perturbations. The sensitivity measures were obtained from 100 independent samples of each sensitivity measure, to yield the averages and standard deviations shown in these figures.

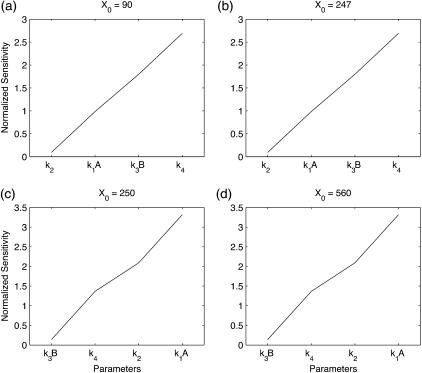
FIGURE 6.

Deterministic sensitivity ordering of the Schlögl model at different initial conditions; (a) X₀ = 80, (b) X₀ = 247, (c) X₀ = 250, and (d) X₀ = 560.

FIGURE 7.

Stochastic sensitivity ordering for the Schlögl model with initial condition X₀ = 247 using different sensitivity measures.

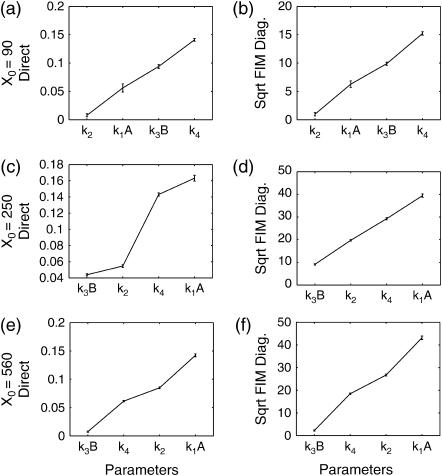
Similar comparisons were also done using an initial condition on the opposite side of the bifurcation point X₀ = 250, as well as initial conditions away from the bifurcation point X₀ = 100 and X₀ = 500 at time t = 20. The last two initial conditions led to unimodal distributions, as expected from Fig. 4. Figs. 6 and 8 present the deterministic and stochastic sensitivity results based on the direct and FIM diagonals. The FIM eigenvalues and standard deviations were in general agreement (not shown). Far from the bifurcation point, the deterministic and stochastic analysis showed good agreement. Around the bifurcation point, the deterministic analysis from both sides of the bifurcation point differed from the stochastic analysis due to one of the discriminating circumstances described in the previous section (see also Fig. 5).

FIGURE 8.

Stochastic sensitivity ordering for the Schlögl model with initial conditions; (a−b) X₀ = 90, (c−d) X₀ = 250, and (e−f) X₀ = 560, based on the direct (left column) and FIM diagonals (right column). The FIM eigenvalues and standard deviations gave similar sensitivity orderings (not shown).

Genetic toggle switch

Systems with multiple steady states including hysteresis effects are widely used in modeling of biological processes, for example, in a cell's decision making (Arkin et al., 1998), cell cycle regulation (Pomerening et al., 2003), and mitogen-activated protein kinase cascades (Ozbudak et al., 2004). In fact, bistability has been a recurrent property observed in networks of cell signaling pathways (Bhalla and Iyengar, 1999) and provides an avenue for cell differentiation and evolution (Laurent and Kellershohn, 1999). Recently, scientists have engineered such systems in vivo based on a simple mathematical model of two repressor-promoter pairs using DNA recombinant techniques (Gardner et al., 2000), which opens the gate for more advanced genetic switch design.

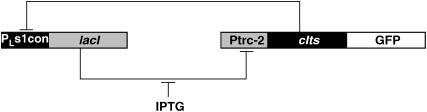
The second example is a model of the aforementioned synthetic genetic toggle switch consisting of two repressor-promoter pairs, lacI repressor with Ptrc-2 promoter and a thermal sensitive λ-repressor cIts with P_Ls1con promoter, aligned in a mutually inhibitory manner (Gardner et al., 2000). Here, the expression of lacI represses the activity of Ptrc-2, which is the promoter of cIts, and vice versa, the expression of cIts inhibits the promoter P_Ls1con of lacI (see Fig. 9). The ON-OFF states are indicated by inserting a green fluorescence protein (GFP) gene downstream of cIts such that the transcription from Ptrc-2 will light up the cell (ON state). Addition of the inducer isopropyl-β-D-thiogalactopyranoside (IPTG) will bias the distribution to the ON state by binding to the lacI repressor and thus inhibiting its activity (Jacob and Monod, 1961). The reverse switch can be accomplished by a thermal pulse, but will not be investigated here. A simple model for this system has been proposed, with two states describing the concentration of each repressor (Gardner et al., 2000):

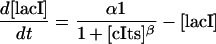(20a)

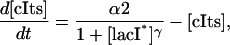(20b)

where

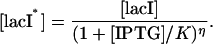(21)

FIGURE 9.

Synthetic genetic toggle switch (PTAK plasmid in Gardner et al., 2000).

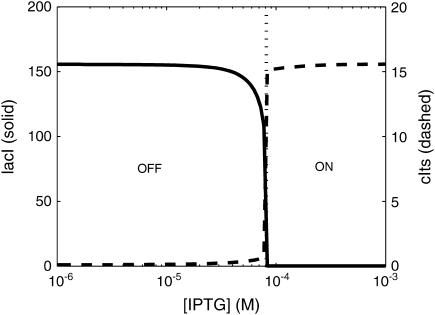
The parameter values are listed in Table 2. Note that the value of parameter K differs from that reported in Gardner et al. (2000), as the stochastic effects around the bifurcation point caused switching from the OFF state to the ON state at lower [IPTG], and thus led to lower observed K for the deterministic model (K = 2.9618 × 10⁻⁵; Gardner et al., 2000). The value of K used here was obtained to better match the flow cytometry measurements for the fraction of ON cells at different [IPTG] concentrations (Fig. 5 b in Gardner et al., 2000). Fig. 10 shows the deterministic switching between the two stable steady states, high [lacI] with low [cIts] (OFF) and low [lacI] with high [cIts] (ON), as a function of the [IPTG] levels. The cells were initially grown in the OFF state.

TABLE 2.

Genetic toggle-switch parameter values

Parameters	Values
α1	156.25
α2	15.6
β	2.5
γ	1
η	2.0015
K	6.0 × 10−5

FIGURE 10.

Switching between the ON-OFF states as a function of [IPTG]. The bifurcation point is ∼[IPTG] = 7.9 × 10⁻⁵. The concentrations [lacI] and [cIts] are taken at the steady-state level (t = 1000).

The stochastic sensitivity analysis started with the formulation of a stochastic version of the model by assigning a representative reaction to each rate equation:

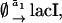(22a)

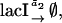(22b)

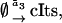(22c)

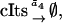(22d)

where 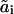are the propensity functions involving possibly non-elementary reactions (e.g., Michaelis-Menten or Hill type expressions). The propensities come directly from the rates in the model normalized to the system volume Ω:

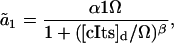(23a)

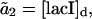(23b)

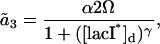(23c)

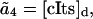(23d)

where the discrete concentrations (denoted by the subscript d) [lacI]_d and [cIts]_d assume integer values and

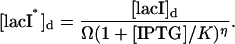(24)

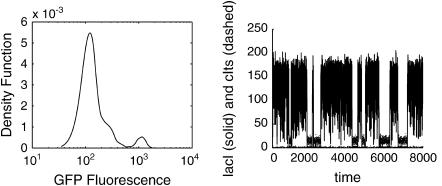
The parameters were the same as in the deterministic model listed in Table 2. Around the bifurcation point, the stochastic system exhibited a bimodal distribution associated with the ON and OFF states, and the stochastic effects introduced flip-flops between the two stable steady states as shown in Fig. 11. The GFP fluorescence distribution in Fig. 11 was computed from the states according to

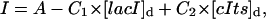(25)

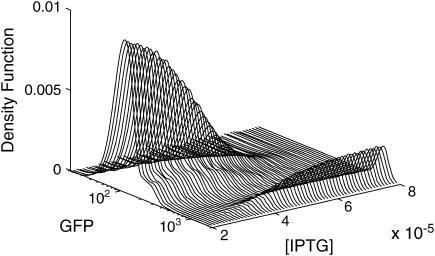
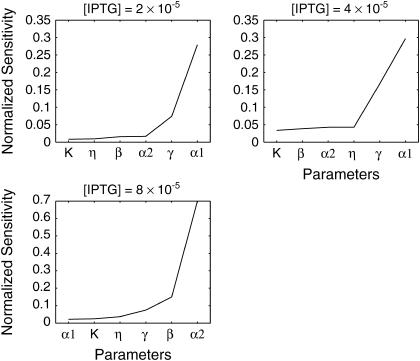
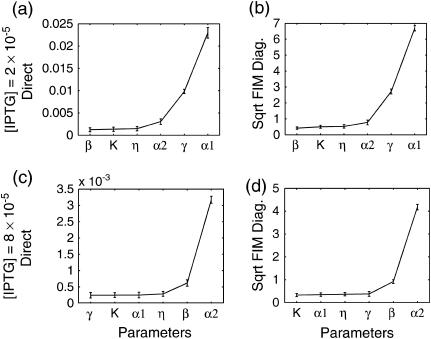
where I is the fluorescence intensity which is assumed to be a linear function of the concentrations (Gaigalas et al., 2001), A is the leakage expression, and C₁ and C₂ represent the efficacy of the lacI repressor and the GFP to cIts expression ratio, respectively. These constants were selected to obtain qualitative matches with the flow cytometry data (Gardner et al., 2000) (A = 420, C₁ = 2, C₂ = 50). As in the Schlögl model, the stochastic transitions from the OFF to the ON state as a function of [IPTG] were smoother than the deterministic simulations, as shown in Fig. 12. Notice that the bimodality exhibited itself with [IPTG] level as low as 3 × 10⁻⁵, far less than the bifurcation point at [IPTG] = 8 × 10⁻⁵. Figs. 13–15 present the deterministic and stochastic sensitivity ordering for different inducer concentrations around the bifurcation point. Again, the density functions were constructed from a run of 10,000 independent SSA realizations and the sensitivity measures were obtained from 100 independent runs. As in the Schlögl example, the deterministic and stochastic sensitivity orderings agreed when the density function is unimodal (see Fig. 14), but differed when the distribution becomes bimodal (see Fig. 15).

FIGURE 11.

Bimodal density function arising from bistability (shown at [IPTG] = 4.0 × 10⁻⁵). The stochastic effects also introduced flip-flops between the two stable steady states.

FIGURE 12.

Stochastic transition from the OFF to ON state as a function of the inducer [IPTG] level.

FIGURE 13.

Deterministic sensitivity ordering for the genetic toggle switch at different inducer concentrations. The bifurcation point occurs at [IPTG] = 7.9 × 10⁻⁵.

FIGURE 14.

Stochastic sensitivity ordering for the genetic toggle switch at an inducer concentration: (a–b) [IPTG] = 2.0 × 10⁻⁵ and (c–d) [IPTG] = 8.0 × 10⁻⁵. At these concentrations, the density functions are unimodal (see Fig. 12). The FIM eigenvalues and standard deviations gave similar sensitivity orderings (not shown).

FIGURE 15.

Stochastic sensitivity ordering for the genetic toggle switch at an inducer concentration [IPTG] = 4.0 × 10⁻⁵.

DISCUSSION

Comparison among the sensitivity orderings in the two examples showed discrepancies between the deterministic and discrete stochastic analysis around the bifurcation point, in particular when the distribution function becomes bimodal. There are (at least) two explanations for the differences in the sensitivity ordering. The main reason is that the stochastic analysis was able to capture the sensitivities of the two attractors simultaneously. In other words, the sensitivity features of both steady states concurrently affected the stochastic analysis, but not the deterministic analysis. In the Schlögl model, the two most sensitive parameters around the bifurcation point in the stochastic analysis (Figs. 7 and 8, c and d) were exactly the most sensitive parameters of both attractors independently, according to the deterministic analysis (see Fig. 6). Similarly, the stochastic sensitivity of the genetic toggle switch showed combinations of deterministic sensitivity ordering of the two attractors. For example, at [IPTG] = 4 × 10⁻⁵, the four most sensitive parameters consisted of the most sensitive parameters from both sides of the bifurcation point.

The second reason for the observed differences was an indirect consequence of the main reason. In the Schlögl model, the more sensitive right attractor induced a waterbed effect, leading to little change in the mean but significant change in the shape of the distribution around the left attractor (see Fig. 5). The waterbed effect arose from the constraint that the integral under the density function should equal to 1 (see Eq. 19). This effect corresponds to the stochastic behavior described in Fig. 2 b. Away from the bifurcation point, however, the stochastic simulations gave unimodal distributions, and the stochastic and deterministic sensitive orderings exhibited good agreement.

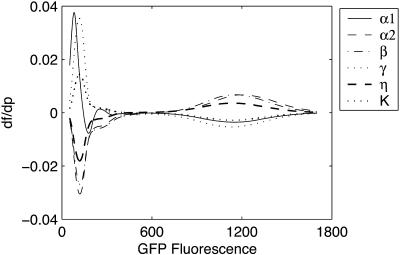
The four sensitivity measures were in general agreement with each other, despite the differences in their interpretations. The direct and FIM diagonals are closely related to the first order sensitivity such as Eq. 1, from their definitions. The FIM eigenvalues and the standard deviations have less direct correlation with the classical sensitivity, but they carry additional information about the system behavior under simultaneous multiple parameter perturbations, and led to the differences shown in Fig. 15. These measures are closely related to information content and parametric uncertainty in parameter estimation problems, i.e., eigenvalues to D-optimality and standard deviations to A-optimality (Emery and Nenarokomov, 1998). The eigenvalue analysis suggests that the sensitivities were correlated, as indicated by the large magnitude of the differences between the largest and the remainder of the eigenvalues. This is confirmed by plotting the sensitivity of density function explicitly, as shown in Fig. 16.

FIGURE 16.

Sensitivity of the density function in the genetic toggle switch at [IPTG] = 4.0 × 10⁻⁵.

The differences between the classical and stochastic analysis above give support for rigorous consideration of the stochastic effects in studying small systems. These differences could lead to different interpretations of the key mechanism(s) responsible for a given phenotype, or strategies in the design and engineering of in vivo biological circuits, in particular bistable switches. In the latter, the design will utilize not only the absolute magnitude of the sensitivity used in this work, but also the overall sensitivity of the density function as in Fig. 16. The engineering of genetic switches and other biological circuits will then aim to achieve the desired distribution of the cell population, not just the average behavior, through manipulation of the sensitive parameters using methods such as genetic mutation and over- or underexpression of certain genes. The design of cell population distribution can borrow approaches in distribution control from other areas, especially particulate systems (Braatz and Hasebe, 2002; Daoutidis and Henson, 2002; Doyle et al., 2002).

The genetic toggle-switch example also motivates explicit treatment of the stochastic effects in model development and parameter estimation. In particular, the early onset of bifurcation due to the stochastic dynamics led to incorrect parameter values, which was only apparent after observing the stochastic simulations. Similar behavior around the bifurcation point has also been observed in the Hopf bifurcation of Drosophila circadian rhythm, leading to an early onset of oscillations (Gonze et al., 2003). In such situations, stochastic paradigms such as the CME or chemical Langevin equation can provide information on the system dynamics that is missing from deterministic models.

CONCLUSIONS

Sensitivity analysis of discrete stochastic processes incorporates the dynamics of the density function explicitly. In small systems exhibiting multistability, the stochastic effects around the bifurcation point manifest as multimodal density functions and spread out the transitions between different steady states (i.e., the stochastic effects annihilate the bifurcation between steady states). The deterministic and stochastic sensitivity analysis around such a bifurcation point can lead to different conclusions, as the deterministic model lacks the information of the true dynamics in the transition. In addition, stochastic effects can induce early/late onset of the bifurcating behavior, which then leads to inaccurate prediction of the observed bifurcation point in the deterministic model. Applications and comparisons of the deterministic and discrete stochastic analysis applied to the Schlögl model and a genetic toggle switch model demonstrated the importance of applying the appropriate sensitivity analysis according to the dynamics of the process.