Abstract
The folding free energy landscape of the C-terminal β-hairpin of protein G is explored using the surface-generalized Born (SGB) implicit solvent model, and the results are compared with the landscape from an earlier study with explicit solvent model. The OPLSAA force field is used for the β-hairpin in both implicit and explicit solvent simulations, and the conformational space sampling is carried out with a highly parallel replica-exchange method. Surprisingly, we find from exhaustive conformation space sampling that the free energy landscape from the implicit solvent model is quite different from that of the explicit solvent model. In the implicit solvent model some nonnative states are heavily overweighted, and more importantly, the lowest free energy state is no longer the native β-strand structure. An overly strong salt-bridge effect between charged residues (E42, D46, D47, E56, and K50) is found to be responsible for this behavior in the implicit solvent model. Despite this, we find that the OPLSAA/SGB energies of all the nonnative structures are higher than that of the native structure; thus the OPLSAA/SGB energy is still a good scoring function for structure prediction for this β-hairpin. Furthermore, the β-hairpin population at 282 K is found to be less than 40% from the implicit solvent model, which is much smaller than the 72% from the explicit solvent model and ≈80% from experiment. On the other hand, both implicit and explicit solvent simulations with the OPLSAA force field exhibit no meaningful helical content during the folding process, which is in contrast to some very recent studies using other force fields.
Protein-folding and -unfolding studies are of great current interest in molecular biology (1, 2). Experiments that probe proteins at different stages of the folding process have helped to elucidate kinetic mechanisms and the thermodynamic stabilities of folding (3–6). However, many of the details of protein-folding pathways remain unknown. Computer simulations performed at various levels of complexity ranging from simple lattice models, models with implicit solvent, to all-atom models with explicit solvent can be used to supplement experiment and fill in some of the gaps in our knowledge about folding pathways. Because explicit solvent simulations require enormous amounts of CPU time, many recent studies have been carried out with implicit solvent models (7–10). However, it is still an open question as to how well these implicit solvent models can predict the thermodynamics as well as the kinetics of protein folding. It will be very interesting to determine whether implicit solvent models can reproduce either the results from explicit solvent simulations or experimental results.
The C terminus β-hairpin of protein G has received much attention recently on both the experimental and theoretical fronts (3–6, 11–16), because it is believed to be one of the smallest naturally occurring systems that exhibit many features of a full-size protein and also because it is a fast folder (folds in ≈6 μs). Understanding the folding of key protein secondary structures such as the β-sheet and the α-helix may provide a foundation for understanding folding in more complex proteins. The breakthrough experiments by the Serrano (3, 4) and Eaton groups (5, 6) recently established the β-hairpin from the C terminus of protein G as the system of choice for studying β-sheets in isolation. These pioneering experiments have inspired much theoretical work on this system using both explicit and implicit solvent models (11–14, 17). For example, Pande and coworkers have studied the kinetics of this β-hairpin with the generalized-Born (GB) continuum solvent model (12). Lazaridis and Karplus have explored the free energy landscape using the CHARMM force field (CHARMM19) with a continuum solvent model EEF1 (10). Very recently explicit solvent simulations have also been used to study this system. Garcia and Sanbonmatsu (14) have studied the free energy landscape of this system in explicit solvent using the AMBER force field (AMBER94) with a short cutoff (9 Å) in the electrostatic interactions. Berne and coworkers (18) have also explored this system with the OPLSAA force field and explicit solvent with no cutoffs in the electrostatic interactions by using the particle-particle particle-mesh Ewald (P3ME) method (19). It is of great interest to compare the free energy landscape calculated using continuum solvent models to that calculated using explicit solvent models. For such comparisons to be self-consistent, it makes sense to use the same force field for the protein (and continuum solvent model parameters parameterized to that force field as well) and at the same time eliminate the sampling issue by using large-scale simulations such as the replica-exchange method (REM; ref. 20). It should be noted that periodic boundary conditions in the explicit solvent simulations may introduce some artifacts in solvation free energies (21, 22) due to the periodicity, but for large enough primary cells and neutral systems such as the one used in our simulations, these artifacts are expected to be very small.
In this article, we use a highly parallel REM and the surface-generalized Born (SGB; ref. 9) implicit solvent model to explore the free energy landscape, and the results are compared with our earlier explicit solvent simulations. A total of 18 replicas are simulated with temperatures spanning 270–690 K, which has the same temperature coverage as the previous explicit solvent simulation (18), although more replicas (64 replicas) have to be used in the explicit solvent simulation (18). Because the force field is normally parameterized at room temperature, we do not expect it to yield accurate results for higher temperatures; nevertheless, these high-temperature replicas permit the system to cross the energy barriers rapidly and thus lead to efficient sampling at the lower temperatures. It is found that the free energy landscape for the continuum solvent model is quite different from that of the explicit solvent model. Some of the nonnative states are heavily overweighted in the continuum solvent model as compared with the explicit solvent model, and more importantly, the lowest free energy state from the continuum solvent model is no longer the native β-strand structure. It is found that the continuum solvent model over-stabilizes salt bridges compared with the hydrophobic interactions between hydrophobic residues and thus in large part leads to the heavy population of this nonnative state. Furthermore, the β-hairpin population at 282 K is found to be less than 40% for the continuum model, as compared with 72% for the explicit solvent model and ≈80% for experiment. On the other hand, both our continuum and explicit solvent simulations with the OPLSAA force field predict no meaningful helical content during the folding process, in agreement with experiment but in contrast to recent simulations using the AMBER force field and the OPLS united atom force field (12, 14).
Methodology
The REM has been implemented in the context of the molecular-modeling package IMPACT (19, 23). Replicas are run in parallel at a sequence of temperatures. Periodically, the configurations of neighboring replicas are exchanged, and acceptance is determined by a Metropolis criterion that guarantees detailed balance. The acceptance criterion used in REM is identical to that in jump-walking methods (23). Because the high-temperature replica can traverse high-energy barriers, there is a mechanism for the low-temperature replicas to overcome the quasiergodicity they would encounter in a one-temperature walk. The replicas themselves can be generated by Monte Carlo (MC), hybrid MC (HMC; ref. 24) as was used in our recent implementation of jump walking and smart walking (23), or molecular dynamics (MD) with velocity rescaling as used by Sugita and Okamoto (25). The HMC method, which uses MD to generate possible conformations, is often called “bad MD but good MC” (24). The HMC method is adopted in this study for the sampling of each of the replicas. In the previous explicit solvent simulation (18) we used Sugita and Okamoto's approach, i.e., MD with velocity rescaling. Both approaches probably are equally good for this study, but in general HMC scales badly with system size and thus is more suitable for smaller systems such as the protein in continuum solvent. It should be recognized that MD simulations of continuum solvent models often omit the required surface-area gradients. Our implementation of HMC allows us to bypass this problem.§ It should be pointed out, though, that since all REM uses the Metropolis criterion for replica exchanges, they are essentially MC methods not MD methods. Thus the MD timings reported here and also in previous REM studies (14, 18, 25) should not be taken as direct kinetic measurements.
The REM itself can be summarized as the following two-step algorithm:
- 1.
Each replica i (i = 1,2,… ,M) at fixed temperature Tm (m = 1,2,… ,M) is simulated simultaneously and independently for a certain number of MC or MD steps.
- 2.
- Pick a pair of replicas, and exchange them with the acceptance probability
where Δ = (βi − βj)[V(xj) − V(xi)], βi and βj are the two reciprocal temperatures, xi is the configuration at βi, xj is the configuration at βj, and V(xi) and V(xj) are potential energies at these two configurations, respectively. After the exchange, go back to step 1.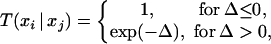
1 In the present work, HMC is used in step 1, and all the replicas are run in parallel on M processors (M = 18). In step 2, only exchanges between neighboring temperatures are attempted, because the acceptance ratio decreases exponentially with the difference of the two β values.
The continuum solvent model adopted in this study is the SGB model, which was developed by Friesner and coworkers (9). In theory, SGB is basically the same as the original GB model of Still et al. (8). The only difference is that SGB uses the surface integral rather than the original volume integral in the single-energy term in GB models (see below, Eq. 4), but it can be proved easily that they are equivalent using Green's theorem (9). Of course, the parametrizations are different also. The SGB model of Friesner and coworkers has been parameterized with the OPLSAA force field to reproduce the experimental solvation free energies for ≈200 small organic molecules (9, 26).
- In typical GB models the total solvation free energy (8, 9) of a protein is expressed as the sum of the “reaction field energy,” Urxn, and the “cavity energy,” Ucav, such that
In the SGB formulation, the total reaction field energy (consult ref. 9 for more details) is expressed as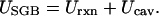
2
where the “single energy” Use is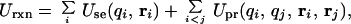
3
where ɛi is the dielectric constant for the interior of the solute (for proteins, it is typically ≈1.0–4.0 in SGB; ref. 9), ɛo is the dielectric constant for outside water (78.5), and the pairwise screened Coulomb energy is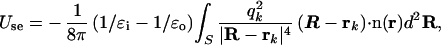
4
with parameter αij =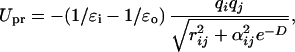
5 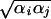 (αi and αj are the Born radius) and parameter D = r
(αi and αj are the Born radius) and parameter D = r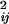 /(2αij)2.
/(2αij)2.
Results and Discussion
The β-hairpin under study here is taken from the C terminus (residue 41–56) of protein G (PDB ID code 2gb1). The 16-residue β-hairpin is capped with the normal Ace and Nme groups, resulting in a blocked peptide sequence of Ace-GEWTYDDATKTFTVTE-Nme, with a total of 256 atoms. The SGB continuum solvation model is used with a dielectric constant of 2.0 for this small β-hairpin (assigning dielectric constants for proteins can be very tricky; refs. 27 and 28). In this study, we also tried 1.0 and 4.0, similar free energy contour maps are obtained, and the general conclusions are basically the same (see below). All the MD simulations are carried out with IMPACT (19, 23). A total of 18 replicas are simulated with temperatures ranging from 270 to 690 K. Before the production run, a conjugate gradient minimization is performed first for each replica, and then a 100-ps MD equilibration is followed with temperature ramping from 0 K to the specified temperature for each replica. The final configurations of the above equilibration then are used as the starting points in the 18 replicas. Each replica is run for 2.0 ns for data collection. The replica exchanges are attempted every 200 fs, and protein configurations are saved every 80 fs, giving a total of 0.45 million configurations.
The optimal temperature distribution in REM should be exponential, i.e., Tn = T0 exp(kn), where Tn is the nth temperature, and T0 and k are constants that can be obtained easily by running a few short trial simulations. In this study, we used a total of 18 replicas with temperatures from 270, 282, 295, 310,… ,649 to 690 K (temperature gaps from 12 to 41 K). With this choice we get an acceptance ratio of ≈40%. We observe that the “temperature trajectory” for one replica (e.g., replica 4 starting at 310 K) visits all the temperatures many times during the 2-ns MD run, and at a given temperature (e.g., 310 K) all the replicas are also visited many times during the same MD run, indicating that our temperature series are optimized reasonably.
The free energy landscape is determined by first calculating the normalized probability distribution function P(X) from a histogram analysis (14) of either an MD or MC simulation. Since the potential of mean force (PMF) W(X), or equivalently the free energy, is related to this probability distribution function through the relation
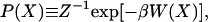 |
6 |
where X is the specified choice set of reaction coordinates (RCs), and Z is the partition function, the relative free energy change corresponding to a change in RC can be obtained easily from
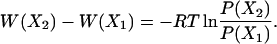 |
7 |
In previous work we determined the free energy surfaces for the β-hairpin in explicit water for different sets of RCs (18) including the number of β-strand hydrogen bonds, the hydrophobic core radius of gyration, the fraction of native contacts, and the radius gyration of the entire peptide, the principal components (29), and found the number of β-strand hydrogen bonds and the hydrophobic core radius gyration to be very informative for this small β-hairpin. Thus, here we compare the free energy contour maps as a function of these two RCs for the explicit with the implicit solvent models.
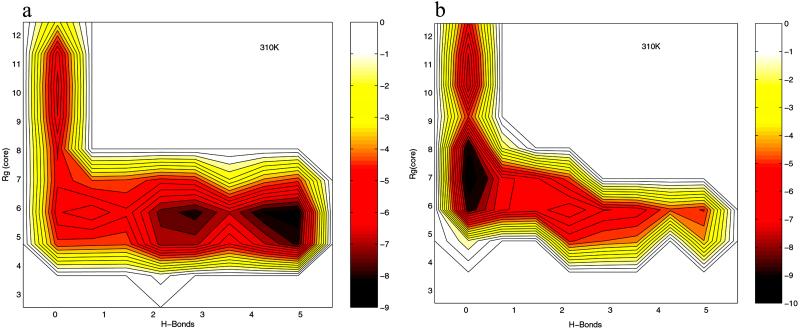
Fig. 1 shows the comparison of the free energy contour maps for explicit (a) and continuum solvent (b) simulations at 310 K. The free energy is plotted against the two RCs mentioned above, i.e., the number of β-strand hydrogen bonds (N ) and the radius of gyration of the hydrophobic core (R
) and the radius of gyration of the hydrophobic core (R ). N
). N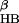 is defined as the number of backbone–backbone hydrogen bonds excluding the two at the turn of the hairpin (18). R
is defined as the number of backbone–backbone hydrogen bonds excluding the two at the turn of the hairpin (18). R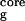 is the radius of gyration of the side-chain atoms on the four hydrophobic residues, W43, Y45, F52, and V54. Surprisingly, the free energy contour maps from these two models are quite different. A closer look at the free energy contour map from the continuum solvent model reveals several important features. (i) The native state (NHB = 5.0 and R
is the radius of gyration of the side-chain atoms on the four hydrophobic residues, W43, Y45, F52, and V54. Surprisingly, the free energy contour maps from these two models are quite different. A closer look at the free energy contour map from the continuum solvent model reveals several important features. (i) The native state (NHB = 5.0 and R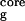 = 5.8 Å) is no longer the lowest free energy state in the continuum solvent model. (ii) The most heavily populated state, or the lowest free energy state, has no meaningful β-strand hydrogen bonds (NHB ≈ 0), and it also has a slightly higher radius of gyration for the hydrophobic core (R
= 5.8 Å) is no longer the lowest free energy state in the continuum solvent model. (ii) The most heavily populated state, or the lowest free energy state, has no meaningful β-strand hydrogen bonds (NHB ≈ 0), and it also has a slightly higher radius of gyration for the hydrophobic core (R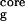 ≈ 7.0 Å). It has ≈2.92 kcal/mol (4.75 RT) lower free energy than the native state [since this state is similar to the intermediate state H from explicit solvent model (11, 14, 18), we also name it the H state for simplicity]. (iii) The overall shape of the free energy contour map, however, is still an “L” shape, which is the same as the contour map for the explicit solvent simulation. This indicates that the folding process probably is still driven by hydrophobic core collapse (18). In preliminary work with the AMBER/GBSA (GB with surface area for cavity) model (30) on this same β-hairpin, we also find large deviations from the explicit solvent model (results will be published elsewhere).
≈ 7.0 Å). It has ≈2.92 kcal/mol (4.75 RT) lower free energy than the native state [since this state is similar to the intermediate state H from explicit solvent model (11, 14, 18), we also name it the H state for simplicity]. (iii) The overall shape of the free energy contour map, however, is still an “L” shape, which is the same as the contour map for the explicit solvent simulation. This indicates that the folding process probably is still driven by hydrophobic core collapse (18). In preliminary work with the AMBER/GBSA (GB with surface area for cavity) model (30) on this same β-hairpin, we also find large deviations from the explicit solvent model (results will be published elsewhere).
Figure 1.
Comparison of the free energy contour maps versus the number of β-sheet hydrogen bonds N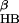 and the hydrophobic core radius gyration R
and the hydrophobic core radius gyration R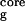 for explicit (a) and implicit (b) solvent simulations at 310 K. A hydrogen bond is counted if the distance between two heavy atoms (N and O in this case) is less than 3.5 Å, and the angle N—H…O is larger than 150.0°. The free energy is in units of RT, and contours are spaced at intervals of 0.5 RT.
for explicit (a) and implicit (b) solvent simulations at 310 K. A hydrogen bond is counted if the distance between two heavy atoms (N and O in this case) is less than 3.5 Å, and the angle N—H…O is larger than 150.0°. The free energy is in units of RT, and contours are spaced at intervals of 0.5 RT.
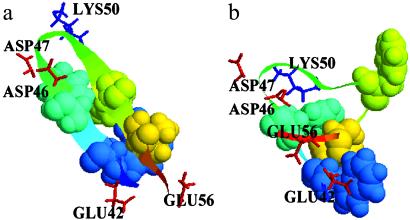
To understand why the continuum solvent model favors nonnative structures, we analyze the heavily populated state H in detail. The structures belonging to that free energy basin are partitioned into clusters defined such that a structure belongs to a cluster if it has an rms deviation no larger than 1 Å from at least one other structure in that cluster. This clustering algorithm allows us to determine the unique structures in a free energy basin and the populations in each cluster bin. Fig. 2 shows one of the most heavily populated structures in state H (b), and for comparison we also show one of the most heavily populated structures from the explicit solvent model, which is really the native structure (a). Two interesting observations emerge from the comparison of these two structures. (i) The hydrophobic residue F52 is expelled from the hydrophobic core in the continuum solvent, while it is well packed with the other three hydrophobic residues (W43, Y45, and V54) in the explicit solvent model. In other words, the four hydrophobic residues form a well packed core in the explicit solvent but not in the continuum solvent. (ii) In explicit solvent, the side chains of charged residues extend fully into the solvent and thus are fully solvated, whereas in the continuum solvent model, the charged residues are clustered to form salt bridges between opposite charges. For example, D46 and D47 form two salt bridges with K50 near the β-hairpin turn, and the C-terminal end residue E56 also swings toward K50 to get closer to the positive charge. The net effect of this salt-bridge formation brings the oppositely charged residues, two near the β-hairpin turn (D46 and D47) and one from the C-terminal end (E56), into closer contact with residue K50, thereby expelling the hydrophobic residue F52 (in the middle of the same β-strand as K50) from the hydrophobic core. This suggests that the balance between electrostatic interactions and the hydrophobic interactions is no longer preserved. The electrostatic interactions between the charged residues (salt bridges) overwhelm the hydrophobic interactions between the four hydrophobic core residues. SGB overestimates the salt bridge, because the loss in “single energies” (compare Eq. 4) when two oppositely charged groups associate is not strong enough to overcome the gain in Coulombic interactions. It is possible also that hydrophobic interactions between hydrophobic residues are underestimated in the SGB and GB models.
Figure 2.
Comparison of the representative structures with the lowest free energy from the explicit (a) and implicit (b) solvent simulations. The hydrophobic residues (W43, Y45, F52, and V54) are represented by space-fill, charged residues (E42, D46, D47, K50, and E56) are represented by sticks with positively charged residues colored blue and negatively charged residues colored red, and the rest are represented by ribbons. The implicit solvent structure show very different features compared with the explicit solvent structure (see text for details).
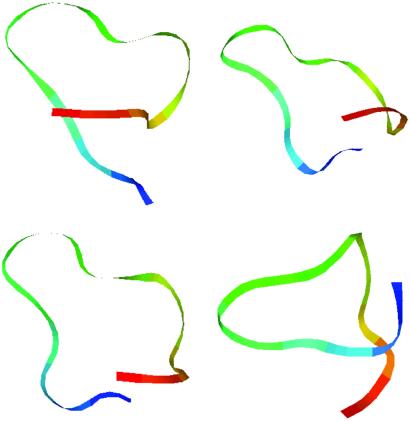
Several other representative structures in the H state found from clustering are shown in Fig. 3. These structures exhibit similar behavior. The hydrophobic core again is destroyed in favor of more stable electrostatic contacts. The erroneous formation of salt bridges probably is exacerbated by the fact that counter ions are not included in implicit solvent models. In explicit solvent simulations, there are three counter ions (3 Na+), which will neutralize the negatively charged residues somewhat (E42, D46, D47, and E56), so that these negative charges may be partially screened, thus reducing the direct electrostatic interactions that would lead to a salt bridge. This is probably a small effect, because the Na+ ions are free ions in solution. It should be pointed out that such salt effects can be included in the Poisson–Boltzmann solvers (31) but are not incorporated easily in GB-type models. As mentioned above, in the continuum solvent model all charged groups interact through a Coulomb potential with a small dielectric constant (between 1 and 4; ref. 9), and thus it is more favorable for oppositely charged residues to come close together instead of being hydrated as they would be in explicit water. One way to fix this is to invoke a stronger dielectric screening (a much larger dielectric constant) in the Coulomb interaction between charged residues as suggested by Warshel and coworkers in another context (32). There is some experimental evidence for this (28). Another possible approach to fix this problem is to introduce a penalty function between oppositely charged residues as was suggested by Jacobson and Friesner in connection with their loop geometry optimizations (unpublished results). Of course the introduction of a larger dielectric constant for charged residues similarly gives rise to a penalty, albeit a different one than that introduced by Jacobsen and Friesner. Some initial testing of the penalty function indicates that it fixes the problem partially. We will address this question in more detail in a separate publication, because it involves a complete refitting of the model. It is possible that other continuum solvent models or other implementations, such as amber/GBSA (preliminary results show a similar effect), might exhibit this salt-bridge effect and may require a similar correction and refitting.
Figure 3.
Representative structures in the lowest free energy basin (state H) in the implicit solvent from clustering with rms deviation (see text for details). All of them show a partially broken hydrophobic core in the favor of stronger electrostatic interactions between charged groups.
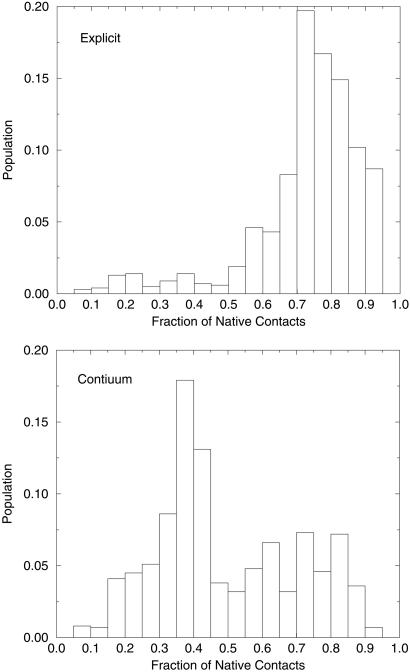
To go one step further, we also calculate and compare the β-hairpin population at various temperatures to the populations determined experimentally from measurements of fluorescence quantum yields (5). It is of interest to calculate this population in both explicit and implicit solvent simulations. Klimov and Thirumalai (17) and Zhou et al. (18) have used the average fraction of native contacts to estimate the β-hairpin population, and here we follow the same approach. Experimentally, it is found that the β-hairpin population at a low temperature of 282 K is ≈80%. From calculating the average fraction of native contacts, we obtained 72% β-hairpin population in the explicit solvent (18) and 39% in the implicit solvent at 282 K. As expected, the β-hairpin population is seriously underestimated in the implicit solvent model. Fig. 4 shows the detailed population histogram at various fractions of native contacts for both explicit and implicit solvent simulations at 282 K. In explicit solvent, the most heavily populated states have 70–80% of the native contacts, while in the implicit solvent the most heavily populated states have only ≈30–40% of the native contacts. This is because these heavily populated states (H state) in implicit solvent have very different structures from the native state as mentioned above. The number of native contacts formed in the H state is significantly less than in the native state. Thus, one finds reasonable populations of β-hairpin in the explicit solvent model at these temperatures but not in the implicit solvent model. Other dielectric constants (e.g., ɛi = 1.0 and 4.0) have also been tried for this peptide, and the β-hairpin population improves slightly (2–3% from ɛi = 2.0 to ɛi = 4.0) with higher dielectric constants, but it is still much too low in the implicit solvent model. This indicates that the erroneous salt-bridge effect and the imbalance between polar and nonpolar interactions in the implicit solvent model are not eliminated. Thus the problem cannot be fixed easily by increasing the overall protein dielectric constant, although it is possible that introduction of a much larger dielectric screening of the charged-residue interactions alone might well do the trick.
Figure 4.
Comparison of the histogram population versus the fraction of native contacts for explicit and continuum solvent models. In the explicit solvent model, the most heavily populated states have ≈70–80% of native contacts, while in the implicit solvent model, the most heavily populated states have only ≈30–40% of the native contacts.
Similarly, one can calculate the hydrogen-bond populations and compare them to NMR results. For example, NMR data show ≈42% of the β-sheet hydrogen-bond population at 310 K (3, 4), whereas our previous explicit solvent simulation found ≈45% average probability for the β-sheet hydrogen bonds, in good agreement with the experiment (18). However, in the implicit solvent model only ≈10% of the hydrogen-bond population is found, a much smaller population than found in experiment. It should be pointed out, nevertheless, that although the explicit solvent model simulation predicts populations in reasonable agreement with experiment near the biological temperatures, it overestimates populations at higher temperatures (18). The temperature dependence of the population in the implicit solvent is also not correct; it underestimates the populations at lower temperatures and overestimates them at higher temperatures.
Another interesting question regarding the folding process and folding intermediates is: to what extent do α-helical structures form during the folding process? Earlier experiments and theoretical works both show no evidence for significant helical contents during the folding process (3–5, 11, 13). However, very recently, in simulations reported by Garcia and Sanbonmatsu (14) using the AMBER (parm94) force field and explicit solvent model significant helical content between 15 and 20% was found at the experimental temperatures. Pande and coworkers also found significant helical intermediates at 300 K from their kinetics simulation using an old version of the OPLS united atom force field and the continuum solvent GB model (no percentage is reported, but from the figures in this paper it seems significant; ref. 12). These authors speculated that significant helical content was not found in earlier simulations because of insufficient sampling (12, 14), but our recent extensive sampling with the explicit solvent model and OPLSAA force field did not find any significant α-helical contents at all (18). It is interesting to see whether this remains the case for the implicit solvent simulation with the OPLSAA force field.
The number of residues in the β-sheet and the α-helix are calculated with the STRIDE program (33). In the implicit solvent simulations we find that the number of helical residues, including both the α-helix and the 310-helix, is less than or equal to 3, and only 1–2% of the conformations exhibit helical content at all temperatures, which is consistent with the results from our previous explicit solvent simulation (18). Furthermore, almost all the helices we find are 310-helices near the original β-turn (residue 47–49). Very few conformations are found to have helical residues in places other than the original β-turn. These findings also agree very well with the results from the explicit solvent model simulations even though the free energy contour maps are quite different. This suggests that the helical content is determined mainly by the protein force field and not by the solvation model in this case. This might make sense, because helix formation is driven mainly by local hydrogen bonds (local in residue sequence) and determined largely by torsional potentials; while β-sheets involve global interactions (global in residue sequence), and both hydrophobic interactions and hydrogen bonds contribute. Thus, β-sheet formation might be influenced more by solvation models, while the formation of helices is probably determined by protein force fields (largely by the torsions). As mentioned above, the minimal helix content predicted by the OPLSAA force field in both the explicit and implicit solvent models is in marked contrast with the simulations based on use of the AMBER94 force field (14) and an old OPLS united-atom force field (12). The OPLSAA results seem to agree with experiments better in this regard.
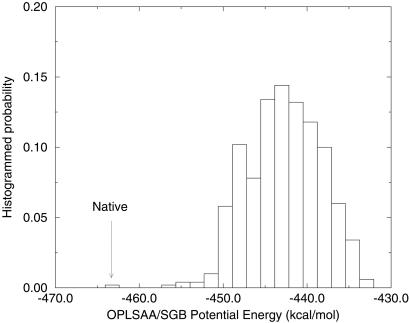
Many groups have been using the implicit solvent model and particularly the OPLSAA/SGB energy (protein potential energy plus the solvation free energy) as a scoring function for protein-structure prediction (34–36). It thus would be of great interest to see whether the global OPLSAA/SGB energy minimum gives the native structure even though the global free energy minimum does not. We have minimized the structures clustered in state H (lowest free energy state) and compared their OPLSAA/SGB energies with the native structure. Fig. 5 plots the energy histogram for these structures. The native structure is found to have the lowest OPLSAA/SGB energy, ≈7.7 kcal/mol lower than the lowest H-state structure. Most of the H-state structures have energies ≈20 kcal/mol higher than the native structure. The large number of conformations found for the H state gives rise to its having a larger entropy and lower free energy than the native state. We have checked other nonnative states, and they show higher OPLSAA/SGB energies than the native structure too. The fact that the native structure is found to have the lowest OPLSAA/SGB energy validates its use in protein-structure prediction for this β-hairpin. It remains to be seen whether this behavior is manifested in other proteins. There is some indirect evidence that this is the case from recent work (34) on detecting native-like structures from a large number of decoys using the OPLSAA/SGB energy-scoring function and other recent work comparing a hydrophobic scoring function with OPLSAA/SGB energies for three decoy sets (36). There seems to be good correlation between the OPLSAA/SGB energy and the rms deviation from the native structure. Thus, despite the salt-bridge problem found above, implicit solvent models still may be useful in providing scoring functions for protein-structure determination. However, for such models to be useful in calculating thermodynamic properties, in sampling or MD, one must devise better implicit solvent models, because the current one overestimates the stability of salt bridges, especially for protein-folding studies where large conformational changes occur.
Figure 5.
The OPLSAA/SGB energy histogram for structures in state H from implicit solvent simulation. The native structure is found to have the lowest OPLSAA/SGB energy in this case (marked in the figure). The fact that the native structure is found to have the lowest energy validates its use in protein structure prediction as a scoring function, since the OPLSAA/SGB energy scoring function still picks the native structure as the best structure.
Conclusion
The free energy landscape of a β-hairpin folding in the implicit solvent SGB model is studied in this paper, and the results are compared with our earlier explicit solvent simulation. A highly parallel REM consisting of 18 replicas spanning from 270 to 690 K has been used for the extensive sampling, and the OPLSAA force field is used for the β-hairpin. The major conclusions are summarized in the following section.
Surprisingly, the free energy landscape found for the implicit solvent model is quite different from that found for the explicit solvent model. Nonnative states are heavily overweighted in the implicit solvent model, and more importantly, the lowest free energy state for the implicit solvent model is not the native β-hairpin structure. We found this to be the case not only for the SGB model but also for the GBSA model implemented in AMBER. A detailed analysis of the most heavily populated state reveals that the electrostatic interaction between charged residues results in an erroneous salt-bridge effect. The strong salt bridge amplifies the imbalance between the polar electrostatic interaction and the nonpolar hydrophobic interaction, which in turn results in a most heavily populated structure with one hydrophobic residue, F52, expelled from the hydrophobic core and the C-terminal end (negatively charged residue E56) swinging toward the charged residue, K50. Furthermore, the β-hairpin population at 282 K is estimated to be less than 40%, as compared with 72% from the explicit solvent model and ≈80% from experiment. We have suggested several possible fixes for this problem. On another front, both the implicit and explicit solvent simulations using the OPLSAA force exhibit no meaningful helical content during the folding process, in agreement with experiment and contrast to recent simulations by others using either the AMBER (with explicit solvent) or OPLS united-atom (with continuum solvent) force fields. The presence or absence of helical content seems to be determined mainly by the protein force fields and not by solvation models in this case.
The global free energy minimum structure found from the implicit model is markedly different from that found from the explicit solvent model. The former has a strong salt bridge with one hydrophobic residue ejected from the hydrophobic core, whereas the latter has the native β-hairpin structure. In addition, thermodynamic averages will be quite different for these two models. Despite this we find evidence that the global potential energy minimum for the OPLSAA/SGB model gives the native structure. Should this be true for other proteins, implicit solvent models still may be quite useful for protein-structure determination as partially shown in some recent works on decoys. However, much work remains to be done to establish a better implicit solvent model that can handle slat bridges correctly. This seems particularly important for protein-folding studies, because large conformational changes are involved.
Acknowledgments
We thank Matthew Jacobson and Richard Friesner for sharing the slat-bridge correction data with us. We also thank Jed Pitera, William Swope, and Robert Germain for useful discussions and comments. This work was supported in part by National Institutes of Health Grant GM4330 (to B.J.B.).
Abbreviations
- GB
generalized Born
- REM
replica-exchange method
- SGB
surface-generalized Born
- MC
Monte Carlo
- HMC
hybrid MC
- MD
molecular dynamics
- RC
reaction coordinate
Footnotes
We generate MD moves using a Hamiltonian H0, and we accept or reject these moves using the Metropolis criterion based on the true Hamiltonian, H. Thus in our treatment H − H0 would give rise to all the forces arising from surface-area gradients and other terms often left out in continuum models. This procedure can be shown to sample the correct distribution function Z−1 exp(−βH) if the MD steps are reversible, as they are here.
References
- 1.McCammon J A, Wolynes P G. Current Opinion in Structural Biology. London: Current Biology Press; 2002. [Google Scholar]
- 2.Wales D J, Scheraga H A. Science. 1999;285:1368–1372. doi: 10.1126/science.285.5432.1368. [DOI] [PubMed] [Google Scholar]
- 3.Blanco F J, Rivas G, Serrano L. Nat Struct Biol. 1994;1:584–590. doi: 10.1038/nsb0994-584. [DOI] [PubMed] [Google Scholar]
- 4.Blanco F J, Serrano L. Eur J Biochem. 1995;230:634–649. doi: 10.1111/j.1432-1033.1995.tb20605.x. [DOI] [PubMed] [Google Scholar]
- 5.Munoz V, Thompson P A, Hofrichter J, Eaton W A. Nature (London) 1997;390:196–199. doi: 10.1038/36626. [DOI] [PubMed] [Google Scholar]
- 6.Munoz V, Henry E R, Hofrichter J, Eaton W A. Proc Natl Acad Sci USA. 1998;95:5872–5879. doi: 10.1073/pnas.95.11.5872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Honig B, Nicholls A. Science. 1995;268:1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 8.Still W C, Tempczyk A, Hawley R C, Hendrickson T. J Am Chem Soc. 1990;112:6127–6129. [Google Scholar]
- 9.Ghosh A, Rapp C S, Friesner R A. J Phys Chem. 1998;102:10983–10990. [Google Scholar]
- 10.Lazaridis T, Karplus M. Proteins. 1999;35:133–152. doi: 10.1002/(sici)1097-0134(19990501)35:2<133::aid-prot1>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 11.Pande V S, Rokhsar D S. Proc Natl Acad Sci USA. 1999;96:9062–9067. doi: 10.1073/pnas.96.16.9062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zagrovic B, Sorin E J, Pande V S. J Mol Biol. 2001;313:151–169. doi: 10.1006/jmbi.2001.5033. [DOI] [PubMed] [Google Scholar]
- 13.Dinner A R, Lazaridis T, Karplus M. Proc Natl Acad Sci USA. 1999;96:9068–9073. doi: 10.1073/pnas.96.16.9068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Garcia A E, Sanbonmatsu K Y. Proteins. 2001;42:345–354. doi: 10.1002/1097-0134(20010215)42:3<345::aid-prot50>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- 15.Roccatano D, Amadei A, Nola A D, Berendsen H J. Protein Sci. 1999;10:2130–2143. doi: 10.1110/ps.8.10.2130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kolinski A, Ilkowski B, Skolnick J. Biophys J. 1999;77:2942–2952. doi: 10.1016/S0006-3495(99)77127-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Klimov D K, Thirumalai D. Proc Natl Acad Sci USA. 2000;97:2544–2549. doi: 10.1073/pnas.97.6.2544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhou R, Berne B J, Germain R. Proc Natl Acad Sci USA. 2001;98:14931–14936. doi: 10.1073/pnas.201543998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhou R, Harder E, Xu H, Berne B J. J Chem Phys. 2001;115:2348–2358. [Google Scholar]
- 20.Hukushima K, Nemoto K. J Phys Soc Jpn. 1996;65:1604–1608. [Google Scholar]
- 21.Hunenberger P H, McCammon J A. J Chem Phys. 1999;110:1856–1872. [Google Scholar]
- 22.Weber W, Hunenberger P H, McCammon J A. J Phys Chem. 2000;B104:3668–3675. [Google Scholar]
- 23.Zhou R, Berne B J. J Chem Phys. 1997;107:9185–9196. [Google Scholar]
- 24.Duane S, Kennedy A D, Pendleton B J, Roweth D. Phys Lett B. 1987;195:216–222. [Google Scholar]
- 25.Sugita Y, Okamoto Y. Chem Phys Lett. 1999;314:141–151. [Google Scholar]
- 26.Gallicchio E, Zhang L Y, Levy R M. J Comput Chem. 2002;23:517–529. doi: 10.1002/jcc.10045. [DOI] [PubMed] [Google Scholar]
- 27.Schutz C N, Warshel A. Proteins. 2001;44:400–417. doi: 10.1002/prot.1106. [DOI] [PubMed] [Google Scholar]
- 28.Garcia-Moreno E, Dwyer J, Gittis A, Lattman E, Spenser D, Stites W. Biophys Chem. 1997;64:211–224. doi: 10.1016/s0301-4622(96)02238-7. [DOI] [PubMed] [Google Scholar]
- 29.Garcia A E. Phys Rev Lett. 1992;68:2696–2699. doi: 10.1103/PhysRevLett.68.2696. [DOI] [PubMed] [Google Scholar]
- 30.Bashford D, Case D. Annu Rev Phys Chem. 2000;51:129–152. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- 31.Chen S W, Honig B. J Phys Chem B. 1997;101:9113–9118. [Google Scholar]
- 32.Burykin A, Schutz C N, Villa J, Warshel A. Proteins. 2002;47:265–280. doi: 10.1002/prot.10106. [DOI] [PubMed] [Google Scholar]
- 33.Frishman D, Argos P. Proteins. 1995;23:566–579. doi: 10.1002/prot.340230412. [DOI] [PubMed] [Google Scholar]
- 34.Wallqvist A, Gallicchio E, Felts A K, Levy R. Adv Chem Phys. 2002;120:459–486. [Google Scholar]
- 35.Sendrovic-Rapp C, Friesner R A. Proteins. 1999;103:1913–1928. [Google Scholar]
- 36.Zhou R, Silverman B D. In: Proceedings of the Pacific Symposium on Biocomputing. Altman R B, Dunker A K, Hunter L, Lauderdale K, Klein T E, editors. Singapore: World Scientific; 2002. pp. 673–684. [Google Scholar]