Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2005 Jan 14;88(4):2737–2744. doi: 10.1529/biophysj.104.052811

Single-Molecule Measurements of the Persistence Length of Double-Stranded RNA

J A Abels 1, F Moreno-Herrero 1, T van der Heijden 1, C Dekker 1, N H Dekker 1
PMCID: PMC1305369  PMID: 15653727

Abstract

Over the past few years, it has become increasingly apparent that double-stranded RNA (dsRNA) plays a far greater role in the life cycle of a cell than previously expected. Numerous proteins, including helicases, polymerases, and nucleases interact specifically with the double helix of dsRNA. To understand the detailed nature of these dsRNA-protein interactions, the (bio)chemical, electrostatic, and mechanical properties of dsRNA need to be fully characterized. We present measurements of the persistence length of dsRNA using two different single-molecule techniques: magnetic tweezers and atomic force microscopy. We deduce a mean persistence length for long dsRNA molecules of 63.8 ± 0.7 nm from force-extension measurements with the magnetic tweezers. We present atomic force microscopy images of dsRNA and demonstrate a new method for analyzing these, which yields an independent, yet consistent value of 62 ± 2 nm for the persistence length. The introduction of these single-molecule techniques for dsRNA analysis opens the way for real-time, quantitative analysis of dsRNA-protein interactions.

INTRODUCTION

Besides the recent discovery of dsRNA's role as a central player in the mechanism of RNA interference (Fire et al., 1998; Timmons and Fire, 1998), it has long been known that dsRNA forms the genome of certain viruses and occurs in the numerous hairpins formed by local base-pairing of ssRNAs. Hence it is clear that dsRNA is an important ingredient in the cell. It is useful to study it in vitro to unravel, for example, its inherent shape and its interaction with important proteins like helicases, polymerases, and nucleases (de la Cruz et al., 1999; Makeyev and Grimes, 2000; Bernstein et al., 2001). Single-molecule techniques, which form an important new class of experiments, yield quantitative information about mechanical properties. We have examined dsRNA using two single-molecule techniques, magnetic tweezers and atomic force microscopy (AFM), to measure its persistence length, which is the basic mechanical property that quantifies its stiffness. The persistence length determines the size of dsRNA in solution and the ease with which it can be bent by dsRNA-binding proteins. Knowledge of its exact value is a prerequisite for quantitative studies of dsRNA-protein interactions.

The most precise bulk biochemical technique used to measure mechanical properties of biomolecules is the cyclization of plasmids (Shore et al., 1981). Estimates of both the stretching and torsional persistence lengths of dsDNA were measured this way. More recently, the stretching persistence length of dsDNA has been measured more accurately using single-molecule techniques (Bustamante et al., 1994, 2003; Wang et al., 1997; Bouchiat et al., 1999).

Possibly due to the difficulty of ligating dsRNA, cyclization techniques have not been widely applied to dsRNA. Instead, measurements of the persistence length of dsRNA have so far relied on electron microscopy, gel electrophoresis, sedimentation velocities, and electrical birefringence (for a review, see Hagerman, 1997). However, these measurements yielded a wide range of values for the rigidity of dsRNA (values from one to three times the rigidity of dsDNA were reported; Hagerman, 1997). The significant spread of values reported makes it difficult to pinpoint an exact value of the persistence length of dsRNA. The increased rigidity of dsRNA compared to dsDNA can be attributed to its A-helical structure, which results from the interference of the 2′ hydroxyl with the arrangement of the sugars in the phosphate backbone (Brown et al., 2000; Charney et al., 1991).

Compared to previous methods, the single-molecule techniques described here present several advantages in quantifying the mechanical properties of dsRNA. In contrast to electron microscopy, both magnetic tweezers and AFM permit measurement of the mechanical properties of molecules in aqueous solutions. Furthermore, they give quantitative information about individual molecules, yielding statistical information which is inaccessible in bulk measurements. Other aspects of our two techniques complement each other. An advantage of the magnetic tweezers is that a single molecule is tethered between a magnetic bead and a surface (Strick et al., 1996), and thus the molecule can freely fluctuate in buffer (Fig. 1 B). In addition, the possibility of tethering a dsRNA molecule between a bead and a surface opens the way to the real-time (typically 10–100 Hz) study of dsRNA-protein interactions (Strick et al., 2001; Bustamante et al., 2003). The strength of the AFM lies in its visualization capability and in its ability to rapidly scan multiple molecules. Using the AFM, it is possible to view both the dsRNA molecule of interest, as well as proteins bound to it (Henn et al., 2001). Since AFM is a surface technique, however, the fashion in which dsRNA molecules adhere to the surface must be addressed.

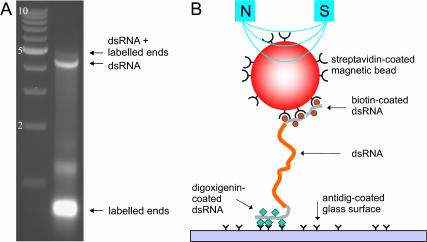
FIGURE 1.

FIGURE 1

Open in a new tab

(A) Gel electrophoresis analysis (nondenaturing agarose, 0.75%) of a dsRNA construct before placement in the magnetic tweezers. The left lane shows a reference ladder of dsDNA fragments at 1-kb intervals, with the qualification that on gel dsRNA is known to migrate slightly slower than dsDNA. The right lane shows four bands. The two most rapidly moving bands correspond to the labeled fragments (with the vast majority corresponding to 0.4-kb labeled fragments and a small minority corresponding to blunt-ended ligated dimers thereof). The slowly moving bands (near 4 kb on the reference ladder) correspond to the 4.2 kb dsRNA molecule without the labeled fragments and the 4.2 kb dsRNA molecule ligated to 0.4 kb biotin- and digoxigenin-labeled ends, respectively. (B) Cartoon of a dsRNA molecule as placed in the magnetic tweezers (not to scale). The dsRNA molecule is tethered to a magnetic bead by a biotin-streptavidin linkage and to the bottom glass surface of a flow cell using an antidigoxigenin-digoxigenin linkage. Magnets are placed above the flow cell to exert a force on the magnetic bead, and hence on the dsRNA molecule. In the experiments, the main part of the dsRNA molecule consists of 4.2 kb or 8.3 kb (∼1 μm or ∼ 2 μm), whereas the labeled ends each have a length of 0.4 kb or ∼ 0.1 μm.

In this article, we demonstrate the incorporation of dsRNA molecules into magnetic tweezers, and the use of magnetic tweezers force spectroscopy as well as visualization by AFM to measure the persistence length of dsRNA. These two independent methods yield a consistent value for the persistence length of dsRNA of 63 ± 2 nm in moderate salt buffer.

MATERIALS AND METHODS

dsRNA constructs

For use in the magnetic tweezers, 0.4 kb, 4.2 kb, and 8.3 kb dsRNA molecules were synthesized using in vitro transcription of specifically designed polymerase chain reaction (PCR) products by T7 RNA polymerase (T7 RNAP). The 0.4 kb PCR product encompassed the sequence [23137,23630] from bacteriophage λ DNA, the 4.2 kb PCR product encompassed the sequence [230,4373] from pBADb10 (a recombinated pBAD vector, gift of V. Rybenkov, University of Oklahoma, Norman, OK), and the 8.3 kb PCR product encompassed the sequence [30286,38650] from bacteriophage λ DNA. The PCR products each contained a single promoter site for T7 RNAP and hence coded for the transcription of a single ssRNA molecule. The transcription reactions included two PCR products designed so that the two ssRNA molecules generated were complementary except for a few nucleotides at their 5′ ends (Dekker et al., 2004). This created sticky ends on the dsRNA molecules which permitted efficient ligation. The transcription reaction was run using a commercial kit (HiScribe kit, New England Biolabs, Beverly, MA) according to the manufacturer's instructions, except that the reactions producing 0.4 kb dsRNA also included labeled nucleotides. The incorporation of labeled nucleotides (biotin-16-UTP and digoxigenin-11-UTP) into 0.4 kb dsRNA was executed by addition of 1–4 molar units of modified UTP to the transcription reactions. The transcription reactions were incubated for 3 h at 37° C. To improve the efficiency of strand annealing, the reactions were heated to 65° C for at least 1 h and cooled down to room temperature by decreasing the temperature by 1.25° C every 5 min in a Mastercycler with heated lid (Eppendorf, Hamburg, Germany). The dsRNA transcription reactions were further treated with five units of RNase-free DNase I (Roche Diagnostics, Almere, The Netherlands) for 1 h at 37° C to remove the PCR products and purified using a RNeasy MinElute Cleanup Kit (Qiagen Benelux, Venlo, The Netherlands). The 4.2 kb and 8.3 kb dsRNA molecules were subsequently ligated to the labeled 0.4 kb dsRNA molecules using high concentration T4 DNA ligase (Fig. 1 A).

For use in the AFM, dsRNA molecules were synthesized using the same HiScribe kit (New England Biolabs). Using 28iMaI plasmid as a substrate and a T7 minimal primer (both included in the HiScribe kit), a PCR was run to create a 935-bp product with promoter sites for T7 RNA polymerase flanking both ends. A transcription reaction was run as described above. This generated a 901-bp dsRNA transcription product. The reaction was subsequently digested with both 5 units of DNase I and 5 units of an RNase mixture (Ambion, Austin, TX) for 1 h at 37° C and purified using a RNeasy MinElute Cleanup Kit (Qiagen). The DNase I digestion removed the dsDNA PCR product whereas the RNase digestion removed the single-stranded overhangs containing the complement of the T7 promoter site from the ends of the dsRNA product. The dsRNA molecules imaged in the AFM were chosen to be shorter than those utilized in the magnetic tweezers so that a 1 μm × 1 μm scan included several complete dsRNA molecules.

dsRNA molecules were synthesized and tested in the magnetic tweezers and in the AFM immediately after being made. In practice, we found that molecules could be maintained in the magnetic tweezers for several days, and we measured the same value of the persistence length from day to day.

Flow cells

Flow cells were fabricated by assembling two glass coverslips separated by a thin layer of parafilm. One glass coverslip was coated with 1% polystyrene and another had two small holes (∅ = 2 mm) drilled into it for fluid exchange. The flow cell was subsequently heated to 150°C to melt the parafilm and form a tight seal. To allow for the attachment of dsRNA molecules, the flow cell was incubated with 0.1 mg/ml antidig oxigenin. To passivate the flow cell, it was subsequently incubated with 10 mg/ml BSA.

Magnetic tweezers

Individual dsRNA molecules were attached at one end to a glass coverslip and at the other end to a magnetic bead (MyOne, Dynal Biotech, Hamburg, Germany) using protocols previously described for the attachment of single DNA molecules (Strick et al., 2001). The buffer utilized was 10 mM potassium phosphate buffer (PB, pH 7.5) supplemented with 0.1% Tween, 10 mM NaN3, and 0.2 mg/ml BSA. The molecules were maintained under tension by the field gradient of two small permanent magnets placed above the sample (Fig. 1 B). The NdFeB magnets (6 × 6 × 5 mm3) were separated by 1.4 mm. The tweezers were calibrated in the x-direction by imaging a grid with etched lines of 10-μm spacing (Meiji Techno, Somerset, UK) and in the z-direction by using a calibrated piezo (P-721, Physik Instrumente, Karlsruhe, Germany). Subsequently, images of the bead grabbed by a charge-coupled device camera (model CV-M30, JAI, Copenhagen, Denmark) were used to determine its distance 〈z〉 from the surface and the magnitude of its transverse fluctuations 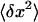Inline graphic. 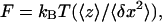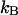From these measurements, we calculate the force exerted on the dsRNA molecule Inline graphic where Inline graphic is Boltzmann's constant and T the temperature in Kelvin. Translation of the magnets in the z-direction controls the magnitude of this force (F <10 pN for MyOne beads of 1-μm diameter). All experiments were conducted at room temperature.

Atomic force microscopy

Freshly cleaved mica discs were treated with a 0.01% polylysine solution (Sigma-Aldrich Chemie, Zwijndrecht, The Netherlands) for 30 s, rinsed with MilliQ-filtered water, and dried in a stream of nitrogen gas. Then, 5 μl of a solution of either dsDNA or dsRNA molecules in either TE (10 mM Tris-HCl, 1 mM EDTA, pH 8.0) or PB was deposited onto the treated mica discs, washed and dried as described above. Concentrations of dsDNA and dsRNA molecules were adjusted by AFM inspection. Samples were imaged in air at room temperature with a commercial AFM microscope (Nanotec Electronica, Madrid, Spain) using noncontact dynamic mode (Moreno-Herrero et al., 2000). Cantilevers with a resonance frequency of 75 kHz and a spring constant of 0.75 N/m were employed (Olympus Europa, Hamburg, Germany). AFM images were processed by subtracting a general plane using WSxM software (www.nanotec.es).

After the AFM imaging, the trajectories of dsDNA and dsRNA molecules were traced semi-automatically using a published routine (Rivetti and Codeluppi, 2001). Our data analyses were implemented in Interactive Data Language (IDL Research Systems, Boulder, CO) and Lab View (National Instruments, Austin, TX).

RESULTS

We conducted measurements in the magnetic tweezers on 4.2 kb and 8.3 kb dsRNA molecules, ligated at their extremities to two 0.4 kb dsRNA fragments multiply-labeled with digoxigenin and biotin, respectively (Fig. 1 A and Materials and Methods). The 4.2 kb molecules were used primarily for controls (Fig. 2 A), whereas the 8.3 kb molecules were used in the measurements of the persistence lengths (Fig. 2, B and C). The molecules were tethered to magnetic beads and suspended in the magnetic tweezers (Fig. 1 B and Materials and Methods). Having attached the dsRNA molecules, we performed several controls to verify that the molecule tethered between the magnetic bead and the surface was indeed dsRNA. While tracking the z-position of the magnetic bead, we added RNase III to the sample (Fig. 2 A, bottom trace). Enzymatic activity of the RNase III would digest the dsRNA and result in movement of the magnetic bead to the top of the flow cell under the influence of the magnets (Fig. 1 B) and a commensurate loss of the tracking of the magnetic bead. Indeed, the tracking of the bead was rapidly lost upon addition of this enzyme to our sample. This indicates that the molecule had been digested and confirmed that the tethered molecule was dsRNA. A control experiment was run in which RNase III was added to a flow cell containing tethered dsDNA molecules (Fig. 2 A, top trace). In this case, the tracking of the molecules' extension was not perturbed, indicating that RNase III was not active on these molecules, as expected.

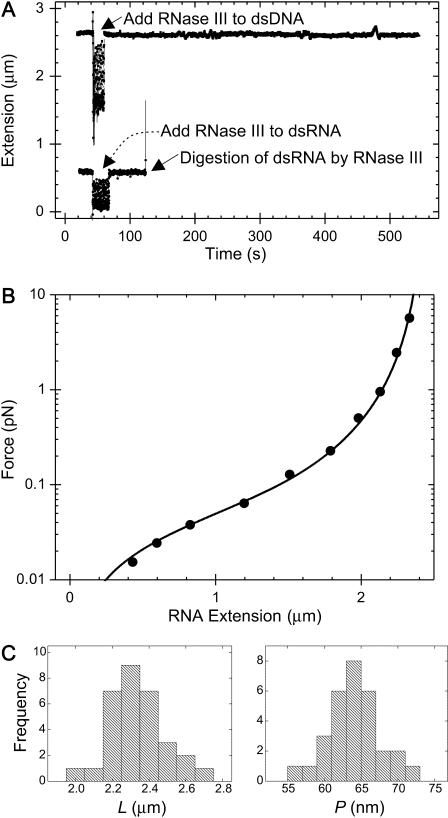
FIGURE 2.

FIGURE 2

Open in a new tab

(A, top) Extension of a dsDNA molecule is tracked in real time using magnetic tweezers. At the point indicated by the arrow, RNase III is added to the sample. Degradation of the molecule by RNase III would result in an upward movement of the magnetic bead and hence a disruption of the tracking of the extension of the molecule. Since this is not observed, we can conclude that the molecule does not contain any dsRNA, as expected. (Bottom) Extension of a dsRNA molecule is tracked in real time using magnetic tweezers. As before, RNase III is added to the flow cell. In this case, at time t∼ 130 s, the tracking of molecule's extension abruptly halts, indicating cleavage of a dsRNA molecule. (B) Example of a force-extension curve for 8.3 kb dsRNA (circles correspond to data points and the smooth curve corresponds to a fit to the wormlike chain model; Bouchiat et al., 1999). The fit yields a value of 63.0 ± 2.5 nm for the persistence length of this dsRNA molecule. (C) Histograms of the contour lengths (left) and the persistence lengths (right) measured for 31 8.3 kb dsRNA molecules. The mean contour length 〈L〉 measured was 2.33 ± 0.03 μm (N = 31) and the mean persistence length 〈P〉 measured was 63.8 ± 0.7 nm (N = 31).

We subsequently measured the end-to-end distance 〈z〉 of the tethered dsRNA as a function of the applied force F, yielding a force-extension curve (Fig. 2 B). The force was typically varied over the range [0.01 pN, 6 pN]. This force-extension curve of a dsRNA molecule can be modeled using the wormlike chain model (WLC):

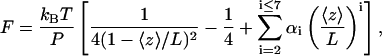graphic file with name M4.gif (1)

where kB is Boltzmann's constant and T the temperature in Kelvin, P is the persistence length, L is the contour length, and the constants αi have values α2 = −0.5164228, α3 = −2.737418, α4 = 16.07497, α5 = −38.87607, α6 = 39.49944, and α7 = −14.17718 (Bustamante et al., 1994; Bouchiat et al., 1999). For the dsRNA molecule depicted in Fig. 2 B, fitting to the WLC model yielded parameters L = 2.46 ± 0.01 μm and P = 63.0 ± 2.5 nm. Repeating this experiment for a number of dsRNA molecules resulted in a mean value of 〈L〉 = 2.33 ± 0.03 μm (N = 31) and a mean value of 〈P〉 = 63.8 ± 0.7 nm (N = 31), where we have quoted the standard error of the mean and the number of molecules measured. Histograms of the contour lengths and of the persistence lengths measured for our 8.3 kb dsRNA molecules are shown in Fig. 2 C. Since the dsRNA molecules were 8340 bp in length, we deduce a mean rise per basepair of 0.279 ± 0.004 nm, which is in excellent agreement with the value of 0.28 nm ± 0.01 nm reported in literature for dsRNA in the presence of monovalent ions (Gast and Hagerman, 1991; Kebbekus et al., 1995). The measured mean persistence length of 〈P〉 = 63.8 ± 0.7 nm can be contrasted with the persistence length of dsDNA in similar buffer conditions which we find to be 54 ± 2 nm.

Next, we consider AFM imaging of dsRNA molecules. The adsorption of biomolecules onto mica surfaces for AFM imaging is typically promoted using either Mg2+ ions (Thomson et al., 1996; Bonin et al., 2000) or polylysine. If Mg2+ ions are used to promote adsorption, it is experimentally found that molecules can re-equilibrate on the two-dimensional (2D) surface. For long polymers equilibrated on the surface in this manner, one can derive an equation relating P to the mean-square end-to-end distance 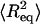Inline graphic:

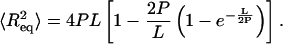graphic file with name M6.gif (2)

For dsDNA, we have measured a value for the persistence length of 52 nm using this method, very similar to the value measured by Rivetti et al. (1996). Obviously, we also tried to adsorb dsRNA molecules on mica using a range of MgCl2 concentrations (4 to 60 mM). Unfortunately, an extremely low adsorption yield was obtained. In addition, the few dsRNA molecules that were adsorbed this way exhibited clustering and irregular lengths. For this reason, we decided to instead use polylysine to adsorb dsRNA molecules onto mica (see Materials and Methods). Since this requires the development of a new method to accurately measure P, described below, we also studied dsDNA molecules as a control.

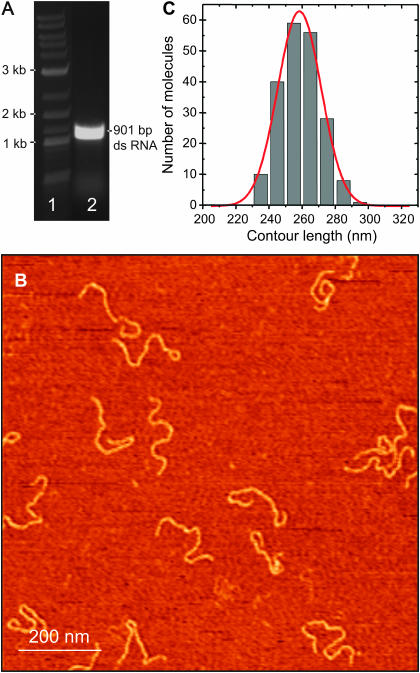
First, we imaged 935-bp dsDNA PCR products adsorbed on mica using polylysine. The length of the dsDNA molecules adsorbed was measured and yielded a mean contour length of 318 ± 16 nm (N = 122 molecules, data not shown). This leads to a rise per base of 0.34 ± 0.02 nm, in agreement with the B-form structure of dsDNA (Watson and Crick, 1953). From the 935-bp dsDNA PCR products, we synthesized 901-bp dsRNA fragments using transcription by T7 RNA polymerase. Fig. 3 A shows the result of the transcription reaction after treatment with DNase I and an RNase mixture that degrades ssRNA (lane 2). A single band at the expected position is clearly visible showing that digestion with the RNase-mixture leaves the molecules intact. Since the RNases in the mixture have a much higher affinity for ssRNA than for dsRNA, this indicated that the molecules measured were purely dsRNA. A large-field image of the 935-bp dsRNA molecules adsorbed on a mica substrate using polylysine is shown in Fig. 3 B. The mean contour length of these molecules (N = 112) was 258 ± 26 nm (Fig. 3 C), corresponding to a rise per base of 0.29 ± 0.03 nm, in agreement with the A-form structure for dsRNA (Arnott et al., 1973).

FIGURE 3.

FIGURE 3

Open in a new tab

(A) Gel electrophoresis (nondenaturing agarose, 0.75%) of 901 bp dsRNA molecules used in the AFM experiments. A reference dsDNA ladder is shown for comparison in lane 1. After the transcription reaction, we digested the products by both DNase I and an RNase mixture (lane 2). Digestion of the product by the RNase mixture ensures that single-stranded overhangs of the transcription product are removed. Hence, the single remaining band is dsRNA. (B) A 1 μm × 1 μm AFM image (256 × 256 pixels) of 901 bp dsRNA molecules deposited on mica using polylysine. (C) Distribution of lengths measured in the AFM for 901 bp dsRNA molecules. We measured a mean contour length of 258 ± 26 nm, corresponding to a rise per basepair of 0.29 ± 0.03 nm.

Molecules adsorbed on a polylysine-modified surface are found to be kinetically trapped rather than re-equilibrated on the surface, and the mean square end-to-end distance is measured to be much lower than that for molecules adsorbed using Mg2+. Rivetti et al. proposed an equation relating the end-to-end distance of kinetically adsorbed molecules 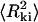Inline graphic to the persistence length P and the contour length L (Rivetti et al., 1996):

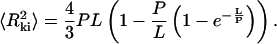graphic file with name M8.gif (3)

However, this equation follows from a direct mathematical projection of the 3D configuration of a polymer onto a 2D surface, which necessarily results in a consequent loss of contour length of the molecule. As demonstrated above, such a decrease in contour length is not experimentally observed. Therefore, it is not surprising that Eq. 3 does not yield correct values of P for kinetically trapped molecules. Indeed, the values of P found for dsDNA (Bussiek et al., 2003, measured 36 nm, van Noort et al., 2004, measured 46 nm, and we measured 36 ± 4 nm) are all significant underestimates.

The kinetics of trapping, which likely initiates through the pinning of a few arbitrary points of the molecule to the surface and proceeds by the adsorption of the intermediate parts of the molecule, suggest that the use of a global property such as the end-to-end distance to deduce P may not be optimal. An improved strategy would rather utilize a local property of the molecules. We have therefore developed a simple method to determine P using the local curvature of kinetically trapped molecules.

We start by considering the angle χ between two consecutive segments of size l of a molecule in 3D (Fig. 4 A), and make the assumption that during kinetic trapping this 3D angle χ between segments of length l is preserved onto the 2D plane. Physically, this corresponds to a local adsorption of the molecule onto the surface in a sequential manner, with transfer of the information stored in the 3D angular distribution. A relationship between the angle χ and P can be derived as follows (Landau and Lifshitz, 1958). The 3D angle χ is related to the radial angle φ and the azimuthal angle θ according to 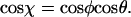Inline graphic One can determine the mean cosine of the angular distribution using 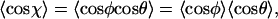Inline graphic since φ and θ are independent. Thermally driven fluctuations of angles between segments in 2D such as φ and θ can be directly related to P using probability distribution functions of the form 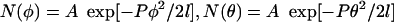Inline graphic where A is a normalization constant. 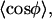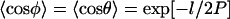Use of the probability distribution functions to determine Inline graphic Inline graphic gives Inline graphic (Landau and Lifshitz, 1958; Frontali et al., 1979; Rivetti et al., 1996). This leads to a very simple relationship between the mean cosine of the angle χ between two segments of length l and the persistence length P, 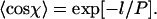Inline graphic This can be rearranged to give:

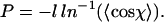graphic file with name M16.gif (4)

FIGURE 4.

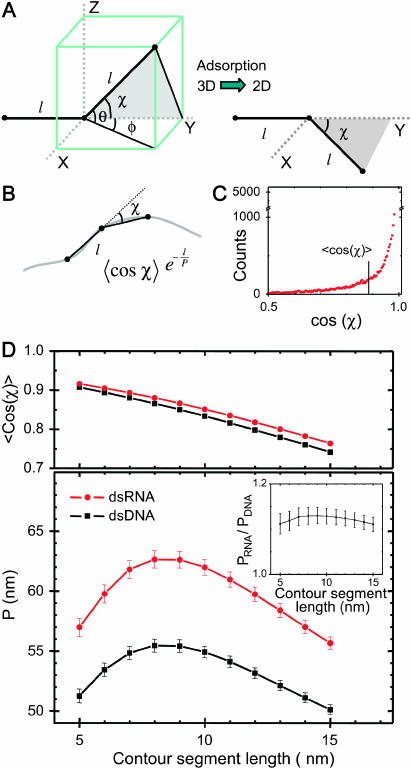
FIGURE 4

Open in a new tab

Local curvature analysis of 935-bp dsDNA molecules and 901-bp dsRNA molecules adhered to a mica substrate by polylysine. (A) Each molecule is viewed as being composed of segments of length l. The angle in 3D between such segments is defined as χ. We postulate that this relative angle between segments is maintained upon adsorption of the molecule onto the surface, which yields a simple equation for the measurement of P for kinetically trapped molecules (Eq. 4). (B) Depiction of a molecule in 2D, with the angle χ between segments of length l indicated. We have measured the distribution of angles χ as a function of the contour segment length l. (C) Distribution of 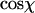Inline graphic for l = 8 nm for dsRNA molecules. Similar distributions were obtained for dsDNA. The average value of this distribution (marked with a black line) is used to determine the persistence length according to Eq. 4. (D) Top: value of 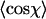Inline graphic for dsDNA (black squares) and for dsRNA (red circles) as a function of contour segment length l. Bottom: From 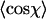Inline graphic, a value of the persistence length can be determined as a function of l using Eq. 4. The persistence lengths of dsDNA (black squares) and dsRNA (red circles) are plotted as a function of l. A clear maximum can be discerned for both dsDNA and dsRNA, which we attribute to the correct values of the persistence lengths of these molecules. Inset: the ratio of the persistence length of dsRNA to the persistence length of dsDNA is nearly constant as a function of l, indicating the robustness of the technique.

Equation 4 has previously been applied in 3D by Bednar et al. (1995) to deduce the persistence length of dsDNA using cryo-electron microscopy. Under the assumption that the angle χ is preserved between segments during kinetic trapping, however, this model therefore establishes a relationship between P and the local curvature of 2D kinetically trapped molecules.

We have experimentally measured the distribution of angles χ between segments as a function of the spacing l between two segments for 122 dsDNA molecules adsorbed on mica using polylysine. For this, we calculated the in-plane angles between segments by using three points spaced by l along the trajectory of the molecules (Fig. 4 B). After the measurement of the first angle along the contour, we slid the three points along the contour at 1-nm intervals, thus measuring the entire angular distribution. A sample angular distribution is shown in Fig. 4 C. After determining 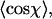Inline graphic this yields a plot of P as a function of the contour segment length l (Fig. 4 D, black squares). One observes a peak value of 55 ± 2 nm in the range l = 7–10 nm. We next measured the distribution of angles χ between segments as a function of the segment spacing l for 112 dsRNA molecules. This yields a range of points which are shifted to higher values of P compared to dsDNA molecules, with a peak value of P = 62 ± 2 nm in the range l = 7–10 nm (Fig. 4 D, red circles). We comment on the values of P for dsDNA and dsRNA below.

DISCUSSION

Using magnetic tweezers, we have measured force-extension curves for dsRNA molecules with random sequences. The force-extension data for dsRNA fitted very well to the WLC model. By analogy with the proven fitting of dsDNA to the WLC model, it is quite reasonable to fit the force-extension behavior of dsRNA similarly. Both molecules form double-stranded helices in which the helical nature prevents stiff segments within the chain from freely rotating with respect to each other. In this case the wormlike chain (and not the freely jointed chain) provides the correct model for the molecule's elasticity. In fitting the force-extension measurements we took particular care to accurately measure the lengths of the molecules, since their contour length was relatively short. (The yield of even longer dsRNA molecules synthesized by in vitro transcription only decreases.) The lengths of the molecules were measured to ∼0.1 μm accuracy. This means that the maximum relative error for the molecules which had a total length of ∼2 μm was ∼5%. Uncertainties in the contour length on this scale did not influence the value of the persistence length. Statistical fluctuations in the measurement of the Brownian motion of the magnetic bead yielded an uncertainty in the persistence length of ∼2–3 nm in each individual measurement. The final mean value we obtained for the measurement of the persistence length of multiple dsRNA molecules in 10 mM PB was 〈P〉 = 63.8 ± 0.7 nm (N = 31). A control of dsDNA measured in the same setup under identical conditions consistently yields values of 54 nm, in agreement with values reported in literature (Bustamante et al., 1994; Bouchiat et al., 1999).

In principle, measurements of the persistence length of dsRNA could be perturbed through degradation of the molecules by RNases. However, in our magnetic tweezers experiments, we did not find that excessive precautions were required to work with dsRNA. The solutions and buffers used were sterile, and addition of 5% hydrogen peroxide (to eliminate RNases) was not found to further increase the lifetime of dsRNA molecules in the flow cell. However, this is not surprising to the extent that most RNases are known to be much less effective on dsRNA compared to ssRNA (Ambion, Technical Reports). Typically, we found that single dsRNA molecules could remain in the magnetic tweezers under an applied tension of 5 pN for at least 24 h.

Next, we consider the AFM measurements. For the analysis of our AFM data, we were forced to develop a model of the adsorption of dsRNA using kinetic trapping, because dsRNA did not adsorb effectively on mica surfaces in the presence of MgCl2. We speculate that the structural differences between dsDNA and dsRNA helices (B-form for dsDNA and A-form for dsRNA; Arnott et al., 1973) may account for this behavior. Typically, the Mg2+ ions bridge the negative charges of the phosphate backbone and the negatively charged mica surface. In A-helices, both the shorter distance between the negatively charged phosphate groups and their orientation (facing each other) may inhibit this bridging. Our model thus needs to account for the adhesion of dsRNA molecules to a mica surface coated with a layer of polylysine. For this kinetic trapping, we developed a method of analysis. Since experimentally kinetic trapping contrasts with equilibrium trapping in which the molecules rearrange themselves to attain a 2D equilibrium, we reasoned that kinetic trapping must reflect information contained in the 3D conformation of the molecules. For this reason, we did not perform a mathematical projection of these segments onto the surface; instead, we suggest that kinetic trapping will maintain the 3D angle χ between two segments upon adsorption onto the surface (Fig. 4 A).

We first tested this procedure for dsDNA molecules and obtained values for the persistence length of dsDNA as a function of the segment length l (Fig. 4 D, black squares). The value of P(dsDNA) peaks between l = 7–10 nm and decreases at lower and higher l. Underestimations of P are expected at high and low l: as l decreases and approaches the pixel resolution utilized in the AFM (4 nm), discretization of angles results in an underestimation of P; at large l, we undercount the number of small angles since large contour segment lengths average over them, similarly leading to underestimation of P. We therefore derive a value of the persistence length of dsDNA of 55 ± 2 nm, which is in good agreement with the commonly accepted value of 54 ± 2 nm. This agreement demonstrates the applicability of the local curvature analysis for the measurement of P for kinetically trapped molecules, and indicates that our model for adsorption captures the essence of kinetic trapping. As an aside, we comment on an additional advantage of such a local method. Along the length of a molecule, typically more than 200 angles χ are calculated. Using local methods allows one to distinguish sequence-dependent features within molecules such as regions of unusual local flexibility (van Noort et al., 2003), provided they are not randomly distributed. In global methods, such small inhomogeneities may greatly perturb the measurement of the global parameter and lead one to deduce an incorrect persistence length.

Applying the same analysis to dsRNA, we deduce a very similar curve for its persistence length as a function of the contour segment length l (Fig. 4 D, red circles). In addition, over the range of l examined, the ratio of P(dsRNA) to P(dsDNA) is nearly constant (inset to Fig. 4 D), indicating the robustness of the technique. From the peak values of the persistence length, since lower values can be deemed unreliable for the same reasons as mentioned for dsDNA, we deduce P(dsRNA) = 62 ± 2 nm. It is gratifying to observe that this value from AFM is in good agreement with the independent value of 63.8 ± 0.7 nm obtained from magnetic tweezers.

Our high-resolution single-molecule techniques thus accurately measure the value of the persistence length of dsRNA to be 63 ± 2 nm in moderate salt buffer. In addition, we note that we were here able to measure the persistence length of an A-helix without the use of special A-tract sequences or the addition of ethanol. Further study of the mechanical properties of A-helices may therefore be facilitated by the methods we have developed to study dsRNA.

CONCLUSIONS

In conclusion, we have introduced two new approaches for the study of dsRNA persistence length: magnetic tweezers and atomic force microscopy. Using magnetic tweezers, we measure a mean persistence length for dsRNA of 63.8 ± 0.7 nm, and using AFM measurements, we obtain 62 ± 2 nm. We expect that this quantification of the mechanical properties of dsRNA is important for several reasons. For example, it governs the typical size of dsRNA molecules when they are injected into cells during RNA interference experiments, and it provides the basis for future quantitative measurements of RNA-protein interactions.

Acknowledgments

We thank Peter Veenhuizen and Daniël Koster for useful discussions and advice, and Ralf Seidel and David Bensimon for a critical reading of the manuscript.

This work is part of the research program of the “Stichting voor Fundamenteel Onderzoek der Materie (FOM)”, which is financially supported by the “Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO)”. F.M.-H. acknowledges funding from the Fundación Ramón Areces as the recipient of a postdoctoral fellowship.

References

  1. Arnott, S., D. W. Hukins, S. D. Dover, W. Fuller, and A. R. Hodgson. 1973. Structures of synthetic polynucleotides in the A-RNA and A'-RNA conformations: x-ray diffraction analyses of the molecular conformations of polyadenylic acid-polyuridylic acid and polyinosinic acid-polycytidilic acid. J. Mol. Biol. 81:107–122. [DOI] [PubMed] [Google Scholar]
  2. Bednar, J., P. Furrer, V. Katritch, A. Z. Stasiak, J. Dubochet, and A. Stasiak. 1995. Determination of DNA persistence length by cryo-electron microscopy. separation of the static and dynamic contributions to the apparent persistence length of DNA. J. Mol. Biol. 254:579–594. [DOI] [PubMed] [Google Scholar]
  3. Bernstein, E., A. A. Caudy, S. M. Hammond, and G. J. Hannon. 2001. Role for a bidentate ribonuclease in the initiation step of RNA interference. Nature. 409:363–366. [DOI] [PubMed] [Google Scholar]
  4. Bonin, M., J. Oberstrass, N. Lukacs, K. Ewert, E. Oesterschulze, R. Kassing, and W. Nellen. 2000. Determination of preferential binding sites for anti-dsRNA antibodies on double-stranded RNA by scanning force microscopy. RNA. 6:563–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bouchiat, C., M. D. Wang, J.-F. Allemand, T. Strick, S. M. Block, and V. Croquette. 1999. Estimating the persistence length of a worm-like chain molecule from force-extension measurements. Biophys. J. 76:409–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Brown, B. A., K. Lowenhaupt, C. M. Wilbert, E. B. Hanlon, and A. Rich. 2000. The Za domain of the editing enzyme dsRNA adenosine deaminase binds left-handed Z-RNA as well as Z-DNA. Proc. Natl. Acad. Sci. USA. 97:13532–13536. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bussiek, M., N. Mucke, and J. Langowski. 2003. Polylysine-coated mica can be used to observe systematic changes in the supercoiled DNA conformation by scanning force microscopy in solution. Nucleic Acids Res. 31:e137. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bustamante, C., Z. Bryant, and S. B. Smith. 2003. Ten years of tension: single-molecule DNA mechanics. Nature. 421:423–427. [DOI] [PubMed] [Google Scholar]
  9. Bustamante, C., J. F. Marko, E. D. Siggia, and S. Smith. 1994. Entropic elasticity of lambda-phage DNA. Science. 265:1599–1600. [DOI] [PubMed] [Google Scholar]
  10. Charney, E., H.-H. Chen, and D. C. Rau. 1991. The flexibility of A-form DNA. J. Biomol. Struct. Dyn. 9:353–362. [DOI] [PubMed] [Google Scholar]
  11. de la Cruz, J., D. Kressler, and P. Linder. 1999. Unwinding RNA in saccharomyces cerevisiae: dead-box proteins and related families. Trends Biochem. Sci. 24:192–198. [DOI] [PubMed] [Google Scholar]
  12. Dekker, N. H., J. A. Abels, P. T. M. Veenhuizen, M. M. Bruinink, and C. Dekker. 2004. Joining of long double-stranded RNA molecules through controlled overhangs. Nucleic Acids Res. 32:e140. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fire, A., S. Xu, M. K. Montgomery, S. A. Kostas, S. E. Driver, and C. C. Mello. 1998. Potent and specific genetic interference by double-stranded RNA in caenorhabditis elegans. Nature. 391:806–811. [DOI] [PubMed] [Google Scholar]
  14. Frontali, C., E. Dore, A. Ferrauto, E. Gratton, A. Bettini, M. R. Pozzan, and E. Valdevit. 1979. An absolute method for the determination of the persistence length of native DNA from electron micrographs. Biopolymers. 18:1353–1373. [DOI] [PubMed] [Google Scholar]
  15. Gast, F. U., and P. J. Hagerman. 1991. Electrophoretic and hydrodynamic properties of duplex ribonucleic acid molecules transcribed in vitro: evidence that A-tracts do not induce curvature in RNA. Biochemistry. 30:4268–4277. [DOI] [PubMed] [Google Scholar]
  16. Hagerman, P. J. 1997. Flexibility of RNA. Annu. Rev. Biophys. Biomol. Struct. 26:139–156. [DOI] [PubMed] [Google Scholar]
  17. Henn, A., O. Medalia, S.-P. Shi, M. Steinberg, F. Franceschi, and I. Sagi. 2001. Visualization of unwinding activity of duplex RNA by DbpA, a DEAD box helicase, at single-molecule resolution by atomic force microscopy. Proc. Natl. Acad. Sci. USA. 98:5007–5012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kebbekus, P., D. E. Draper, and P. Hagerman. 1995. Persistence length of RNA. Biochemistry. 34:4354–4357. [DOI] [PubMed] [Google Scholar]
  19. Landau, L. D., and E. M. Lifshitz. 1958. Statistical Physics, Course of Theoretical Physics. Pergamon, London.
  20. Makeyev, E. V., and J. M. Grimes. 2000. RNA-dependent RNA polymerases of dsRNA bacteriophages. Virus Res. 101:45–55. [DOI] [PubMed] [Google Scholar]
  21. Moreno-Herrero, F., P. J. de Pablo, J. Colchero, J. Gómez-Herrero, and A. M. Baró. 2000. The role of shear forces in scanning force microscopy: a comparison between the jumping mode and tapping mode. Surf. Sci. 453:152–158. [Google Scholar]
  22. Rivetti, C., and S. Codeluppi. 2001. Accurate length determination of DNA molecules visualized by atomic force microscopy: evidence for a partial B- to A-form transition on mica. Ultramicroscopy. 87:55–66. [DOI] [PubMed] [Google Scholar]
  23. Rivetti, C., M. Guthold, and C. Bustamante. 1996. Scanning force microscopy of DNA deposited onto mica: equilibration versus kinetic trapping studied by statistical polymer chain analysis. J. Mol. Biol. 264:919–932. [DOI] [PubMed] [Google Scholar]
  24. Shore, D., J. Langowski, and R. L. Baldwin. 1981. Energetics of DNA twisting. II. topoisomer analysis. Proc. Natl. Acad. Sci. USA. 78:4833–4837.6272277 [Google Scholar]
  25. Strick, T., J.-F. Allemand, D. Bensimon, A. Bensimon, and V. Croquette. 1996. The elasticity of a single supercoiled DNA molecule. Science 271:1835–1837. [DOI] [PubMed] [Google Scholar]
  26. Strick, T. R., J.-F. Allemand, D. Bensimon, and V. Croquette. 2001. The manipulation of single biomolecules. Phys. Today. 54:46–51. [Google Scholar]
  27. Thomson, N. H., S. Kasas, B. L. Smith, H. G. Hansma, and P. K. Hansma. 1996. Reversible binding of DNA to mica for AFM imaging. Langmuir. 12:5905–5908. [Google Scholar]
  28. Timmons, L., and A. Fire. 1998. Specific interference by ingested dsRNA. Nature. 395:854–857. [DOI] [PubMed] [Google Scholar]
  29. van Noort, J., T. van der Heijden, M. de Jager, C. Wyman, R. Kanaar, and C. Dekker. 2003. The coiled-coil of the human Rad50 DNA repair protein contains specific segments of increased flexibility. Proc. Natl. Acad. Sci. USA. 100:7581–7586. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. van Noort, J., S. Verbrugge, N. Goosen, C. Dekker, and T. T. Dame. 2004. Dual architectural roles of HU: formation of flexible hinges and rigid filaments. Proc. Natl. Acad. Sci. USA. 101:6969–6974. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Wang, M. D., H. Yin, R. Landick, J. Gelles, and S. Block. 1997. Stretching DNA with optical tweezers. Biophys. J. 72:1335–1346. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Watson, J. D., and F. H. C. Crick. 1953. Molecular structure of nucleic acids: a structure for deoxyribose nucleic acid. Nature. 171:737–738. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES