Pause Point Spectra in DNA Constant-Force Unzipping

Abstract

Under constant applied force, the separation of double-stranded DNA into two single strands is known to proceed through a series of pauses and jumps. Given experimental traces of constant-force unzipping, we present a method whereby the locations of pause points can be extracted in the form of a pause point spectrum. A simple theoretical model of DNA constant-force unzipping is presented, which generates theoretical pause point spectra through Monte Carlo simulation of the unzipping process. The locations of peaks in the experimental and theoretical pause point spectra are found to be nearly coincident below 6000 basepairs for unzipping the bacteriophage λ-genome. The model only requires the sequence, temperature, and a set of empirical basepair binding and stacking energy parameters, and the good agreement with experiment suggests that pause point locations are primarily determined by the DNA sequence. The model is also used to predict pause point spectra for the bacteriophage φX174 genome. The algorithm for extracting the pause point spectrum might also be useful for studying related systems which exhibit pausing behavior such as molecular motors.

INTRODUCTION

The unbinding of double-stranded DNA (dsDNA) into single-stranded DNA (ssDNA) is a ubiquitous event central to many cellular processes. Much research has focused on understanding the thermal unbinding of dsDNA (Wartell and Benight, 1985). These studies have revealed quantitative aspects of the thermal unbinding transition through the extraction of sequence-dependent free energy differences between bound and unbound DNA (Blossey and Carlon, 2003; Rouzina and Bloomfield, 1999a,b; SantaLucia et al., 1996). In living cells, however, the unbinding of dsDNA is typically achieved using molecular motors which utilize chemical energy and exert forces to pull apart the strands of dsDNA. To have a quantitative understanding of these processes it is important to first study the simpler case of unbinding dsDNA by a controllable mechanical probe.

Early studies on unzipping large dsDNA molecules made use of microneedles to measure the forces generated when the dsDNA was unzipped at a constant rate (Bockelmann et al., 1997, 1998; Essavaz-Roulet et al., 1997). For slow enough unzipping velocities, these experiments were shown to measure the equilibrium force versus extension curve of the growing portion of the ssDNA as the molecule was unzipped. The force versus extension curves exhibited jagged features corresponding to the unzipping of large portions of the dsDNA, giving rise to “stick-slip motion” of the junction between the bound and unbound strands, also known as the unzipping fork. These jagged features were shown to be related to the local basepair (bp) content of the dsDNA near the unzipping fork.

An alternative is to measure the position of the unzipping fork as the dsDNA is pulled apart under a constant applied force (see Fig. 1 for a schematic illustration of the experiment). Most interesting to real-time biological processes involving dsDNA unzipping is the out-of-equilibrium measurement of the position of the unzipping fork, for various forces, versus time. Moreover, in the constant-force ensemble, both the equilibrium statistical mechanics and dynamics of the unzipping are more amenable to explicit analytical calculations than studies in the “constant-extension” ensembles associated with slow unzipping at constant velocity (Lubensky and Nelson, 2002). Recently, single-molecule experiments have allowed study of this process. Both theory (Bhattacharjee, 2000; Cocco et al., 2001, 2002; Kafri et al., 2002; Lubensky and Nelson, 2000, 2002; Marenduzzo et al., 2002; Nelson, 2004; Sebastian, 2000) and experiments (Danilowicz et al., 2004) show that at a given temperature the dsDNA separates into ssDNA when the applied force exceeds a critical value F_c. Moreover, for forces near F_c, the dynamics of the unzipping process is highly irregular (Danilowicz et al., 2003). Rather than a smooth time evolution, the position of the unzipping fork progresses through a series of long pauses separated by rapid bursts of unzipping.

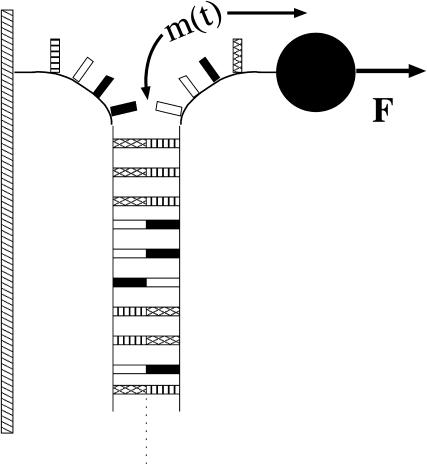
FIGURE 1.

Schematic diagram of the DNA constant-force unzipping experiment. One strand of the dsDNA is attached to a fixed support, typically via a linker DNA strand (not shown). The other strand is pulled with a constant force, F, via a magnetic bead (not to scale) attached to the strand. If the force is large enough, the dsDNA separates into two ssDNA strands. The position of this separation, measured in bps opened, m(t), locates the unzipping fork. See Fig. 2 for a more detailed depiction of the experimental setup used in this study.

Pauses and jumps in constant-force unzipping can have several origins. For temperatures near the dsDNA melting transition, portions of the dsDNA can unbind and form transient “bubbles” below the unzipping fork. In addition, because of the helical nature of the dsDNA structure, a natural twist can be accumulated during the force-induced unzipping process. If the unzipping fork encounters a thermal bubble in the course of its progress, then we would expect a jump in its position. Furthermore, if the unzipping occurs on timescales much faster than the timescales associated with untwisting, then one would expect pauses when the DNA has to unravel accumulated twist (Thomen et al., 2002). Moreover, since AT and CG bps have different interaction strengths (and associated bp stacking energies—see Table 1), pauses and jumps could also be due to effects associated with the particular sequence of the DNA, as observed in the constant velocity studies (Bockelmann et al., 1998).

TABLE 1.

Base quartet free energies ΔG_qt for the bound to unbound transition for T = 298 K (25°C) taken from SantaLucia et al. (1996), using ΔG_qt = ΔH_qt−TΔS_qt

Base quartet	ΔGqt/kBT
5′-GC-3′	4.46
CG	4.22
GG	3.46
GA	2.79
GT	2.96
CA	2.79
CT	2.20
AA	2.31
AT	1.52
TA	1.33

Only two nucleotides of the base quartet are shown. The other two are obtained from the usual complementarity A-T and G-C. Free energies are expressed in units of k_BT = 0.59 kCal/mol at T = 298 K (25°C).

Sequence related pausing has also been observed in the motion of motor proteins along dsDNA tracks such as RNA polymerase (RNAp) (Davenport et al., 2000; Neuman et al., 2003; Wang et al., 1998) and exonuclease (Perkins et al., 2003). For the case of RNAp, pausing was shown to occur at specific sequence locations along the dsDNA, and a mechanism involving sequence specific interactions with the enzyme binding pocket was proposed (Neuman et al., 2003). Recent theoretical analysis of general models of molecular motors on heterogeneous tracks has shown that anomalous dynamics and the associated pauses and jumps can be caused by the sequence heterogeneity alone (Kafri et al., 2004). In these models, motor movement is described as the motion of a random walker on a one-dimensional free energy landscape (FEL), representing the natural reaction coordinate of the motor along the track. Sequence heterogeneity on the track leads to a special form for the FEL, which turns out itself to be a random walk about a well-defined mean. Such random forcing FELs are known to give asymptotic anomalous dynamics, where under certain conditions the displacement of the motor grows sublinearly in time (Bouchaud et al., 1990). As discussed below, theoretical descriptions of DNA unzipping also lead to dynamics on random forcing FELs, and thus display the same global phenomena as molecular motors on heterogeneous tracks.

In this respect, dsDNA unzipping is an ideal system to study anomalous dynamics because of its simplicity and its direct relevance to the behavior of biologically important molecular motors such as RNAp and exonuclease. In particular, studying DNA unzipping will lead to a better understanding of the biologically relevant pausing behavior of these motors.

Studying DNA unzipping is also important from the point of view of protein-DNA interaction assay development. Recently, DNA unzipping was used to probe protein-DNA interaction in the case of binding of the restriction enzyme BsoBI (Koch and Wang, 2003). Unzipping experiments revealed large forces necessary to unzip the DNA when the unzipping fork encountered a bound protein. The same pauses and jumps were observed in unzipping fork dynamics and were attributed to protein binding sites. It is important to distinguish pauses due to sequence heterogeneity alone, and those due to protein binding, which makes the study of anomalous dynamics in DNA unzipping of great importance for this type of protein-DNA interaction assay development and interpretation.

Unzipping experiments on multiple identical copies of the same DNA have shown that locations of pauses are highly conserved from one strand to another (Danilowicz et al., 2003). Hence, it seems likely that in these experiments at least, transient bubbles and accumulated twist play only a minor role in determining the jumps and pauses. In this work we study the location of the pause points both experimentally and theoretically. To facilitate this study, we introduce a pause point spectrum which is a function of the number of bps unzipped. The locations of peaks in the pause point spectrum signify the location of pause points in unzipping, and peak areas can be used as a measure of the strength of pause points. We predict pause point locations by adapting a model of the dynamics of the unzipping fork in a constant-force unzipping experiment on heterogeneous DNA (Lubensky and Nelson, 2002). The only input information into the analysis is the DNA sequence, free energy differences between dsDNA and ssDNA obtained using melting experiments, and temperature. Both thermal bubbles and build up of twist are ignored within our treatment. We find that we can predict most experimentally observed pause points, thus confirming that pause point locations are primarily a function of sequence. Our algorithm might also prove useful for analyzing pause points arising in the single-molecule molecular motor experiments mentioned above (Davenport et al., 2000; Neuman et al., 2003; Perkins et al., 2003; Wang et al., 1998).

The article is organized as follows: In the Experimental Method section, we describe constant-force unzipping experiments performed on λ-phage DNA. In the section Pause Point Algorithm, we present an algorithm for constructing a pause point spectrum from experimental traces of unzipping fork position versus time. The section “Defining the free energy landscape” describes a theoretical model of DNA constant-force unzipping which defines a FEL as a function of the number of bases unzipped, m, used to describe the unzipping process. In the section Dynamics, this FEL is used as a surface on which to perform Monte Carlo simulations mimicking the unzipping experiments. In the same way as performed for experimental unzipping trajectories, these trajectories are combined to form theoretical pause point spectra, which are compared with experiment in the Discussion.

EXPERIMENTAL METHOD

The experimental procedure has been discussed previously (Assi et al., 2002; Danilowicz et al., 2003). As shown in Fig. 2, our setup consisted of two pieces of λ-phage DNA, covalently bound to each other. One strand of DNA was used as a spacer between the glass capillary and the other strand, which was to be unzipped. The spacer strand of DNA was attached to the capillary with a digoxigenin/antidigoxigenin antibody bond. The capillary was coated with digoxigenin antibody, whereas the spacer strand of DNA was hybridized with a digoxigenin labeled oligonucleotide. One end of the strand of DNA to be unzipped was hybridized and ligated with a hairpin to prevent the complete separation of the unzipped DNA molecule. The other end of the strand was hybridized and ligated with a biotinylated oligonucleotide which specifically bound to a streptavidin-coated superparamagnetic bead. When a magnetic field was applied, the force induced on the bead slowly unzipped the DNA. The unzipping direction (order of nucleotides unzipped) was controlled by the selection of oligonucleotides.

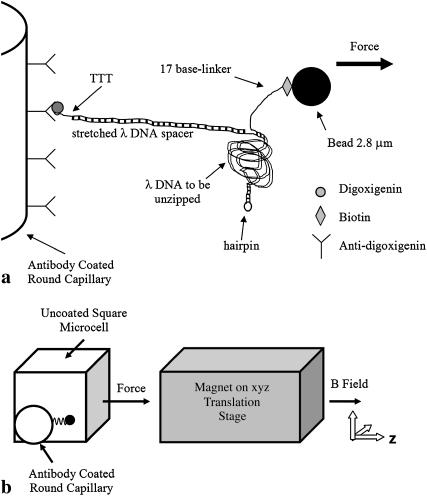
FIGURE 2.

Molecular construction and square cell. (a) Schematic of the DNA binding to the inner glass capillary and the magnetic bead such that pulling the bead away from the surface will cause the dsDNA shown on the right side of the diagram to be separated into two single DNA strands. Note that the figure is not to scale, considering that λ-DNA contains 48,502 bp. (b) Schematic of the side view of the square capillary containing the round glass capillary to which the DNA molecules are bound. The magnetic tweezer apparatus exerts the controlled force on the magnetic beads, a microscope is used for observation, and two thermoelectric coolers are used to control the temperature of the sample during the initial incubation. The magnetic beads are pulled to the right in a direction parallel to the bottom and top surfaces of the square capillary and perpendicular to the surface of the round capillary at a height equal to the radius of the round capillary, where we focus the microscope. This design allows us to view DNA molecules that are offset from the surfaces of the square capillary and to infer the number of separated bps by measuring the separation between the magnetic bead and the surface of the round capillary.

Fig. 2 b shows the round, antibody-coated capillary inside an uncoated square microcell. The round capillary was 0.5 mm in diameter, whereas the square microcell was 0.8 mm across, leaving a space for a solution of DNA, beads, and buffer inside the microcell but outside the sealed, empty, round capillary. The capillary was incubated in a solution containing digoxigenin antibody at 5^oC for at least 2 days. The DNA solution and bead suspension were also individually kept at 5^oC before the experiment. We inserted a digoxigenin antibody-coated capillary and the DNA and bead suspension into the microcell and then incubated it at 37^oC for 45 min, allowing the DNA to bind to the capillary via the antigen-antibody bond. Finally, we rotated the microcell so the beads that had settled on top of the round capillary were hanging off of its side. We focused using a microscope objective on the beads that were attached to the outermost point on the capillary so that we could accurately measure the distance between the beads in our field of view and the capillary.

The optical resolution of the current setup was determined through parallel measurements of the stretched length of identical dsDNA molecules. A histogram of the observed lengths yielded a standard deviation of ∼0.5 microns. Pause points with smaller variations than this resolution may be the same.

We applied a magnetic force by bringing a stack of small magnets mounted on an xyz translation stage near the microcell. The magnets could be approximated as a solenoid with its long axis in the z-direction, so the field gradient acted in the z-direction only and was essentially uniform (Assi et al., 2002) over our field of view, which was much smaller than the solenoid radius.

We measured the distance the DNA molecules had unzipped by tracking their attached beads. We took still digital photographs of the field of view through a 10× objective lens once every 10 s. An image processing program found the coordinates of each bead in each frame. Fig. 3 shows part of our field of view at two different times. In Fig. 3 a, we had just applied the magnetic field. Fig. 3 b shows the same beads 28 frames, or just over 4 min, later.

FIGURE 3.

Photographs from above the square capillary shown in Fig. 2 b. The dark bar on the left is the inner round capillary to which the beads are tethered. The dark dots are the beads. (a) The beads immediately after a 15 pN force was introduced. (i) Bead attached to fully zipped DNA. (ii) Bead attached to partially unzipped DNA. Most of the beads are in the fully zipped position, ∼17 μm from the surface of the capillary. (b) The beads 4 min later. More DNA strands have unzipped, causing the beads to jump farther from the round capillary.

In each experiment, we saw ∼50 beads in our field of view. Approximately 10 beads unzipped slowly over the course of the experiment, pausing at various points. An individual bead paused at fixed extension until, through thermal fluctuations, the unzipping proceeded. After overcoming an energy barrier which we attribute to sequence heterogeneity, the strand unzipped up to the next pause point, where the same process repeated. Pause points seemed very reproducible in experiment from bead to bead (each attached to a genetically identical DNA), even when the applied force varied considerably. This statement will be quantified below.

To compare simulation results to experimental data, we converted microns unzipped to the numbers of bps unzipped. The centers of beads attached to fully zipped strands of λ-phage DNA under a force near 15 pN were observed 16.5 μm from the round capillary in experiments. The centers of beads attached to fully unzipped strands of λ-phage DNA under a force of 15 pN were observed 77.4 μm from the round capillary in experiments. Thus the two fully unzipped dsDNA strands (with a ligated oligonucleotide to prevent dissociation—Fig. 2) were stretched to a length of 60.9 μm. λ-phage DNA is 48,502 bps long, so to convert from μm to bps, we use the conversion factor 48,502 bp/60.9 μm ≈ 800 bp/μm. That is, ∼800 bps are broken when the bead moves 1 μm under this force. Since two strands of ssDNA are produced during unzipping, the monomer spacing along an ssDNA strand is found from the inverse of this factor divided by two to be a ≈ 0.6 nm. This is consistent with the monomer spacing calculated from the contour length of ss λ-phage DNA of ≈ 30μm (Smith et al., 1996); 30 μm/48,502 bases ≈ 0.6 nm/base. Such a linear interpolation seems reasonable given the fairly large forces (∼15–20 pN) acting on the unzipped “handles”.

PAUSE POINT ALGORITHM

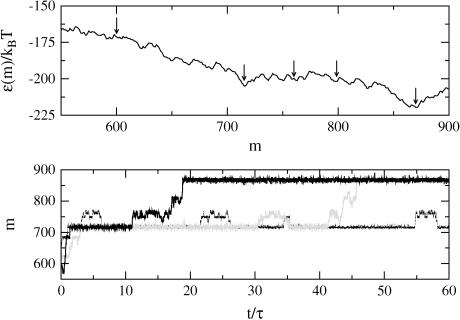
Fig. 5, b and c, displays several experimental unzipping trajectories. As can be seen in the trajectories, the unzipping fork progresses through long pauses at specific locations, separated by rapid transitions between these pauses. Moreover, a sample of trajectories from identical DNA sequences display a uniformity in the locations at which the DNA unzipping pauses. Note also that pauses at certain locations seem consistently longer than others. From these considerations, we are motivated to develop a method for combining many trajectories to form a distribution reflecting the location and relative strengths of pause points.

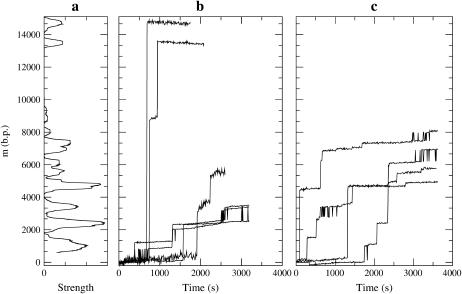
FIGURE 5.

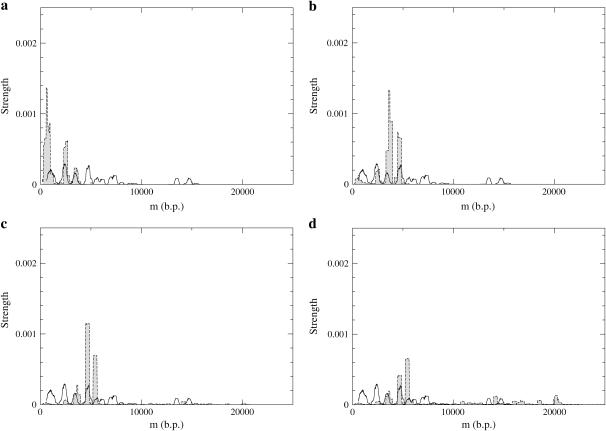
(a) Experimental pause point spectrum alongside sample experimental unzipping trajectories at T = 298 K (25°C) with (b) F = 15 pN and (c) F = 20 pN. The experimental spatial resolution is 0.5μm (∼400 bp), which determined the size of the window used to calculate the spectrum. The structure of some peaks indicates multiple underlying pause points that are only partially resolved at this resolution. The full experimental pause point spectrum was computed with 15 experimental trajectories, only 10 of which are shown. The two uppermost plateaus in b decrease in position in time due to sliding of the inner capillary inside the square cell during the acquisition of those trajectories.

A pause point “spectrum” can be computed as follows (see Fig. 4 for an example):

1. Create a histogram (area normalized to 1) based on the position of the unzipping fork during the time duration of the experiment for all trajectories using the highest resolution possible. In the case of this setup, the bead tracking software produced position data to 0.001 μm.

2. To smooth this histogram according to the effective experimental resolution, define a window centered around each position of the histogram, with a width equal to the experimental resolution.

3. Compute the average histogram peak height within this window, and assign the value of this average to the position of the center of the window in the pause point spectrum.

FIGURE 4.

Sample window averaged results. The high resolution (1 bp) pause time histogram is shown in black, and in this case was generated from theoretical simulations (Theoretical Study of Pause Points). The shaded spectrum is created by sliding a window of size 400 bp along the x axis, and assigning a y-value to the midpoint of the window equal to the average of the high resolution histogram within that window. A window of 400 bp corresponds to an experimental resolution of 0.5 μm. Note that highly localized pause points appear as broad peaks according to a much lower resolution in the window average.

The locations of the peaks in a pause point spectrum correspond to the distances at which the trajectories paused and thus correspond to pause points. In addition, the peak areas are proportional to the amount of time trajectories spent at the peak locations. Hence, relative peak area can be used as a measure of the relative strength of pause points. As can be seen from direct comparison between the spectrum and trajectories (Fig. 5), this method of analysis provides an excellent summary of pauses and jumps observed in experiment. From this intuition, we expect that higher experimental spatial resolution would allow us to resolve further peaks in the spectrum.

The experimental pause point spectrum was computed using 15 unzipping trajectories of which 10 are shown in Fig. 5, b and c. In addition to applying the above algorithm, the following steps were taken: Trajectories were first individually shifted so that the starting position of each trajectory was 0 μm. This was done to subtract the linker length from the measured distance for each bead. To collect as many trajectories as possible for better statistics, the experimental resolution was 0.5 μm. The spectrum was thus created with a window of 0.5 μm, corresponding to ∼400 bp. In each of the experimental trajectories, there was a period in the beginning that was noisy due to transient bead adjustments in the turning on of the magnetic field (Fig. 5). These regions were not included in the experimental spectra. To convert from μm to bp, we multiplied by 48,502 bp/60.9 μm, which represents the appropriate bp/μm factor for λ-phage under these experimental conditions (Experimental Method).

THEORETICAL STUDY OF PAUSE POINTS

Defining the free energy landscape

We consider the DNA unzipping experiment (Fig. 1) as a chemical reaction from dsDNA → 2 ssDNA. This system possesses a natural one-dimensional reaction coordinate, namely the number of bps unzipped m, or equivalently the spatial location of the unzipping fork. Theoretical descriptions can then be naturally reduced from a complicated, three-dimensional system to a one-dimensional description with some of the interactions renormalized, expressing the three-dimensional nature of the problem.

A very simple one-dimensional effective model (Lubensky and Nelson, 2000; Lubensky and Nelson, 2002) can then be written down based on the above picture. We define a free energy as a function of the number of bases unzipped, 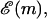which represents the difference in free energy between the state with m bps unzipped and the fully zipped state (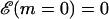). There is a contribution to 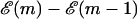from the free energy difference between the bound and unbound mth bp, 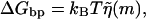as well as a contribution due to adding two additional monomers to the free ssDNA strands under a tension, F, denoted as 2k_BTg(F). The function g(F) represents the dimensionless free energy per bp of a single-stranded polymer under a constant force, F. Depending on the range of F considered, g(F) can be derived from a Gaussian or Freely Jointed Chain (FJC) model (Lubensky and Nelson, 2002)

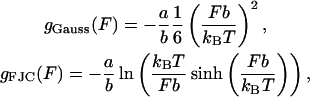(1)

where a is the monomer-monomer spacing on the ssDNA backbone and b is the Kuhn length of ssDNA. For quantitative comparison, the FJC model is used in this work when necessary. We can write these contributions as

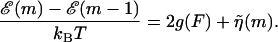(2)

The DNA sequence information is stored in the function 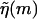. In principle, this function might depend on time due to transient bubbles or twists in the DNA. At forces low enough (F ≤ 5 pN) such that hairpin formation in the unzipped handles is possible (Dessinges et al., 2002; Montanari and Mézard, 2001), g(F) could also be sequence dependent. These complications are neglected here. If we iterate Eq. 2 until we reach m = 0, we have

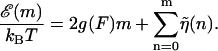(3)

Here we are setting 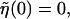which ensures 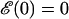. The long DNA sequences we are considering should be insensitive to such edge effects.

Thermodynamically we expect in equilibrium that unzipping of a dsDNA molecule of M bases will occur when 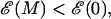with the transition region between ds and ssDNA occurring when 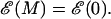If we define the shifted function 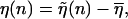where 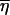is the average of 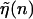over the sequence, we can rewrite Eq. 3 in the form

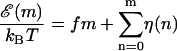(4)

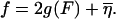(5)

The parameter f is a reduced force, which defines the overall tilt of the FEL, with the particular base sequence overlaid on this tilt with the function 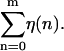For a given f, the experimental force, F, can be calculated by inverting Eq. 5 for a particular choice of g(F) (here the FJC form (Eq. 1)). Since g(F) represents the free energy per monomer of a ssDNA strand under force, relative to the free strand, g(F) decreases with increasing F. Thus larger F values give rise to more negative f values, causing the landscape to tilt downward, favoring unzipping. With this definition, the critical reduced force is defined by the equation f = 0. Values of f > 0 represent forces too low to unzip, whereas values of f < 0 represent forces where full equilibrium unzipping is thermodynamically favorable. In all of the above, we have assumed that thermal bubbles do not form under the experimental unzipping conditions. This simple model can be defined in a more rigorous fashion by integrating out three-dimensional degrees of freedom in a statistical mechanical microscopic definition of the system. Effects due to bubbles can be incorporated into a coarse grained model with renormalized parameters (Lubensky and Nelson, 2002).

It is interesting to note that even for this simple model, nontrivial phenomena can occur due to the buildup of free energies naturally present in Eq. 4. In fact, for a random DNA sequence, Eq. 4 shows that the FEL itself is a random walk around the tilted mean 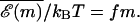Such landscapes are known as random forcing landscapes because the randomness comes in the derivative of 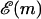. Anomalous dynamics on these landscapes is well studied (Bouchaud et al., 1990) and is caused by large energy barriers due to the buildup of random variables. Indeed, for the case of a completely random base sequence of length M, a sum over the independent random variables in Eq. 4 would give an energy barrier 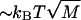(Lubensky and Nelson, 2002). Since GC bps are ∼ k_BT stronger than AT pairs at room temperature (Table 1), we expect large peaks to appear due to the presence of long GC-rich regions. For a sequence of length M = 48,000, one expects barriers on the order of 200 k_BT. Although not studied in this work, averages over an ensemble of different sequences can be performed to investigate the nature of sequence to sequence variation in the unzipping transition associated with this model (Lubensky and Nelson, 2002).

In practice, FELs are computed for a particular genome sequence using the experimentally determined free energies of base quartet formation (SantaLucia et al., 1996). There are 10 distinct base quartets, where m now represents the mth base quartet, whereas 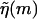represents this base quartet's free energy (Table 1). These free energy parameters are determined through thermal denaturation studies on short dsDNA fragments and were found for temperatures of ∼310 K. By using base quartet free energies, base stacking interactions are included, which are thought to be more important for overall dsDNA stability than the hydrogen bonds in between bps (Blossey and Carlon, 2003; Grosberg and Khokhlov, 1994). To compute FELs for different temperatures, the free energies for a given quartet were calculated from 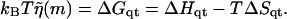Here ΔH_qt (ΔS_qt) is the enthalpy (entropy) difference between the bound and unbound DNA base quartet. Once temperature and f are specified, the FEL is computed with Eq. 2 or Eq. 4.

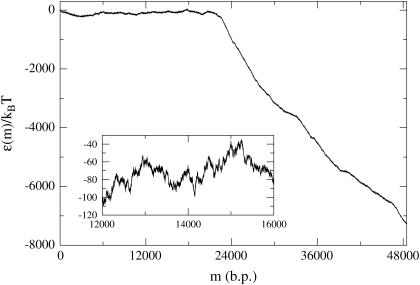
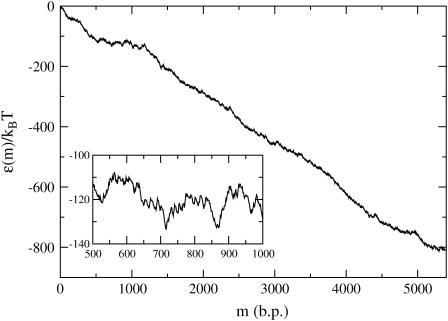
The case of λ-phage DNA is particularly interesting since it is known that this genome consists of a GC-rich half connected to an AT-rich half. (The λ-phage genome can be found at http://www.ncbi.nih.gov/ with sequence accession number NC_001416.) Using the free energy parameters of SantaLucia et al. (1996), one finds that the large GC-rich region creates a peak of ∼3000 k_BT at f = 0 and T = 298 K (25°C), representing an insurmountable barrier to unzipping, and which is much larger than that expected for a random sequence. For the λ-phage genome, we thus define an operational critical reduced force of unzipping as the value of f such that 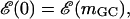where m_GC is the boundary of the GC-rich region. As can be seen in Fig. 6, this operational critical reduced force corresponds to approximately f = −0.15. Forces greater than this should allow easier unzipping since the AT-rich portion of the FEL has a negative slope for these forces. However, even at these large forces, there are barriers on the order of 20 k_BT to unzip (Fig. 6, inset). Using an FJC model for the single strands, with monomer spacing, a = 0.6 nm (corresponding to the bp/μm conversion factor in the Experimental Method section), and Kuhn length, b = 1.9 nm (Montanari and Mézard, 2001), we invert Eq. 5 to find a reduced force value of f = −0.15 corresponds to an experimental force value of F ≈ 16 pN.

FIGURE 6.

FEL for the λ-phage genome at f = −0.15, T = 298 K (25°C) corresponding to F ≈ 16 pN. A closer view is given in the inset. Because the λ-phage genome splits into a GC-rich “front end”, followed by an AT-rich region, the effective critical unzipping force is the one shown here, which produces an approximately flat energy landscape for the first ∼20,000 bps. Note that there are still energy barriers ∼20 k_BT in this region due to sequence heterogeneity.

Dynamics

To study the location of the pause points, one has to study the dynamics related to moving along the chemical reaction coordinate, m. Macroscopic unzipping occurs only if f < 0, when the equilibrium state of the system is unbound. In this case, the experimental traces of DNA unzipping represent the approach of the system toward its equilibrium single-stranded state.

As outlined in Lubensky and Nelson (2002), there are four dynamical timescales associated with DNA constant-force unzipping in the setup shown in Fig. 1: τ_end and τ_bulk represent base pairing and unpairing at the end of the strand and in the bulk, respectively; τ_ss(m) represents the relaxation time of the liberated single strands; and τ_rot(m) represents the relaxation time of twist built up in the zipped portion of the strand due to the helical nature of the DNA. The latter two timescales vary as a function of m. The dynamics of unzipping are determined by the slowest of these timescales. Here we assume that this timescale, for any value of m, is related to the unbinding of bps.

In the analysis below, we assume that the slowest timescale is m-independent. Furthermore, it can be argued that bubble formation is suppressed in DNA for the relevant experimental conditions because of strong base stacking interactions (Blossey and Carlon, 2003).

We will be interested in the unzipping dynamics for f < 0, that is for forces above the critical force of unzipping where it is thermodynamically favorable to unzip. However, even under these conditions, the approach to thermodynamic equilibrium is far from simple. Smooth progress of the unzipping fork is hampered by very large energy barriers in 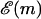that can be caused by the buildup of positive η(m). As mentioned above, for random DNA sequences of length M, these barriers can grow as 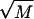. Forces slightly above the critical force are unable to remove these barriers through tilting the landscape, and we expect to observe difficulty in traversing these barriers. Since the barriers are sequence dependent, it is possible that the dynamics of unzipping display characteristic signatures of the sequence.

To study the behavior of a particular DNA sequence and to make direct contact with experiments, it is useful to have a dynamical model that closely mimics the experiment. This can be achieved most simply through Monte Carlo simulations of a random walker on the one-dimensional FEL for the specific DNA sequence under study, at the specified reduced force and temperature conditions. The position of the walker on the FEL represents the position of the unzipping fork in experiments. The walker moves from position m to a nearest neighbor position m ± 1 with the rate

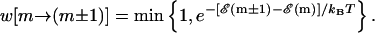(6)

Details of the algorithm are outlined in Appendix A.

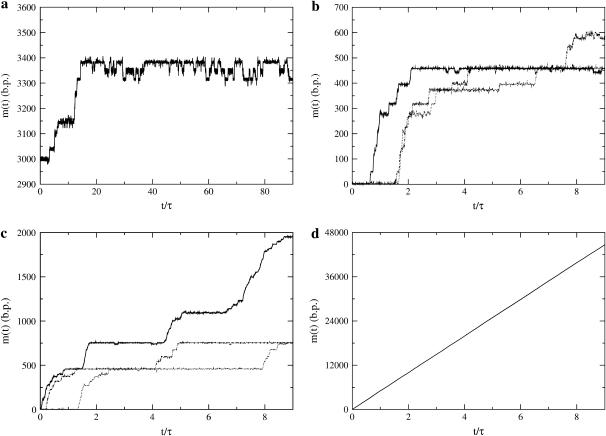
A simulation consists of specifying the FEL (DNA sequence, temperature, and reduced force) and propagating the Monte Carlo algorithm for a specified number of steps. The initial condition is such that the walker starts at m = 0, representing the experimental circumstance of tracking DNAs that begin as fully zipped. What results is trajectory data, m(t), which contains the same information obtained in experiments. Sample theoretical trajectories are shown in Fig. 7. There are clear pauses and jumps of the trajectories for reduced forces much higher than the critical force (−0.39 ≤ f ≤−0.5). Only extremely large reduced forces (f = −5) are sufficient to remove all barriers and allow smooth unzipping.

FIGURE 7.

Sample theoretical unzipping trajectories, m(t), where τ = 10,000 steps. (a) f = −0.26, (b) f = −0.39, (c) f = −0.50, and (d) f = −5. For t/τ ≥ 15, a shows intricate two-state behavior caused by nearly degenerate minima on the FEL. In d, the unzipping is smooth, but does not fully unzip in 80,000 time steps, indicating dwell time at some sites. Note that pause points are reproducible in the simulations, and that very large forces are required to smooth out the large barriers present in λ-phage DNA and allow smooth unzipping.

It must be stressed that there is a certain freedom in choosing particular Monte Carlo algorithms (Appendix A). Algorithms can differ in how long it takes random walkers to traverse energy barriers, and thus we do not expect to be able to compare timescale information between experiment and theory, quantitatively. Although pause point locations can be predicted, we do not expect pause point strengths to match between experiment and theory.

To calculate the theoretical pause point spectra, simulations were performed at a variety of reduced forces, f, and on FELs at the same temperature of the experiments. Each simulated trajectory consisted of 10⁷ Monte Carlo steps, and 300 trajectories were used to create the theoretical histograms with a resolution of 1 bp (Fig. 4). Corresponding to the 0.5 μm experimental resolution, the window averages were taken over 400 bps with a length per bp for λ-phage DNA under these conditions of 60.9 μm/48,502 bp as discussed in the Experimental Method section. For f values in which some of the trajectories reached the fully unzipped state (m = 48,502 bp), the trajectories were cut off past 48,000 bps before being included in the spectra.

Previous theoretical studies used the assumption of equilibrium to calculate experimental observables. In particular, for the constant pulling velocity studies, the applied force and the location of the unzipping fork can be computed via thermodynamic averages using the Boltzmann distribution under this experimentally verified assumption (Bockelmann et al., 1998, 2002). We note, however, that the plateaus seen in the equilibrium average of the number of bps unzipped as a function of sample displacement in this case are different from the plateaus seen in the position of the unzipping fork observed in this study due to dynamical effects in the constant-force experiment.

We would like to emphasize that the theoretical description in this study aims to reproduce the nonequilibrium dynamical effects of DNA unzipping, which is also the relevant process in the context of molecular motors. Since the model needs only several physical parameters and the DNA sequence under study, the pauses and jumps observed in the simulations demonstrate that this dynamical behavior can arise due to sequence effects.

DISCUSSION

An examination of a few experimental unzipping trajectories (Fig. 5) reveals that the pausing locations are often encountered by multiple copies of the same DNA. These copies are subject to different realizations of thermal noise but share the same base sequence, an indication that sequence is a strong factor in governing pause point locations.

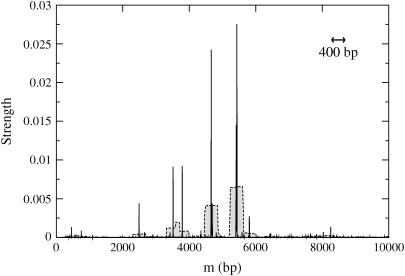
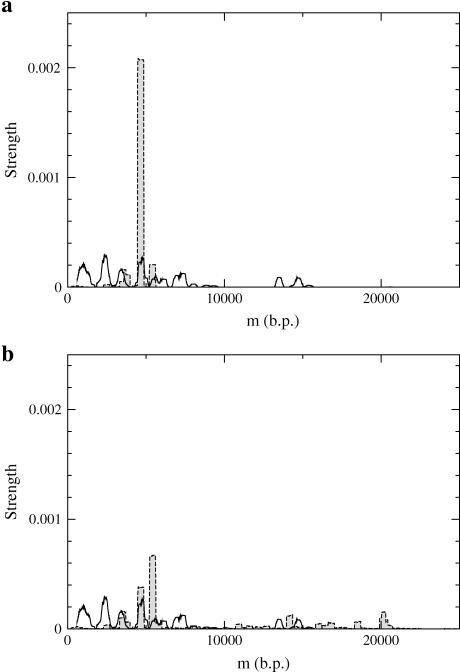
Experimental and theoretical pause point locations can be compared by examining the peak positions in the corresponding pause point spectra (Table 2). Every theoretical peak <6000 bp is within the error bars of an experimental peak. In addition, theory predicts a gap in the pause point spectra of ∼9000 bp starting at 5400 bp, which is similar in size and location to that observed in experiment. We must emphasize that the match between the location and size of the gaps in the spectrum is evidence that we are not observing fortuitous matching between peak locations. The fact that the positions of the pause points and gaps match to such a high degree between experiment and theory demonstrates that for these experimental conditions, the approximations inherent in the concept of dynamics on the FEL representing DNA constant-force unzipping as a model for the experiments are sound. Since the theoretical model only requires the base sequence and thermodynamic parameters for base quartet formation, the agreement is proof that pause point locations are strongly governed by base sequence. The good comparison also shows that neglect of bubble formation for these temperatures is appropriate, as is also found by other means (Blossey and Carlon, 2003).

TABLE 2.

Experimental versus theoretical pause point locations (bp) for the first 15,000 bp corresponding to unzipping the front half of the λ-phage genome (Fig. 6)

Experiment (±200 bp)	Theory (±200 bp)
1000	600
2400	2500
3400	3400
4700	4600
5600	5400
6100
7100
Gap = 6400	Gap = 8800
13,500
	14,200
14,700

The pause point locations are the positions of the centers of the peaks in the pause point spectra (Fig. 8), and have error bars of ±200 bp due to experimental resolution. The theoretical pause points include those found for f = −0.29,−0.39,−0.47, and−0.50. Also listed is the size of the gap regions in the spectra where no pause points are found. Note that every theoretical peak <6000 bp is within the error bars of an experimental peak, and the theoretical and experimental gaps are roughly the same size and in the same location in the pause point spectra.

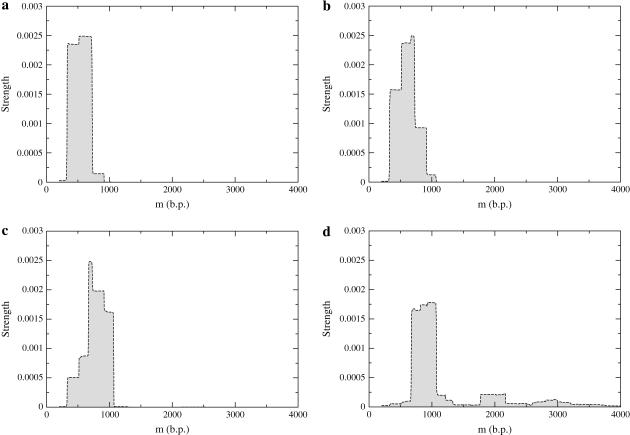
Theoretical and experimental pause point spectra are shown in Fig. 8. The values of f used in the simulations lie in the range−0.25 ≤ f ≤ −0.5. Recall that f = −0.15 corresponds roughly to a flat average FEL in the GC-rich region of the λ-phage DNA (Fig. 6). A value of F ≈ 17 pN corresponds to f = −0.37 under these conditions, which is within this range. We have compared experimental and theoretical pause points in the front half of the unzipping process. The much steeper energy landscape in the back half (see Fig. 6) eliminates most pause points. As the values of f are gradually decreased from f = −0.25, the theoretical pause point spectra grow into more peaks at larger distances, although low bp peaks are still preserved. Thus the locations of pause points are fairly robust with respect to f values. Once the forces are high enough to allow exploration of the whole FEL, the location of the peaks in the spectra do not change, and peak areas are adjusted reflecting a changing of the strength of the pause points.

FIGURE 8.

Experimental (black) and theoretical (shaded) pause point spectra for λ-phage at T = 298 K (25°C). The section Pause Point Algorithm outlines how the spectra were created using a sliding window average based on a 0.5 μm experimental resolution. Experiments were done with F = 15 pN and F = 20 pN, and the spectrum was obtained from 15 experimental traces (see Fig. 5). Theoretical spectra are at (a) f = −0.29, (b) f = −0.39, (c) f = −0.47, and (d) f = −0.50, and where created using 300 traces of 10⁷ steps each.

Two experimental spectra features are not observed in the theoretical spectra. The experimental doublet peak at 7100 bp was not observed in any theoretical spectra for a variety of parameters, including longer simulation times. The pair of peaks centered around 14,000 bp in the experimental spectra is also not picked up in the theoretical spectra, rather a single peak lying in the middle of the experimental peaks is found. The doublet of experimental peaks represents data from two separate runs, and thus a slight miscalibration in the 800 bp/μm conversion factor (Experimental Method) for those particular runs could cause the two peaks to separate since a miscalibration has a larger effect for longer distance pause points. For strong enough forces, theoretical pause point spectra also display many more peaks than present in the experimental spectra. We suspect that more experimental trajectories will reveal these additional peaks.

We might also expect discrepancies between experimental and theoretical pause point locations to be due to large A-rich regions in the genome since these are more susceptible to bubble formation due to the weaker base pairing and stacking interactions (Table 1). Thus further investigation into these pause point discrepancies can lead to interesting genomic information. Experiments involving higher temperatures and different ionic conditions will help elucidate these discrepancies (Danilowicz et al., 2004).

The theoretical spectra ultimately rely on the input base pairing and stacking free energy parameters used to calculate the FEL on which the simulations are performed. Because the parameters used in this study were determined through melting studies (SantaLucia et al., 1996), we must also attribute some differences between experimental and theoretical spectra to errors in these parameters. Because of the good agreement between pause point locations, however, we believe our basic model to be correct and that the majority of fine tuning is involved in bp parameter choice. The lack of reliable free energy parameter sets at a variety of temperatures prevented us from investigating the effect of temperature on unzipping.

Through a more detailed comparison of experimental and theoretical pause point spectra on a variety of carefully selected DNA sequences, an assay could be developed to determine DNA base pairing free energy parameters from unzipping experiments. Since unzipping experiments can be performed for a variety of temperature and buffer conditions (Danilowicz et al., 2004), this assay could be used to determine these parameters for any relevant conditions. This was not possible in this study for reasons discussed below.

In addition to pause point locations, pause point spectra also contain information about the strengths of pause points. Larger peak areas signify more trajectories paused at a given location for a longer time, and thus indicate stronger pause points. Thus the peak areas reflect the timescales of DNA unzipping. Each step in the Monte Carlo propagation of the unzipping can be thought to occur on the microscopic timescale governing the DNA unzipping, which is estimated to be ∼10⁻⁷ s (Danilowicz et al., 2003), with a large error in the exponent (Mathé et al., 2004). The accuracy of this figure is not high enough to allow direct comparison with theoretical and experimental timescales. As mentioned above, the particular choice of the Monte Carlo algorithm can change the characteristic unzipping times of simulations and could account for the discrepancy between theoretical and experimental peak areas and pause point strengths.

To investigate any discrepancy between experimental and theoretical timescales, we calculated spectra for simulations of 10⁸ steps (Fig. 9). A reduced force of f = −0.39 is not strong enough to allow DNAs to unzip under this length of time. Comparing to the 10⁷ step simulations (Fig. 8), we see that longer times in this case allow peaks at slightly higher bp to be observed, but mainly result in a change in peak area. For f = −0.50, which allows for some fraction of unzipping even with 10⁷ step runs, longer runs only serve to change peak areas, and not locations (compare with Fig. 8). Longer simulation times do not give spectra that approach the experimental pause point spectrum. Thus increasing the simulation time does not seem to resolve the discrepancy between experimental and theoretical timescales. We expect investigations into alternative Monte Carlo algorithms could lead to simulations that mimic experimental timescales with reasonable computing cost.

FIGURE 9.

Experimental (black) and theoretical (shaded) pause point spectra for λ-phage simulations of 10⁸ steps at 298 K (25°C). (a) f = −0.39 and (b) f = −0.50. The longer run times in the simulations produce different pause point strengths, but similar pause point locations to Fig. 8.

The discrepancy in timescale leads to a discrepancy in peak area and thus pause point strengths. This prohibits a more quantitative comparison of theoretical and experimental spectra such as an overlap integral describing the degree to which the spectra match. Such an overlap would not reflect the strong agreement in pause point locations due to the mismatch in peak areas. With a more sophisticated choice of Monte Carlo algorithm, and more experimental data, we expect such a quantitative comparison to be possible. With this in hand, an assay to determine bp free energy parameters, as mentioned above, could be developed.

This procedure to investigate pause points in DNA unzipping is easily extended to the study of other genomes since all that is required is the base sequence and temperature of interest. As an example, we theoretically investigated the pause point unzipping spectrum for the microvirus bacteriophage φX174 (BP-φX174; M = 5386). (The BP-φX174 genome can be found at http://www.ncbi.nih.gov/ with sequence accession number NC_001422.) The FEL for BP-φX174 has barriers that are on the order of 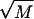and is a good example of a landscape which can be approximated by an integrated random walk (Fig. 10). Fig. 11 plots several sample simulation trajectories alongside a segment of the BP-φX174 FEL for f = −0.25, and Fig. 12 plots pause point spectra for several values of f, all at T = 298 K (25°C). Once again we see that for low values of f, the spectra grow into peaks at higher bp as the value of f is increased. A value of f = −0.45 is large enough to cause unzipping, and we can see that the spectrum at this value has contributions from the whole surface. For BP-φX174, f = −0.45 corresponds to F ≈ 17 pN at 298 K (25°C).

FIGURE 10.

FEL for the BP-φX174 genome at f = −0.15, T = 298 K (25°C) corresponding to F ≈ 16 pN. A closer view is given in the inset of the approximately horizontal plateau region.

FIGURE 11.

Sample simulation trajectories displayed below the relevant segment of the BP-φX174 FEL at f = −0.25 (25°C). The three trajectories start at the left of the figure at m = 600 bp, t = 0. Simulation time has units τ = 5385 steps corresponding to the genome length. Pause points are denoted by arrows on the FEL. Note that very intricate multistate behavior is seen in the walker trajectories. In particular, the region from 725 to 775 bp shows the presence of several minima of the same depth on the FEL, and shows up as oscillations in the trajectories.

FIGURE 12.

Theoretical pause point spectra for BP-φX174 at T = 298 K (25°C): (a) f = −0.15, (b) f = −0.20, (c) f = −0.25, and (d) f = −0.45. Each spectrum was created using 300 traces of 10⁷ steps each. A value of f = −0.45 corresponds to F ≈ 17 pN.

CONCLUSION

We have presented experimental evidence that the dynamics of DNA constant-force unzipping are not smooth, but rather display characteristic pauses and jumps. Furthermore, we have given strong evidence that the locations of these pauses are primarily governed by the DNA sequence at room temperature (25°C). Because of the relationship between theoretical descriptions of DNA unzipping and movement of molecular motors (Kafri et al., 2004), this provides evidence that pausing of molecular motors on heterogeneous tracks can be due to purely sequence effects. Furthermore, the details of this study of pauses of λ-phage unzipping will lead to more precise interpretation of protein-DNA interaction assay results which utilize DNA unzipping (Koch and Wang, 2003).

The free energy parameters of base pairing used in this study were determined through melting studies which employ conditions outside of biological relevance (SantaLucia et al., 1996). Through a more detailed and systematic comparison of theoretical and experimental pause point spectra, bp binding energies could be determined at more biologically relevant conditions (Danilowicz et al., 2004). This could lead to a general assay to determine these parameters at a variety of temperature and buffer conditions.

We have also presented a general scheme for computing pause point spectra for any DNA sequence, with the only inputs being the sequence, temperature, and a set of 10 empirical parameters representing DNA duplex stability.

The ideas presented above can be applied to any system in which the concept of a pause point can be well defined, or in which a “spectrum” representation of trajectory data can be useful in other ways. We can then enumerate the steps involved in constructing a theoretical representation of the system to facilitate comparison with experiments:

1. Using chemical intuition, reduce the system to one degree of freedom. Equilibrium statistical mechanics can be used to justify, or derive, the resulting FEL description of the system.

2. To model experiments, use Monte Carlo simulation with the appropriate algorithm to create theoretical trajectories.

3. Compute trajectory spectra using the above procedure for both experimental and theoretical trajectories.

Such systems, of which DNA constant-force unzipping is one, also include topics of current interest such as the motion of molecular motors on biopolymers (Davenport et al., 2000; Keller and Bustamante, 2000; Neuman et al., 2003; Perkins et al., 2003; Wang et al., 1998).

APPENDIX A: MONTE CARLO ALGORITHM

The Monte Carlo technique is designed to sample an ergodic system according to the equilibrium distribution for long simulation times. The distribution is specified by the detailed balance condition

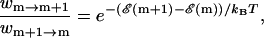(A1)

where w_{m →m+1} is the rate of taking the step from m to m + 1 bps unzipped. The ratio on the right hand side of Eq. A1 ensures relaxation to the Boltzmann distribution for long times (Newman and Barkema, 1999). Specifying the distribution, and thus the detailed balance criterion, still offers a large degree of flexibility in choosing an algorithm. Our goal in this study is to be able to predict the pause points of the DNA unzipping process, and to this end, we expect many choices of the Monte Carlo algorithm to give equivalent pause points. The simplest algorithm to achieve the detailed balance is known as the Metropolis Criterion (Newman and Barkema, 1999). For an unzipping fork location at m,

1. Choose a direction to move (m + δ, δ = ± 1).

2. If 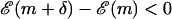, accept the move and GOTO 1.

3. If 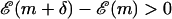, accept the move with the probability according to the Boltzmann distribution (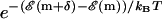). Else stay at this m. GOTO 1.

To prevent the random walkers from trying to unzip (rezip) beyond the end (beginning) of the dsDNA strand, we artificially inserted infinite barriers to these transitions in the simulations.