3-D Particle Tracking in a Two-Photon Microscope: Application to the Study of Molecular Dynamics in Cells

Abstract

We developed a method for tracking particles in three dimensions designed for a two-photon microscope, which holds great promise to study cellular processes because of low photodamage, efficient background rejection, and improved depth discrimination. During a standard cycle of the tracking routine (32 ms), the laser beam traces four circular orbits surrounding the particle in two z planes above and below the particle. The radius of the orbits is half of the x,y-width of the point spread function, and the distance between the z planes is the z-width of the point spread function. The z-position is adjusted by moving the objective with a piezoelectric-nanopositioner. The particle position is calculated on the fly from the intensity profile obtained during the cycle, and these coordinates are used to set the scanning center for the next cycle. Applying this method, we were able to follow the motion of 500-nm diameter fluorescent polystyrene microspheres moved by a nanometric stage in either steps of 20–100 nm or sine waves of 0.1–10 μm amplitude with 20 nm precision. We also measured the diffusion coefficient of fluorospheres in glycerol solutions and recovered the values expected according to the Stokes-Einstein relationship for viscosities higher than 3.7 cP. The feasibility of this method for live cell measurements is demonstrated studying the phagocytosis of protein-coated fluorospheres by fibroblasts.

INTRODUCTION

Within the past few years, single-particle tracking techniques have been increasingly used for studying biological systems. In contrast to large ensemble measurements, in which only average quantities are obtained, single-particle methods provide information about the distribution of molecular properties in inhomogeneous systems. Analysis of single molecule trajectories is useful to understand several aspects of the motion of molecules and their interactions with the environment. It has been used to measure diffusion coefficients of molecules (Hicks and Angelides, 1995), recognize different molecular populations according to their mobility (Daumas et al., 2003), and explore mechanisms involved in the particle motion (Smith et al., 1999).

Fluorescence microscopy has been used to visualize, locate, and track single particles (Goulian and Simon, 2000; Kues et al., 2001) in a wide variety of biological systems. For example, Noji et al. (1997) followed the movement of a fluorescent actin filament attached to the γ-subunit of F1-ATPase and determined that this protein acts as a rotary motor. In another application, Seisenberger et al. (2001) studied the process of virus infection by imaging single viruses labeled with fluorescent probes. Their work revealed important aspects about the initial interaction between the virus and the cell and the virus motion in the cytoplasm and the nucleus.

Most of the methods used so far for particle tracking in fluorescence microscopy rely on ultrafast video cameras that can detect single particles with accuracy of 10–100 nm in the range of ms (see for example, Kubitscheck et al., 2000). Recently, Yildiz et al. (2003) described a method for tracking single fluorescent particles with higher position accuracy (1.5 nm) but with 0.5 s of temporal resolution. Fujiwara et al. (2002) and Murase et al. (2004) studied the dynamics of lipids (labeled with 40-nm diameter colloidal gold particles) in cell membranes using a high-speed video camera, which allows the tracking of the tagged-lipids in brightfield mode with a temporal resolution of 25 μs and a spatial precision of 17 nm at this recording rate. The main limitation of these methods is that they can only detect particles moving within the focal plane, and thus they are generally limited to applications such as studying molecular processes in membranes (Dahan et al., 2003; Smith et al., 1999; Wilson et al., 1996).

To localize and track fluorescent particles in three dimensions, most techniques are based on imaging the sample with a camera at different z-positions and then analyzing the resulting image z-stacks as a function of time (see for example, Bornfleth et al., 1999; Thomann et al., 2002). These methods have a time resolution in the range of seconds and can only be applied to slow moving particles. In addition, as they require illumination of large sample volumes, their use in biological applications is limited because of photodamage and bleaching.

Speidel et al. (2003) presented a method for three-dimensional (3-D) tracking with a different basis. The method uses standard epifluorescence video imaging in off-focus mode and allows the tracking of particles with 100-ms temporal resolution. However, it is limited to particles moving <3 μm in the z-direction.

Recently, Kis-Petikova and Gratton (2004) described a method to locate fluorescent particles in two dimensions and suggested an algorithm for tracking them which was further developed into a tracking procedure (Levi et al., 2003). Here, we extend these ideas to three dimensions and develop a new method to locate and track single particles in a two-photon microscope. Two-photon microscopy is of increasing utility to the field of cell biology because of the reduction in out-of-focus photobleaching and photodamage, allowing the study of living cells including those cases where UV imaging is not possible due to these factors (Piston, 1996). In this context, we consider that the technique presented in this work can be of great potential for the study of dynamics of fluorescently tagged particles in biological systems.

To illustrate the applications of this method in living systems, we explore the phagocytosis process. Phagocytosis is a key mechanism of eukaryotic cells for the uptake and degradation of microorganisms, damaged or senescent cells, and particulates such as pollutants (Rabinovitch, 1995). To quantify this process, several authors make use of fluorescent beads since the uptake of these particles by cells is easily quantifiable (Schroeder and Kinden, 1983). In mammals, phagocytosis is mainly the work of specialized cells as macrophages. However, it has been demonstrated that several cells can uptake particles both in vivo and in vitro (Rabinovitch, 1995, and references therein). Particularly, Arlein et al. (1998) demonstrated that fibroblasts—despite not being “professional phagocytes”—ingest fluorescent beads. By using collagen-coated beads, several authors studied collagen phagocytosis by fibroblasts, which is an essential process to maintain tissue homeostasis in healthy mammalian soft connective tissue (Segal et al., 2001).

Particle tracking is an appealing approach to study phagocytosis because it can provide a detailed description of the initial interaction between the cell and the particle as well as the characteristics of the motion and the destination of the particle in the cell.

MATERIALS AND METHODS

Fluorescent microspheres

Carboxylate modified yellow-green fluorescent polystyrene microspheres (500, 100, 20, 10 nm nominal diameters) and collagen-coated microspheres (1 μm diameter) were purchased from Molecular Probes (Eugene, OR). For the phagocytosis experiments, 500-nm beads were coated with bovine serum albumin (BSA; Sigma Chemical; St Louis, MO) as described by Lee and McCulloch (1997) and Segal et al. (2001). The BSA and collagen-coated beads were suspended in the cell culture medium at concentrations of 2 × 10⁸ and 2 × 10⁶ fluorospheres/ml, respectively, calculated according to Haughland (1998).

Cell culture

Murine embryonic fibroblast cells were cultured and maintained in Dubecco's modified Eagle's medium (Gibco, Paisley, UK) supplemented with fetal bovine serum (10% v/v) and streptomycin/ampicillin at 37°C in a humidified atmosphere of 5% CO₂. Trypsinized cells were seeded into 35 mm diameter dishes with optic glass in the bottom and cultured for 72 h before the tracking experiments.

Microscope setup

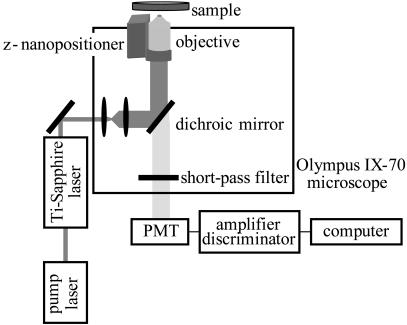
All the tracking experiments were carried out with an Olympus IX70 microscope (Fig. 1). The two-photon excitation source was a mode-locked titanium-sapphire laser (Mira 900; Coherent; Palo Alto, CA) pumped by an argon ion laser (Innova 300; Coherent) and tuned at 780 nm. The laser power at the sample ranged from 1 to 10 mW. The light is directed into the microscope by two galvomotor-driven scanning mirrors (Cambridge Technologies, Watertown, MA) through a scanning lens.

FIGURE 1.

Schematic diagram of the two-photon fluorescence microscope setup.

The laser light is reflected with a low-pass dichroic mirror (transmission from 370 to 630 nm; Chroma Technology; Brattleboro, VT) and focused on the sample with a 20× (dry) 0.75-NA plan apochromat objective. Fluorescence emission is collected by the objective and passes through a dichroic and short-pass filter to eliminate any reflected excitation light. It then exits the microscope to the detector (Hamamatsu (Tokyo, Japan) H7422P-40 photomultiplier tube) on the side port. The output of this unit was amplified and passed through a discriminator (PX01 Photon Counting Electronics; ISS; Champaign, IL). Photons were counted with a data acquisition card (ISS).

During the tracking procedure, the two scanning mirrors are moved independently by voltages generated in a computer card (3-axis card; ISS). When they are synchronized to move following sine waves shifted 90° relative to one another, the laser beam moves in a circular path. The position of the scanning center is determined by the offset values of the sine waves.

A piezoelectric z-nanopositioner (Polytec PI; Auburn, MA) equipped with a linear voltage differential transformer feedback sensor and operated in closed-loop configuration is placed below the objective to enable changes of the focal plane. During each cycle of the tracking routine, the 3-axis card generates a square wave voltage which drives the motion of the z-nanopositioner between two z planes separated by a distance given by the amplitude of the square wave. Similar to the x and y coordinates, the position of the center of z-scanning is given by the DC offset.

The experiments are controlled by a data acquisition program (SimFCS; LFD; Champaign, IL). This program, which also contains the tools used for trajectory analysis, can be downloaded from the Laboratory for Fluorescence Dynamics website (www.lfd.uiuc.edu).

Differential interference contrast (DIC)

The microscope was modified with an IR LED (Optodiode, Newbury Park, CA) and a cMOS camera (Pixelink; Otawa, ON, Canada) for imaging the cells. This configuration allows us to take IR-DIC and fluorescence images simultaneously.

Transmission electron microscopy

TEM images were taken with a Philips CM12 microscope (Philips, Eindhoven, The Netherlands) at an accelerating voltage of 120 kV. Samples were prepared by placing 20 μl of an ethanol dispersion of the beads on a carbon-coated copper grid 300 mesh.

Tracking procedure

The tracking routine starts with a fast raster scan of a large area of the sample in which the particle of interest can be observed. Then, we select the particle to be tracked by clicking on top of its image. This directs the laser beam to the chosen particle by changing the DC offset values of the output of the 3-axis card for the x, y, and z coordinates. This point is considered as the initial coordinates for the tracking.

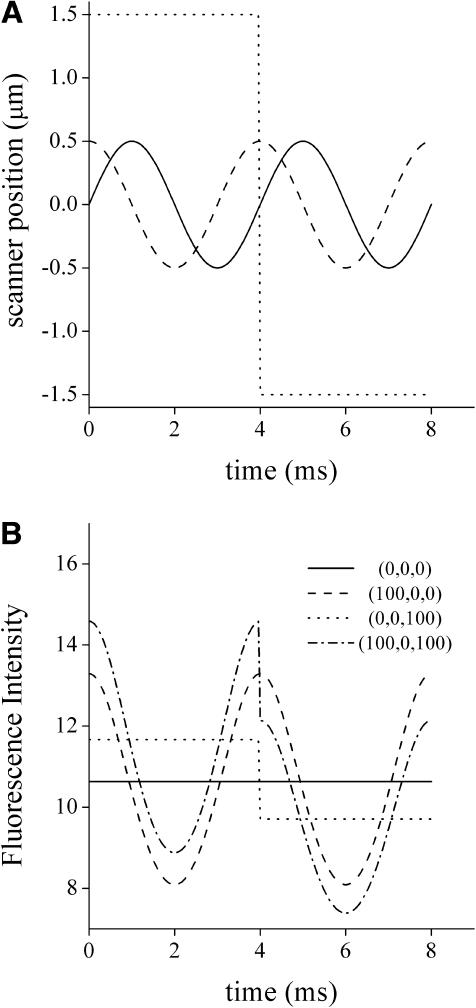
During each cycle of the tracking routine, the excitation beam traces n circular orbits in a plane above the particle and n orbits in a plane below (Fig. 2 A). The diameter of the orbit is equal to the x,y-width of the point spread function (PSF), and the scanned z planes are separated in a distance equal to the z-width of the PSF.

FIGURE 2.

Intensity profile simulated during a cycle of the tracking routine. (A) The coordinates x (solid), y (dashed), and z (dotted) of the scanner during one cycle of tracking are represented as a function of time. (B) The fluorescence intensity signal as a function of time was calculated according to Eqs. 1 and 2 considering the following positions for the particle (in nm): (0,0,0), (100,0,0); (0,0,100); (100,0,1000). For the simulation, we considered the following parameter values: w_o = 500 nm, B = 0, F_o = 10⁶, r_x,y = 500 nm, r_z = 1500 nm, f = 250 Hz, λ = 780 nm.

The PSF was measured from an image stack obtained by raster scanning a bright small fluorescent particle at different z planes. The dimensions of the PSF were calculated by fitting one-dimensional Gaussian functions to the intensity profiles in the x-, y-, and z-directions.

In a typical experiment, the frequency of the z-square wave is 8 or 16 times slower than that of the x and y sine waves. Thus, the x,y-scanning mirrors trace n = 4 or 8 circular orbits in each focal plane (2n orbits per cycle). The fluorescence intensity is averaged over the n orbits in each plane to improve the signal/noise ratio (S/N). Fluorescence data is collected at high frequency (f_data = 16 or 32 kHz) as the laser moves around the particle.

As demonstrated by Kis-Petikova and Gratton (2004) and Berland et al. (1995), the fluorescence intensity (F) during the scanning is a periodic function of time (t):

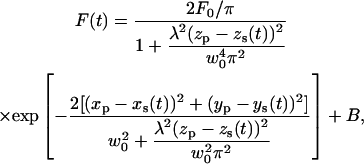(1)

where w_o is the beam waist, λ is the wavelength, B is the background intensity, and F_o is a constant. The subscripts p and s refer to the particle and the scanner coordinates, respectively.

For the scanning routine described above, the coordinates of the scanner vary as a function of time as follows:

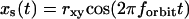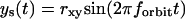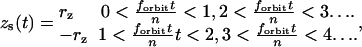(2)

where r_x,y is the x,y-circular orbit radius, r_z is half the amplitude of the z-square wave, and f_orbit is the frequency of the circular orbit.

According to these equations, the absolute position of the particle (x_p, y_p, z_p) can be determined by measuring the fluorescence intensity while moving the laser beam as a function of time. Fig. 2 B represents intensity profiles simulated for particles situated at different positions relative to the center of the scanner. It is clear that the intensity signal is very sensitive to the position of the particle.

After each cycle of the tracking routine, the current coordinates of the particle are determined on the fly from the phase and modulation of the fluorescence signal calculated by Fast Fourier Transform. Then, the center of scanning is moved to this new position and a new cycle of the tracking routine starts. In other words, during the tracking routine, the scanner follows the particle by changing its position to that calculated for the particle in the previous cycle. In an ideal tracking experiment, the scanner is always on top of the particle and the positions of the scanner and the calculated for the particle are identical.

If the measured intensity drops below a set threshold value corresponding to the background intensity, it is assumed that the scanner is no longer tracking the particle. In this case, the diameter of the circular orbit will gradually increase, and the center of z-scanning will progressively change. Thus, the laser beam explores a larger volume until it finally detects the lost particle. Once the particle is found, the center of scanning jumps to its position and the tracking routine resumes as before.

The method described above can also be used to track two particles simultaneously. The initial positions for the particles are set by clicking them on the fluorescence image. The tracking routine starts on top of one of the particles; after one tracking cycle, the laser jumps to the position of the second particle and does another cycle. Once this cycle is finished, the center of scanning is moved to the new position determined in a previous cycle for the first particle, thus the positions of the particles are recovered alternately. If one or both particles are lost, the procedure for finding them is similar to that described above for the case of one particle tracking.

Analysis of single-particle trajectories

Single-particle trajectories were analyzed in a similar manner to that described by Saxton and Jacobson (1997) with the exception that the particle motion was extended at three dimensions instead of two. Briefly, we calculated the mean-square displacement (MSD) as a function of a lag time (τ) for lags <¼ of the total data points:

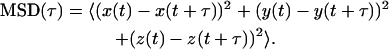(3)

To quantitatively analyze the motion of the particles, it is helpful to classify the trajectories in terms of simple models. Analytical forms of the equations for various types of motion have been derived (Saxton and Jacobson, 1997):

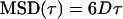(4)

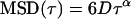(5)

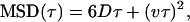(6)

where D is the diffusion coefficient, v is velocity, and α is a constant <1. These equations consider normal random diffusion (Eq. 4), anomalous subdiffusion (Eq. 5), and directed motion with diffusion (Eq. 6) in three dimensions.

These models were fitted to the experimental data, and the best fitting model provides the parameters D, v, and/or α for the particle motion.

RESULTS

Evaluation of the performance of the tracking method

In the previous section, we described a method for tracking particles in three dimensions. To quantify the accuracy and performance of this method, we mounted a linear voltage differential transformer feedback-controlled x,y-piezo stage (Polytec PI) on the microscope, allowing us to move the sample in defined trajectories in the focal plane by changing the applied voltage to the piezo stage.

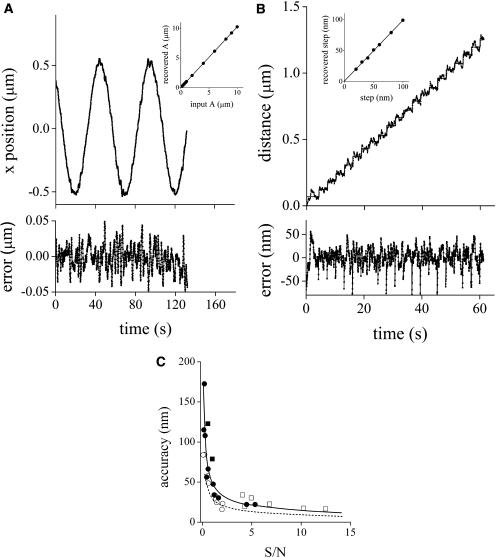
In the first calibration experiment, we dried a dispersion of 500-nm fluorescent beads onto a coverslip and applied a sine wave voltage to the x- or y-direction of the piezo stage with a frequency of 0.02 Hz and amplitudes increasing from 0.1 to 10 μm. The recovered amplitude of the particle motion was linearly related to the input amplitude with slopes of 1.026 ± 0.003 (x axis) and 1.078 ± 0.005 (y axis) and ordinates equal to zero. Fig. 3 A shows the recovered trajectory for a bead moving in a sine wave of 1 μm amplitude in the x direction. The inset to this figure shows the calibration curve obtained for this axis.

FIGURE 3.

Tracking accuracy. 500-nm fluorescent beads dried onto a coverslip were moved in a sine wave of amplitudes in the range 0.1–10 μm and frequency of 0.02 Hz (A) or in 20 steps of 20–100 nm separated in time by 3 s (B). The tracking routine was run as described in Materials and Methods with f_data = 16 kHz, f_orbit = 250 Hz, n = 8, r_x,y = 0.7 μm, and r_z = 2.5 μm. Trajectories recovered for beads moving 1 μm in a sine wave (A) or in 60 nm steps (B). The insets to the figures show the amplitude recovered by fitting the bead trajectories to sine waves plotted as a function of the input amplitude (A) and the average step size recovered plotted as a function of the input step size (B). Dependence of the tracking accuracy on the signal/noise ratio (C). The position of fixed beads with diameters (nm): 552 (□), 100 (○), 24 (▪), and 14 (•) were determined at different laser powers in the range 0.1–15 mW, using the following parameters for the tracking routine: f_data = 32 kHz, f_orbit = 250 Hz, n = 16, r_x,y = 0.7 μm, and r_z = 2.5 μm. The accuracy of the tracking was calculated as described in the text. The continuous line represents the fitting of the following function: 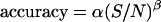with α = 49 ± 5 nm, β = 0.54 ± 0.08. The dashed line represents the theoretical accuracy.

To test the ability to track in the z-direction, we mounted the piezo stage perpendicular to the microscope stage, allowing the sample to be moved along the optical axis of the microscope. By following a procedure similar to that described above, we verified that the trajectories recovered for particles moving in the z-direction agreed with that of the input sine waves. The recovered amplitude of the particle motion was linearly related to the input amplitude with a slope of 0.97 ± 0.02 and ordinate equal to zero.

To assess the performance of the tracking method for distances in the nanometer range, we used a nanometric stage (Mad City Labs (Madison, WI) Nano-Bio 2) with 0.7 nm position accuracy in closed-loop scanning mode. The slide was moved in defined x- or y-steps ranging from 20 to 100 nm. Fig. 3 B shows the trajectory recovered for a particle moving in steps of 60 nm in the x direction. The recovered step size was linearly related to the input step size (inset to the figure) with slopes of 1.00 ± 0.01 (x axis) and 1.005 ± 0.006 (y axis) and ordinates equal to zero.

For the experiments tracking immobilized beads in three directions, the calculated error in the particle position was 20 nm along each axis. This value was calculated by averaging the standard deviations obtained for the x, y, and z coordinates after 600 tracking cycles. It is important to mention that the theoretical error for the particle position determination—due to the Poissonian noise in the photon counting—decreases with the square root of the S/N ratio (Kis-Petikova and Gratton, 2004). This relation indicates that the accuracy of the tracking would increase, for example, by increasing the integration time or by improving the signal (e.g., using brighter particles).

Fig. 3 C shows the accuracy on the determination of the position measured for beads of different sizes (10–500 nm diameter) as a function of the signal/noise ratio, which was modified by varying the excitation laser power. The figure shows that the accuracy of the tracking is approximately constant for S/N higher than 2 and increases with square root dependence for lower values of S/N, as predicted by theory. It is also seen that the accuracy is independent of the size of the fluorescent beads.

In addition, the figure shows the theoretical accuracy of the particle position as a function of S/N. These values were obtained by using the tracking program to simulate and track a particle with diffusion coefficient equal to zero, variable brightness, and considering a PSF of dimensions identical to that determined experimentally. For this simulation, the fluorescence of the background was set to a constant value. The accuracy was determined by tracking the simulated particle using the same set of parameters that were used in the experiment shown in Fig. 3 C. It can be observed that the theoretical limit cannot be reached experimentally due to instrumental factors such as thermal and mechanical jitter that contribute to the noise of the measurements. Also, we were able to verify that the experimental z-accuracy is limited by the time-response of the nanopositioner. Control experiments indicated that this parameter is critical when tracking with short integration times (data not shown).

Taken together, these results show that the method allows an accurate tracking of particles in three dimensions.

Diffusion of beads in glycerol

In the previous section, it was shown that the 3-D tracking method developed here is suitable for tracking particles moving in predefined trajectories in the x-, y-, or z-directions. However, as a more realistic test of its potential for tracking particles in live cells, we decided to explore the performance of the tracking routine in solution. With this aim, we studied the random diffusion of 500-nm fluorescent beads in solutions of increasing glycerol concentration. A small volume of each sample (80 μl) was placed between a coverslip and a slide previously treated for 20 min with 5 mM octadecyltrichlorosilane in toluene and washed with toluene, acetone, and ethanol. This chemical treatment was done to coat the glass surface with hydrophobic groups, thus preventing the adsorption of beads on the surface and minimizing its effects on the random motion of the particles.

After the procedure previously described, we measured 20–30 trajectories for each glycerol concentration. For beads in solutions of low glycerol concentration, selecting a bead to track from the initial image was nearly impossible due to its fast diffusion rate. Instead, we started the tracking in an arbitrary position and left the scanner to find a particle by itself, following the routine described in the Materials and Methods section.

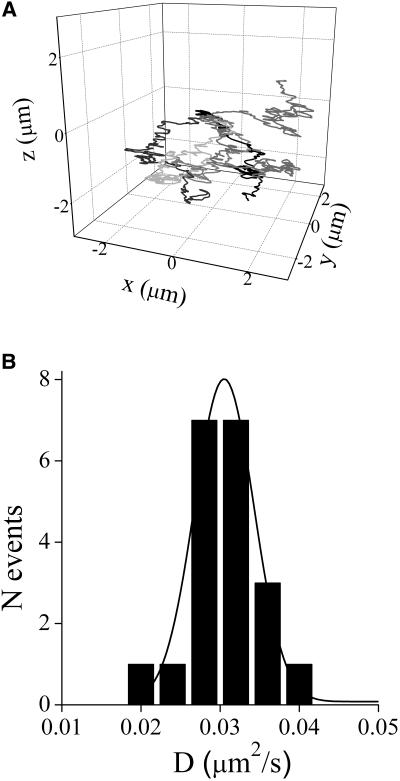
Fig. 4 A shows some of the trajectories measured for the 80% glycerol sample. The calculated MSD as a function of time lag for these trajectories verifies that in most cases, the MSD varies linearly with time, as is expected for a normal random diffusion process (see Eq. 4).

FIGURE 4.

Tracking fluorescent beads in glycerol solutions. Suspensions of 500 nm fluorospheres in solutions of glycerol (0%–80%) were placed between a slide and a coverslip previously treated with octadecyltrichlorosilane. (A) Trajectories obtained for six different beads in 80% glycerol. The initial point for the trajectories was arbitrarily set in (0,0,0). (B) Histogram of diffusion coefficients obtained by fitting Eq. 5 to the MSD versus τ plot for trajectories of beads in 80% glycerol. The continuous line represents the Gaussian distribution function fitted to the experimental data. The tracking routine was run as described in Materials and Methods with f_data = 16 kHz, f_orbit = 250 Hz, n = 4, r_x,y = 0.7 μm, and r_z = 2.5 μm. The temperature was 23.0°C.

For each glycerol concentration, we constructed a histogram of the calculated diffusion coefficients. The mean value of D and its error were obtained by fitting the histogram with a Gaussian distribution (Fig. 4 B). Fig. 5 shows the measured values of D at different glycerol concentrations as a function of the inverse of the viscosity. According to the Stokes-Einstein relationship, these parameters are related by (Atkins, 1978):

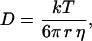(7)

where T is the absolute temperature, k is the Boltzmann's constant, r is the particle radius, and η is the viscosity of the solution.

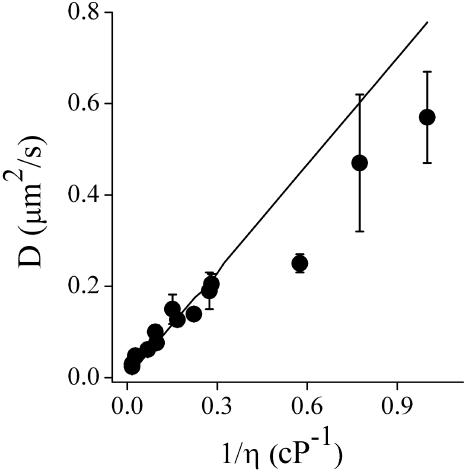
FIGURE 5.

Diffusion of fluorescent beads in glycerol solutions. The experimental diffusion coefficients obtained as described in the legend to Fig. 4 are represented as a function of the inverse of the viscosity (circles). The continuous line represents the values of D obtained from the Stokes-Einstein relation (Eq. 7).

We took transmission electron microscopy (TEM) images of a beads sample to precisely determine the average radius of the beads and obtained a value of 276 ± 5 nm. The continuous line in Fig. 5 represents the theoretical values of D, calculated using Eq. 7 considering this value for the beads radius. Comparing this to the measured values, a negative deviation from the expected behavior is seen. This deviation can be explained by considering that the Brownian motion is affected by the trapping of beads in the focus of the laser beam (Chirico et al., 2002). To test this hypothesis, we tracked beads suspended in water using three different values for the laser power (0.8, 1.3, and 3.4 mW) and obtained the following values for D: 0.5 ± 0.1, 0.3 ± 0.1, and 0.02 ± 0.01 μm²/s, respectively. This indicates that the motion of the beads is restricted by optical trapping, explaining the deviation between the theoretical and experimental values.

To better assess the performance of the tracking routine in the high-viscosity limit (η > 3.7 cP), we used Eq. 7 to fit the data in Fig. 5 over this range and calculated the experimental particle radius from the best-fit parameters. We obtained a value of r = 290 ± 36 nm, which agrees with the measured TEM value (within the error range). Note that a slightly larger size for the particles in solution relative to the TEM measurements may be expected due to hydration.

Phagocytosis of fluorescent beads by fibroblasts

To illustrate the broad range of biological applications possible with the 3-D particle tracking method, we studied the phagocytosis of beads by fibroblasts. Carboxylate-coated yellow-green fluorescence polystyrene beads were coated with BSA and incubated in the culture medium with fibroblasts previously starved in Dulbecco's phosphate buffered saline for 2 h at 37°C. To select the beads that are interacting with the cells, we register simultaneously the IR-DIC and fluorescence images of the sample. The fluorescence image allows us to detect a fluorescent bead, whereas the IR-DIC image provides the details of its position with respect to the cell and allows us to follow the motion of the cell during the tracking. Generally, we took IR-DIC images every 10–15 s and, after tracking the bead, constructed a movie overlaying the cell with the bead trajectory.

During the first few minutes after adding the beads, we observed that most of them that are in contact with cells had a high mobility and some of them even detached from the cell. After 2–4 h of incubation, we observed a more directed motion for the beads interacting with cells. Fig. 6 shows a two-dimensional (2-D) projection of trajectories for beads moving according to this description overlapped with the DIC images of the cells. In the case of the trajectory shown in Fig. 6 B, the DIC image shows that the bead is moving toward the perinuclear region of the cell. To determine if the bead movement is due to their interaction with the cell, we incubated fibroblasts with BSA-coated beads for 2 h and fixed the cells with 1.6% formaldehyde in Dulbecco's phosphate buffered saline. We verified that, after fixation, the beads only move several nm or less, i.e., within the error of the tracking method (data not shown).

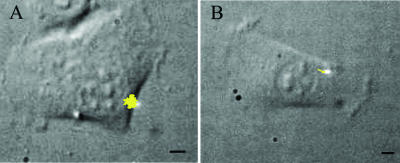
FIGURE 6.

Phagocytosis of BSA-coated beads. Trajectories of a bead loosely attached to a cell (A) and of another bead moving through a linear path toward the perinuclear region (B). The bright spot corresponds to the position of the laser at the beginning of the tracking. The yellow lines correspond to the 2-D projections of the trajectories. The tracking routine was run as described in Materials and Methods with f_data = 16 kHz, f_orbit = 250 Hz, n = 8, r_x,y = 0.7 μm, and r_z = 2.5 μm and lasted 11 min (A) and 16 min (B). Bars = 5 μm.

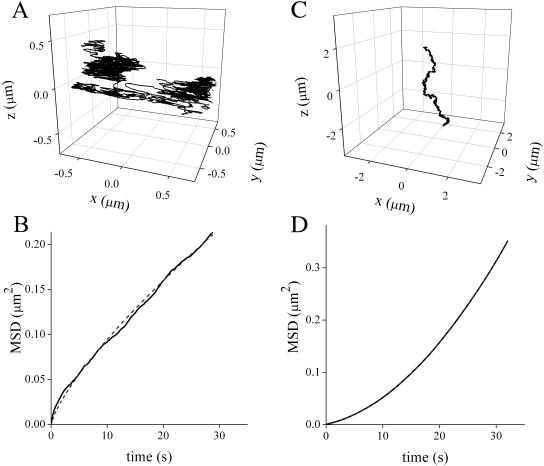
As mentioned before, collagen phagocytosis by fibroblasts is a key process to maintain tissue homeostasis in healthy mammalian soft connective tissue. To explore this process, we assayed the phagocytosis of collagen-coated beads. In this case, we observed a similar behavior to that previously described for albumin-coated beads. During the first moments of incubation, the beads attached to the cell membrane and moved in a restricted region. Fig. 7 A shows the 3-D trajectory measured for a bead whose motion follows this pattern. We plotted MSD as a function of τ for these trajectories and obtain the best-fit with an anomalous diffusion model (Fig. 7 B), suggesting that the random motion of the particle is restricted by interaction with the membrane. The best fitting parameters were D = 4 × 10⁻³ ± 4 × 10⁻³ μm²/s and α = 0.7 ± 0.3 (N = 7).

FIGURE 7.

Phagocytosis of collagen-coated beads. 3-D trajectories of a collagen-coated bead loosely attached to a cell (A) and following a linear path (C). (B) and (D) MSD versus τ plots for these trajectories. The dashed lines correspond to the fitting of anomalous motion (Eq. 5) and diffusion + transport (Eq. 6) models, respectively. The best fitting parameters for these trajectories were D = 2.75 × 10⁻³ ± 2 × 10⁻⁵ μm²/s and α = 0.759 ± 0.002 (B) and D = 4.4 × 10⁻⁴ ± 1.6 × 10⁻⁷ μm²/s and v = 1.6 × 10⁻² ± 9 × 10⁻⁶ μm/s (D). The trajectories lasted for 5 and 8.7 min, respectively. The tracking routine was run as described in Materials and Methods with f_data = 16 kHz, f_orbit = 250 Hz, n = 4, r_x,y = 0.7 μm, and r_z = 2.5 μm.

After 3–4 h of incubation, it was seen that some of the beads moved through the cell following a linear path. Fig. 7 C shows the 3-D trajectory of a particle moving in this manner. For phagocytosed beads, we saw that the experimental data were best fit with a directed motion plus slow diffusion model (Fig. 7 D), suggesting that there is an active process driving the motion of the bead. The best-fit parameters were D = 4 × 10⁻⁴ ± 3 × 10⁻⁴ μm²/s and v = 9 × 10⁻³ ± 4 × 10⁻³ μm/s (N = 7). To verify that the beads exhibiting this behavior were actually phagocytosed, we incubated the cells with collagen-coated beads for 3 h. After incubation, the cells were trypsinized and washed with fresh medium. By following this procedure, the beads that are loosely bound to the cells are removed (McKeown et al., 1990). Then the cells were plated in a fibronectin-coated dish and incubated for 1 h.

We observed that ∼30% of the tracked beads followed linear trajectories. The rest of them showed highly restricted motion and were located in the perinuclear region (data not shown), suggesting that they were already transported through the cytoplasm and arrived at their final destination as a consequence of the long incubation required for this experiment. This result agrees with Caspi et al. (2001), who observed that after reaching the perinuclear region, the engulfed beads show a restricted random diffusion.

Tracking two particles

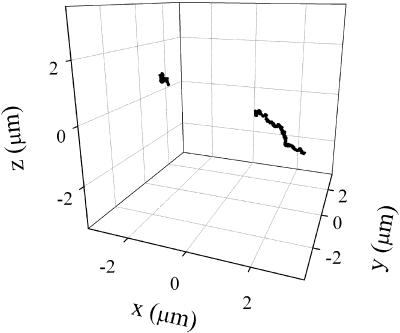
As mentioned before, the method described in this article is easily extended to allow the tracking of two particles simultaneously. This can be used, for example, to measure the relative distance between two particles as a function of time. To illustrate this possibility, we followed the motion of two beads interacting with the same cell. Fig. 8 shows the trajectories recovered for this pair of beads, one of them showing a constrained motion and the other showing a directed motion.

FIGURE 8.

Tracking two particles. 3-D trajectories obtained simultaneously for two beads coated with collagen interacting with a cell. The tracking routine was run as described in Materials and Methods with f_data = 16 kHz, f_orbit = 250 Hz, n = 4, r_x,y = 0.7 μm, and r_z = 2.5 μm. The tracking lasted 4 min.

DISCUSSION

In this work, we described a method that allows the tracking of fluorescent particles in three dimensions over a wide distance range using two-photon microscopy. The control experiments—tracking fluorescent microspheres moving in known paths—demonstrated that the method can recover trajectories up to 10 μm (Fig. 3) with 20 nm precision and a time resolution of 32 ms. The performance of the tracking was shown to be equally good in the x-, y-, and z-directions. We have not yet explored the performance of the tracking system for distances >10 μm. However, in the x- and y-directions, there are no limitations for the tracking and, in the z-direction, the system is only limited by the working distance of the objective and the maximum travel distance of the z-piezo, which is 100 μm.

We verified that the time resolution of this new method is between 32 and 64 ms in three dimensions, depending on the signal/noise ratio. When tracking in two dimensions, the time resolution can be lowered to 16 ms.

For the data presented in this work, a 20× (dry) objective was used. Calibration experiments similar to that described in Fig. 3 were also done using other objectives (results not shown). The tracking was equally accurate using either a 63× (NA 0.8, dry) or a 60× (NA 1.2, water immersion) objective. However, when using an oil immersion objective, we failed to recover the trajectory of the beads when they were moving out of the focal plane. In this case, it seems that the objective and coverslip may “stick” together and move more or less rigidly with the z-nanopositioner.

The performance of the tracking algorithm is not sensitive to the exact shape of the PSF. The tracking is achieved by minimizing the modulation of the signal as the beam orbits around the particle. The only necessary condition is that a minimum exists and that the shape of the minimum does not change over time. In practice, the algorithm only minimizes the modulation of the first harmonic. If the PSF or the particles lack symmetry, then the higher-order harmonics are affected. Extending this work to include the analysis of higher-order harmonics may be useful for such things as following the rotational dynamics of nonsymmetric particles.

The tracking method was also shown to be suitable for measuring the trajectories of particles moving freely in solution. Figs. 4 and 5 show that the diffusion coefficients of 500-nm beads in solutions of high viscosity (η > 3.7 cP) can be measured with high precision. Experiments done changing the laser power show that as the power decreased, the apparent value of the diffusion coefficient increased, suggesting optical trapping of the beads.

To illustrate the potential for this new technique in studying cellular processes, we explored the phagocytosis process. By combining the particle tracking with IR-DIC imaging, it was possible to track the particle and observe its motion within the cell simultaneously. This provides valuable information about the location and dynamics of the particle in the cellular environment.

During the incubation of fibroblasts with fluorescent beads, we saw that in the initial moments some of them attached to the cells, following trajectories that were best fit with an anomalous diffusion model (see Eq. 5). According to Saxton (1994), this may be explained by the binding of the particle to certain membrane elements. Thus, the anomalous motion could be a consequence of the initial adsorption of the beads to certain domains in the membrane and/or interactions with the receptors.

After 2–3 h of incubation, it was seen that the beads tended to move in linear paths, heading mainly in the direction of the perinuclear region. The trajectories of these beads followed a directed motion model (see Eq. 6) characterized by a diffusion coefficient of 10⁻⁴ μm²/s and a velocity of 0.01 μm/s. The latter value is on the order of the average velocity determined by Caspi et al. (2001) for 3-μm polystyrene beads engulfed by SV80 human fibroblasts (0.008–0.03 μm/s), suggesting that a similar mechanism may be responsible for the observed motion despite the differences in cell type and bead size.

Several authors (e.g., see Blocker et al., 1997; Caspi et al., 2001; Toyohara and Inaba, 1989) have suggested that the cytoskeleton is involved in the motion of phagosomes through the cytoplasm toward the perinuclear region. This directional movement facilitates maturation of phagosomes by favoring their interaction with the endocytic compartments (Blocker et al., 1997). In this way, a possible explanation for the linear trajectories observed for phagocytosed beads is that they move along microtubules through the action of molecular motors. The first term in Eq. 6 reflects the random diffusion of the bead when it is not bound to the cytoskeleton. The second term is related to the motion due to molecular motors. The fitting of Eq. 6 to the experimental data shows that the contribution of free diffusion is much lower than that of active transport, suggesting that the phagocyte remains bound to the cytoskeleton most of the time.

From these results, it is seen that 3-D particle tracking can provide a detailed description of the molecular dynamics in living cells. Conversely, when using a 2-D tracking method, important information about the motion of the particle along the optical axis is often neglected. Also, the longer trajectories obtained in 3-D tracking result in a better description of the particle motion and a higher precision for the diffusion coefficients and other parameters determined from the MSD analysis. This improvement can be seen in the low errors of the parameters obtained by fitting the data shown in Fig. 7. For all of the parameters, the error was <0.7%.

On the other hand, from the combination of IR-DIC and tracking we could obtain simultaneous information about the characteristics of the motion of the particle; calculate diffusion coefficients, velocities, etc.; and locate with high precision the particle in the cell. This can provide important information regarding the mechanisms involved in the particle motion.

The method presented in this work also allows for the simultaneous tracking of two particles, even when they are located in different focal planes. This is a useful option since it can be applied to study the relative distance between two particles as a function of time. When measuring in live cells, this can help to decouple the motion of the particles from the overall motion of the cell.

Using two-photon microscopy makes this method well suited for biological applications since it provides significantly lower out-of-focus photodamage and photobleaching than other fluorescence microscopies. Also, during the tracking we focused the laser in a small volume surrounding the particle, resulting in reduced photodamage of the rest of the sample. In contrast, methods that employ video cameras (see for example, Anderson et al., 1992; Hicks and Angelides, 1995; Wilson et al., 1996) require repetitive exposures of large sample volumes that could result in significant damage.

In summary, we demonstrated that using a simple scanning technique with a two-photon microscope, we are able to track fluorescent particles moving in three dimensions, with a time resolution of 30–60 ms and spatial resolution in the 20 nm range, depending on the particle brightness and integration time. Also, we demonstrated that the method is suitable for studying the dynamics of particles in biological systems. To our knowledge, this is the first method described for the fast tracking of particles in three dimensions using a two-photon microscope.

We are currently applying this new method to explore the dynamics of DNA in the cell nucleus. The new method is allowing us to obtain a description of the DNA motion with temporal and spatial resolutions not reached before. We hope that further progress in this project will provide valuable information regarding DNA dynamics.