Abstract
Cochlear outer hair cells (OHCs) are thought to play an essential role in the high sensitivity and sharp frequency selectivity of the hearing organ by generating forces that amplify the vibrations of this organ at frequencies up to several tens of kHz. This tuning process depends on the mechanical properties of the cochlear partition, which OHC activity has been proposed to modulate on a cycle-by-cycle basis. OHCs have a specialized shell-core ultrastructure believed to be important for the mechanics of these cells and for their unique electromotility properties. Here we use atomic force microscopy to investigate the mechanical properties of isolated living OHCs and to show that indentation mechanics of their membrane is consistent with a shell-core organization. Indentations of OHCs are also found to be highly nonhysteretic at deformation rates of more than 40 μm/s, which suggests the OHC lateral wall is a highly elastic structure, with little viscous dissipation, as would appear to be required in view of the very rapid changes in shape and mechanics OHCs are believed to undergo in vivo.
INTRODUCTION
The mammalian hearing organ contains two types of sensory cells, the inner and outer hair cells (OHCs), which are both essential to the mechano-electrical transduction process leading to sound detection (von Bekesy, 1960). Whereas inner hair cells are usually considered to function as true sensors, OHCs are thought to be involved in the “cochlear amplifier”, an active tuning process responsible for the extreme sensitivity and frequency selectivity of the hearing organ. Isolated OHCs undergo rapid length changes in response to changes in their transmembrane potential (Ashmore, 1987; Brownell et al., 1985). This so-called OHC electromotility can work in phase with electric stimuli at frequencies reaching 80 kHz and more, leading to the production of forces at similar frequencies (Frank et al., 1999). The mechanical properties of OHCs also change in response to voltage stimulation, in a way that is tightly correlated with the length changes (He and Dallos, 1999). Motile or mechanical responses of OHCs presumably occur also in vivo, driven by variations in the receptor potential of the cells. Such changes are believed to be at the heart of the feedback mechanism at work in the cochlear amplifier.
The electromotile properties of OHCs are thought to be caused by conformational changes of voltage-sensitive motor units situated in their plasma membrane (Dallos et al., 1991; Hallworth et al., 1993; Kalinec et al., 1992), one prominent candidate for the motor being the protein prestin (Oliver et al., 2001; Zheng et al., 2000). The large magnitude, short response time, and directionality of the length changes observed in OHCs are probably dependent on the special structure of these cells. OHCs are cylindrical in shape with a radius slightly smaller than 5 μm and lengths ranging between 15 and 100 μm or more, depending on their location along the cochlea. The basal part of the OHC contains the nucleus, and its apex supports a cuticular plate from which a bundle of stereocilia projects. Between the base and apex lies an axial core circumscribed by the lateral wall, which comprises the largest portion of the cell body. This lateral wall appears 100 nm thick by electron microscopy with a unique trilayer organization composed of an outermost plasma membrane, the cortical lattice, and the innermost subsurface cisternae (Brownell et al., 2001, and references therein). The cortical lattice is a protein skeleton located ∼25 nm below the plasma membrane, which extends the length of the cell. It is principally composed of actin filaments oriented on average circumferentially, and cross-linked transversally by spectrin (Holley and Ashmore, 1988; Wada et al., 2003). The plasma membrane appears to be attached to an array of ‘pillars’ of unknown composition that are fixed to the actin filaments of the cortical lattice (Flock et al., 1986). The subsurface cisternae are a complex of membrane-bound organelles of unclear function, situated immediately beneath the cortical lattice.
In addition to the above ultrastructural features, the OHC appears to have a small turgor pressure estimated to ∼1kPa, which is known to affect the expression of electromotility (Adachi et al., 2000; Chertoff and Brownell, 1994; Ratnanather et al., 1993). This turgor is assumed to apply a prestress to the lateral wall that helps maintain the cylindrical shape of the cell and contributes to its rigidity. This has led to a picture of the OHC as composed of a thin elastic shell enclosing a pressurized fluid core (Brownell et al., 2001). As a result, models of OHC mechanics have been developed mainly on the basis of elastic shell theory (e.g., Flügge, 1960). First models (Iwasa and Chadwick, 1992; Ratnanather et al., 1996) described the OHC wall as a thin elastic cylinder with isotropic elastic properties, but more refined models were also developed, taking account of the orthotropic properties of the cortical lattice (Spector et al., 1996, 1998; Tolomeo and Steele, 1995; Tolomeo et al., 1996) as well as the composite structure of the OHC lateral wall (Raphael et al., 2000; Spector et al., 1998, 2002; Sugawara and Wada, 2001).
The above models assume that the mechanical properties of the OHC are attributable to a shell-core organization of the cell. Although this view seems well accepted, there has been little evidence supporting it at the experimental level. A large amount of research has focused on measuring the mechanical properties of OHCs, using various experimental techniques, e.g., calibrated probes (Chan and Ulfendahl, 1999; Hallworth, 1995; Holley and Ashmore, 1988; Ulfendahl et al., 1998) and microchamber or micropipette aspiration techniques (Frank et al., 1999; Gitter et al., 1993; Lue and Brownell, 1999; Nguyen and Brownell, 1998; Sit et al., 1997). However, these experiments were designed to measure the stiffness of the OHC body as a whole, and they did not probe the local mechanics of the lateral wall.
The possibility of using atomic force microscopy (AFM) to investigate the ultrastructure and mechanics of isolated OHCs have been demonstrated in a number of recent studies (Le Grimellec et al., 2002; Sugawara et al., 2002, 2004; Wada et al., 2003). In two of these reports, chemical fixation was applied to the cells. It is, however, known that chemical fixation affects the morphology of the OHCs (e.g., Slepecky and Ulfendahl, 1988) and, as shown in other cell types, alters cellular mechanical properties as well (Hoh and Schoenenberger, 1994). Thus, Sugawara et al. (2002) studied by AFM the mechanical properties of OHCs in physiological conditions and, more recently (2004), of inner hair cells and several supporting cells of the hearing organ. Here we used AFM to investigate more closely the mechanical behavior of isolated, living OHCs in relation to their ultrastructure. We measured the indentation response of the cells at different locations along their lateral wall and investigated their viscoelastic properties. Our results provide direct mechanical evidence of a highly elastic shell-core organization of the OHC clearly in line with what is known about the function of these cells and their behavior in vitro.
METHODS
Cell preparation
Pigmented guinea pigs (200–400 g) were anaesthetized and decapitated. The temporal bones were excised and the middle ear cavities opened to expose the cochleas. Each cochlea was detached and transferred to medium bath, Eagle's minimum essential with Hanks' salts (without L-glutamate, Gibco-BRL, Life Technologies, Gaithersburg, MD). The bony shell was gently removed and the organ of Corti was scraped off from the basilar membrane. Coils of the organ of Corti were enzymaticaly treated for 3 min with collagenase (Sigma (St. Louis, MO) c-0130, concentration 0.5 mg/ml). A constricted glass pipette was used to mechanically separate cells from each other. The suspension of OHCs was transferred to a petri dish coated with either Cell-Tack (Becton Dickinson Labware, Franklin Lakes, NJ; 25% dilution in 0.1 M NaHCO3) or polylysine (Sigma P-6407, concentration 0.1mg/ml). CellTak is a preparation derived from the mussel adhesive protein that is widely used to promote cell attachment to plastic or glass, and polylysine is another widely used adhesive. The cells were left for ∼2 min in the middle of the dish in 1–2 ml medium to make them attach on a smaller area. The rest of the medium (10 ml) was then added and the petri dish was placed on the AFM stage. All experiments were performed at room temperature. The use of animals in this study was done in accordance with Swedish regulations for animal care and use (permit No. N10/01).
Attaching the cells to a substrate
Of the two adhesive substrates that we tested for immobilizing freshly isolated, living OHCs on a plastic petri dish, polylysine turned out to be the most effective; however, cells attached with this substrate fairly quickly showed morphological signs of deterioration. Using Cell-Tak was less effective for immobilizing the cells, and often dozens of OHCs had to be examined before identifying one that was well attached. Nevertheless, these cells were usually in much better shape than cells attached with polylysine. Their appearance remained healthy for the duration of the experiments (up to 2 h after dissociation), and enough of them attached on the dish surface (up to a few tens per cm2) to allow for AFM experiments.
Atomic force microscopy
Experiments were performed using a Bioscope AFM equipped with a conventional fluid cell, mounted on a Zeiss (Jena, Germany) Axiovert 135 and controlled by a Nanoscope IIIa controller (Digital Instruments, Santa Barbara, CA). Unsharpened V-shaped silicon nitride “Microlever” cantilevers (Digital Instruments) with a nominal spring constant 0.01 N/m were used. These cantilevers had the expected resonant frequency, and conservatively their nominal spring constant is accurate to within a factor of three.
Visualization and selection of isolated OHCs
The cells were viewed with the inverted light microscope on which the Bioscope is mounted. All experiments were recorded on videotape with a charge-coupled device camera to monitor both the cells and the AFM cantilever and to measure the cells' length and other morphological characteristics off-line. With the isolation procedure used, short OHCs usually survived poorly, and mainly long OHCs remained in good conditions. Care was taken to choose cells with healthy appearance (showing no shrinking, swelling, dislocation of the nucleus, or visible motion of organelles in the cytoplasm) and well attached to the substrate. The lengths of the selected OHCs ranged from 50 μm to 100 μm. Attachment of the cells was tested by tapping the side of the sample stage while monitoring the cell to see if it moved on the petri dish.
Force curve acquisition
In a typical indentation experiment, the cantilever was placed at three positions along the OHC body, corresponding to the basal, middle, and apical regions, and force-distance curves were acquired (scanning the cantilever vertically over 5 μm and collecting 1024 data points per curve). For each position the force-distance curve was recorded at three slow, but different, scanning rates (1, 5, and 10 μm/s) for cross-checking. Regions close to the nucleus or the cuticular plate were avoided, to minimize the contributions to the force curves due to the mechanical response of cell components other than the lateral wall. In a number of experiments, the cantilever was placed in the middle part of the cell body and force curves were collected continuously during 1 h at a rate of 0.5 μm/s while monitoring the shape of the cell with the video camera.
To investigate the viscosity of the OHC lateral wall, the cantilever was placed in the middle position of the cell body, and force curves were acquired at increasing scanning rates (0.5 μm/s up to 93μm/s), averaging 10–20 curves for each frequency. The force curve hysteresis as a function of scanning rate was then analyzed as described below.
Comparison experiments on MDCK cells
Madine-Carby canine kidney (MDCK) cells were grown in Dulbecco's modified Eagle's medium (DMEM, Gibco-BRL, Life Technologies) supplemented with 10% fetal bovine serum at 37°C, 5% CO2; ∼6 × 104 cells were plated onto 15-mm glass coverslips glued to steel disks and used when they were confluent after 4–5 days. Imaging solution was either complete medium or DMEM with 25 mM HEPES buffer. A commercial AFM was used with unsharpened cantilevers with a nominal radius of curvature 50 nm and a nominal spring constant of 0.01 N/m. The measurements were performed at room temperature and atmospheric CO2.
Data analysis
Estimation of contact point and cell indentation
The basic data recorded by the AFM is a force-distance curve, giving the deflection d(z) of the cantilever in contact with the sample (in nanometers) as a function of the height z of the piezo stage used to move the sample. Each force curve shown in the Results section was obtained from an average of 10 curves recorded in series. Before plotting this average, the curves were redressed for any linear bias in the noncontact region, and the location of the contact point z0 was estimated as described by Radmacher (1997), using a least-squares fit of a phenomenological model describing the force-indentation relationship in the contact region. As a model we used a quadratic polynomial in z − z0, to account for both the observed linear behavior of d(z) near contact and for the nonlinearity seen in the curves at larger indentations. This simple model turned out to allow a fairly precise fit in most cases, reproducing closely the break at the contact point with a good estimation of the location of this point and of the initial slope of the curve. The cell indentation is given by δ(z) = z − z0 − d(z). Note that the z axis is directed downwards, as is standard in contact mechanics.
Analysis of elasticity—Epp plot
For purpose of comparison with other AFM studies on living cells, a standard elasticity analysis was applied to the force curves with a custom set of software tools written in the Interactive Data Language (IDL, Research Systems, Boulder, CO). For the analysis, all curves were shifted to the same zero deflection, and selected portions were compared to the expected behavior, derived from the classical solution for the indentation of a linear elastic half-space by a rigid cone (Love, 1939; Sneddon, 1965):
 |
(1) |
where E is the Young's modulus; ν is the Poisson's ratio and is taken to be 0.3 (Maniotis et al., 1997); α is the half angle of cantilever tip (35°); and kc is the spring constant of the cantilever. As above, z is the piezo position and d is the cantilever deflection. According to this formula, an estimate of Young's modulus E can be deduced from the constant term in a linear fit of the dependency between log(δ) = log(z − z0 − d) and log(d). For an ideal (infinitely thick and homogeneous) sample, the modulus estimated in this way is independent of the range of deflection values used in the fit. To assess deviations from the ideal case, it is informative to use, for each deflection value d = d0, the value of E estimated from the tangent at d0 to the function log(δ) = f(log d) (best linear fit near d0), and to plot this value as a function of d0 (so-called Epp-plot). When comparing fresh and swollen cells, we used the same cantilever and the same experimental setup without changing the optical lever sensitivity. Thus changes in modulus when expressed as a ratio are accurate to within the precision of the measurement (better than 10%).
Analysis of force curve hysteresis
We used the surface hysteresis between the approach and retract curves as a relative measure of viscosity. The two force curves (approaching and retracting) were first shifted to the same free deflection value (zero) to account for the effects of extracellular fluid friction acting on the cantilever. This subtraction does not remove additional contributions due to fluid friction acting on the sample. The area under the retract curve was subtracted from the area under the approach curve and then divided by the area under the approach curve and defined as the relative viscosity (Mathur et al., 2001). The relative viscosity was plotted as a function of scanning velocity for MDCK cells (Hoh and Schoenenberger, 1994) and for the OHCs.
RESULTS AND DISCUSSION
Evidence for a shell-core organization of the OHC
AFM indentation measurements on freshly isolated OHCs produced an unusual force versus distance relationship. Most cells that have been examined by AFM show a nonlinear deflection of the cantilever after contact with continuous changes in the slope of the indentation curve (Radmacher, 1997). Such a contact is predicted from Sneddon mechanics (Sneddon, 1965) for the indentation of an infinitely thick, homogeneous and isotropic, elastic half-space by an axisymmetric indenter. Although this model has proven very useful to interpret AFM measurements, cells are neither infinitely thick nor homogeneous. This is apparent when Sneddon mechanics is used to analyze the indentation of thin cells, for which the estimated elastic modulus typically increases as a function of indentation depth. This is a result of the solid support contributing to the indentation measurement, making the cell appear effectively stiffer as the probe approaches the substrate (Akhremitchev and Walker, 1999). Nevertheless, a nonlinear force curve is observed in most cases, reflecting the variation with indentation depth of the contact area between the tip and the sample. For indenters that are not flat-ended, e.g., spherical, conical, or even pyramidal (to which the analysis of Sneddon does not strictly apply), the force curve slope is proportional to the square root of the contact area (Pharr et al., 1992). Since this area is zero at zero indentation, the force curve is expected to be flat at contact.
In contrast to this, indentation measurements on fresh OHCs show distinct breaks in the force curve, with a nonzero slope at contact (Fig. 1 B). The presence of such a break is reminiscent of the behavior of bacteria, which also show a linear force-distance relationship under indentation by AFM (Arnoldi et al., 2000). The ultrastructural analogies between the lateral membranes of OHCs and bacteria have been pointed out (Brownell, 2002). Both appear to be relatively stiff and enclose a pressurized fluid core relatively devoid of skeletal structures. Bacteria have a high turgor pressure (∼100 kPa) to which corresponds a large membrane tension given, according to Laplace's law, by T = PR, where P is the turgor pressure and R is the mean curvature radius of the membrane. In this case the force-distance relationship is linear with a slope determined by the membrane tension, which dominates the force acting on the AFM tip (Arnoldi et al., 2000). The turgor is much smaller in OHCs but should still give a contribution to the force acting on the AFM tip proportional to the indentation distance δ. In addition, the tip force receives contributions from the elastic reaction of the cell membrane (due to its bending and in-plane compression or extension near the indentation dimple), which for the OHC can a priori not be neglected. For an elastic shell of finite geometry under local indentation, the elastic reaction force is a complicated nonlinear function Fshell(δ) of δ. However, it can be shown that Fshell is proportional to δ near contact (Landau and Lifshitz, 1959) with a constant of proportionality kshell defining the elastic contact stiffness of the shell. As a consequence, indentation curves measured on OHCs by AFM are expected to be linear for small indentations, as we observed experimentally. The slope of the curve at δ = 0 defines the contact stiffness of the OHC membrane, given by kOHC = kc dd/dδ|δ=0 = kc (1 − dd/dz)−1 dd/dz|z=0. Estimating kOHC on eight healthy OHCs of lengths ranging between 75 μm and 100 μm, we found very small values in the range 1.6–8.5 × 10−4 N/m, with an average of (3.7 ± 1.8) × 10−4 N/m (n = 23). Performing similar estimates on four cells with lengths in the range 50–65 μm, we found larger values in the range 0.5–2.1 × 10−3 N/m, with an average of (1.5 ± 0.6) × 10−3 N/m (n = 10). Hence a significant dependency of kOHC upon cell length was observed, which we proceed to analyze further below.
FIGURE 1.
(A) Micrograph showing the experimental setup of the experiments: An isolated OHC with the AFM cantilever placed over it. (B) Approach deflection curves acquired on a fresh healthy OHC and on a swollen OHC (the deflection curve on a hard surface is also plotted as reference). The inset shows a zoom of the curves in the region of the contact point.
Thin shell analysis of the OHC contact stiffness
The OHC contact stiffness kOHC receives a priori contributions from both the turgor pressure of the cell and the elastic reaction of the lateral wall. To estimate the elastic contribution kshell, we need to consider the indentation of a thin elastic cylindrical shell under boundary conditions relevant to the OHC. A case relatively simple to understand physically is that of a cylinder free of constraints at both ends, undergoing pure bending (without in-plane compression or extension) under indentation. The indentation is then governed by a nonlocal bending mode in which the cylinder flattens over its whole length. A scaling law for the contact stiffness of the cylinder in this case can be derived from a simple energy argument: the bending energy per unit area of a thin shell under deformation is equal to κ c2, where κ is the bending stiffness of the shell (defined by κ = 1/12 Eh3/(1 − ν2), where E, ν, and h are the shell's Young modulus, Poisson ratio, and thickness, respectively) and c is the change in shell curvature caused by the deformation (Landau and Lifshitz, 1959). For a flattening of height δ, c is of order δ/R2 all along the cylinder. The total bending energy Ebend(δ) for a cylinder of length L and radius R is thus of order κ δ2/R4 × 2πRL ∝ κ L/R3 δ2, which corresponds to a bending spring constant kbend = d2Ebend(δ)/dδ2 ∝ κ L/R3. In the case of a concentrated load applied in the middle point of the cylinder on one side, while the other side is fixed, a detailed calculation of the bending energy of a thin cylindrical shell under flattening (Timoshenko and Woinowsky-Krieger, 1959) leads to the more precise result kbend = AE*h3L/R3, where E* = E/(1 − ν2) and A ≈ 2.24. Unfortunately, this scaling law does not apply to our case because the OHC is not free at both ends. The lateral wall might be considered loosely constrained on the nucleus side, but it is almost rigidly constrained on the apical side by the thick and stiff cuticular plate. Under these conditions, longitudinal extension of the OHC membrane is expected to occur during local indentation. In fact, in their cell poking experiments Ulfendahl et al. (1998) reported a decrease of the OHC lateral indentation stiffness with cell length, contrary to what one would expect for a pure bending deformation.
Using energy arguments similar to the one above, de Pablo et al. (2003) derived a scaling law for the contact stiffness of a thin cylinder of infinite length undergoing local indentation. In this case, the cylinder flattens over a finite distance governed by the equilibrium between shell bending and the longitudinal stretching caused by the flattening. Although their analysis is still not directly applicable to the OHC, it can be extended to the case of a closed cylinder of finite length and constrained at both ends, assuming that the primary mode of deformation is a flattening of the cylinder. Note that this assumption neglects the possible contribution of local bending modes (in which the cylinder surface is stretched within a small dimple around the point of load while being compressed along the circular sections below the dimple). However, under local deformation, one would not expect a dependency of indentation stiffness upon the length of the cylinder. Therefore, the above assumption was taken as a reasonable approximation for the OHC.
Thus, for a flattening of height δ over a length l, the contact stiffness has two contributions, the bending contribution kbend ≈ AE*h3 l/R3 and the contribution kstretch due to longitudinal stretching, which can be shown to scale like kstretch ∝ E*h R3/l3 (de Pablo et al., 2003). As the actual mode of deformation involved in the indentation is the softest mode, the deformation occurs over the distance l* that minimizes the total shell stiffness kshell = kbend + kstretch. For a very long cylinder (the case considered by de Pablo et al., 2003), the flattening occurs over a finite length of order l0 = R√(R/h), and kshell has a scaling ∝ E*h5/2/R3/2 independent of the cylinder length. For a cylinder of length L comparable to l0 or shorter, the deformation involves the whole length of the cylinder, and we obtain for the contact stiffness the estimate
 |
(2) |
in which B is a constant. To apply this to the OHC we need an estimate for the Young modulus of the OHC membrane. Using a three-point bending test, Tolomeo et al. (1996) estimated the average resultant modulus of the intact OHC, defined as the product of Young's modulus by the wall's thickness, to be EOHCh ≈ 0.003 N/m. Using axial and circumferential measurements on demenbranated cells, Tolomeo and Steele (1995) found that the axial resultant modulus EOHC//h of the cortical lattice had about the same value as EOHCh, whereas the circumferential modulus was one order of magnitude smaller (EOHC⊥h ≈ 0.0004 N/m). These values were confirmed by Spector et al. (1998), who modeled the OHC as an orthotropic shell to analyze micromechanical experiments on this cell (including the experiments of Tolomeo and Steele, 1995) and found values in the range 1–2 × 10−3 N/m for EOHC//h and 3–7 × 10−3 N/m for EOHC⊥h.
To obtain a definite scaling model for kshell, we take the average EOHC in the range 1–7 × 104 Pa, ν = 0.3 for the Poisson ratio, R = 5 μm, and h = 100 nm for the shell radius and thickness, respectively. Finally we take A = 2.24 as above, and we let B be a free parameter, which may be fitted to our measurements of kOHC. The characteristic length l0 = R√(R/h) is ∼35 μm for the OHC. It is useful to introduce the cutoff length L* for which the above expression is minimum, namely L* = (3B/A)1/4 l0. Fig. 2 shows a plot of our measured values of kOHC as a function of cell length. The curves are best fits of these measurements to the above scaling law, using two values of EOHC (namely 104 N/m and 7 × 104 N/m). Clearly a good agreement between measurements and model was obtained. The values of the cutoff length L* corresponding to these best fits were L* ≈ 160 μm for EOHC = 7 × 104 N/m and L* ≈ 260 μm for EOHC = 104 N/m. These are longer than the lengths of the longest OHCs, though not much, which provides a check a posteriori of the assumption made in the above scaling law, i.e., that the cell flattens over a distance comparable to its length.
FIGURE 2.
Plot of the OHC contact stiffness as a function of cell length. The measurements were performed on 12 OHCs with lengths in the range 50–100 μm. Superimposed are best fits of the scaling model (Eq. 2). The dotted and dashed curves correspond to EOHC = 10 kPa and EOHC = 70 kPa, respectively (other parameters being as given in the text). The symbols O, □, and Δ correspond to measurements performed along the lateral wall in regions A, B, and C, respectively, as defined in Fig. 5.
Constraints on the turgor contribution to kOHC
According to the analysis of Arnoldi et al. (2000), when the dominant mode of deformation of the membrane is a local indentation dimple near the point of load, the turgor contribution to the contact stiffness is given by the membrane tension, kturgor (local) ∝ T, up to some factor of order unity. The situation is different in the case of a cylindrical shell undergoing nonlocal flattening, where kturgor may be much smaller than T. In fact, if the ends of the cylinder are free and the deformation inextensive, the membrane tension does not produce any work and kturgor vanishes. If the ends of the cylinder are constrained, under flattening each circular section bends without changing length, but the cylinder must extend along its main axis. For a cylinder of radius R and length L indented by a distance δ, this produces a change in surface area proportional to R/Lδ2 (each generator of the cylinder changing length by about δ2/L). The work produced by membrane tension in this case is thus ∝ TR/Lδ2, corresponding to a stiffness kturgor (flatten) ∝ TR/L.
Let us examine the above estimates in the case of the OHC. Assuming a perfectly cylindrical geometry, the membrane tension T is related to the cell turgor pressure P by Laplace law T = PR. Using the common estimate P = 1 kPa, with R = 5 μm as above, and a cell length in the range L = 80–100 μm, we obtain the estimates kturgor (local) ∼ PR = 5 × 10−3 N/m and kturgor (flatten) ∼ PR2/L = 2.5–3.1 × 10−4 N/m. Hence kturgor (local) is more than 10 times larger than the measured contact stiffness for these cell lengths (kOHC ≈ 3.7 × 10−4 N/m), whereas kturgor (flatten) is of the same order.
These estimates are consistent with the assumption that the primary mode of indentation in our experiments was a flattening of the membrane and suggest that in a cell with a turgor pressure P = 1 kPa, the elastic and turgor contributions to kOHC might be of the same order. It is, however, difficult to assess this point in our experiments because we had no way of measuring the turgor pressure. In fact, after disruption of the cytoskeleton, the cells did not show appreciable membrane tension (see below), and the actual value of P was probably significantly lower than 1 kPa. Moreover, the above analysis does not take into account the possibility of small axial undulations (or ripples) in the OHC plasma membrane, as observed by electron microscopy (Smith, 1968; Ulfendahl and Slepecky, 1988). If present in living OHCs, such ripples would give the plasma membrane a high axial curvature, in effect reducing its tension (hence kturgor). The presence of an excess of OHC plasma membrane (Li et al., 2002; Morimoto et al., 2002) also suggests that this membrane is capable of rather large deformations without appreciable stretching.
Hence the true turgor contribution in our experiments might well have been much smaller than the elastic contribution kshell. In addition, the 1/L scaling predicted by the above estimate kturgor (flatten) is too weak to explain the observed dependency of kOHC upon cell length. Our main justification for assuming a nonlocal flattening of the OHC membrane is therefore to be seen in the good agreement obtained with the above scaling model for kshell.
Comparison with previous measurements
Using a glass probe ∼2μm in diameter as a cell poker, Ulfendahl et al. (1998) reported an indentation stiffness of ∼2–3 mN/m in the mid-region of the OHC membrane. For a flat punch indenting an elastic half-space, the contact stiffness is proportional to the diameter of the punch (Pharr et al., 1992). For a punch inducing a nonlocal flattening of a cylindrical shell, the indenter size should not affect the measured indentation stiffness very much; but if a local stretching of the shell contributes, a rough proportionality would be expected. Thus, the measurements obtained by cell poking are in reasonable agreement with our AFM measurements. Our observation of a decrease of kOHC with cell length confirms this agreement.
It is also interesting to consider our AFM measurements in light of the three-point bending test estimate Eh = 0.003 N/m of Tolomeo et al. (1996). This estimate was based on Euler beam theory, by which Eh, the resultant stiffness modulus of the OHC membrane, can be related to the measured bending stiffness kcell of the cell body. For a load applied in the middle of the cell, while the base and the apex are maintained stationary a distance L apart, the relation reads kcell ≈ 48π Eh R3/L3 (Tolomeo et al., 1996). Up to a prefactor, kcell obeys the same scaling law as the stretching contribution kstretch, defined above, for the indentation of a cylinder under flattening. This is to be expected since the bending of a long hollow beam (a tube) involves a flattening of the beam in the region where it bends. Applying the above formula with L = 80 μm and R = 5 μm, the value Eh = 0.003 N/m corresponds to kcell ≈ 1.1 × 10−4 N/m, comparing well with the value of kOHC measured for that cell length.
Although Sugawara et al. (2002) did not observe a contact break in their AFM force curves, the tip forces reported by these authors on living OHCs (∼1 nN for a 1-μm indentation) are very similar to the ones we measured (∼0.5 nN for the same indentation; cf. the curve acquired on a fresh OHC in Fig. 1 B). Using Sneddon mechanics, Sugawara et al. (2004) estimated the Young modulus of OHCs in the apical turn of the cochlea to be ∼2 kPa. This is larger than our Epp estimates (Fig. 3), though not dramatically so. Note that these estimates provide only a measure of the apparent stiffness of the OHC assimilated with a solid elastic body. As such they cannot be compared directly to the Young modulus EOHC of the OHC membrane. In fact, they appear to underestimate the value of EOHC found by Tolomeo et al. (1996) and other estimates based on shell theory (Spector et al., 1998) by a factor roughly equal to h/R.
FIGURE 3.
Plot of estimated Young's modulus as a function of cantilever deflection (Epp-plot) for a fresh OHC (upper trace) and for a swollen OHC (lower trace). In addition to the disappearance of the break in the force curve, the swollen OHC appears ∼3 times softer than the healthy one.
As a side remark, although Sneddon mechanics is clearly not a correct description of the indentation response of the OHC lateral wall near contact, it reliably reproduced the force curves outside that region. The Epp plot of the response did not show appreciable variation of the apparent elastic modulus as a function of cantilever deflection. Such analysis is also useful to measure relative variations in the elastic properties of the cells. It is in particular clear from Fig. 3 that the lateral wall of the healthy OHC was stiffer than that of the swollen cell.
Mechanical lability of the OHC contact stiffness
Differences between fresh and swollen OHCs
OHCs placed in standard saline medium after isolation showed gradual signs of deterioration with time and eventually started to swell, becoming rounded or even spherical. This degradation process was relatively slow, and OHCs initially fresh and left undisturbed maintained their normal cylindrical shape with a healthy appearance for a couple of hours or more. We do not know if the swelling that occurred in the end was caused by gradual changes in turgor pressure or by a slow degradation of the cytoskeleton. However, it was clear that the fragility of the cells with respect to mechanical stimulation increased with time. The curve labeled fresh cell in Fig. 1 B was acquired a few minutes after isolation. Several force curves could be recorded at different positions on the cell body without inducing appreciable changes in cell morphology. The other curve (swollen cell) was acquired on a different OHC ∼2 h after isolation. In this case, at the beginning of the stimulation, the cell had a normal cylindrical shape, and the force curves showed a break at contact. However, after a few acquisitions, the cell started to swell near the point of stimulation, and in 5–7 min it became spherical. It was striking in this experiment that the break of the force curve disappeared when the cell started to become rounded. (The curve displayed in Fig. 1 B was acquired on the cell after this point.) Clearly the integrity of the cytoskeleton must have been lost after the cell had swollen. We can also affirm that swollen cells had no appreciable turgor pressure. Indeed, even a moderate turgor should have given these cells a contact stiffness (of order T = PR) larger than the contact stiffness of fresh cells. On the contrary, swollen cells did not have a sizeable contact stiffness. Although the cell underwent dramatic changes in shape in the example of Fig. 1 B, for all we can say its membrane was not ruptured. Hence it is reasonable to assume that any turgor pressure had been lost after 2 h in this case, even before we started stimulating the cell.
Behavior of the OHC lateral wall under continuous stimulation
To provide control of our indentation experiments on fresh OHCs, a continuous stimulation for 1 h was applied to the membrane of several OHCs of initial healthy appearance. For all the cells used (n = 3), the force curves maintained a break at contact for a period of stimulation of ∼10–20 min or more (an example is shown in Fig. 4). During that time the force curve showed only minor changes in shape, apart from a noticeable decrease in the slope at contact (meaning that the contact stiffness kOHC decreased). We therefore concluded that the break was not an artifact of our acquisition and reflected a stable mechanical feature of the OHC lateral wall. After this initial period, the stimulated OHC entered a phase of transition lasting 5–10 min, during which the cell showed signs of swelling: its radius increased, its length decreased concomitantly, and the cell body as a whole straightened. During this phase the force curve remained qualitatively unchanged and showed a break at contact, but the cell's contact stiffness increased significantly (by a factor of 3 or more), suggesting an increase in membrane tension. Apparent oscillations in kOHC values, such as seen in Fig. 4 B, were observed in the three cells, but they might represent noise artifacts and we did not try to interpret them. However, the significant increase was reproducible. At a particular time of the stimulation, the shape of the force curve changed qualitatively. Its slope decreased abruptly and the break at contact disappeared, suggesting a collapse due to rupture either of the cytoskeleton or of the membrane itself. After this time the cell body appeared rounded near the region where the stimulation had been applied. However, over the timescale of the experiment, the swelling remained localized around the point of stimulation. (By contrast, in the case of Fig. 1 B the cell lost its cylindrical shape rapidly and completely.) Since we do not know if the membrane was ruptured during the collapse, it is difficult to tell whether the increase of contact stiffness reflected an increase of turgor pressure or a mechanical reaction of the membrane. In any case, the integrity of the cytoskeleton was lost after the collapse, and the indentation response of the cell (similar to that of the swollen cell in Fig. 1 B) was no longer consistent with the presence of a turgor pressure.
FIGURE 4.
(A) Plots of force-distance curves at different times during continuous stimulation of an isolated OHC with the AFM tip. (B) Plot of the contact stiffness (kOHC) of the OHC membrane as a function of time. (C) Series of images showing the aspect of the cell at different stages during the experiment. (1, 2, 3, 4, and 5 correspond to 3, 12, 20, 26, and 37 min of stimulation, respectively.)
We point out that an apparent increase of membrane tension in response to mechanical stress has also been observed by Oghalai et al. (1998) (here the stress was applied by aspiration with a micropipette).
Mechanical uniformity of OHCs along their lateral wall
No obvious correlation between the shape of the force curve and the position on the OHC body was observed. Minor differences were seen in the force curves recorded for different regions, but as shown in Fig. 5 A, there were no clear patterns in these differences. The values measured for the contact stiffness kOHC didn't show a clear correlation with position either (Fig. 5 B). The dispersion in the values was significant (reflecting the observed variation of kOHC with cell length) but similar for all the positions tested along the lateral wall. Ulfendahl et al. (1998) reported lower indentation stiffnesses in the middle region of the cell as compared to the cuticular plate and the nucleus region. However, in these experiments the OHC body was subject to much larger indentations, and structures below the cell membrane presumably contributed more to the mechanical response. In our experiments, positions directly above the cuticular plate and the nucleus were not probed. Overall, our measurements support the idea that the OHC lateral wall is on average homogeneous in its mechanical properties. We emphasize that this homogeneity is to be understood in a statistical sense and does not preclude the presence of local inhomogeneities in a particular OHC. Such variations are expected from the domain structure of the lateral wall observed by electron microscopy (Holley, 1996) and have been confirmed by recent AFM studies (Le Grimellec et al., 2002; Sugawara et al., 2002; Wada et al., 2003, 2004).
FIGURE 5.
(A) Examples of force curves acquired on four different OHCs at different locations on the lateral wall (A: basal region; B: middle cell body; C: apical region). (B) Values of the OHC contact stiffness kOHC estimated for seven different cells. Repeated symbols for positions A, B, and C belong to the same cell.
Little viscosity in the deformations of OHCs
To probe the viscosity of the OHC membrane, we recorded several indentation curves on OHCs at the same location on the cell membrane and for increasing scanning frequencies. In AFM force curves, the hysteresis seen in the contact portion of the curve is related to the viscous properties of material being indented, as sample friction introduces a phase lag in the cantilever deflection with respect to the scanning position of the piezo scanner (A-Hassan et al., 1998). This phase lag increases as the indentation frequency increases. Thus for a given material, the force curves display larger hysteresis at faster indentation rates, and the rate dependence provides a relative measure of local viscosity of the sample (Mathur et al., 2001). In most measurements we observed a clearly detectable and increasing hysteresis in the force curves measured for scanning rates increasing between 1 and 40 μm/s (Fig. 6 A). However, this hysteresis was much smaller than for other cell types. This is evident in the graph shown in Fig. 6 B, where the hysteresis values measured in our experiments and in experiments performed with MDCK cells are compared. MDCK cells have an elastic modulus in the range of 1kPa, with an apparent spring constant of 0.002 N/m within 1 μm of indentation (Hoh and Schoenenberger, 1994). This is larger than the contact stiffness of the OHC, though in the same range. It is thus clear that viscosity has much less effect on the indentation mechanics of the OHC than on that of MDCK cells.
FIGURE 6.
(A) Force curves acquired at the same position but different scanning rates on the membrane of an isolated OHC, showing increasing hysteresis with increasing cantilever velocity. (The curves have been shifted to the same free deflection to subtract hydrodynamic contributions.) (B) Plots of force-relative hysteresis as a function of scanning velocity, for indentation of an isolated OHC, and an MDCK cell. Note the small hysteresis on the OHC compared to the one measured on the MDCK cell.
It is of interest to analyze further our results in terms of the relaxation times implied for the OHC membrane. After subtraction of noncontact friction contributions and multiplication by the cantilever spring constant, the hysteresis area between the approach and retract curves gives the work Wfriction of sample friction forces acting on the cantilever during one cycle of motion (cf. the Appendix). Note that Wfriction reflects not only the viscosity of the OHC membrane, but also the viscosity of the fluid set in motion by the membrane (the subtraction removes only hydrodynamic contributions acting directly on the cantilever) and possibly small contributions due to friction on the substrate. We did not try to separate these contributions. To perform an order of magnitude calculation, let us adopt a simple linear viscosity model in which the sample friction force Ffriction is proportional to the indentation velocity. We then have Ffriction = γOHC dδ/dt, where the constant γOHC defines the effective friction coefficient of the OHC membrane under local indentation. In our case, the indentation velocity was close to the scanning velocity dz/dt = v, up to an error (due to cantilever deflection) less than a few percent. To a good approximation, we then have Wfriction ≈ 2γOHC v(ΔZ − 2Δd), where ΔZ and Δd denote the vertical distance scanned by the cantilever while in contact with the cell, and the total cantilever deflection, respectively (cf. the Appendix). The friction coefficient γOHC can therefore be estimated from hysteresis measurements with the formula
 |
(3) |
For the curves shown in Fig. 6 A where ΔZ ≈ 2 μm, we found values for γOHC in the range 0.5–0.7 × 10−5 Ns/m. The ratio τ = γOHC/kOHC represents the relaxation time of the OHC membrane under local lateral indentation. Using the above values for kOHC, we obtain the estimates τ ≈ 0.02 s for OHCs with lengths in the range 75–100 μm, and τ ≈ 0.004 s for OHCs with lengths in the range 50–65 μm. Such small relaxation times are consistent with a highly elastic behavior of the OHC membrane. OHC electromotility would seem to require even smaller relaxation times (of the order of 10 μs or smaller); however, this clearly involves a mode of membrane deformation different from the one studied here.
Ehrenstein and Iwasa (1996) did an experiment in which they punctured an OHC after an osmotic challenge inflating the cell. By measuring the time it took for the cell membrane to recover its shape, they found a relaxation time of ∼40 s. It is difficult to compare this estimate to ours since the membrane was not punctured in our experiments, and the indentation did not involve changes of intracellular pressure. In particular, the large relaxation time measured by Ehrenstein and Iwasa suggested an adaptation of the membrane to osmotic stress, which would not be expected to play a role in our indentation experiments.
More relevant to our case are the viscosity estimates obtained by Li et al. (2002), who used small beads manipulated by optical tweezers to pull tethers from the plasma membrane of living OHCs. By pulling on the membrane at a constant speed they could measure both the effective spring constant and the friction coefficient of the tethers. Interestingly, it required significantly larger pulling forces to form the tether than to develop it once it was formed (this was attributed to the strong attachment expected to exist between the plasma membrane and the cortical lattice). For a developed tether, Li et al. measured a friction coefficient γtether ≈ 0.24–0.53 × 10−5 Ns/m, which is quite close to our estimate of γOHC. The effective spring constant of a developed tether was of ktether ≈ 3.7 × 10−6 N/m, giving a relaxation time ≈ 0.6–1.4 s. Li et al. do not provide an estimate for the spring constant of a forming tether; however, this can be estimated from their pulling curves to be kform ≈ 1.5 × 10−4 N/m. The relaxation time for the forming tether would therefore be in the range 0.015–0.04 s, a surprisingly good agreement with our results.
CONCLUSIONS
Our main conclusion is that AFM indentation measurements performed on fresh isolated OHCs are consistent with a shell-core organization of these cells. This is seen in the presence of a break in the force-distance curves at the contact point, with a linear relationship between force and indentation near the contact region, the mechanical signature of a thin elastic layer enclosing a pressurized fluid. Hence the OHC lateral wall possesses a small, but finite, contact stiffness kOHC, which we measured to be in the range 0.2–2.1 × 10−3 N/m for healthy cells. We also found that there is a significant dependency of kOHC upon cell length, which is well explained by a simplified scaling model for the indentation of a cylindrical shell, assuming that the primary mode of deformation is a flattening of the cylinder around the point of load. The observed contact stiffness was a characteristic of healthy OHCs. It was not present in swollen cells and disappeared after a too long stimulation by the AFM tip. The turgor pressure of the OHC influences its membrane tension, adding a contribution to the contact stiffness that could be comparable to kOHC. However, this contribution could have been significantly reduced in our experiments due to a low turgor pressure of the cells. It would be further diminished by the presence of small ripples and excess in the OHC plasma membrane.
Another important finding is that the OHC lateral wall shows a highly elastic behavior, little affected by viscosity. It is plausible that the structure of the lateral wall helps keep friction forces very small in deformations of the OHC, as one would expect from a structure whose function involves force production at several tens of kHz. It should be noted that all the cellular components of the cochlear partition are subject to rapid motion during sound stimulation, and this should be reflected in their mechanics.
Finally, our study provides confirmation of the relative uniformity (on average) of the mechanical properties along the OHC lateral wall, in agreement with the observations of Sugawara et al. (2002) and Wada et al. (2003).
To date, elastic shell models have been used to analyze AFM experiments in several contexts, including bacteria (Arnoldi et al., 2000), microtubules (de Pablo et al., 2003), and viruses (Ivanovska et al., 2004). A more precise analysis of the indentation of isolated OHCs, using models that take into account the special organization of the OHC lateral wall and its orthotropic nature, remains to be developed.
Acknowledgments
We thank Mr. Tom Warwick and Veeco Instruments (UK) for generously providing the AFM used for this work.
This work was supported by grants from the Human Science Frontier Program, the Swedish Research Council, the Foundation Tysta Skolan, and the Petrus and Augusta Hedlund Foundation.
APPENDIX: RELATION BETWEEN THE HYSTERESIS AREA AND THE WORK OF FRICTION
Since, to a good approximation, only the friction forces acting on the cantilever induce hysteresis in our experiments, the work of these forces during one cycle of motion is equal to the work of the full tip force Fc = kcd during the same cycle. By definition, this work is given by
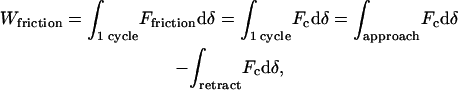 |
(A1) |
where, as before, δ is the sample indentation, which relates directly to the displacement of the AFM tip in contact mode. Since δ = z − d, we may rewrite Eq. A1 as
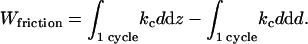 |
(A2) |
The second term in the right-hand side of the last equation is equal to zero since this is the variation of the cantilever elastic energy ½kcd2 during the entire cycle. Hence Wfriction is equal to the first term, which is just the product of kc by the force curve hysteresis area as defined in the text.
Using a linear viscosity model Ffriction = γOHC dδ/dt, the work of friction is also equal to
 |
(A3) |
where a dot denotes time derivative. The last term in this equality is of order γOHC vΔd × Δd/ΔZ, much smaller than the previous terms. Neglecting it, we obtain the relation used in the text to estimate γOHC.
References
- Adachi, M., M. Sugawara, and K. H. Iwasa. 2000. Effect of turgor pressure on outer hair cell motility. J. Acoust. Soc. Am. 108:2299–2306. [DOI] [PubMed] [Google Scholar]
- Akhremitchev, B. B., and G. C. Walker. 1999. Effect of finite sample thickness on elasticity determination using atomic force microscopy. Langmuir. 15:5630–5643. [Google Scholar]
- Arnoldi, M., M. Fritz, E. Bäuerlein, M. Radmacher, E. Sackmann, and A. Boulbitch. 2000. Bacterial turgor pressure can be measured by atomic force microscopy. Phys. Rev. E. 62:1034–1044. [DOI] [PubMed] [Google Scholar]
- Ashmore, J. F. 1987. A fast motile response in guinea-pig outer hair cells: the cellular basis of the cochlear amplifier. J. Physiol. 388:323–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Bekesy, G. 1960. Experiments in Hearing. McGraw-Hill, New York.
- Brownell, W. E., C. R. Bader, D. Bertrand, and Y. de Ribaupierre. 1985. Evoked mechanical responses of isolated cochlear outer hair cells. Science. 227:194–196. [DOI] [PubMed] [Google Scholar]
- Brownell, W. E., A. A. Spector, R. M. Raphael, and A. S. Popel. 2001. Micro- and nanomechanics of the cochlear outer hair cell. Annu. Rev. Biomed. Eng. 3:169–194. [DOI] [PubMed] [Google Scholar]
- Brownell, W. E. 2002. On the origins of outer hair cell electromotility. In Hair Cell Micromechanics and Otoacoustic Emissions. C. I. Berlin, L. J. Hood, and A. J. Ricci, editors. Delmar-Thomson Learning, Albany, NY. 25–47.
- Chan, E., and M. Ulfendahl. 1999. Mechanically evoked shortening of outer hair cells isolated from the guinea pig organ of Corti. Hear. Res. 128:166–174. [DOI] [PubMed] [Google Scholar]
- Chertoff, M. E., and W. E. Brownell. 1994. Characterization of cochlear outer hair cell turgor. Am. J. Physiol. 266:C467–C479. [DOI] [PubMed] [Google Scholar]
- Dallos, P., B. N. Evans, and R. Hallworth. 1991. Nature of the motor elements in electrokinetic shape changes of cochlear outer hair cells. Nature (Lond.). 350:155–157. [DOI] [PubMed] [Google Scholar]
- de Pablo, P. J., I. A. Schaap, F. C. MacKintosh, and C. F. Schmidt. 2003. Deformation and collapse of microtubules on the nanometer scale. Phys. Rev. Lett. 91:098101. [DOI] [PubMed] [Google Scholar]
- Ehrenstein, D., and K. H. Iwasa. 1996. Viscoelastic relaxation in the membrane of the auditory outer hair cell. Biophys. J. 71:1087–1094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flock, Å., B. Flock, and M. Ulfendahl. 1986. Mechanisms of movement in outer hair cells and a possible structural basis. Arch. Otorhinolaryngol. 243:83–90. [DOI] [PubMed] [Google Scholar]
- Flügge, W. 1960. Stresses in Shells. Springer-Verlag, Berlin.
- Frank, G., W. Hemmert, and A. W. Gummer. 1999. Limiting dynamics of high-frequency electromechanical transduction of outer hair cells. Proc. Natl. Acad. Sci. USA. 96:4420–4425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gitter, A. H., M. Ruder, and H. P. Zenner. 1993. Forces involved in length changes of cochlear outer hair cells. Pflueg. Arch. Eur. J. Physiol. 424:9–14. [DOI] [PubMed] [Google Scholar]
- Hallworth, R. 1995. Passive compliance and active force generation in the cochlear outer hair cell. J. Neurophysiol. 74:2319–2328. [DOI] [PubMed] [Google Scholar]
- Hallworth, R., B. N. Evans, and P. Dallos. 1993. The location and mechanism of electromotility in guinea pig outer hair cells. J. Neurophysiol. 70:549–558. [DOI] [PubMed] [Google Scholar]
- A-Hassan, E., W. F. Heinz, M. D. Antonik, N. P. D'Costa, S. Nageswaran, C. A. Schoenenberger, and J. H. Hoh. 1998. Relative microelastic mapping of living cells by atomic force microscopy. Biophys. J. 74:1564–1578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He, D. Z., and P. Dallos. 1999. Somatic stiffness of cochlear outer hair cells is voltage-dependent. Proc. Natl. Acad. Sci. USA. 96:8223–8228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoh, J. H., and C. A. Schoenenberger. 1994. Surface morphology and mechanical properties of MDCK monolayers by atomic force microscopy. J. Cell Sci. 107:1105–1114. [DOI] [PubMed] [Google Scholar]
- Holley, M. C., and J. F. Ashmore. 1988. A cytoskeletal spring in cochlear outer hair cells. Nature. 335:635–637. [DOI] [PubMed] [Google Scholar]
- Holley, M. C. 1996. Outer hair cell motility. In The Cochlea. P. Dallos, A. N. Popper, and R. R. Fay, editors. Springer, New York. 386–434.
- Ivanovska, I. L., P. J. de Pablo, B. Ibarra, G. Sgalari, F. C. MacKintosh, J. L. Carrascosa, C. F. Schmidt, and G. J. L. Wuite. 2004. Bacteriophage capsids: tough nanoshells with complex elastic properties. Proc. Natl. Acad. Sci. USA. 101:7600–7605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwasa, K. H., and R. S. Chadwick. 1992. Elasticity and active force generation in cochlear outer hair cells. J. Acoust. Soc. Am. 82:1667–1678. [DOI] [PubMed] [Google Scholar]
- Kalinec, F., M. C. Holley, K. H. Iwasa, D. J. Lim, and B. Kachar. 1992. A membrane-based force generation mechanism in auditory sensory cells. Proc. Natl. Acad. Sci. USA. 89:8671–8675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landau, L. D., and E. M. Lifshitz. 1959. Theory of Elasticity. Pergamon, London.
- Le Grimellec, C., M. C. Giocondi, M. Lenoir, M. Vater, G. Sposito, and R. Pujol. 2002. High-resolution three-dimensional imaging of the lateral plasma membrane of cochlear outer hair cells by atomic force microscopy. J. Comp. Neurol. 451:62–69. [DOI] [PubMed] [Google Scholar]
- Li, Z., B. Anvari, M. Takashima, P. Brecht, J. H. Torres, and W. E. Brownell. 2002. Membrane tether formation from outer hair cells with optical tweezers. Biophys. J. 82:1386–1395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Love, A. E. H. 1939. Boussinesq problem for a rigid cone. Quart. J. Math. 10:161–175 (Oxford series). [Google Scholar]
- Lue, A. J., and W. E. Brownell. 1999. Salicylate induced changes in outer hair cell lateral wall stiffness. Hear. Res. 135:163–168. [DOI] [PubMed] [Google Scholar]
- Maniotis, A. J., C. S. Chen, and D. E. Ingber. 1997. Demonstration of mechanical connections between integrins, cytoskeletal filaments, and nucleoplasm that stabilize nuclear structure. Proc. Natl. Acad. Sci. USA. 94:849–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathur, A. B., A. M. Collinsworth, W. M. Reichert, W. E. Kraus, and G. A. Truskey. 2001. Endothelial, cardiac muscle and skeletal muscle exhibit different viscous and elastic properties as determined by atomic force microscopy. J. Biomech. 34:1545–1553. [DOI] [PubMed] [Google Scholar]
- Morimoto, N., R. M. Raphael, A. Nygren, and W. E. Brownell. 2002. Excess plasma membrane and effects of ionic amphipaths on mechanics of outer hair cell lateral wall. Am. J. Physiol. Cell Physiol. 282:C1076–C1086. [DOI] [PubMed] [Google Scholar]
- Nguyen, T. V., and W. E. Brownell. 1998. Contribution of membrane cholesterol to outer hair cell lateral wall stiffness. Otolaryngol. Head Neck Surg. 119:14–20. [DOI] [PubMed] [Google Scholar]
- Oghalai, J. S., A. A. Patel, T. Nakagawa, and W. E. Brownell. 1998. Fluorescence-images microdeformation of the outer hair cell lateral wall. J. Neurosci. 18:48–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliver, D., D. Z. Z. He, N. Klöker, J. Ludwig, U. Schulte, S. Waldegger, J. P. Ruppersberg, P. Dallos, and B. Fakler. 2001. Intracellular anions as the voltage sensor of prestin, the outer hair cell motor protein. Science. 292:2340–2343. [DOI] [PubMed] [Google Scholar]
- Pharr, G. M., W. C. Oliver, and F. R. Brotzen. 1992. On the generality of the relationship among contact stiffness, contact area, and elastic modulus during indentation. J. Mater. Res. 7:613–617. [Google Scholar]
- Radmacher, M. 1997. Measuring the elastic properties of biological samples with the AFM. IEEE Eng. Med. Biol. Mag. 16:47–57. [DOI] [PubMed] [Google Scholar]
- Raphael, R. M., A. S. Popel, and W. E. Brownell. 2000. A membrane bending model of outer hair cell electromotility. Biophys. J. 78:2844–2862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratnanather, J. T., W. E. Brownell, and A. S. Popel. 1993. Mechanical properties of the outer hair cell. In Biophysics of Hair Cell Sensory Systems. H. Duifhuis, J. W. Horst, P. van Dijk, and S. M. van Netten, editors. World Scientific, Singapore. 199–206.
- Ratnanather, J. T., M. Zhi, and W. E. Brownell. 1996. The ratio of elastic moduli of cochlear outer hair cells derived from osmotic experiments. J. Acoust. Soc. Am. 99:1025–1028. [DOI] [PubMed] [Google Scholar]
- Sit, P. S., A. A. Spector, A. J. Lue, A. S. Popel, and W. E. Brownell. 1997. Micropipette aspiration on the outer hair cell lateral wall. Biophys. J. 72:2812–2819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slepecky, N. B., and M. Ulfendahl. 1988. Glutaraldehyde induces cell shape changes in isolated outer hair cells from the inner ear. J. Submicrosc. Cytol. Pathol. 20:37–45. [PubMed] [Google Scholar]
- Smith, C. A. 1968. Ultrastructure of the organ of Corti. Adv. Sci. 122:419–433. [PubMed] [Google Scholar]
- Spector, A. A., W. E. Brownell, and A. S. Popel. 1998. Elastic properties of the composite outer hair cell wall. Ann. Biomed. Eng. 26:157–165. [DOI] [PubMed] [Google Scholar]
- Spector, A. A., W. E. Brownell, and A. S. Popel. 1996. A model of cochlear outer hair cell deformations in micropipette experiments: an analytical solution. Ann. Biomed. Eng. 24:241–249. [DOI] [PubMed] [Google Scholar]
- Spector, A. A., M. Ameen, and R. A. Schmiedt. 2002. Modeling 3-D deformation of outer hair cells and their production of the active force in the cochlea. Biomech Model Mechanobiol. 1:123–135. [DOI] [PubMed] [Google Scholar]
- Sneddon, I. N. 1965. The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 3:47–57. [Google Scholar]
- Sugawara, M., Y. Ishida, and H. Wada. 2002. Local mechanical properties of guinea pig outer hair cells measured by atomic force microscopy. Hear. Res. 174:222–229. [DOI] [PubMed] [Google Scholar]
- Sugawara, M., Y. Ishida, and H. Wada. 2004. Mechanical properties of sensory and supporting cells in the organ of Corti of the guinea pig cochlea—study by atomic force microscopy. Hear. Res. 192:57–64. [DOI] [PubMed] [Google Scholar]
- Sugawara, M., and H. Wada. 2001. Analysis of elastic properties of outer hair cell wall using shell theory. Hear. Res. 160:63–72. [DOI] [PubMed] [Google Scholar]
- Timoshenko, S. P., and S. Woinowsky-Krieger. 1959. Theory of Plates and Shells. McGraw-Hill, New York.
- Tolomeo, J. A., and C. R. Steele. 1995. Orthotropic piezoelectric properties of the cochlear outer hair cell wall. J. Acoust. Soc. Am. 97:3006–3011. [DOI] [PubMed] [Google Scholar]
- Tolomeo, J. A., C. R. Steele, and M. C. Holley. 1996. Mechanical properties of the lateral cortex of mammalian auditory outer hair cells. Biophys. J. 71:421–429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulfendahl, M., E. Chan, W. B. McConnaughey, S. Prost-Domasky, and E. L. Elson. 1998. Axial and transverse stiffness measures of cochlear outer hair cells suggest a common mechanical basis. Pflüg. Arch. Eur. J. Physiol. 436:9–15. [DOI] [PubMed] [Google Scholar]
- Ulfendahl, M., and N. Slepecky. 1988. Ultrastructural correlates of inner ear sensory cell shortening. J. Submicrosc. Cytol. Pathol. 20:47–51. [PubMed] [Google Scholar]
- Wada, H., H. Usukura, M. Sugawara, Y. Katori, S. Kakehata, K. Ikeda, and T. Kobayashi. 2003. Relationship between the local stiffness of the outer hair cell along the cell axis and its ultrastructure observed by atomic force microscopy. Hear. Res. 177:61–70. [DOI] [PubMed] [Google Scholar]
- Wada, H., K. Kimura, T. Gomi, M. Sugawara, Y. Katori, S. Kakehata, K. Ikeda, and T. Kobayashi. 2004. Imaging of the cortical cytoskeleton of guinea pig outer hair cells using atomic force microscopy. Hear. Res. 187:51–62. [DOI] [PubMed] [Google Scholar]
- Zheng, J., W. Shen, D. Z. He, K. B. Long, L. D. Madison, and P. Dallos. 2000. Prestin is the motor protein of cochlear outer hair cells. Nature. 405:149–155. [DOI] [PubMed] [Google Scholar]








