Probing the Viscoelastic Behavior of Cultured Airway Smooth Muscle Cells with Atomic Force Microscopy: Stiffening Induced by Contractile Agonist

Abstract

Complex rheology of airway smooth muscle cells and its dynamic response during contractile stimulation involves many molecular processes, foremost of which are actomyosin cross-bridge cycling and actin polymerization. With an atomic force microscope, we tracked the spatial and temporal variations of the viscoelastic properties of cultured airway smooth muscle cells. Elasticity mapping identified stiff structural elements of the cytoskeletal network. Using a precisely positioned microscale probe, picoNewton forces and nanometer level indentation modulations were applied to cell surfaces at frequencies ranging from 0.5 to 100 Hz. The resulting elastic storage modulus (G′) and dissipative modulus (G″) increased dramatically, with hysteresivity (η = G″/G′) showing a definitive decrease after stimulation with the contractile agonist 5-hydroxytryptamine. Frequency-dependent assays showed weak power-law structural damping behavior and universal scaling in support of the soft-glassy material description of cellular biophysics. Additionally, a high-frequency component of the loss modulus (attributed to cellular Newtonian viscosity) increased fourfold during the contractile process. The complex shear modulus showed a strong sensitivity to the degree of actin polymerization. Inhibitors of myosin light chain kinase activity had little effect on the stiffening response to contractile stimulation. Thus, our measurements appear to be particularly well suited for characterization of dynamic actin rheology during airway smooth muscle contraction.

INTRODUCTION

Airway smooth muscle (ASM) cells have unique structural and mechanical properties that set them apart from skeletal muscle and nonmuscle cells (Murphy, 1994; Small, 1995). The complex mechanics and contraction of ASM tissues, being both length and history dependent, are largely responsible for airway narrowing and airway hyperresponsiveness in asthmatic subjects (Brusasco and Pellegrino, 2003; Fredberg, 2004; Ma et al., 2002; Woolcock et al., 1984). To explain these pathological phenomena, investigators have studied ASM microstructure (Daniel, 1988; Kuo et al., 2003), cellular complex microrheology (An et al., 2002; Fabry et al., 2001a, 2001b; Hubmayr et al., 1996), and the biochemical pathways activated during contractile events (Gerthoffer and Gunst, 2001; Morgan and Gangopadhyay, 2001; Pfitzer, 2001; Schramm and Grunstein, 1992; Somlyo and Somlyo, 2003). The prospect of understanding the link among these observations has been a difficult challenge.

An emerging description of ASM rheology is that of the soft-glassy material hypothesis, which does not rely on specific molecular mechanisms but embodies the concepts of structural disorder and metastability, allowing for mechanical rigidity as well as the ability of cells to flow and remodel (Fabry et al., 2001a; Fabry and Fredberg, 2003; Sollich, 1998). This hypothesis links the measurable hysteresivity (the ratio of the dissipative to the elastic components of the complex shear modulus) and the dependence of the complex modulus on deformation frequency (the power-law exponent) to an effective noise temperature of molecular agitations in the intracellular environment. Structural disorder in the cell explains the absence of any characteristic time constant of the complex rheology or specific mode of deformation. Metastability is understood as weak confinement of structural elements in the cell, in that the energy of stochastic forces is comparable to confinement potentials, and thus structural rearrangements are probabilistic events. In this way the rigidity of the cell acquires a weak (power-law) dependence on frequency of perturbation, as stress relaxation can occur over long time scales and is progressively less probable at higher frequencies. If the source of random forces is nonthermal in nature (e.g., ATP hydrolysis by motor proteins or dynamic actin filaments), it is possible for the cell to rapidly modulate its mechanical state.

The applicability of this description as an integrative framework encompassing the diversity of underlying mechanisms involved in ASM contractile events has recently been reviewed (Gunst and Fredberg, 2003). In this framework, the onset of contractile processes is described by a rapid increase in microscale agitations (interpreted from a transient increase in hysteresivity), force and stiffness increase, and then gradual freezing or solidification (decreased hysteresivity). The two main elements within the cell's mechanical structure that are implicated in ASM contractile processes are actomyosin cross-bridge cycling and actin filament polymerization. Increased actomyosin cross-bridge activity is initiated by receptor stimulated elevation of the concentration of intracellular calcium ions, which promotes myosin light chain phosphorylation via calmodulin and myosin light chain kinase (MLCK). This activation results in force production and sliding of adjacent actin and myosin filaments (Huxley and Hanson, 1954) and is widely accepted as the key step in smooth muscle contraction (Kamm and Stull, 1986; Murphy, 1980). The rapid cycling of cross-bridges is proposed to explain the transient increase in hysteresivity, and the subsequent decay is attributed to the formation of latch-state binding of myosin heads to actin filaments (Fredberg et al., 1996; Murphy, 1994). Enhanced actin polymerization and dynamic remodeling is observed during the onset of contraction (An et al., 2002; Hirshman and Emala, 1999; Mehta and Gunst, 1999). The actin cytoskeleton is suggested to provide a fortified environment for tension development and to strengthen membrane contacts of the contractile apparatus, thus playing a key role in force transmission to the extracellular matrix and neighboring cells. Actin polymerization may also be involved in sensing and adapting to mechanical forces (Gunst et al., 2003).

Measurable quantities, like tension, stiffness, hysteresivity, and noise temperature, are all integrative parameters, typically sensitive to both actomyosin activity and actin polymerization (An et al., 2002; Jones et al., 1999; Mehta and Gunst, 1999). What is required is a technique to precisely target individual mechanisms with a mechanical probe. This may only be possible if there is a spatial segregation of nonmyosin-associated actin and the actomyosin contractile apparatus in the ASM cell. There is evidence to suggest that such a distinction between contractile (α-) and cytoskeletal (β-) actin in ASM is present (Small, 1995) where cytoskeletal actin may be selectively localized to membrane-associated structures. However, this segregation is still a point of dispute (Song et al., 2000; Stromer et al., 2002).

Atomic force microscopy (AFM; Binnig et al., 1986) is established as a versatile tool for imaging and measuring nanoscale elastic properties of living cells (A-Hassan et al., 1998; Radmacher et al., 1996), with sensitivity to underlying cytoskeletal elements such as actin filaments (Rotsch and Radmacher, 2000). Recent advances have measured complex (viscoelastic) rheology (Alcaraz et al., 2003; Mahaffy et al., 2000). In this study, we employ AFM to map the mechanical structure and explore the frequency-dependent complex rheology of ASM cells in culture. We observe stiffening events induced by a known contractile agonist and test the sensitivity of these measurements to MLCK inhibitors and actin polymerization dynamics. We also compare our work with recent studies of ASM rheology and contractile stiffening in tissue strips (Fredberg et al., 1996) and in cultured cells by using magnetic twisting cytometry (MTC; An et al., 2002; Fabry et al., 2001a). AFM allows for versatile control over the spatial localization of the measurement probe and the mechanical stimulus with the goal of separating characteristic effects of actomyosin interactions from cytoskeletal rearrangements.

MATERIALS AND METHODS

Cell culture and treatments

Tracheal smooth muscle cells from 7- to 9-week-old male Fisher rats (Harlan Sprague Dawley, Wallkerville, MD) were isolated and cultured according to previously described methods (Tolloczko et al., 1995). Briefly, the cells were enzymatically dissociated with 0.05% elastase type IV and 0.2% collagenase type IV and cultured in 1:1 Dulbecco's modified Eagle's medium, Ham's F12 medium supplemented with 10% fetal bovine serum, 0.224% NaHCO3 and 100 U/ml penicillin, 100 μg/ml streptomycin and 25 μg/ml amphotericin in the presence of 5% CO₂. Cell culture reagents were purchased from GIBCO (Mississauga, Ontario, Canada). Confluent first or second passage cells were rendered quiescent by incubation in medium containing 0.5% fetal bovine serum for 4 days before experiments. Confirmation of a smooth muscle phenotype was based on typical morphology, positive smooth muscle specific α-actin staining, negative keratin staining, and contractile responses to agonists.

For AFM experiments, cells were mounted on the microscope stage in ∼300 μl of Hanks' balanced salt solution (Invitrogen Canada, Burlington, Ontario, Canada), pH 7.3, at room temperature. Time-course measurements were made for 10–12 min before and for 15 min after addition of 10 μM contractile agonist 5-hydroxytryptamine (5-HT; serotonin). To inhibit MLCK, cells were preincubated with 1 μM wortmannin or 5 μM 1-(5-iodonaphthalene-1-sulfonyl)-1H-hexahydro-1,4-diazepine hydrochloride (ML-7) for 10 and 25 min, respectively (Nakanishi et al., 1992; Saitoh et al., 1987). To cause actin depolymerization, actin capping agent cytochalasin-D was added to the cells after treatment with 5-HT for 15 min and the measurements continued for 10–15 min. Cytochalasin-D, wortmannin, and ML-7 were obtained from Sigma-Aldrich Canada (Toronto, Ontario, Canada).

Measurement of cell contraction

Cells used for contraction measurements were plated on homologous cell substrate (Tao et al., 2003) and rendered quiescent by serum deprivation at ∼70% confluence. The cells were incubated for 10 min with 1 μM wortmannin or for 25 min with 5 μM ML-7 or with the appropriate vehicle (DMSO or ethyl alcohol, respectively). Images of cells stimulated with 5-HT were acquired at the rate of one image per minute using a video camera (Hamamatsu Photonics, Hamamatsu City, Japan) mounted on a microscope equipped with Nomarski optics (Nikon Diaphot, Nikon, Tokyo, Japan) and PTI (Photon Technology International, Princeton, NJ) software. The length of the cells was measured before and 10 min after stimulation. Each experimental group consisted of 31–37 cells. Data are expressed as percentage of cell length decrease. Negative values indicate increase in cell length.

Atomic force microscopy

Measurements were performed with a Bioscope AFM equipped with a G-type scanner, Nanoscope IIIa control electronics, and software version 4.43r8 (Digital Instruments, Veeco Metrology Group, Santa Barbara, CA). Silicon nitride triangular microlevers (TM Microscopes, Veeco) with a nominal spring constant of k = 0.01 N/m were used for both force volume and complex modulus measurements. For the latter, a 4.5 μm diameter polystyrene bead (Polysciences, Warrington, PA) was fixed to the tip of each probe with UV light curable adhesive (Elecro-lite, Danbury, CT) using a custom procedure. The deflection sensitivity of the optical lever was calibrated before and after each experiment by measuring the slope of the contact region of a force-distance curve acquired on a clean glass cover slip in Hanks' balanced salt solution.

Elasticity mapping via force volume

In this AFM imaging mode (supported by Nanoscope control software, version 4.23 b6 or higher), the cantilever is scanned vertically to obtain a force-distance curve at each point in an x-y array over the cell surface. The probe indents the surface with a predetermined maximum force relative to baseline on each approach (relative trigger mode) then is retracted again before moving laterally to the next point in the array. The height (z-piezo scanner voltage) at which the maximum force is reached is used as the height image value. The inverse slope of the indentation region of each force curve is measured to first order by taking the force value at a fixed height above the maximum-force height for that curve. These values are plotted as the elasticity map, providing a qualitative measure of the variations of the inverse local elastic modulus of the cell surface. Parameters used for the force volume imaging were: 1 μm z-scan, 64 data points per curve, 64 × 64 array, 10 Hz vertical scan rate, 14 Hz lateral scan rate, and ∼0.4 nN maximum force (although ∼0.1 nN was attributed to the hydrodynamic force on the probe). The total time required for each image was 15 min.

Indentation modulation, complex modulus measurements

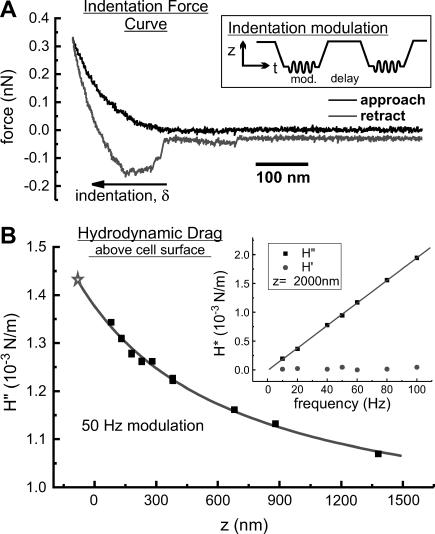
To measure the complex microrheology of the cells, beaded probes were used to indent the surface at a specified location on each cell. Although the lateral resolution of the force volume imaging is not maintained, the use of beaded probes provides a better assessment of the cells rheology by averaging over a larger area of the cell surface with well-defined contact geometry. Also, smaller local strains are applied to the cell, reducing the chance of nonlinear or destructive deformation (Dimitriadis et al., 2002). The relative trigger mode was used to control the maximum force applied on each indentation. Force curves were acquired at a much slower rate (0.317 Hz, 1.5 μm z-scan, 4096 data points). At this scan speed, the hydrodynamic force on the lever was insignificant compared to the maximum loads used (∼0.3 nN). We did not rely on force curve analysis for quantitative evaluation of complex cellular rheology but instead used the indentation modulation procedure described below. The only parameter obtained from force curves (example in Fig. 1 A) was the value of operating indentation depth (δ₀). A 15 s delay was used after each approach (i.e., at the point of maximum indentation force) and each retraction from the cell surface. During the indentation delay, a sinusoidal oscillation was added to the vertical scan control voltage, with small amplitude (5–8 nm) and variable frequency (0.5–100 Hz). An external digital lock-in amplifier (SR 830, Stanford Research Systems, Sunnyvale, CA) was used for drive signal generation and measurement of the resulting amplitude and phase of the deflection signal. These outputs were sampled with a 12-bit data acquisition board (PCI-6024E, National Instruments, Dallas, TX) and recorded on a computer for further analysis.

FIGURE 1.

(A) Typical force curve obtained from vertical scanning of a beaded AFM probe (at a rate of 0.317 Hz) such that it approaches, indents, retracts, and releases from a cell's surface. The inset is an illustration of a typical signal applied to the vertical scanner to perform indentation modulations. (B) A sample calibration of the hydrodynamic drag on a beaded AFM probe above a cell surface. The fit to the scaled spherical drag function (see text) and its extrapolation to surface indentation (⋆) are shown. The inset shows the linear dependence of the hydrodynamic drag on modulation frequency, and the purely viscous nature of this drag (H′ is the in-phase elastic component which is negligible compared to the out-of-phase viscous component, H″).

Time-course profiles were constructed from repeated indentations with modulation at constant frequency (typically 10 Hz). Frequency-dependent measurements were acquired during periods of stable mechanical response of the cell. On alternate indentations, the modulation frequency was toggled between the time-course (control) frequency and other frequencies used (in random order), such that the control frequency was used before and after each measurement at another frequency. In this way small but persistent shifts in the response to the control frequency were used to scale measurements at other frequencies relative to the average response at control frequency modulations. These changes were typically <10%, but in those cases where larger changes occurred, the corrected values were consistent with cases in which the changes were small.

The hydrodynamic drag on the lever was calibrated for each probe used (Alcaraz et al., 2002). These measurements were made by modulating the probe (at 50 Hz) at different heights (0.2–2 μm) above the cell surface at the same location and with the same amplitude (5–8 nm) as used for the indentations experiments. The phase response of the AFM z-piezo was calibrated by bringing a stiff probe (k = ∼42 N/m, Olympus etched Si tapping-mode probe) into contact with a clean glass cover slip (in air), modulating the z-piezo at all frequencies used in this study, and recording the phase of the lever deflections relative to the drive signal. The frequency-dependent phase shift was subtracted off of all other phase measurements.

Data analysis

The Hertzian contact mechanics model (Hertz, 1882; Johnson, 1987) for a spherical indenter relates the force experienced by the probe (F) to the indentation depth (δ) for elastic deformations of linear, homogeneous samples of infinite thickness. It is commonly used to extract values of elastic modulus from AFM indentation data. We used the first term of the Taylor expansion of this model to compute the complex shear modulus, G*, of the cell from the small amplitude indentation oscillations, δ₁, (Alcaraz et al., 2003; Mahaffy et al., 2000)

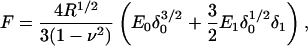(1)

where ν is the Poisson ratio of the cell, R is the radius of the spherical probe, δ₀ is the operating indentation, and E₀ the zero frequency value of the elastic modulus obtained from the slow approach force curve. E₁ is the frequency-dependent elastic modulus related to G* by E₁ = 2(1 + ν)G* for a continuous medium (Landau and Lifshitz, 1986). The indentation depth is calculated as δ = z − d, were z is the controlled vertical position of the base of the probe (measured as positive values extending down from the point of contact between the bead and the cell surface) and d (= F/k) is the measured deflection of the lever. Note that δ₁ and F₁ = 2(Rδ₀)^1/2E₁δ₁/(1 − ν²) are both complex values having both amplitudes and phases relative to the vertical drive oscillation, thus E₁ and G* have both real (in-phase) and imaginary (90° out-of-phase) components. The Poisson ratio is taken to be 0.5 for incompressible materials (Mahaffy et al., 2004).

Further extension of the Hertz model to include the effects of finite sample thickness and adherence to the substrate required a detailed knowledge of the cells thickness (Dimitriadis et al., 2002; Mahaffy et al., 2004). AFM topography of nonconfluent cells and optical focal plane measurements of confluent cells estimate cell thickness at h = ∼3 μm. For this thickness and the indentation depths used (∼100 nm), rheology coefficients could be overestimated by as much as 20% ([Rδ₀]^1/2/h).

Correction for the hydrodynamic drag forces experienced by the probe moving through the surrounding liquid was done by calculating the hydrodynamic drag function iH″ = F₁/δ₁ = ib(h)f (b is the drag factor, i is the imaginary unit, i² = −1, and f is the oscillation frequency) for different heights (h) above the cell and extrapolating to h = 0 (Alcaraz et al., 2002). As a model for the drag factor dependence on h, we used the scaled spherical function with an added constant to account for the nonzero drag on probe oscillations far from the surface: 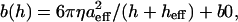where a_eff and h_eff are the effective radius and height of the lever, respectively, η is the liquid viscosity, and b₀ is the drag far from the cell surface. For these measurements, without contact or adhesion to the cell surface, the real component of the drag was negligible and the imaginary component scaled linearly with frequency, as expected for purely viscous drag. An example of a fit of the imaginary component of the drag to the functional height dependence of a scaled spherical oscillating probe with nonzero decay at long distance is shown in Fig. 1 B (modulation frequency 50 Hz). This fit was used to determine a value for the drag factor at zero height, b(0). The hydrodynamic drag on the lever was subtracted from complex shear modulus measurements (at any frequency).

Finally, we calculate the complex shear modulus of the cell as

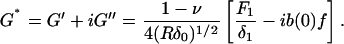Here the complex shear modulus has been separated into its real (storage modulus, G′) and imaginary (loss modulus, G″) components and has only a weak dependence on the operating indentation and probe radius (G*∼(Rδ₀)^−1/2). For time-course plots of G′ and G″ we define a parameter k₀ = k(1 − ν)/4(Rδ₀)^1/2, and calculate only the ratios G′/k₀ and G″/k₀ so that any uncertainty associated with k (probe spring constant), ν, R, and δ₀ are not included. This is justified because only δ₀ changes throughout the course of each measurement and these variations have little impact on variations of G*. We also calculate the loss tangent or hysteresivity (η = G″/G′), which provides a measure of solidlike (η ≪ 1) or fluidlike (η ≫ 1) behavior of the cell, and where dependence on k, ν, R, and δ₀ is eliminated (and thus the common errors associated with determination of the contact point, control of the maximum force, and uncertainty associated with Hertzian contact mechanics). Values of G′, G″, and η reported in the text (and in Table 1) are averages over 5 min of individual indentation measurements (including calculated values of k₀), then averaged among all cells tested, reported as mean ± SE. Percent change of responses (R) relative to baseline (B) values are calculated as (R − B)/B × 100% for each cell then averaged within the population, where values in the stimulated or treated states are 5 min averages taken between 5 and 10 min after addition of the drug. Statistical significance of differences between reported means was determined by a two-sample t-test at a level of p < 0.05.

TABLE 1.

Population average complex rheology of ASM cells under various treatments

	G′ (kPa)*	G″ (kPa)*	η*	α†	μ (Pa·s)†
Baseline (n = 16)	1.2 ± 0.2	0.32 ± 0.05	0.27 ± 0.03	0.120 ± 0.005	5.1 ± 0.4
5-HT (n = 11)	2.7 ± 0.5	0.52 ± 0.09	0.20 ± 0.02	0.055 ± 0.005	21 ± 2
Cytochalasin-D (n = 5)	0.5 ± 0.1	0.25 ± 0.05	0.53 ± 0.05	0.160 ± 0.009	7.2 ± 0.6
Wortmannin (n = 5)	1.3 ± 0.3	0.35 ± 0.09	0.25 ± 0.06	–	–
Wortmannin + 5-HT (n = 5)	2.4 ± 0.2	0.34 ± 0.07	0.14 ± 0.02	0.069 ± 0.002	5.1 ± 0.4
ML-7 (n = 7)	0.6 ± 0.2	0.20 ± 0.04	0.40 ± 0.06	0.158 ± 0.009	4.1 ± 0.5
ML-7 + 5-HT (n = 7)	1.1 ± 0.3	0.26 ± 0.06	0.26 ± 0.04	0.101 ± 0.004	4.4 ± 0.6

^*Measured at 10 Hz modulation.

^†Parameters from fits of frequency-dependent rheology.

Frequency-dependent cellular mechanics model

To describe the functional dependence of G′ and G″ on oscillation frequency, we used the power-law structural damping model (Fabry et al., 2001a; Fredberg and Stamenovic, 1989; Hildebrandt, 1969):

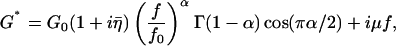(2)

where the structural damping coefficient 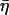is not an independent parameter but is related to the power-law exponent α by 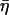= tan(πα/2), G₀ is a modulus scale factor, f₀ is a frequency scale factor, Γ denotes the gamma function, and μ is the Newtonian viscous damping coefficient. The factor Γ(1 − α)cos(πα/2) is close to unity for small values of α and is ignored in interpretations and discussions, although included in data fits. This model implies that the loss modulus consists of a component (with scale factor 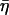G₀) that is coupled to the storage modulus, both having the same power-law dependence on frequency, interpreted as frictional damping. Additionally, the loss modulus contains a Newtonian viscosity component that behaves linearly with frequency. With this term, the structural damping constant (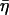) is not equivalent to the hysteresivity (η = G″/G′) but approaches it at low frequencies (when α ≪ 1). Measurements of G′ and G″ versus f were fit to this model with a global nonlinear regression analysis using 1/(SE)² weighting (Origin 7.0, OriginLab Corp., Northampton, MA), determining values of α and μ for the cells in unstimulated, stimulated, and drug treated states. In fitting individual data sets, f₀ and G₀ are not independent parameters and thus can not be determined uniquely. However, multiple data sets (cells under multiple treatments) were fit concurrently, and universal scaling identified unique values for both f₀ and G₀ that are common to all cellular states (similar to the analysis of Fabry et al., 2001a).

RESULTS

Elasticity maps

Force volume imaging was performed on a confluent culture of ASM cells for two different lateral scan sizes (40 μm and 5 μm; Fig. 2). The height under constant force profile for the larger scan (Fig. 2 A) clearly shows one cell with three other neighboring cells contacting each other at the cell boundaries. The elasticity profile shows that the thick central region (likely the nucleus) is softer than the surrounding regions of the cell (roughly a fourfold difference in force-indentation slope) and a nodal fiber network that spans the entire area of the cell surface. This microstructure is even more striking in the smaller scan of the perinuclear region (Fig. 2, C and D). The fibrils are not aligned with any particular direction in the cell, but form a network of interconnected nodes. The observed fibrils, and especially the nodes, appear stiff relative to the surrounding cellular material (>2-fold difference in compliance). This rich elasticity contrast on the submicron length scale is part of the motivation for using a large (4.5 μm) bead on the AFM cantilever as an indentation probe for single-location measurements, providing some local averaging of the cell's shear modulus.

FIGURE 2.

Force volume height (A, C) and elasticity (B, D) profiles of a confluent culture of rat tracheal smooth muscle cells using a constant maximum applied force of ∼0.4 nN (height color scale spans 1 μm in A and 0.3 μm in C; dark is stiff and light is soft in the elasticity maps). A and B covers an entire apical surface of a cell and portions of three neighboring cells. C and D are of the area within the square marked in A. These images reveal a stiff fibrous network that is highly nodal and spans the entire cell, although the nuclear region appears to provide a very soft background (large light region in the top left quarter of B). The higher resolution images in C and D clearly identify the nodes as well as their interconnecting fibers as the structures of mechanical rigidity within the cell.

Although the force volume imaging provided a qualitative view of the spatial variations of the cells' mechanical structure, it was not useful for quantitative assessment of elasticity, lacking both in accuracy and temporal resolution. The major limitation was the presence of viscous forces on the AFM probe, as well as adhesion to the cell surface. The hydrodynamic drag force on the probe and the viscoelastic nature of the cell caused a significant hysteresis between the approach and retraction in the indentation region of the force curves (Fig. 1 A). This made measurement of elastic modulus via slope analysis, or even a fit to Hertzian indentation model, highly convoluted with viscosity effects. Averaging approach and retraction curves in an attempt to eliminate viscous forces from the analysis (Radmacher et al., 1996) was complicated by surface adhesion artifacts. Many kinetic processes involved in ASM contraction occur within minutes (Gunst and Fredberg, 2003), but sustained contractions can last for 15 min or longer and therefore it was possible to obtain force volume maps (15 min per image) before and during contractile activation with 10 μM 5-HT. Some structural rearrangements were observed near the cell periphery as well as subtle changes in structure and apparent elasticity contrast throughout the cell; however, these effects were difficult to quantify and distinguish from random variations (data not shown).

Complex modulus time-course response

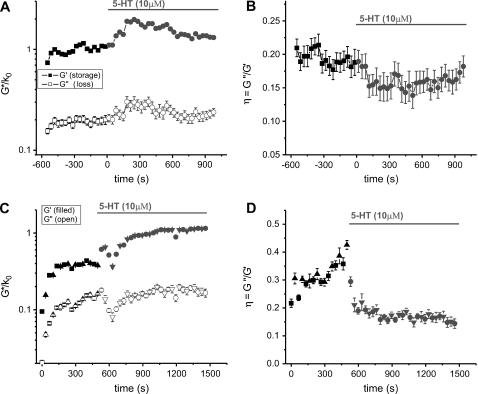
The AFM probe was positioned onto an ASM cell surface in the region between the nucleus and the periphery using the Bioscope optics (40× objective). This was the region where the highest detail in the cytoskeletal network was observed in the force volume images. Indentation modulation (at 10 Hz) was used to compute the storage modulus (G′), loss modulus (G″), and loss tangent (η = G″/ G′). The elastic storage modulus values are typically in the range 0.5–3 kPa (G′ = 1.25 ± 0.20 kPa, n = 16, 5 min averages), with dissipative loss moduli one fifth to one third of these values (η = 0.27 ± 0.03) although in some cases as large as 0.5G′. Addition of the contractile agonist 5-HT (10 μM) causes a dramatic increase in G′ (150 ± 30% increase relative to baseline values, n = 11), which is often paralleled by a similar increase in G″ (67 ± 15%). Two examples are shown in Fig. 3. The loss tangent time courses tend to be much less noisy than the time courses for G′ and G″, indicative of coupling between elastic and dissipative processes within the cell (the structural damping hypothesis). The time-course plots of η show a definitive decrease after addition of 5-HT (−28 ± 5%), interpreted as a shift toward solidlike behavior.

FIGURE 3.

Complex shear modulus (A and C) and hysteresivity (B and D) time-course measurements on two different cells, stimulated with the contractile agonist 5-HT (serotonin). The solid symbols in A and C are the elastic storage moduli and the open symbols are the dissipative loss moduli obtained from repetitive indentation modulation measurements (plotted without the coefficient, k₀ = k(1 − ν)/4(Rδ₀)^1/2). After an initial increase, likely a mechanosensitive response, the complex modulus reaches a relatively stable baseline before stimulation. 5-HT induces a dramatic stiffening response and reduced hysteresivity with variable kinetics. Two different modulation amplitudes were used in C and D (6.2 nm: squares for baseline and circles after 5-HT; 2.5 nm: triangles pointing up for baseline and pointing down for 5-HT) producing identical results, which indicates that cell rheology was probed in a linear deformation regime.

These changes in G′, G″, and η all occur within the first few minutes after addition of 5-HT, sometimes within the first 30 s (one or two data points). However, the amplitude and kinetics of the contractile stiffening varies among cells. Typically cells with larger G′ and smaller η baseline values responded less than cells with smaller G′ and larger η baseline values, as if there is an upper threshold stiffness (or lower threshold for the loss tangent) beyond which the cell cannot stiffen any further. The threshold for G′ seemed to be ∼2.5 kPa and ∼0.15 for η, although this has not been rigorously quantified. Cells with baseline G′ values significantly above this stiffness threshold were eliminated from the analysis. Another significant heterogeneity in the response profiles was that for some cells the stiffness increased to a peak value then decayed slowly (over ∼5 min) toward baseline levels, but for other cells (the majority) the stiffness increases were unimodal, reaching a plateau that did not decay within the measurement time span.

When two modulation amplitudes, 2.5 and 6.2 nm, were used on alternating indentations (Fig. 3, C and D), the results for G′, G″, and η at these two amplitudes are indistinguishable in both the baseline and stimulated states. This suggests that the modulations used fall within a linear deformation regime, in support of the use of only the first Taylor expansion term of the Hertz model (Eq. 1), so that results do not depend on the precise choice of modulation amplitude.

Baseline values of G′ and G″ often exhibit an increase from the onset of indentation probing (Fig. 3, especially Fig. 3 C). This stiffening occurs mainly in the first minute of probing, decaying to a gradual increase (barely detectable) or flat-line response after that. This implies evidence for a mechanosensitive response of the ASM cells to the mechanical perturbation from the AFM probing. For this reason we probed each cell continuously for 8–10 min before adding 5-HT, to establish a relatively stable baseline level of the storage and loss moduli.

Effects of cytochalasin-D and MLCK inhibitors

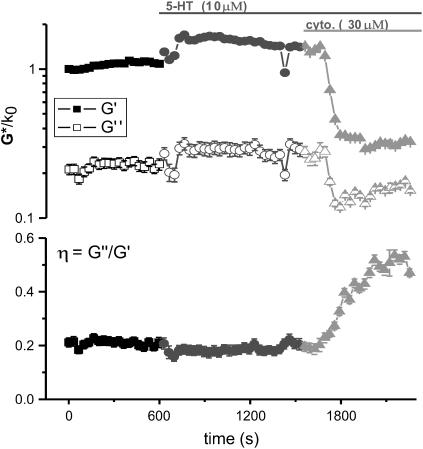
The dependence of the ASM complex modulus on the polymerized actin content in the contractile state was tested with the actin capping agent, cytochalasin-D (30 μM) after stimulation with 5-HT. A dramatic decrease in both the storage and loss moduli was observed within 3 min after addition of cytochalasin-D, indicative of cellular softening or relaxation (Fig. 4). The hysteresivity exhibits a large increase from ∼0.2 to 0.53 over a 5-min period after the onset of the softening response. This is interpreted as a shift toward fluidlike behavior. The average values of G′, G″, and η from all cells tested for baseline, 5-HT stimulated, and cytochalasin-D treated states are presented in Table 1. With cytochalasin-D present, storage modulus values drop to a level not only well below the contractile level, but also significantly below the baseline level (n = 5). The contractile stiffening and solid- versus liquidlike behavior of ASM cells is clearly sensitive to the degree of actin polymerization.

FIGURE 4.

Example of the effects of the actin capping agent, cytochalasin-D, on the complex shear modulus and hysteresivity of an ASM cell after stimulation with 5-HT. The severe decrease in storage (G′) and loss (G″) modulus, to levels well below baseline, indicate that dynamic actin polymerization is largely responsible for maintenance of cellular rigidity in the contractile and resting states. The large increase in hysteresivity (η) characterizes the inhibition of actin polymerization as a transition toward fluidlike behavior of the cell.

Inhibitors of MLCK (wortmannin) and ML-7 were used to test the sensitivity of ASM baseline rheology and response to contractile stimulation to the activity of actomyosin cross-bridge cycling. Results are listed in Table 1. Wortmannin treatments had no effect on baseline rheology as the storage and loss moduli average values after treatment (n = 5) were not significantly different than control baseline values (n = 16). Furthermore, 5-HT resulted in a stiffening response that was not significantly different in amplitude or kinetics for wortmannin treated cells than for control cells. Loss tangent values showed a large decrease after 5-HT stimulation in wortmannin treated cells similar to those for 5-HT stimulated control cells. Therefore, a 5-HT-induced contractile stiffening and transition toward solidlike behavior was still present in wortmannin treated cells.

Cells treated with ML-7 had significantly smaller storage moduli and larger loss tangents on average (n = 7), compared to untreated cells. Due to the length of time needed for ML-7 treatment, we were not able to track the time course of this decrease in G′. After stimulation of these cells with 5-HT, G′ values increased, although not to the same level as was reached in control cells after 5-HT. Loss tangent values were larger for ML-7 treated cells and showed significant decrease after 5-HT stimulation. Thus, ML-7 has a softening (liquefying) effect on ASM cells but does not prevent the stiffening (solidifying) effect of 5-HT stimulation.

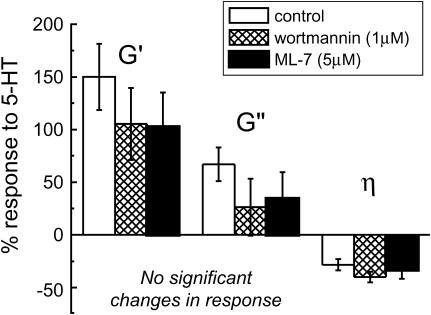
To illustrate this stiffing response, independent of baseline levels, we calculated the percent response to 5-HT relative to baseline values for each cell, then averaged the percent responses for control, wortmannin treated, and ML-7 treated cells (Fig. 5). Although some slight differences in G′, G″, or η mean response to 5-HT are observed between control and treated cells (for example, a decrease in G′ percent response from 150% in control cells to 104% in MLCK inhibited cells), these changes were not statistically significant.

FIGURE 5.

Relative responses to stimulation (percent difference from baseline) calculated for each cell tested and averaged for control and MLCK inhibited conditions. Although mean values are reduced, there is no significant inhibition of the contractile responses (P > 0.05).

Optical measurements of cell contraction confirmed that the MLCK inhibitory treatments used were sufficient to block 5-HT-induced cell shortening (Table 2). Contraction was reduced by the ML-7 vehicle (ethanol control response is half the DMSO control), but was substantially blocked by both wortmannin and ML-7.

TABLE 2.

5-HT-evoked contraction of ASM cells treated with MLCK inhibitors or appropriate vehicle

Treatment:	DMSO* 5-HT	Wortmannin 5-HT	Ethanol†5-HT	ML-7 5-HT
% contraction:	20.7 ± 2.7	−2.4 ± 2.6	9.7 ± 2.7	0.85 ± 0.07

^*Vehicle for wortmannin.

^†Vehicle for ML-7.

Frequency-dependent profiles

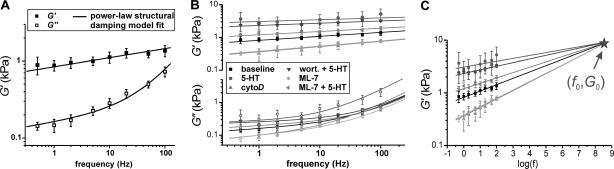
To investigate further the details of ASM rheology and the changes in cellular mechanics involved in contractile activation, we studied the frequency dependence of the complex shear modulus. Results show a weak power-law dependence of G′ on deformation frequency (Fig. 6 A, baseline conditions, n = 10). The behavior of G″ is more complicated, approaching the weak power-law dependence at low frequencies (parallel to G′) but having a much stronger dependence at higher frequencies. This complex behavior is well fit by the power-law structural damping model with additional Newtonian viscosity, described above (Eq. 2). The coupled data-set fit shown (fitting G′ and G″ simultaneously) provides values for the power-law exponent α = 0.120 ± 0.005, the Newtonian viscosity coefficient μ = 5.1 ± 0.4 Pa·s, and the scaling term G₀ = 0.77 ± 0.03 kPa (using f₀ = 1 Hz, an arbitrary choice for this single data-set fit).

FIGURE 6.

(A) Frequency dependence of the complex modulus of untreated ASM cells. Data are well fit by the weak power-law structural damping model with an additional Newtonian viscosity component (Eq. 2). The weak power-law behavior of the elastic modulus, spanning the entire frequency range tested, supports the hypothesis that cells behave as soft-glassy materials close to the glass transition (α = 0). (B) Frequency-dependent complex moduli under all treatment conditions, with a global fit to Eq. 2. The power-law exponent and Newtonian viscosity varied among treatments (fit parameters giving in Table 1). (C) Extrapolation of the storage moduli (G′) fits to the universal coordinate (f₀ = 10⁹ Hz and G₀ = 9.3 kPa).

This assay was repeated after the stimulation of the ASM cells with contractile agonist, 5-HT, and inhibitory drug treatments (Fig. 6 B). The parameters α and μ varied among treatments and are listed in Table 1. The power-law exponent showed anticovariance with the level of stiffness. Contractile stimulation, with or without MLCK inhibitors present, increased G′ at all frequencies tested and decreased the power-law exponent (slope in Fig. 6 B). Treatments that decreased stiffness, such as actin depolymerization with cytochalasin-D or MLCK inhibition with ML-7 (although not with wortmannin) resulted in stronger power-law frequency dependence (increased α). This behavior was fit well using the constraint of a universal coordinate (f₀, G₀) at much higher frequency than accessible with current technique, where all data fits for G′ converge (Fig. 6 C). The global nonlinear regression (lines in Fig. 6, B and C) determined log(f₀) = 9.0 ± 0.7 and log(G₀) = 0.97 ± 0.05 (or f₀ = 10⁹ Hz and G₀ = 9.3 kPa). Values of α were identical to those found if data sets were fit individually for each treatment (not shown). The Newtonian viscosity coefficient varied among treatments but without consistent correlation with any other parameter of the model. It increased by ∼4-fold under stimulation with 5-HT and remained slightly elevated after relaxation with cytochalasin-D. Unlike the changes in stiffness and α, μ showed no significant variation in the presence of MLCK inhibitors (wortmannin or ML-7).

DISCUSSION

Mechanical structure

The force volume images presented here provide maps of spatial variations of cultured ASM cells' mechanical structure under constant applied normal force (∼0.4 nN). With this level of force the cells plasma membrane is expected to be easily deformed (Evans, 1989) but is rarely punctured (as observed by inspection of our force curves). Indentation depths are typically 50–100 nm but can be as large as 200 nm when probing a very soft region of the cell (i.e., the nucleus). This allowed us to probe the underlying (yet still relatively superficial) cytoskeleton of the ASM cells. The observed cross-linked fiber network, with no striations or alignment with any particular direction in the cell, is a hallmark of smooth muscle microstructure (Small, 1995). The stiff nodes we observe appear very similar to the dense bodies or the membrane-associated dense plaques that have been extensively studied in smooth muscle with electron microscopy (Ashton et al., 1975; Draeger et al., 1990; Gunst and Tang, 2000). Our observations are more likely of dense plaques due to the superficial nature of the surface indentations used. These structures are critical for maintaining the structural integrity of the cells as well as being heavily involved in mechanical signaling and contraction. Dense plaques are known to be associated with actin filaments and interconnected by the more stable intermediate filaments, whereas cytosolic dense bodies connect actomyosin contractile fibers to the actin filament cytoskeleton (Draeger et al., 1990). The lateral resolution in AFM measurements on soft surfaces is limited mainly by the tip-surface convolution during indentation and the decay of the resulting stress field within the cell (Charras et al., 2001). A good estimate for the resolution for our probes and indentation level is 50–80 nm. The distance between individual measurements in Fig. 2 B is 78 nm, so we are measuring features at the scale of our resolution. This is comparable to, if not better than, the resolution limits of optical techniques in studying the cytoskeleton of living cells. Our force-based imaging demonstrates the ability of AFM to identify specifically mechanical structures in ASM cells and gives an appropriate length scale for the variations in cellular mechanics.

AFM force volume imaging provides additional information contained in the elasticity contrast. The enhanced stiffness of the fiber network relative to the surrounding cellular material supports the concept that it is the stress bearing structure of the cell. Within the tensegrity model for cellular biomechanics (Ingber, 1997), the fiber stiffness is related not only to its intrinsic rigidity but to existing prestress in the fiber network, recently confirmed for ASM cells (Stamenovic et al., 2004; Wang et al., 2002). Modeling of adherent cell poking experiments (Coughlin and Stamenovic, 2003) show that prestress in the peripheral actin cytoskeleton provides the key resistance to indentation at forces comparable to those used here. The soft-glassy material model involves structural elements that are in close interaction (confinement) yet still undergo nonequilibrium remodeling events (Fabry and Fredberg, 2003; Sollich, 1998). In cells, the identity of these structural elements is not known, but it seems reasonable that (for ASM cells) the stiff nodes we observe are potential candidates. Force volume mapping could be used to target individual elements and test the malleability of the interconnecting fibers, which likely define the confinement interactions.

Complex rheology

We characterized the microscale viscoelasticity of cultured ASM cells with AFM indentation modulation in the fibrous perinuclear region. The complex shear modulus, measured in response to nanoscale oscillatory perturbations, exhibited soft-glassy rheology. The elastic (storage) modulus scaled as a weak power-law (G′ ∼ f ^0.120±0.005) and the loss modulus, ∼1/5 G′ at low frequencies (in agreement with the structural damping relation 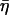= tan(πα/2) = 0.191), scaled with the same power-law dependence on frequency. Weak power-law behavior of the loss modulus, coupled to the elastic modulus, is referred to as frictional damping, as opposed to viscous damping which has a much stronger dependence on frequency. This behavior has been observed from microrheology measurements of ASM and other cell types with MTC (Fabry et al., 2001a) and in lung epithelial cells by AFM measurements (Alcaraz et al., 2003). The structural damping relation between G′ and G″ is also observed in tissue-level rheology (Fredberg and Stamenovic, 1989) and suggests that the elastic and dissipative processes in the cell are fundamentally linked at the level of the stress bearing element. An example of such a linkage was postulated using actomyosin cross-bridge formation and stretching as the energy storage process and their release as the energy loss process (Fredberg et al., 1996). In this way the ratio between G′ and G″ is independent of the number of actomyosin bridges and only on their cycling rate. Analogously, one could describe a structural damping mechanism based on dynamic actin polymerization, where the addition of G-actin monomers to F-actin filaments acts to resist deformation (storing elastic energy) and is coupled to the energy loss process of depolymerization, or removal of actin monomers from filaments.

Scale-free rheology is an indication of disordered mechanical structure in that the cell cannot be modeled by a defined set of elastic springs and dissipative sinks yielding a finite set of characteristic deformation frequencies. Rather, the cells demonstrate a continuous distribution of relaxation time constants, and thus there are no distinguishing inflections in the shear modulus frequency spectrum. The power-law exponent has been attributed to an effective ‘noise’ temperature, x = 1 + α, defining the cells as a nonequilibrium (metastable) system existing close to the glass transition (α = 0) and relatively far from the liquid state (α = 1). Currently, no theoretical description exists to explain the microscopic origin of soft-glassy rheology. Rather, these properties have been described with a model constitutive equation (Sollich, 1998), reasoning that mechanical properties are not a result of specific molecular interactions, but of a higher level of structural organization (confined structural elements with a heterogeneous distribution of confinement energies). The effective noise temperature is expected to be an integrative function of many forms of molecular agitations, the foremost of which being cross-bridge cycling and dynamic actin polymerization. This was confirmed in our study by the sensitivity of baseline mechanics to both cytochalasin-D and ML-7, although conflicting results were observed between the ML-7 and wortmannin treatments. Low levels of myosin light chain phosphorylation are typically observed in unstimulated ASM (Kamm and Stull, 1986).

At high frequencies, the loss modulus, G″, contains a component that is fit by a linear dependence on f and is attributed to Newtonian viscosity of the cells. Accurate measurement of this term relies directly on the calibration of the hydrodynamic drag on the measurement probe, as the two phenomena have the same functional behavior. For this reason we measured the lever drag and its decay with increasing height from the cell surface for each probe used. Errors in this method could arise from hydrodynamic coupling between the lever/fluid motions and the cell surface. In this case, simply subtracting the drag calibration from rheology measurements may not be appropriate as this coupling could drive cell deformations, producing a nonlinear effect that depends on cell viscoelasticity. Our calibrations varied considerably between probes (∼30%) and different surfaces (∼10%), but no consistent dependence on surface compliance was identified (tested over glass, cells, and cells stimulated with 5-HT). Improved calibration techniques and modeling of hydrodynamic effects are desired. Interpretation of Newtonian viscosity in terms of molecular mechanisms is also difficult. It characterizes the degree of purely dissipative particle interactions in a fluid, without reference to the elements involved or specific chemical bond formation/release. Nevertheless, this term has important implications for rapid reshaping, flow, and internal motions in the cell, as it is the source of greatest resistance at high frequencies. This term has commonly been treated as a constant property of the cytosol with no dynamic modulation in cellular processes. We have shown that this is not true for ASM contractile events (further discussion below).

Baseline measurements made in this study may not represent the unperturbed state of the ASM cells. Activation of a mechanotransduction mechanism is suspected in response to the mechanical stimulation of the AFM probing, often observed as an initial stiffening response over the first minute or so of the complex modulus measurements. Cyclic mechanical strain applied to ASM cultures via flexible substrate techniques has been shown to increase cellular contractile proteins and force production, Ca²⁺ sensitivity, cytoskeletal and focal adhesion reorganization, and stiffness (Smith et al., 2000, 2003a), but these changes are observed after many days of mechanical stimulation. Recently, localized mechanical stress applied to ASM cells with MTC has been shown to induce actin accumulation and stiffening over the time scale of our experiments (∼30 min; Deng et al., 2004). Possible mechanical sensing mechanisms have been proposed for ASM involving tyrosine phosphorylation of paxillin and focal adhesion kinase (Tang et al., 1999) and activation of RhoA (Smith et al., 2003b), also implicated in regulating contractility (Gunst et al., 2003). AFM has been shown to activate mechanotransduction signals in the form of an intracellular Ca²⁺ increase in osteoblasts (Charras et al., 2001). ASM cells experience mechanical strains in vivo during breathing, but reproducing physiologically relevant mechanical conditions for ASM rheological studies is nontrivial (Latourelle et al., 2002). We have demonstrated the potential for study of rapid mechanosensitive stiffening in ASM using AFM, as a mechanical probe which does not rely on specific membrane-receptor attachment (as does MTC).

Stiffening response to stimulation

We observed dynamic stiffening of ASM cells in response to the contractile agonist 5-HT. The fractional increase in storage modulus (150 ± 30%) is paralleled by a similar, but unequal increase in the loss modulus (67 ± 15%). The coupling is in keeping with the structural damping hypothesis for cellular mechanics, but the unbalanced response is indicative of a more fundamental change of the mechanical ordering state of the cell. Structural damping predicts that the hysteresivity parameter (loss tangent, η = G″/G′) is a constant index of the coupling between storage and loss processes. After stimulation, the definitive decrease in hysteresivity (−28 ± 6%) signifies the increased prevalence of the elastic, solidlike nature of the cell. A model proposed to explain decreased hysteresivity of ASM tissue after contractile stimulation is based on conversion of actomyosin bridges from the rapidly cycling phosphorylated cross-bridge state to the more stable latch-state when bound myosin heads become dephosphorylated (Fredberg et al., 1996; Murphy, 1994). However, we do not observe the fast transient increase in η at the onset of stiffening that was observed in the measurements published by Fredberg et al. (first 20–30 s, preceding the slow definitive decrease), interpreted as the increased cross-bridge cycling from the mostly inactive baseline state. Transient increases in hysteresivity have also been observed in MTC experiments (Fabry et al., 2001b), although the amplitude was smaller and decay was within 10–15 s. It is possible that a similar transient occurs before our first indentation after stimulation, but this is unlikely because the complex modulus usually does not respond until at least 50–100 s after addition of 5-HT. This apparent discrepancy is an indication that we are probing a fundamentally different mechanism of ASM contractile stiffening. Alternatively, the absence of the hysteresivity transient could be due to a difference in cross-bridge kinetics in rat ASM compared to human ASM such as used for the studies of Fredberg et al. and Fabry et al. (Lecarpentier et al., 2002).

Actomyosin activity is also a common mechanism for describing the actuation of ASM contraction. It is therefore intriguing that inhibition of myosin phosphorylation through MLCK had very little effect on the stiffening response. Both of the inhibitory agents, wortmannin and ML-7, at the doses and durations used are known to block the ability of MLCK to induce phosphorylation and thus activation of myosin motors in smooth muscle (Nakanishi et al., 1992; Saitoh et al., 1987). Our observation that contractile shortening is blocked by the wortmannin and ML-7 (Table 2) confirms the efficacy of these treatments in inhibiting MLCK activity. A recent MTC study reported a stiffening response of cultured ASM to 5-HT, which was significantly suppressed by 1 μM ML-7 (paralleled by a similar reduction of baseline stiffness), but complete ablation of the response required a dose of 20 μM (An et al., 2002). We do not discount the possibility that our MLCK inhibitory treatments were only partially effective and that further study of dose-dependent effects is warranted. However, our observation that ML-7 (5 μM) reduced baseline stiffness by 50%, yet did not significantly alter the relative response to 5-HT (Fig. 5), suggests that there was some sensitivity to myosin activity; but the stiffening response we measured probed a cellular mechanical process that is largely independent of actomyosin interactions. It is also possible that the vehicle used for ML-7 delivery (ethanol) was responsible for the decrease in baseline stiffness as it reduced the shortening response by 50%.

The conflict of our results with those of An et al. may be partly due to differences in the measurement techniques. In MTC, Arg-Gly-Asp (RGD)-containing peptides are used to couple the measurement beads directly to the cell surface integrin receptors, key components of focal adhesions or dense plaques in ASM and known to be the sites of mechanical coupling from the extracellular matrix to the intracellular contractile fibers (Burridge et al., 1988; Draeger et al., 1989; Gunst and Tang, 2000; Schoenwaelder and Burridge, 1999). Therefore, it is not surprising that stiffness changes measured with MTC are dominated by the activity of actomyosin contractile elements. Integrin receptor binding is also known to stimulate a number of biochemical signals that could have pronounced effects on cellular mechanics (Meyer et al., 2000; McNamee et al., 1996; Plopper and Ingber, 1993). The use of chemically nonspecific AFM probes avoids this potential effect. One can also reason that the geometry and direction of the applied force in MTC (lateral twists) and AFM (vertical oscillations) has a significant influence on the mechanical structures being probed. These arguments require a detailed examination of the induced intracellular strains and stress transmission (Charras et al., 2001), which are particularly difficult to quantify/model for MTC (Coughlin and Stamenovic, 2003).

Complete frequency-dependent assays before and after contractile stimulation confirmed the description of contractile stiffening as a transition toward solidlike glassy rheology and revealed the relative contribution of frictional and viscous damping to the observed changes in complex rheology. Further support for the soft-glassy framework is provided by the extrapolation of our frequency-dependent results to the universal coordinate (f₀, G₀) common to all treatments, leaving the noise temperature (α + 1) as the key determinant of the cells' mechanical state. However, our observation that the high-frequency component of the loss modulus, described by Newtonian viscosity, is dynamic between baseline and stimulated states is unique. Newtonian viscosity may be useful in distinguishing between contractile events (myosin dependent) and other stiffening processes, as its dynamics during stimulation seems to be blocked by MLCK inhibitors (unlike the stiffening response). Highlighted by the behavior under wortmannin treatment, the variations in Newtonian viscosity response appear to be independent of changes in stiffness. This supports our claim that Newtonian viscosity dynamics are not an artifact of hydrodynamic coupling at the cell surface (stiffness-dependent effect discussed above). ML-7 treatment also inhibited the 5-HT-induced Newtonian viscosity increase (but not the stiffness increase). Although a mechanism for such processes is unclear, we have shown that Newtonian viscosity, as well as the power-law exponent (noise temperature), are critical in characterizing ASM contractile mechanics.

Dynamic actin polymerization

The results presented here point to dynamic actin polymerization as a good candidate for a myosin-independent stiffening response, due to the high sensitivity to modulation of actin polymerization dynamics. Cytochalasin-D, a filament capping agent, is suspected to only affect actin that is in a state of dynamic polymerization-depolymerization and not stable actin filaments. Thus, it can be reasonably stated that the mechanical integrity of the cells as probed by AFM surface indentations, relies to a large extent on dynamic cycling, or treadmilling, of actin filaments (Wegner, 1976), also known to generate propulsive force in motile cells (Mogilner and Oster, 2003). Actin filaments of the contractile apparatus in smooth muscle may be dynamic (i.e., cytochalasin-D sensitive; Tseng et al., 1997), thus interpretation in terms of nonmyosin-associated actin depends also on the MLCK inhibitor tests discussed above.

Increased actin polymerization has been previously observed during contractile events in ASM (An et al., 2002; Herrera et al., 2004; Hirshman and Emala, 1999; Mehta and Gunst, 1999). These and subsequent studies implicate a number of signaling and regulatory molecules of actin polymerization, which are not directly dependent on myosin light chain phosphorylation, and myosin ATPase activity. Gerthoffer and Gunst (2001) review the evidence for contractile agonist stimulation of tyrosine phosphorylation of focal adhesion kinase, c-Src, and paxillin, which lead to actin remodeling through the Rho (or Rac) family of GTPases and the 27-kDa heat shock protein. Since these pathways are also involved in mechanotransduction, they are stimulated by tension development during contraction and thus are partially dependent on cross-bridge cycling and force production. Membrane attachments of the actin cytoskeleton (via vinculin and talin) are altered and strengthened during contractile activation (Gunst and Fredberg, 2003). Other actin regulatory pathways may involve activation or modulation of phosphoinositides, Arp2/3, profilin, cofilin, filamin, or α-actinin, as known from studies of nonmuscle cells (Pollard et al., 2000; Stossel et al., 2001; Yin and Janmey, 2003).

The functional role of dynamic actin polymerization and remodeling during contraction of ASM is suggested to be necessary for optimal energy utilization during contraction (Jones et al., 1999). Increased stiffness of the actin cortex may enhance force transmission from the contractile apparatus to the extracellular matrix (and thus to neighboring cells) by strengthening the region surrounding focal adhesions (Gunst and Fredberg, 2003; Janmey, 1998; Kuo and Seow, 2004). Similarly mechanotransduction and mechanoprotective mechanisms may enhance the cytoskeletal-membrane junction, strengthening specifically at sites of high tension or strain. Similarity of the viscoelastic characteristics of the contractile apparatus, the connective layer beneath the membrane, and the extracellular matrix is of critical importance for cooperative, coordinated muscle contraction (the so-called hysteretic matching; Fredberg and Stamenovic, 1989). Therefore, this study stands as an important step in characterizing the components of a complete model of airway contraction.

CONCLUSIONS

Atomic force microscopy provides a unique tool to probe the nanoscale mechanical structure and complex rheology at the surface of living cells, with the ability to track variations of these properties in the space, time, and frequency domains. We show that force volume imaging can identify mechanical structures of interest for modeling cytoskeletal mechanics. The indentation modulation technique allowed for measurement of the elastic and dissipative components of the complex shear modulus, which increased dramatically with contractile stimulation and showed a definitive shift in fundamental mechanical behavior. We presented evidence implicating actin polymerization and not actomyosin activity as the dominant mechanism actuating the stiffening response. Thus, actin dynamics has a prevalent role in near-surface mechanics of ASM cells during contraction. The frequency dependence of the complex modulus under all treatments supports the soft-glassy rheology model of cellular mechanics with an additional term describing the Newtonian viscosity (or purely fluid behavior) at high frequencies. The soft-glassy behavior of ASM cells, governed largely by the level of molecular agitations (noise temperature) is the key determinant of the cells' mechanical state. We revealed significant changes in the Newtonian viscosity term that vary independently of the soft-glassy properties (showing stronger correlation with actomyosin activity). Thus, with further study of frequency-dependent ASM cell surface rheology, it should be possible to distinguish features of actin polymerization and cross-bridge interactions during cellular mechanical events. Measurement and characterization of these phenomena require a precision nanoscale probe with picoNewton force sensitivity and detailed analysis of frequency-dependent complex rheology, as is possible with AFM.