Abstract
Ezrin plays a key role in coupling signal transduction to cortical cell organization. This actin–membrane linker undergoes a series of conformational changes that modulate its interactions with various partners and its localization in membrane or cytosolic pools. Its mobility and exchange rates within and between these two pools were assessed by two-photon fluorescence recovery after photobleaching in epithelial cell microvilli. Analysis of ezrin mutants with an altered actin-binding site revealed three ezrin membrane states of different mobilities and exchange properties, reflecting sequential association with membrane components and F-actin in the context of a fast overall turnover.
Ezrin is a member of the ezrin/radixin/moesin (ERM) family of actin–membrane linkers that play a key role in coupling signal transduction pathways with the maintenance of the cortical cytoskeleton architecture and its dynamic response to external stimuli (1, 2). ERM linkers concentrate in cell-surface structures rich in actin such as microvilli and filopodia, and their impaired expression or inactivation severely alters cell surface morphology, motility, and adhesion (1).
Ezrin is present in membrane and soluble pools, and its dynamic localization between these two compartments is an important determinant of its activity. In the cytoplasm, ezrin is mainly present in a so-called “masked” form, in which intramolecular interactions between the N and C termini block its binding sites (3). Conformational masking is also achieved by similar interactions in an intermolecular head-to-tail fashion (4). The formation of the fully active state of cytoskeleton–membrane linker of ezrin/radixin/moesin (ERM) proteins is thought to be achieved by a succession of conformational changes that involve binding to PIP2 and membrane/peripheral proteins (intercellular adhesion molecules, CD44/43, and EBP50), as well as the phosphorylation of a Thr present in the actin-binding site (5–11). Deactivation of ERM linkers might be triggered by dephosphorylation, because in vivo dephosphorylation correlates with microvilli breakdown (12, 13).
The two-way exchange between the cytosolic and membrane pools plays a crucial role, because it controls not only the relative amount of ezrin molecules in the active membrane form but also the relative amount of time spent by each molecule at the membrane and the total flux of ezrin turnover. However, the exact sequence of these events, as well as the lifetimes of the different conformation states, is unknown and poses a fundamental challenge to understanding the morphogenetic properties of ezrin. Key parameters controlling these different states could be either static (relative amounts of active vs. inactive forms at a given time point) or dynamic (residence times, mobilities, fluxes).
In the present work, mobility studies resolving ezrin membrane and cytosol contributions have been performed in epithelial LLC-PK1 cells. These cells display, on their apical surface, microvilli that are well characterized ultrastructurally and biochemically. In the microvilli, ezrin is thought to link bundles of actin filaments to the plasma membrane. To analyze the ezrin membrane-bound pool and resolve its behavior from that of the cytosolic pool, we combined the method of fluorescence recovery after photobleaching (FRAP) (14) with two-photon fluorescence microscopy (15), which uses restricted excitation to analyze selectively the cortical region of cells. The present data describe the dynamic behavior of GFP-tagged actin and ezrin, with a high temporal and spatial resolution of 10 ms and ≈1 μm. We also analyzed the behavior of ezrin mutants to elucidate the molecular determinants of their dynamic properties. Numerical simulations were used to extract a physical interpretation that leads to a new model for the serial engagements of ezrin at the membrane.
Materials and Methods
Molecular Biology, Cell Cultures, and Transfections.
GFP-actin (16), ezrin-GFP (17), ezrin-GFP internal (GFPi) (18), and ezrin-Δ53-GFP (18) constructs have been previously described. GFP was fused at the C-terminal end of ezrin-T567A and -T567D (6). LLC-PK1 cells (CCL 101; American Type Culture Collection, Rockville, MD) were grown in DMEM supplemented with 10% FCS. DNA transfer to LLC-PK1 cells was performed as previously described (6). Transiently transfected cells were analyzed after 2–3 d of cDNA expression. Ezrin-GFP transfected cells were selected for the generation of stable transfectants as previously described (6). Similar results of FRAP experiments were obtained whether cells were stably or transiently transfected with the different constructs. Experiments were performed at 37°C in growth medium, with confluent cells seeded on 25-mm glass coverslips. When indicated, cells were treated with 3 μM jasplakinolide (Molecular Probes) for 10–30 min.
Two-Photon Fluorescence Imaging.
An IX70 inverted microscope coupled with a Fluoview confocal scanner (Olympus, Tokyo) was modified for two-photon fluorescence imaging. A tunable pulsed Ti:Sapphire laser (Tsunami; Spectra Physics, Mountain View, CA) pumped by a ND-YVO4 laser (Milennia; Spectra Physics) provided 70-fs pulses with a 80-MHz repetition rate. GFP fluorescence was excited at 900 nm with a high numerical aperture objective (×63 oil immersion, numerical aperture 1.25, Zeiss PlanNeofluar) and collected through the same objective via a GFP 500- to 520-nm bandpass filter (HQ510/20, Chroma Technology, Brattleboro, NY). Fluorescence was detected with the built-in Fluoview photomultiplier in the descanned configuration (R928, Hamamatsu Photonics, Hamamatsu City, Japan). In the above conditions, the excitation volume that gives the point-spread function can be represented as an ellipsoid with a z-axial symmetry, and dimensions dw = 0.6 μm and dz = 1.5 μm in the focal plane and along the optical axis z, respectively.
FRAP Setup.
Laser power was rapidly switched (0.1 ms) by an electrooptical modulator (model 350–50, Conoptics, Danbury, CT) driven from a home-written labview 5.1 (National Instruments, Austin, TX) interface that also controlled a 1-MHz A/D computer board (PCI-MIO-16E-4, National Instruments, Austin, TX) that acquired the descanned fluorescence signal detected by the R928 photomultipliers.
FRAP Experiments
Localized FRAP Experiments.
In most of our experiments, the GFP fluorescence of one selected point was followed along with illumination, which allows a high temporal resolution of 10 ms, in a sequential manner: (i) observation for 1 s with a 2-mW power (observation power); (ii) bleaching with a 20-mW power for 50 ms; and (iii) observation of the recovery for 10 s.
Control experiments were aimed at checking that: (i) the photobleached region did not move relative to the laser beam; (ii) photobleached molecules did not recover their lost fluorescence; (iii) the intensity level was proportional to the number of molecules returning into the focal volume. These experiments are detailed in Supporting Methods, which is published as supporting information on the PNAS web site, www.pnas.org. Briefly: (i) microvilli moved at a velocity of 0.1 μm per 10 s. Consequently, the observation was limited to 10 s. (ii) The recovery of immobile GFP was very limited (7% in 10 s) and did not interfere significantly with the interpretation of the present data. (iii) Under continuous illumination during the observation period, fluorescent proteins undergo a limited photobleaching process (observation bleaching). Observation bleaching is 100 times slower than pulse bleaching, because the two-photon fluorescence excitation rate is proportional to the squared intensity. To quantify the effect of observation bleaching, the postpulse recovery sampled at 10 s only (“end-point sampling”) was compared with the value obtained at 10 s with the standard protocol. The observation bleaching did not affect the measurement of fast-moving proteins but led to an underestimate of the recovery amplitude for low mobility proteins by typically 15% at 10 s. This fact was taken into account, and fractions given in Results and in Table 1 are normalized by using the “end-point sampling” level, whereas raw data are shown in Figs. 4 and 5.
Table 1.
Fast- and slow-moving pools for ezrin and actin in microvillus
| % fast A | % slow B–F | Relative percentage in the slow-moving pool
|
||||
|---|---|---|---|---|---|---|
| B (fast) | F (exchange) | B (slow) | C (immobile) | |||
| Actin | 55 | 45 | 100 | |||
| Ezrin | 30 | 70 | 25/[0] | 0/[70] | 75/[30] | |
| Ezrin-GFPi | 10 | 90 | 25/[0] | 0/[70] | 75/[30] | |
| Ezrin-Δ53 | 0 | 100 | 70 | 30 | ||
| Ezrin-T567A | 15 | 85 | 40/[30] | 25/[0] | 0/[50] | 35/[20] |
| Ezrin-T567D | 0 | 100 | 15/[0] | 0/[30] | 85*/[70] | |
The nomenclature of Fig. 3 (A–F) was adopted. For each construct, the percentage of fast-diffusing component (soluble fraction in situation A, with D = 10–30 μm2⋅s−1) or slow-moving components (membrane or actin-bound, in situations B–F) in microvilli is indicated. Relative percentages in the slow-moving pool are indicated. B (fast) refers to the situation of membrane diffusion with D = 0.8 μm2⋅s−1, B (slow) with D = 0.1 μm2⋅s−1, F to reaction-limited exchanges with τ = 5 s. In this latter case (F column), the percentages represent the amount of the fraction bound to discrete membrane ligands.
indicates that the estimated immobile fraction C is statistically significantly greater for ezrin-T567D than for WT-ezrin (-GFP or -GFPi). Situations D and F do not appear in the table, because they do not account explicitly for the exchange between two membrane pools, which is suggested by the present data. Fractions given between brackets correspond to an alternative interpretation to the Fig. 6 model that was not proposed, because it would imply a more complex model with other states of intermediate mobility.
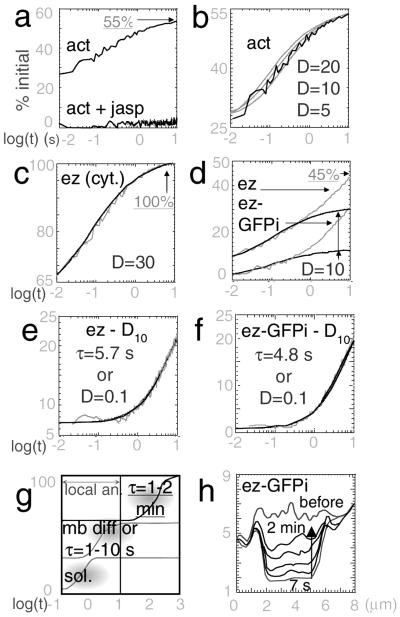
Figure 4.
Dynamic behavior of GFP-actin, ezrin-GFP, and ezrin-GFPi in the cytoplasm and in the microvilli. (a–f) Local measurements. For all figures, mean recovery curves are drawn. (a) Actin-GFP in microvilli, before (Upper) and after (Lower) jasplakinolide treatment (n = 73 and SEM = 2%). (b) Numerical fits of GFP-actin recovery (black), with D = 5, 10 and 20 μm2⋅s−1 (gray). (c) Cytoplasmic ezrin-GFP (gray) (n = 53, SEM = 2%) fitted with a diffusive curve of D = 30 μm2⋅s−1 (black). (d) Ezrin-GFP (Upper, gray, n = 117 and SEM = 1.4%) and ezrin-GFPi (Bottom, gray, n = 118 and SEM = 1.5%) in microvilli. Black: fits of the short time regions with diffusive curves of D = 10 μm2⋅s−1. (e) The difference between the ezrin-GFP recovery curve and the fast-diffusing curve of D = 10 μm2⋅s−1 (gray) was fitted with a slow diffusive process of D = 0.1 μm2⋅s−1 or with reaction-limited exchange process modeled by an exponential of τ = 5.7 s (both fits overlap: black). (f) The difference between the ezrin-GFPi recovery curve and the fast-diffusing curve of D = 10 μm2⋅s−1 (gray) was fitted with a slow diffusive process of D = 0.1 μm2⋅s−1 or an exchange process of τ = 4.8 s (both fits overlap: black). (g) Synopsis of the different time domains of relaxation, accessible either by local analysis or time-lapse imaging FRAP experiments, with arbitrary vertical scale. (h) Relaxation in a typical time-lapse imaging FRAP experiment. The profiles are similar for ezrin-GFP and -GFPi, shown here. The recovery was analyzed in terms of the average fluorescence intensity profile (y, arbitrary units) along the direction perpendicular to the bleached band. Successive profiles before photobleaching and at 7 s, 14 s, 30 s, 1 min, and 2 min after photobleaching are shown.
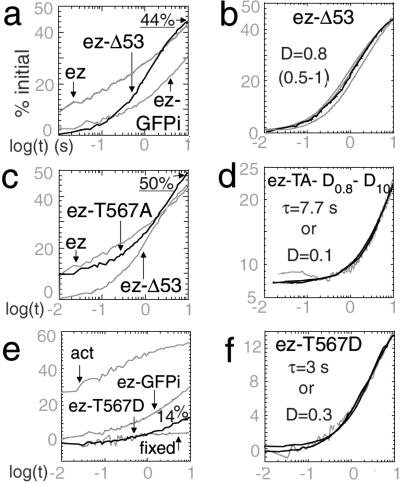
Figure 5.
Dynamic behavior of ezrin-GFP mutants in microvilli. (a) Ezrin-Δ53-GFP (black), ezrin-GFP and ezrin-GFPi (gray) in microvilli (n = 172 and SEM = 1.2% for ezrin-Δ53). (b) Ezrin-Δ53-GFP (black) fitted with diffusive relaxation (D = 0.5, 0.8 and 1 μm2⋅s−1) (gray). (c) Ezrin-Τ567Α-GFP (black, n = 115 and SEM = 1.6%), ezrin-Δ53-GFP (gray, Bottom) and ezrin-GFP (gray, Upper) in microvilli. The recovery of ezrin-T567A was analyzed by successive subtractions, first of 45% of D = 0.8 μm2⋅s−1, second of 15% of D = 10 μm2⋅s−1. Possible fits after these two subtractions with a slow diffusive process (D = 0.1, μm2⋅s−1) or a reaction-limited process (τ = 7.7 s) are shown (both fits overlap: black). (e) Ezrin-T567D-GFP (black, n = 34 and SEM = 1.5%), ezrin-GFPi and GFP- actin (gray) in microvilli. The recovery curve of immobile proteins is shown (gray, Bottom). (f) Fit of ezrin-T567D-GFP (gray) with a slow diffusive process (D = 0.3 μm2⋅s−1) or a reaction-limited process of τ = 3 s (black lines).
Time-Lapse FRAP in Imaging Mode.
To gain insight into the dynamics beyond the 10-s time scale, two-photon time-lapse imaging FRAP experiments were carried out. A band 5 μm in width and 20 μm in height was photobleached in the apical plane for 2 s, and fluorescence recovery was monitored by imaging the whole initial frame, at a rate of one image/7 s.
FRAP Data Presentation.
Fluorescence relaxation curves are shown in such a way that 100% corresponds to the intensity before the bleaching pulse and 0% to the level at the end of that 50-ms pulse for an immobilized GFP-tagged protein. This normalization scheme displays the actual photobleaching depth relative to its maximal possible value achieved in the immobile situation: immobile proteins reproducibly yield an 80% bleaching depth after 50-ms bleaching.
Interpretation Frame, Simulations, and Fitting Procedures.
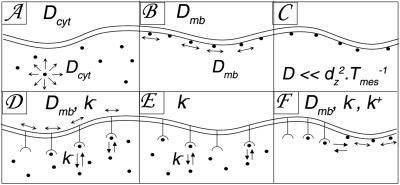
We interpreted the FRAP data in terms of the elementary situations depicted in Fig. 3 that consist of reaction-limited exchanges or diffusion in/between membrane and cytosol. Here are the main points of our approach, further developed in Supporting Methods.
Figure 3.
Classification of relaxation processes. Elementary situations used for modeling recovery curves. (A) Diffusion in the cytosol with a diffusion coefficient Dcyt. (B) Membrane diffusion with a coefficient Dmb. (C) Slow membrane diffusion or immobility. If D ≪ d ⋅T
⋅T (≈0.25 μm2⋅s−1), molecules appear immobile during the observation time of Tmes = 10 s. (D–F) Two-compartment situations, where recovery quantitatively reflects the kinetic parameters k+, k− of reaction-limited relaxations, either (D) between a membrane-diffusive and a cytoplasmic population, (E) a slowly or nondiffusing membrane population and a cytoplasmic population, or (F) two membrane populations, one diffusing and one virtually immobile (see Supporting Methods on the PNAS web site).
(≈0.25 μm2⋅s−1), molecules appear immobile during the observation time of Tmes = 10 s. (D–F) Two-compartment situations, where recovery quantitatively reflects the kinetic parameters k+, k− of reaction-limited relaxations, either (D) between a membrane-diffusive and a cytoplasmic population, (E) a slowly or nondiffusing membrane population and a cytoplasmic population, or (F) two membrane populations, one diffusing and one virtually immobile (see Supporting Methods on the PNAS web site).
In the exchange situation, fluorescence recovery can occur only when bleached molecules present on the saturable sites have gone away, explaining that a koff can be measured with this technique. Under the assumption of first-order processes, reaction-limited exchanges were modeled by exponentials.
For the diffusive case, the equation ∂tC(r, t) = DΔC(r, t) − kbI2(r)C(r, t) was solved numerically in the approximation of a unidimensional geometry (C, concentration; r, position; D, diffusion coefficient; I(r), illumination intensity distribution; kb, bleach constant).
When experimental data could not be explained by a single fit to diffusion or exponential relaxation, they were considered as the sum of two relaxations determined by two fits in a sequential manner: first the fast diffusive component and then the slow one. Procedures for fitting numerical simulation results with experimental data were carried out with the recovery amplitude and diffusion coefficient as free parameters. The error on diffusion coefficients was estimated graphically by bracketing experimental data.
Results
Ezrin and Actin GFP-Fused Constructs and Subcellular Localizations.
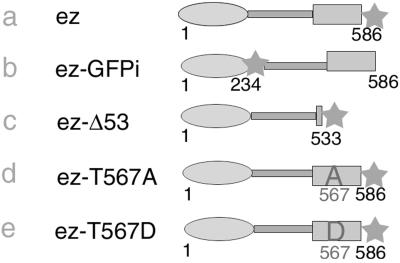
To analyze the dynamics of actin and ezrin in microvilli, the proteins were fused with GFP. The GFP-actin construct has been previously described (16). GFP was either added at the C terminus of ezrin (ezrin-GFP, Fig. 1a) or inserted inside the molecule at position 234 (ezrin-GFPi; Fig. 1b), which represents a constitutively active form of ezrin (18). To test for the effect of ezrin binding to actin, the F-actin-binding site of ezrin was either deleted or altered. A deletion of the 53 C-terminal amino acids, which comprise the binding site to F-actin, was performed (ezrin-Δ53-GFP; Fig. 1c). We also tested the mobility of ezrin carrying a point mutation in T567 (Fig. 1 d and e). It was previously shown that the phosphorylation of the residue T567 was involved in ezrin binding to actin (6). Impairing T567 phosphorylation with a T567A mutation resulted in reduced binding to actin, whereas mimicking constitutive phosphorylation with a T567D mutation led to constitutive binding to actin.
Figure 1.
Ezrin constructs. Schematic representations of ezrin fused to GFP. Ezrin contains an N-terminal membrane-binding domain, followed by an α-helical domain and a C-terminal actin-binding domain. GFP is represented by a star.
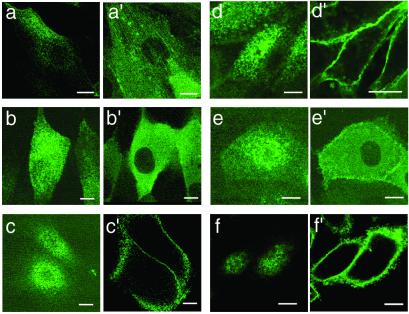
Actin-GFP was present in a variety of cell structures, including stress fibers and microvilli (Fig. 2 a and a′). Like endogenous ezrin (19), ezrin-GFP was present in microvilli as well as in the cytoplasm (Fig. 2 b and b′), whereas ezrin-GFPi was present in microvilli, in a characteristic punctate distribution, and at the cell periphery of LLC-PK1 cells but was not detected in the cytoplasm (Fig. 2 c and c′). Ezrin-Δ53 was associated with the apical and lateral membrane of LLC-PK1 cells (Fig. 2 d and d′). Ezrin-T567A-GFP showed an apical distribution but was also strongly expressed in the cytoplasm (Fig. 2 e and e′). Ezrin-T567D-GFP was present in the lateral regions and in microvilli and was not detected in the cytoplasm (Fig. 2 f and f′).
Figure 2.
Subcellular localization of actin and ezrin constructs fused to GFP in LLC-PK1 cells. Images were acquired by two-photon microscopy, using a 900-nm pulsed laser delivering 70-fs pulses, with a ×63 oil-immersion objective (Zeiss). Individual cells were imaged successively in two planes: through the apical surface (simple letters) and through the middle plane of the cells (primed letters). GFP-actin (a and a′), ezrin-GFP (b and b′), ezrin-GFPi (c and c′), ezrin-Δ53-GFP (d and d′), ezrin-Τ567Α-GFP (e and e′), and ezrin-T567D-GFP (f and f′). (Bar = 10 μm.)
FRAP Strategy and Interpretation.
To evaluate the mobility of proteins present in both membrane-bound and cytosolic forms, we used a microscopy technique capable of resolving in three dimensions the behavior in these two compartments separately. This was achieved by two-photon FRAP, in which the excitation and thus the photobleaching are confined in the axial direction, as opposed to classical one-photon FRAP in which excitation occurs along the whole optical axis. This excitation confinement to a micrometer-size volume corresponds to the typical dimensions of one microvillus. Fluorescence relaxation was assessed at a single-focus position, which allowed a high temporal resolution on the order of milliseconds. A quantitative analysis of the data was developed, taking into consideration that fluorescence relaxation can result from either a single diffusion or reaction-limited return of fluorescence into the excitation volume. These processes were considered in a limited number of elementary situations with different membrane and cytosol pools (Fig. 3). Time constants for these different situations were resolved by using fits with theoretical simulation curves.
Actin and Ezrin Behaviors in Microvilli and Cytosol.
For actin in microvilli, the relaxation started from a fluorescence level after the photobleaching pulse above zero (27 ± 2%, n = 73) (Fig. 4a). From our numerical simulations, an initial fluorescence level superior to zero is indicative of a large amount of fast-moving proteins, as relaxation of fast-moving proteins already starts during the bleach pulse of 50 ms, thus limiting the photobleaching depth. This fast relaxation was fitted as a diffusion process with D = 10 μm2⋅s−1 (5–20 μm2⋅s−1) (Fig. 4b) but accounted for only a part of the fluorescence recovery (55%). The fast movements were completely suppressed by the F-actin stabilizer jasplakinolide (Fig. 4a), which inhibits F-actin depolymerization and therefore strongly reduces the ratio G-/F-actin, suggesting that the fast mobile pool corresponded to the G-actin pool. The remaining “immobile” fraction (45% of the signal) probably corresponded to the F-actin pool, the movement of which was not detected on this time scale. (The estimated amounts of fast- and slow-moving pools for actin and ezrin constructs are listed in Table 1.)
The mobility of ezrin-GFP was evaluated in both the cytoplasm and microvilli. In the cytoplasm, the fluorescence recovered rapidly and completely (Fig. 4c). The high initial intensity of 65 ± 0.6% (n = 53) reflected a large amount of fast-moving proteins. The fit with numerical curves was best with a D = 30 μm2⋅s−1 (10–100 μm2⋅s−1), which was, like for actin, in the range expected for free diffusion in aqueous solution, strongly suggesting that the cytosolic ezrin pool essentially contained freely diffusing proteins.
In microvilli, ezrin-GFP did not completely recover after 10 s (level reached: 45 ± 4%, n = 117) (Fig. 4d). Two distinct behaviors could be resolved. At short times, the initial fluorescence level was above 0 (9.4 ± 0.8%), indicating a fast-moving pool representing about 30% of molecules. Because the ratio of initial fluorescence level to saturation value was close to the one of actin in microvilli (0.3–0.4), we modeled the behavior of this pool with a similar D = 10 μm2⋅s−1 (Fig. 4d).
At longer times, ezrin-GFP relaxed with an approximately constant flux between 2 and 10 s. This slow relaxation was studied by subtracting the fast component from the raw relaxation curve (Fig. 4e). Because the relaxation was not complete at 10 s, the saturation could not be observed. Thus two distinct fits had to be considered (Fig. 4e): either a unique slow diffusion with D = 0.1 μm2⋅s−1 (0.03–0.2 μm2⋅s−1) or a reaction-limited exchange with a typical time τ = 5.7 s, involving 25% of the molecules present at the membrane.
Like ezrin-GFP, ezrin-GFPi showed an incomplete recovery in microvilli (level reached: 30 ± 2%, n = 118) with fast and slow behaviors (Fig. 4d). The fast-diffusing fraction of ezrin-GFPi was reduced compared with ezrin, as deduced from the low initial recovery level (2.4 ± 0.01%). This fast-moving pool was fitted as 10% of diffusive pool with D = 10 μm2⋅s−1 (Fig. 4d). Apart from this difference in the soluble fraction, the slow-moving fractions of ezrin-GFP and -GFPi were very similar. In particular, the slow component of ezrin-GFPi fitted also either with a slow diffusive process (D = 0.1 μm2⋅s−1) or with a reaction-limited process (τ = 4.8 s, for 25% of molecules) (Fig. 4f).
The local FRAP experiments described so far, with observation time limited to 10 s, allowed us to observe cytosol and membrane diffusion, as well as fast-exchange phenomena (Fig. 4g). To determine the temporal scale of slower movements for ezrin (-GFP or -GFPi), typically exchanges with τ>10-s, time-lapse experiments were also performed, in which a significant renewal of ezrin cytoskeleton was observed with a typical t1/2 of 1–2 min in microvilli (Fig. 4h).
Ezrin Mutants with Altered Dynamic Behavior.
To test for the effect of ezrin binding to actin, we studied the mobility of ezrin-Δ53, -T567A, and -T567D proteins in microvilli.
The initial recovery level of ezrin-Δ53 (0 ± 0.5%, n = 172) indicated no detectable soluble fraction. A slow recovery was then observed over 10 s and began to saturate over that time scale, unlike ezrin wild type (WT) (Fig. 5a). The recovery curve was well fit with the theoretical curve obtained for diffusion with D = 0.8 μm2⋅s−1 (0.5–1 μm2⋅s−1) (Fig. 5b) and not with an exponential (not shown). Such a diffusion coefficient falls within the range of diffusion coefficients known for membrane proteins. The mobile fraction estimated from the diffusive fit was 70%. Ezrin-Δ53 is thus, for the most part, present in a freely diffusing form at the membrane.
The dynamic behavior of ezrin-T567A-GFP was intermediate between that of WT-ezrin and ezrin-Δ53 (Fig. 5c). Three components with decreasing time constants were observed. First, the initial recovery intensity (7 ± 1%, n = 115) indicated a minor soluble pool in the bleached volume, with a D = 10 μm2⋅s−1 (for 15% of molecules). Second, half of the remaining signal fit to a curve with a D = 0.8 μm2⋅s−1 (not shown). Third, the remaining relaxation signal could be fit either by a slow diffusive process (D = 0.1 μm2⋅s−1) or by a first-order reaction process (τ = 7.7 s, 25% of molecules) (Fig. 5d). The remaining immobile fraction was estimated to only 35% with “exchange” fit.
Ezrin-T567D relaxation was similar in shape to ezrin-WT relaxation but of smaller amplitude (Fig. 5e). No soluble component was observed, as estimated from the initial recovery level of 0 ± 1% (n = 34). As for ezrin-GFP and GFPi, because the relaxation was not complete at the end of the observation time, two fits remained possible: either a slow diffusion (D = 0.3 μm2⋅s−1, between 0.1 and 0.5 μm2⋅s−1), involving 30% of the molecules, combined with an immobile fraction, or a reaction-limited process (τ = 3 s, 17% exchange) (Fig. 5f). Our results suggest, therefore, that the relaxation process is similar in nature for WT-ezrin and ezrin-T567D, and hence that the reduced recovery at 10 s for ezrin-T567D indeed reflects an increase of the immobile pool for ezrin-T567D (Table 1).
Discussion
Two-Photon FRAP.
The interaction of ezrin with both membrane components and actin cytoskeleton is thought to involve serial engagements through a succession of conformational changes that are not fully understood. Understanding the functional properties of ezrin inside cells thus requires an understanding of the spatiotemporal behavior of the molecule as it interacts with its molecular partners. The method proposed here combines the intrinsic three-dimensional localization of two-photon fluorescence excitation with the well established FRAP method, as first described in ref. 20. We propose here a quantitative analysis of the microscopic dynamics of a cellular protein with high temporal and spatial resolution, combined with a molecular analysis by using mutants and theoretical modeling based on numerical simulations.
Soluble Pools.
FRAP experiments allowed us to assess the soluble fractions of ezrin and actin in the cytoplasm as well as in the microvillus region (Table 1). In the microvillus region, the soluble pool was important for ezrin-GFP and -T567A (15–30%), but less abundant for ezrin-GFPi, that no longer forms the dormant (“masked”) cytosolic form. There was no detectable cytosolic pool for ezrin-Δ53, which is associated with the membrane, and ezrin-T567D, which is a constitutively active form associated with actin.
A diffusion coefficient of 30 μm2⋅s−1 was found for cytosolic ezrin, similar to the one of cytosolic GFP (21). Because translational FRAP experiments are not very sensitive to the degree n of oligomerization (D is approximately proportional to 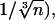 this coefficient indicates that cytosolic ezrin forms monomers or low number oligomers, in agreement with fractionation data (6). A reduced diffusion coefficient (10 μm2⋅s−1) was estimated for actin or ezrin in the microvillus region, which might be accounted for by the confinement of the molecules inside apical structures and the geometry of the probe volume.
this coefficient indicates that cytosolic ezrin forms monomers or low number oligomers, in agreement with fractionation data (6). A reduced diffusion coefficient (10 μm2⋅s−1) was estimated for actin or ezrin in the microvillus region, which might be accounted for by the confinement of the molecules inside apical structures and the geometry of the probe volume.
Membrane and Actin-Bound Ezrin.
At the membrane, the recovery seen in time-lapse imaging occurs typically with a t1/2 of 1–2 min for ezrin and ezrin-GFPi, which may reflect the basal rate of ezrin cycling between membrane and cytosol. It is important to note that ezrin recruitment to the membrane also occurs on the order of minutes on stimulation of cells. For instance, epidermal growth factor treatment induces membrane extensions that contain ezrin in 30 s (22), whereas pervanadate causes a redistribution from cytosol to lateral membrane in 5 min (23).
To study ezrin membrane behavior in more detail, localized measurements were performed on different ezrin constructs. Importantly, ezrin and ezrin-GFPi showed the same dynamic behavior, despite their different structures and biochemical properties (M.M. and P.M., unpublished results), suggesting that the fusion of GFP does not alter the linker function of ezrin.
Mutants with altered binding to actin allowed us to characterize three membrane pools with different mobility: a highly mobile pool observed for mutants with reduced binding to actin; an “immobile” pool that was best observed for a mutant with enhanced binding to actin; and a pool of intermediate mobility observed with WT-ezrin. Given the strong differences between the relaxation curves of the different mutants, we can safely assume that the relaxation mainly results from the properties of the exogenous protein population, with a minimal influence of a possible association with endogenous ezrin. Ezrin oligomerization might cause such an association, but it will not be discussed here because little is known about oligomerization processes.
The maximal membrane mobility was found for the ezrin-Δ53 and -T567A proteins with D = 0.8 μm2⋅s−1. This value is typical for membrane proteins that do not interact with the cytoskeleton, and PIP2 molecules have the same coefficient in lipid bilayers (24). We suggest that these ezrin mutants accumulate in the freely diffusing membrane intermediate form that precedes the binding to actin, probably reflecting their lost ability to reach a stable actin-bound state. This membrane freely diffusing form was not detected with WT-ezrin, either because the residence time is too short or the relative population too small.
An “immobile” form was observed for a fraction of WT-ezrin molecules (Table 1) and best observed for ezrin-T567D that dissociates from the filaments at a slower rate. This immobile state probably corresponds to a slowly exchanging actin-binding state of ezrin, with no reaction-limited exchange faster than 10 s, because F-actin itself appears immobile over 10 s. The enhancement of that state by the ezrin-T567D mutation is in agreement with the fact that T567 phosphorylation is an important determinant for stable binding to actin. Table 1 shows nevertheless that a weak immobile fraction was still estimated from fits of ezrin-Δ53 and -T567A mutants, suggesting that they could reach, albeit marginally, an immobile state without T567 phosphorylation.
An intermediate mobility situation was also observed for WT-ezrin, as well as for ezrin-T567A and, to a lesser extent, for ezrin-T567D. Within our modeling frame, this situation might reflect either a slow membrane diffusion with D = 0.1 μm2⋅s−1, or a reaction-limited exchange with τ = 5 s (Table 1). The latter interpretation was preferred because it leads to a model that accounts for the irreversibility of the engagement of ezrin.
Model for Ezrin Activation.
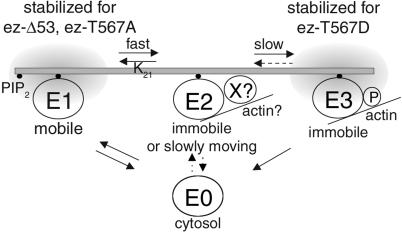
To account for the three distinct relaxations observed—corresponding to free membrane diffusion, reaction-limited exchange, and minimal mobility—we propose the following model (Fig. 6). Cytosolic ezrin first binds to the membrane as a high mobility state termed E1, with a residence time that is not kinetically limiting in comparison with the downstream steps. Proteins in the E1 state are then available for reversibly exchanging with an actin-binding state, termed E2, that progressively leads to irreversible binding called E3. A direct transition from cytosolic state to actin-bound state E2 cannot be ruled out, but for dimensional reasons, such a direct binding is likely to be less efficient than the transition from a membrane state (E1). The lifetime in the intermediate state E2, 5 s, corresponds to the dissociation time toward the free membrane or cytosolic form. It also sets the minimal possible value for the conversion time toward the stable fully phosphorylated actin-binding state E3. In turn, the E3 state dissociates upon dephosphorylation, over a much larger time scale of 1–2 min. In this scheme, ezrin turnover results from a sequence of diffusion periods, in which ezrin behaves reversibly, and of irreversible molecular events.
Figure 6.
Proposed model for ezrin association with the membrane. We propose that cytosolic ezrin first binds to membrane, entering state E1 with high lateral mobility. From that state on, ezrin enters state E2, whereby its mobility is much reduced, with a lifetime of 3–5 s that might be interpreted as the typical time of a reverse transition leading ezrin backwards to E1. The fraction of ezrin molecules that do not dissociate over that time scale proceeds irreversibly to the E3 state with virtually zero mobility. E3 might dissociate slowly, on the order of minutes, most likely to the cytosolic pool E0. (Plain arrows represent the main elements of the model and dashed arrows open alternative possibilities.)
In this model, the intermediate state E2 is proposed as a key state where ezrin binds to a membrane multiprotein complex of reduced mobility, in which state it might bind to actin indirectly, or directly through other actin-binding regions present in its N-terminal domain (25). Ezrin, while in E2, might undergo successive reversible and irreversible transitions which would then lock it in a stable actin-bound conformation E3. The mechanism of the conversion from a reversible to a stable state remains elusive, but the T567 phosphorylation is an important step of this process. First, the efficiency of this conversion is much reduced by the T567A mutations, which leads to a relative accumulation in E2 vs. E3 (in contrast, ezrin-Δ53 is not seen in E2, probably because of a more profoundly modified structure). Second, the conversion from reversible to stable state is more efficient for ezrin-T567D, mimicking a constitutively phosphorylated form, than for WT-ezrin. Nevertheless, T567 phosphorylation is only part of the activation process, as suggested by the observation that ezrin-T567D is also present in the reversible state E2, although to a weaker extent than WT-ezrin. A possibly analogous example of such a progressive activation has been described for the serial molecular events leading to calmodulin kinase II activation (26).
Concluding Remarks
In this study, local two-photon FRAP and site-directed mutagenesis were used to investigate simultaneously ezrin biochemistry and mobility at a local scale in microvilli, and to characterize three different ezrin membrane states, in the context of a very dynamic behavior with fast exchanging pools and a residence time at the membrane on the order of minutes. A fundamental issue raised by these observations is the relationship between ezrin dynamics and the maintenance of the steady-state apical morphology and its ability to respond to stimuli. Consequently, further investigation should aim at elucidating whether and how ezrin dynamics is coupled to the dynamic control of epithelial cell morphology and to the activity of associated membrane and peripheral proteins involved in ion transport, endocytosis, or actin polymerization. The approach established in the present work should be applicable to a large number of problems in which protein localization and mobility must be assessed at a microscopic scale. This is the case, for instance, of most signaling molecules for which the dynamics within and between the cytosolic and the membrane pool is a key determinant of their activity.
Supplementary Material
Acknowledgments
We thank Jacques Prost, Evelyne Coudrier, and Patricia Bassereau for sharing important ideas at the inception of the project and for constant support throughout the work; Claire Brown, Luc Fetler, Bruno Fiévet, and Véronique Bastouill for helpful discussions; and Julie Plastino and Edith Heard for careful reading of the manuscript. S.C. was supported by fellowships from the Ecole Polytechnique and Association de la Recherche contre le Cancer (ARC). This work was supported by grants from the Institut Curie, the Fondation de la Recherche Médicale, the ARC, and the Centre National de la Recherche Scientifique (CNRS).
Abbreviations
- FRAP
fluorescence recovery after photobleaching
- GFPi
GFP internal
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Bretscher A, Chambers D, Nguyen R, Reczek D. Annu Rev Cell Dev Biol. 2000;16:113–143. doi: 10.1146/annurev.cellbio.16.1.113. [DOI] [PubMed] [Google Scholar]
- 2.Mangeat P, Roy C, Martin M. Trends Cell Biol. 1999;9:187–192. doi: 10.1016/s0962-8924(99)01544-5. [DOI] [PubMed] [Google Scholar]
- 3.Gary R, Bretscher A. Mol Biol Cell. 1995;6:1061–1075. doi: 10.1091/mbc.6.8.1061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bretscher A, Gary R, Berryman M. Biochemistry. 1995;34:16830–16837. doi: 10.1021/bi00051a034. [DOI] [PubMed] [Google Scholar]
- 5.Barret C, Roy C, Montcourrier P, Mangeat P, Niggli V. J Cell Biol. 2000;151:1067–1080. doi: 10.1083/jcb.151.5.1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gautreau A, Louvard D, Arpin M. J Cell Biol. 2000;150:193–203. doi: 10.1083/jcb.150.1.193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Nakamura F, Huang L, Pestonjamasp K, Luna E J, Furthmayr H. Mol Biol Cell. 1999;10:2669–2685. doi: 10.1091/mbc.10.8.2669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Huang L, Ichimaru E, Pestonjamasp K, Cui X, Nakamura H, Lo G Y, Lin F I, Luna E J, Furthmayr H. Biochem Biophys Res Commun. 1998;248:548–553. doi: 10.1006/bbrc.1998.9009. [DOI] [PubMed] [Google Scholar]
- 9.Matsui T, Maeda M, Doi Y, Yonemura S, Amano M, Kaibuchi K, Tsukita S. J Cell Biol. 1998;140:647–657. doi: 10.1083/jcb.140.3.647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yonemura S, Tsukita S. J Cell Biol. 1999;145:1497–1509. doi: 10.1083/jcb.145.7.1497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Oshiro N, Fukata Y, Kaibuchi K. J Biol Chem. 1998;273:34663–34666. doi: 10.1074/jbc.273.52.34663. [DOI] [PubMed] [Google Scholar]
- 12.Chen J, Cohn J A, Mandel L J. Proc Natl Acad Sci USA. 1995;92:7495–7499. doi: 10.1073/pnas.92.16.7495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kondo T, Takeuchi K, Doi Y, Yonemura S, Nagata S, Tsukita S. J Cell Biol. 1997;139:749–758. doi: 10.1083/jcb.139.3.749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Axelrod D, Koppel D E, Schlessinger J, Elson E, Webb W W. Biophys J. 1976;16:1055–1069. doi: 10.1016/S0006-3495(76)85755-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Denk W, Strickler J H, Webb W W. Science. 1990;248:73–76. doi: 10.1126/science.2321027. [DOI] [PubMed] [Google Scholar]
- 16.Ballestrem C, Wehrle-Haller B, Imhof B A. J Cell Sci. 1998;111:1649–1658. doi: 10.1242/jcs.111.12.1649. [DOI] [PubMed] [Google Scholar]
- 17.Lamb R F, Ozanne B W, Roy C, McGarry L, Stipp C, Mangeat P, Jay D G. Curr Biol. 1997;7:682–688. doi: 10.1016/s0960-9822(06)00295-8. [DOI] [PubMed] [Google Scholar]
- 18.Dard N, Louvet S, Santa-Maria A, Aghion J, Martin M, Mangeat P, Maro B. Dev Biol. 2001;233:161–173. doi: 10.1006/dbio.2001.0192. [DOI] [PubMed] [Google Scholar]
- 19.Crepaldi T, Gautreau A, Comoglio P M, Louvard D, Arpin M. J Cell Biol. 1997;138:423–434. doi: 10.1083/jcb.138.2.423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Brown E B, Wu E S, Zipfel W, Webb W W. Biophys J. 1999;77:2837–2849. doi: 10.1016/S0006-3495(99)77115-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kohler R H, Schwille P, Webb W W, Hanson M R. J Cell Sci. 2000;113:3921–3930. doi: 10.1242/jcs.113.22.3921. [DOI] [PubMed] [Google Scholar]
- 22.Bretscher A. J Cell Biol. 1989;108:921–930. doi: 10.1083/jcb.108.3.921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wu Y X, Uezato T, Fujita M. J Cell Biochem. 2000;79:311–321. doi: 10.1002/1097-4644(20001101)79:2<311::aid-jcb140>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 24.Wagner M L, Tamm L K. Biophys J. 2001;81:266–275. doi: 10.1016/S0006-3495(01)75697-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Roy C, Martin M, Mangeat P. J Biol Chem. 1997;272:20088–20095. doi: 10.1074/jbc.272.32.20088. [DOI] [PubMed] [Google Scholar]
- 26.Hanson P I, Meyer T, Stryer L, Schulman H. Neuron. 1994;12:943–956. doi: 10.1016/0896-6273(94)90306-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.