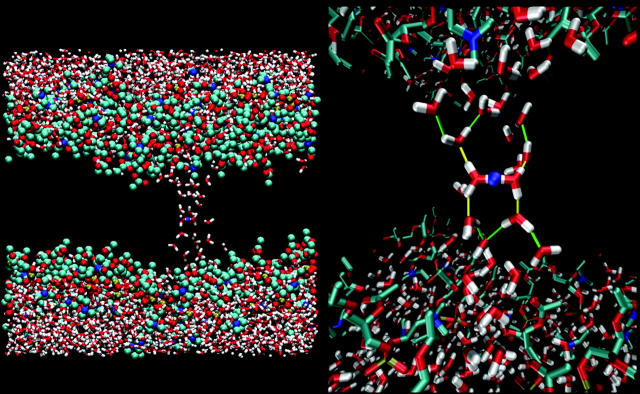
Abstract
Protons are known to permeate pure lipid bilayers at a rate that is anomalous compared to those of other small monovalent cations. The prevailing mechanism via which they cross the membrane is still unclear, and it is unknown how to probe the mechanism directly by experiment. One of the more popular theories assumes the formation of membrane-spanning single-file water wires providing a matrix along which the protons can “hop” over the barrier. However, free energy calculations on such structures (without the presence of an excess proton) suggest that this mechanism alone cannot account for the observed permeation rates. We use the multistate empirical valence bond method to directly study water structures surrounding a (delocalized) excess proton on its way through the membrane. We find that membrane-spanning networks, rather than single-file chains, are formed around the proton. We also find that such structures are considerably stabilized in the presence of the proton, with lifetimes of several hundreds of picoseconds. The observed structures are suggestive of a new, concerted, mechanism and provide some direction for further investigation.
INTRODUCTION
Proton transport across membranes is of vital importance for many cellular activities. Prokaryotes and eukaryotic organelles (mitochondria and chloroplasts) maintain proton gradients across their membranes, which are used to drive processes including ATP synthesis, active molecular transport, and flagellar rotation (Alberts et al., 2002). The concept that (electro)chemical gradients are actively maintained across membranes to provide energy for dedicated tasks was first introduced by Peter Mitchell in the 1960s as “chemiosmotic coupling” (Mitchell, 1961). This mechanism requires two structural elements: an (effectively) impermeable membrane that acts as a capacitor and a collection of gates that can selectively transport chemical species toward the intra- or extracellular space. Over the past few decades, several such gates have been found and characterized as membrane-embedded proteins that act as selective transporters.
One class of such proteins, proton channels, facilitate proton transport by stabilizing a single file of water molecules across a lipid bilayer (Decoursey, 2003). Permeation of protons along the water wire is thought to occur via a hopping mechanism—also referred to as the Grotthuss mechanism—in which the molecular topology and the identity of the conducting proton are constantly changed. This explains why proton transport is anomalously different from the transport of other small positive ions and proceeds up to several orders of magnitude faster.
The fatty inner core of lipid bilayers presents an efficient block against passage of ions and polar molecules, and thus evolved as the abovementioned capacitor. However, it has long been known that leakage does take place, even in the absence of channels (Decoursey, 2003; de Gier, 1992). In this case also, the proton permeability is orders of magnitude higher than the permeability of other cations indicating that the two processes must occur via fundamentally different mechanisms. Even though speculation has existed since long before the discovery of channel proteins (Hinkle and Yu, 1979; Nichols and Deamer, 1980), the prevailing mechanism of channel-less proton transport is still unknown. This rather unsatisfactory situation can be ascribed to the fact that many disparate pathways are imaginable, in sharp contrast with the dedicated channels, where the confining geometry severely limits the number of possibilities.
Here we will discuss the current theories (Decoursey, 2003; Haines, 2001), restricting ourselves to pure systems, i.e., neglecting the possibility of carrier molecules that can take up a proton on one side of the membrane and release it on the other.
Transient water wires
In analogy with dedicated proton channels, it has been suggested that transient single-file chains of water can span the membrane, facilitating proton transport via a Grotthus-type mechanism (Nichols and Deamer, 1980; Nagle, 1987). The positively charged proton would be partly stabilized in the fatty membrane core by the hydrogen-bonded network of the water file. Using molecular dynamics (MD) simulations, Marrink and Berendsen (Marrink et al., 1996) have estimated the free energy for the formation of such a water wire at 26 kcal/mol. This value could only be made consistent with measured proton permeabilities by assuming that protons permeate instantaneously and that their entry rate is anomously high. This is unlikely, since the same MD study reports maximum lifetimes of these water wires of only 10 ps (a later independent study reports an average lifetime of 37 ps and a maximum lifetime of 90 ps (Venable and Pastor, 2002)). By contrast, transport through channels like gramicidin A takes place on the order of several hundreds of picoseconds to nanoseconds.
Long-lived hydrophilic pores
When pores are formed in a membrane, above a critical pore radius the lipid headgroups will start to reorient toward the pore region. This can create a hydrophilic pore that will stabilize water molecules inside. Conversely, the water molecules will stabilize the pore as well. It has been suggested that such pores can be responsible for the passage of ions and polar molecules across membranes (Lawaczeck, 1988). In a recent simulation study, pores were created by applied tension and it was shown that—at least under tension—they remained stable over several tens of nanoseconds (Leontiadou et al., 2004). The free energy of pore formation was estimated at 10–24 kcal/mol. The critical pore radius was estimated at 0.7–0.9 nm, accommodating up to 100 water molecules in the pore region. At this level of confinement, water tends to show bulk-like behavior. Since in bulk water the self-diffusion constants of excess protons and potassium ions differ only by a factor of 5 (Cukierman, 2000), this mechanism would not seem to account for the order of magnitude difference in permeation rates between protons and other cations.
Intramembrane clusters
Recently, Haines (2001) proposed a “cluster-contact” mechanism for proton leaks. For stabilization of a proton in a bilayer, a small surrounding cluster of water molecules—as opposed to a membrane-spanning wire—might suffice. Haines suggested that such structures be present as separate clusters in the two monolayers. Proton translocation could then take place when two clusters meet and a proton hops from one to the other. Three possible events were identified: 1), an excess proton in a positively charged cluster hopping to a neutral cluster in the adjacent monolayer; 2), a proton from a water molecule in a neutral cluster hopping to a hydroxyl ion in a negatively charged cluster; or 3), proton exchange by clusters with an excess proton and an excess hydroxyl ion, respectively. The last event would be favored over the first two due to an extra charge attraction, but this would be offset by the fact that such encounters would be rarer (in terms of classical transition-state theory, a smaller “attempt frequency”). Proton blockage from intramembrane hydrocarbons (sterols, isoprenes) that occupy the interlayer spacing was given by the author as circumstantial evidence for these mechanisms. It is not clear, however, that this is decisive evidence for the proposed mechanism since it seems that such blocking molecules could also inhibit the other proposed mechanisms.
Thus far, neither experiments nor calculations have made it possible to pinpoint the prevailing mechanism of proton leakage through lipid bilayers. Experimentally, the problem is challenging: the medium is very dense and the length scales involved are tiny. It is therefore virtually impossible to directly probe the process of interest. The experimental “evidence” is thus largely circumstantial, via dependence of the permeability on such parameters as the pH, the counterion flux, the composition of the membrane, etc. Computer simulations may therefore be useful in achieving a microscopic understanding of this process.
Given the small length scales involved, any serious simulation attempt needs to be at the atomistic level of detail. A popular method that provides such detail, and at the same time can be used to study a full-scale membrane on a nanosecond timescale, is molecular dynamics. This approach has been used in the earlier simulations of water wires (Marrink et al., 1996; Venable and Pastor, 2002) as well as in the study of hydrophilic pores (Leontiadou et al., 2004). A drawback of MD simulations, however, is that the description is purely classical, whereas the proton is expected to display quantum behavior, i.e., through the rearrangement of chemical binding patterns via the Grotthuss shuttling process. The above studies have thus addressed the problem of intramembrane proton transport indirectly, by calculating the free energy of formation of some structural water matrix (single file or more bulk-like pores) to infer the permeability of protons along such a matrix. This approach only holds if the two processes are well separated in time (and if matrix formation is the rate-limiting process), whereas it will fail if there are important pathways where the proton and other coordinates move in a more concerted way. This question can only be answered by explicitly including the excess proton in the description.
True quantum simulations are still prohibitively expensive for simulating a full system of a membrane in solution. Even hybrid (quantum mechanical/molecular mechanical, or QM/MM) simulations are out of reach, since the effective interaction length of the delocalized proton would demand the treatment of a large QM region. To bridge this methodological gap, the multistate empirical valence bond (MS-EVB) method has been developed (Schmitt and Voth, 1998, 1999; Day et al., 2002). In this approach, an excess proton is described as a linear combination of accessible hydronium states. The system can continuously change its (classical) molecular topology while the transition probabilities between states are parameterized to model the true ab initio energy surface. The MS-EVB method has been succesful in describing the properties of proton transport in the bulk (Schmitt and Voth, 1999) as well as in confined geometries (Brewer et al., 2001; Smondyrev and Voth, 2002b; Wu and Voth, 2003).
In the next section of this article we will briefly summarize our methodology and describe the simulated system. Thereafter we will investigate the hypothesis that the presence of an excess proton stabilizes water chains in geometries in which they would normally not be stable. We conclude that the effect is not sufficient to enhance the lifetime of single-file chains of water in dimyristoylphosphatidylcholine (DMPC) membranes. In the subsequent section we study the formation of solvent structures around an excess proton that is quasistatically pulled through a DMPC membrane. We show that the evolved structures are hydrogen-bonded networks of water (and lipid headgroups), rather than single chains. We also show that the excess proton plays a crucial role in the stabilization of these structures and discuss the importance of other reaction coordinates, such as large-scale membrane modes. Finally we suggest a new mechanism for proton transport and end the article with conclusions and directions for future investigations.
METHOD
The MS-EVB approach (Schmitt and Voth, 1998, 1999; Day et al., 2002) can be regarded as a smooth interpolation method between force fields. At every instant in time, possible molecular topologies of the system are constructed and their interaction energies and forces are calculated via standard MD force fields. In practice, this means that the excess proton in its environment is described as a superposition of (empirical) valence bond states (Warshel and Weiss, 1980; Warshel, 1991). Each EVB state represents one hydronium ion surrounded by water and other molecules. Thus, an EVB Hamiltonian is constructed in which the diagonal elements are given by the energy of each state and the off-diagonal elements are parameterized to obtain the correct transition probabilities between states. The parameterization is generally carried out a priori using ab initio calculations on representative molecular clusters, although alternatives are possible.
Diagonalization of the EVB Hamiltonian at each time step defines the current state of the system via the ground-state eigenvector as a linear combination of all possible states. The forces on each atom are found via the Hellmann-Feynman theorem:
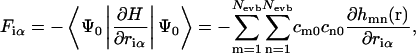 |
(1) |
with hmn(r) the elements of the EVB Hamiltonian matrix, riα the coordinate of particle i in the direction α, and Nevb the current number of EVB states. We will refer to the parameters cm0 as the “EVB amplitudes”, where m stands for the EVB state and 0 denotes the ground state eigenvector.
After evaluation of all the particle forces, the system is classically propagated to the next time step at which a new construction of states is carried out. This procedure maps onto a well-defined conserved Hamiltonian, i.e., the equations of motion are uniquely determined by the nuclear coordinates only. Thus all the usual statistical thermodynamics applies and all available methods for (enhanced) sampling of statistical mechanical ensembles can be used.
In the above description, the excess proton itself has become an ill-defined concept since it is now delocalized over different hydronium states. Thus we need an appropriate coordinate to describe proton transport. We choose to define the “center of excess charge” (CEC) as a linear combination of the oxygen positions in all accessible hydronium states, weighted by the EVB amplitudes (Smondyrev and Voth, 2002a):
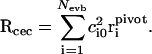 |
(2) |
Here, the sum is over all empirical valence bond states and 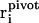 denotes the position of the hydronium oxygen (“pivot oxygen”) for each state.
denotes the position of the hydronium oxygen (“pivot oxygen”) for each state.
The reader is referred to earlier works for a more detailed description of the method and its parameters. Throughout the work described here we have made use of the MS-EVB2 parameter set (Day et al., 2002).
Force field
Throughout this study, we have used a system composed of a DMPC lipid bilayer with 100 DMPC molecules (50 per monolayer), 2089 water molecules, one excess proton, and one chloride counterion. The lipid molecules were modeled with united atom force field parameters (Smondyrev and Berkowitz, 1999; Smondyrev and Voth, 2002a). The water model was an adjusted version of the flexible point charge model used by us before (Randa et al., 1999). Upon moving from the bulk to the membrane interior, molecules will experience a large change in dielectric environment. It is therefore essential to have a water model that reproduces the experimental dielectric constant reliably. This is not the case for current simple point charge (SPC) models. In a separate study, the O-H equilibrium bond length (rOH) and H-O-H equilibrium bond angle (θHOH) were optimized in a self-consistent manner to reproduce the experimental values of the static dielectric constant εr and self-diffusion coefficient Ds of bulk water. Since εr turned out to be very sensitive with respect to changes in θHOH and, alternatively, Ds very sensitive with respect to changes in rOH, the abovementioned properties could be optimized without substantial changes in the molecular geometry. The resulting model was compared extensively against existing models in terms of thermodynamic, kinetic, and structural properties. The new model appeared much improved with respect to the SPC and TIP3P models, and the overall performance is comparable to or better than the extended SPC model. The parameters of the new model and some other models are shown for comparison in Table 1. Details about the simulations and the optimization procedure will be published elsewhere (Y. Wu, H. L. Tepper, and G. A. Voth, unpublished data).
TABLE 1.
Parameters of the modified water potential used in this study (SPC/Fw)
| kb (kcal mol−1 Å−2) |
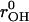 (Å) (Å) |
kθ(kcal mol−1 rad−2) |
 (°) (°) |
|
|---|---|---|---|---|
| SPC/Fw | 1059.162 | 1.0120 | 75.900 | 113.24 |
| TIP3P/Fs | 1059.162 | 0.9600 | 68.087 | 104.50 |
| SPC/E | ∞ | 1.0000 | ∞ | 109.47 |
| TIP3P | ∞ | 0.9527 | ∞ | 104.52 |
| SPC/Fd | 1054.20 | 1.0000 | 75.900 | 109.50 |
| εOO (kcal mol−1) | σOO (Å) | qO (e) | qH (e) | |
| SPC/Fw | 0.1554253 | 3.165492 | −0.8200 | 0.4100 |
| TIP3P/Fs | 0.1522000 | 3.150600 | −0.8340 | 0.4170 |
| SPC/E | 0.1554253 | 3.165492 | −0.8476 | 0.4238 |
| TIP3P | 0.1521000 | 3.150574 | −0.8200 | 0.4100 |
| SPC/Fd | 0.1554253 | 3.165492 | −0.8200 | 0.4100 |
For comparison, other models are listed as well: TIP3P/Fs, a flexible TIP3P model as used in the MS-EVB2 parameter set (Day et al., 2002); SPC/E (Berendsen et al., 1987); TIP3P (Jorgensen et al., 1983); and SPC/Fd, a flexible SPC model (Dang and Pettitt, 1987). All potentials are of the same form, an intramolecular term  and an intermolecular term
and an intermolecular term 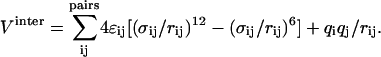
Other system parameters
We used an integration time step of 1 fs and a Nosé-Hoover thermostat (relaxation time 0.5 ps) to keep the temperature at 310 K. The electrostatic interactions were calculated via Ewald summation with a tolerance of 10−4 and a real-space cutoff of 9 Å. We used a box size of 55.7 × 55.7 × 53.68 Å3 with periodic boundary conditions applied in all directions. Initial configurations were taken from previous multinanosecond simulations on the same system (Smondyrev and Voth, 2002a). All simulations were performed with our in-house MS-EVB variant of the DL_POLY simulation package (Smith and Forester, 1996).
TRANSIENT WATER WIRES
For some time now, a popular theory for proton permeation has been Grotthuss shuttling along hydrogen-bonded water chains that would transiently span the membrane (Nagle, 1987). The concept is appealing, since it is analogous to presumed mechanisms of transport in, e.g., ice and biological proton channels. To this day, however, the mechanism remains unconfirmed in pure bilayers. Past simulation studies have failed to generate water wires with long enough lifetimes to allow proton transport. Reported lifetimes range from ∼10 ps (Marrink et al., 1996) to 37 ps (Venable and Pastor, 2002), whereas proton transport along these wires would be expected to take at least 50–100 ps or more.
The lack of stability of single-file water chains can be understood in the light of recent work on model hydrophobic channels, independently carried out by the groups of Hansen (Allen et al., 2002, 2003) and Sansom (Beckstein et al., 2001; Beckstein and Sansom, 2003). Both groups studied the water occupancy of hydrophobic pores, with both ends immersed in a bath of bulk water. They showed that for intermediate pore sizes, the system fluctuates between filled and completely empty states. For typical pore sizes that would only accommodate single-file chains (pore radius <4 Å), the pores remained unoccupied over nanosecond timescales. In lipid bilayers, where the pore formation would itself be an activated process, such timescales would seem not to suffice to make it a plausible proton permeation mechanism.
Hummer et al. (2001) studied water conduction through carbon nanotubes of similar size (radius 4.05 Å) and showed that those pores could sustain single-file chains of water over nanosecond timescales. The nanotubes in this study, however, were immersed in a bath of water, which constitutes a substantially different dielectric environment from that of the abovementioned model pores. At first sight it seems that the systems of interest for our study are more closely related to the above model structures than to Hummer's nanotubes.
It was implied by Beckstein and Sansom that an unoccupied pore would also provide a closed state for ionic transport (Beckstein and Sansom, 2003), but Allen et al. (2003) showed that the presence of an ion could significantly change the behavior. In fact, when they put a monovalent cation in the center of the pore it would spontaneously fill, even with single-file water chains for the smallest pore radii. It is not clear, though, if this effect would enhance the lifetime of transient water wires, since in the abovementioned study, the ion itself was kept at a fixed position (R. Allen, FOM-AMOLF, Amsterdam, private communication, 2004). In a later study, the same authors did relax the ion, but then permeation was only observed in the presence of a substantial electric field (Dzubiella et al., 2004).
In the context of this study, it is interesting to ask whether the presence of an excess proton could stabilize the very same transmembrane water wire along which it diffuses. There are two reasons to believe that this is true: 1), the abovementioned influence of a positive charge on the water chain; and 2), the amphiphilic nature of the excess proton: From several studies within our group (with varying levels of description for the quantum-like proton transport), it has been found that the hydronium ion has a tendency to move out of bulky water regions (Petersen et al., 2004). This somewhat counterintuitive result can be explained by the hydrogen bonding environment of the protonated species. In bulk, a water molecule has, on average, just less than four hydrogen bonds with other water molecules. A hydronium ion, however, disrupts this structure because it can accommodate a maximum of three hydrogen bonds. This effect causes a tendency to repel the excess proton out of the bulk.
We set out to investigate the effect of the excess proton by creating artificial pores in a DMPC membrane, putting the excess proton at the mouth and monitoring whether the pore would spontaneously fill with the proton surrounded by water molecules. The pores were made from an initial equilibrium system by slowly introducing a chain of repulsive particles along the z axis (perpendicular to the membrane), in the origin of the xy plane. These repulsive particles were static “ghost” particles in the sense that their equations of motion were not integrated. Their interactions with any other atom in the system (regardless of its identity) were defined by a Gaussian potential:
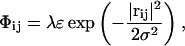 |
(3) |
with rij the distance between regular particle i and ghost particle j. We used σ = 2 Å and ε = kBT and put ghost particles at coordinates (0, 0 – 21 Å), (0, 0 – 19 Å), …(0, 0 – 21 Å). The dimensionless parameter λ allowed us to slowly (quasistatically) turn on the repulsive particle chain during successive simulations. A Gaussian interaction potential was chosen because of its smoothness over the entire range. Any repulsive potential that is unbounded at r → 0, like the Weeks-Chandler-Andersen potential, would introduce singularities in the system, even for small values of λ.
There are some important differences between our pores and those of the Sansom and Hansen groups. First of all, the membrane was included in full detail, with no difference between molecules at the pore boundary and molecules farther away. The pore boundaries were atomically rough and subject to thermal fluctuations (analogous to the pores of Beckstein and Sansom (2003), but different from the smooth pores of Allen et al. (2003)). And lastly, the repulsive potential in Eq. 3 only imposed a minimum pore size, not a maximum one. That is, the lipids were, in principle, free to open up even more.
During the first stage of the simulations, the ghost particles were repulsive for all other atoms (both water and lipid). We started with a 100-ps simulation at λ = 0.5, used its end configuration for a new 100-ps simulation at λ = 1.0, and so on up till λ = 10.0. Simultaneously with building up these initial configurations, each λ window was extended to a full production run of 500 ps. This created equilibrated systems with artificial pores of different sizes, ranging from no discernable pore at λ = 0.5 to a pore radius of ∼4 Å at λ = 10.0.
During stage II, we gradually decreased the interaction of the ghost chain with the water molecules only. This was done by introducing a second set of ghost particles superposed on the first ones, but now defined by an attractive potential between the ghost particles and water atoms:
 |
(4) |
The idea behind this two-step process was that they would represent two distinct reversible perturbation paths, one for the formation of a cavity and one for bringing in water molecules that could eventually fill the pores.
RESULTS
Fig. 1 shows the end configuration of stage II for λ = 6.0. Clearly, a pore has formed with more or less cylindrical shape. During the entire run of several hundred picoseconds this pore remained completely empty of water. (The water molecules occupying the pore region in the picture are actually situated above and below the membrane, not inside). Up to λ = 10.0 no occupation of the pores by pure water was observed, in accordance with the findings in the earlier studies on model hydrophobic pores.
FIGURE 1.

Top view of an artificially constructed pore in the membrane. Throughout the simulations, the pore remained completely empty (water molecules projected on the pore region are actually situated above and below the pore mouths).
Next, an hydronium ion was placed at the pore mouth. This did not change the situation. In all cases the hydronium remained located close to the pore mouth and the pore never filled with water nor did the excess proton show a tendency to enter the pore.
Finally, runs were initiated where the hydronium ion was put in the center of the pore. In all cases it immediately relocated to one of the pore mouths long before any water entered the pore.
One could imagine that the pore-filling process might not be spontaneous but could rather be an activated process with a slight barrier. That barrier could be calculated by an appropriate free energy method, but this is beyond the scope of our study. We feel that any barrier higher than kBT would make this mechanism a highly unlikely candidate for proton permeation, especially since transient pores of these sizes are not stable on their own (Leontiadou et al., 2004). Going to even larger pore sizes would finally lead to (meta)stable pores of a hydrophilic nature (Leontiadou et al., 2004), but we have argued above that their bulk-like occupancy cannot account for the anomalous proton permeation rates observed experimentally.
IN SEARCH OF A CONCERTED REACTION COORDINATE
A key aspect of the transient water wire proposal is the separation of timescales between the formation of a membrane-spanning water matrix (the rate-limiting step) and the subsequent diffusion of the excess proton along that matrix. In the previous section we extended that picture to include the formation of a transient membrane pore, followed by the (possibly concerted) diffusion of water and proton through that pore. It was concluded that a proton together with a single-file chain of water in the pore is not stable enough to make a mechanism likely where the membrane-spanning matrix is just a single-file water chain.
The above observation does not exclude the possibility of a proton moving across a membrane while surrounded by a water structure in a more concerted way. A surrounding water structure seems to be essential for two reasons: first, it would shield the positive charge and thus lower the barrier for traversing the hydrophobic membrane core; and second, without an (at least local) hydrogen-bonded matrix through which the proton can hop, the anomalous permeation rates with respect to other cations cannot be explained. The objective of this section is to find plausible structures without any a priori assumptions and eventually to suggest a complete pathway involving such structures.
Finding optimal reaction coordinates without prior knowledge of their nature is a significant challenge in free energy calculations for any complex system. There are ways to identify metastable sets in a multidimensional space of reaction coordinates (Schütte and Huisinga, 2003), but they generally apply only if a representative part of phase space can be sampled. That is not the case here, since proton permeation is a rare event and will never be observed spontaneously in an equilibrium simulation. An alternative is transition path sampling (Bolhuis et al., 2002), but that relies on generating several reaction paths from an initial reactive event and integrating them forward and backward in time until the proton has reached one of the basins. At present, that procedure is computationally prohibitive for our large system with EVB dynamics. Moreover, it relies on the availability of an initial reactive pathway close enough to the global minimum of the transition path ensemble, which might not be trivial to find in this case.
In the following, we will present free energy calculations for just one reaction coordinate, the z-position of the CEC. This coordinate is simple and conceptually attractive, since any path that takes the CEC position from one side of the membrane to the other side by definition constitutes a reactive event. Since it is highly improbable that this coordinate will be the optimal one in terms of classical transition-state theory, we cannot expect to find the true free energy barrier (Jóhannesson and Jónsson, 2001), although it might provide a reasonable upper bound. By inspecting other candidate reaction coordinates and correlating them with the chosen one, we seek to gain insight into the collective motion of solvent and bilayer that brings the proton over the barrier. This procedure also leads to a structure that we suggest may be representative of the transition state. Together, the findings presented here should facilitate later studies on the true transition path ensemble.
Umbrella simulations
In this section, we describe the use of umbrella simulations to enhance the sampling of the proton in the region of the membrane where its probability distribution is low (high free energy). There are several ways to do this, which lead to different results. First, we could have started with an equilibrium simulation of a DMPC bilayer in water and then put a hydronium ion at various positions in the membrane. Then, after some energy minimization to a local minimum, the local proton distribution could be sampled with the aid of a restraining umbrella potential. This procedure would lead to a symmetric free energy profile because of the symmetric structure of the membrane. Alternatively, we could start at one end of the membrane, perform local sampling with a restraining potential and use an equilibrated configuration of that sample as initial configuration in the next umbrella simulation, in which the restraining potential would be moved slightly closer to the center of the membrane. A successive series of such simulations will also bring the proton to the other side of the membrane.
Note that the latter procedure does not necessarily lead to a symmetric free energy profile. This is because the procedure itself is asymmetric in nature. While the proton is quasistatically “dragged” into the membrane, it can be accompanied by simultaneous motion of solvent molecules with it or deformation modes of the membrane. Though a symmetric profile is appealing, we propose that the second procedure gives potentially much more information about other (slow) degrees of freedom that are important in the optimal reaction coordinate and provide a picture of proton transfer that is much closer to true reactive pathways. Supposing that on reactive paths, the proton is always surrounded by a cluster of water molecules, but the free energy for water permeation through the apolar membrane core is much higher than the thermal energy, then the first procedure described in the previous paragraph will never show water molecules around the hydronium since it is impossible for them to cross the intermediate barrier during the sampling time. In other words, the “free energy” measure is an average over a subspace that is irrelevant for the process of interest.
The symmetry breaking in the second procedure does not mean that statistical mechanics is violated, because if the procedure were to be repeated starting from the other side, we would find exactly the opposite free energy profile. The average of these two profiles would be symmetric. That latter average, however, clearly contains just as little information as the profile from the first procedure. As a word of caution, we state that our free energy profile will also be a local average over a subspace. However, we suggest that that subspace has much more relevance for the optimal reaction coordinate.
The first umbrella simulation was started close to the bulk region at zcec = 20 Å. After 50 ps, we gathered the end configuration and used it as the initial configuration for the next simulation, with the umbrella origin at zcec = 19 Å. This procedure was repeated with steps of 1 Å until the excess proton had reached the center of the membrane. All runs were subsequently extended to 250 ps per window. In all cases we used a harmonic umbrella potential:
 |
(5) |
with spring constant k = 5 kcal/(mol Å2). Note that even though the interaction range of this potential is locally peaked around the position of the excess proton, it strictly affects all particles, since the coefficients ci0 in Eq. 2 are an implicit function of all particle coordinates. The force on particle m in the z-direction due to Uumb is equal to
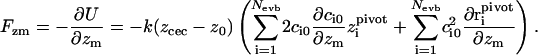 |
(6) |
Clearly, the last sum is only nonzero if particle m is the pivot oxygen of one of the Nevb MS-EVB states, but the first term is nonzero for all particles. The derivative of the (ground state) EVB amplitudes c0 with respect to the particle positions can be related to the complete set of eigenvalues and eigenvectors of the MS-EVB Hamiltonian (A. M. Smondyrev and G. A. Voth, unpublished results) via:
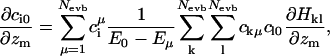 |
(7) |
where ciμ denotes the EVB amplitudes of all energy levels above the ground state. Since the Hamiltonian matrix is sparse, the evaluation of Eq. 7 does not present much computational overhead.
The potential of mean force (PMF) along a coordinate z is defined as the free energy along that coordinate. In our specific case:
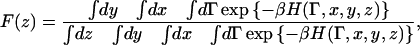 |
(8) |
where x, y, and z stand for the position of the CEC, and Γ for the remaining set of (generalized) coordinates. In principle, the integrals over x and y here are unbounded, since the system itself is infinitely replicated in those directions. Based on symmetry, though, every subspace defined in x and y should give a trivially identical free energy profile in z. (The membrane is a two-dimensional fluid). This allows for two routes to perform the sampling. 1), The xy space accessible to the CEC can be restricted by imposing restraining walls. This was done for ion transport in gramicidin A, where the one-dimensional PMF outside the restricted geometry of the channel becomes truly undefined (Allen et al., 2004). 2), Without imposing restrictions in xy, simulate over timescales sufficient to ensure that a representative part of the xy plane has been sampled.
Since it is not a priori clear which approach provides the most efficient sampling, we tried both. First, xy-restrained windows were simulated for 250 ps, of which the last 150 ps were used for use in the free energy calculation. The runs were then extended for another 250 ps without xy restraints, of which, again, the last 150 ps were used for production. Two representative trajectories are shown in Fig. 2. It can be seen that both of the trajectories sample a small region in xy space, far smaller than the space defined by the restraining cylindrical walls (here with a radius of 4 Å). It appears that the CEC (gray curve) has become trapped by the restraining walls (dashed line). This is confirmed by the successive unrestrained trajectory that immediately transcended the cylindrical boundaries (black curve). We concluded that although the membrane is known to be a two-dimensional fluid, the motions of the membrane matrix are much slower than the CEC motions through that matrix. Imposing extra restraining walls can then create local traps that slow down the sampling rate of the CEC in space. Without restraining walls it is likely to be much easier for the CEC to quickly sample a representative (though not exhaustive) space around its starting point. Note that in the earlier mentioned study on ion transport in gramicidin (Allen et al., 2004), a cylinder radius of 8 Å was used, which makes it very doubtful that the full phase space was sampled properly (since simulation times per window were comparable to ours).
FIGURE 2.
Trajectories (150 ps) of the CEC from an umbrella simulation with umbrella origin at zcec = 17 Å. The shaded trajectory has restraining walls in the xy plane (with a cylinder radius of 4 Å, as denoted by the dashed line). The black trajectory is unrestrained in both x and y.
From the successive umbrella simulations, a PMF can be reconstructed via the weighted histogram analysis method (Kumar et al., 1992). Fig. 3 shows the resulting PMF for both the restrained and the unrestrained windows. The fact that the unrestrained approach gives lower free energy minima inside the membrane could be seen as further confirmation that the CEC was able to find local basins.
FIGURE 3.
Potential of mean force (free-energy barrier) for the full region from the bulk (26 Å) to the membrane core (0 Å). Shown are the results for the simulations with (dashed line) and without (solid line) cylindrical restraints in the xy plane.
Several things can be learned from this potential of mean force. First, there is a small free energy drop in going from the bulk region (z > 22 Å) to the membrane interface. This is also known as the “antenna effect”: the membrane collects protons from the bulk which can then surface-diffuse toward channels or other functional regions (Williams, 1978; Haines, 1983). This result agreed with an earlier study by our group (Smondyrev and Voth, 2002a), where the minimum was also found around z = 18 Å. In the study described here, we found a slightly different profile from bulk to the first minimum, which we attribute to our more extensive sampling. The free energy difference between bulk and interface in Fig. 3 amounts to 2 ± 0.5 kcal/mol.
Upon extending our simulation further toward the membrane center, we found a surprising second metastable minimum at zcec ≈ 12 Å. A representative configuration from that region is depicted in Fig. 4. Apparently, a structure is formed in which the hydronium is stabilized by both water molecules and hydrogen-accepting oxygen atoms of the lipid headgroups. The network is dynamic in the sense that interchange takes place between pure water hydrogen bonds and hydrogen bonds with the lipid headgroups. This behavior should be unique to protons; it is hard to imagine how another cation would be stabilized in such a manner. This simulation therefore seems to give a first glimpse of new intermediates relevant to proton permeation of the lipid bilayer.
FIGURE 4.

Representative phospholipid headgroup structure around the excess proton (blue), residing in the second metastable minimum around zcec = 12 Å. The cooperative hydrogen-bonded networks of solvent and lipid headgroups is evident.
From this second minimum onward, the PMF rises monotonously to the membrane center. This is not surprising, since the apolar membrane core cannot facilitate charges easily. Interestingly, the free energy cost to reach the membrane center is not prohibitively high: only 18 kcal/mol. Comparing this to the 25 kcal/mol previously reported for water wire formation, one can conclude that both values are of the same order of magnitude, thus creating room for speculation about competing mechanisms. The two values do not, however, refer to the same process: the latter constitutes a free energy for wire formation through the entire membrane (albeit not particularly stable wires), but without explicit proton transport, whereas our value constitutes the free energy for a proton (including a substantial surrounding water structure) to reach the membrane core. At this point one can suggest the feasibility of a mechanism analogous to the cluster-contact proposal of Haines (see Introduction); if we very roughly assume a hydroxyl ion could approach the proton from the opposite side with a free energy cost similar to that of the proton to reach the core—and for simplicity assuming their additivity—we would arrive at an estimate of 36 kcal/mol. This is clearly an upper bound, because of the extra and significant charge-charge attraction between the proton and the hydroxyl. (As a rough estimate, the free energy reduction for moving two oppositely charged monovalent ions from 20-Å to 2-Å separation in a medium with effective static dielectric constant εr = 50 amounts to −3.0 kcal/mol. For εr = 10 this becomes more negative, to −14.9 kcal/mol). Alternatively, a neutral water cluster could enter the membrane from the opposite side and pick up the proton. This process would not benefit from the extra charge attraction, but would have a much higher “attempt frequency” (in terms of classical transition-state theory) simply because of the higher concentration of water molecules. In fact, we have seen spontaneous formation of such candidate “water wires” at the opposite side of the membrane in our simulations. One such structure is shown in Fig. 5. Note that the two opposing clusters do not have to completely touch. It is possible that the connecting structure would be composed of two clumps with a small wire in between, like an hourglass. We will more closely look into possible transition-state structures in the section entitled In search of a proton permeation pathway.
FIGURE 5.

Representative water structure showing only the water molecules in which a transversal wire has spontaneously formed on the side opposite to the excess proton (blue sphere).
Clearly, the above suggestions would have to be confirmed by more detailed free energy calculations, but the order of magnitude of the current numbers makes them at least plausible. Assessing the true free energy profiles is still a challenging task, since the reaction coordinates describing such coordinated cluster-like motions are not easily defined.
Water structure around the excess proton
In the previous section, the free energy cost was calculated for moving an excess proton from the bulk to the core of the membrane, and it was argued that this free energy barrier is low enough to be relevant to true proton permeation pathways. Here, we will present a more detailed investigation of the evolving solvent structure along that path. The average number of accessible MS-EVB states as identified by the algorithm was calculated during the umbrella simulations. The result for the first and second solvation shells is depicted in Fig. 6. The number of MS-EVB states reflects the degree of delocalization of the excess proton over the solvating water molecules via a transient Grotthuss hopping process.
FIGURE 6.
Average number of MS-EVB states in the first (thick dashed line) and second (thick solid line) hydration shells around the excess proton, as a function of zcec. Also shown are the distributions (from a simulation with the excess proton far out in the bulk) of water atoms (thin dotted line), lipid headgroups (thin solid line), and lipid tails (thin dashed line).
In the bulk water region (z > 22 Å), the excess proton is always threefold coordinated. Upon going toward the interface, this coordination remains intact until a substantial lipid bilayer headgroup density is reached (at ∼18 Å). Simultaneously, the second solvation shell gradually becomes less populated. Note the striking correlation of this with the decreasing water density in that region.
Upon going further into the headgroup region, the number of MS-EVB states in the first hydration shell also decreases. This is because hydrogen bonds with the lipid headgroup oxygens mix in with the solvating network and stabilize the localized hydronium cation (see also Fig. 4). Once the density of the lipid tailgroups starts to build up, the second solvation shell loses its second molecule. This reveals that the excess proton is only connected to a (local) water chain from one side. This behavior makes sense since the local water density goes down to very low values in the increasingly apolar environment. Apparently, the excess charge is shielded by a water chain on one side and the headgroup oxygens on the other side.
Interestingly, once the headgroup density has dropped substantially (z < 8 Å), the number of water molecules participating in the second solvation shell of the excess proton comes back up to two. Here, the excess proton is stabilized from both sides by a connecting water wire. However, it is not a single-file wire perpendicular to the membrane plane, as suggested in the transient water wire proposal, or as sketched in the cluster-contact picture (Haines, 2001). Rather, the water molecules remain in the polar headgroup region as much as possible, aligning parallel to the interface. This leads to what we call “transversal water wires”, some representative structures of which are displayed in Fig. 7. The water molecules represented by beads are the molecules constituing the EVB complex, plus molecules from further hydration shells that are hydrogen-bonded to this complex. Apparently, transversal wires constitute the best balance between water molecules exposed to an apolar environment and the shielding of the excess proton's positive charge. This leads us to propose a mechanism based on linear water structures parallel to the membrane instead of perpendicular to it: We suggest that the excess proton leaks into the membrane core while being shielded by two or three transversal water wires. Gradually, the wires will get more and more bent until they collapse unto each other, forming a small network-like structure around the excess proton. At the same time, similar wires might approach from the opposide of the membrane that could “pick up” the proton and eventually release it on the other side. Spontaneous formation of such a wire can actually be seen in the bottom of Fig. 5. Note that this mechanistic suggestion cannot be tested within the framework of umbrella simulations, since they only give information about static structures. For full assertion of the permeation mechanism, one has to resort to dynamic simulation methods. We will come back to that in later sections.
FIGURE 7.

Snapshots from the umbrella simulations showing transversal water wires surrounding the excess proton. The panels are configurations from simulations with different origins of the umbrella potential (z0 in Eq. 5). From top to bottom: z0 = 8 Å, z0 = 4 Å, and z0 = 2 Å. The pivot hydrogen of the most protonated state is colored blue. Note that close to the headgroup region lipid oxygens can participate in the wires (top panel, yellow bead).
Eventually, in the free energy sampling, the excess proton reaches the core of the membrane, where the density of lipid tail atoms goes down. This reduces the free energy cost for water molecules to move in and the figure nicely shows that the excess proton second shell coordination rises with decreasing lipid tail density. Somewhere in moving the excess proton toward this region, the transversal water wire has bent so much that the two parts touch and form a more network-like structure. Then, in the low-density lipid tail region, more water molecules come in to extend the size of the local network.
Note that the separation of the above-mentioned structural features into distinct regions corresponds closely with the four-region model for membranes introduced by Marrink and Berendsen (1994). Note also that, although we referred to the cluster-contact mechanism as a valid one in the previous section, there are two important differences with the illustration of Haines' article. First, as stated above, local water wires (clusters) formed transversal, rather than perpendicular, to the membrane. Second, the hydrogen-bonded network in our study never completely lost contact with the bulk water region. In that sense we did not observe local clusters inside a monolayer disconnected from the bulk.
Beyond the core region
Even though the results presented here suggest that the optimal reaction coordinate will involve solvent entering the membrane from both sides, we decided to carry on the successive umbrella simulations through the core region to the other side until contact was made with the opposing bulk region. This way, we could explore whether a membrane-spanning solvent structure could evolve (or, alternatively, the structure behind the proton would “snap” before contact was made with the opposite side) and, if so, how stable such a structure would be.
The resulting free energy profile is shown in Fig. 8. Not surprisingly, it keeps going up as long as the solvent surrounding the CEC is only connected to the upper bulk region. Beyond zcec = −9 Å the profile starts to level off. The plot also shows the result averaged over a shorter time segment from the end of the umbrella sampling in each window. There the change from the steep to the shallow profile is more pronounced. This means that some other coordinate (other than zcec) has pushed the system over some barrier into a new metastable region during the overall 250 ps of the umbrella sampling window, and that the shorter time segment at the end of the run emphasizes more of that physical effect. We associated this behavior with the water structure becoming hydrogen-bonded to the opposite headgroup region, which is seen in a representative structure of zcec = −12 Å, depicted in Fig. 9. It is clear that the solvent structure has become membrane-spanning (not losing contact with the other bulk region) and in Fig. 8 it can be seen that this constitutes a small but noticeable local free energy minimum. Note also that the membrane-spanning structure is not single-file.
FIGURE 8.
Free energy profile for umbrella simulations beyond the core region. The dashed line represents an average over the last 150 ps of 250 ps umbrella window runs. The two dotted lines are averages over the last 100 ps (both curves represent the same data, but shifted).
FIGURE 9.
Hydrogen-bonded network around the excess proton just after the formation of a membrane-spanning solvent structure.
In search of a proton permeation pathway
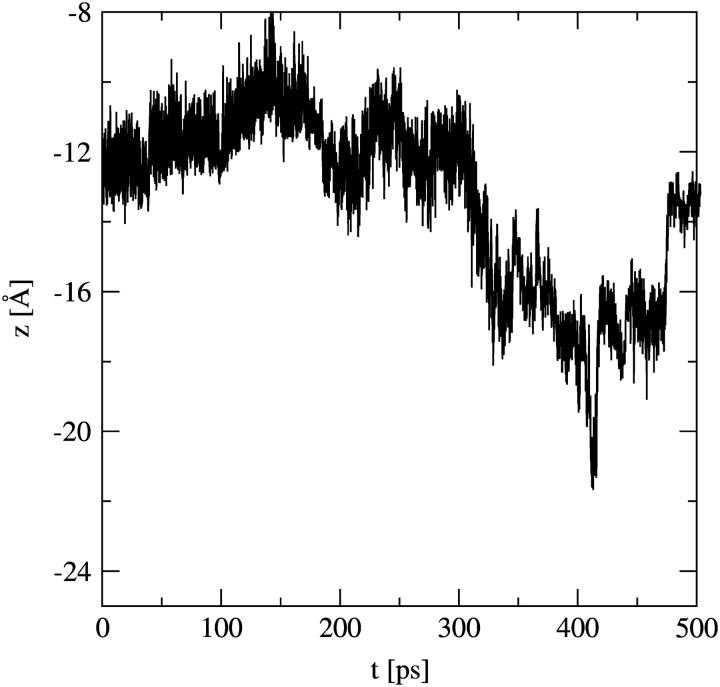
To test the stability of the structure in Fig. 9 (in the presence of the proton), the umbrella potential was released and an unrestrained equilibrium simulation was carried out with that structure as the initial configuration. The resulting trajectory is plotted in Fig. 10. It can be seen that the excess proton stayed at around the same location for >300 ps before it was released into the bulk region. Inspection of the corresponding configurations showed that only at that moment in time did the membrane-spanning water structure break. The proton moving back to z = −14 Å at the end of the trajectory did not constitute a rebuilding of the membrane-spanning structure. Instead, it was the excess proton moving to the second local minimum just beyond the headgroup region (as discussed in “Umbrella simulations”).
FIGURE 10.
Trajectory of an unrestrained simulation started from the configuration in Fig. 9.
The estimated lifetime obtained from this single trajectory is much longer than lifetimes previously reported for membrane-spanning single-file water wires. This could be due both to the presence of the proton and to the (network-like) structure itself. In none of the 250-ps umbrella simulations (up till z = −16 Å) was breakage of the water structure observed, which shows the stabilizing factor of the excess proton. This behavior might even suggest that structures like this can exist for long enough for a second proton to permeate as well (and extend the lifetime even further). Such a “double occupancy” effect, where a second proton comes in and pushes the first one out, has also been suggested for proton channels like gramicidin A (Roux et al., 1995).
As a final part of this study, more insight was sought on the structure of the transition state. This is important for two reasons: First, should we be able to construct structures that are representative of the transition-state region, then they could be used to “shoot” trajectories backward and forward in time to generate a reactive path for transition path sampling. Second, the transition-state structure itself generally contains a lot of information about possible pathways. One interesting question is how relevant certain membrane modes might be in the optimal reaction coordinate. In the structure of Fig. 9, it was seen that the membrane itself was slightly narrowed at the entrance and exit points of the water structure, so one might naturally wonder whether the same holds for the transition state.
Clearly, because of physical symmetry of the bilayer system, the true transition state should be at zcec = 0 Å, but because of our asymmetric free energy sampling procedure the structure for that point was somewhat removed from the transition state (any structure released there would show the excess proton moving back to the upper bulk region and never finding its way to the other side). Believing, however, that the newly found membrane-spanning structure might be a relevant one for true pathways, we reversed the successive umbrella windows, i.e., a new umbrella simulation was started with the umbrella potential at zcec = −11 Å, and initialized from the end configuration of the window at zcec = −12 Å. This step was followed by an umbrella simulation at zcec = −10 Å, and so on back to the membrane center. The structure found with the excess proton in the center is drawn in Fig. 11. Surprisingly, in this structure the membrane itself is completely flat. Of course this does not mean that certain membrane breathing modes could not be involved in the initiation of reactive paths, but at least they do not seem important in the saddle-point region (the region that determines the free energy barrier and hence the rate). It is also interesting to see that the local proton structure is an almost perfect Zundel complex, but oriented in the plane of the membrane. Apparently that constellation of solvating water molecules provides the best shielding of the positive excess proton charge.
FIGURE 11.
Transition-state structure. Shown are the excess proton (blue), the water molecules, and the lipid headgroup atoms.
It remains to be seen whether the network structure of transmembrane solvent in the transition state can account for the orders-of-magnitude difference in permeation rates between protons and other cations. An earlier article on proton conduction in artificial cylinders (Brewer et al., 2001) showed that the highest proton hopping rates were found in the cylinders with the smallest radii. However, the full kinetics of membrane permeation will be determined by both the diffusion along the transmembrane structure and the formation free energy of that structure. An investigation of the latter is the scope of a future study.
CONCLUDING REMARKS
By quasistatically pulling an excess proton through a lipid bilayer we have found a new membrane-spanning structure that could be highly relevant for true proton permeating pathways. We have shown that this structure is stable in the presence of the excess proton, having a lifetime of hundreds of picoseconds, much longer than previously reported lifetimes of single-file water chains. This result suggests that protons can permeate lipid bilayers via a complex concerted mechanism that cannot be described by pure water molecule coordinates alone.
We have also analyzed the solvating water structure around an excess proton upon moving from the bulk region toward the membrane core. Four different regions with different structural features were clearly identified, suggesting that inside the more apolar bilayer region the proton will be stabilized by transversal water wires, rather than perpendicular ones.
The emerging mechanism for proton permeation is one of an excess proton entering the membrane core and being carried over to another cluster (neutral or negatively charged) entering the membrane from the opposite side. This mechanism has strong similarities with the cluster-contact mechanism proposed by Haines, with the difference being that separate clusters are not involved, but that at some point along the pathway the solvating structure spans the entire membrane.
A strong contribution of hydrogen-bond acceptors in the lipid headgroup domain has also been identified in this work. This clearly suggests the uniqueness of the permeation mechanism for protons and may partly explain the disparate permeabilities measured between protons and other cations. This behavior also points to the possibility that proton hops along the lipid headgroups could play a role in the dynamical pathways as well. In turn, this would mean that these hydrogen-bond acceptors may need to be explicitly included in the MS-EVB Hamiltonian to allow for the dynamical protonation/deprotonation of the phospholipid headgroups. This is at present not included in the model but will be the focus of a future study. Suffice it to say here that headgroup protonation would probably change the free energy profile in the region zcec = 14–20 Å, but not the free energy cost for the transition from bulk to the membrane core.
To conclude, this study has revealed some new insight on the possible proton permeation pathways through pure lipid bilayers. Furthermore, it has provided information as to the relevant reaction coordinates to study this phenomenon. The identification of a possible transition-state structure also opens the way for future studies of the full transition path ensemble for proton permeation, which is at present too computationally expensive to undertake.
Acknowledgments
We thank Rosalind Allen for helpful discussions and a careful reading of the manuscript.
This research was supported by the National Institutes of Health (RO1 GM053148). The computational resources for this project have been provided by National Institutes of Health grant NCRR 1 S10 RR17214-01, on the Arches Metacluster, administered by the University of Utah Center for High Performance Computing. Some of the computations were performed on the National Science Foundation Terascale Computing System at the Pittsburgh Supercomputing Center, which is also gratefully acknowledged. The molecular images in this article were created with the molecular graphics program VMD (Humphrey et al., 1996).
Harald L. Tepper's present address is FOM Institute for Atomic and Molecular Physics (AMOLF), Kruislaan 407, 1098 SJ Amsterdam, The Netherlands.
References
- Alberts, B., A. Johnson, J. Lewis, M. Raff, K. Roberts, and P. Walter. 2002. Molecular biology of the cell. 4th ed. Garland Science, New York.
- Allen, R., J. P. Hansen, and S. Melchionna. 2003. Molecular dynamics investigation of water permeation through nanopores. J. Chem. Phys. 119:3905–3919. [Google Scholar]
- Allen, R., S. Melchionna, and J.-P. Hansen. 2002. Intermittent permeation of cylindrical nanopores by water. Phys. Rev. Lett. 89:175502. [DOI] [PubMed] [Google Scholar]
- Allen, T. W., O. S. Andersen, and B. Roux. 2004. Energetics of ion conduction through the gramicidin channel. Proc. Natl. Acad. Sci. USA. 101:117–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckstein, O., P. C. Biggin, and M. S. P. Sansom. 2001. A hydrophobic gating mechanism for nanopores. J. Phys. Chem. B. 105:12902–12905. [Google Scholar]
- Beckstein, O., and M. S. P. Sansom. 2003. Liquid-vapor oscillations of water in hydrophobic nanopores. Proc. Natl. Acad. Sci. USA. 100:7063–7068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berendsen, H. J. C., J. R. Grigera, and T. P. Straatsma. 1987. The missing term in effective pair potentials. J. Phys. Chem. 91:6269–6271. [Google Scholar]
- Bolhuis, P. G., D. Chandler, C. Dellago, and P. L. Geissler. 2002. Transition path sampling: Throwing ropes over rough mountain passes, in the dark. Annu. Rev. Phys. Chem. 53:291–318. [DOI] [PubMed] [Google Scholar]
- Brewer, M. L., U. W. Schmitt, and G. A. Voth. 2001. The formation and dynamics of proton wires in channel environments. Biophys. J. 80:1691–1702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cukierman, S. 2000. Proton mobilities in water and in different stereoisomers of covalently linked gramicidin A channels. Biophys. J. 78:1825–1834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dang, L. X., and B. M. Pettitt. 1987. Simple intermolecular model potentials for water. J. Phys. Chem. 91:3349–3354. [Google Scholar]
- Day, T. J. F., A. V. Soudackov, M. Cuma, U. W. Schmitt, and G. A. Voth. 2002. A second generation multistate empirical valence bond model for proton transport in aqueous systems. J. Chem. Phys. 117:5839–5849. [Google Scholar]
- Decoursey, T. E. 2003. Voltage-gated proton channels and other proton transfer pathways. Physiol. Rev. 83:475–579. [DOI] [PubMed] [Google Scholar]
- de Gier, J. 1992. Permeability barriers formed by membrane lipids. Bioelectrochem. Bioenerg. 27:1–10. [Google Scholar]
- Dzubiella, J., R. J. Allen, and J.-P. Hansen. 2004. Electric field-controlled water permeation coupled to ion transport through a nanopore. J. Chem. Phys. 120:5001–5004. [DOI] [PubMed] [Google Scholar]
- Haines, T. H. 1983. Anionic lipid headgroups as a proton-conducting pathway along the surface of membranes: a hypothesis. Proc. Natl. Acad. Sci. USA. 80:160–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haines, T. H. 2001. Do sterols reduce proton and sodium leaks through lipid bilayers? Prog. Lipid Res. 40:299–324. [DOI] [PubMed] [Google Scholar]
- Hinkle, P. C., and M. L. Yu. 1979. The phosphorus/oxygen ratio of mitochondrial oxidative-phosphorylation. J. Biol. Chem. 254:2450–2455. [PubMed] [Google Scholar]
- Hummer, G., J. C. Rasaiah, and J. P. Noworyta. 2001. Water conduction through the hydrophobic channel of a carbon nanotube. Nature. 414:188–190. [DOI] [PubMed] [Google Scholar]
- Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD: visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- Jóhannesson, G. H., and H. Jónsson. 2001. Optimization of hyperplanar transition states. J. Chem. Phys. 115:9644–9656. [Google Scholar]
- Jorgensen, W. L., J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
- Kumar, S., D. Bouzida, R. H. Swendsen, P. A. Kollman, and J. M. Rosenberg. 1992. The weighted histogram analysis method for free-energy calculations on biomolecules. 1. The method. J. Comput. Chem. 13:1011–1021. [Google Scholar]
- Lawaczeck, R. 1988. Defect structures in membranes: routes for the permeation of small molecules. Ber. Bunsen-Ges. Phys. Chem. 92:961–963. [Google Scholar]
- Leontiadou, H., A. E. Mark, and S. J. Marrink. 2004. Molecular dynamics simulations of hydrophilic pores in lipid bilayers. Biophys. J. 86:2156–2164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrink, S.-J., and H. J. C. Berendsen. 1994. Simulation of water transport through a lipid membrane. J. Phys. Chem. 98:4155–4168. [Google Scholar]
- Marrink, S.-J., F. Jähnig, and H. J. C. Berendsen. 1996. Proton transport across transient single-file water pores in a lipid membrane studied by molecular dynamics simulations. Biophys. J. 71:632–647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell, M. 1961. Coupling of phosphorylation to electron and hydrogen transfer by a chemiosmotic type of mechanism. Nature. 191:144–148. [DOI] [PubMed] [Google Scholar]
- Nagle, J. F. 1987. Theory of passive proton conductance in lipid bilayers. J. Bioenerg. Biomembr. 19:413–426. [DOI] [PubMed] [Google Scholar]
- Nichols, J. W., and D. W. Deamer. 1980. Net proton-hydroxyl permeability of large unilamellar liposomes measured by an acid-base titration technique. Proc. Natl. Acad. Sci. USA. 77:2038–2042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen, M. K., S. S. Iyengar, T. J. F. Day, and G. A. Voth. 2004. The hydrated proton at the water liquid/vapor interface. J. Phys. Chem. B. 108:14804–14806. [Google Scholar]
- Randa, H. S., L. R. Forrest, G. A. Voth, and M. S. P. Sansom. 1999. Molecular dynamics of synthetic leucine-serine ion channels in a phospholipid membrane. Biophys. J. 77:2400–2410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roux, B., B. Prod'hom, and M. Karplus. 1995. Ion transport in the gramidin channel: molecular dynamics study of single and double occupancy. Biophys. J. 68:876–892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitt, U. W., and G. A. Voth. 1998. Multistate empirical valence bond model for proton transport in water. J. Phys. Chem. B. 102:5547–5551. [Google Scholar]
- Schmitt, U. W., and G. A. Voth. 1999. The computer simulation of proton transport in water. J. Chem. Phys. 111:9361–9381. [Google Scholar]
- Schütte, C., and W. Huisinga. 2003. Biomolecular conformations can be identified as metastable sets of molecular dynamics. In Handbook of Numerical Analysis, Vol. 10: Computational Chemistry. P. G. Ciarlet and J. L. Lions, editors. North-Holland, Amsterdam, The Netherlands. 699–744.
- Smith, W., and T. R. Forester. 1996. DL_POLY_2.0: A general-purpose parallel molecular dynamics simulation package. J. Mol. Graph. 14:136–141. [DOI] [PubMed] [Google Scholar]
- Smondyrev, A. M., and M. L. Berkowitz. 1999. United atom force field for phospholipid membranes: constant pressure molecular dynamics simulation of DPPC/water system. J. Comput. Chem. 20:531–545. [Google Scholar]
- Smondyrev, A. M., and G. A. Voth. 2002a. Molecular dynamics simulation of proton transport near the surface of a phospholipid membrane. Biophys. J. 82:1460–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smondyrev, A. M., and G. A. Voth. 2002b. Molecular dynamics simulation of proton transport through the influenza A virus M2 channel. Biophys. J. 83:1987–1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venable, R. M., and R. W. Pastor. 2002. Molecular dynamics simulations of water wires in a lipid bilayer and water/octane model systems. J. Chem. Phys. 116:2663–2664. [Google Scholar]
- Warshel, A. 1991. Computer Modeling of Chemical Reactions in Enzymes and Solutions. Wiley, New York.
- Warshel, A., and R. M. Weiss. 1980. An empirical valence bond approach for comparing reactions in solutions and in enzymes. J. Am. Chem. Soc. 102:6218–6226. [Google Scholar]
- Williams, R. J. P. 1978. The multifarious couplings of energy transduction. Biochim. Biophys. Acta. 505:1–44. [DOI] [PubMed] [Google Scholar]
- Wu, Y., and G. A. Voth. 2003. A computer simulation study of the hydrated proton in a synthetic proton channel. Biophys. J. 85:864–875. [DOI] [PMC free article] [PubMed] [Google Scholar]