Normal-Modes-Based Prediction of Protein Conformational Changes Guided by Distance Constraints

Abstract

Based on the elastic network model, we develop a novel method that predicts the conformational change of a protein complex given its initial-state crystal structure together with a small set of pairwise distance constraints for the end state. The predicted conformational change, which is a linear combination of multiple low-frequency normal modes that are solved from the elastic network model, is computed as a response displacement induced by a perturbation to the system Hamiltonian that incorporates the given distance constraints. For a list of test cases, we find that the computed response displacement overlaps significantly with the measured conformational changes, when only a handful of pairwise constraints are used (≤10). The performance of this method is also shown to be robust against different choices of pairwise distance constraints and errors in their values. This method, if supplied with the experimentally derived distance constraints (for example, from NMR or other spectroscopic measurements), can be applied to the analysis of protein conformational changes toward transient states.

INTRODUCTION

Quantitatively correct description of conformational changes is central to the understanding of functional mechanisms for many biomolecular complexes. Such description is routinely obtained by doing structural comparison between the two crystal structures solved for the initial state and the end state, respectively. In case only the initial-state crystal structure is known, computational prediction of the conformational changes is highly desirable. However, simulating the conformational changes with atomic details is made difficult by its requirement of long-time simulation up to a microseconds to milliseconds timescale. Recent work by a number of researchers has suggested another computational route that avoids this difficulty: the lowest-frequency normal modes that are computed from a highly simplified elastic network model (ENM), can give surprisingly good descriptions of the functionally relevant dynamics of macromolecular systems (Atilgan et al., 2001, Isin et al., 2002, Keskin et al., 2002, Kim et al., 2002, Kundu and Jernigan, 2004, Xu et al., 2003, Zheng and Brooks, 2005). Many biologically interesting dynamical transitions were found to be dominated by just a handful of lowest-frequency normal modes (Delarue and Sanejouand, 2002, Tama and Sanejouand, 2001, Zheng and Doniach, 2003). However, without knowing both the initial and the end structures in the first place, it is still elusive to pinpoint the relevant modes from the low-frequency spectrum: in many cases, the most relevant mode may not be the lowest-frequency mode; sometimes two or more modes are almost equally relevant. Therefore, it is desirable to “predict” the conformational change by computing a linear combination of multiple low-frequency normal modes as a good approximation. To achieve this task, we need additional structural information about the end state in addition to the crystal structure for the initial state. In a recent study (Tama et al., 2004), Tama and co-workers used a linear combination of low-frequency normal modes for flexible fitting of high-resolution structures into low-resolution maps of macromolecular complexes from electron microscopy. Here we explore the possibility of using another kind of experimental constraints—a small set of pairwise distance constraints as a guide to probe protein conformational changes.

Experimentally, pairwise distances between specified atoms of a protein in its native state (in solution) can be obtained by NMR. There are other techniques that utilize fast spectroscopy (for example, site-direct spin labeling combined with electron paramagnetic resonance spectroscopy; see Hubbell et al., 2000) to probe pairwise distances of a protein in a transient state. Computationally, it has been well known that even a small number of pairwise distance constraints can improve the protein structure modeling significantly (Skolnick et al., 1997; Debe et al., 1999). In the framework of ENM, because functionally relevant conformational changes generally involve a small number of low-frequency normal modes, it is natural to expect that a small number of pairwise distance constraints, if chosen properly, would be sufficient for obtaining a good approximation to the conformational changes.

Technically, in the framework of normal-modes analysis the distance constraints can be either enforced directly as “hard” constraints or incorporated indirectly as “soft” constraints (or restraints):

1. The “hard” constraints are enforced by first linearizing the constraints at the lowest-order perturbation and then solving the resulting linear equations (see Materials and Methods); for N pairwise distance constraints, a linear combination of the N or more lowest-frequency normal modes is solved to satisfy them. Although this method appears to be mathematically sound, it lacks physical basis because the N low-frequency modes are treated equally regardless of their differences in frequency.

2. The “soft” constraints (or restraints) can be incorporated into a quadratic perturbation to the system Hamiltonian, and then the response displacement is computed (see Materials and Methods). The physical essence of this method is, by exerting forces to the few chosen pairs of residues to force them to approach the desired distance constraints, such local perturbation is propagated to the whole structure to eventually induce global conformational changes that are biologically relevant (Zheng and Doniach, 2003). The above perturbation may be physically driven, for example, due to ligand binding or interaction with other proteins (such as an inhibitor). Compared with the “hard” constraints-based method, this method employs the linear-response theory that naturally favors lower-frequency over higher-frequency modes (see Materials and Methods).

We will use the above “soft” constraints-based method to computationally predict the conformational changes. We will test this method on a list of test cases to evaluate its performance in terms of both accuracy and robustness.

MATERIALS AND METHODS

Elastic network model

Given the C_α atomic coordinates for a protein's native structure, we build an elastic network model by using a harmonic potential with a single force constant to account for pairwise interactions between all C_α atoms that are within a cutoff distance (R_C = 10 Å). The energy in the elastic network representation of a protein is:

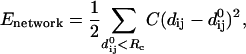(1)

where d_ij is the distance between the dynamical coordinates of the C_α atoms i and j, and is the distance between C_α atoms i and j, as given in the crystal structure.

For the above harmonic Hamiltonian we can perform the standard normal-modes analysis , and using the eigenvectors of the lowest-frequency normal modes (starting from mode No. 1 after excluding the six zero modes for translations and rotations) we can compute the overlaps with the conformational changes between two states with known structures (Zheng and Doniach, 2003). The drastic simplification of representing the complex protein structure by an effective harmonic potential is justified by a study (Tirion, 1996), which showed that a single spring constant potential reproduces the slow dynamics that is computed from the normal modes analysis of a complex all-atom potential.

We note that the cutoff distance R_C = 10 Å is selected as a trade-off between the following two considerations: first, R_C should be large enough to avoid additional zero modes besides the six rotational and translational modes; second, R_C should be small enough to avoid introducing too much nonphysical long-range interaction. In practice, we find similar results for slightly different cutoff distances (data not shown).

Predict conformational changes from distance constraints

Motivation

Assume we have the three-dimensional coordinates of the initial protein structure's C_α atoms, and N pairwise distance constraints for the unknown end structure. The goal is to predict the conformational change from the initial structure to the end structure. Here we limit our attention to the directionality of the conformational change (a 3L-dimensional vector where L is the length of sequence) but not its amplitude.

There are two different ways to achieve this goal:

Hard distance constraints

One can use the linear combination of M lowest-frequency modes to satisfy N linearized pairwise distance constraints () (n = 1, 2…N):

Assume then it must satisfy the following N linear equations (n = 1, 2,…N):

(2)

where is the perturbational change of the pairwise distance for (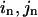) caused by the eigenvector of mode m; 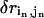is the change of the pairwise distance for () derived from the given distance constraint.

To satisfy N independent constraints as in Eq. 2, M should be no less than N. If N is equal to M, there is only one solution to Eq. 2; when M > N, there will be multiple solutions.

Our tests have shown that the direct satisfaction of the “hard” distance constraints (M = N) often results in poor overlap between the computed displacement by Eq. 2 and the measured one (see Table 2).

TABLE 2.

Summary of results from both ideal and nonideal tests

					Nonideal test result
			Ideal test result		Test 1		Test 2
PDB codes	Mode No. (overlap)	Pool size	No. pairs	Overlap	No. pairs	Overlap	No. pairs	Overlap
8adh 6adh	No. 3(0.680)	49	–	–	–	–	–	–
			10	0.564	8	0.622(0.100)	10	0.528(0.081)
			4	0.300
1avr 1avh	No. 2(0.412)	14	2	0.538	9	0.423(0.134)	–	–
			3	0.550	9	0.423(0.134)	1	0.406(0.000)
			3	0.455
4dfr 5dfr	No. 1(0.611)	9	–	–	–	–	–	–
			2	0.588	9	0.390(0.000)	3	0.297(0.308)
			1	0.612
1ddt 1mdt	No. 2(0.564)	147	1	0.640	2	0.607(0.067)	1	0.640(0.000)
			7	0.650	9	0.646(0.011)	7	0.650(0.000)
			2	0.421
3enl 7enl	No. 1(0.345)	49	1	0.499	8	0.366(0.107)	1	0.499(0.000)
			10	0.500	8	0.366(0.107)	10	0.500(0.003)
			1	0.346
1hhp 1ajx	No. 3(0.70)	6	1	0.784	–	–	–	–
			1	0.784	5	0.187(0.069)	1	0.517(0.589)
			1	0.068
1lfh 1lfg	No. 1(0.613)	62	1	0.671	5	0.620(0.236)	1	0.671(0.000)
			8	0.882	10	0.737(0.170)	10	0.867(0.025)
			4	0.663
2lao 1lst	No. 1(0.886)	40	1	0.932	1	0.918(0.028)	1	0.932(0.000)
			3	0.942	10	0.937(0.006)	3	0.942(0.000)
			3	0.920
3tms 2tsc	No. 4(0.503)	15	4	0.563	2	0.536(0.133)	4	0.556(0.040)
			7	0.664	10	0.648(0.025)	7	0.637(0.043)
			1	0.438
1ypt 1yts	No. 6(0.470)	23	1	0.662	1	0.626(0.117)	1	0.662(0.000)
			9	0.759	10	0.756(0.020)	9	0.754(0.014)
			1	0.383
1l3s 1lv5	No. 5(0.696)	56	5	0.704	–	–	5	0.695(0.044)
			7	0.719	10	0.633(0.174)	7	0.710(0.026)
			6	0.103
1bpx 1bpy	No. 1(0.710)	31	1	0.755	3	0.756(0.103)	1	0.755(0.000)
			7	0.759	10	0.807(0.038)	8	0.759(0.001)
			1	0.711
1ih7 1ig9	No. 2(0.804)	82	1	0.815	3	0.809(0.110)	1	0.815(0.000)
			5	0.817	10	0.874(0.017)	5	0.817(0.000)
			1	0.058
2ktq 3ktq	No. 4(0.504)	40	1	0.755	4	0.564(0.295)	1	0.755(0.000)
			10	0.790	10	0.710(0.167)	10	0.786(0.024)
			1	0.116
4q21 5p21	No. 2(0.494)	29	1	0.579	8	0.499(0.109)	2	0.590(0.047)
			10	0.660	10	0.515(0.091)	9	0.615(0.061)
			3	0.191
1tag 1tnd	No. 3(0.385)	49	1	0.478	3	0.405(0.185)	1	0.478(0.000)
			9	0.531	10	0.572(0.096)	9	0.526(0.012)
			2	0.217
9aat 1ama	No. 6(0.515)	37	4	0.545	–	–	–	–
	No. 7(0.459)		8	0.604	9	0.505(0.153)	8	0.491(0.100)
			5	0.210
1cll 1ctr	No. 5(0.405)	28	1	0.695	1	0.484(0.119)	1	0.695(0.000)
	No. 4(0.380)		1	0.695	8	0.578(0.057)	1	0.695(0.000)
			2	0.313
1hil 1him	No. 4(0.598)	13	1	0.684	10	0.664(0.198)	–	–
	No. 1(0.460)		6	0.809	10	0.664(0.198)	8	0.479(0.384)
			1	0.477
1omp 1anf	No. 2(0.675)	60	1	0.711	3	0.765(0.184)	1	0.711(0.000)
	No. 1(0.650)		8	0.861	10	0.862(0.069)	8	0.857(0.010)
			2	0.823
1dfl 1kk7	No. 1(0.518)	102	1	0.638	5	0.516(0.217)	1	0.638(0.000)
	No. 3(0.475)		10	0.813	10	0.657(0.109)	10	0.800(0.015)
			1	0.518
1vom 1mma	No. 1(0.558)	89	1	0.734	7	0.561(0.172)	1	0.734(0.000)
	No. 2(0.371)		2	0.752	10	0.618(0.086)	2	0.752(0.001)
			2	0.674

For each test case, the first row shows the minimal number of pairs needed to match the maximal overlap between any single mode and the measured conformational change; the second row shows the number of pairs when the maximal overlap between the computed and the measured conformational changes is obtained. For the two nonideal tests, both the average overlap and its standard deviation (inside parentheses) are shown. For the ideal test, the third row shows the corresponding result for the “hard constraint” method as a comparison.

Soft distance constraints

We incorporate the constraints into a perturbation to the Hamiltonian, and then compute the response displacement induced by this perturbation. Details are shown as follows.

First, we introduce N pairwise distance constraints () (n = 1,2…N) as a perturbation to the Hamiltonian of the elastic network:

(3)

where a constant term is omitted, and the perturbational Hessian matrix δH and the force vector δF are computed as follows:

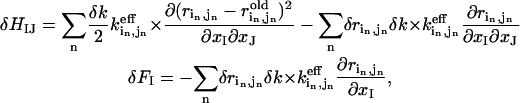(4)

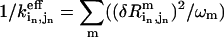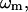where is the inverse of the “effective” spring constant for pair () in the old structure ( the eigenvalue of mode m; 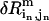, the perturbational change of the pairwise distance for () caused by the eigenvector of mode m); δk gives the overall amplitude of the perturbation; 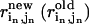is the pairwise distance for pair (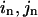) in the end (initial) structure.

Second, the response displacement 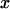induced by the above perturbation (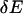) at second-order approximation is computed as follows:

(5)

where H₀ is the Hessian matrix for the unperturbed ENM. In practice, we find first-order approximation (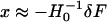) is generally as accurate as second order (adding second-order term makes little difference). The factor of 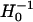favors low-frequency modes in their contribution to x.

It is straightforward to verify the following: under the assumption of linear response, the contribution to the energy perturbation in Eq. 3 from each individual pairwise constraint, by itself, results in the change of that pairwise distance that satisfies the constraint perturbationally. However, when all contributions are added up, none of those constraints are satisfied any more. So the basic assumption is: every pairwise constraint can be enforced by a pairwise force applying on that particular pair “independently”, and the interpair interference can be ignored (for example, one can ignore the change in the pairwise distance for pair 2 caused by the forces applied on pair 1). The interpair interference can be taken into account by tuning the as variables to satisfy the constraints exactly and meanwhile minimize the energy in Eq. 5. However, our test of such alternative method (data not shown) showed, surprisingly, significantly degraded performance. We suspect that the interpair interferences are probably much weaker in real proteins than described by the ENM.

The response displacement as computed above is used as an approximation to the conformational change. Its accuracy can be assessed by calculating its overlap with the measured conformational change (generalized cosine between these two vectors; see Tama and Sanejouand, 2001); the higher the overlap is, the more accurate the prediction will be.

Criteria for selecting residue pairs

Pairwise distance constraints can be experimentally retrieved by a variety of techniques. Intuitively, only residue pairs with significant change of distance (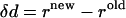) during the transition will be useful for predicting the conformational changes. Therefore, the selection criteria are needed before the method can be tested. Here for the purpose of testing cases for which both crystal structures are known, we use the following criteria:

1. The pairwise distance jumps across the cutoff distance 10 Å during the transition, which results in breaking of an old bond of spring or generation of a new bond of spring in the elastic network.

2. There is relatively significant change in the pairwise distance (|δd|) during the transition; the significance is assessed by a Z-score: 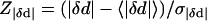and we keep those with Z_|δd| > 1.

In summary, we select those residue pairs that satisfy the above two conditions and keep them as a pool of pairwise distance constraints for further testing. The pairwise distance constraints used for the later testing can only be obtained from this pregenerated pool. Of course, in practice, when only the initial crystal structure is known, this pool of pairwise distance constraints is obtained by experiments.

Test protocol

We propose the following two procedures to test the accuracy and robustness of the method:

Ideal test

We use the top N residue pairs (ranked by the pairwise distance change |δd|) as the input of distance constraints (N = 1, 2, …, 10), then we compute the response displacement and its overlap with the measured conformational change to assess the performance.

We define the success criteria as follows. A test case is said to successfully pass the ideal test if there exists N ≤ 10 such that using the top N pairs as input results in a higher or similar overlap with the measured conformational change than any single mode.

Nonideal test: including the following two tests

Test 1. We randomly pick N pairs from the pool of significant pairs as generated above. For a given N (N = 1, 2, … , 10), we repeat the calculation 100 times with different randomly selected N pairs and then compute the average and standard deviation of the computed overlaps. The average assesses the average performance whereas the standard deviation gives the robustness of the method.

Test 2. We introduce a random fractional error (following the uniform distribution between −50 and 50%) to the new pairwise distance values. For a given input of top N pairwise constraints, we repeat the calculations 100 times with different inaccurate values of distance constraints and then compute the average and standard deviation of the overlaps. The average assesses the average performance whereas the standard deviation gives the robustness of the method.

We define the success criteria as follows. A test case is said to successfully pass the nonideal tests if there exists N ≤ 10 such that: a), the average overlaps obtained from the above two tests are both higher than or similar to the maximal overlap between the measured conformational change and any single mode; b), the standard deviation is much smaller than the average overlap.

Test cases

We test this method for a list of protein pairs with both structures available in the Protein Data Bank (PDB). Fourteen pairs in the list are obtained from a recent study (Tama and Sanejouand, 2001); we only exclude four pairs for reasons such as the lack of dominance of low-frequency modes among the lowest 10 modes. We then supplement by eight additional pairs of proteins from our own studies.

RESULTS AND DISCUSSION

We now perform a systematic test of the accuracy and robustness of the method. For the test cases, we select a list of protein transition pairs where both the initial and the end structures are available in the PDB (Table 1). These proteins vary significantly in size and function, and their conformational changes involve hinge bending or shear motion (as classified in Gerstein and Krebs, 1998). The diversity of the test cases facilitates a strict test on the generality of the method.

TABLE 1.

Information about the 22 pairs of protein structures as test cases: the PDB codes of the corresponding pair of initial and end crystallographic structures

Protein names	No. residues	PDB codes
Alcohol dehydrogenase	373	8adh, 6adh
Annexin V	317	1avr, 1avh
Aspartate aminotransferase	401	9aat, 1ama
Calmodulin	144	1cll, 1ctr
Dihydrofolate reductase	159	4dfr, 5dfr
Diphtheria toxin	523	1ddt, 1mdt
Enolase	436	3enl, 7enl
HIV-1 protease	99	1hhp, 1ajx
Immunoglobulin	418	1hil, 1him
Lactoferrin	691	1lfh, 1lfg
LAO binding protein	238	2lao, 1lst
Maltodextrin binding protein	370	1omp, 1anf
Thymidylate synthase	264	3tms, 2tsc
Tyrosine phosphatase	278	1ypt, 1yts
Scallop myosin s1	772	1dfl, 1kk7
Dictyostelium myosin	730	1vom, 1mma
Bacillus DNA polymerase	580	1l3s, 1lv5
DNA polymerase-β	331	1bpx, 1bpy
rb69 DNA polymerase	897	1ih7, 1ig9
Taq DNA polymerase	528	2ktq, 3ktq
ras p21 protein	169	4q21, 5p21
Transducin-α	314	1tag, 1tnd

For the purpose of method testing, we generate a pool of “useful” pairwise distance constraints (see Materials and Methods), and we require that the pairwise distance constraints as input to our method can only come from this “pregenerated” pool.

Then we run the following two tests:

Ideal test

To demonstrate the best performance this method can offer, assume we are given the top N pairs (sorted by |δd|, the pairwise distance change during the transition) from the pool as the input of distance constraints (N = 1, 2, … 10). For those top N pairwise constraints, we compute the response displacement as defined in Eq. 5, and then calculate its overlap with the measured conformational change. We compare it with the maximal overlap between any single mode and the measured conformational change. We then ask the following two questions to assess the performance: 1), What is the minimum N needed to get a similar or higher overlap than any single mode? 2), What is the highest overlap attained as N varies from 1 to 10. We record these two numbers in Table 2 for all the test cases.

A test case is said to successfully pass the ideal test if our method obtains a better or similar performance than any single mode (see Materials and Methods for details of the success criteria).

Nonideal test

We design the following two nonideal tests to assess the robustness of our method:

1. In practice, there is no guarantee that we can get precisely the top N pairwise distance constraints from the pregenerated pool as assumed in the ideal test. So it is natural to ask whether the performance is sensitive to different choices of pairwise distance constraints from the pool as input. To address this question we randomly pick N pairs from the pool of significant pairs and evaluate statistically the performance of the method (Materials and Methods). For a given N (N = 1, 2, … 10), we repeat the calculation with different randomly selected N pairs and then compute the average and standard deviation of the computed overlaps. The average assesses the average performance whereas the standard deviation gives the robustness of the method. These results are also recorded in Table 2.

2. Another practical issue is that the experimentally measured pairwise distances for the end state are inaccurate. Therefore it is critical to test if our method is robust against such inaccuracy. We introduce a random fractional error (Materials and Methods) to the new pairwise distance values. For a given input of top N pairwise constraints (defined in the ideal test), we repeat the calculations with different inaccurate values of distance constraints and then compute the average and standard deviation of the overlaps. The average assesses the average performance whereas the standard deviation gives the robustness of the method. These results are also recorded in Table 2.

A test case is said to successfully pass the nonideal tests if our method “statistically” obtains a better or similar performance than any single mode (see Materials and Methods for details of the success criteria).

Then we go into a detailed discussion of the results. To clearly analyze the results, we classify the 22 test cases into the following three categories:

Successful cases with single-mode dominance

Among the test cases that successfully pass both the ideal and nonideal tests, for 12 of them (see the top part of Table 2 for details) there is a single mode that dominates the measured conformational change. Among these 12 cases, only three are dominated by precisely the lowest-frequency mode (mode No. 1) and four by the second-lowest-frequency mode (mode No. 2); the remaining five have their dominant mode ranging from mode No. 3 to No. 6 (Table 2). Therefore, even for cases with single-mode dominance, a simple choice of the dominant mode based solely on lowest frequency is generally not feasible.

For example, the transition (1ddt → 1mdt) is dominated by mode No. 2 (overlap = 0.564). In both the ideal and nonideal tests, our method captures mode No. 2 as the dominant mode (see Fig. 2. The nonideal test with different choices of input pairs reveals high robustness with slightly reduced performance (average overlap ∼ 0.7, and SD ≤0.1). It is noted that the robustness against errors in the input distance constraints is very strong: for N = 1…10 pairs, the standard deviation is virtually zero.

FIGURE 2.

Summary of results for transition (1ddt → 1mdt). Panel a shows the overlap between the computed and the measured conformational changes versus the number of pairwise distance constraints. Panel b shows the overlap between the computed conformational change and mode No. 2 versus the number of pairwise distance constraints. Line with pluses, result for the ideal test; horizontal line, the maximal overlap between any single mode and the measured conformational change; x-marks with error bars, result for the nonideal test 1, where the error bar shows 1 SD.

Similar results are obtained for the other two examples: (1ypt → 1yts; see Fig. 3) and (2lao → 1lst; see Fig. 4). In both transitions, both nonideal tests reveal very robust performance (small standard deviation).

FIGURE 3.

Summary of results for transition (1ypt → 1yts). Panel a shows the overlap between the computed and the measured conformational changes versus the number of pairwise distance constraints. Panel b shows the overlap between the computed conformational change and mode No. 6 versus the number of pairwise distance constraints. Line with pluses, result for the ideal test; horizontal line, the maximal overlap between any single mode and the measured conformational change; x-marks with error bars, result for the nonideal test 1, where the error bar shows 1 SD.

FIGURE 4.

Summary of results for transition (2lao → 1lst). Panel a shows the overlap between the computed and the measured conformational changes versus the number of pairwise distance constraints. Panel b shows the overlap between the computed conformational change and mode No. 1 versus the number of pairwise distance constraints. Line with pluses, result for the ideal test; horizontal line, the maximal overlap between any single mode and the measured conformational change; x-marks with error bars, result for the nonideal test 1, where the error bar shows 1 SD.

To summarize, for the 12 successful cases with single-mode dominance we find that our method correctly captures the dominant mode that also dominates the predicted conformational change and thus achieves a comparable or better performance than any single mode alone. Depending on different cases, although the nonideal test gives somewhat reduced performance (with more pairs needed) than the ideal test, it is generally robust and the results are not sensitive to the choices of pairs from the pool and the accuracy of the input distance constraints. The robustness against the latter is particularly impressive: in 11 out of 12 cases, the standard deviation is ≪0.1 (except for transition 1avr → 1avh).

Successful cases with multimodes dominance

Among the test cases that successfully pass both the ideal and nonideal tests, for five of them (see the bottom part of Table 2) there are two modes that dominate the measured conformational change.

We discuss these cases in details as follows.

Transition (9aat → 1ama) is dominated by mode No. 6(overlap = 0.515) and No. 7 (overlap = 0.459). In the ideal test, our method (with ≥4 pairs as input) can capture mode No. 6 as the dominant mode together with mode No. 1. This is not surprising because mode No. 1 frequency (0.000326) is much lower than mode No. 6 (0.057652), which favors its presence in the response displacement. The nonideal test reveals reasonable robustness with different choices of pairs as input (average overlap ∼ 0.5, ± SD ≤0.15 for N ≥ 4 pairs). The robustness against errors in the input distance constraints is relatively strong (for N = 1…10 pairs, the SD is always ≤0.1).

Transition (1cll → 1ctr) is dominated by three modes: No. 3(overlap = 0.374), No. 4 (overlap = 0.380), and No. 5 (overlap = 0.405). Our method captures mode No. 3 as the dominant and No. 4 as subdominant mode (see Fig. 1). This explains its high overlap of 0.69 with the measured conformational change. The nonideal test with different choices of pairs reveals good robustness with slightly reduced performance (average overlap ∼ 0.5, and ± SD ≤0.1). It is noted that the robustness against errors in the input distance constraints is extremely strong: for N = 1…10 pairs, the SD is always <0.003.

FIGURE 1.

Summary of results for transition (1cll → 1ctr). Panel a shows the overlap between the computed and the measured conformational changes versus the number of pairwise distance constraints. Panel b (panel c) shows the overlap between the computed conformational change and mode No. 3 (No. 4) versus the number of pairwise distance constraints. Line with pluses, result for the ideal test; horizontal line, the maximal overlap between any single mode and the measured conformational change; x-marks with error bars, result for the nonideal test 1, where the error bar shows 1 SD.

Transition (1omp → 1anf) is dominated by mode No. 2(overlap = 0.675) and No. 1 (overlap = 0.650). Our method correctly captures mode No. 2 as dominant mode and mode No. 1 as subdominant mode. The nonideal test with different choices of pairs offers almost as good performance as the ideal test (average overlap ∼ 0.8, and ± SD ≤0.2) for ≥4 pairs as input. It is noted that the robustness against errors in the input distance constraints is also very strong: for N = 1…10 pairs, the SD is always <0.02.

Transition (1dfl → 1kk7) is dominated by mode No. 1(overlap = 0.518) and No. 3 (overlap = 0.475), both of which are correctly captured as dominant or subdominant mode by this method. The nonideal test with different choices of pairs as input reveals slightly reduced performance than the ideal test and good robustness (average overlap ∼ 0.5–0.6, ± SD ≤0.2) for N ≥ 5 pairs. The robustness against errors in the input distance constraints is relatively strong (for N = 1…10 pairs, the SD is always ≤0.1).

Transition (1vom → 1mma) is dominated by mode No. 1(overlap = 0.558), and No. 2 (overlap = 0.371). Both modes are captured by our method as dominant or subdominant modes. The nonideal test with different choices of pairs as input reveals somewhat reduced performance than the ideal test and reasonable robustness (average overlap ∼ 0.5–0.6, ± SD ≤0.2) for N ≥ 5 pairs. The robustness against errors in the input distance constraints is very strong (for N = 1…10 pairs, the SD is always ≤0.01).

To summarize, in the above five successful cases our method correctly captures one or both of the dominant modes that also dominates the predicted conformational change and thus achieves a comparable or better performance than any single mode alone. Although the nonideal test gives somewhat reduced performance than the ideal test (with more pairs needed and a small variation in the overlap), it is generally robust and the results are not sensitive to the choices of pairs from the pool and the accuracy of the input distance constraints. The robustness against the latter is particularly impressive.

Unsuccessful cases

There are five unsuccessful cases that are discussed as follows:

Transition (8adh → 6adh). There is a dominant mode No. 3 (overlap = 0.68); the ideal test gives reasonable performance (although the overlap 0.56 is lower than 0.68 of mode No. 3), and the nonideal test gives reduced performance with good robustness against both the choices of pairs from the pool and the inaccuracy of the input distance constraints. Therefore, this case is actually partially successful.

Transition (3enl → 7enl). There is a weakly dominant mode No. 1(overlap = 0.345). We obtain good ideal test result but worse nonideal test result although with good robustness.

In the remaining three cases (including 4dfr → 5dfr, 1hhp → 1ajx, and 1hil → 1him), the ideal test result is good but the nonideal test fails to give robust results (the standard deviation is comparable to the average overlap); namely, the performance is sensitive to either the choices of pairs or errors of distance constraints or both. We note that the size of the pool of significant pairs is relatively small for these three cases, which may result in relatively strong susceptibility to the contribution of each individual pair and therefore cause weak robustness. Indeed, for the transitions 1hhp → 1ajx and 1hil → 1him, when we enlarge the pool size the robustness is significantly improved (data not shown).

SUMMARY

As indicated by the results of the ideal test (Table 2), for most of the test cases (21 out of 22), by using just a small number (≤10) of pairwise distance constraints, we have obtained a good overlap between the computed conformational change and the measured one, which is higher than (or close to) the maximal overlap between any single mode and the measured one. In particular, in cases where more than one normal mode dominates, the predicted conformational change can correctly capture all or some of the dominant modes and give a better overlap than any single mode. We also find that increasing the number of constraints generally does not significantly improve the overlap values.

The results of the nonideal test are also encouraging: for most of the test cases (17 out of 22), slightly more constraints are needed to match the performance of the ideal test, and the robustness against different choices of pairs of constraints and errors in the values of distance constraints is generally strong. The dependence on the number of constraints is stronger than in the ideal test; the average overlap improves and the variance of the overlap decreases as more constraints are used. Therefore, for practical use of this method, we need to use slightly more constraints than suggested by the ideal test, which improves not only the average performance but also the robustness.

It is noted that the dependence on the accuracy of distance constraints is very weak for most of the test cases even for a relative large fractional error (up to 50%). This is critical to the practical application of this method with experimentally derived distance constraints that are usually of limited accuracy.

CONCLUSION

In conclusion, we have developed an ENM-based method that predicts the conformational changes of a protein complex given the initial state crystal structure together with the input of a small set of pairwise distance constraints for the end state. The predicted conformational change, which is a linear combination of multiple low-frequency normal modes, is computed as a response displacement induced by a quadratic perturbation to the Hamiltonian of the elastic network that incorporates the given distance constraints. For most of the test cases we studied, we find that the computed response displacement overlaps well with the measured conformational change, when only a handful of pairwise constraints (≤10) are used; in several cases even a single constraint has already yielded very good results. This method generally performs better than using any single normal mode, especially in cases where more than one mode dominates the transition. The robustness of the method against different choices of residue pairs and errors in the values of distance constraints has also been shown to be fairly strong.

The success of this method lends support to the critical roles of collective low-frequency motions in facilitating biomolecular functions. The easy and accurate triggering of such collective mode(s) by manipulating just a small number of interacting pairs of residues may be essential to the mechanism of allostery initiated by ligand binding or protein-protein interactions.

Compared with other computational methods that utilize the distance constraints to model protein structures (for example, using molecular dynamics simulation with additional energy terms from the constraints as restraints, as implemented in CHARMM by Brooks et al., 1983), this method has the following advantages: first, its implementation is fast and easy; second, it is free from any trapping in local minima; and third, it is applicable to large protein complexes. Furthermore, the conformational change predicted by this method can serve as a zero-order approximation that can be further refined by more sophisticated methods (for example, using dynamical simulations based on all-atom potentials).

Before ending, we acknowledge that there is limitation and inaccuracy in the ENM and there exist some protein conformational changes that cannot be described by the low-frequency normal modes (for example, some local structural changes). However, the basic idea proposed here is not limited to the ENM and it can be applied to the normal modes analysis of other force fields like the all-atom potentials.

For future work, we will apply this method with the experimentally derived distance constraints (for example, from NMR or other optical spectroscopy probes) to the analysis of protein conformational changes toward transient states that are difficult to capture by NMR or x-ray crystallography.