Self-Organized Density Patterns of Molecular Motors in Arrays of Cytoskeletal Filaments

Abstract

The stationary states of systems with many molecular motors are studied theoretically for uniaxial and centered (asterlike) arrangements of cytoskeletal filaments using Monte Carlo simulations and a two-state model. Mutual exclusion of motors from binding sites of the filaments is taken into account. For small overall motor concentration, the density profiles are exponential and algebraic in uniaxial and centered filament systems, respectively. For uniaxial systems, exclusion leads to the coexistence of regions of high and low densities of bound motors corresponding to motor traffic jams, which grow upon increasing the overall motor concentration. These jams are insensitive to the motor behavior at the end of the filament. In centered systems, traffic jams remain small and an increase in the motor concentration leads to a flattening of the profile if the motors move inwards, and to the buildup of a concentration maximum in the center of the aster if motors move outwards. In addition to motor density patterns, we also determine the corresponding patterns of the motor current.

INTRODUCTION

Cytoskeletal motors such as kinesin, dynein, and myosin are proteins which convert the chemical free energy released from the hydrolysis of adenosine triphosphate (ATP) into directed movements along filaments of the cytoskeleton. In cells, these motors drive various transport processes, and are also involved in cell division, cell locomotion, and reorganization of the cytoskeleton (Schliwa and Woehlke, 2003; Howard, 2001). A lot of knowledge has been obtained from in vitro motility assays that allow for the measurement of single motor properties such as their velocities, average walking distances, step sizes, and the forces they exert (Howard, 2001). These quantities have been measured for various types of processive motors including conventional kinesin (Howard et al., 1989; Block et al., 1990; Svoboda et al., 1993; Meyhöfer and Howard, 1995; Vale et al., 1996; Schnitzer and Block, 1997), Myosin V (Mehta et al., 1999; Veigel et al., 2002), the processive monomeric kinesin KIF1A (Okada and Hirokawa, 1999; Tomishige et al., 2002), and cytoplasmic dynein (Wang and Sheetz, 2000; King and Schroer, 2000). These motility assays study systems consisting either of mobile motors and immobilized filaments or of immobilized motors and mobile filaments. In addition, systems where both motors and filaments are mobile and filaments can be displaced by motors have also been studied (see e.g., Takiguchi, 1991; Urrutia et al., 1991; Nédélec et al., 1997; Surrey et al., 2001; Kruse and Jülicher, 2000).

In all of these systems, motors and filaments interact via hard core interactions arising from their mutual exclusion. Indeed, both motors and filaments occupy a certain spatial volume which cannot be occupied by another molecular structure. In particular, motors bound to filaments exclude other motors from the binding sites of the filaments. The latter exclusion effects were first addressed in our previous work (Lipowsky et al., 2001) in which we introduced a general class of driven lattice gas models for this purpose.

In the following, we use these driven lattice gas models to explore how the arrangement of the filaments affects the motor transport in closed compartments. We consider uniaxial and centered filament arrangements and present results for the stationary patterns of both motor density and motor current. Both types of arrangements are accessible to in vitro experiments and mimic structures of the cytoskeleton as observed in vivo. The uniaxial systems mimic the geometry of axons or fungal hyphae, whereas centered systems are realized, for example, in the asterlike structures of microtubules extending from centrosomes. For the uniaxial systems, we have previously shown that traffic jams build up easily as a consequence of mutual exclusion (Lipowsky et al., 2001), whereas previous work on centered systems (Nédélec et al., 2001) did not incorporate this mutual exclusion.

We will show in the following that uniaxial and centered systems exhibit rather different jamming behavior. While in uniaxial systems jammed regions grow upon increasing the motor concentration and spread over the whole system, the effect of jamming in centered systems is less dramatic and jams remain small in this case. Increasing the motor concentration, however, influences the density profile in the nonjammed region. In addition, we show that the traffic jams in uniaxial systems are rather insensitive to the motor behavior at the end of the filaments. In contrast, the latter behavior is crucial for the presence of jams in centered systems.

The density profiles discussed here theoretically can be directly measured in biomimetic experiments in vitro, and, in fact, such density profiles have recently been measured for the case of centered or asterlike systems (Nédélec et al., 2001). However, the latter experiment did not address the jamming behavior, which could be studied by increasing the motor concentration in these systems. In addition, our theoretical density profiles can be compared to motor density profiles measured for the corresponding systems in vivo. Such in vivo density profiles have been reported for fungal hyphae, which represent uniaxial systems. Seiler et al. (2000) have observed motors localized at the tip of these hyphae, which corresponds again to the case of low motor density. In vivo, the motor concentration can be changed by changing the level of expression of the corresponding gene; in that way jamlike density profiles have recently been observed for another fungal kinesin-like motor (Konzack, 2004; Konzack et al., 2005). The effect of exclusion (and, thus, jamming) is enhanced if the motors transport large cargoes such as membranous organelles. Jamlike behavior of organelles has been observed in axons (W. Saxton, private communication); extreme cases induced by mutations of motors (which are lethal in later stages of development) are accompanied by strong swelling of the axon (Hurd and Saxton, 1996; Martin et al., 1999).

Our article is organized as follows. We introduce the theoretical model in the following section. In the sections Density Profiles for Uniaxial Filament Systems and Density Profiles for Centered Filament Systems, we discuss jamming effects in two types of filament systems and present results for the motor density patterns obtained from Monte Carlo simulations and from a two-state model. Finally, we relate our results to recent experiments in the Discussion. The Appendices describe the theoretical methods used in this article and some analytical calculations.

THEORETICAL MODEL

Lattice models for molecular motors and filaments

In this article, we study the stationary profiles of the motor density that build up within closed compartments containing filaments. These stationary states are characterized by the balance of bound and unbound motor currents (Lipowsky et al., 2001). Unbinding of motors from the filaments reflects the finite binding energy of the motor-filament complex that can be overcome by thermal fluctuations and leads to peculiar random walks of the motors, which consist of alternating sequences of directed motion along filaments and nondirected diffusion in the surrounding fluid (Ajdari, 1995; Lipowsky et al., 2001; Nieuwenhuizen et al., 2002, 2004), see Fig. 1 a. To study these random walks, we have recently introduced lattice models (Lipowsky et al., 2001). One useful feature of these models is that one can incorporate motor-motor interactions such as the mutual exclusion in a rather natural way (Lipowsky et al., 2001; Klumpp and Lipowsky, 2003, 2004). Motor-motor interactions are especially important on the filaments: motors are strongly attracted to filaments, so that the local density of motors on these filaments will typically be large even if the overall motor concentration is rather small. The importance of motor-motor interactions is further increased if motors accumulate in certain regions of closed compartments.

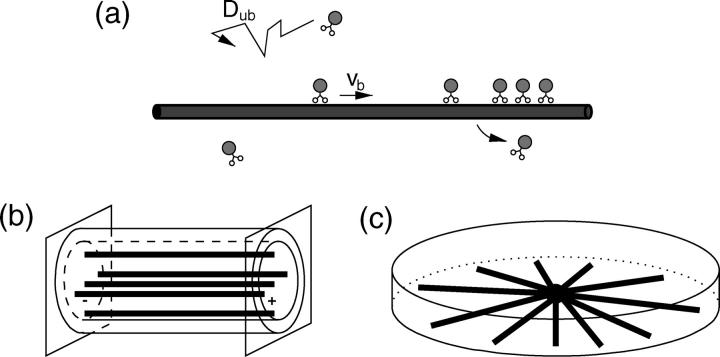
FIGURE 1.

(a) Molecular motors perform active directed movements characterized by the bound-state velocity v_b along a cytoskeletal filament. After unbinding from the filament, the motor undergoes nondirected Brownian motion with diffusion coefficient D_ub. As motors are strongly attracted to filaments, mutual exclusion of motors from binding sites leads to molecular traffic jams. We study stationary states for two geometries: (b) uniaxial arrangements of filaments in closed tubelike compartments and (c) radial or asterlike arrangements of filaments in closed disklike compartments.

Mutual exclusion of motors from binding sites of the filaments has two effects:

1. Binding of motors to the filament is reduced for those filament segments which are already occupied by many motors. This effect is directly observed in decoration experiments (see, e.g., Song and Mandelkow, 1993; Harrison et al., 1993).

2. The mutual hindrance slows down the movement of motors in regions of high motor density. This second effect has not yet been studied experimentally, but there are indications of it in microtubule gliding assays (Böhm et al., 2000). In addition, there is indirect evidence for such a slowing-down from the self-organization of microtubules and motors, where an increase of motor concentration can induce a transition from vortex to aster patterns of microtubules (Surrey et al., 2001). From computer simulations, such a transition is expected if the motors spend more time close to the end of a filament. This should happen if the motors are slowed down at the filament end by a traffic jam which builds up upon increasing the motor concentrations.

Bound and unbound motor movements

In the following, we describe the movements of molecular motors as random walks on a three-dimensional cubic lattice (Lipowsky et al., 2001; Nieuwenhuizen et al., 2002, 2004). One or several lines of lattice sites represent one or several filaments. The lattice constant ℓ is taken to be the repeat distance of the filament (which is 8 nm for kinesins moving along microtubules), so that filament sites of the lattice correspond to binding sites of the filament. A motor bound to a filament performs a biased random walk, which describes the active movements along the filament. Per unit time τ, it attempts to make forward and backward steps with probability α and β, respectively. As backward steps are rare for cytoskeletal motors, we take β = 0 in the following, which eliminates one parameter from our systems. Rather similar behavior is found for small nonzero values of β. With probability γ, the bound motor makes no step, and with probability ε/6, it unbinds to each of the four adjacent nonfilament sites. The sum of all hopping probabilities per unit time τ is one, i.e., the probabilities are related by

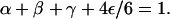(1)

When the motor particle reaches the end of the filament, it does not have the possibility to step forward to another filament site. We will consider two different unbinding processes for this last filament site as in our previous work (Klumpp and Lipowsky, 2003):

• Thermal unbinding. The motor particle detaches from the last filament site with probability ε/6 to the unbound site in the forward direction, but remains at the last site with probability γ′ ≡ γ + α −ε/6, whereas the backward probability β and the sideward probability ε/6 remain unchanged. Adjusting the no-step probability implies the modified normalization

  (2)

  for the hopping probabilities at the last filament site.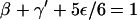

• Active unbinding. The motor particle detaches from the last site with probability α in the forward direction and with probability ε/6 in the four sideward directions as for all other filament sites. In this case, the normalization of the hopping probabilities at the last filament site is given by Eq. 1.

An unbound motor performs a symmetric random walk, which corresponds to nondirected diffusive movement. It attempts to step to each adjacent lattice site with equal probability 1/6. If an unbound motor reaches a filament site, it can bind to this site with probability π_ad. The random walk probabilities can be chosen in such a way that one recovers the measured transport properties of specific motors such as the bound state velocity, the unbound diffusion coefficient, and the average walking distance (see Lipowsky et al., 2001; Klumpp and Lipowsky, 2003). (Note that the model used here does not account for the bound state diffusion coefficient or, equivalently, the randomness parameter of the motor movements. This parameter can be incorporated by introducing a second timescale for the movements of the bound motors; see Lipowsky et al., 2001. Such an extended model leads to density profiles that are very similar to those described here. This indicates that the overall diffusion is essentially governed by the unbound diffusion process.) The unbound diffusion coefficient D_ub fixes the basic timescale τ = ℓ²/D_ub. The probabilities α, β, γ, and ε are determined from the velocity v_b = (α − β)ℓ/τ of a single bound motor, the average walking distance along the filament Δx_b = 3v_bτ/(2ε), the condition β = 0, and Eq. 1.

Mutual exclusion of motors is taken into account by rejecting all hopping attempts to lattice sites which are occupied by other motors. We take the motor particles to have a linear size comparable to the filament repeat distance ℓ and to occupy a volume ℓ³. If the motors are attached to larger cargoes, exclusion is enhanced. In particular, a large cargo of linear size nℓ, when bound to the filament, effectively covers between nℓ and (2n − 1)ℓ filament sites depending on the bound density. However, the functional relationships between the different densities and current are rather similar (MacDonald et al., 1968; McGhee and von Hippel, 1974). We will briefly discuss this case at the end of the article in Discussion.

These lattice models for systems with many molecular motors are related to driven lattice gas models which have been studied extensively in the context of nonequilibrium phase transitions (Katz et al., 1983; Krug, 1991). In the models studied here, the driving, i.e., the active directed movement, is restricted to the linear subspaces corresponding to the filaments.

In the following, we will usually express all lengths and times in units of the filament repeat distance ℓ and the basic timescale τ, respectively. This means that the bound and unbound motor densities ρ_b and ρ_ub that we will consider in the following are local particle number densities satisfying 0 ≤ ρ_b ≤ 1 and 0 ≤ ρ_ub ≤ 1, which corresponds to 0 ≤ ρ_b ≤ 1/ℓ³ and 0 ≤ ρ_ub ≤ 1/ℓ³ in dimensionful units. Dimensionful units will be used when presenting results for specific motor molecules.

Filament arrangements and compartment geometries

In this article, we study two types of filament arrangements within closed compartments as shown in Fig. 1, b and c. The first type is a uniaxial filament system where a closed cylindrical tube contains a number N_f of uniaxially arranged filaments, i.e., filaments oriented parallel to the cylinder axis and with the same orientation. We denote the coordinate parallel to the filament by x and the coordinates perpendicular to it by y and z. The tube has length L and radius R.

The second type of system which we will study is a centered filament system, i.e., a radial or asterlike arrangement of filaments within a closed disklike compartment. The number of filaments is again N_f. In this case, we denote the radial coordinate by r. The linear extension of the compartment along the direction of the filaments, i.e., the disk radius, is denoted by L and the disk height by h.

In both cases, we take all filaments to have the same length, which is equal to the corresponding linear extension of the compartment, i.e., to the tube length and to the disk radius in the case of uniaxial and centered filament systems, respectively. Shorter filaments lead to very similar results. An example would be filaments in radial arrangements that are nucleated from a centrosome and extend from r = R_c, the centrosome radius, to the disk radius r = R. In addition, since the compartments are closed, the number of motors, denoted by N, stays constant within each compartment.

DENSITY PROFILES FOR UNIAXIAL FILAMENT SYSTEMS

We first consider uniaxial arrangements of filaments within a closed tube as shown in Fig. 1 b. On the one hand, placing one or several filaments and motors inside a tube should be experimentally feasible. The tube could be either a glass tube as used for micropipettes, a topographic channel as used for filament guiding (Clemmens et al., 2003), or a liquid microchannel on a chemically structured surface (Gau et al., 1999; Brinkmann and Lipowsky, 2002). In all cases, tube diameters down to a few micrometers can be achieved. On the other hand, tubelike geometries are also quite common in cells, the most prominent example being the axon of a nerve cell, a tubular cell compartment with a diameter in the range of few micrometers and a length of up to a meter, which contains tens of microtubules per μm² (Alberts et al., 2002); typical distances of the microtubules are in the range of 100 nm. Similar compartments, the hyphae, exist in the case of fungal cells. In addition, some compartments inside the cell have tubular shapes and contain filaments such as strands of cytosol crossing vacuoles in plant cells, again with diameters in the micron range.

We will now focus on the case of a single filament, since the case of N_f isopolar parallel filaments in a tube with cross-section φ is essentially equivalent to a single filament in a tube with cross-section φ/N_f, provided that the filaments are equally distributed within the tube. (If the filaments are concentrated in a certain region, i.e., if the distance between filaments is small compared to the distance between filaments and the tube wall, depletion of motors is enhanced; depletion effects are rather weak, however.) Let us consider a cylindrical tube of length L and radius R with one filament located along its symmetry axis. Imagine now that a certain number of motors are placed in this tube. In the absence of ATP, the system attains an equilibrium state, where binding to and unbinding from the filament balance each other locally, i.e., at every single binding site. Both the bound and the unbound motor densities are constant and related by the radial equilibrium condition

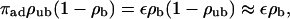(3)

where the terms (1 − ρ_b) and (1 − ρ_ub) describe mutual exclusion of bound and unbound motors, respectively, with (1 − ρ_ub) ≈ 1 for typical experimental situations.

When ATP is added to the system, the motors start to move along the filament. We use the convention that the filaments are oriented in such a way that the bound motors move to the right. The motor current along the filament builds up a density gradient, which generates a diffusive current. In the stationary state, this diffusive current balances the drift current of bound motors. As a first approximation, we assume that Eq. 3 is also valid in the presence of ATP (which is justified if the velocity v_b is sufficiently small, as we will show below). The balance of currents can then be expressed by

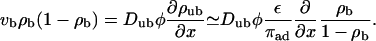(4)

It follows from this relation that, for low motor densities, the motor density increases exponentially along the filament and that motors accumulate at the right end of the filament, further increasing the importance of exclusion effects there.

Simulation results

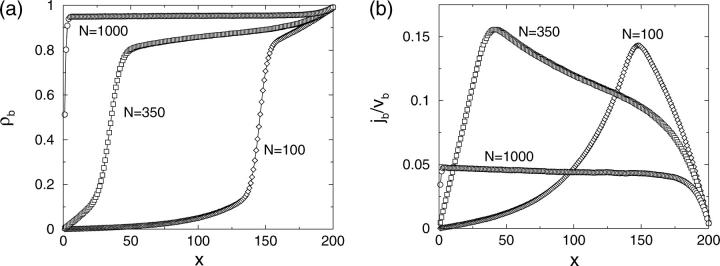
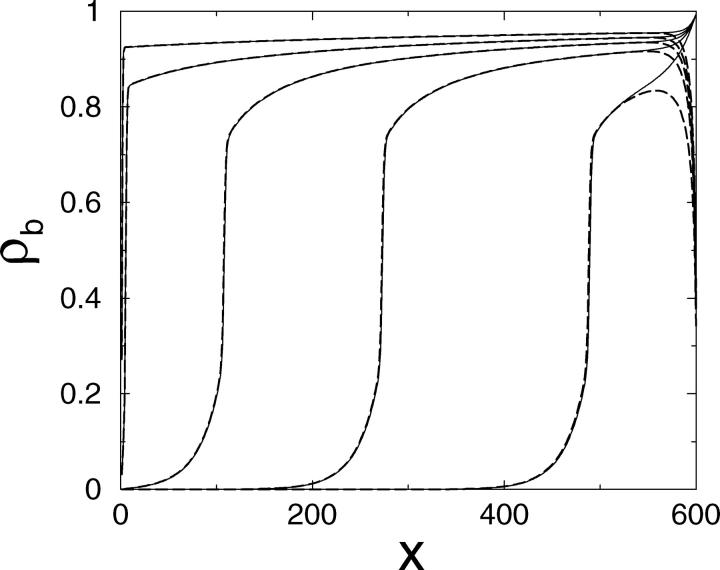
Typical density profiles as obtained from Monte Carlo simulations are shown in Fig. 2 a. If the total number N of motors is relatively small—one example is provided by N = 100 in Fig. 2—motors are essentially localized at the right end of the tube. Crowding of motors occurs only in a short region at the end of the filament where motors form a kind of traffic jam. To the left of the traffic jam, the density has an exponential profile as predicted by the simple balance of active directed currents and diffusive currents. If a motor detaches from the filament in the crowded region, it will diffuse back over a certain distance and most likely rebind to the filament in the region to the left of the traffic jam. In the jammed region rebinding is strongly reduced, since essentially all binding sites are already occupied. Upon rebinding to the filament, the motor will move relatively fast to the right until it ends up in the jammed region again.

FIGURE 2.

Profiles of (a) the bound motor density ρ_b and (b) the corresponding bound motor current j_b as functions of the coordinate x along the filament in the closed tube for three different motor numbers N as obtained from Monte Carlo simulations. The tube has length L = 200ℓ and radius R = 25ℓ. The transport parameters are 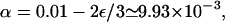β = 0, γ = 0.99, ε = 10⁻⁴, and π_ad = 1.

These observations imply the coexistence of a low-density region with an exponential density profile and a crowded high-density region, separated by a relatively sharp domain wall or interface which corresponds to the beginning of the traffic jam. If the number of motors in the tube is increased, the jammed region spreads further to the left and the domain boundary is shifted toward smaller values of the spatial coordinate x, as shown in Fig. 2 for N = 350. Now, motors diffuse backward over larger distances, since attempts to rebind to the filament fail, if the binding sites are already occupied.

Finally, if the motor concentration is very large, there is only one domain with a high density of bound motors: The filament is crowded over its whole length and the bound density profile is essentially constant except for the regions close to the two ends of the filament (see the case N = 1000 in Fig. 2). In this case, motors may diffuse back over the whole system length, but both the diffusive current and the bound current along the filament are very small.

The corresponding profiles of the bound motor current along the filament are shown in Fig. 2 b. The diffusive current of unbound motors integrated over the tube cross-section has the same absolute value, but the opposite sign. The current depends strongly on the position x along the filament as long as the filament is not completely jammed. Like the motor densities, it increases exponentially in the low density region. In the jammed region at the right end of the tube, the current decreases rapidly. It reaches its maximum close to the end of the traffic jam. Note that the maximal current accessible in these systems is smaller than v_b/4, i.e., smaller than the maximally possible current in a system with constant densities such as a tube system with periodic boundary conditions (Klumpp and Lipowsky, 2003). For the case of the completely jammed filament, the current profile is nearly flat, whereas the absolute current is small.

To obtain a global characterization of transport in the system, we determined the average current defined by

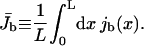(5)

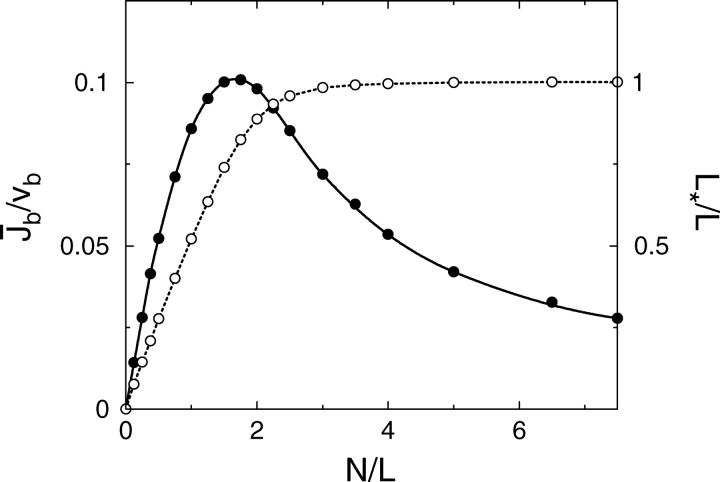
This quantity exhibits a maximum at an optimal motor concentration as a function of the total number N of motors in the system, i.e., as a function of the overall motor concentration (see Fig. 3). For small N, it grows linearly with the number of motors, whereas for large N it decreases again since motion of the bound motors is slowed down by the increasing traffic jam. However, this decrease of the currents is rather slow, since additional motors introduced into the system can only rarely find free binding sites. For the system shown in Fig. 3, the maximal current occurs for 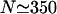motors, which corresponds to the intermediate case of the profiles in Fig. 2.

FIGURE 3.

Average current 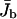of bound motors (solid circles) and traffic jam length L_* (open circles) as functions of the total number N of motors in the tube. Geometry and parameters of motion are the same as in Fig. 2. The data points at N/L = 0.5, 1.74, and 5 correspond to the profile shown in Fig. 2.

A second quantity, which gives a global characterization of the profiles, is the traffic jam length L_* of the crowded domain. L_* can be defined by the condition ρ_b(x_*) = 1/2 via L_* = L − x_*. Results for L_* are also shown in Fig. 3. The three cases discussed above can now be distinguished as follows. For very small L_*/L, crowding of motors only occurs in a small region at the filament end and the profile decays exponentially to the left over a large fraction of the system size. For intermediate values of L_*/L with 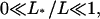the density profiles exhibit coexistence of domains with high and low bound motor densities. Finally, for L_*/L ≈ 1 the whole filament is crowded. Comparing the functional dependence of the traffic jam length L_* with the average bound current 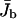shows that the optimal transport occurs when a large part of the filament is crowded, 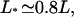but the traffic jam is not yet too dense.

Two-state model

To get some further insight into the properties of these self-organized density profiles, we studied the stationary states of these systems using a two-state model. In this model, which is described in detail in Appendix A, the dependence of the concentration profiles on the radial coordinate is neglected and motors can be in two states, namely bound and unbound. This approximation is justified, because the profile of the unbound motor density depends only weakly on the radial coordinate. The two-state approximation captures most of the relevant features of these profiles and numerical solutions for the stationary profiles are obtained much faster than by Monte Carlo simulations.

For the uniaxial systems, the two-state model as defined in Appendix A is given by

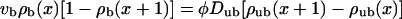(6)

and

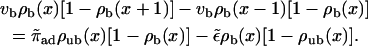(7)

These equations express the balance of bound and unbound currents and the binding to and unbinding from the filament, respectively (see Appendix A).

For the nonjammed low density region, some analytical results can be obtained from these equations which are presented in Appendix B. In particular, an exponential increase of the density profile is obtained as ρ_b ≈ 𝒩e^χ/ξ (except for the region close to the left boundary) with a length scale ξ as given by Eq. B6.

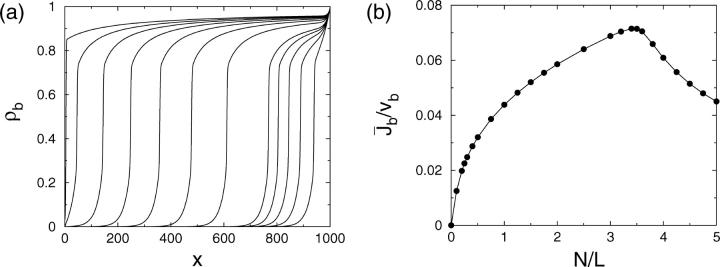
To obtain results for arbitrary densities, we solved the two-state Eqs. 6–7 numerically. Some profiles of the bound motor density as well as the average current as a function of the number of motors are shown in Fig. 4 for a relatively large system with L = 1000. Although the main features are the same as for the smaller system discussed above, some additional details can be seen here. The current increases linearly with the number N of motors for small N, but at a certain point, 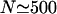or 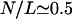in Fig. 4 b, the slope begins to change. The current then increases more slowly, but again nearly linearly, until it reaches its maximum. This change in slope of the current corresponds to the formation of a plateau in the density profile, where the density in the traffic jam is approximately constant and changes only little upon addition of motors.

FIGURE 4.

Two-state model. (a) Profiles of the bound motor density ρ_b as a function of the spatial coordinate x parallel to the filament and (b) average bound motor current 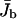as a function of the number N of motors in the tube as obtained from the numerical solution of the discrete two-state model. The chosen tube has length L = 1000 and radius R = 25. The parameters of motion are v_b = 0.01, D_ub = 1/6, ε = 10⁻⁴, and π_ad = 1. The numbers of motors in a are from right to left) N = 100, 200, 300, 400, 500, 1000, 1500, 2000, 2500, 3000, 3500, and 4000.

Until now, we have assumed thermal detachment, i.e., that detachment at the end of the filament occurs with the same rate as detachment at any other site of the filament. As mentioned before (see Eq. 2), a second possibility is active unbinding, i.e., that motors detach with an increased rate at the end by making an active step which leads to unbinding. There is some indirect evidence for a quicker detachment of kinesin motors at the microtubule end from experiments and computer simulation of the formation of aster and vortex patterns of microtubule by motors (Surrey et al., 2001). In simulations, quick detachment at the microtubule end leads to the formation of vortex (or spiral-like) structures, whereas slow detachment is necessary for the formation of asterlike centered arrangements. Kinesin is able to form both asters and vortices, suggesting that detachment at the microtubule end is relatively quick, whereas the kinesin-related motor, Ncd, only forms asters and thus probably detaches slowly at the microtubule end (Surrey et al., 2001).

We have determined density profiles for both cases using the two-state approach (see Fig. 5). These density profiles show that the jamming behavior is rather insensitive to the motor behavior at the end of the filaments. Except for the region very close to the filament end, the profiles for the two cases agree well. In particular, the domain wall or interface represented by the steep increase of the density profile at the beginning of the traffic jam is the same in both cases. This observation shows that the traffic jam is not due to the slow unbinding at the end, but due to the accumulation of motors with an exponential density profile, which follows from the balance of bound drift current and unbound diffusive currents in a uniaxial geometry. On the other hand, the density profile within the jammed region depends strongly on the detachment rate at the filament end. Although there is a weak increase of the bound density inside the jammed region for small detachment rate at the filament end, the bound density decreases strongly in this region in the case of an increased detachment rate at the end (see Fig. 5).

FIGURE 5.

Two-state model. Profiles of the bound motor density ρ_b for active and thermal unbinding of motors at the filament end. A motor at the end of the filament detaches with the same probability as at any other filament site (thermal unbinding, solid lines) or by a forward step, i.e., with rate α (active unbinding, dashed lines). L = 600, R = 25, parameters of motion as in Fig. 4; and N = 200, 800, 1400, 2000, and 2600 (from right to left).

Comparing the density profiles obtained from the two-state model with those obtained from simulations for the same parameter set, we find quite good agreement in the case where the entire filament is crowded by motors. For smaller overall motor concentrations, qualitative agreement is still good, but there are small quantitative discrepancies. We find that the length scale ξ of the exponential increase of the density is smaller in the two-state model than in the simulations. Correspondingly, the crowded region is slightly longer in this approximation. This difference is due to neglecting a depletion zone close to the filament in the two-state model. Close to the filament, the unbound motor density is smaller than its radial average in the low-density region. Taking it as independent of the radial coordinate, we thus overestimate binding of motors to the filament. Therefore there are more motors bound to the filament in the two-state model than in the simulations, which results in a longer traffic jam, and the maximum of the current is shifted to a smaller number of motors in the system.

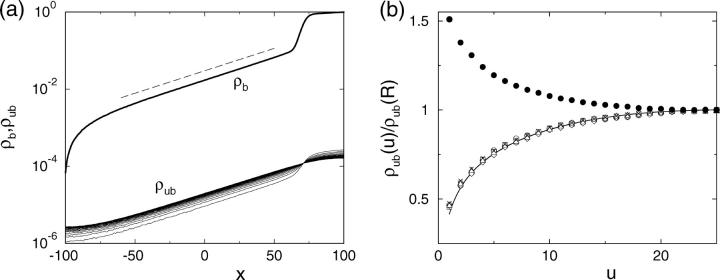
To obtain a quantitative description of the radial density profiles, we have solved the full three-dimensional diffusion equation for the low-density region and derived an analytical expression for the depletion layer close to the filament as shown in Appendix C. It follows from the latter expression that the radial profile of the unbound density is nearly flat far from the filament and exhibits a logarithmic depletion zone close to the filament. This confirms the observation that the unbound motor density depends only weakly on the radial coordinate which justifies the two-state approach. Comparing the results from this calculation with the simulation of the full model, good agreement is found. In Fig. 6, we have plotted both the longitudinal (Fig. 6 a) and radial profiles (Fig. 6 b) as obtained by both methods. The radial profiles exhibit the predicted depletion layer close to the filament in the low density region to the left of the traffic jam. In the crowded region, the unbound density is enhanced close to the filament in comparison to the value far from the filament. The full diffusion equation also leads to a condition for the length scale ξ given by Eq. C6 and we obtain 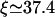for the parameters used in Fig. 6, in good agreement with the value from simulations which is 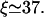In contrast, the two-state approximation yields the smaller value 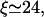because it overestimates the current of motors binding to the filament.

FIGURE 6.

(a) Profiles of the bound motor density ρ_b (thick line) and the radius-dependent unbound motor density ρ_ub as functions of the spatial coordinate x parallel to the filament. The lines for the unbound density show the profile at different distances from the filament (u = 1 to u = 25, bottom to top in the left part of the jam and top to bottom right of the jam). The dashed line indicates the exponential ∼exp(x/37.4) as obtained from the linearized equations C1–C3. (b) Radial profile of the unbound density in the low density region, x = −40 (○), −20 (□), 0 (⋄), 20 (▵), 40 (×), and in the crowded region, x = 80 (•). The solid line shows the analytical result given in Eq. C5. The simulation data at all positions in the low density region agree with each other and with the analytical result, which shows that the profile has the product form (Eq. C4). The transport parameters are as in Fig. 2, and the tube has length L = 201 and radius R = 25.

DENSITY PROFILES FOR CENTERED FILAMENT SYSTEMS

In this section, we consider profiles of the motor concentration in centered filament systems or asterlike arrangements of filaments as shown in Fig. 1 c. Such arrangements can be formed for microtubules in vitro either by nucleation from microtubule-organizing centers (Holy et al., 1997) or by self-organization of microtubules and motor complexes (Nédélec et al., 1997; Surrey et al., 2001). Centered filament systems mimic the most common organization of microtubules in cells. Motivated by the restructuring of this organization during cell division and the formation of the mitotic spindle (Hyman and Karsenti, 1996), many experiments have focused on the case where the filaments are also mobile.

In the following, we consider immobilized asterlike arrangements of filaments which are not reorganized by the action of motors. The asters consist of N_f filaments of length L arranged radially in a thin disk of radius L and height h. We take the filaments to extend from r = 0 to r = L within the disk, but again smaller filaments lead to very similar results. In that case, active directed currents of motors along the filaments and diffusive motor currents will again be balanced in a stationary state. For the aster geometry some theoretical and experimental results for low motor densities have recently been reported by Nédélec et al. (2001). We confirm their main theoretical result, an algebraic density profile far from the center of the aster, and extend the study of concentration profiles in asters by exploring the effect of mutual exclusion. (Note that in the experiments of Nédélec et al., 2001, the dynamics is more complicated, since they used mobile filaments and their motor constructs can also displace these filaments with respect to each other, so that the motor density profiles and the filament patterns develop in coordination. After some time, however, these systems reach a steady state, in which the filament pattern is stationary—although not completely immobile—and can, on average, be represented by a fixed filament system. In addition, once the asterlike structure is formed, the filaments are usually sufficiently separated from each other, with the exception of the center of the aster, so that the additional dynamics plays only a minor role. Indeed, in the low density case, the theoretical density profiles agree well with the experimental profiles, as we will discuss below. To exclude the more complicated dynamics, one could immobilize the filaments once the stationary state has been reached or, alternatively, use centered microtubule systems nucleated from centrosomes, Holy et al., 1997, and conventional kinesins, which cannot bind to two filaments at the same time.)

Two-state equations for centered systems

Centered filament systems are implemented in the two-state model by substituting the coordinate n used in the general expressions with the radial coordinate r, by using Eqs. A4–A6 for the bound and unbound motor currents and introducing a geometrical weight factor φ(r) ≈ φ₀r as described in Appendix A. The latter factor implements the fact that with increasing r, the volume available for unbound diffusion increases. The two-state model equations are then given by

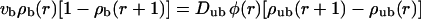(8)

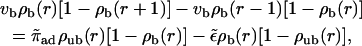(9)

for the case of motors moving outwards in an aster. If motion of motors is directed inwards, i.e., if v_b < 0, the two-state equations are given by

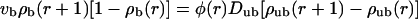(10)

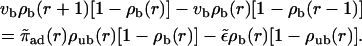(11)

In the low density limit, these equations lead to the algebraic density profile ρ_b ∼ r^η reported by Nédélec et al. (2001) (see Appendix B). The exponent η ∼ v_b is positive if motors move outwards and negative if motors move inwards.

Numerical results

To study the effect of hard core exclusion in asters, we used the parameters given by Nédélec et al. (2001) for the motor constructs used in their experiments. In the numerics all parameters are given in units of the microtubule periodicity ℓ = 8 nm and the step time τ_s = 10 ms. Parameters of the bound state are v_b = 0.8 μm/s = ℓ/τ_s and 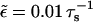corresponding to unbinding after 100 steps, and those of the unbound state are D_ub = 20 μm²/s = 3125 ℓ²/τ_s and 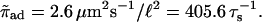Parameters which correspond to kinesin with beads as used by Lipowsky et al. (2001) lead to similar results. All results shown in the following are obtained for an aster of N_f = 300 microtubules of length 50 μm = 6250 ℓ, which is confined in a slab of height 9 μm = 1125 ℓ.

Motors moving inwards

We consider first the case where motors move inwards. For this case, experimental results have been reported by Nédélec et al. (2001). Accumulation of motors in the center of the aster is observed by fluorescence microscopy. Profiles of the total motor concentration, i.e., the concentration averaged over bound and unbound motors,

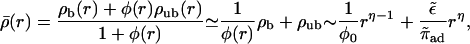(12)

can be extracted from the fluorescence images. The last expression is valid for small motor densities and sufficiently large values of r and predicts that the density profile exhibits a crossover from a decay ∼r^η−1 for small r to ∼r^η for large r. This crossover behavior is seen in the experimental data of Nédélec et al. (2001).

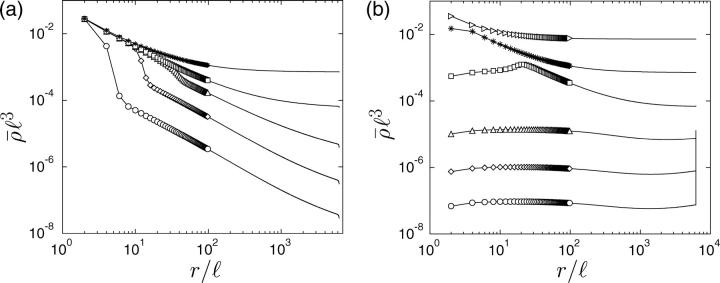
For small overall motor concentrations, the numerical solution of the master equations exhibits the power law behavior predicted theoretically by neglecting exclusion effects. For the chosen parameters we find ρ_ub(r) ∼ r^η with from the data for N = 10⁴ shown in Fig. 7 a in agreement with Eq. B14. In the center of the aster, a traffic jam is obtained already for small total number of motors. The traffic jam is, however, rather short and, in contrast to the case of uniaxially aligned filaments, does not grow substantially in length when the number of motors in the system is increased (see Fig. 7 a). Jamming of motors occurs only for small r (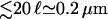). For this range of r, no experimental data are available. In contrast to the case of uniaxial systems, the motor behavior at the end of the filaments is crucial for the presence of jams in centered filament systems: If motors unbind actively at the filament ends (in the center of the aster), traffic jams are absent (as shown in Fig. 8 a). In the regions with low motor densities, the density profiles for thermal (slow) and active (fast) detachment at the ends of the filaments agree perfectly.

FIGURE 7.

Concentration profiles for motors moving (a) inwards and (b) outwards in asterlike arrays of filaments as functions of the radial coordinate r. Parameters are for motor complexes as described by Nédélec et al. (2001), see text. The numbers of motors are (from bottom to top) N = 10⁴ (○), 10⁵ (⋄), 10⁶ (▵), 10⁷ (□), 10⁸ (*), and 10⁹ (▹). The profiles shown are profiles of the total motor concentration 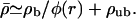Because of the logarithmic scale, discrete data points are only indicated for small r.

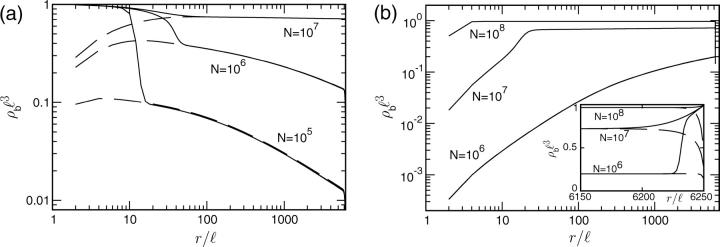
FIGURE 8.

Thermal versus active unbinding of motors at the filament end in centered systems. Profiles of the bound motor density ρ_b as a function of the radial coordinate r for motors moving (a) inwards and (b) outwards in asterlike filament arrays. At the end of the filaments, motors detach with the same probability as at any other filament site (solid lines) or by a forward step, i.e., with rate α (dashed lines). The inset in b shows the region close to the filament ends where the profiles for the two cases differ. The parameters are as in Fig. 7.

The main effect of the mutual exclusion is that density profiles get more and more flat with increasing motor concentration in the system (see Fig. 7 a). This means that the power law profile is found only for small overall motor concentrations. The average current in the system again exhibits a maximum at an optimal motor concentration. The maximum occurs at a motor concentration, where the bound motor density becomes nearly constant and the power law behavior is hardly identified.

Motors moving outwards

For motors moving outwards in an aster we obtain profiles as shown in Fig. 7 b. For small numbers of motors (and not too close to the boundaries) the bound density follows the power law obtained from the linear equations. Now the exponent η is positive but small. With increasing motor concentration, the profile of the bound density again gets more and more flat and the filaments become more and more crowded. As in the case of outward movements, however, the jams at the end of the filaments grow only very weakly and remain rather small (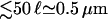). The motor behavior at the filament ends is also crucial for the presence of these jams in this case, and jams are absent if motors unbind quickly at the filament ends (see Fig. 8 b).

The new feature compared to the previous case is that the profile of the total motor concentration, which is rather flat for small motor concentration, develops a pronounced maximum in the center of the aster as the number of motors is increased beyond the optimal motor concentration (see Fig. 7 b). This can be understood in the following way: If no ATP is added to the system, motors will accumulate in the center of the aster, simply because they bind strongly to the filaments, and, in the center, the number of binding sites per unit area is maximal. If ATP is added, motors are driven outwards by active directed motion. Now if the number of motors in the system is increased, so that the motor movements are slowed down by the exclusion effect, the outward drift is suppressed and accumulation in the center is successively restored.

DISCUSSION

We have presented theoretical results for the density profiles of molecular motors in arrays of cytoskeletal filaments. Motors were described as particles which move actively, i.e., in a directed manner, when they are bound to cytoskeletal filaments, but undergo nondirected diffusion upon unbinding from filaments. In addition, motor particles interact via mutual exclusion. On the one hand, these models are designed to describe the generic behavior of the movements of molecular motors; on the other hand, the model parameters can be adapted to the transport properties of specific motor molecules. In general, these models involve certain simplifications compared to real systems. We have therefore tested a few modifications of the models to check that a more detailed modeling does not change our conclusions.

Mutual exclusion of motors is obviously enhanced, if the motors carry large cargoes such as latex beads or vesicles. Furthermore, microtubules consist of 12–14 protofilaments, which correspond to 12–14 parallel tracks (see also Nieuwenhuizen et al., 2002, 2004). For the uniaxial geometry, we have performed simulations of lattice models for which these two features have been incorporated. In these latter simulations, motors which occupy a cubic volume of M³ lattice sites move on a microtubule consisting of 12 protofilaments arranged in a tubular geometry. In the simulations we chose M = 3 and M = 5. These cargoes can mimic small vesicles with diameters of some tens of nanometers. In vivo, the cargo diameters lie between a few nanometers for a single protein or RNA molecule and hundreds of nanometers for a large organelle. In addition, these model cargoes attach to the filament only with one of their surface sites, which represents the motor. Therefore, those cargoes which are not bound to the filament have an additional rotational degree of freedom. The resulting density profiles are averaged over M subsequent lattice sites, because the unrealistic cubic shape of the cargoes and the rigidity of their attachment to the motors leads to an artificial sublattice structure in the crowded region. We then obtain density profiles that resemble the ones discussed above, but the value of the bound density in the crowded region is smaller, because a smaller number of motors can block the filaments. In particular, a motor bound to one protofilament also blocks binding sites of the adjacent protofilaments because of the steric hindrance induced by its large cargo.

Finally, let us relate our results to experiments. We have determined profiles of the motor density and motor currents in uniaxial and centered filament systems. On the one hand, these systems are directly accessible to experiments in biomimetic model systems in vitro. Density profiles as discussed here have so far only been measured for the case of centered or asterlike systems (Nédélec et al., 2001) (see Density Profiles for Centered Filament Systems, above, for a discussion of the dynamics in these experiments). The latter experiment shows the power law profile that is obtained from the theory for low motor densities. Higher motor densities and the corresponding jamming behavior have not been explored in this experiment, but could be studied in the same way by increasing the overall motor concentration. For the latter case, our theoretical study makes detailed predictions for the density and current profiles which could be checked in such an experiment. In addition, it would be quite interesting to construct other filament arrangements and compartment shapes and to study the corresponding motor transport experimentally.

On the other hand, we can also compare our theoretical results about motor traffic in closed compartments with experimental studies on motor traffic in biological cells, where, however, additional phenomena such as the dynamics of the filaments, the regulation of the motor activity, and the presence of other cellular structures also play important roles. Using fluorescence probes, several groups have measured the density profiles of molecular motors in vivo. One particularly interesting system is that of the kinesin motors in fungal hyphae. These hyphae are tubular compartments which contain uniaxial filament systems. In one experiment, strong localization of kinesin has been observed at the tip of these fungal hyphae (Seiler et al., 2000). The cometlike density profiles of these motors localized at the tip correspond to the case of low motor density in our model. However, this localization is only found for kinesin mutants lacking a certain regulatory domain, i.e., for motors which move actively, but which are not regulated by cargo binding (see also Verhey et al., 1998). The underlying regulatory mechanism is the deactivation of the motor via folding of its tail if no cargo is bound to it (Coy et al., 1999; Seiler et al., 2000). The deactivated motors do not exhibit active movement along filaments and can diffuse back over larger distances. Further regulatory mechanisms have mainly been discussed for the case of axons where the question, whether and how motors are transported back, is most prominent (Goldstein and Yang, 2000). The mechanisms include local degradation of motors at the axon terminal (Dahlström et al., 1991) and backward transport by motors of opposite directionality (Hirokawa et al., 1990, 1991).

Very recently, another fungal kinesin was also shown to localize at the tip of the hyphae and to exhibit these cometlike profiles. In this case, larger motor concentrations were induced by increasing the level of expression of the corresponding gene. This leads to density profiles with regions of high motor density which increase in length with increasing expression level (Konzack, 2004; Konzack et al., 2005). According to our model, these density profiles should represent growing traffic jams. It would be highly desirable to repeat these experiments in vitro.

In summary, we have discussed theoretically the stationary density and current profiles of molecular motors in uniaxial and centered asterlike arrangements of cytoskeletal filaments. In particular, we have explored the effects of exclusion and jamming which can be addressed in these systems by varying the overall motor concentration. The two types of filament systems, which we studied, exhibit different density profiles and different jamming behavior. For small overall motor concentrations, the profiles are exponential in uniaxial systems, but algebraic in centered systems except for the crowded region close to the filament ends. Increasing the overall motor concentration, the jammed region grows in the uniaxial geometry, resulting in the coexistence of large regions of high and low density of bound motors; whereas the crowded region remains small in centered systems, in which larger overall motor concentrations lead to a flattening of the profile if the motors move inwards, and to the buildup of a concentration maximum in the center of the aster if motors move outwards. In addition, the jamming in the uniaxial systems is rather insensitive to the motor behavior at the ends of the filaments, while the latter behavior is crucial for the presence of jams in centered systems.

Both geometries studied here mimic arrangements of filaments in cells and are accessible to in vitro experiments. The predictions for both geometries can thus be tested experimentally. Some density profiles have already been determined experimentally. These profiles correspond mainly to the case of low motor density (Nédélec et al., 2001; Seiler et al., 2000)—only one recent experiment (Konzack, 2004; Konzack et al., 2005) addresses higher motor densities—and are in agreement with our theoretical description.

APPENDIX A: THEORETICAL METHODS

Monte Carlo simulations

We performed Monte Carlo simulations for the case of uniaxial arrangements of filaments, where filaments are located within cylindrical tubelike compartments and aligned parallel to the cylinder axis, which we take to be the x axis. We take the filaments to have the same length L as the tube, but we checked that shorter filaments lead to very similar results. The cylindrical tube with radius R is taken to consist of all channels, i.e., lines of lattice site parallel to the filament, with u ≡ (y² + z²)^1/2 ≤ R and 0 ≤ x ≤ L. Reflecting boundary conditions are implemented by rejecting all moves to lattice sites outside this range. Within the closed tube the number N of motors is fixed. Each Monte Carlo step, corresponding to a unit of the basic timescale τ, consists of N Monte Carlo moves. At each move, a motor particle is chosen randomly and updated according to the random walk probabilities.

Two-state model

Our Monte Carlo simulations show that the stationary profiles of the unbound motor density depend only weakly on the coordinates perpendicular to the filaments. To determine the stationary state, we can therefore use a two-state approximation, in which all unbound channels are treated as equivalent and the motors can be in two states, bound and unbound. The stationary state is then characterized by the balance of bound and unbound currents, j_b and j_ub, respectively, as given by

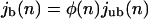(A1)

with 0 < n < L, and by the change of the bound current as a function of the spatial coordinate n arising from the binding and unbinding of motors, which leads to

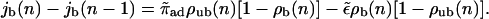(A2)

The latter equation expresses the fact that, in the stationary state, the sum of all outgoing currents is equal to the sum of all incoming currents at any filament site n and corresponds to Kirchhoff's first rule for electric circuits. Here, ρ_b and ρ_ub are the local number densities of bound and unbound motors, respectively. (In the next step, we will express the currents j_b and j_ub in terms of these densities.) The coordinate n along the filament is given by the spatial coordinate x along the cylinder axis and the radial coordinate r for uniaxial and radial arrangements of filaments, respectively. φ(n) is a geometrical factor and will be explained below. The binding and unbinding rates have been rescaled in Eq. A2, 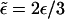and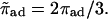

In addition, we express the bound and unbound motor currents as functions of the motor densities. For the tube geometry, we use the convention that the bound motors move to the right (the case that they move to the left is then obtained via the reflection symmetry). The bound motor current is then given by

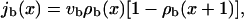(A3)

where v_b is the velocity in the absence of other motors. In the presence of many motors, forward steps are only possible if the filament site in front of a motor is not occupied. The probability of a vacant site is given by [1 − ρ_b], which leads to the reduction of the current as a function of density expressed in Eq. A3.

For radial arrangements of filaments, we have to distinguish inward and outward movements of bound motors. The bound motor current is given by

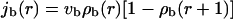(A4)

and

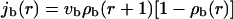(A5)

for outward and inward movements, respectively.

In all cases, the diffusive current of unbound motors is given by

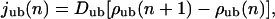(A6)

with the diffusion coefficient D_ub of unbound motors. Note that the latter expression is a discrete version of the usual diffusive current D_ub∂ρ_ub/∂n.

The geometrical factor φ introduced in Eq. A1 describes the relative weight of the bound and unbound currents and is given by the number of filament channels per nonfilament channel. In general, φ is a function of the coordinate n. For N_f isopolar parallel filaments within a cylindrical tube, φ is given by φ ≈ πR²/N_f. In particular, for a single filament, φ is given by the tube cross-section. Notice that, within the two-state model, the number of filaments appears only via this geometrical factor and leads to a rescaling of the accessible volume for the diffusion of unbound motors. In the case of centered filament systems, the volume available for the unbound diffusion depends on the radial coordinate r, and the geometrical factor φ increases linearly with r. In this case, φ is given by the ratio of the free surface (i.e., not covered by filaments) to the area covered by filament channels, which leads to

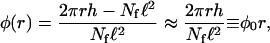(A7)

where N_f is the number of filaments, ℓ² is the cross-section of a single channel, and h is the height of the slab, into which the aster is confined.

At the boundaries, x = 0 and x = L, terms corresponding to currents through the tube walls have to be omitted in Eq. A2. Together with the normalization condition

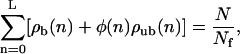(A8)

which fixes the total number N of motors in the tube, these equations form a system of 2L nonlinear equations for the 2L unknown densities ρ_b(n) and ρ_ub(n) with 0 < n ≤ L. We have solved this system of nonlinear equations numerically using Newton's method with backtracking (Press et al., 1992). The advantage of the two-state approach over the Monte Carlo simulations is that it requires less computation time, so that larger systems are accessible. In addition, simulations take particularly long computation times, if unbound diffusion is fast compared to bound movement, which is the case for cytoskeletal motors without large cargoes. In this case, the basic timescale τ of the simulations is much smaller than the step time 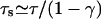of the bound movements because γ is close to 1. In contrast, in the two-state approach, the necessary computation time is independent of the parameter values. In addition, within the two-state approximation, the computation time for several filaments (arranged in parallel or in an aster) is the same as for a single filament.

As we do not distinguish between the different nonfilament channels in the two-state model, we neglect depletion layers close to the filaments as we discuss in Appendix C in some detail for the tube geometry. In addition, a mean field approximation is implicit in the relations for the bound motor current as given by Eqs. A3–A5. However, a comparison of the stationary profiles from the two-state approach with simulation results obtained for the case of truly equivalent unbound channels, for which the two-state approximation is exact, shows very good agreement. We therefore conclude that, in contrast to the open tube systems discussed by Klumpp and Lipowsky (2003), the mean field approximation is quite accurate for the closed systems discussed here.

APPENDIX B: LOW DENSITY LIMIT OF THE TWO-STATE MODEL

Some analytical results can be obtained for the nonjammed low density regions both in uniaxial and centered filament systems. For this purpose, we consider the continuum version of the two-state equations.

Uniaxial systems

The continuum two-state equations for uniaxial filament systems are obtained by expanding Eqs. 6 and 7 up to second order in the lattice constant. (Note that we expand Eq. 6 taken at positions x and x − 1 and average the results to get an non-ambiguous result. This agrees with the result obtained by expanding the time-dependent equations. The expansion leads to D_b = v_bℓ/2, but within the continuum equations, we can also treat D_b as an independent parameter.) This leads to

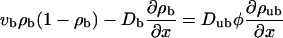(B1)

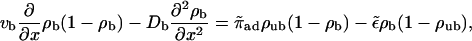(B2)

with the boundary conditions j_b = v_bρ_b(1 − ρ_b) − D_b∂ρ_b/∂x = 0 at x = 0 and x = L, which express the fact that no motors enter or leave the tube. These boundary conditions also imply, via Eq. B1, that the unbound motor currents vanish at the boundaries. In the low-density limit, hard core repulsion or exclusion can be neglected. This is appropriate in the noncrowded region, where For simplicity, we also neglect the bound diffusion terms, i.e., we consider the case D_b = 0. On the one hand, this can be understood as taking into account only the first nonvanishing terms in the derivation of the continuum equations. On the other hand, a comparison of numerical solutions of the continuum equations with and without these terms shows that the precise value of D_b is largely irrelevant for the solution, as long as the detachment rate is small (which, however, is the case for processive motors). In the low-density limit the equations become linear,

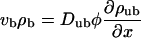(B3)

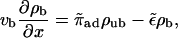(B4)

and, in general, the solution is given by a sum of two exponential terms. One term, however, decreases exponentially with x and therefore contributes only close to the left boundary, where it ensures the boundary condition of vanishing current and leads to a larger initial slope of the density profile. For sufficiently large x, the solution is therefore increasing exponentially along the tube,

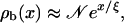(B5)

where 𝒩 is a constant and

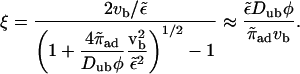(B6)

The last approximation is valid for small v_b and is also obtained from our first approximation, Eq. 4 above, where we assumed that unbinding and rebinding are equilibrated. The unbound density is given by

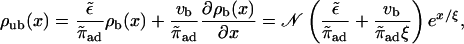(B7)

i.e., bound and unbound density are proportional in the low-density limit. The first term of the factor relating bound and unbound density is the one obtained in the case of equilibrated transitions between the bound and unbound states (e.g., from linearizing Eq. 3), the second one is a correction which shows that binding and unbinding are also driven out of equilibrium if v_b ≠ 0. (Note, however, that this term is of order 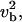since ξ ∼ 1/v_b, so that up to linear order in v_b, radial equilibrium still holds.) This correction term is positive, thus the current of motors binding to the filament at a given site, 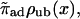is larger than the current of unbinding motors at the same site, 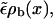which is easy to understand, since the motors bound to the filament are driven away by the drift v_b. For small driving velocity v_b, we can replace the local balance of binding and unbinding currents at a site x by the condition

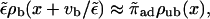(B8)

which states that motors binding to the filament at site x, move for a distance 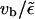before they unbind at site 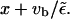Inserting the solution given above, we can check that this is fulfilled for small :

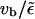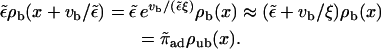(B9)

The fact that more motors attach to the filament than detach from it, indicates that this solution cannot be correct for all x. In a system without mutual exclusion, unbinding will be larger than binding to the filament only at the end of the filament. In that case, we can account for unbinding at the filament end by assuming that all motors that would have detached in the interval [L, L + v_b/ε] are forced by the boundary to wait at the last binding site of the filament until they detach. Therefore the density at the filament end, ρ_b(x = L), is given by

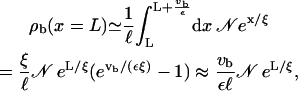(B10)

where ℓ is again the size of the binding site and the last relation is valid for small velocity v_b, for which the ansatz given in Eq. B8 is justified. A comparison with simulations for the case without mutual exclusion shows good agreement of the density at the last lattice site with the values obtained by this procedure. In reality, however, there is hard core exclusion and the present solution holds only as long as the bound density is sufficiently small and breaks down at a certain x because of the exponential increase of the bound density.

Centered systems

For centered filament systems, the continuum limit of the two-state equations for low motor densities leads to

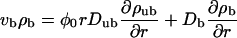(B11)

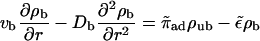(B12)

for both inward and outward movements. In the case D_b = 0, these equations are equivalent to those used by Nédélec et al. (2001) to describe their experimental results. These equations lead to

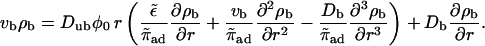(B13)

To recover the asymptotic solution of Nédélec et al. (2001) we assume ρ_b ∼ r^η and neglect terms of order r^η−1. We obtain

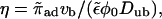(B14)

which can be larger or smaller than zero, depending on the sign of the velocity v_b. Note that the bound diffusion coefficient does not contribute to this asymptotic result. Interestingly, neglecting terms of order r^η−1 is equivalent to the assumption that binding to and unbinding from the filament are balanced locally. Hence asymptotically, bound and unbound densities are related by 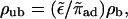in contrast to the case of uniaxial systems, and ρ_ub decays with the same power law as ρ_b.

APPENDIX C: DEPLETION LAYER

In this Appendix, we derive an analytical expression for the radial profile of the unbound motor density for the case of a single filament located along the symmetry axis of a cylindrical tube. We consider the linearized diffusion equations that are appropriate for the low density limit or the noncrowded region to the left of the traffic jam.

The balance of bound and unbound currents is given by

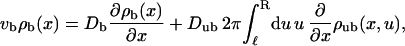(C1)

and the unbound motor density fulfills the stationary diffusion equation with cylindrical symmetry

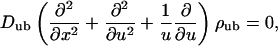(C2)

which holds for values of the radial coordinate u with ℓ ≤ u ≤ R with the filament radius 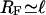and the tube radius R. The solution has to fulfill the boundary condition ∂ρ_ub/∂u = 0 at u = R. The longitudinal boundary conditions are the same as in the two-state model. Binding to and unbinding from the filament are described by

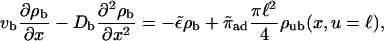(C3)

which represents the boundary condition for ρ_ub at u = ℓ. The separation ansatz

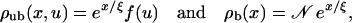(C4)

where 𝒩 is a constant, leads to

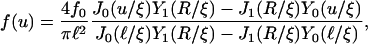(C5)

where J₀ and Y₀ are Bessel functions of order zero of the first and second kind, respectively, and J₁ and Y₁ are the corresponding Bessel functions of the first order (Abramowitz and Stegun, 1984). For small u the radial profile behaves as f(u) ∼ ln(u/ξ).

The balance of bound and unbound currents, Eq. C1, yields the condition

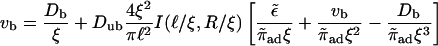(C6)

with

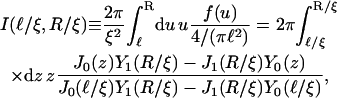(C7)

from which the localization length ξ is determined numerically.

APPENDIX D: LIST OF SYMBOLS

Db	(One-dimensional) diffusion coefficient of bound motors.
Dub	Diffusion coefficient of unbound motors.
f(r)	Radial part of the concentration profile in a tube.
h	Height of the slab to which a filament aster is confined.
jb	Local current of bound motors.
jub	Local current of unbound motors.
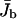	Spatially averaged current of bound motors in a closed tube.
λ	Lattice constant, given by the filament repeat distance.
L	Linear extension of the compartment, i.e., length of the tube or radius of the disk.
L*	Length of crowded region (traffic jam).
n	Coordinate along the filament in the general case, n = x and n = r for uniaxial and radial filament arrangements, respectively.
N	Number of motors.
Nf	Number of filaments.
N	Normalization constant.
r	Radial coordinate in the aster geometry.
R	Radius of closed tube.
t	Time variable.
u	Radial coordinate in the tube geometry.
vb	Velocity of bound motor.
x	Spatial coordinate parallel to the filament.
y, z	Spatial coordinates perpendicular to the filament.
α	Probability for a forward step of a bound motor per unit time τ.
β	Probability for a backward step of a bound motor per unit time τ.
γ	Dwell probability of a bound motor per unit time τ.
ε	Detachment parameter, for which ε/6 is the detachment probability per nonfilament neighbor site per unit time τ.
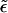	Rescaled detachment probability,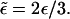
η	Exponent of the asymptotic density profiles in asters.
ξ	Localization length or decay length of the density profiles.
πad	Sticking probability for a motor hopping to the filament.
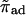	Rescaled sticking probability,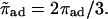
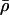	Average motor density (bound and unbound motors).
ρb	Density of motors bound to the filament.
ρub	Density of unbound motors.
τ	Basic time unit, defined by τ = ℓ2/Dub.
τs	Step time.
φ	Ratio of the number of filament channels to the number of nonfilament channels; uniaxial arrangements: tube cross-section/filament number, asters: radius-dependent effective cross-section/filament number.
φ0	Parameter for the ratio of bound to unbound channels in the case of asters.