Abstract
We present a directed essential dynamics (DED) method for peptide and protein folding. DED is a molecular dynamics method based on the essential dynamics sampling and the principal component analysis. The main idea of DED is to use principal component analysis to determine the direction of the most active collective motion of peptides at short intervals of time (20 fs) during the folding process and then add an additional force along it to adjust the folding direction. This method can make the peptides avoid being trapped in the local minima for a long time and enhance the sampling efficiency in conformational space during the simulation. An S-peptide with 15 amino acids is used to demonstrate the DED method. The results show that DED can lead the S-peptide to fold quickly into the native state, whereas traditional molecular dynamics needs more time to do this.
INTRODUCTION
Protein folding is one of the most important and unresolved problems in life science. It has been studied for many years, and many methods for investigating it have been developed, from lattice to all-atom ones (Boczko and Brooks, 1995; Gutin et al., 1995; Irback et al., 2000; Kaya and Chan, 2000; Shakhnovich and Gutin, 1993; Takada et al., 1999). After decades of extensive research, some comparably sophisticated theories have been proposed. Among them, the folding funnel theory is widely accepted (Bryngelson et al., 1995; Leopold et al., 1992; Mirny and Shakhnovich, 2001). According to this theory, proteins go down along the energy landscape during the folding process and quickly approach their native states.
Many folding/unfolding simulations have been carried out on proteins at the atomic level (Gsponer and Caflisch, 2002; Jaenicke, 2000; Knapp-Mohammady et al., 1999; Luque et al., 1996; Majeux et al., 2001; Galzitskaya et al., 2000; Pande and Rokhsar, 1999; Zagrovic et al., 2001; Zhang et al., 2001). These studies enable a thorough understanding of protein folding/unfolding. One of the important results is that both folding and unfolding processes of proteins go through a few conformational clusters (so called local minima) before they arrive at their native states. In the past, most of the simulations of protein folding were done under traditional molecular dynamics (MD). It was found that traditional MD is not very efficient for exploring conformational space because it spends too much time on staying in local minima and is hard to find an outdoor to get out (Pande and Rokhsar, 1999). So to get a full folding path of a protein, simulations must be carried out from different initial structures to enhance the probability of getting out of local minima and reaching the native state, or simply increase the simulation time. For example, Duan and Kollman have made a successful 1-μs simulation at 300 K for a 36-residue peptide, and the final structure of the peptide was very close to the native state (Duan and Kollman, 1998). This encourages using simulation to study protein folding.
In the last 10 years, many methods have been proposed to improve sampling efficiency on energy landscape. A lot of them are based on the normal mode analysis (NMA; Brooks and Karplus, 1983; Go et al., 1983; Levitt et al., 1983) or the principal component analysis (PCA; Amadei et al., 1993; Balsera et al., 1996; Kitao and Go, 1999; Teeter and Case, 1999; Zhang et al., 2003). In NMA, the potential energy is approximated as harmonic terms and normal modes are obtained by diagonalization of the Hessian matrix of a structure, which stays in a local minimum. In other words, NMA describes the atomic motions in terms of single frequency modes within a harmonic energy minimum, and so it can give important information on protein structure, such as flexibility and stability. However, since NMA assumes that the system is harmonic, when dealing with anharmonic systems, like peptides and proteins at ordinary temperatures, it is not really useful. Furthermore, the Hessian matrix is calculated from the second derivation of the potential energy described by an all-atom force field, and so NMA costs too much CPU time.
PCA provides a more useful tool to study protein folding. It does not use any harmonic assumption and simply provides those collective degrees of freedom, in general not at all associated to a single frequency, which decompose the whole conformational fluctuation into the largest-smallest components. It is known that protein structure is always represented by three-dimensional Cartesian coordinates, and so the degrees of freedom of a protein are very large (i.e., 3N − 6, where N is the number of atoms). It is difficult to explore the energy landscape in this multidimensional space by traditional MD. PCA tries to solve the problem by generating new 3N − 6 vectors from those Cartesians coordinates. Then we can pick out the main collective degrees of freedom necessary to describe dynamics of protein folding. These special collective degrees of freedom span an essential subspace, and all the conformations in the MD trajectories can be projected into it and form a visual image of the folding process. A lot of researches have reported that this subspace can reflect global motion of proteins with a high approximation. Using some special sampling techniques in this space, it is possible to explore the energy landscape more extensively and get a general view of protein folding. In the last 10 years, there were some successful applications of PCA in protein simulations (Amadei et al., 1993; De Groot et al., 2001; Elmaci and Berry, 1999; Garcia, 1992; Hayward et al., 1995; Ota and Agard, 2001; Van Aalten et al., 1995), which exhibit that PCA is perspective and can help us to investigate the protein folding problem in depth.
Essential dynamics sampling (EDS; Amadei et al., 1993, 1996) is one of the simulation methods based on PCA. In EDS, a simulation is done at first (typically lasting for nanoseconds), and the principal components or collective degrees are derived from it. Then these principal components can be used to lead protein folding in subsequent normal simulation. Recently Daidone et al. (2003) studied protein folding in explicit water with EDS and obtained a full folding path for a real protein (cytochrome c) successfully. EDS is also robust in analyzing relative motion, for example, hinge-bending between domains in protein (Cregut et al., 1998; Van Aalten et al., 1998). But it must be noted that the principal components may vary significantly during protein folding, i.e., when the conformations undergo large transformations. So, when applying EDS to protein folding, we should pay more attention to conformation change.
Recently some improvements to EDS have been reported for protein folding. For example, Zhang et al. have proposed a useful technique named amplified collective motion (ACM; Zhang et al., 2003) to supplement EDS. They analyzed the recorded trajectory and obtained normal modes at short intervals. Then they coupled the normal modes in different subspaces with different thermal baths. The normal modes in the essential subspace are coupled to a higher temperature bath, and the rest are coupled to a normal temperature bath. This method is effective in practice and enables short peptides to fold into the native state successfully, but there is one thing to be considered: in this method all the normal modes are obtained from the anisotropic network model (Atilgan et al., 2001). The anisotropic network model is an elastic network model and can be seen as a reduced model of NMA. It treats protein structures as many beads connected by harmonic springs. The potential energy of this system is very different from that of an all-atom force field and is related with cumulated harmonic energies of residue pairs. So the normal modes derived from this model may not be consistent with all-atom models, especially with protein structures far away from the native state.
In this study, we present a new method for peptides and protein folding, i.e., a directed essential dynamics (DED) analysis, which is motivated by EDS and ACM. The main idea of DED is as follows: we hope to make the peptide move away from the local minima quickly and try to use the most active collective degrees of freedom to do this. EDS tells us that the dynamics of the molecule can be described by some essential collective degrees of freedom, whereas PCA provides a method to obtain these essential degrees. In practice, we use PCA to capture the essential motions from the most recent structures in the trajectories at short intervals (20 fs) during protein folding. Then, instead of coupling with different temperatures as in ACM, we add a weak force on the peptide along the resultant direction of these essential motions to direct the folding of the peptide. The main difference between EDS and DED is the simulation time used to obtain collective motions. In EDS, nanosecond simulations are typically used, whereas in DED only 20 fs are utilized. This is because EDS and DED have different aims. EDS wants to get the collective degrees of freedom of peptide in its native state accurately to use them as acceptance conditions in the subsequent folding or unfolding simulation to guide the molecule moving toward or away from the native state and thus enhance the sampling efficiency. The aim of DED is to use the most active collective degrees of freedom of peptide in the unfolded state to guide the molecule to jump out of local minima or across barriers. So it does not need the information of the collective motions in the native state but the most flexible collective degrees of current conformation at intervals. The intervals should not be too large because the structures in the intervals would vary too much and the calculated collective degrees would not be suitable for current conformation. We have applied DED to the folding simulation of S-peptide and analyzed typical physical characteristics, such as folding path, hydrogen bond formation, and so on. The results show that DED is efficient in exploring conformation space and provides a novel tool to study protein folding.
MATERIALS AND METHODS
Now let's have a brief review on PCA. It works as follows: When we have done a folding simulation of a peptide, we can get a covariance matrix C from the trajectory X(t). The element 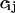 of the matrix C is determined by
of the matrix C is determined by
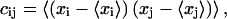 |
(1) |
where 〈 〉 donates the average over all the structures sampled in the trajectory and 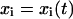 is the ith Cartesian coordinate of the conformation at time t. So the covariance matrix C represents the correlation between atomic motions in Cartesian coordinate space. Then the collective degrees of freedom can be derived from the eigenvectors of the diagonalized matrix C.
is the ith Cartesian coordinate of the conformation at time t. So the covariance matrix C represents the correlation between atomic motions in Cartesian coordinate space. Then the collective degrees of freedom can be derived from the eigenvectors of the diagonalized matrix C.
Since C is symmetric, it can be diagonalized by using an orthogonal transformation matrix T:
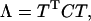 |
(2) |
where Λ is a diagonal matrix and every diagonal element 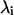 in it is an eigenvalue of the covariance matrix C, and its corresponding eigenvector is the ith column in the matrix T. Each eigenvalue and eigenvector pair represents one collective motion. The eigenvectors corresponding to larger eigenvalues represent more flexible directions in the trajectory. So the eigenvectors with the largest eigenvalues will hold most of the characters of the motions or, in other words, all the complex motions of protein can be reduced to only approximately a few collective motions.
in it is an eigenvalue of the covariance matrix C, and its corresponding eigenvector is the ith column in the matrix T. Each eigenvalue and eigenvector pair represents one collective motion. The eigenvectors corresponding to larger eigenvalues represent more flexible directions in the trajectory. So the eigenvectors with the largest eigenvalues will hold most of the characters of the motions or, in other words, all the complex motions of protein can be reduced to only approximately a few collective motions.
Based on this idea, DED determines the collective motions at short intervals during the simulation. We analyze the trajectory every 20 fs and construct a covariance matrix for all the nonhydrogen atoms immediately. This means that we only consider the collective motions of nonhydrogen atoms. This is because these “heavy atoms” can describe the conformation of the molecule adequately and furthermore can reduce the calculation time. We choose 20 fs because unfolded states are not stable and the conformations of S-peptide change quickly. So we select this short interval to make a reliable evaluation on the collective motions of the current conformation.
Then we pick out the six eigenvectors 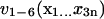 (as collective coordinates) corresponding to the six largest eigenvalues
(as collective coordinates) corresponding to the six largest eigenvalues 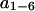 in the covariance matrix and build a new vector
in the covariance matrix and build a new vector 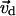 by the linear combination of these eigenvectors with their eigenvalues as the coefficients
by the linear combination of these eigenvectors with their eigenvalues as the coefficients
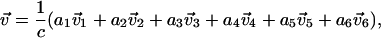 |
(3) |
where c is
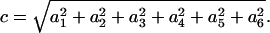 |
(4) |
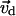 is considered as the principal component of the motions in the local state, and the peptide is directed to move along this direction by adding a weak force:
is considered as the principal component of the motions in the local state, and the peptide is directed to move along this direction by adding a weak force:
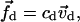 |
(5) |
where 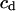 is a coefficient. Here we select only the first six eigenvectors because we found that the sum of the first six eigenvalues is always more than 90% of the sum of the total eigenvalues. So we assume that the first six eigenvectors are enough to describe the peptide motion. Furthermore, after many tests, we find that, when
is a coefficient. Here we select only the first six eigenvectors because we found that the sum of the first six eigenvalues is always more than 90% of the sum of the total eigenvalues. So we assume that the first six eigenvectors are enough to describe the peptide motion. Furthermore, after many tests, we find that, when 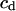 equals 5.0 kcal/mol Å, the force is strong enough to pull the molecule and, at the same time, is weak enough to avoid distorting the molecule. Since the force
equals 5.0 kcal/mol Å, the force is strong enough to pull the molecule and, at the same time, is weak enough to avoid distorting the molecule. Since the force 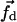 breaks contacts quickly, it can increase the probability of the molecule to jump out of the local minima. Thus the simulation based on DED may overcome the difficulty met by traditional MD.
breaks contacts quickly, it can increase the probability of the molecule to jump out of the local minima. Thus the simulation based on DED may overcome the difficulty met by traditional MD.
It must be pointed out that, to increase the sampling efficiency, the particular choice of the number of eigenvectors used and the linear combination in Eq. 3 are not unique. Our simulation results show that any choice of the number of eigenvectors and the linear combination can give a similar effect, i.e., any steering that breaks and forms contacts quickly can lead the peptide fold correctly and rapidly. However, we suggest using the eigenvectors corresponding to the first largest eigenvalues to investigate the folding pathway of the molecule. This is because the first modes are the most flexible motions and adding forces to them can avoid disturbing the original folding pathway of the molecule too much. If we apply forces to the less flexible direction, we disturb the original motion of the molecule significantly although we still can enhance the sampling efficiency.
The model system we used in this study is an S-peptide, which forms a helix in proteins (Søgaard et al., 1999; Tirado-Rives and Jorgensen, 1991). It is selected from 15 N-terminal amino acids of ribonuclease A and capped with the acetyl and N-methyl groups: KETAAAKFERQHMDS.
In this study, we use a GA/SA model (Qiu et al., 1997; Still et al., 1990) as an implicit solvent model to simulate the aqueous environment. GB/SA is a reduced model from the continuum model, which treats the water as a continuous medium, and there are usually three terms included in the free energy of solvation:
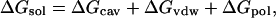 |
(6) |
where 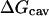 is a solvent-solvent cavity term corresponding to the free energy of creating a cavity of solute in the solvent continuum;
is a solvent-solvent cavity term corresponding to the free energy of creating a cavity of solute in the solvent continuum; 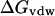 is the free energy term representing the interactions between the solute and solvent; and
is the free energy term representing the interactions between the solute and solvent; and 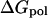 denotes electrostatic interactions between the solute and solvent.
denotes electrostatic interactions between the solute and solvent.
The advantage of this model is that it need not treat solvent molecules explicitly and costs much less time, although some accuracy may be lost. The MD software we used is Tinker (see http://dasher.wustl.edu/tinker/) with Charmm27 force field (MacKerell et al., 1998). All the simulations were done under 298 K and 1 atm.
To test DED, we carried out “native simulations” and “folding simulations” by traditional MD and DED, respectively. The native simulations and folding simulations refer to the simulations with the native and unfolded structures as their initial structures, respectively. The time for all the simulations is 20 ns. We carried out four DED and four traditional MD native simulations and eight DED and four traditional MD folding simulations. We found that the corresponding results of each kind of simulation are similar. So we only present the most typical trajectory in the following analysis.
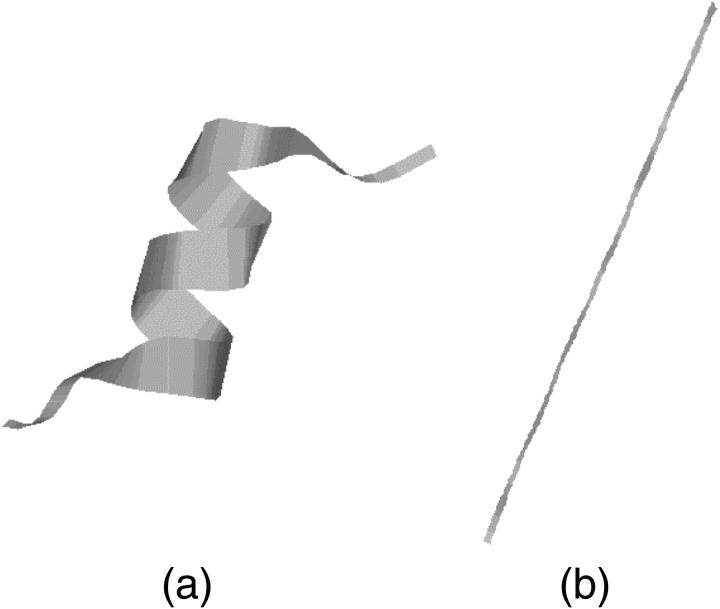
The initial structure of the S-peptide in native simulation is obtained from its crystal structure directly (Fig. 1 a). And for folding simulations, we set its initial structure as a β-strand (Fig. 1 b) to eliminate the correlations between the initial and native structures. Some parameters, such as radius of gyration and hydrogen bonds, are calculated from all the backbone atoms (including two caps). RMSD is calculated from backbone atoms too, but only between residues 3 and 13 to avoid the end effect. This is because the native structure (Fig. 1 a) is cut from the whole protein structure, and so its two ends are connected with other parts of the protein. But in our simulation, the two ends of the S-peptide are free and interact with water molecules directly.
FIGURE 1.
Initial structures for the S-peptide in (a) native simulations and (b) folding simulations.
To investigate whether the DED will introduce distortions or drift in a large system simulation, we did a 0.23 ns simulation for chymotrypsin inhibitor 2 (CI2) starting from the native conformation of CI2. The simulation was also done under NPT ensemble (298 K and 1 atm).
RESULTS AND DISCUSSION
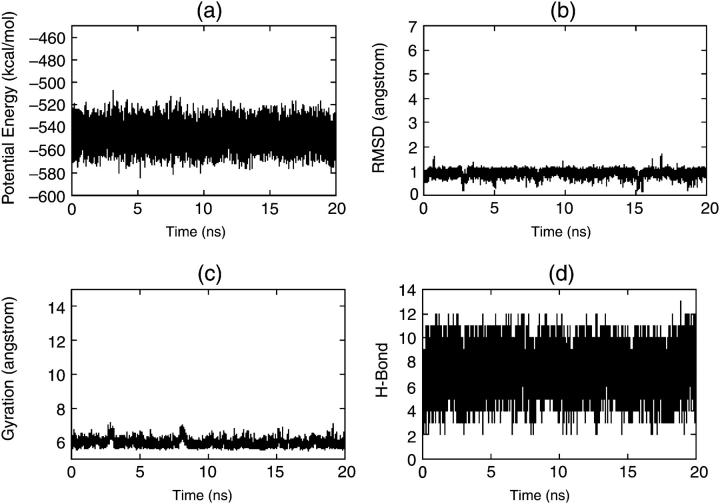
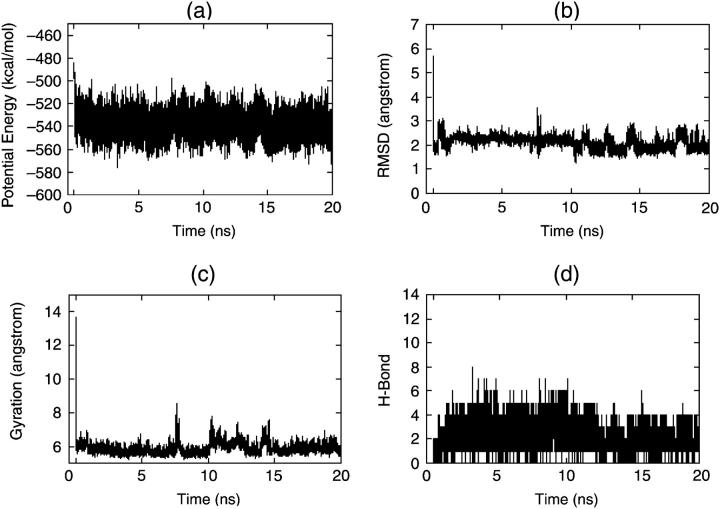
Figs. 2 and 3 show the results of native simulations under traditional MD and DED methods, respectively. From Fig. 2 we can see that when the S-peptide is in its native state, it shows high stability under the traditional MD simulation. The root mean-square difference (RMSD) of its conformations from its native state is ∼1.0 Å all the time (Fig. 2 b), and its radius of gyration and hydrogen bonds (Fig. 2, c and d) also conform to this. But in the DED simulation, we find that the S-peptide is more active. Fig. 3 b shows that the RMSD has some large fluctuations and even exceeds 4.0 Å once in a while, although it maintains ∼1.0 Å on the whole. This is because DED finds the collective motions in every short period (20 fs), and immediately directs the S-peptide to move along its directions in the next period. So during the DED simulation, the S-peptide is always trying to move in the most flexible direction. However, it does not go away from the native state for a long time and comes back to it quickly. It is just one of the advantages of DED to prevent peptides from staying in the local energy minima for a long time.
FIGURE 2.
Four parameters via time for native simulations by traditional MD: (a) potential energy, (b) RMSD, (c) radius of gyration, and (d) H-bond.
FIGURE 3.
Four parameters via time for native simulations by DED: (a) potential energy, (b) RMSD, (c) radius of gyration, and (d) H-bond.
We show in the following that if the S-peptide is in a local minimum but not the global one (the native state), DED will let the S-peptide leave it quickly and go to a lower energy state instead of coming back to it, whereas the traditional MD simulation will spend most of its time in the local minimum. This is why DED has high efficiency in sampling the conformation space. This feature of DED makes it easier to find the native state of the peptide than traditional MD during the folding simulation.
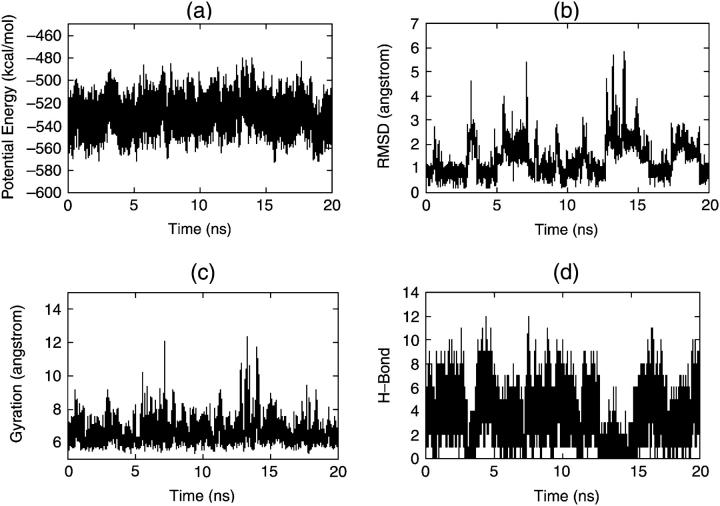
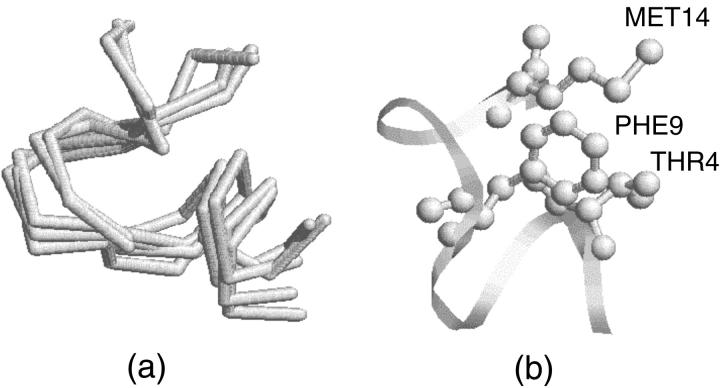
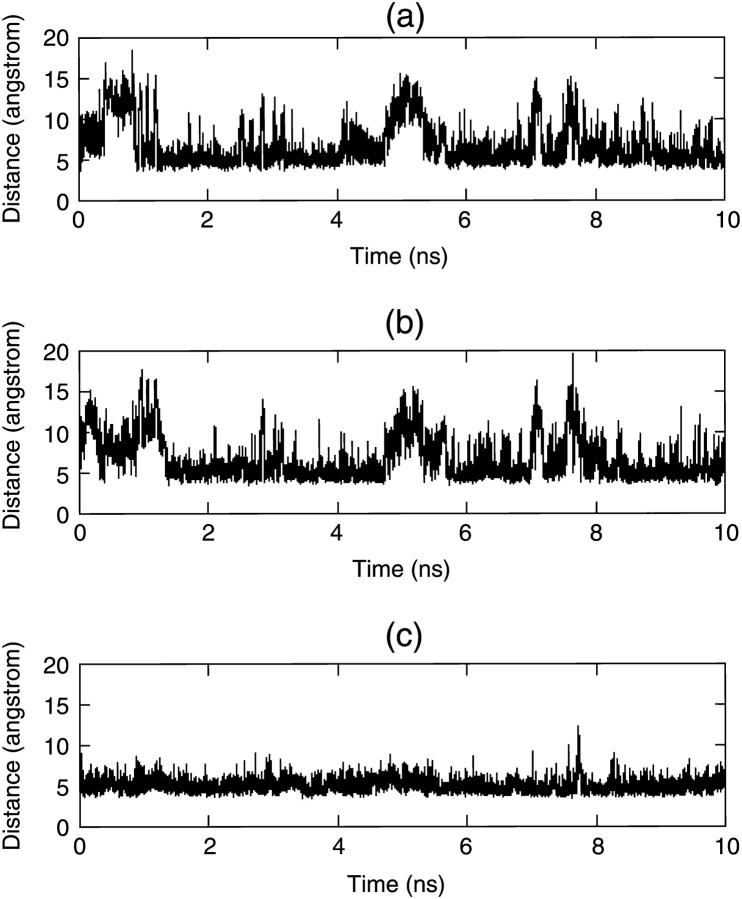
Fig. 4 describes the folding of the S-peptide beginning from a β-strand under traditional MD simulation. The RMSD curve in Fig. 4 b shows that the S-peptide cannot fold to its native state in 20 ns and the RMSD is up to 2.0 Å all along and without large fluctuations, so it may have been trapped into a local stable state. To check our guess, we selected five structures every 2 ns from 2 ns to 10 ns and found that these five structures overlapped with each other on the whole (Fig. 5 a). We found that in most of these structures LYS2-ALA6, GLU3-ALA7, and PHE9-GLN12 form stable backbone hydrogen bonds, and the side chains of THR4, PHE9, and MET14 are almost always packed together tightly (Fig. 5 b). Fig. 6 gives a detailed description for this. It shows that, although the distances between the three pairs (THR4-PHE9, THR4-MET14, and PHE9-MET14) vary with time, they maintain at 5 Å for most of the simulation time and only move away from each other once in a while. So they form a core for most of the time. Obviously, this is a stable conformation cluster different from the native state. When the S-peptide goes into this cluster, it can hardly jump out. This is the notable problem encountered by traditional MD. Of course, if the simulation time is long enough, it may overcome all the local minima eventually, just as the work of Duan and Kollman on a 36-residue peptide found (Duan and Kollman, 1998).
FIGURE 4.
Four parameters via time for folding simulations by traditional MD: (a) potential energy, (b) RMSD, (c) radius of gyration, and (d) H-bond.
FIGURE 5.
(a) Overlapped five structures selected every 2 ns from 2 ns to 10 ns during traditional MD folding simulation. (b) Highlight presentation of THR4, PHE9, and MET14, which packed together tightly. The structure is picked up at 6 ns.
FIGURE 6.
Distances between the centers of the side chains of three residues via time: (a) THR4-PHE9, (b) THR4-MET14, and (c) PHE9-MET14.
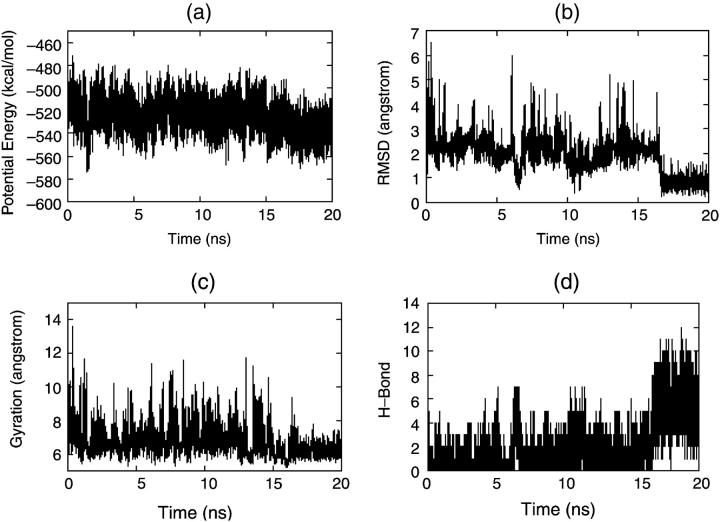
On the other hand, Fig. 7 shows the folding simulation with DED starting from a β-strand. Just like the native simulation, all the parameters undergo large fluctuations. For example, although the RMSD decreases to 2.0 Å at the beginning of the folding (at ∼1 ns), it goes back to 5.0 Å immediately. We can see that all the parameters vary in a large range. This means that the S-peptide under DED can go through many different conformations and will not be trapped in a local minimum for a long time. This is very important for folding simulation because the degrees of freedom of a protein molecule are very large and there are many local minima in the folding path. If it does not have a high mobility, it would be trapped by these minima and cannot get to its native state. In this folding simulation, the S-peptide is active all the time until it reaches the native state at ∼17 ns (the RMSD decreases to 1.0 Å and the number of hydrogen bonds increases to eight), then it keeps stable and all the parameters vary in a small range. This simulation gives the main feature of DED: higher mobility in the folding process but stable enough in the native state. This virtue of DED enables us to get the full folding trajectory for the S-peptide eventually. In the following, we shall use it to analyze the folding process.
FIGURE 7.
Four parameters via time for folding simulations by DED: (a) potential energy, (b) RMSD, (c) radius of gyration, and (d) H-bond.
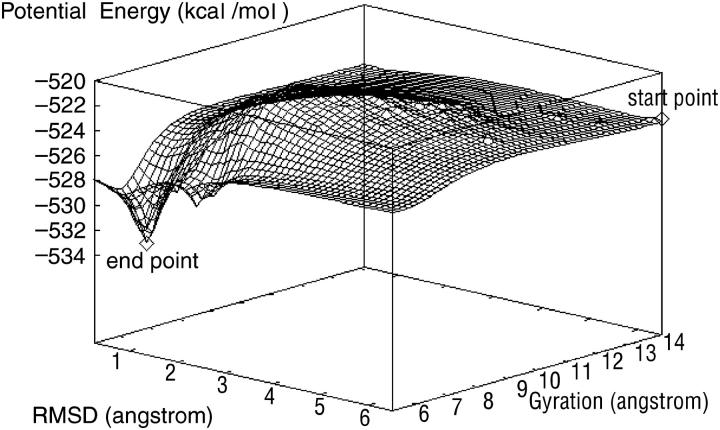
First we sample the conformations in the folding trajectory to give a visual view of the smoothed energy landscape along the parameters RMSD and radius of gyration in Fig. 8. The S-peptide goes from the starting point (an unfolded state) and, through a very complex terrain, reaches the end point (the native state). From Fig. 8, we note that to fold successfully, the S-peptide must overcome many obstacles, such as high energy barriers, low deep valleys, long narrow fosses, and so on. All of these will block the peptide from folding into the native state directly. Traditional MD needs a lot of time to overcome these obstacles. However, DED solves this problem successfully. When DED is being implemented in simulation, the local environment of the peptide is analyzed at intervals. If the S-peptide is held back by some obstacles, it will try to find the most convenient way to get across or turn around them. So it would not be trapped in a local site for a long time. From this aspect, DED increases the sampling efficiency greatly on the energy landscape.
FIGURE 8.
Smoothed energy landscape for the S-peptide constructed from the RMSD and radius of gyration. The “start point” donates the initial position in the simulation. Similarly, the “end point” donates the final position in the simulation. From this picture, we can clearly see that the energy landscape for the S-peptide is full of frustrations, but at the end point, the energy is much lower than other places.
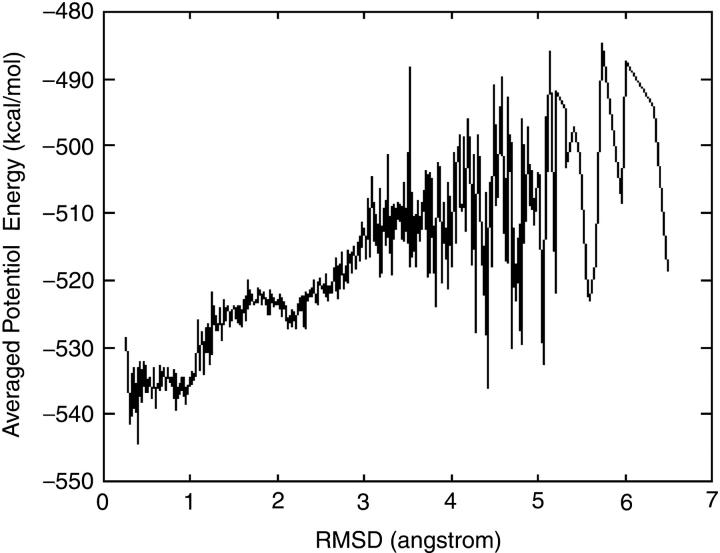
Fig. 9 is a view of the variety of the average potential energy along one reaction coordinate—RMSD. We averaged the potential energies of all conformations according to their RMSD relative to the native state. From the figure, we can see that when the S-peptide's structure is far from the native state (large RMSD), the average potential energy is high and fluctuates with large amplitude. But when it comes closer to the native state, at ∼3.0 Å, the fluctuations reduce suddenly and the average potential energy goes down to a stable point rapidly. This stable point is at 2.1 Å, and the energy curve at this point likes a local minimum: the energy is higher on both sides. When the RMSD gets close to 1.0 Å, the S-peptide reaches a global minimum. This is a basin-like shape. The energies of the conformations here are much lower than other areas. So whenever the S-peptide folds into this “basin”, it would hardly jump out. This provides some fundamental knowledge on the native state. Another interesting feature in this figure is that some unfolded states (large RMSD) have very low potential energy too, which is close to that of the native state. Because the generalized Born/surface area model has considered the contribution of water, the potential energy can be approximately viewed as the free energy. The fact that the unfolded state and the native state have similar free energy coincides with the phenomenon of the enthalpy-entropy compensation, which has been observed in many experimental and theoretical studies (Creamer and Rose, 1992; Lee et al., 1994; Makhatadze et al., 1995; Pickett and Sternberg, 1993). In detail, the phenomenon shows that in many folding or unfolding processes the change in enthalpy is partially or almost compensated by a corresponding change in entropy. So the variance of free energy is small and sometimes can be neglected.
FIGURE 9.
Average potential energies for different RMSDs in the DED folding simulation. It shows that the potential energies for the structures far away from the native state fluctuate very much, and some of them are even close to that of the native state.
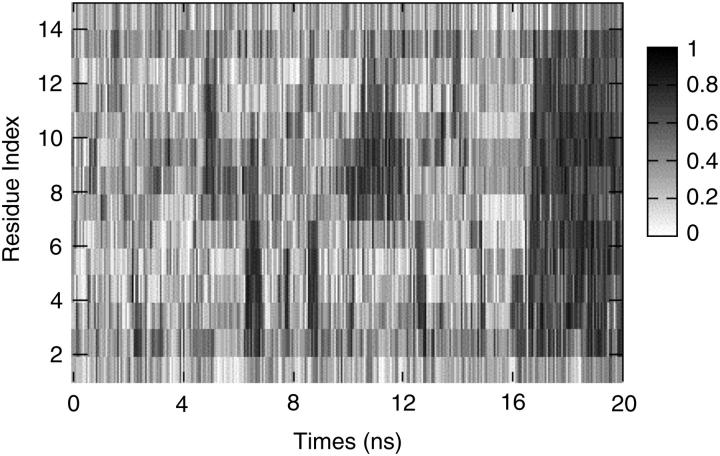
Fig. 10 shows the formation of the helix in S-peptide. All the residues are represented by gray color. When the structure of residue is more similar to the helix (i.e., φ is −58, ψ is −47), its corresponding color will be deeper. From this picture we find that helical structure is often formed in one-half of the S-peptide (residue 2–7 or residue 8–13) during the folding process. Until 16 ns, the helical structure in one-half extends to the other successfully, and then the total structure becomes stable after that time.
FIGURE 10.
The residue's conformations via time. The darker the color is, the closer it is to the standard helical conformation.
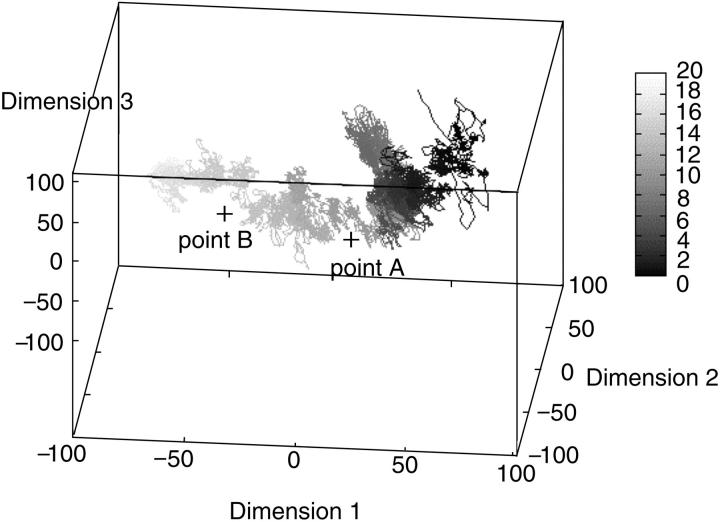
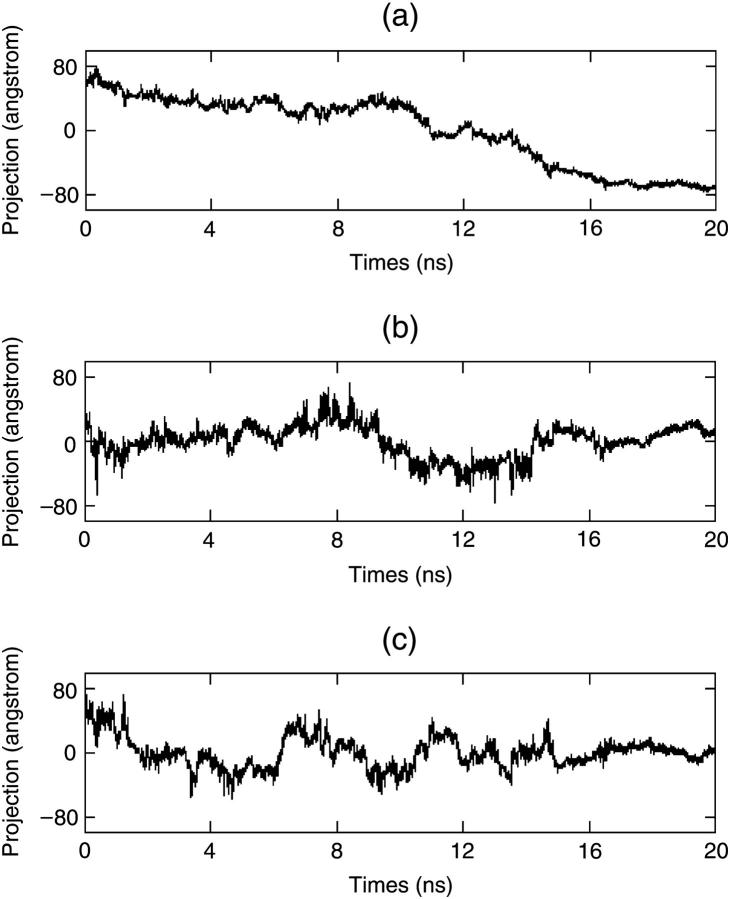
Now we analyze the whole trajectory with PCA. PCA provides a robust tool to view the protein folding process. As usual, we calculate the covariance matrix of all the conformations in the trajectory and get the principal components. We only select the three principal components with the largest eigenvalues. Then all the conformations are projected onto them and connected with lines (see Fig. 11). The S-peptide folds from one terminus of the line (black) to the other (white). In this figure we find that during the folding of the S-peptide, most of its conformations congregate together and form only a few clusters. The time used to move from one cluster to another is very short. Fig. 12 gives the curves of these three principal components along time respectively. It shows that only the first principal component (i.e., the most flexible direction during the S-peptide folding) varies broadly. It has not only some features of the three dimension PCA curve (Fig. 11), but also those of the RMSD curve (Fig. 7 b). In Fig. 12 a, the first principal component has three flat areas, which correspond to the three conformation clusters in Fig. 11. It decreases quickly at 10 ns and 13.5 ns, which correspond to point A and point B in Fig. 11, respectively. When time goes up to 16.6 ns, the first principal component reaches a stable state, which can be validated in the RMSD curve too (Fig. 7 b). We find that all this information can not be derived from the other two principal components. Both of them fluctuate around zero. This implies that the first principal component plays a much more important role in the simulation.
FIGURE 11.
PCA on the DED folding simulation. From this we can see that all the conformations in the trajectory aggregate to a few clusters. The time used to transfer between the clusters is very short.
FIGURE 12.
Projections of all the conformations on the first three principal components via time on the first (a), second (b), and third (c) principal components. It is noted that only the first principal component varies greatly and the other two principal components only fluctuate randomly around zero.
As mentioned in the introduction, Daidone et al. (2003) recently obtained a full folding path for cytochrome c successfully with EDS. In their work, they first did a 2.66 ns simulation of the native state at 300 K to obtain collective motions of the system. Then they sorted the eigenvectors according to the eigenvalues and divided them into three subsets. The first one-third represented the large concerted motions of the system and the last one-third the collective quasi-constraint (or near constraint) vibrations. They found that the main mechanical information of the folding process was associated with the last one-third of the eigenvectors. This seems contradictory to our results, because we use the first few eigenvectors to direct peptide folding. In fact, this is due to the different aims to apply the eigenvectors. They use the last one-third eigenvectors (near constraint) in the native simulation to lead protein to fold into the native state and therefore they use the most inactive collective degrees of freedom, which characterizes the stable native structure, whereas we use the first six eigenvectors in the unfolded state to make protein jump out of local minima or across barriers and so we use the most active ones.
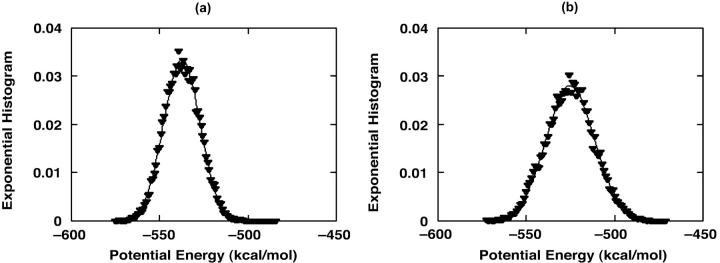
Finally, it is noted that DED can be considered as a kind of biased sampling method. Fig. 13 shows that the samplings in energy space in both traditional MD and DED methods have the similar Gaussian distributions. The exponential histogram is calculated by using the formula
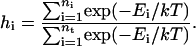 |
(7) |
Here 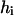 is the exponential histogram between
is the exponential histogram between 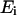 and
and 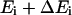 ,
, 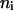 is the number of conformations in this energy gap, and
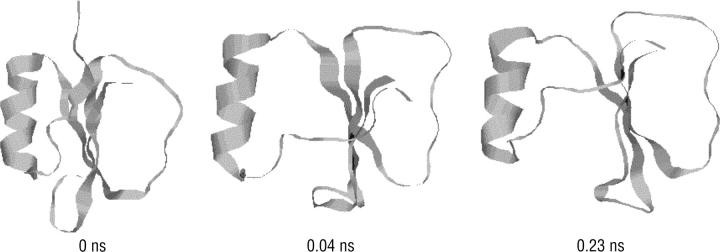
is the number of conformations in this energy gap, and 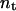 is the total number of conformations. Ei is the total energy of the system, including the free energy term due to the implicit solvent. The curves are those of the fitted Gaussian functions. The main difference is that the distribution for DED is wider than that for traditional MD, i.e., the sampling space of the former is larger than the later. As mentioned above, the force (5.0 kcal/mol Å) is strong enough to pull the molecule but, at the same time, is too weak to distort the molecule. Furthermore, the steering direction changes rapidly in a very short time. So DED is not as the standard steered molecular dynamics and will not introduce significant distortions or drift in the steering direction. This can be clearly seen from the DED unfolding simulation of CI2 (Fig. 14). The motions of the structure are similar to those of high temperature unfolding simulation (Day et al., 2002). In the work of Day et al., an unfolding simulation of CI2 is performed. At the first stage of the simulation (0–0.26 ns), where most of structures are near the native conformation, the motion of CI2 is mainly present at its loop, whereas in the two relatively rigid groups, one consists of three β-sheets and the other consists of one helix, is almost maintained. It is noted that the behavior of CI2 seems different from that of the S-peptide, which fluctuates around the native state as shown in Fig. 3 b. This is due to the short simulation time (only 0.23 ns), which strongly restricts the sampling in the conformation space of CI2. The whole conformation space for CI2 is much larger than S-peptide. So even though the same simulation time as for S-peptide is used for CI2, the sampling is still not sufficient. Here, the short time simulation of CI2 is only used to show that the DED will not introduce significant distortions or drift in the steering direction as the standard steered molecular dynamics.
is the total number of conformations. Ei is the total energy of the system, including the free energy term due to the implicit solvent. The curves are those of the fitted Gaussian functions. The main difference is that the distribution for DED is wider than that for traditional MD, i.e., the sampling space of the former is larger than the later. As mentioned above, the force (5.0 kcal/mol Å) is strong enough to pull the molecule but, at the same time, is too weak to distort the molecule. Furthermore, the steering direction changes rapidly in a very short time. So DED is not as the standard steered molecular dynamics and will not introduce significant distortions or drift in the steering direction. This can be clearly seen from the DED unfolding simulation of CI2 (Fig. 14). The motions of the structure are similar to those of high temperature unfolding simulation (Day et al., 2002). In the work of Day et al., an unfolding simulation of CI2 is performed. At the first stage of the simulation (0–0.26 ns), where most of structures are near the native conformation, the motion of CI2 is mainly present at its loop, whereas in the two relatively rigid groups, one consists of three β-sheets and the other consists of one helix, is almost maintained. It is noted that the behavior of CI2 seems different from that of the S-peptide, which fluctuates around the native state as shown in Fig. 3 b. This is due to the short simulation time (only 0.23 ns), which strongly restricts the sampling in the conformation space of CI2. The whole conformation space for CI2 is much larger than S-peptide. So even though the same simulation time as for S-peptide is used for CI2, the sampling is still not sufficient. Here, the short time simulation of CI2 is only used to show that the DED will not introduce significant distortions or drift in the steering direction as the standard steered molecular dynamics.
FIGURE 13.
The sampling distributions in energy space for traditional MD (a) and DED (b) during the folding simulation, respectively. The data are fitted by Gaussian functions (real line).
FIGURE 14.
A 0.23 ns unfolding simulation for CI2 starting from its native state.
CONCLUSIONS
In this article, we present a variation of EDS and provide a new method for molecular simulation, i.e., a DED analysis. It analyzes the principal components during protein folding at short intervals and builds the most flexible direction to adjust peptide motion. By applying DED in the folding simulation of an S-peptide, it is found that DED is more efficient than traditional MD. From the energy landscape we validated that the peptide folding goes though many local minima and energy barriers and these increase the simulation time of traditional MD. But DED can overcome these quickly. DED can find the most convenient way to get across or to turn around the obstacles and so can lead S-peptide to fold into its native state rapidly.
The DED simulation results of the S-peptide are also in agreement with the current viewpoint on protein folding. First, the energies of most unfolded structures are very high, but there are still a few structures having much lower energy close to that of the native state. Second, short peptides do not move smoothly during the folding process. The conformations in the trajectory aggregate to a few clusters or, in other words, intermediates. These results in turn validate the practicability of DED simulation. DED may provide an alternative approach to simulate the folding of peptides and proteins.
Acknowledgments
This work was supported by the National Natural Science Foundation of China under grant No. 90103031 and the Foundation of the Ministry of Education.
References
- Amadei, A., A. B. M. Linssen, and H. J. C. Berendsen. 1993. Essential dynamics of proteins. Proteins Struct. Funct. Genet. 17:412–425. [DOI] [PubMed] [Google Scholar]
- Amadei, A., A. B. M. Linssen, B. L. de Groot, D. M. F. van Aalten, and H. J. C. Berendsen. 1996. An efficient method for sampling the essential subspace of proteins. J. Biomol. Struct. Dyn. 13:615–625. [DOI] [PubMed] [Google Scholar]
- Atilgan, A. R., S. R. Durrell, R. L. Jernigan, M. C. Demirel, O. Keskin, and I. Bahar. 2001. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 80:505–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balsera, M. A., W. Wriggers, Y. Oono, and K. Schulten. 1996. Principal component analysis and long time protein dynamics. J. Phys. Chem. 100:2567–2572. [Google Scholar]
- Boczko, E. M., and C. L. Brooks. 1995. First principle calculation of the folding free energy of a three-helix bundle protein. Science. 269:393–396. [DOI] [PubMed] [Google Scholar]
- Brooks, B. R., and M. Karplus. 1983. Harmonic dynamics of proteins: normal modes and fluctuations in bovine pancreatic trypsin inhibitor. Proc. Natl. Acad. Sci. USA. 80:6571–6575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryngelson, J. D., J. N. Onuchic, N. D. Socci, and P. G. Wolynes. 1995. Funnels, pathways, and the energy landscape of protein folding—a synthesis. Proteins Struct. Funct. Genet. 21:167–195. [DOI] [PubMed] [Google Scholar]
- Creamer, T. P., and G. D. Rose. 1992. Side chain entropy opposes alpha-helix formation but rationalizes experimentally-determined helix-forming propensities. Proc. Natl. Acad. Sci. USA. 89:5937–5941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cregut, D., G. Drin, J. P. Liautard, and L. Chiche. 1998. Hinge-bending motions in annexins: molecular dynamics and essential dynamics of apo-annexin V and of calcium bound annexin V and I. Protein Eng. 11:891–900. [DOI] [PubMed] [Google Scholar]
- Daidone, I., A. Amadei, D. Roccatano, and A. D. Nola. 2003. Molecular dynamics simulation of protein folding by essential dynamics sampling: folding landscape of horse heart cytochrome c. Biophys. J. 85:2865–2871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day, R., B. J. Bennion, S. Ham, and V. Daggett. 2002. Increasing temperature accelerates protein unfolding without changing the pathway of unfolding. J. Mol. Biol. 322:189–203. [DOI] [PubMed] [Google Scholar]
- De Groot, B. L., X. Daura, A. E. Mark, and H. Grubmuller. 2001. Essential dynamics of reversible peptide folding: memory-free conformational dynamics governed by internal hydrogen bonds. J. Mol. Biol. 309:299–313. [DOI] [PubMed] [Google Scholar]
- Duan, Y., and P. A. Kollman. 1998. Pathways to a protein folding intermediate observed in a 1-microsecond simulation in aqueous solution. Science. 282:740–744. [DOI] [PubMed] [Google Scholar]
- Elmaci, N., and R. S. Berry. 1999. Principal coordinate analysis on a protein model. J. Chem. Phys. 110:10606–10622. [Google Scholar]
- Galzitskaya, O. V., J. Higo, M. Kuroda, and H. Nakamura. 2000. β-hairpin folds by molecular dynamics simulations. Chem. Phys. Lett. 326:421–429. [Google Scholar]
- Garcia, A. E. 1992. Large-amplitude nonlinear motions in proteins. Phys. Rev. Lett. 68:2696–2699. [DOI] [PubMed] [Google Scholar]
- Go, N., T. Noguti, and T. Nisikawa. 1983. Dynamics of a small globular protein in terms of low-frequency vibrational modes. Proc. Natl. Acad. Sci. USA. 80:3696–3700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gsponer, J., and A. Caflisch. 2002. Molecular dynamics simulations of protein folding from the transition state. Proc. Natl. Acad. Sci. USA. 99:6719–6724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutin, A. M., V. I. Abkevich, and E. I. Shakhnovich. 1995. Evolution-like selection of fast-folding model proteins. Proc. Natl. Acad. Sci. USA. 92:1282–1286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayward, S., A. Kitao, and N. Go. 1995. Harmonicity and anharmonicity in protein dynamics normal mode analysis and principal component analysis. Proteins. 23:177–186. [DOI] [PubMed] [Google Scholar]
- Irback, A., F. Sjunnesson, and S. Wallin. 2000. Three-helix-bundle protein in a Ramachandran model. Proc. Natl. Acad. Sci. USA. 97:13614–13618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaenicke, R. 2000. Stability and stabilization of globular proteins in solution. J. Biotechnol. 79:193–203. [DOI] [PubMed] [Google Scholar]
- Kaya, H., and H. S. Chan. 2000. Polymer principles of protein calorimetric two-state cooperativity. Proteins Struct. Funct. Genet. 40:637–661. [DOI] [PubMed] [Google Scholar]
- Kitao, A., and N. Go. 1999. Investigating protein dynamics in collective coordinate space. Curr. Opin. Struct. Biol. 9:164–169. [DOI] [PubMed] [Google Scholar]
- Knapp-Mohammady, M., K. J. Jalkanen, F. Nardi, R. C. Wade, and S. Suhai. 1999. L-alanyl-L-alanine in the zwitterionic state: structures determined in the presence of explicit water molecules and with continuum models using density functional theory. Chem. Phys. 240:63–77. [Google Scholar]
- Lee, K. H., D. Xie, E. Freire, and L. M. Amzel. 1994. Estimation of changes in side chain configurational entropy in binding and folding: general methods and application to helix formation. Proteins. 20:68–84. [DOI] [PubMed] [Google Scholar]
- Leopold, P., M. Montal, and J. Onuchic. 1992. Protein folding funnels: a kinetic approach to the sequence-structure relationship. Proc. Natl. Acad. Sci. USA. 89:8721–8725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt, M., C. Sander, and P. S. Stern. 1983. Normal-mode dynamics of a protein: bovine pancreatic trypsin inhibitor. Int. J. Quant. Chem: Quant. Biol. Symp. 10:181–199. [Google Scholar]
- Luque, I., O. L. Mayorga, and E. Freire. 1996. Structure-based thermodynamic scale of alpha-helix propensities in amino acids. Biochemistry. 35:13681–13688. [DOI] [PubMed] [Google Scholar]
- MacKerell Jr., A. D., D. Bashford, M. Bellott, R. L. Dunbrack Jr., J. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, I. W. E. Reiher, B. Roux, M. Schlenkrich, J. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-hydrogen empirical potential for molecular modeling and dynamics studies of proteins using the CHARMM22 force field. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- Majeux, N., M. Scarsi, and A. Caflisch. 2001. Efficient electrostatic salvation model for protein-fragment docking. Proteins Struct. Funct. Genet. 42:256–268. [DOI] [PubMed] [Google Scholar]
- Makhatadze, G. I., G. M. Clore, and A. M. Gronenborn. 1995. Solvent isotope effect and protein stability. Nat. Struct. Biol. 2:852–855. [DOI] [PubMed] [Google Scholar]
- Mirny, L. A., and E. I. Shakhnovich. 2001. Protein folding theory: from lattice to all-atom models. Annu. Rev. Biophys. Biomol. Struct. 30:361–396. [DOI] [PubMed] [Google Scholar]
- Ota, N., and D. A. Agard. 2001. Enzyme specificity under dynamic control II: principal component analysis of α-lytic protease using global and local solvent boundary conditions. Protein Sci. 10:1403–1414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pande, V. S., and D. S. Rokhsar. 1999. Molecular dynamics simulations of unfolding and refolding of a β-hairpin fragment of protein G. Proc. Natl. Acad. Sci. USA. 96:9062–9067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickett, S. D., and M. J. E. Sternberg. 1993. Empirical scale of side-chain conformational entropy in protein folding. J. Mol. Biol. 231:825–839. [DOI] [PubMed] [Google Scholar]
- Qiu, D., P. S. Shenkin, F. P. Hollinger, and W. C. Still. 1997. The GB/SA continuum model for solvation. A fast analytical method for the calculation of approximate born radii. J. Phys. Chem. A. 101:3005–3014. [Google Scholar]
- Shakhnovich, E., and A. Gutin. 1993. Engineering of stable and fast-folding sequences of model proteins. Proc. Natl. Acad. Sci. USA. 90:7195–7199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Søgaard, T. M. M., C. G. Jakobsen, and J. Justesen. 1999. A sensitive assay of translational fidelity (readthrough and termination) in eukaryotic cells. Biochemistry (Mosc). 64:1408–1417. [PubMed] [Google Scholar]
- Still, V. C., A. Tempezvk, R. C. Hawley, and T. Hendrickson. 1990. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 112:6127–6129. [Google Scholar]
- Takada, S., Z. Luthey-Schulten, and P. G. Wolynes. 1999. Folding dynamics with nonadditive forces: a simulation study of a designed helical protein and a random heteropolymer. J. Chem. Phys. 110:11616–11629. [Google Scholar]
- Teeter, M. M., and D. A. Case. 1999. Harmonic and quasiharmonic descriptions of crambin. J. Phys. Chem. 94:8091–8097. [Google Scholar]
- Tirado-Rives, J., and W. L. Jorgensen. 1991. Molecular dynamics simulations of the unfolding of an α-helical analogue of ribonuclease A S-peptide in water. Biochemistry. 30:3864–3871. [DOI] [PubMed] [Google Scholar]
- Van Aalten, D. M. F., A. Amadei, A. B. M. Linssen, V. G. H. Eijsink, and G. Vriend. 1995. The essential dynamics of thermolysin-conformation of the hinge-bending motion and comparison of simulations in vacuum and water. Proteins Struct. Funct. Genet. 22:45–54. [DOI] [PubMed] [Google Scholar]
- Van Aalten, D. M. F., E. Grotewold, and L. Joshua-Tor. 1998. Essential dynamics from NMR clusters: dynamic properties of the Myb DNA-binding domain and a hinge-bending enhancing variant. Methods. 14:318–328. [DOI] [PubMed] [Google Scholar]
- Zagrovic, B., E. J. Sorin, and V. S. Pande. 2001. β-hairpin folding simulations in atomistic detail using an implicit solvent model. J. Mol. Biol. 313:151–169. [DOI] [PubMed] [Google Scholar]
- Zhang, L., E. Gallicchio, R. Friesner, and R. M. Levy. 2001. Solvent models for protein-ligand binding: comparison of implicit solvent poisson and surface generalized born models with explicit solvent simulations. J. Comput. Chem. 22:591–607. [Google Scholar]
- Zhang, Z., Y. Shi, and H. Liu. 2003. Molecular dynamics simulations of peptides and proteins with amplified collective motions. Biophys. J. 84:3583–3593. [DOI] [PMC free article] [PubMed] [Google Scholar]