A Consistent Experimental and Modeling Approach to Light-Scattering Studies of Protein-Protein Interactions in Solution

Abstract

The osmotic second virial coefficient, B₂, obtained by light scattering from protein solutions has two principal components: the Donnan contribution and a contribution due to protein-protein interactions in the limit of infinite dilution. The Donnan contribution accounts for electroneutrality in a multicomponent solution of (poly)electrolytes. The importance of distinguishing this ideal contribution to B₂ is emphasized, thereby allowing us to model the interaction part of B₂ by molecular computations. The model for protein-protein interactions that we use here extends earlier work (Neal et al., 1998) by accounting for long-range electrostatic interactions and the specific hydration of the protein by strongly associated water molecules. Our model predictions are compared with measurements of B₂ for lysozyme at 25°C over pH from 5.0 to 9.0, and 7–60 mM ionic strength. We find that B₂ is positive at all solution conditions and decreases with increasing ionic strength, as expected, whereas the interaction part of B₂ is negative at all conditions and becomes progressively less negative with increasing ionic strength. Although long-range electrostatic interactions dominate this contribution, particularly at low ionic strength, short-range electrostatic/dispersion interactions with specific hydration are essential for an accurate description of B₂ derived from experiment.

INTRODUCTION

Recent interest in the use of light scattering to characterize protein solution thermodynamics has been generated by studies showing that the osmotic second virial coefficient of protein solutions, the quantity extracted from light-scattering measurements, can be correlated with the protein crystallization tendency of those solutions (George and Wilson, 1994). This observation is founded on the earliest description of light scattering, where the scattering properties of a macromolecular solute in solution are related to the osmotic pressure of the solution, written as

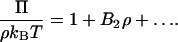(1)

Here Π is the osmotic pressure, ρ is the solute density, or equivalently the solute concentration, and B₂ is the osmotic second virial coefficient, which characterizes pairwise interactions between solute molecules in dilute solution. A positive B₂ corresponds to repulsive intermolecular interactions, and a negative B₂ to attractive interactions. Thus, the slightly negative values of B₂ that are found to favor protein crystallization, it is argued, must reflect weakly attractive protein-protein interactions in solution (George and Wilson, 1994). This picture is, however, more complicated for solutions of (poly)electrolytes, which by definition consist of more than two components. Indeed, a nonzero B₂ can be obtained even for an ideal solution of (poly)electrolytes in which there are no intermolecular interactions. Appreciating this point calls for careful consideration of B₂ as a measure protein-protein interactions alone. It is this point and its consequences that are discussed in this article from the perspective of coupling light-scattering measurements with molecular computations of protein-protein interactions to predict B₂ as a function of solution conditions. Our motivation is to develop a consistent experimental and modeling approach to light-scattering studies of protein solutions that in turn can be used to devise rational strategies for inducing protein crystallization.

The earliest studies on light scattering from simple solutions were largely the pioneering efforts by Einstein, Smoluchowski, Zernicke, and Debye (Kerker, 1969; Stacey, 1956). Following their work, Brinkman and Hermans (1949), Kirkwood and Goldberg (1950), and Stockmayer (1950) presented statistical mechanical analyses of light scattering from multicomponent solutions that naturally contained the earlier two-component results as a special case. Shortly thereafter, Edsall et al. (1950), Kirkwood and Shumaker (1952), and Timasheff et al. (1955, 1956) applied this analysis of multicomponent solutions to light-scattering studies of protein solutions. Their work, which unfortunately has been overlooked in some studies over the last decade or so (including by two of the coauthors on this article), showed the impressive insights one could obtain from light-scattering studies of protein solutions, if interpreted properly.

We pursue this point here, starting with the analysis of Stockmayer (1950), and reemphasizing key points already appreciated by Edsall and co-workers (1950). We also identify an interaction part of B₂ as the target for molecular computations, which leads to a reconsideration of our earlier model of protein-protein interactions (Asthagiri et al., 1999; Neal et al., 1998). In particular, we find it necessary to account for the specific hydration of protein molecules and long-range electrostatic interactions in the current model to describe the solution behavior observed in our light-scattering studies.

This article is organized as follows. First, we present the theory of light scattering from multicomponent solutions derived by Stockmayer (1950). No new results are obtained, but aspects of that analysis are emphasized in the context of our current work. We then apply the theory to a prototypical two-component solution, emphasizing that osmotic quantities are recovered only in the limit of vanishingly small solute concentrations for this simple solution. Experimentally probing this regime of infinite dilution reveals aspects of the light-scattering measurements that are masked when protein concentrations are not sufficiently dilute. Next, we consider a solution comprising a protein component, added salt component, and the solvent, where a component is defined to be electroneutral, although each electroneutral component consists of charged constituents. This notion of components versus constituents is identical to that adopted by Scatchard (1946) and later specialized to light-scattering studies of protein solutions (Edsall et al., 1950). However, our definition of components is more direct than that of Edsall et al. (1950) (see also Prins and Hermans, 1954). Our analysis of this three-component solution leads directly to consideration of the Donnan contribution, and after accounting for this contribution, the identification of the interaction part of B₂ as our target for molecular computations. Finally, we compare calculations of B₂ based on our new model for protein-protein interactions to those extracted from light-scattering measurements.

THEORY

Light scattering from protein solutions

Stockmayer's (1950) expression for the turbidity of a solution due solely to composition fluctuations is given by

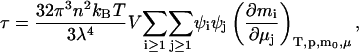(2)

where m_i is the number of molecules and μ_i is the chemical potential of component i, n is the refractive index of the solution, λ is the wavelength of incident light, k_BT is the thermal energy, V is the volume, and ψ_i = ∂n/∂m_i is the refractive index increment upon adding component i at constant temperature and pressure. The subscripts, μ and m₀, imply that this partial derivative is also evaluated at constant chemical potentials of all components, except that for the solvent, the number of molecules of which, m₀, is fixed. The summations exclude the pure solvent (index 0). Note the coupling between fluctuations in the chemical potential of component j with the amount of component i. This quantity is at the heart of the multicomponent approach, and connects directly to Kirkwood-Buff solution theory (Kirkwood and Buff, 1951), where again similar quantities are encountered.

It is convenient to use concentration units (number density or mol density) and βμ instead of μ, where β = 1/k_BT. With these changes,

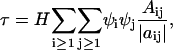(3)

where the ψ_i are now derivatives of the refractive index with respect to concentration variables, ρ_i = m_i/N_AV (mol/volume) with N_A Avogadro's number, H is an optical constant equal to 32π³n²/3λ⁴N_A, |a_ij| is the determinant of the coefficients of a_ij given by

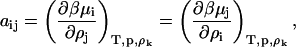(4)

and A_ij is the cofactor of the element a_ij.

For a two-component, single-phase system, the chemical potential of the solute, component 2, can be expressed as

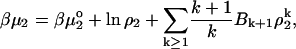(5)

where B_n is the n^th virial coefficient. Retaining only the second virial coefficient, we have at dilute solute concentrations,

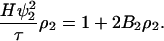(6)

This expression is the one commonly used in light-scattering studies of protein solutions. Because this system has three degrees of freedom, there is only one free variable with temperature and pressure fixed. As is naively supposed, if μ₀ is indeed fixed as in “osmotic” conditions, the system is completely defined. Alternatively, if we change the composition of the solute at constant T, p, then clearly μ₀ cannot be held constant. The osmotic conditions are obtainable only for vanishingly small changes in the amount of the solute. Under such conditions, one does indeed recover osmotic conditions, and B₂ can be legitimately identified as the osmotic virial coefficient.

Consider a three-component system consisting of the solvent (water, component 0), salt (component 1), and a protein (component 2). For simplicity we take the salt to be NaCl, and the protein, P, to carry a positive charge z. Therefore, we define the protein component as PCl_z. All components are electrically neutral. We assume the concentrations of free HO⁻ and H⁺ ions in solution to be negligible in comparison (cf. Edsall et al., 1950). The concentration of NaCl is ρ₁ and that of the protein is ρ₂. Chemical potentials of the salt and the protein components, respectively, take the form:

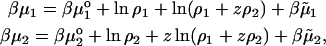(7)

where 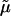is the excess chemical potential. Defining α₁ = ln ρ₁ + ln(ρ₁ + zρ₂) for the ideal contribution and 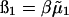for the excess contribution, and similarly for component 2, we obtain

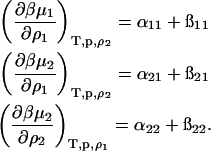The expression for the turbidity, Eq. 3, can be simplified using the physically reasonable assumption ψ₂ ≫ ψ₁ (Edsall et al., 1950). Thus,

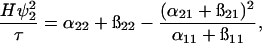(8)

which for an ideal solution becomes

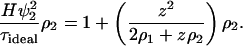(9)

Comparing Eq. 9 with Eq. 6, we find that even for an ideal solution consisting of a charged protein and salt in water, B₂ is not zero. The Donnan term z²/(2ρ₁ + ρ₂) arises solely due to electroneutrality and conveys no additional molecular information.

Typically protein concentrations are on the order of 5 mg/ml and salt concentrations are roughly 0.1 M. Assuming 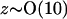and a protein molecular weight of 15 kDa, we have 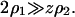The quantities ß₂₁ and ß₁₁ represent the nonideal contributions arising from the preferential partitioning of the salt ions relative to the protein. These effects, including specific binding of ions to the protein, become important for high protein charge and/or high ionic strengths (Casassa and Eisenberg, 1964). We provisionally neglect these contributions and write

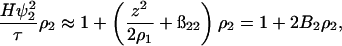(10)

where the coefficient B₂ is identified as the osmotic second virial coefficient. Note that this quantity once again contains ideal contributions that must be accounted for to probe the protein-protein interactions of primary interest that are embodied in the quantity ß₂₂.

Protein-protein interactions

For infinitely dilute concentrations of protein in the salt-water solution we have (Kirkwood and Shumaker, 1952; Timasheff et al., 1955, 1956)

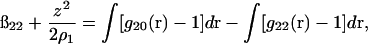(11)

where g₂₀ is the protein-solvent pair correlation function and g₂₂ is the protein-protein pair correlation function. This expression is derived from Kirkwood-Buff solution theory (Kirkwood and Buff, 1951) for a two-component system. Our application here to a three-component system is an approximation, but likely a very good one for ß₂₂ in the limit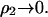

In practice, the first integral on the right-hand side of Eq. 11 makes a small contribution, and in adopting the McMillan and Mayer approach (1945), as is the usual case, one simply ignores it. Recognizing, however, that the dominant contribution to this integral is the protein excluded volume, we take

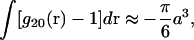where a is the nominal diameter of the protein.

To evaluate the second integral, we focus on w₂₂(r), the potential of mean force (PMF) between protein molecules, where g₂₂(r) = exp[−βw₂₂(r)]. For large separations, we adopt a Debye-Hückel model (Hill, 1986a) of protein-protein interactions, and consider a distinguished protein molecule in solution while treating other protein molecules and added salt as a statistical distribution of counterions and coions,

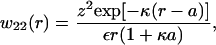(12)

where ε is the solution dielectric constant and κ is given by the usual expression,

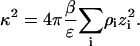(13)

In the limit 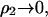κ² is proportional to ρ₁, the ionic strength of the solution due to the added salt. A further simplification is to write

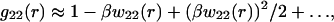and retain only the dominant terms. Taking as our operational definition of large protein-protein separations, protein surfaces separated by more than a Debye length, or r > (a + κ⁻¹), we obtain

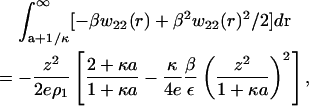(14)

where e is the base of the natural logarithm. The first term on the right-hand side of this expression is the Donnan contribution multiplied by (2 + κa)/e(1 + κa). Indeed, if the integration were carried out from 0 to ∞, the precise Donnan contribution in Eq. 10 would be recovered. This result is simply a consequence of the fact that Eq. 12 is consistent with electroneutrality for the added salt solution. Moreover, the contribution to the PMF given by Eq. 14 decreases in magnitude with increasing ionic strength, as expected, due to the factor of 1/ρ₁ (inverse ionic strength) multiplying the terms in brackets on the right-hand side of this equation.

The long-range contribution to ß₂₂ is obtained by substituting Eq. 14 into Eq. 11. Thus,

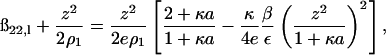(15)

and the additional subscript l emphasizes that this contribution corresponds to just the long-range part of ß₂₂. An identical expression has been derived by Hill (1986b) for ionic solutes in solution with short-range interactions taken into account by treating them as hard-sphere, excluded volume interactions. The left-hand side of Eq. 15 is twice the osmotic second virial coefficient (Eq. 10) where the second term, the Donnan contribution, makes a positive contribution to 2B₂. Subtracting this ideal contribution from both sides of the equation leads to the observation that ß_22,l is negative. The physical interpretation of

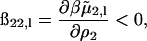is that adding protein in the limit 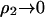increases the ionic strength of the solution, which screens these long-range electrostatic interactions.

For protein-protein interactions at separations between a and a + κ⁻¹, Eq. 12 is clearly a poor approximation, primarily because it does not account for specific charge-charge interactions and neglects short-range dispersion and hydration effects. In this regime, we use our earlier models (Neal et al., 1998) with full accounting for protein shape and charge anisotropy to compute the PMF. With these considerations, the short-range contribution to ß₂₂ is given by

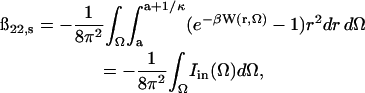(16)

where W(r, Ω) is the PMF between the two protein molecules, and Ω comprises the three Euler and two polar angles that specify their relative orientation (Neal et al., 1998). For a given Ω, the radial integration in Eq. 16 can be carried out to yield I_in(Ω) (Neal et al., 1998). For orientations corresponding to favorable interactions, I_in(Ω) is positive.

Our final expression for ß₂₂ is

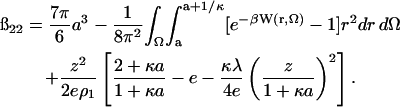(17)

The short-range dispersion (vdW) and electrostatic contributions are embodied in W(r, Ω). For the electrostatic contributions, our earlier model (Neal et al., 1998) was adopted. The protein is represented as a sphere with dielectric constant 4 (Gilson and Honig, 1986; Simonson et al., 1991; Pitera et al., 2001) and the angular charge distribution assigned according to the crystal structure. The surrounding solvent has a dielectric constant of 80. The interaction free energy is obtained by numerically solving the governing Poisson and linear Poisson-Boltzmann equations in the appropriate domains.

Dispersion interactions are modeled using a hybrid Lennard-Jones/Lifshitz-Hamaker approach described earlier (Asthagiri et al., 1999). This hybrid approach captures the essential features of surface complementarity in intermolecular interactions, but the effect of strongly associated water molecules is lost. In the quasichemical description of hydration (Paulaitis and Pratt, 2002), it is natural to view these water molecules as part of the protein. The solution thermodynamics is then described in terms of quasicomponents comprising the protein and bound water molecules immersed in a statistical field due to the exterior medium. Here, we identify strongly associated water molecules through explicit molecular dynamics simulations and retain the statistical description for the remainder.

The configurational integral in Eq. 17 was estimated by Monte Carlo sampling of the configurational space (Press et al., 1992). A total of 10⁴ configurations were generated for each calculation.

MOLECULAR DYNAMICS SIMULATIONS

A water density map around lysozyme (Protein Data Bank code 1LYZ) was generated from a molecular dynamics (MD) simulation as follows. The protein molecule was solvated in a cubic box of edge length ∼62 Å containing 7107 nonoverlapping TIP3P (Jorgensen et al., 1983) water molecules. The protein atoms were fixed throughout the simulation, as the modeling of ß₂₂ is based on rigid crystal structures. The system was first energy minimized by 20,000 steps of steepest descent minimization. All simulations were carried out in the NPT ensemble using NAMD (Kalé et al., 1999) and the CHARMM27 force field (MacKerell et al., 2000). The equations of motion were integrated with a 2-fs time step. The system temperature was held constant at 298 K by applying the Langevin dynamics method to all nonhydrogen atoms with a damping coefficient of 1 ps⁻¹. The system pressure was maintained at 1 bar using a Nose-Hoover Langevin piston with a period of 200 fs and a decay set to 100 fs. Electrostatic interactions were treated by the particle-mesh Ewald method using a real space cutoff of 12 Å. The same cutoff was used for nonbonded nonelectrostatic interactions. Water geometry was constrained by the SHAKE algorithm (Ryckaert et al., 1977). Equilibration for 200 ps was followed by a production run of 2 ns where configurations were saved every 0.1 ps for analysis.

The configuration files were used to generate a water density map on a 1.0-Å grid placed around the protein molecules. The sites were classified based on the mean density values calculated within the cubic grid volumes. These density values were represented in dimensionless form as η = log(ρ/ρ_b), where ρ and ρ_b are the densities at a given site and in bulk water, respectively. Sites with densities that correspond to η ≥ 2.0 were selected as the sites for strongly associated water molecules in the first hydration shell, defined to be within 3.5 Å of heavy surface atoms of LYS. Using a cutoff value of η = 2.0 gives ∼150 strongly associated water molecules. Water molecules placed at these sites are shown as red spheres in Fig. 1 with protein atoms depicted with green spheres. Crystallographic waters are shown as blue spheres.

FIGURE 1.

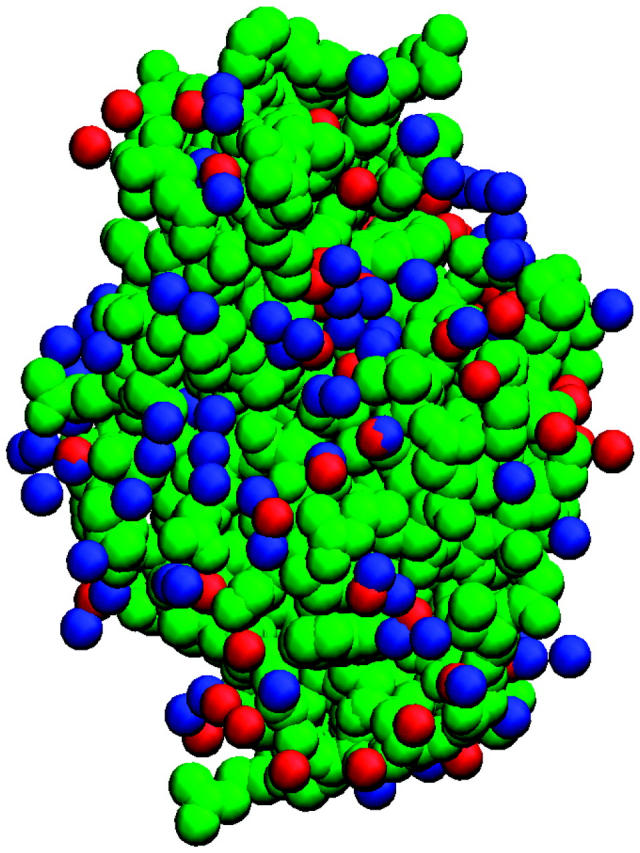
Structure of hen egg white lysozyme (Protein Data Bank code 1LYZ). Heavy atoms are depicted as green spheres. High water density sites obtained from MD simulations are displayed as red spheres. Crystallographic waters are shown as blue spheres.

EXPERIMENTAL METHOD

Hen egg white lysozyme (3× crystallized, L-7651) was obtained from Sigma-Aldrich (St. Louis, MO). NaCl (S9888, Sigma-Aldrich) was used to adjust the ionic strength of the protein samples. Buffer salts—sodium acetate (3470-01, J. T. Baker, Phillipsburg, NJ), bis-Tris (156663, Sigma-Aldrich), and Tris (T-1503, Sigma-Aldrich)—were used for pH stability at pH values of 5.0, (6.5, 7.0) and (8.0, 9.0), respectively. The pH was measured using a Mettler Toledo MP220 pH meter and was adjusted by adding small quantities of 0.1–0.5 M HCl (9535-33, J. T. Baker) and NaOH (3722-01, J. T. Baker). All samples for static light scattering (SLS) were prepared with filtered deionized water obtained from a Barnstead NANOpure ultraviolet water filter system (Barnstead International, Dubuque, IA). The buffer solutions were filtered with Whatman 20-nm inorganic filters (Whatman PLC, Brentford, UK) and were used to prepare stock solutions of ∼10 mg/ml lysozyme at various solution conditions. The protein solutions were filtered before the SLS measurements using Amicon Ultrafree MC centrifugal filter devices (Millipore, Billerica, MA) with a 100-nm pore size. All glassware was first treated with detergent, stored overnight in HELLMAMEX II alkaline cleaning solution, and then washed thoroughly with filtered and deionized water shortly before an experiment.

SLS data were collected at an angle of 90° on a Malvern 4700C system, equipped with a LEXEL95 Ar-ion laser operating at a wavelength of 488 nm and a Malvern MULTI8 computing correlator, 7032 CN. Toluene (TX 0735-6, EMD Chemicals, Gibbstown, NJ) was used as an index matching fluid in the glass vat that held the sample cell. All experiments were run at 25 ± 0.1°C. A Neslab RTE-210 water bath was used to control the temperature by circulating water through the metal casing enclosing the glass container that holds the index matching fluid.

In the SLS measurement, the Rayleigh ratio is related to turbidity by R_θ = 6τ/16π(1 + cos² θ). At a scattering angle of 90°, R₉₀ = 6τ/16π, and Eq. 10 can be rewritten as

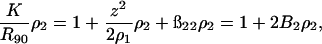(18)

where 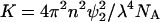is an optical constant. It is customary to use units of (g/vol) for the protein concentration. In such cases, ρ₂ = c₂/M_w, with c₂ in g/vol and M_w the molecular weight of the protein. With these units, a plot of the left side of Eq. 18 as a function of protein concentration, c₂, gives 1/M_w as the intercept and 2B₂ as the slope, where units of B₂ are mol ml/g².

The excess Rayleigh ratio of each sample was calculated by calibration with benzene (high-performance liquid chromatography grade; 27079, Sigma-Aldrich),

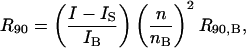where I, I_S, and I_B are the measured intensities at 90° for the protein and buffer solutions and benzene, respectively, n_B is the refractive index of benzene, and R_90,B is the absolute Rayleigh ratio of benzene, taken to be 38.6 × 10⁻⁶cm⁻¹ (Velev et al., 1998). A value of ψ₂ = ∂n/∂c₂ = 0.2 ml/g was used (Velev et al., 1998). R = R₉₀ is implied in the discussion below.

RESULTS

Light-scattering measurements

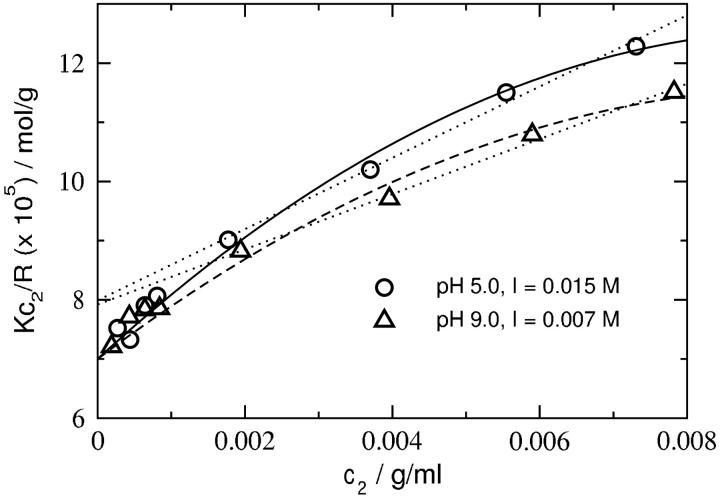
We measured osmotic second virial coefficients for lysozyme across a wide range of pH and ionic strength. Fig. 2 shows plots of Kc₂/R as a function of protein concentration at low ionic strengths for pH values of 5.0 and 9.0. The behavior is distinctly nonlinear, and data collection must be extended to protein concentrations much lower than 2 mg/ml to avoid underestimating the slope and overestimating the intercept. The protein concentrations in SLS measurements typically range from 2 to 10 mg/ml. From Fig. 2, it is clear that this practice would consistently predict a protein molecular weight much lower than the actual value derived from the amino acid sequence of lysozyme. Similar nonlinear behavior was noted in previous SLS studies of bovine serum albumin under conditions of high protein charge and low ionic strength (Edsall et al., 1950). The physical basis for this curvature is related to an increase in the total ionic strength of the solution with increasing protein concentration; i.e., interactions beyond pairwise protein-protein interactions become important.

FIGURE 2.

SLS plots for lysozyme (cf. Eq. 18) at low ionic strengths. The solid and dashed lines are quadratic fits to the data. The dotted line is a linear fit to the data corresponding to c₂ ≥ 1.8 mg/ml. Note that even these curves give a consistent intercept (1/M_w), but the molecular weight thus calculated is nearly 2 kDa lower than the value (14,285 Da) that well constrains the full data set. M_w based on amino acid sequence information is 14,320 Da.

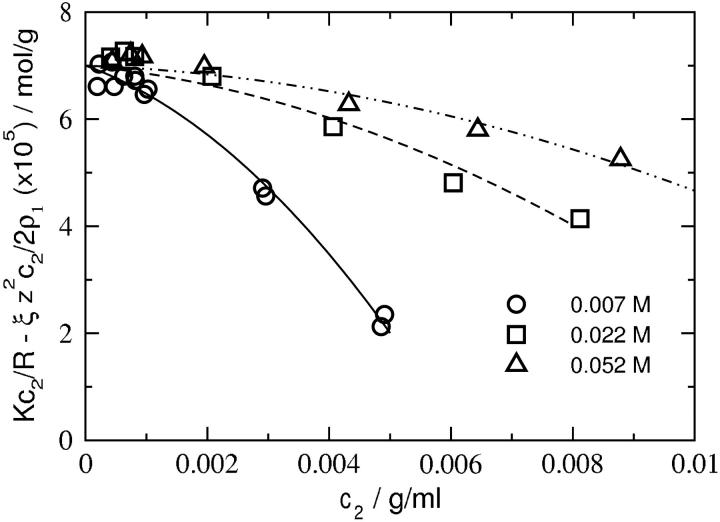
Fig. 3 shows plots of Kc₂/R adjusted for the Donnan contribution, 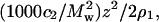as a function of protein concentration at pH 7.0 and three ionic strengths. The limiting slopes give ß₂₂ and are obtained by fitting the data to a quadratic function of c₂, then evaluating the derivative at c₂ = 0. We find that ß₂₂ is negative at all ionic strengths, but becomes progressively less negative with increasing ionic strength. The same behavior is observed at all pH. These results are summarized in Table 1. The values of 2B₂ are reported here as the sum of z²/2ρ₁ and ß₂₂. Because these values match those obtained directly from the limiting slope of Kc₂/R as a function of c₂, the latter values are not reported in Table 1. We find that B₂ is positive at all pH and decreases with increasing ionic strength, as expected based on screening of repulsive electrostatic interactions. The same trend is observed for an ideal solution: z²/2ρ₁ is positive and decreases with increasing ρ₁. However, the magnitude of B₂ at all conditions is lower than that for the ideal contribution, which reflects the importance of attractive protein-protein interactions. Finally, the molecular weight of lysozyme (14,320 Da based on amino acid sequence) is input in our calculations, but M_w = 14,285 Da best describes the data. This agreement reflects the high quality of the data and the accuracy of the data analysis.

FIGURE 3.

SLS plots for lysozyme at pH 7.0 and various ionic strengths adjusted for the Donnan contribution, 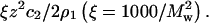The curves are quadratic fits to the data. ß₂₂ is obtained from the slopes of these curves in the limit c₂ = 0.

TABLE 1.

SLS results for lysozyme

pH	z	I	2B2	z2/2ρ1	ß22
5.0	10.2	0.015	117.7	169.6	−51.9
5.0	–	0.030	63.0	84.8	−21.8
5.0	–	0.060	36.7	42.4	−5.7
7.0	8.0	0.007	165.0	223.6	−58.6
7.0	–	0.022	57.0	71.1	−14.1
7.0	–	0.052	25.1	30.1	−5.0
9.0	6.7	0.007	100.5	156.8	−56.3
9.0	–	0.022	31.0	49.9	−18.9
9.0	–	0.052	13.6	21.1	−7.5

B₂, z²/2ρ₁, and ß₂₂ are in units of ×10⁴ mol ml/g². I is the ionic strength (including buffer) in mol/liter; z is the charge carried by the protein, obtained from titration experiments (Kuehner et al., 1999). An average M_w = 14,300 Da is used in the calculations.

Modeling protein-protein interactions

Results of the calculations of ß₂₂, ß_22,s, and ß_22,l are given in Table 2. Calculated values of ß₂₂ are in reasonable agreement with the SLS results, given the sensitivity of these calculations to the value of z (see also Fig. 4, top), and the correct dependence on ionic strength is also recovered (Table 2); i.e., ß₂₂ is large and negative at low ionic strength, and becomes progressively less negative with increasing ionic strength. Interestingly, ß_22,s and ß_22,l have diametrically opposite dependences on ionic strength. ß_22,s is positive at low ionic strength and decreases with increasing ionic strength, suggesting a greater influence of repulsive electrostatic interactions relative to attractive vdW interactions. In contrast, ß_22,l is negative at low ionic strength, but becomes progressively less negative with increasing ionic strength. The contribution to ß₂₂ from ß_22,l dominates, particularly at low ionic strength, and therefore, the ionic strength dependence of ß₂₂ follows that of ß_22,l.

TABLE 2.

Calculation of ß₂₂ and contributing terms based on Eq. 17

pH	z	I	ß22,s + 7πa3/6	ß22,l	ß22,calc	ß22,exp
5.0	10.2	0.015	35.0	−108.9	−73.9	−51.8
5.0	–	0.030	22.3	−55.6	−33.3	−21.8
5.0	–	0.060	13.0	−28.1	−15.1	−5.7
7.0	8.0	0.007	31.1	−123.5	−92.4	−59.0
7.0	–	0.022	19.6	−42.3	−22.7	−14.1
7.0	–	0.052	10.2	−18.5	−8.3	−5.0
9.0	6.7	0.007	27.2	−81.9	−54.7	−56.3
9.0	–	0.022	16.4	−28.3	−11.9	−18.9
9.0	–	0.052	7.8	−12.5	−4.7	−7.5

The sphere diameter for the electrostatics calculations is 38.2 Å. Following Neal et al. (1998), this diameter is 20% greater than that for an equivalent volume defined as density/molecular weight (Roth et al., 1996). The mean excluded volume from the MD simulations gives a diameter of 36.4 Å. The contribution from 7πa³/6 is 5.9 × 10⁻⁴ mol ml/g². Other details as in Table 1.

FIGURE 4.

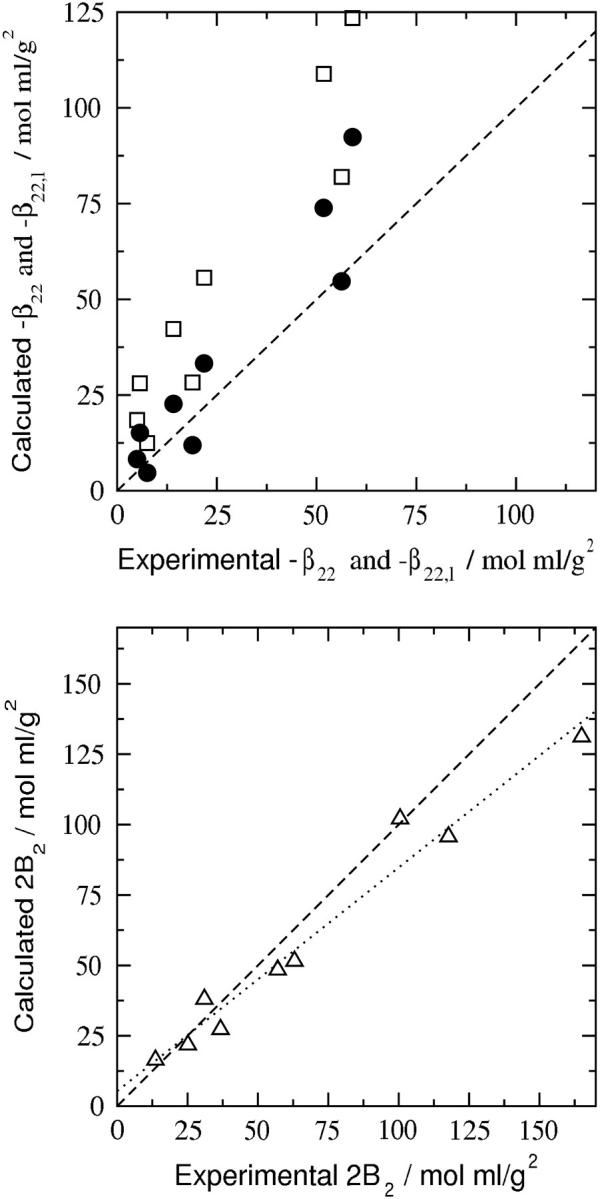
Comparison of experimental and calculated values of ß₂₂, −ß_22,l, and 2B₂. (Top) −ß₂₂ (•), the interaction contribution to the osmotic second virial coefficient, B₂; −ß_22,l (□), the purely long-range contribution to ß₂₂. (Bottom) 2B₂ (▵). The dotted line is a linear fit of the data with a correlation coefficient R² = 0.98 and slope of 0.8. The statistical uncertainty due to the Monte Carlo integration of the configurational integral in Eq. 17 is less than the size of the symbols and hence is not shown.

Nonetheless, the long-range contribution, ß_22,l, alone does not provide an accurate description of the experimental ß₂₂, as shown in Fig. 4 (top); the short-range contribution, ß_22,s, is essential. We also note that deviations in the calculated values of ß₂₂, which are greater at low ionic strength, are amplified due to the subtraction of a positive Donnan term that likewise is larger at low ionic strength. Thus, even small fluctuations in the net charge of the protein can significantly affect the predicted ß₂₂ at these solution conditions. Of course, the experimental values represent averages over all possible fluctuations, whereas our model uses only one set of charges, in this case obtained from titration experiments (Kuehner et al., 1999). We expect, therefore, that satisfactory agreement between the experimentally derived and calculated values of ß₂₂ will be nontrivial to obtain. The agreement for B₂ shown in Fig. 4 (bottom) is substantially better, indicating that the approximations inherent to our model offset one another to some extent. It should be noted that all parameters in the model are assessed independently (Asthagiri et al., 1999; Neal et al., 1998).

DISCUSSION

The osmotic second virial coefficient derived from SLS measurements using Eq. 10 has two principal components: the Donnan contribution and ß₂₂, the contribution due to protein-protein interactions in the limit of infinitely dilute protein solutions. The Donnan term is positive and can be the dominant contribution when the protein has a large net charge and/or when the ionic strength associated with the added salt is low. Indeed, a dominant Donnan contribution explains the large positive values of B₂ that have been reported in the literature (Edsall et al., 1950; Velev et al., 1998). The importance of distinguishing this contribution from the interaction part of B₂ has been emphasized here, thereby opening up the possibility of determining the latter by molecular computations.

The model for protein-protein interactions that we use in this study (Eq. 17) extends our earlier work (Neal et al., 1998) in two respects. First is the consideration of long-range electrostatic interactions. In the earlier work, the electrostatic interactions were sampled up to 13(a + 5.5 κ⁻¹) using 13 unevenly spaced points, with intermediate points interpolated using a spline. This technique has the undesirable effect of coarsely describing the short-range contributions and not completely capturing the long-range effects. Here we recognize the importance of electrostatic interactions for r > a + κ⁻¹, and account for these long-range interactions using a Debye-Hückel model (Eq. 12). Between a and a + κ⁻¹, we sampled the short-range component of the electrostatic interactions using a fine (0.1 Å) grid. In our analysis, ß_22,l is derived by considering a distinguished protein molecule in solution and treating other protein molecules as part of a statistical distribution of counterions and coions, which leads to

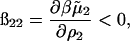in Table 2. Our physical interpretation of this result is that the addition of protein in the limit of 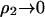increases the ionic strength of the solution, which reduces the free energy of charging the distinguished protein molecule; i.e., the effect of adding protein is to screen long-range protein-protein interactions, which dominate ß₂₂, especially at low ionic strength.

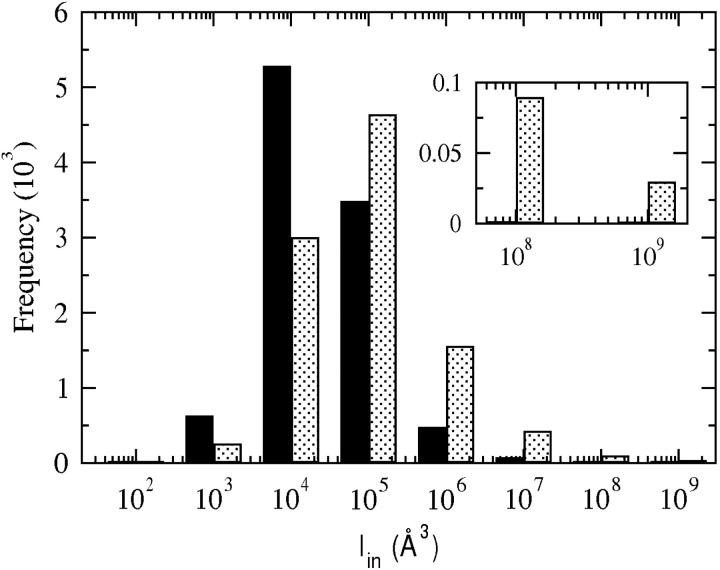
The second extension from the earlier work is the consideration of specific hydration of the protein molecule; protein-protein interactions modeled here account for an ensemble of water molecules that are strongly associated with the protein. Including these explicit water molecules reduces the frequency of occurrence of interactions that involve highly complementary protein-protein orientations, as shown in Fig. 5. A more extensive discussion of specific hydration is given in a subsequent article (A. Paliwal, D. Asthagiri, D. Abras, A. M. Lenhoff, and M. E. Paulaitis, unpublished results). The effect is to reduce short-range vdW attractions. Thus, accounting for specific hydration will offset to a certain extent the added consideration of long-range electrostatic interactions in extending our earlier model. More importantly, though, separating these long-range electrostatic interactions from the short-range electrostatic/vdW interactions makes possible an accurate assessment of the latter contribution to the protein-protein PMF by molecular computations.

FIGURE 5.

Distribution of I_in with (solid bars) and without (dotted bars) specific hydration. Positive I_in values represent favorable orientations. The inset highlights the distribution for the highly complementary configurations. See “Protein-protein interactions” section for the definition of I_in.

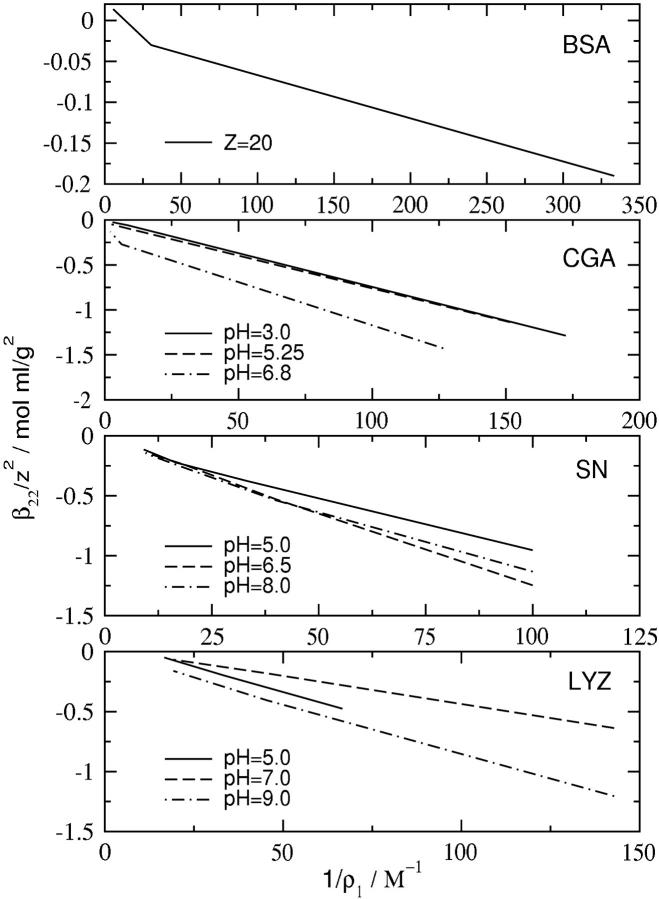
The influence of both short-range and long-range interactions in ß₂₂ (and B₂) can lead to interpretations of SLS data that confuse the length scale of relevant interactions for certain solution conditions. From Eq. 17, a plot of ß₂₂/z² as a function of 1/ρ₁ (inverse ionic strength) will be linear when long-range electrostatic effects dominate protein-protein interactions. This plot is shown in Fig. 6 for several different proteins for which SLS data are available. A linear dependence is obtained in all cases, which confirms the general observation that long-range electrostatic interactions dominate at low to moderate ionic strength.

FIGURE 6.

ß₂₂/z² as a function of 1/ρ₁ (inverse ionic strength) for different proteins. The protein in each panel is (top to bottom): BSA, bovine serum albumin; data (Table V in Edsall et al., 1950). CGA, chymotrypsinogen; data (Figure 4 in Velev et al., 1998) where we have adjusted for the presence of citrate buffer by considering ionization of the buffer at each given pH. SN, staphylococcal nuclease; data (A. Paliwal, D. Asthagiri, D. Abras, A. M. Lenhoff, and M. E. Paulaitis, unpublished results). LYZ, lysozyme; data from Table 1 in this article.

The results for chymotrypsinogen (Fig. 6) are particularly illustrative when compared with an earlier analysis of the same data, based instead on the behavior of B₂ (Velev et al., 1998). In that analysis, the ionic strength dependence of B₂ showed opposite trends at low and high pH. At low pH, the trend is consistent with that depicted in Fig. 6: increasing ionic strength reduces a positive B₂, which implies that long-range electrostatic repulsions are screened. In contrast, B₂ is negative at high pH and low ionic strength, and becomes progressively less negative with increasing ionic strength. This behavior suggests that there are protein-protein configurations corresponding to attractive electrostatic interactions that are screened at higher ionic strengths. As shown in Fig. 6, this behavior is not observed if one considers ß₂₂.

The picture one obtains from this analysis is that B₂ characterizes short-range (i.e., molecular scale) protein-protein interactions solely when the net charge on the protein is low. This picture is also supported by calculations of B₂ based on our earlier model (Neal et al., 1998). Although those calculations were of limited statistical quality, protein-protein configurations were found at neutral pH (low net charge on the protein) corresponding to attractive electrostatic interactions that are screened at high ionic strength. Interestingly, more extensive calculations (A. Paliwal, D. Asthagiri, D. Abras, A. M. Lenhoff, and M. E. Paulaitis, unpublished results) based on the model presented here likewise uncover configurations corresponding to attractive electrostatic interactions that play a dominant role in ß_22,s. These calculations also reveal a fortuitous balance between a (positive) Donnan contribution and the (negative) contribution from ß_22,l such that B₂ follows the same ionic strength dependence as the ß_22,s.

As the results in Fig. 6 indicate, z² largely captures the principal electrostatic interactions between protein molecules, and thus serves as a scaling factor for ß₂₂ in the low to moderate ionic strength regime. Nonetheless, protein interactions on the molecular scale are of primary interest in self-assembly phenomena, and as such, the hard-sphere virial coefficient, B_hs = 2πa³/3, is often used as a scale for protein-protein interactions in this regime. This scaling can, however, lead to problematic conclusions. For example, the SLS results for lysozyme at pH = 5.0 and I = 0.015 M (Table 1) give B₂/B_hs ≈ 20. This result implies an effective range of interactions for a protein molecule on the order of four times the Debye length, κ⁻¹, which naturally jolts our intuition of the virial coefficient characterizing molecular scale interactions. The problem here is in not appreciating the constraints that electroneutrality imposes. Separating long-range and short-range effects (Eq. 16) by introducing a cutoff at a + κ⁻¹, is one possible approach, but by no means the only approach to probe molecular scale phenomena in these systems. The scheme proposed by Weeks and co-workers (Chen et al., 2004) for electrolytes appears to have significant strengths. In their approach, one attempts to extract the short-range component by appropriately screening entirely the long-range component. Our attempt to include their idea of screening long-range interactions to better reveal short-range interactions shows a rich subtlety of local interactions. Adapting this idea in a pragmatic way for protein solutions, however, requires further development.

In attempting to correlate protein crystallization with protein solution thermodynamics and B₂, it must be recognized that the salt concentration at crystallization conditions is often high; thus, for all practical purposes 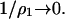In this regime, long-range electrostatic effects are unimportant, and the hard-sphere virial coefficient is indeed the best metric to guide the development of such correlations, an aspect that is illustrated in work by Rosenbaum and Zukoski (Rosenbaum et al., 1996). However, modeling protein interactions in this regime is much more demanding, because contributions from ß₁₁ and ß₂₁ (Eq. 8) can no longer be ignored, and these quantities are still amongst the most challenging to describe at the molecular level for proteins. Recent interpretations of light-scattering measurements of B₂ have also focused on the role of alcohols as additives in crystallizing media (Farnum and Zukoski, 1999; Liu et al., 2004). These systems contain four or more components, and the application of the two-component approximation (Eq. 11) used here must be considered with care. Still, the theoretical framework provided more than half a century ago (Brinkman and Hermans, 1949; Kirkwood and Goldberg, 1950; Stockmayer, 1950) remains relevant, and coupled with recent advances in molecular modeling and simulations of protein-protein interactions, is likely to provide the framework to address these challenges.

CONCLUSIONS

Our analysis of the osmotic second virial coefficient, B₂, obtained by light scattering from protein solutions highlights the importance of distinguishing the Donnan contribution from ß₂₂, the contribution due to protein-protein interactions in the limit of infinite dilution. The Donnan contribution accounts for electroneutrality in multicomponent solutions of (poly)electrolytes, and separating this ideal contribution from the interaction part of B₂ leads directly to the identification of ß₂₂ as the target for molecular computations.

The model for ß₂₂ presented here represents an extension of earlier work (Neal et al., 1998), and incorporates long-range electrostatic interactions, which we describe by adopting a simple Debye-Hückel model, and the specific hydration of the protein by an ensemble of strongly associated water molecules, which we determine from molecular simulations. The effect of including specific hydration is to reduce short-range attractive dispersion interactions by eliminating a number of highly complementary protein-protein configurations. The key finding of this study is that short-range electrostatic/dispersion interactions with specific hydration must be taken into account to achieve an accurate description of B₂, although long-range electrostatic interactions can make a dominant contribution to ß₂₂, particularly at low ionic strength. These short-range contributions, in particular, are amenable to molecular computations, and therefore, we anticipate that further applications of molecular modeling and simulations can lead to even greater insights from the analysis of light-scattering studies of protein-protein interactions.