Conformational Dynamics of the Ligand-Binding Domain of Inward Rectifier K Channels as Revealed by Molecular Dynamics Simulations: Toward an Understanding of Kir Channel Gating

Abstract

Inward rectifier (Kir) potassium channels are characterized by two transmembrane helices per subunit, plus an intracellular C-terminal domain that controls channel gating in response to changes in concentration of various ligands. Based on the crystal structure of the tetrameric C-terminal domain of Kir3.1, it is possible to build a homology model of the ATP-binding C-terminal domain of Kir6.2. Molecular dynamics simulations have been used to probe the dynamics of Kir C-terminal domains and to explore the relationship between their dynamics and possible mechanisms of channel gating. Multiple simulations, each of 10 ns duration, have been performed for Kir3.1 (crystal structure) and Kir6.2 (homology model), in both their monomeric and tetrameric forms. The Kir6.2 simulations were performed with and without bound ATP. The results of the simulations reveal comparable conformational stability for the crystal structure and the homology model. There is some decrease in conformational flexibility when comparing the monomers with the tetramers, corresponding mainly to the subunit interfaces in the tetramer. The β-phosphate of ATP interacts with the side chain of K185 in the Kir6.2 model and simulations. The flexibility of the Kir6.2 tetramer is not changed greatly by the presence of bound ATP, other than in two loop regions. Principal components analysis of the simulated dynamics suggests loss of symmetry in both the Kir3.1 and Kir6.2 tetramers, consistent with “dimer-of-dimers” motion of subunits in C-terminal domains of the corresponding Kir channels. This is suggestive of a gating model in which a transition between exact tetrameric symmetry and dimer-of-dimers symmetry is associated with a change in transmembrane helix packing coupled to gating of the channel. Dimer-of-dimers motion of the C-terminal domain tetramer is also supported by coarse-grained (anisotropic network model) calculations. It is of interest that loss of exact rotational symmetry has also been suggested to play a role in gating in the bacterial Kir homolog, KirBac1.1, and in the nicotinic acetylcholine receptor channel.

INTRODUCTION

K channels (Yellen, 2002) are a ubiquitous family of integral membrane proteins, whose role is to enable and to regulate the passive flux of K⁺ ions across cell membranes. They are both of physiological and biomedical interest (Ashcroft, 2000). K channel regulation occurs via a conformational change that allows the protein to switch between two alternative conformations (closed versus open), a process known as gating. Gating is thus an inherently dynamic process that cannot be fully characterized by static structures alone.

The elucidation of the structures of several bacterial K channels (Mackinnon, 2003) has shed considerable light on the structural basis of the mechanisms of ion selectivity and permeation (Doyle et al., 1998; Jiang et al., 2002a,b; Kuo et al., 2003; Morais-Cabral et al., 2001; Zhou and MacKinnon, 2003). These structures share a common core transmembrane (TM) pore-forming domain, which is tetrameric, the monomers surrounding a central pore. The pore-forming domain can exist in two or more conformations according to whether the channel is in an open or closed state. The various K channels differ in the domains present on either side of (i.e., N-terminal or C-terminal) the core TM domains. These additional domains confer different gating mechanisms: KcsA, gated by low pH; MthK, gated by Ca²⁺ ions; KvAP, gated by TM voltage; and KirBac, gating mechanism unknown. The central pore-forming domain is formed of a M1-P-F-M2 motif, where M1 and M2 are helices, and the short P-helix and extended filter region form a reentrant loop between the two TM helices. The filter is the structural element mainly responsible for the selective conduction of K⁺ ions.

The inward rectifier (Kir) class of K channels has two main physiological roles: they regulate cell excitability by stabilizing the membrane potential close to the K-equilibrium potential, and they are involved in K-transport across membranes (Nichols and Lopatin, 1997; Reimann and Ashcroft, 1999). For example, Kir3.1/Kir3.4 channels modulate cardiac electrical activity, and Kir6.2 is involved in insulin release from pancreatic β-cells. Two recent structures, of the intracellular domain of a mammalian Kir (Kir3.1 = GIRK1; Nishida and MacKinnon, 2002) and of the complete structure of a bacterial Kir homolog (KirBac1.1; Kuo et al., 2003), offer a detailed understanding of structure/function relationships in this important family of K channels. The Kir channels are somewhat simpler in their TM architecture than are Kv channels. Kir channels have two TM helices per subunit (as do KcsA and MthK), whereas Kv channels have six. Kir channels have a large intracellular domain composed of ∼50 residues from the N-terminal tail of the protein plus a C-terminal domain of ∼200 residues. This domain plays an important functional role via binding cytosolic regulators of Kir activity, such as ATP and PIP₂.

To understand the structure/function relationships of complex channel proteins, the individual structural and functional domains may be studied in isolation. For example, the x-ray structures of TM domains of the KcsA and MthK channels provide examples of the closed and open conformations of this domain, enabling modeling of the changes in gate structure, dynamics, and energetics upon channel opening (Holyoake et al., 2003; Jiang et al., 2002b). By combining such information with the closed state structure of KirBac and the high resolution structure of the intracellular domain of Kir3.1, it may be possible to arrive at a more unified model of Kir gating. A comparable approach has been applied to the nicotinic acetylcholine receptor, for which a high resolution structure of a protein homologous to the receptor ligand-binding domain is available (Brejc et al., 2001; Celie et al., 2004), in addition to an electron-microscopy derived model of the TM domain (Miyazawa et al., 2003).

In this study, we use molecular dynamics (MD) simulations to explore aspects of the conformational dynamics of the intracellular C-terminal domain of Kir channels that may be related to control of channel gating. Although the timescale of channel gating (<1 ms) is too long to be addressed directly by MD simulation, the intrinsic flexibility of the C-terminal domain on a 10-ns timescale provides clues as to the nature of the overall gating mechanism. Recent studies of other K channels, both crystallographic (Jiang et al., 2002a,b) and mutational (Niu et al., 2004), indicate the role of the intracellular domains in regulating gating transitions between the open and closed states of the TM domain. Thus, we wish to examine how the conformational dynamics of the Kir3.1 C-terminal domain may be integrated within a more general model of Kir channel gating.

One question that must be addressed in any simulation study is that of the significance of the motions observed. However, one may try to evaluate the biological significance of the motions by asking whether or not they are conserved across related members of a protein family (Pang et al., 2003). We have therefore extended our simulation study of the Kir3.1 C-terminal domain to include simulations of a homology model of the related Kir6.2 C-terminal domain. (The two domains share 48% sequence identity.) This also enables us to explore the conformational stability of the homology model of the Kir6.2 C-terminal domain on a 10-ns timescale. We have also analyzed the simulations to address two subsidiary questions: i), how C-terminal domain motions differ between the monomeric and tetrameric forms of the domain, and ii), how motions of the Kir6.2 C-terminal domain are modified by the presence of bound ATP.

METHODS

Kir6.2 model building

A model of the mouse Kir6.2 C-terminal domain was generated as described previously (Trapp et al., 2003), using Modeller v6.2 (Sali and Blundell, 1993) to construct a homology model based on the mouse Kir3.1 C-terminal domain (Protein Data Bank entry 1N9P) template. The template and the target sequence were aligned using clustalX (Jeanmougin et al., 1998) and are 48% identical. The fourfold symmetry of the Kir3.1 C-terminal domain crystal structure was imposed during the modeling procedure. The N-terminal sequence fragment (residues 43–57) present in the Kir3.1 C-terminal domain structure was omitted from the model. An ensemble of 25 structures was constructed, and these models were ranked by Modeller energy function and by deviation from the template structure. The best model according to both these criteria was selected. The stereochemistry of this model was evaluated using ProCheck (Laskowski et al., 1993) and judged to be satisfactory. The x-ray crystal structure of the Kir3.1 C-terminal domain (Protein Data Bank entry 1N9P) was also simulated. The incomplete N-terminal region in the structure was removed before the simulation, as were the crystallographic waters.

ATP docking to the Kir6.2 model

To a first approximation, the binding of ATP to each subunit is independent of binding to adjacent subunits. Thus, the Kir6.2 monomer was used for ATP docking, as described previously (Trapp et al., 2003). Docking was performed using AUTODOCK 3.0 (Goodsell et al., 1996; Morris et al., 1998). Partial charges were assigned using MOPAC (Stewart, 1990) in InsightII, and rotatable bonds in the ligand were treated using DefTors within AutoDock. None of the rotatable bonds in the ATP molecule was restrained during docking. Simulated annealing was employed to perform automated ligand docking.

MD simulations

MD simulations were performed using GROMACS v3.1.4 (Berendsen et al., 1995; Lindahl et al., 2001; www.gromacs.org) employing the GROMOS87 force field (van Gunsteren and Berendsen, 1987). For each simulation (Table 1), the protein molecule was solvated with SPC waters (Berendsen et al., 1981) in a box of size 9 nm³ for monomer and 11 nm³ for tetramer simulations. Counterions were added to neutralize the system. This yielded ∼72,000 atoms for the monomer systems, and ∼128,000 atoms for the tetramers. Before running simulations, the system was energy minimized for 1000 iterations of steepest descents. The system was then equilibrated for 0.25 ns, during which the protein atoms were restrained using a force constant of 1000 kJ/mol/nm². During this equilibration process, the water molecules and the ions were free to move, but the ATP was restrained. All restraints were then removed and each simulation was run for 10 ns.

TABLE 1.

Summary of simulations

Simulation name	Protein	Ligand	All residues Cα RMSD* (Å)	Core residues Cα RMSD* (Å)
Kir3.1	Kir3.1 monomer	-	2.8	2.2
Kir3.14	Kir3.1 tetramer	-	2.6	1.9
Kir6.24	Kir6.2 tetramer	-	2.7	2.2
Kir6.24 + ATP	Kir6.2 tetramer	ATP	3.4	2.6
Kir6.2	Kir6.2 monomer	-	4.1	2.4
Kir6.2 + ATP	Kir6.2 monomer	ATP	3.7	2.3

All simulations were of 10 ns duration (see Methods for details).

^*Cα RMSD = RMSDs of Cα atoms from their positions in the starting structure, evaluated for the final 8 ns of each simulation. Core residues are defined as those with an RMSF (see Fig. 2, A, C, and E) of <2.5 Å.

Simulations employed Berendsen coupling (Berendsen et al., 1984) to maintain a constant temperature of 300 K and a constant isotropic pressure of 1 Bar. Van der Waals interactions were modeled using 6–12 Lennard-Jones potentials with a 1.3 nm cutoff. Long-range electrostatic interactions were calculated using the Particle Mesh Ewald method (Darden et al., 1993; Essmann et al., 1995), with a cutoff for the real space term of 1.2 nm. Covalent bonds were constrained using the LINCS algorithm (Hess et al., 1997). The time step employed was 2 fs, and coordinates were saved every 10 ps for analysis. Analysis used the GROMACS suite of packages and local scripts. Structural diagrams were generated using VMD (Humphrey et al., 1996) or RasMol (Sayle and Milner-White, 1995). Porcupine plots of eigenvectors were calculated using an approach derived from Tai et al. (2001, 2002) as implemented in the Dynamite server (Barrett et al., 2004).

Anisotropic network models were generated using a modified version of the ANM code from the Jernigan laboratory (http://ribosome.bb.iastate.edu/; Atilgan et al., 2001; Keskin et al., 2000). A cutoff of 11 Å was used, above which distance no springs were defined and below which all springs were defined as having equal forces. An (arbitrary) spring constant of 1 was used.

RESULTS

The simulations are based upon the crystal structure of the Kir3.1 C-terminal domain or upon a model of the homologous (see below) Kir6.2 C-terminal domain. Note that the Kir3.1 C-terminal domain crystal structure corresponds to an artificial construct in which residues 41–63 of the intact channel protein were joined directly to residues 190–371 (Nishida and MacKinnon, 2002). Thus in the simulations, only residues 190–371 were included. The Kir6.2₄ model (Fig. 1) exhibits an overall Cα RMSD of 1.3Å from the template Kir3.1₄ crystal structure for 181 × 4 = 724 Cα atoms. This value lies within the range expected for proteins sharing 25% or more sequence identity (0.7–2.3 Å; Russell et al., 1997). The stereochemistry of the model, as analyzed by ProCheck (see below), was judged to be acceptable.

FIGURE 1.

(A) Sequence alignment of the C-terminal domains of Kir3.1 (mGIRK) and Kir6.2. The loops between strands βD and βE (DE) and between strands βL and βM (LM) are boxed and labeled. (B) Model structure of the monomeric Kir6.2 C-terminal domain, with a docked ATP molecule (red). The mobile loops (DE and LM) and termini are labeled and shown in blue. (C) Model structure of the Kir6.2 C-terminal domain tetramer, with ATP in red. The view is looking down the central pore axis from the membrane (channel) side of the C-terminal domain. The DE and LM loops are labeled.

In examining the structure of the Kir6.2₄ tetramer, we note that the loops between strands βD and βE (i.e., the loop around residues 226–228 in Kir6.2 and 239–241 in Kir3.1) and between βL and βM (i.e., the loop around residues 322–324 in Kir6.2 and 334–336 in Kir3.1) are highly surface exposed in the monomer but packed against the adjacent subunit in the tetramer. Thus we may anticipate differences in their mobility between the monomeric and tetrameric states of the protein (see below).

The results obtained from docking ATP to the monomeric Kir6.2 C-terminal domain are in agreement with the experimental mutagenesis data, as has been described previously (Trapp et al., 2003). The ATP molecule fits into the putative binding site such that its adenine ring is separated from its phosphate tail by a β-strand in the model. This short β-strand is just before the equivalent of the βB-strand in the Kir3.1 crystal structure. Such an orientation separates the charged tail from the hydrophobic conjugated ring system sitting in a hydrophobic environment. The docking results are also consistent with the experimental results that suggest that the β-phosphate of ATP interacts with the side chain of K185 (see below) and also the residues S184, H186 are close to the phosphate tail of the bound ATP molecule. The γ-phosphate points outward from the rest of the structure.

Thus, we have three tetrameric structures upon which to base simulations: Kir3.14, Kir6.24, and Kir6.24 with bound ATP. All three tetramers were used as starting points for simulations, as were the corresponding monomers (see Table 1).

Structural stability and residue flexibility in the simulations

The root mean-square deviation (RMSD) of, e.g., the Cα atoms of a protein over the course of a simulation, may be used as a measure (albeit a crude measure) of the conformational stability of a protein structure or model during that simulation. In the context of the Kir C-terminal domain structures, we were interested to examine the conformational stability of the domain structures in isolation (i.e., not as part of an intact Kir channel structure) and to compare the crystallographic structure with the homology model.

If first we examine the Kir3.1 simulations (Fig. 2 B), we note that for both the monomer and the tetramer there is an initial rise in RMSD over the first ∼1 ns, after which a plateau is reached. This is commonly observed in protein simulations and is thought to reflect the relaxation of the protein once removed from the crystal packing environment. The overall value of the Cα RMSD for the monomer (2.8 Å; Table 1) is a little higher than that for the tetramer (2.6 Å), as might be anticipated. If one excludes the higher mobility loops (i.e., those with a Cα RMSF of >2.5 Å) from the RMSD calculation, then both of these values drop to ∼2 Å, indicative of stable simulations on a 10-ns timescale.

FIGURE 2.

Cα RMSFs versus residue number (A, C, and D) and RMSDs from initial structure versus time (B, D, and E). (A) RMSFs for the Kir3.1 (monomer, shaded line) and Kir3.1₄ (tetramer, black line) simulations. The residues corresponding to the DE and LM loops are labeled. (B) RMSDs for all residues of the Kir3.1 (monomer, thick shaded line) and Kir3.1₄ (tetramer, thick black line) simulations and for the core residues of Kir3.1₄ (thin black line). (C) RMSFs for the Kir6.2₄ (shaded line) and Kir6.2₄ + ATP (black line) simulations. (D) RMSDs for all residues of the Kir6.2₄ (thick shaded line) and Kir6.2₄ + ATP (thick black line) simulations and for the core residues of Kir6.2₄ (thin black line). (E) RMSFs for the Kir6.2 (shaded line) and Kir6.2 + ATP (black line) simulations. (F) RMSDs for all residues of the Kir6.2 (thick shaded line) and Kir6.2 + ATP (thick black line) simulations and for the core residues of Kir6.2 (thin black line). (For the tetramer simulations, both the RMSF and the RMSD curves are averages across the four monomers.)

We may compare the RMSD of the Kir6.2₄ simulation with that of the Kir3.1₄ simulation, the former based on a homology model, the latter on a (1.8 Å resolution) x-ray structure. The homology model is remarkably stable, at least on the timescale of the 10-ns simulation. Whether one compares the core residues (i.e., those with an RMSF <2.5 Å) or all residues, the Cα RMSDs for the model and the structure are very similar. Thus, as far as one may judge from analysis of RMSDs, the Kir6.2₄ model and simulation merit detailed analysis. In particular, if the Kir6.2₄ model was globally incorrect (e.g., due to a sequence poor alignment), we would anticipate a higher Cα RMSD than that observed. This has been the case in previous studies when we have used simulations to compare multiple homology models of either the Kir6.2 channel TM domain (Capener et al., 2002; Sansom et al., 2002) or aquaporin (Law and Sansom, 2004). However, we cannot exclude the possibility that individual side-chain conformations may be inaccurate or incorrect.

Interestingly, the RMSD for the Kir6.2₄ +ATP simulation is significantly higher than for the Kir6.2₄ simulation, and may not have reached a plateau within 10 ns. This is true whether or not one omits the mobile loops. This suggests that the presence of ATP may be initiating some structural drift. On a 10-ns timescale, sampling of such conformational change will be incomplete (Faraldo-Gómez et al., 2004) although simulations studies of, e.g., glutamine binding protein and of glutamate receptors (Pang et al., 2003), suggest that large scale protein conformational changes can begin to be sampled on a 10-ns timescale.

The all residue Cα RMSD for the Kir6.2 (monomer) simulation is significantly higher than that for the Kir6.2₄ (tetramer) simulation. This is perhaps not unexpected (although a comparable difference was not observed for the Kir3.1 simulations). However, the difference is less marked if the RMSDs of the core fold are compared. This suggests that tetramerization may lead to reduction in flexibility of some of the loops.

A more detailed picture of differences in residue mobility within and between simulations can be obtained from graphs of the root mean-square fluctuation (RMSF) of Cα atoms relative to the average structure (Fig. 2, A, C, and E). Examining first the RMSF profile for the Kir3.14 simulation, we see that the overall pattern is close to that observed in the crystallographic B-values. In particular, the peaks in the RMSF profile, as anticipated, coincide with the surface loops between the secondary structure elements. The regions of greatest flexibility correspond to the termini of the simulated domain (as is generally the case) and also loops DE and LM (see above). Interestingly, the flexibility of both the DE and LM loop regions is reduced on going from the monomer to the tetramer, confirming the role of these loops in intermonomer contacts (see above). A similar decrease in flexibility of the DE and LM loops in going from the monomer to the tetramer is seen for the Kir6.2 model, for which the reduction in the mobility of the DE loop on tetramerization (compare Fig. 2, C and E) is quite marked.

Comparison of the Kir6.2₄ simulations with and without ATP (Fig. 2 C) reveals surprisingly few changes in flexibility. The only noticeable changes are a decrease in flexibility upon binding ATP of two loops: the LM loop and a loop (∼295) between strands βH and βI, which lies near the central pore axis. Interestingly, neither of these loops is close to the ATP binding site, i.e., the reduction in mobility occurs at a distance from the ligand interactions. We note that in the complete channel model (S. Haider, F. M. Ashcroft, and M. S. P. Sansom, unpublished) the 295 loop is close to slide helix of the membrane-embedded domain, a region that has been suggested to play a role in Kir channel gating (Kuo et al., 2003).

Essential dynamics

To examine overall patterns of motions of the C-terminal domain tetramers, we have employed principal components (i.e., essential dynamics) analysis (Amadei et al., 1993). By calculating the eigenvectors from the covariance matrix of a simulation and then filtering the trajectories along each of the different eigenvectors, it is possible to identify the dominant motions observed during a simulation by visual inspection. Application of such analysis to Cα atom motion in our simulations of tetramers revealed that the first eigenvector accounts for ∼45%, 33%, and 51% of all motion in Kir3.1₄, Kir6.2₄, and Kir6.2₄ + ATP simulations, respectively (Fig. 3 A). Thus we have restricted further analysis to the first eigenvector.

FIGURE 3.

(A) Eigenvalue versus eigenvector index for the first 10 eigenvectors of the Kir3.1₄ (solid shaded line), Kir6.2₄ (solid black line), and Kir6.2₄ + ATP (broken black line) simulations. (B) Subspace overlap analysis, showing the fractional overlap between the first 10 eigenvectors of trajectory 1 as a function of the number of eigenvectors included from trajectory 2. The upper group of curves (labeled AD vs. AD) correspond to comparing subunits A and D in trajectory 1 with subunits A and D in trajectory 2 (see inset schematic diagram for subunit nomenclature). The trajectories compared are Kir6.2₄ versus Kir6.2₄ +ATP (solid black line), Kir3.1₄ versus Kir6.2₄ (broken black line), and Kir3.1₄ versus Kir6.2₄ + ATP (solid shaded line). The lower curve (labeled AD vs. BC) corresponds to comparing subunits A and D in trajectory 1 with subunits B and C in trajectory 2, where trajectory 1 is Kir6.2₄ and trajectory 2 is Kir6.2₄ + ATP (broken shaded line).

We were interested in the relative motions of the four subunits of each tetramer, particularly in the context of recent discussions of symmetry-breaking (asymmetric) motions of subunits within the pentameric rings of the ligand-binding domain of the α7 nicotinic receptor (Henchman et al., 2003). We therefore analyzed the overlap of the principal components of each system onto the essential spaces (e.g., the first 10 eigenvectors) extracted from the trajectories of different subunits pairs in all our simulations. The results (Fig. 3 B) indicate that, despite starting off from symmetrical structures/models, if one chooses an equivalent pair (e.g., subunits A and D in simulation 1 with A and D in simulation 2), then the overlap of the first 10 eigenvectors is ∼35%, whereas if one chooses a nonequivalent pair (e.g., subunits A and D in simulation 1 with subunits B and C in simulation 2), the overlap is significantly less (<20%). Thus, even though sampling of motions is inevitably incomplete, there is clear evidence for an asymmetry in the motion of the tetramer, whereby it appears to move as a “dimer-of-dimers”. As will be seen, this is suggestive of possible gating models and so merits more detailed examination.

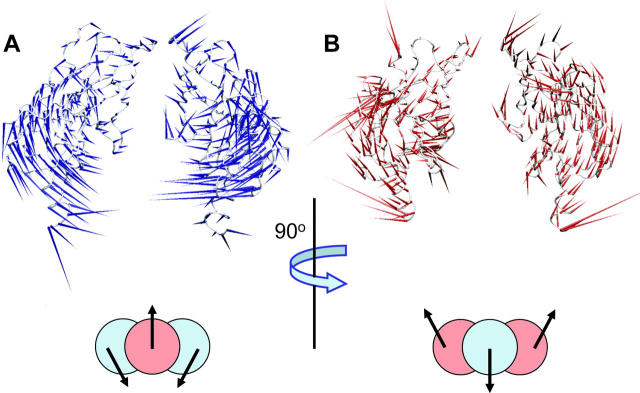
We may visualize this motion by using “porcupine” plots (Tai et al., 2001, 2002) to illustrate the direction and magnitudes of selected eigenvectors for each Cα atom. This is shown in Fig. 4 for the Kir6.2₄ simulation. It is evident that the four subunits of the tetramer move as two groups of two, in a dimer-of-dimers fashion. Thus, looking “down” onto the tetramer along the central fourfold axis from the membrane side, two opposite subunits (e.g., A and D) move “upward”, while the other two (e.g., B and C) move “downward”. This may correspond to an “intrinsic” motion of a tetrameric assembly of subunits.

FIGURE 4.

“Porcupine” plots of the first eigenvector for simulation Kir6.2₄. The protein is shown as a Cα trace. The arrows attached to each Cα atom indicate the direction of the eigenvector and the magnitude of the corresponding eigenvalue. Subunits A and D are shown in A and subunits B and C in B. (The two views are related by a 90° rotation). The schematic diagrams summarize the motions of the four subunits (A, D = blue; B, C = red) revealed by the eigenvectors.

As will be discussed in more detail below, this is suggestive of a mechanism for coupling of C-terminal domain motions to gating of the TM channel. As stressed above, 10-ns simulations are too short to reveal details of channel gating motions directly. However, they may provide some clues. We are aware that sampling of protein motions in such simulations is far from complete. However, we do have a test of the significance of the motions observed, namely, comparison between simulations of homologous proteins. This has proved valuable in several other systems (Pang et al., 2003). Therefore in Fig. 5, we compare porcupine plots for the first eigenvectors of the four tetramer simulations. Although there are differences between the simulations with respect to the motions sampled, it is evident the basic dimer-of-dimers pattern (i.e., two subunits moving “up” while the other two move “down”) is conserved. This increases our confidence concerning the significance of this result. This conclusion is further supported by examination of the second eigenvector. This also indicates dimer-of-dimers motion. This is encouraging as taken together the first and second eigenvectors account for between 50% and 60% of the motions in the simulation.

FIGURE 5.

Porcupine plots of the first eigenvector for simulations (A) Kir3.1₄, (B) Kir6.2₄, and (C) Kir6.2₄ + ATP. In each case all four subunits are shown, and the tetramer is oriented such that the “upward” moving subunits are on the left and right sides of the diagram.

This result is suggestive of a possible mechanism for channel gating, as will be discussed below. The simulations, as they are only of the C-terminal domains, cannot reveal the details of coupling between the intracellular and TM domains. However, they are suggestive of a model of how these motions may be coupled. The analysis of the eigenvectors did not, however, provide any indication of a difference in Kir6.2₄ motions in the presence and absence of ATP. This may require more extended simulations than are currently feasible, and also the inclusion of the N-terminal tail component of the intracellular domain.

Kir6.2/ATP interactions

It has been shown experimentally that K185 binds to β-phosphate of ATP (Fig. 6 A). Mutation of this residue to Asp or Glu completely abolishes the binding of ATP to the channel (Reimann et al., 1999). The tight K185/ATP interaction is maintained in the Kir6.2 monomer (Fig. 6 B) and in one subunit in the Kir6.2₄ (tetramer) simulation (Fig. 6 C; in the three remaining subunits, the average distance is slightly greater than would be consistent with H-bonding, i.e., >3.5 Å, but is still consistent with an electrostatic interaction). There does not seem to be any modulation of K185 flexibility by the presence or absence of ATP in the tetramer simulations, whereas in the Kir6.2 monomer simulations, there is a small increase in Cα flexibility in this region in the absence of ATP (Fig. 2 E).

FIGURE 6.

(A) Interaction of the K185 side chain with the β-phosphate of ATP in model/simulation Kir6.2₄ + ATP (illustrated using the starting model for the simulation). This interaction is maintained in (B) the Kir6.2 + ATP (monomer) simulation, and in (C) one subunit in the Kir6.2₄ + ATP (tetramer) simulation. In both B and C, the distance between the P atoms of the β-phosphate of ATP and the Nζ atom of the side chain of K185 is shown as a function of time.

During the course of the simulation, the adenine ring of ATP undergoes substantial motion while remaining within the binding site. This motion may result from the absence of N-terminal residues from the model. It results in disruption of interactions: of the backbone carbonyl oxygen of R301 with N6 in the pyrimidine ring of ATP and between the side chain carbonyl oxygen of E179 and N6 of the pyrimidine ring. However, the ATP molecule is not fully displaced from its binding site in any of the simulations, and the RMSF values for residues that interact with and contribute to the binding site of ATP are quite low. It has also been shown experimentally that R50 (Trapp et al., 2003) interacts with the β-phosphate of ATP. However, this interaction is absent from our simulations due to the absence of a complete N-terminus from the template structure. This may explain why we do not see a conformational change triggered by ATP in our simulations. Alternatively, such a conformational change may also require the presence of the TM domain. However, this does not exclude a possible role for the dimer-of-dimers motion in gating. Rather, we would suggest that the dimer-of-dimers motion is an intrinsic property of the intracellular domain that may be modulated by the binding of ATP to the intact channel.

Coarse-grained simulations

One criticism of MD simulations is that a 10-ns timescale is insufficient to reveal conformational changes underlying gating. Of course, we do not as yet know the timescale of the gating transition per se (as opposed to the mean duration between gating transitions), but it is likely to be on at least a microsecond timescale. Therefore, even if the current simulations were extended 10-fold, we would remain uncertain about whether we had adequately sampled the conformational changes. We have therefore used an alternative, coarse-grained model of protein dynamics to investigate the Kir3.1 intracellular domain. These simulations are based upon an anistropic network model that has been used to investigate the dynamics of a number of proteins (Atilgan et al., 2001). Network models (both anisotropic and Gaussian) have been shown to be capable of reproducing crystallographic B-values (Atilgan et al., 2001; Bahar et al., 1997; Keskin et al., 2000).

To evaluate the different approaches to Kir3.1 intracellular domain dynamics, we have compared mean-square fluctuations for each residue (i.e., Cα atom) calculated from the MD simulation and from the ANM (see Fig. 7 A). The overall agreement is good, with the same regions showing higher and lower than average flexibility in the two approaches. A scatter plot of the MSFs (Fig. 7 B) gives a correlation coefficient of 0.87 for MD versus ANM. Thus the coarse-grained and atomistic simulations seem to be providing similar pictures of the overall dynamics of the Kir3.1 intracellular domain.

FIGURE 7.

(A) Comparison of Cα atom mean-square fluctuations (MSFs) MD simulation (shaded line) and anisotropic network modeling (ANM; black line) for Kir3.1₄, as a function of residue number. Note that the MSFs have been normalized to a unit average and so are in arbitrary units. (B) Scatter plot of MD-derived MSFs versus ANM-derived MSFs, with a correlation coefficient of R = 0.87. (C) Porcupine plots of the first eigenvector (i.e., the lowest frequency mode) for the ANM analysis of Kir3.1₄. The tetramer orientation is similar to that in Fig. 4 A.

Having compared the ANM with the MD simulations, one may probe the ANM results in a little more detail. In particular, the first eigenvector from the ANM (corresponding to the lowest frequency mode) for Kir3.1₄ supports an asymmetric dimer-of-dimers motion of the protein similar to that observed in the MD simulations (Fig. 7 B). Thus, both atomistic and coarse-grained simulations suggest dimer-of-dimers motion is an intrinsic property of the intracellular domain tetramer structure.

DISCUSSION

Biological relevance of the simulation results

It is possible to interpret the simulation data in the context of a general model for Kir channel gating. First, let us review some of the relevant experimental data. Structural studies by MacKinnon and colleagues comparing the conformations of the bacterial K channels KcsA and MthK (Jiang et al., 2002b) have implicated a hinge-bending transition, at a conserved glycine, of the pore-lining M2 helices in gating of K channels. In this model, control of channel gating by ligand or protein binding to a C-terminal domain would require transmission of a conformational change in the C-terminal domain to the pore-lining helices. It is also suggested that that Kir3.1 C-terminal domain may fit the MthK (open) channel conformation “more naturally” than the KcsA (closed) channel (Nishida and MacKinnon, 2002). The nature of the linker region between a C-terminal domain and the pore-lining helices has not been resolved crystallographically for any K channel other than KirBac, for which there are as yet no functional data. However, studies of mutant BK channels in which S6-RCK1 linkers of different length were created by either deleting or adding amino acids to each linker suggested that the linker might act as a spring conveying conformational change from the C-terminal domain to the pore-lining helix gate (Niu et al., 2004). Structural studies of KirBac (Kuo et al., 2003) have revealed dimer-of-dimers symmetry in the (bacterial) intracellular domain and are suggestive of a model in which inner helices bend to open the channel. Such bending motions of the pore-lining (M2) helices are supported by MD simulations of the isolated TM domain of KirBac (Domene et al., 2004; also Grottesi et al., 2005), although one should recall that recent studies of, e.g., Kv channels, suggest that different K channels may have different patterns of distortion of their pore-lining helices (Webster et al., 2004).

We may combine these experimental and simulation data with the results of this study to formulate a plausible general model for Kir gating (Fig. 8). In particular, the results of the principal components analysis of the simulations suggest that adjacent subunits move in opposite directions with respect to each other, i.e., a dimer-of-dimers type motion. These motions are suggestive of larger scale subunit motions that could be conveyed by the (crystallographically unresolved) linkers to the TM domain. Based on MacKinnon and colleagues' suggestion that the Kir3.1 C-terminal domain fits better to the open state of the TM domain, this might suggest that the transition from a tetrameric to a dimer-of-dimers arrangement of the C-terminal domains could be associated with closing of the channel (Fig. 7). We would expect ATP binding to modulate this transition. However, the effect of ATP is difficult to model given the absence of key residues from the various template structures.

FIGURE 8.

Proposed gating mechanism. Of the TM domain, only the M2 helices (cyan) of two opposite subunits are shown embedded (for clarity). In the open state, these helices are kinked. Asymmetric movements of the C-terminal domains (pale blue and pink circles), as indicated by the arrows, lead to closure of the channel via adoption of a dimer-of-dimers like packing by the M2 helices (which also lose much/all of their kink upon closure).

These simulation results are therefore supportive of a model in which “symmetry breaking” of a ring of intracellular “gatekeeper” domains plays an important role in gating of the channel per se. In this respect, it is of interest that MD simulations of a homology model of the ligand-binding domain of the α7 nicotinic acetylcholine receptor (Henchman et al., 2003) suggest that symmetry-breaking motions in this homopentameric receptor also may be related to channel gating. We also note that dimer-of-dimers symmetry has been observed in the intracellular domains in the crystal structure of the KirBac (in its closed channel conformation; Kuo et al., 2003). It has also been suggested that the cyclic nucleotide-binding intracellular domain of the HCN channel (Zagotta et al., 2003) may undergo a dimer-of-dimers to tetramer gating switch upon binding cAMP (Ulens and Siegelbaum, 2003). A dimer-of-dimers structure has also been suggested for the ligand-binding domain of glutamate receptor channels (Sun et al., 2002), the TM domain of which has some distant homology with that of K channels (Kuner et al., 2003). Thus, deviations from exact rotational symmetry in gatekeeper domains may prove to be a general property of ion channels, although in different channels the switch may be associated with either opening or closing a channel.

Methodological issues and limitations

One methodological implication of this study is that it adds to the evidence that MD may be used to evaluate and study homology models of channels and related proteins (Capener et al., 2002). This is of especial importance in the context of membrane proteins and ion channels for which the majority of the structure are either of bacterial homologs and/or of fragments of more complex proteins (Armstrong et al., 1998; Armstrong and Gouaux, 2000; Brejc et al., 2001; Celie et al., 2004; Gouaux and Furukawa, 2003; Mayer et al., 2001).

There are two principal limitations of this study: it is restricted to the C-terminal domain rather than the intact channel; and from a purely statistical point of view, it is well understood that even ∼10-ns simulations do not fully sample the motions of the protein in question (Faraldo-Gómez et al., 2004). To answer the second question, we have some confidence in the significance of the simulation results given that all three simulations of tetramers exhibited similar motions. The correlation between the motions observed for the Kir.3.1₄ tetrameric crystal structure simulation and the Kir6.2₄ tetrameric homology model simulation suggests we may have captured an essential aspect of the motion of Kir intracellular domains. However, more extended simulations will be required to evaluate the adequacy of sampling of motions in the conformational space for these structures.

Coarse-grained (ANM) calculations also provide support for dimer-of-dimers motion of the Kir intracellular domain tetramer. However, one still cannot be certain that larger scale conformational changes may occur. Both approaches to intracellular domain dynamics (MD simulations and ANM calculations) sample, with differing granularity, the local free energy surface. Thus, they may reveal the “first step” toward gating but cannot reveal or exclude larger-scale conformational changes. However, we draw some encouragement from studies of gating motions of the TM domain of K channels. In this latter case, comparison of crystallographic structures (Jiang et al., 2002b), normal modes analysis (Shen et al., 2002), and MD simulations (Biggin and Sansom, 2002; Grottesi et al., 2005) all support a model in which motion of the M2 helices opens the channel.

To explore the relationship of intracellular domain motions to those of intact Kir channels, models and extended simulations of, e.g., an intact channel model, will be needed (S. Haider, F. M. Ashcroft, and M. S. P. Sansom, unpublished). Even if one has such models and simulations, it is of considerable value to determine the intrinsic dynamics of the isolated C-terminal domain (this study) and of the TM domain (Domene et al., 2004) to dissect out the roles, respectively, of the gatekeeper and the gate in the mechanism of Kir function.

In summary, our MD simulations of Kir C-terminal domains suggest a dimer-of-dimers like motion that may be related to gating of Kir channels. This provides an experimentally testable hypothesis, which could be addressed using a variety of techniques including, e.g., FRET (Cha et al., 1999; Glauner et al., 1999; Tsuboi et al., 2004), site-directed spin labeling (Perozo et al., 1999), or cross-linking of cysteine mutants with Cd²⁺ (Loussouarn et al., 2000; Webster et al., 2004), all of which have been applied to K channels.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.