Electrogenic Partial Reactions of the Gastric H,K-ATPase

Abstract

The fluorescent styryl dye RH421 was used to identify and investigate electrogenic reaction steps of the H,K-ATPase pump cycle. Equilibrium titration experiments were performed with membrane vesicles isolated from hog gastric mucosa, and cytoplasmic and luminal binding of K⁺ and H⁺ ions was studied. It was found that the binding and release steps of both ion species in both principal conformations of the ion pump, E₁ and P-E₂, are electrogenic, whereas the conformation transitions do not contribute significantly to a charge movement within the membrane dielectric. This behavior is in agreement with the transport mechanism found for the Na,K-ATPase and the sarcoplasmic reticulum Ca-ATPase. The data were analyzed on the basis of the Post-Albers reaction cycle. For proton binding, two pK values were found in both conformations: 6.7 and ≤4.5 in the E₁ conformation; 6.7 and ≤2 in the P-E₂ conformation. The equilibrium dissociation constants for K⁺ binding on the cytoplasmic side were 11 and 16 mM. The respective equilibrium dissociation constants on the luminal side were obtained via K⁺ concentration dependence of the enzyme activity and determined to be 0.11 mM for both luminal binding sites.

INTRODUCTION

The enzyme responsible for HCl secretion by parietal cells in the gastric mucosa is the H,K-ATPase (Durbin et al., 1974; Sachs et al., 1976). This protein is a member of the family of P₂-type ATPases, closely related to the Na,K-ATPase and the sarcoplasmic reticulum (SR) Ca-ATPase (Shull and Lingrel, 1986; Sweadner and Donnet, 2001). Numerous publications showed that the gastric H,K-ATPase exchanges H⁺ for K⁺ by a mechanism similar to that of the Na,K-ATPase (Helmich-de Jong et al., 1985; Lorentzon et al., 1988; Rabon et al., 1982; Wallmark et al., 1980). The stoichiometry of the H,K-ATPase is 2 H⁺/2 K⁺/1 ATP (Rabon et al., 1982), so that the overall transport is electroneutral at pH ≥ 6.1 (Fig. 1), but must fall to 1 H⁺/1 K⁺ at the very acidic luminal pH of the stimulated parietal cell due to the thermodynamic limitation of energy yield from the hydrolysis of ATP. Nevertheless, two elementary charges have to be translocated through the membrane in each half-cycle under our pH conditions. This process, a movement of charge through the membrane dielectric, is termed “electrogenic”, and it is characterized by two properties: 1), it generates a current component that affects the membrane potential in cells, and 2), the kinetics of electrogenic transport steps can be modulated by the membrane potential (Läuger, 1991). In the case of the H,K-ATPase the electrogenicity of the H⁺ transporting half-cycle was demonstrated by a biophysical technique (van der Hijden et al., 1990).

FIGURE 1.

Simplified pump cycle of the H,K-ATPase on the basis of the Post-Albers scheme of P-type ATPases. E₁ and E₂P represent the two basic conformations of the protein. In E₁ the ion-binding sites are accessible from the cytoplasmic side (left side of the cycle), in E₂P from the luminal side (right side of the cycle). In both occluded states, (H₂)E₁P and (K₂)E₂, the ions are unable to exchange with either aqueous phase. The stoichiometry of two H⁺ and two K⁺ ions, which are moved in opposite directions, accounts for the overall electroneutrality of the transport process.

Because the H,K-ATPase-containing membrane preparations are small vesicles purified from parietal cells, direct electrophysiological techniques cannot be applied to analyze the pump cycle in terms of electrogenic reaction steps. An alternative method is the use of an electrochromic styryl dye (Klodos, 1994). Such dyes have been already successfully applied to identify and analyze the electrogenic reaction steps of the Na,K-ATPase and the SR Ca-ATPase (Pedersen et al., 2002; Peinelt and Apell, 2002; Stürmer et al., 1991). From these studies, it was shown that in both ATPase species the main electrogenic events are binding and release of the transported ions on both sides of the membrane. In addition, in equilibrium titration experiments, the binding affinities of the transported ions could be determined as well as a number of rate constants of the rate-limiting steps in the investigated partial reactions (for review, see Apell, 2003).

Therefore, we extended this technique to investigations of the H,K-ATPase to gain detailed information on the transport mechanism of this ion pump, which could not be obtained by other methods, and to compare it with the results obtained for other closely related members of the family of P-type ATPases. In this article we present the results from steady-state ligand-binding experiments.

MATERIALS AND METHODS

Materials

Phosphoenolpyruvate, pyruvate kinase, lactate dehydrogenase, NADH, and ATP (disodium salt, special quality) were obtained from Boehringer (Mannheim, Germany). The ionophore nigericin was ordered from Sigma (Steinheim, Germany) and the fluorescent dye RH421 from MoBiTec (Göttingen, Germany). Dye purity was checked by thin-layer chromatography. SCH28080 was from Altana Pharma (Konstanz, Germany). All other reagents were the highest grade commercially available.

Enzyme preparation

The gastric H,K-ATPase was derived from hog gastric mucosa by previously published methods, which involve differential and density gradient centrifugation (Rabon et al., 1988). The crude gastric mucosal membranes were collected from the stomach and homogenized in a solution of 0.25 M sucrose, 5 mM PIPES/Tris, pH 6.8, and 1 mM EGTA. The homogenate was centrifuged at 11,000 rpm in a Sorvall GSA rotor for 45 min. The supernatant was centrifuged at 30,000 rpm in a Beckman (Fullerton, CA) type-30 rotor for 1 h. The microsomal pellet was resuspended in a solution of 0.25 M sucrose, 5 mM PIPES/Tris, pH 6.8, and 1 mM EGTA. The microsomal suspension was purified using Z-60 zonal rotor. In the isolated vesicles ∼90% of the H,K-ATPase is oriented as in the parietal cell with the cytoplasmic side outward.

Specific ATPase activity of the H,K-ATPase was determined by two methods. 1), The pyruvate kinase/lactate dehydrogenase assay (Schwartz et al., 1971); the specific activity of the H,K-ATPase-containing vesicles preparations was in the range of 80–120 μmol P_i per milligram total protein and hour at 37°C. The enzyme activity could be blocked completely by the H,K-ATPase-specific inhibitor SCH28080. 2), K⁺-stimulated ATPase activity was measured by P_i determination with malachite green (Vagin et al., 2002); the membrane fractions were incubated at 37°C for 1 h in Na⁺ free buffer (25 mM imidazole, 1 mM EDTA, and 5 mM MgCl₂, pH 7.2, 0.03 mM ouabain, 0.02 μM bafilomycin, 0.03 μM tharpsigargin) with 4.8 mM TRIS-ATP and the indicated K⁺ concentration. In the presence of 2 mM K⁺ a specific activity of 143 μmol P_i per milligram total protein and hour was obtained. In the presence of 450 μM SCH28080 no significant residual ATP hydrolysis was found.

Detection of partial reactions by the electrochromic styryl dye RH421

Fluorescence measurements were carried out in a Perkin-Elmer (Rodgau, Germany) LS 50B fluorescence spectrophotometer as described before (Schneeberger and Apell, 1999). The excitation wavelength was set to 580 nm and the emission wavelength to 650 nm (slit width 15 and 20 nm, respectively). Equilibrium titration experiments were started in standard buffer (25 mM imidazole, 1 mM EDTA, and 5 mM MgCl₂, pH 8.5, adjusted with NaOH). Before the fluorescence experiments 10 μg H,K-ATPase (in the form of purified vesicles) was incubated at room temperature for 30 min in 43 μl standard buffer and 0.5 mM nigericin. Thereafter, 200 nM RH421 and 3 min later the incubated protein preparation were added to a thermostated fluorescence cuvette containing 1 ml standard buffer. The solution was equilibrated until a stable fluorescence signal was obtained. This fluorescence amplitude, F₀, at pH 8.5 and in the absence of K⁺ ions was registered, and used as a reference level for all subsequent determinations of electrogenic responses. Titration experiments were carried out by adding small aliquots of concentrated salt solutions or HCl until no further changes of fluorescence intensity could be observed. To allow a comparison between different titration experiments or averaging of data, relative fluorescence changes, ΔF(t)/F₀ = (F(t) − F₀) / F₀, were calculated with respect to the initial reference intensity, F₀. Specific fluorescence levels could be assigned to defined states of the pump cycle of the H,K-ATPase, corresponding to the experimental results obtained from substrate-dependent partial reactions of the Na,K-ATPase (Heyse et al., 1994). All experiments were performed at 18.5 ± 0.5°C.

To exclude unspecific fluorescence changes that could have been produced by processes other than ion binding or release, a series of control experiments was performed. Other ionophores, such as gramicidin D (1 μM) and valinomycin (1 μM) were used in addition to nigericin to short-circuit the vesicle membrane for all kinds of monovalent cations. Under these conditions the fluorescence changes in K⁺ and H⁺ titration experiments were not significantly different. This finding demonstrated that no transmembrane electric potentials were detected by RH421. The H,K-ATPase-containing vesicles were also incubated at 56°C for 30 min to inactivate the ion pump completely. Thereafter, with no enzymatic activity no fluorescence changes could be observed when highest concentrations of K⁺, H⁺, or ATP were added in the presence or absence of nigericin and/or gramicidin.

RESULTS

In the case of the SR Ca-ATPase and Na,K-ATPase it was demonstrated that the major charge-moving reactions of the pump cycle are the ion binding and release steps of the pump cycle (for a review, see Apell, 2003). Due to the close homology of the amino acid sequence of the Na,K-ATPase and the H,K-ATPase (Fagan and Saier, 1994; Maeda et al., 1990) it may be expected that the fluorescence method that was successfully applied to study these reaction steps (Bühler et al., 1991; Stürmer et al., 1991; Apell and Diller, 2002), should provide similar insight into the ion-transport mechanism of the H,K-ATPase.

Identification of electrogenic partial reactions

The electrogenicity of partial reactions that can be induced by substrate addition were studied by fluorescence experiments performed as described in the Methods section, starting in a buffer at pH 8.5 and without K⁺ present. If a pK of the cytoplasmic binding sites is assumed to be ∼6.7 for the first and below 4.5 for the second site (see below), then <1% of the sites would be occupied by H⁺ at pH 8.5. Under this condition most of the ion pumps are trapped with empty binding sites in state E₁ (Fig. 1). This state is defined as the reference state to allow the comparison of the fluorescence signals from various experiments. According to the Post-Albers cycle of the H,K-ATPase (Fig. 1), a series of experiments were performed in which defined states could be stabilized by substrate additions. In Fig. 2 four of such exemplary measurements are shown. In the first experiment (Fig. 2 A) HCl was added to the enzyme in state E₁ to obtain pH 6.5 so that ∼30% of all binding sites can be assumed to be occupied by H⁺ ions. This is reflected by a fluorescence decrease of ∼10%. Subsequent addition of 2 mM ATP induced the conformation transition of ion pumps that passed through the state (H₂)E₁-P into the phosphorylated states E₂P (cf. Fig. 1). The relaxation into a new equilibrium was fast, most probably controlled by mixing of the cuvette contents with a magnetic stirrer. Due to the presence of the ionophore nigericin the luminal pH was also ∼6.5. Because the fluorescence level did not change, it may be concluded that the amount of charges in the binding sites did not change, and the majority of pumps are in state P-E₂H. Further addition of saturating KCl (240 mM) led to binding of K⁺ and a relaxation into a new steady-state condition. For the H,K-ATPase it was found that, in contrast to the Na,K-ATPase, enzyme dephosphorylation (and K⁺ occlusion) as well as low-affinity ATP binding to the E₂ conformation of the protein the K⁺-occluded state are not stabilized at low K⁺ concentrations (Helmich-de Jong et al., 1986; Lorentzon et al., 1988). In the presence of cytoplasmic H⁺, luminal K⁺, and ATP, all substrates are present to allow repetitive turnover of the ion pump. Addition of high concentrations of K⁺ (>20 mM), however, locks a major part of ion pumps in the state (K₂)E₂ by a strong shift of the equilibrium in the reaction, E₁ + 2 K⁺ ↔ K₂E₁ ↔ (K₂)E₂, to the right. This process, the so-called K⁺ back-binding, prevents most of the pumps from running through their cycle.

FIGURE 2.

Time course of the fluorescence signal of the electrochromic styryl dye RH421 indicating substrate-dependent partial reactions of the H,K-ATPase. The initial state of all four experiments shown was E₁ (Fig. 1), which was obtained with 10 μg H,K-ATPase in standard buffer at pH 8.5 and with no K⁺ ions present. This level was defined to be F₀. The fluorescence scale on all four panels is the same. (A) Addition of HCl (14.5 mM) produced a pH decrease to 6.5, ATP was added to obtain a concentration of 2 mM in the cuvette, and KCl was added to obtain a final concentration of 240 mM. (B–D) Addition of the substrates in varying order produced different sequences of protein states as indicated in the panels. The label “E₂(K₂) + ?” was chosen to point out that in the presence of 30 μM (free) H⁺ and 2 mM ATP the pump has all substrates to cycle, and the reduced fluorescence decrease, when compared to the maximal possible in the state (K₂)E₂, indicates that other states were also populated. Although most responses upon substrate addition were fast, i.e., within stirring time in the cuvette, binding of H⁺ to the luminal binding sites showed a slow kinetics with time constants τ > 10 s (B).

In Fig. 2 B, 2 mM ATP was added to the enzyme in state E₁ at pH 8.5. A small drop in pH to ∼8.15 occurred, because imidazole has only a low buffering capacity at such a high pH, and ATP is a buffer substance itself. Even under this condition it may be expected that the small fraction of enzyme populates state H₂E₁ (<0.1‰, according to the model discussed below). It will be phosphorylated and make the transition into the E₂P conformation. How much of the E₁ state is removed in the absence of K⁺ depends, however, on the rate of spontaneous dephosphorylation of E₂P. This rate was found to be detectable and in the order of 0.2% of the maximum activity (Vagin et al., 2001). In this partial reaction (Fig. 2 B) no significant difference of the specific fluorescence intensity of the initial and final state, E₁ and P-E₂, respectively, was found. Therefore, this finding does not allow a discrimination between the preferred state of the pump at high pH, which may be E₁ or P-E₂. When subsequently the H⁺ concentration was increased to pH 6.5, a significant drop of fluorescence signal was observed to the same level as observed in panel A after addition of HCl and ATP. This level corresponds to state P-E₂H. The slow fluorescence decrease of this partial reaction into the new equilibrium state is remarkable. In several of these experiments the time course could always be fitted by a single exponential with a time constant of between 10 and 30 s. A reasonable explanation is an increased reaction flux, HE₁ → P-E₂H, because at pH 6.5 the H₂E₁ population may be estimated to be ∼0.5%. The increased phosphorylation reaction at pH 6.5, which is now probably larger than the proposed spontaneous dephosphorylation at pH 6.5, leads to a relaxation into the new steady state that is shifted toward the E₂P states. The time course of this relaxation process is controlled by the rate constants of the conformation transition and of the dephosphorylation, and can be expected to be slow. Addition of 240 mM KCl produced a same fast response as found in the experiment of Fig. 2 A. The fast response with subsequent K⁺ addition contradicts the possible assumption that a slow ion exchange across the membrane caused the slow response on the H⁺ addition.

When 240 mM KCl was added first (Fig. 2 C) while buffer pH was 8.5, an instantaneous fluorescence decrease in the order of 25% occurred, representing the partial reaction, E₁ → (K₂)E₂. Subsequent addition of 2 mM ATP was without detectable effect but addition of H⁺ ions (to obtain pH 6.5) led to a fluorescence increase of ∼7%. This observation points to the fact that in a small fraction of the ion pumps, K⁺ is displaced from the binding sites by binding of H⁺ even at extremely high K⁺ concentrations. In principle, this buffer composition provided all substrates for turnover condition of the pump cycle, however, as mentioned above, such a high K⁺ concentration strongly inhibits turnover. The fluorescence level obtained under this condition was in agreement with the final level in Fig. 2, A and B. When the sequence of KCl and ATP addition was altered (Fig. 2 D) the resulting final fluorescence level was the same as in Fig. 2 C, indicating that ATP did not affect formation of the state (K₂)E₂ at pH 8.5.

Cytoplasmic ion binding

The fluorescence decreases observed after addition of H⁺ or K⁺ in both conformations as shown in Fig. 2 were induced by the highest concentrations of substrates used in the experiments. When additions were performed in small aliquots, titration curves could be recorded, which provided insight into the binding kinetics of the ions to the sites in both principal conformations, E₁ and P-E₂.

To study the interaction of both ion species with the ion binding sites and their competition, series of RH421 fluorescence measurements were performed. In the E₁ conformation H⁺ binding was studied in the absence and presence of K⁺ ions (0–100 mM KCl), as well as K⁺ binding at pH values between pH 6.3 and 8.5. As a lower experimental pH limit a value of ∼6.3 was chosen to avoid artifacts that were found at pH < 5.5. When buffer pH was lowered beyond this value, a dramatic fluorescence decrease was observed down to a level similar to that before the addition of the membrane vesicles. This phenomenon may be explained probably by precipitation of the RH421-containing vesicles in the standard buffer used. This effect was not further studied because it was not relevant for the understanding of protein function.

Various measurements could be compared by normalization of the fluorescence levels as described in the Materials and Methods section, because all experiments were started in standard buffer at pH 8.5 and 0 K⁺ to obtain the reference level, F₀. The desired pH was adjusted by addition of HCl before a stepwise addition of KCl. In the case of pH titration experiments, KCl was added after having recorded F₀ and before stepwise additions of HCl. The results of both types of experiments are plotted in Fig. 3. Each data point represents the average of three or four titration experiments. Error bars were omitted for sake of clarity. As can be seen in Fig. 3 A, in the presence of 10 mM KCl the fluorescence signals were almost pH independent, whereas at lower K⁺ concentrations, the fluorescence decreased with increasing H⁺ concentration. According to the detection mechanism of the styryl dye, RH421, a fluorescence decrease indicates uptake of additional positive charge into the membrane domain of the protein. At K⁺ concentrations >10 mM the observed fluorescence increase at pH < 7 indicates a partial replacement of two K⁺ ions by one H⁺. The information obtained from K⁺ titration experiments at various pH is consistent with the results of the H⁺ binding experiments. At ∼10 mM K⁺ all titration curves merge, whereas at lower K⁺ concentrations the fluorescence levels decrease with pH, and increase with pH at higher K⁺ concentrations (Fig. 3 B).

FIGURE 3.

Titration of the cytoplasmic binding sites of the H,K-ATPase with H⁺ and K⁺ ions as detected by the RH421 fluorescence. The mutual effect of both ions on each other indicates competitive behavior in the binding sites. (A) pH titration experiments in the presence of the indicated K⁺ concentrations. (B) K⁺ titrations in buffer of various pH as indicated. The lines drawn through the experimental data were obtained by least-square fits of Eq. A12 with the one set of kinetic parameters: K_H,1 = 2.0 × 10⁻⁷ M (pK 6.7), K_H,2 = 3.2 × 10⁻⁵ M (pK 4.5), K_K,1 = 11 mM, and K_K,2 = 16 mM. Data points are mean values of at least three sets of experiments. The error bars were removed for the sake of clarity.

Luminal ion binding

Corresponding experiments were performed to study binding and competitive behavior of ions at the luminal binding sites of the H,K-ATPase. The experiments were also started in standard buffer at pH 8.5. Addition of 2 mM ATP reduced buffer pH to 8.15. Even at this high pH the pumps are able to perform with a very low rate the partial reaction 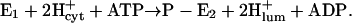The fraction of the pumps that is maintained in the state P-E₂ (due to the absence of K⁺ ions) depends on the ratio of phosphorylation and dephosphorylation rates of the pumps. At low pH, when the phosphorylation reaction is significantly overcoming spontaneous dephosphorylation of the enzyme, the forward rate dominates, and the phosphorylated states, P-E₂H and P-E₂, will be populated preferentially. Because the vesicles were incubated with nigericin before the measurements, H⁺ and K⁺ ions added to the buffer in the cuvette were able to equilibrate rapidly across the vesicle membrane and were able to bind to the ion sites accessible from the luminal phase. In Fig. 4 the results of these experiments are shown. Again, the presented data are the average of three or four identical titrations. (The pH titration in the absence of KCl represents the average of six measurements.) In control experiments incubations were also performed in the presence of 440 μM nigericin + 20 μM valinomycin + 20 μM gramicidin to obtain definitely nonlimiting conductance for K⁺ and H⁺ across the vesicle membrane. No significant differences to experiments with nigericin only could be observed.

FIGURE 4.

Titration of the luminal binding sites of the H,K-ATPase with H⁺ and K⁺ ions as detected by the RH421 fluorescence. The mutual effect of both ions on each other indicates competitive behavior in the binding sites. (A) pH titration experiments in the presence of the indicated K⁺ concentrations. (B) K⁺ titrations in buffer of various pH as indicated. The lines drawn through the experimental data were obtained by least-square fits according to Eq. A26 of the reaction model described in Appendix II. The reaction constants are given in Table 1. Data points are mean values of at least three sets of experiments. The error bars were removed for the sake of clarity.

In the absence of K⁺ (uppermost curve in Fig. 4 A) the reaction observed upon addition of H⁺ could be fitted with the phenomenological Hill function for a logarithmic plot,

(1)

and a pK of 6.7 ± 0.07, n_H = 1.23 ± 0.18, and ΔF_max/F₀ = −0.17 ± 0.01 were obtained. When the data were analyzed by the analytical solution under the assumption of the simple reaction scheme, P-E₂ ↔ P-E₂H ↔ P-E₂H₂, the pK values for the two binding steps were determined to be 6.7 for the first and 1 for the second H⁺ bound.

In the presence of saturating concentrations of ATP, a pH and K⁺ dependence of the fluorescence was observed (Fig. 4) similar to findings obtained by cytoplasmic ion binding (Fig. 3). This observation indicates comparable binding kinetics. When compared with the experiments in the E₁ conformation of the ion pump, significant differences in the K⁺-concentration dependence are obvious: a pH-independent fluorescence signal was found at the higher K⁺ concentration of 20 mM (Fig. 4 A), which corresponds to a merging of the K⁺ titration curves at ∼20 mM in Fig. 4 B. The second difference between luminal and cytoplasmic binding behavior is the stronger pH effect below pH 7 at high K⁺ concentrations on the luminal side. The more pronounced increase of the fluorescence signal indicates either a higher H⁺ or a lower K⁺ affinity on the luminal side. When the pH-titration curves in the absence of K⁺ are compared in both conformations (uppermost trace in Figs. 3 A and 4 A), the differences are not large. The reason is that at high pH on the one hand a significant fraction of the enzyme is still in E₁ due to spontaneous dephosphorylation of the enzyme, and on the other hand that the H⁺ affinity for the first proton bound, P-E₂ → P-E₂H, is rather similar in both enzyme conformations.

Enzyme activity

From experiments in which the H,K-ATPase was activated by KCl additions in the presence of saturating ATP, a half-maximum enzyme activity was obtained at ∼0.2 mM (Wallmark et al., 1980). This finding is in contrast to the apparent K⁺ affinity as found in the experiments presented in Fig. 4, in which equilibrium titrations were detected by RH421 experiments. Therefore, K⁺-stimulated ATPase activity was investigated with the same enzyme preparation by determination of the amount of P_i released upon ATP hydrolysis at pH 7.2 and 37°C, under otherwise identical conditions to the experiments of Fig. 4. The results from experiments on K⁺-dependent enzyme activity are shown in Fig. 5. The K⁺-concentration dependence could be fitted by a simple binding isotherm, with a half saturating K⁺ concentration, K_m = 0.11 ± 0.01 mM and a maximal specific enzyme activity of 141 ± 3 μmol P_i per milligram protein and hour. At K⁺ concentrations above 10 mM the enzyme activity was reduced with increasing ion concentrations (data not shown). These findings agree well with previously published data (Wallmark et al., 1980).

FIGURE 5.

Dependence of the specific enzymatic activity on K⁺ concentration in the buffer. The activity was measured by P_i determination with malachite green at 37°C. The concentration dependence was fitted by simple binding isotherm with a K_m = 0.11 ± 0.01 mM and E_A,max = 140.5 ± 3 μmol P_i per milligram protein and hour.

Ion selectivity

The selectivity of the ion-binding sites in both conformations for other cations was investigated by titration experiments corresponding to those for K⁺ binding. Starting in the standard buffer at pH 8.5 (as level F₀) titration experiments were performed with NaCl and NH₄Cl. The normalized fluorescence decrease as function of the ion concentration is plotted in Fig. 6 A. For comparison, K⁺ titration data are included. The data could be fitted by an equation according to a single binding isotherm,

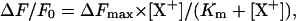(2)

where ΔF_max is the maximum fluorescence change at saturating concentrations of the ion [X⁺] and K_m is the half-saturating ion concentration. ΔF_max was determined to be −0.27 ± 0.01 for all three ion species in the measurements presented. K_m was ∼9.8 ± 1.1 mM for K⁺, 13.52 ± 0.6 mM for and 35.7 ± 1.8 mM for Na⁺ ions. When the data were analyzed in addition according to the model of Appendix I, two equilibrium dissociation constants could be determined for each ion species. They were 10 and 17 mM for K⁺ (see also Table 1), 15 and 50 mM for and 36 and 81 mM for Na⁺ ions.

FIGURE 6.

Ion selectivity of the binding sites in the two principal conformations, (A) E₁ and (B) P-E₂ in standard buffer at pH 8.5 for Na⁺, K⁺, and The fluorescence decrease is proportional to the occupation of the binding sites with cations and could be fitted with a simple binding isotherm (Eq. 2). For details see text.

TABLE 1.

Overview of the equilibrium dissociation constants of the H,K-ATPase determined from the experiments presented

Reaction	Constant	Fit value	Determination by
E1 ↔ HE1	pKH,1	6.7	pH titration without K+; Fig. 3 A
HE1 ↔ H2E1	pKH,2	≤4.5
E1 ↔ KE1	KK,1	11 mM	pH and K+ titrations in E1; Fig. 3 A
KE1 ↔ (K2)E2	KK,2	16 mM
P-E2 ↔ P-E2H	pLH,1	6.7 ± 1	pH titration in the presence of ATP and without K+; Fig. 4 A
P-E2H ↔ P-E2H2	pLH,2	≤2
P-E2 ↔ P-E2K	LK,1	0.11 mM	Enzyme activity; Fig. 5
P-E2K ↔ P-E2K2	LK,2	0.11 mM

Constants were used to fit the reaction scheme of Fig. 7 B to the experimental data of Figs. 3 and 4. The temperature of the experiments was 18.5 ± 0.5°C. (pK = 10^−K, pL = 10^−L).

Experiments were also performed in the E₂P conformation, which was induced by addition of 2 mM ATP before the titration of the ion binding sites with different cations. Under this condition a slightly different pattern was found (Fig. 6 B); again ΔF_max was the same for all three ion species (−0.23 ± 0.01). K_m was approximately the same for (12 mM) and K⁺ (13.4 mM). Na⁺ had, however, a significantly higher binding affinity (22.8 mM) when compared with binding to the sites in the E₁ conformation.

DISCUSSION

The experiments, performed with H,K-ATPase-containing vesicles isolated from parietal cells and with the styryl dye RH421, demonstrate that it is possible to investigate electrogenic partial reactions of the H,K-ATPase by the method published for two other P-type ATPases, the Na,K-ATPase and the SR Ca-ATPase (Butscher et al., 1999; Heyse et al., 1994; Pedersen et al., 2002). The observed fluorescence-intensity changes of the membrane-bound dye molecules are not generated by transmembrane potentials but by changes of the local electric field in the membrane dielectric, based on the mechanism of electrochromicity (Bühler et al., 1991; Pedersen et al., 2002). In this study the partial reactions of the H,K-ATPase were identified in which ions migrate into or out of the membrane domain of the pump protein, and the ion binding affinities were determined by equilibrium titration experiments in the form of equilibrium dissociation constants.

All ion binding and release reactions are electrogenic

When preparations of H,K-ATPase-containing vesicle are kept in specific but unphysiological buffers, defined protein conformations, or even a single state of the ion pump can be stabilized by an appropriate choice of ions and substrates. This property of the pump protein was exploited in fluorescence experiments with RH421 to detect charge movements correlated to transitions between several states of the pump cycle (Fig. 1) that were induced by respective substrate additions. Similar experiments have been performed with the Na,K-ATPase (Heyse et al., 1994; Stürmer et al., 1991) and the SR Ca-ATPase (Butscher et al., 1999) and provided valuable insight into the electrogenicity of these ion pumps.

The results presented in Fig. 2 reveal that all partial reactions in which ions bind to or are released from the H,K-ATPase are accompanied by changes of the RH421 fluorescence. This finding visualizes an electrogenic movement of ions into the interior of the protein's membrane domain. In contrast, the ATP-induced partial reactions, which include enzyme phosphorylation, ion occlusion, and the conformation transition, H₂E₁-P → P-E₂H₂, showed no remarkable fluorescence changes. This indicates that no significant charge movements occur in these reaction steps. Such a behavior may be explained by an (almost) immobile position of the ion-binding sites in the membrane domain of the pump while the pump runs through its cycle, found to be a common property of P-type ATPases (Apell, 2003). These findings are also supported by recent simulations of the ion binding sites in the H,K-ATPase (Munson et al., 2005).

Significant differences of fluorescence were obtained after addition of HCl or KCl (Fig. 2, A and C). The K⁺-induced fluorescence changes were a factor of two larger than that induced by H⁺ binding. This observation allows two different explanations. One explanation is that at the lowest tested pH of 6, only one H⁺ ion is bound to the two binding sites. In contrast, at saturating K⁺ concentrations, such as <100 mM, both binding sites are occupied by K⁺ ions. Buffer pH could not be decreased below a value of 6 (see above). Therefore, it was not possible to check whether higher H⁺ concentrations would lead to a further, H⁺ binding-specific fluorescence decrease. The difference of a factor of almost 2 in the (maximum) fluorescence change between K⁺ and H⁺ is in favor of this explanation, and a simulation of the data under the assumption that the second H⁺ binds with a pK of 4.5 (or below) from the cytoplasmic side fits very well (Fig. 3). A second possibility would be that both H⁺ ions bind in different and less “deep” positions in the membrane domain than the K⁺. Such an assumption could be explained by a transient binding of an H⁺ before enzyme phosphorylation to a charged amino acid side chain that is situated spatially between the aqueous phase and the ion binding sites. The detailed mechanism has to be explored by future, time-resolved investigations.

Kinetic analysis of ion binding and release reactions

In both principal conformations, E₁ and E₂P, the ion binding sites are accessible from the cytoplasmic or luminal aqueous phase, respectively. When the pump is working under physiological conditions beginning at pH 6.1 (Rabon et al., 1982; Skrabanja et al., 1984), two H⁺ ions replace two K⁺ in the E₁ conformation; in the E₂P conformation the reverse process occurs (Fig. 1). Kinetic properties of both ion binding and release processes can be investigated by equilibrium-titration experiments shown in a comprehensive form in Figs. 3 and 4. From these results it is immediately obvious that the presence of one ion species affects the binding behavior of the other. The following analysis is performed under the assumption that the presence of H⁺ as well as Mg²⁺ and ATP promotes a transition into the states of the E₂P conformation.

H⁺ binding can be studied in the absence of competing K⁺, whereas in the case of K⁺ binding titration experiments, at least low H⁺ concentrations are present. The highest tested buffer pH in which enzyme activity remained unaffected over the period of the titration experiments (∼1 h) was 8.5. When pK values of the binding sites are assumed to be below 7, at a pH of 8.5, >98% of the protein would be in the state E₁, with no H⁺ bound. Therefore, we assigned this fluorescence level to state E₁. The simplest reaction scheme, which covers the whole series of titration experiments presented in this article, is given by the detailed Post-Albers cycle shown in Fig. 7 B, and it consists of a purely linear reaction sequence, i.e., it does not contain mixed populations of ions in the binding sites.

FIGURE 7.

Expanded version of ion binding and release steps of the pump scheme in Fig. 1. (A) The simplest possible mechanism for the binding sites presented to the cytoplasm is a linear, sequential arrangement that excludes mixed occupation of the ion-binding sites. State K₂E₁ is shown in parentheses to indicate that it is not explicitly treated in the mathematical treatment due to the fact the steady state of the reaction K₂E₁ ↔ K₂E₂ is strongly shifted to the right side. This reaction scheme has the minimum number of kinetic parameters, the four equilibrium dissociation constants, K_H,2, K_H,1, K_K,1, K_K,2. (B) In the presence of ATP the pump is able to present the sites alternatively to both aqueous phases. Therefore, the whole cycle of Fig. 1 has to be expanded. The luminal equilibrium dissociation constants were introduced as L_H,2, L_H,1, L_K,1, and L_K,2. Since this model was applied on equilibrium titration experiments, all other reaction steps may be comprised in two reaction steps with the rate constants, k_A and k_P. (Due to the negligible ADP and P_i concentrations in the experimental buffer, back reactions were omitted.) In addition, the rate constant, k_D, is included. It indicates the proposed pathway for spontaneous dephosphorylation of the enzyme in the absence of luminal K⁺.

To obtain the equilibrium dissociation constants for the H⁺ and K⁺ binding/release steps in both principal conformations, increasingly complex experimental situations were studied. At first, H⁺ binding in the E₁ conformation was analyzed in the absence of K⁺ and ATP (Fig. 3 A, uppermost trace), and fitted by the analytical solution of the reaction sequence, E₁ ↔ HE₁ ↔ H₂E₁, leading to the first two equilibrium dissociation constants, and 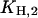(Fig. 7 A). The first one, 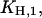can be determined precisely, whereas for 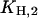only an upper limit can be given due to the restricted pH range of the buffer. In a next step all H⁺ and K⁺ titration experiments performed in the E₁ conformation (Fig. 3) were fitted simultaneously by the reaction scheme in Fig. 7 A (see Appendix I) using the previously determine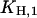d and 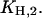By this treatment the other two cytoplasmic equilibrium dissociation constants, 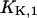and 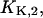were obtained (cf. Table 1).

The third step was the analysis of the titration experiments in the presence of ATP and the absence of K⁺. Under these conditions, the pump is able to perform the transition into states of E₂P. The pump process is, however, fixed in P-E₂ due to the absence of K⁺. Implicit in this treatment is that at high pH, when the forward reaction is limited by H⁺ binding in the E₁ state of the pump, spontaneous dephosphorylation of the state P-E₂ has to be included. To describe the spontaneous dephosphorylation, the reversal of the forward reaction of the Post-Albers scheme may be excluded due to the low H⁺ binding affinity (pK ≤ 2) of the reaction step, P-E₂H + H⁺ → P-E₂H₂. Therefore, dephosphorylation has to occur from either P-E₂ or in P-E₂H. The pH dependence of the dephosphorylation in the absence of K⁺, showing a higher rate at high pH (Stewart et al., 1981), indicates a preference for the reaction P-E₂ → E₁. From P-E₂, the partial reaction would be electroneutral; from P-E₂H, one net charge would be moved through the membrane. Data on an electrogenic contribution of this reaction are not available so far. A critical discussion of the role of spontaneous dephosphorylation is given below.

pH titration experiments reflect, depending on the buffer pH, “back binding” of H⁺ to its binding site from the luminal side of the protein in state P-E₂H and H⁺ binding in state HE₁. The data (Fig. 4, uppermost trace) can be analyzed either by the simple reaction scheme, P-E₂ ↔ P-E₂H ↔ P-E₂H₂, or by the scheme of Fig. 7 B with [K⁺] = 0 (Appendix I). As a result the equilibrium dissociation constants, and 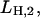could be estimated. On the basis of the amplitude of the detected fluorescence changes the second H⁺ has to bind with an equilibrium dissociation constant, L_H,2 ≥ 10 mM (pK₂ ≤ 2). The binding affinity of the first H⁺ could not be determined accurately because the dephosphorylation rate, k_D, is unknown (see below).

When in the last step of the analysis the complete set of ion binding experiments in the E₂P conformation (Fig. 4) was performed to reveal the effect of H⁺ on K⁺ binding and vice versa on the luminal side, an unexpectedly low K⁺ affinity of the binding sites was obtained. An inspection of Fig. 4 B shows that it would be expected to be ∼20 mM. From the literature it is known, however, that the affinity is below 1 mM as measured by the K⁺ dependence of enzyme activity (Wallmark et al., 1980). When the (permeabilized) vesicles were incubated in the presence of ATP and in the absence of K⁺, the protein is trapped in the state P-E₂. Addition of a low concentration of KCl allows progress of the pumping process, but the K⁺ binding reaction, P-E₂ + 2 K⁺ → P-E₂K₂, still remains a rate-limiting step until at higher K⁺ concentrations, binding is no longer the rate-limiting step. When the experiments of Wallmark et al. (1980) were repeated with our preparation a half-saturating K⁺ concentration of 0.11 mM was obtained (Fig. 5) in agreement with the published data. The Hill function (Eq. 1) was fitted to the experimental results, and the best fit was obtained with K_1/2 = 0.11 mM and the Hill coefficient n_H = 1.0. When we used the analytical solution to fit the reaction sequence, P-E₂ ↔ P-E₂K ↔ P-E₂K₂ to the data, the best fit was obtained again with both binding sites having the same equilibrium dissociation constant, L_K,1 = L_K,2 = 0.11 mM. This observation indicates a sequential binding to two sites, and implies that they are not accessible at the same time, because in such a case the dissociation constants would have to differ by a factor of 4 due to statistical reasons.

Luminal H⁺ binding

The two pK values of H⁺ binding in the E₂P conformation were determined from all data in Fig. 4 to be 6.7 ± 1 and ≤2 (Table 1). Only when we have access to the dephosphorylation rate, k_D, and with buffer conditions that allow a further decrease of pH these numbers can be determined with higher accuracy.

It has been stated that in the absence of K⁺ and at pH 7.4 only ∼23% of the enzyme is phosphorylated in equilibrium at 100 μM ATP (Wallmark et al., 1980). This fact would be in agreement with the low and limiting population of the state H₂E₁ at physiological pH and a significant spontaneous dephosphorylation rate. The numbers above imply that at a pH 7.4 the dephosphorylation rate would be about three times larger than the phosphorylation rate. Under physiological conditions in nonstimulated parietal cells (i.e., when the lumen of the vesicles is K⁺ depleted and pH ∼ 7) such a large dephosphorylation rate would produce a tremendous ATP consumption and energy dissipation. This waste of energy is, however, prevented by the high cytoplasmic K⁺ concentration that locks the pump mostly in its (K₂)E₂ state, until the H,K-ATPase relocates from the intracellular tubulo-vesicles to the apical membrane and K⁺ ions become available at the luminal side of the H,K-ATPase so that the intended pump function can occur.

To pump H⁺ into the gastric lumen that has a pH in the range of 1, the high pK value for the second H⁺ ion to be released seems to be counterproductive, because the binding sites would be mostly occupied by a proton and, therefore, decelerate the propagation of the pump cycle.

It is possible, however, to meet the physiological requirements with such a high pK as determined by our simulation. A mechanistic explanation would be that the proton is not only transported but also utilized in the absence of the counter ion K⁺ to neutralize negatively charged side chains in the binding site by formation of a hydrogen bond. Such a concept is supported by the recent discussion of the SR Ca-ATPase structure. Toyoshima and Inesi found that binding of protons is needed to stabilize the ion binding sites in the transmembrane domain of the Ca pump in the absence of Ca²⁺ (Toyoshima and Inesi, 2004). Similarly, it was shown for the Na,K-ATPase that in its E₁ conformation, two H⁺ are bound in or close to the ion-binding sites in the absence of Na⁺ and K⁺ ions at physiological pH (Apell and Diller, 2002). Therefore, it seems to be reasonable to expect a comparable mechanism in the case of the closely related H,K-ATPase.

Although a proton within the membrane domain of the H,K-ATPase produces an effect on the RH421 fluorescence signal comparable to that of bound K⁺, it is significantly less strongly bound to the protein when compared to sixfold coordinated alkali cations. Because protonated side chains do not produce a spatial hindrance or Coulomb repulsion, K⁺ can enter the ion binding sites almost unperturbed. The state with K⁺ in the binding site and a H⁺ at the same time would be only a short-lived transient state, the proton would be displaced rapidly, leave the membrane domain, and thus allow progress in the pump cycle, i.e., dephosphorylation and ion occlusion, P-E₂K₂ → (K₂)E₂.

Luminal K⁺ binding

To understand the discrepancy between the K⁺ concentration dependence obtained from the enzyme activity and from the equilibrium titration experiments we have to assess the two different experimental methods, and what they detect. In the case of enzyme activity ATP hydrolysis is measured as production of inorganic phosphate as a function of time, and this production is directly proportional to the turnover number of the H,K-ATPase. In contrast, the RH421 method reports the distribution of the ion pumps between the variously charged states in the pump cycle under steady-state conditions. In the case of the Na,K-ATPase (and similarly also in the SR Ca-ATPase) the rate-limiting step of the pump cycle is at low ATP concentrations the conformational transition, (K₂)E₂ → K₂E₁, and (K₂)E₂ is the preferentially populated state. Therefore, in the presence of Na⁺ and ATP, K⁺ titration experiments report the same binding affinity when measured by enzyme activity and in RH421 experiments (Bühler and Apell, 1995). In contrast, in the case of the H,K-ATPase the K⁺-occluded state is not stabilized at low K⁺ concentrations (Helmich-de Jong et al., 1986) and, in consequence, the conformation transition, (K₂)E₂ → K₂E₁, is not rate limiting. Therefore, the enzyme can accumulate under steady-state conditions in considerable amounts in states that have no K⁺ bound (e.g., in the E₁ or P-E₂ state), although the turnover rate is still controlled by the K⁺ concentration. In the presence of high K⁺ concentrations (>10 mM) the K⁺ reverse-binding reaction_, E₁ + 2 K⁺ → … → (K₂)E₂, takes over and populates, at increasing K⁺ concentration, the (K₂)E₂ state. This process is reported correctly by both the RH421 experiments (Fig. 4 B) as well as the enzyme activity (Wallmark et al., 1980).

On the basis of the independently determined eight equilibrium dissociation constants (Table 1) it is possible to simulate all the experimental data from fluorescence experiments presented in Figs. 3 and 4 with the reaction scheme of Fig. 7 B (according to its mathematical representation shown in Appendix II). The only free parameters to fit the data are the rate constants k_A and k_P. The fit of the data shown in Fig. 4 was obtained with a ratio of k_P/k_A = 1. These results demonstrate, that the ion-concentration dependence of the fluorescence data and of the enzymatic activity can be simulated by the Post-Albers cycle with the same set of equilibrium dissociation constants. The real values of k_A and k_P, however, can be determined only by time-resolved experiments.

Ion selectivity

When K⁺ ions were replaced by Na⁺ or 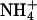ions, only the titration experiments in the E₁ conformation provide reliable information, due to the arguments discussed in the previous paragraph. The results of the experiments in E₁ show (Fig. 6 A) that 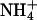ions are able to replace K⁺ ions fairly well, whereas the affinity of the binding sites for Na⁺ ions is lower by a factor of almost 4. Studies of congeners of K⁺ in the H,K-ATPase were performed, so far only for the dephosphorylation reaction (Wallmark et al., 1980). When Na⁺ replaced K⁺ on the cytoplasmic side in experiments with gastric membrane vesicle, proton secretion could not be detected, and ATP hydrolysis was reduced to 7% when compared with K⁺ containing buffer (Sachs et al., 1976). 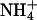When these authors compared this reaction in the presence of (luminal) K⁺, or Na⁺ ions, then was less effective by a factor of two for inducing dephosphorylation when compared to K⁺, and Na⁺ was more than a factor of 10 less effective. When electrogenic H⁺ transport was studied in the presence of monovalent cations on the cytoplasmic side, ∼2 mM K⁺ could reduce the maximum of the transient current to 50% whereas up to 9 mM Na⁺ did not affect the current at all (van der Hijden et al., 1990). The reduction was probably caused by “reverse binding” of K⁺ in the E₁ state of the pump. This reverse-binding effect was clearly shown by Lorentzon and collaborators (Lorentzon et al., 1988). They also showed that 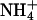is able to fully replace K⁺, however, at ∼10-fold higher concentrations. The effect of back binding of cations in E₁ started at 0.2 mM in the case of K⁺, whereas 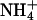became effective only at concentrations >2 mM. This effect (0.2 vs. 2 mM) on the enzyme activity is significantly larger than the difference between the two half-saturating concentrations of both ions in the E₁ conformation of the H,K-ATPase (9.8 vs. 13.5 mM) as presented in Fig. 6 A. Which conditions or reaction steps are responsible for the differences will be investigated in further studies.

Comparison with the Na,K-ATPase and SR Ca-ATPase

When experimental investigations of the H,K-ATPase are compared with the closely related Na,K-ATPase and SR Ca-ATPase, so far significantly less data for the H,K-ATPase are available in literature. The main reason is the overall electroneutrality of the H,K-ATPase that makes detailed studies difficult. Another obstacle is that the transport of H⁺ in the upper half of the pump cycle (Fig. 1) cannot be studied by tracer isotopes due to the rapid exchange of tritium in water molecules, which diffuse almost freely through the membrane. In contrast, radioactive Na⁺ or Ca²⁺ ions were applied very successfully to study transport kinetics of the Na,K-ATPase and Ca-ATPase, respectively.

Therefore, the styryl dye method is a valuable tool because it allows analysis of the electrogenic partial reactions of the H,K-ATPase pump cycle. One important finding of this presentation is the fact that all ion-binding and ion-release steps are electrogenic, as it was found likewise for the Na,K-ATPase and SR Ca-ATPase.

Based on findings from the other P-type ATPases, of which the electrogenicity was investigated in great detail, recently a “general” mechanism was discussed (Apell, 2003). According to this model, the binding sites are situated deep inside the membrane domain of the protein. In the case of the SR Ca-ATPase they are formed by the transmembrane α-helices M4–M6 and M8 (Toyoshima et al., 2000), and comparable arrangements are proposed for the Na,K-ATPase (Ogawa and Toyoshima, 2002) and for the H,K-ATPase (Hermsen et al., 2001). In consequence, the ion-binding sites of all three ion pumps do not move significantly perpendicular to the membrane plane when the protein switches between its two principal conformations, and binding and release occurs through narrow, ion-well-like, gated access channels from the cytoplasm in the E₁ conformation or from the luminal phase in P-E₂.

Appendix I: NUMERICAL ANALYSIS OF THE EQUILIBRIUM TITRATION EXPERIMENTS

The simplest reaction scheme of substrate-ion binding and release on the basis if the Post-Albers scheme (Fig. 1) is a linear sequential model (Fig. 7). In the case of equilibrium titration experiments for all states of E₁ the condition holds: d[E₁X_n]/dt = 0 (X = H or K, n = 0,1,2). Therefore, the four coupled equations can be represented by a system of linear equations.

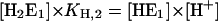(A1)

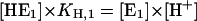(A2)

(A3)

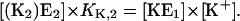(A4)

For sake of simplicity the two states E₁K₂ and (K₂)E₂ are taken together as “(K₂)E₂”, because equilibrium between both is not dependent on [K⁺] or [H⁺], and the equilibrium constant provides a strong shift to the state (K₂)E₂. In addition, the conservation condition of states has to hold

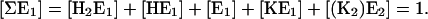(A5)

For this system of five coupled equations, the solution was calculated to be

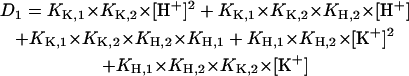(A6)

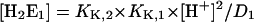(A7)

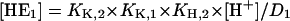(A8)

(A9)

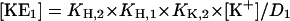(A10)

(A11)

To obtain the calculated fluorescence intensity of the normalized experimental data, specific fluorescence levels have to be introduced: f(E₁) = 0 (requirement of the normalization procedure) and f(H E₁), f(H₂ E₁), f(K E₁), f((K₂)E1), which can be determined from the experimental data at saturating high substrate concentrations.

The fitting curves through the data in Fig. 3 were calculated according to

(A12)

In the absence of K⁺ ions ([K⁺] = 0), the analytical form of the remaining three states of the sequential model, [E₁], [E₁H], and [E₁H₂] (Fig. 3 A) can be simplified, and become independent of the K⁺-binding affinities.

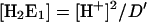(A13)

(A14)

(A15)

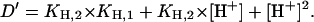(A16)

The pH titration experiments without K⁺ were fitted with this simplified form to obtain the equilibrium titration constants, which are 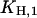and (Fig. 7 A).

In the presence of ATP the pH titration experiments include also three states in the P-E₂ conformation, P-E₂H₂, P-E₂H, and P-E₂ (Fig. 7 B). They are accounted for by:

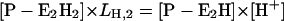(A17)

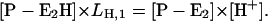(A18)

Eq. A5 has to be replaced by:

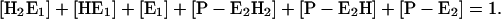(A19)

In the case of the H⁺ titration experiments in the P-E₂ conformation of the protein (when no K⁺ is present in the system the partial reaction, H₂E₁ ↔ (H₂)E₁-P ↔ P-E₂H₂, and the spontaneous dephosphorylation can be covered by the equation:

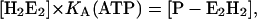(A20)

where K_A is an apparent equilibrium constant that controls the amount of enzyme in the states of E₁ or P-E₂. In this simple model K_A is just a fit parameter because no detailed information on the kinetics of the spontaneous dephosphorylation is available so far. The solution of this linear equation system (similar to that presented in Eqs. A6–A11) was used to obtain L_H,1 and L_H,2.

Appendix II: NUMERICAL ANALYSIS OF THE STEADY STATE OF THE H,K-ATPASE UNDER CYCLING CONDITIONS

The simplest reaction cycle including all ion binding and release steps on both sides of the membrane on the basis of Fig. 1 is shown in Fig. 7 B. In the case of experiments under steady-state conditions all states of the ion pump have to be included. To simulate the experimental results in Fig. 4, when only equilibrium dissociation constants are known, partition equilibrium for all binding and release steps in both principal conformations, E₁ and P-E₂, may be assumed as the simplest approach. Two reaction steps, however, are not in equilibrium: enzyme phosphorylation and dephosphorylation. Therefore, the pump cycle can be represented by Eqs. A1–A4, A17 and A18, and

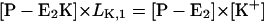(A21)

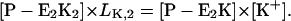(A22)

(The solution of the equilibrium state of Eqs. A17–A20 corresponds to that of Eqs. A1–A4.) The normalization condition of Eq. A5 has to be replaced by:

(A23)

Under steady-state conditions, when all substrates, H⁺, K⁺, and ATP are present and the pump runs under turnover conditions, the reaction flux, Φ, of all reaction steps has to be the same. For the reaction flux in sequence

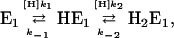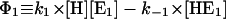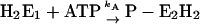as an example, one obtains and and under steady-state conditions the equation holds. This is also true for the phosphorylation and dephosphorylation steps in Fig. 7 B, and 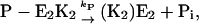respectively, with 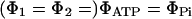or

(A24)

Due to the partition equilibrium [H₂E₁] is a well-defined fraction (Eq. A7) of the total amount of the enzyme in E₁, [Σ E₁]. The same holds for [P-E₂K₂] and [Σ E₂P]. That leads to

(A25)

and

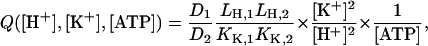(A26)

where

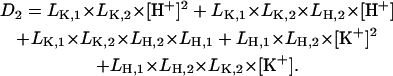(A27)

All the other variables are as defined before.

From Eq. A25 it can be seen that at any given pH, K⁺, and ATP concentration the population of the E₁ and P-E₂ states is controlled by the ratio of the rate constants of enzyme phosphorylation and dephosphorylation, k_A and k_P.

The ratio of the parameters k_A and k_P was used as free-fit parameter and produced reasonable fits when set to 1 (Fig. 4). The real values of the rate constants cannot be determined without time-resolved data.

To simulate the experimental fluorescence intensities the fluorescence amplitude was calculated according to

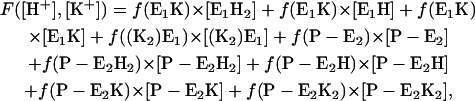(A28)

making use of the specific fluorescence levels of the E₁ states, f(E₁H) = −0.17, f(E₁H₂) = −0.26, f(E₁K) = −0.18, f((K₂)E₂) = −0.26, and newly introduced levels for the P-E₂ states, f(P-E₂) = 0, f(P-E₂H) = −0.17, f(P-E₂H₂) = −0.26, f(P-E₂K) = −0.18, and f(P-E₂K₂) = −0.26. (The numbers were taken from the simulations of the data in Figs. 3 and 4).