Differences in the Modulation of Collective Membrane Motions by Ergosterol, Lanosterol, and Cholesterol: A Dynamic Light Scattering Study

Abstract

A dynamic light scattering setup was used to study the undulations of freely suspended planar lipid bilayers, the so-called black lipid membranes, over a previously inaccessible range of frequency and wave number. A pure synthetic lecithin bilayer, 1,2-dielaidoyl-sn-3-glycero-phoshatidylcholine (DEPC), and binary mixtures of DEPC with 40 mol % of cholesterol, ergosterol, or lanosterol were studied. By analyzing the dynamic light scattering data (oscillation and damping curves) in terms of transverse shear motion, we extracted the lateral tension and surface viscosity of the composite bilayers for each sterol. Cholesterol gave the strongest increase in lateral tension (approximately sixfold) with respect to the DEPC control, followed by lanosterol (approximately twofold), and ergosterol (1.7-fold). Most interestingly, only cholesterol simultaneously altered the surface viscosity of the bilayer by almost two orders of magnitude, whereas the other two sterols did not affect this parameter. We interpret this unique behavior of cholesterol as a result of its previously established out-of-plane motion which allows the molecule to cross the bilayer midplane, thereby effectively coupling the bilayer leaflets to form a highly flexible but more stable composite membrane.

INTRODUCTION

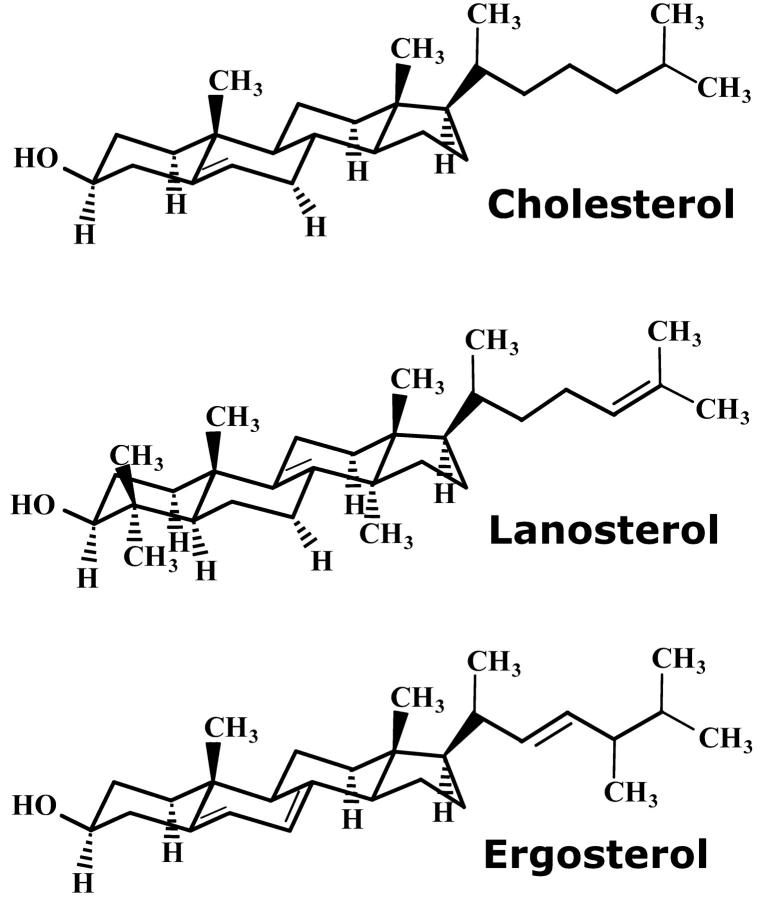
Cholesterol, which can account for up to 35% of the total lipid content in certain eukaryotic cells, is by far the best studied sterol found in membranes and plays a central role in the formation of domain structures (so-called rafts) in artificial and natural membranes. Other related sterols (Fig. 1) are less well understood regarding their effect in membranes, and it is not yet clear whether the liquid-ordered phase (i.e., significant ordering effect without loss of membrane fluidity) as established for cholesterol even exists, e.g., for lanosterol (the evolutionary precursor of cholesterol) or for ergosterol (found in the cells of fungi and yeast).

FIGURE 1.

Chemical structures of cholesterol, lanosterol, and ergosterol.

In previous work we compared the molecular dynamics of cholesterol in lecithin bilayers with other structurally and functionally related sterols like lanosterol and ergosterol at high sterol concentrations (40 mol %). Using quasielastic neutron scattering we observed an out-of-plane motion of 1-nm amplitude that was unique to cholesterol. The conclusion drawn from these experiments suggested that part of the cholesterol molecule can cross the bilayer midplane at a high frequency in the GHz range, which in turn provides an effective coupling between the two bilayer leaflets by increasing the frictional drag. In contrast, it was concluded that lanosterol and ergosterol remain confined within the individual bilayer leaflets. It can be expected that these differences in the molecular dynamics will manifest themselves in the collective motion of the membrane since an increased intrabilayer frictional drag would provide a significant (viscous) damping to thermally excited undulations. By comparing the effects of three sterols on the collective motions of lecithin bilayers in the mesoscopic regime, we may gain further insights into the implications of molecular properties on function. Furthermore, it may provide a deeper understanding of why cholesterol has become the dominant sterol of eukaryotic cells in the course of cellular evolution.

Thermally excited undulations of membranes are of functional importance for the cell, in particular for cell-cell and cell surface-substrate interactions. Undulations or, more generally, collective membrane motions, are well-characterized both experimentally and theoretically in the low-frequency regime (Helfrich and Servuss, 1984; Sackmann, 1996; Seifert and Langer, 1993). The methods used at low frequencies are based on microscopic interferometry (reflection interference contrast microscopy, RICM) coupled with video data acquisition where the restricted bandwidth of the latter limits the access to motions with frequencies below 100 Hz (Sackmann, 1996; Zilker et al., 1987). Owing to this restriction, RICM is best suited for studying the low-frequency undulations that arise in tension-free systems. In contrast, for freely suspended planar bilayers, so-called black lipid membranes (BLM), the lateral tension dominates all other membrane viscoelastic properties. As a result, the collective undulations of BLMs are in the mesoscopic range, extending up to the MHz frequency regime. Collective motions in the mesoscopic range have rarely been studied, mainly due to the scarcity of suitable experimental methods. Dynamic light scattering (DLS) has emerged as one of the few experimental approaches which combines sensitivity (single membrane measurements) and dynamic range (measurements of correlation times over eight orders of magnitude in time) to probe collective membrane motions on the mesoscopic scale (Crilly and Earnshaw, 1983, 1985; Grabowski and Cowen, 1977; Hirn et al., 1998, 1999a,b). Subsequent analysis of DLS data in terms of hydrodynamic theory yields a measure of parameters such as lateral membrane tension and surface viscosity (Helfrich and Servuss, 1984; Kramer, 1971; Fan, 1973).

Theoretically, the DLS technique can probe all collective motions that give rise to a fluctuation of the dielectricity constant at the membrane surface. We have: 1), transverse shear (the motion of membrane constituents in the direction normal to the interface) coupled with the splay mode describing the tilt motion of the long axis of anisotropic molecules; and 2), lateral compression (in-plane motion of the membrane constituents leading to fluctuations of the local density) coupled with the order fluctuation mode. Experimentally, only the transverse shear contributes significantly to the DLS signal owing to the limited frequency range that is accessible for state-of-the-art hardware. It is this constraint that facilitates the analysis of the DLS data. For the measurements presented in this article, we have employed a new dedicated DLS setup that overcomes several limitations of the past. In particular, the upper-q limit has been greatly improved compared to all previous work. The new setup has facilitated measurements in the range from 100 cm⁻¹ to 80,000 cm⁻¹ (0.8 μm < λ < 600 μm) and over eight orders of magnitude in time (from 10 s to 10⁻⁷ s).

THEORY

The undulation behavior of freely suspended planar membranes in solution was treated theoretically in terms of linear (i.e., Navier-Stokes) hydrodynamics by Kramer (1971). In this theory, all interactions were treated as linear functions and the anisotropic structure and dynamics of the lipid molecules, owing to their partial ordering in the bilayer, were ignored. For the special case of a membrane consisting of isotropic molecules symmetrically immersed in a homogeneous liquid, it was concluded that the transverse shear mode is the only collective motion accessible by DLS on a physically meaningful timescale. All other modes are either completely insensitive to DLS or, like the lateral compression mode, exist at higher frequencies only (GHz range and higher), which are hardly resolvable. The transverse shear mode describes the out-of-plane motions of isotropic molecules. For the case of a BLM, this would correspond to the shearing between adjacent lipids in the direction of the membrane normal and leads to an effective fluctuation of the membrane. The fluctuation is opposed by the membrane tension arising from the interaction between the BLM-forming lipids and the edge of the BLM bearing hole. This renders the collective BLM motion dominated by tension, and the dispersion relation of this transverse shear mode is given by Kramer (1971) as

(1)

where m = (q² − iρω/η)^1/2, q = 2π/λ is the scattering vector, ω = ω₀ − iΓ is the complex frequency consisting of the Eigen-frequency ω₀ and the damping constant Γ, ρ, and η are density and viscosity of the bulk fluid, and γ = γ₀ − iωγ′ is a complex tension with the real part, γ₀, being the membrane tension and γ′, the surface viscosity.

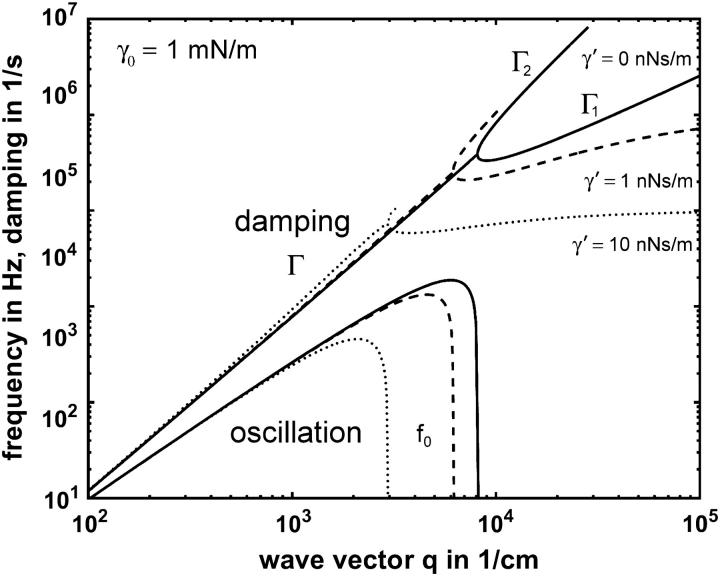
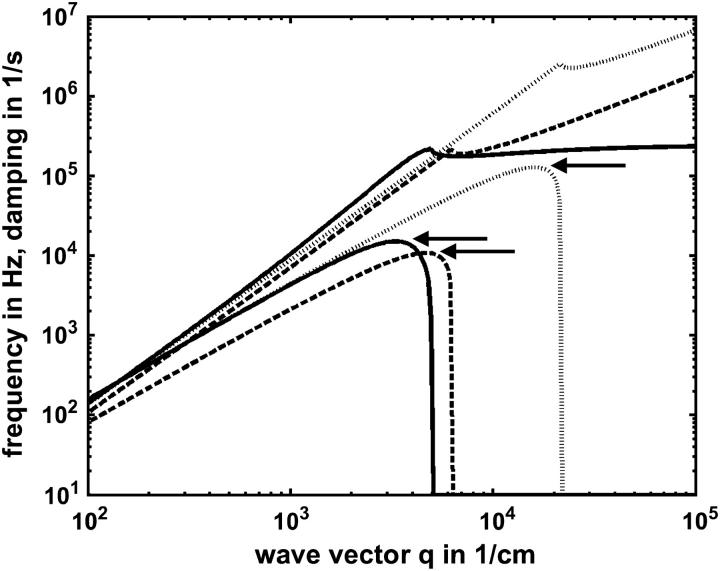
Fig. 2 shows a plot of f₀ = ω₀/2π and Γ versus q according to Eq. 1 using parameters typical for BLMs. A detailed discussion of the dispersion equation is given in Crilly and Earnshaw (1983) and Kramer (1971).

FIGURE 2.

Theoretical dispersion curve of the transverse shear mode of a membrane according to Eq. 1. The mode frequencies f₀ = ω₀/2π and damping Γ versus mode wave vector q for the parameter γ₀ = 1 mN/m, ρ = 1 mg/ml, and η = 1 mPa are shown at different surface viscosities γ′: 0 nNs/m (—), 1 nNs/m (- - -), and 10 nNs/m (⋯). The damping Γ splits after the bifurcation point into the slow damping mode Γ₁ and the fast damping mode Γ₂. The fast damping Γ₂ cut off at the same value to which the slow damping Γ₁ converges asymptotically.

For BLMs with tensions in the range 0.1 mN/m < γ₀ < 4 mN/m, the left side of Fig. 2 describes an oscillating regime, whereas the right one is characteristic of an overdamped regime. The crossover between the two regimes occurs quite abruptly. The damping constant Γ in the oscillating regime splits above the transition (bifurcation) point into two branches Γ₁ for the slower and Γ₂ for the faster mode. For higher q-values the slower mode Γ₁ propagates asymptotically toward the limiting value ξ = γ₀/γ′. When the faster mode Γ₂ approaches this value, it merges into the bulk mode, which has the dispersion relation

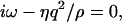(2)

and vanishes for ξ-values above this limit. Because this bulk mode might couple to the fast undulation mode Γ₂ it is likely that this thermally driven fast undulation mode dissipates its energy into the bulk by this coupling. However, as the bulk mode is insensitive to DLS, a detection of Γ₂ is not possible.

By additionally considering the geometrical anisotropy of the lipids, Fan (1973) extended Kramer's theory by introducing an additional splay mode coupled to the transverse shear mode with a coupling strength depending on the free energy variation arising from tilting the molecular director of a lipid molecule away from those of the adjacent lipids.

Thus, in Fan's treatment the membrane tension γ₀ is no longer a constant but depends on the curvature energy κ and the undulation wave vector q, giving rise to an effective tension

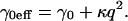(3)

Equation 3 shows that at high q-values κ dominates the undulation behavior. However, for typical BLM parameters, the κ-induced modifications of Eq. 1 would be non-negligible only at q-values well beyond the upper q-limit (80,000 cm⁻¹) of our DLS setup.

MATERIALS AND METHODS

Materials and membrane preparation

For all samples the BLM-forming solution was 1 wt % lipid dissolved in n-decane. The n-decane with 99+ % purity (Sigma-Aldrich, Steinheim, Germany) was additionally purified using an alumina column until it became completely colorless. The phospholipid 1,2-dielaidoyl-sn-3-glycero-phosphocholine (DEPC) was purchased from Avanti Polar Lipids (Alabaster, AL). The purity of cholesterol was >98% (Avanti Polar Lipids). Lanosterol (purity > 97%) and ergosterol (purity > 95%) were obtained from Sigma-Aldrich (Steinheim, Germany). The sterols were used without further examinations. The buffer (pH = 7.0, adjusted with NaOH) was 20 mM HEPES in ultra-pure water, filtered through sterile 0.1-mm filter units (Millipore, Bedford, MA) before the DLS measurements.

BLMs of DEPC and of DEPC/sterol mixtures were prepared by gliding a Teflon loop carrying the BLM-forming solution over a 3.5-mm-diameter Teflon hole. The water level in the scattering cell was adjusted to 3 mm above the upper edge of the Teflon wall (see below), thus eliminating hydrostatic pressure differences. Before this, the hole was pretreated by spreading a methanol solution containing 2 wt % lipids, followed by solvent evaporation under atmospheric air pressure. After formation, the BLMs were allowed to equilibrate overnight before measurements commenced. Equilibration has been established by observing the slow positional variation of the reflected laser spot. DLS measurements were performed after 12 h equilibration of the BLMs.

Experimental setup

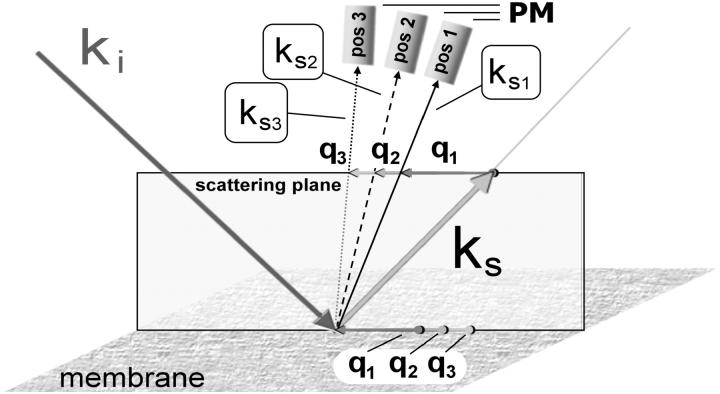
The BLM-containing scattering cell was a standard square glass cuvette of dimensions 45 × 10 × 10 mm (Hellma, Mühlheim, Germany). A hole of 4.5 mm was embedded in a rectangular Teflon wall of 2 mm that divides the cell diagonally into two compartments. Across this hole a 25-μm-thick Teflon foil with a circular hole of 3.5 mm diameter (the BLM bearing hole) was attached concentrically by Prism 406 Surface Insensitive Instant Adhesive (Loctite, Munich, Germany). We found that the use of the thin foil and the 3.5-mm-wide bearing hole provided the conditions required for having a largely planar and stable BLM that allowed for high q-resolution and eliminated any laser reflections from the Teflon. Moreover, the low thickness of the foil prevented positional fluctuations of the whole BLM that would otherwise reduce the q-resolution. The long-time stability of the BLM (a typical membrane lasted for ∼2 days) was achieved only for a perfectly smooth edge of the bearing hole. Capillary waves of the water surface were eliminated by a suitable stopper in the upper part of the cell (∼1 cm above the BLM bearing hole) in direct contact with the water. The cuvette was mounted inside a water-circulating system to control the cell temperature (22°C for all measurements) via a water bath thermostat (Neslab Instruments, Portsmouth, NH). The argon ion laser used (Innova 70–4 from Coherent, Santa Clara, CA) was operated on its 488.0 nm line in the TEM_oo mode at 75 mW. The laser beam was focused on the BLM using a lens of 50-cm focal length to achieve a small angle of divergence (0.11°) and thus high q-resolution. The illuminated spot on the BLM (scattering area) had a diameter of 160 μm. The scattering geometry is shown in Fig. 3. The photomultiplier (PM) was mounted on a goniometer (both from ALV GmbH, Langen, Germany) at an angle of 45° with respect to the BLM normal and at 30-cm distance from the scattering area. The q-regime of interest was selected by placing a pinhole (∅ 800 μm) near the BLM and a second one (∅ 100 μm) in front of the PM. For higher q-values (q > 3400 cm⁻¹) the 100-μm pinhole was replaced by a vertical slit aperture (200 × 2000 μm) to additionally collect the out-of-plane scattering intensity. The rationale for using a slit aperture has been discussed in detail elsewhere (Hirn, 1999a); in brief, it increased the signal/noise ratio of the detector signal by a factor of 80 without any reduction of signal quality. The PM signal was preamplified and processed by autocorrelation in 320 channels using an ALV-5000/E equipped with an FAST TAU Extension (ALV GmbH, Langen, Germany). Measurements were done in the heterodyne mode using the diffuse scattering arising from the molecular roughness of the BLM as a local oscillator. The time increments used varied from 12.5 ns to 0.84 s. The whole DLS setup was capsulated for dust protection and mounted on a 200-kg laser table (Melles-Griot, Voisins le Bretonneux, France) which was shock-insulated by four air-damping modules.

FIGURE 3.

Schematic depiction of the scattering geometry used in our DLS setup, showing the incident vector k_i, the specular reflected vector k_s (reflection angle 45°), in-plane wave vectors q₁ < q₂ < q₃, and the scattered vectors k_s1, k_s2, k_s3, which were detected by the photomultiplier (PM) at the corresponding angles (pos1, pos2, pos3).

Data analysis

In the oscillating regime, the autocorrelation functions G_o(t) were fit to the theoretically expected function

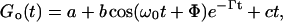(4)

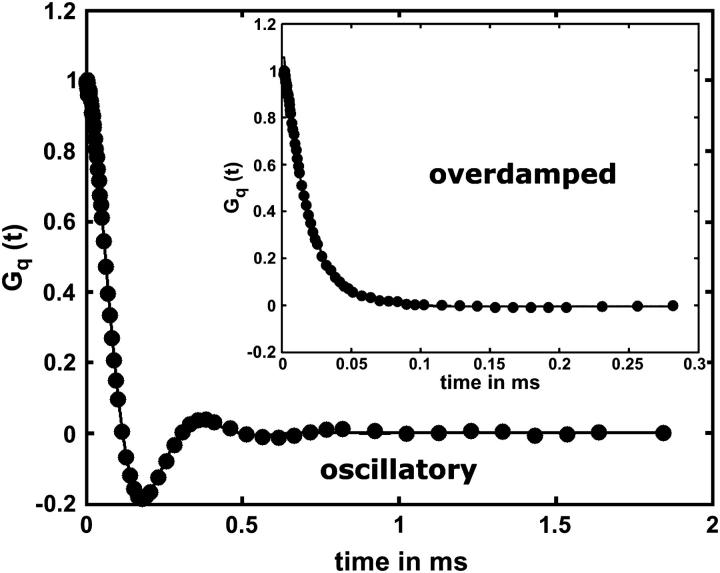
where a is the baseline offset and b is the amplitude. The linear baseline correction of the function is represented by ct and Φ adjusts the phase. Corrections of G_o(t) in the limit of small q to compensate for instrumental effects, as suggested in Crilly and Earnshaw (1983), were not performed since these deviations from Eq. 4 were found completely negligible for q > 400 cm⁻¹. An example obtained for a BLM of pure DEPC is shown in Fig. 4.

FIGURE 4.

Example of experimental correlation functions G_q(t) of a DEPC-BLM (circles) at 22°C obtained in the oscillating and in the overdamped regime (inset). Full lines represent data fits according to Eq. 4 and Eq. 6.

At the transition point (bifurcation) between oscillating and overdamped regime and its vicinity (±400 cm⁻¹), the data were fit to the function

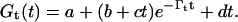(5)

This is the general expression for the asymptotic limit of classical harmonic oscillators, and indicates that in this transition region both overdamped modes, Γ₁ and Γ₂, are detectable.

Finally, in the overdamped regime, two damping modes are predicted (Eq. 1)—thus the data were fit to

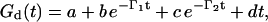(6)

with a linear baseline correction dt.

However, beyond the point where Γ₂ approaches the value γ₀/γ′, the fast overdamped mode disappeared by coupling to the bulk mode. Hence, for q-values beyond this point only the slow overdamped mode Γ₁ was considered in the fitting procedure, as shown in Fig. 4.

Measuring autocorrelation functions with a signal/noise ratio like that shown in Fig. 4 required acquisition times between 30 s and 5 h, depending on q and membrane tension. The latter is particularly important at high tensions, since the amplitudes, and thus the scattering intensity, are reduced with increasing tension.

Fitting the autocorrelation functions with the appropriate equations (Eqs. 4, 5, or 6), provided the mode frequency f₀ and the damping constant Γ.

The relationship between the q-value and the corresponding scattering angle ϕ, adjusted with the goniometer, is given by

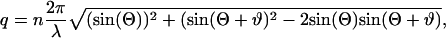(7)

where n = 1.33 is the refractive index of water, λ = 488.0 nm is the wavelength of the incident laser light, Θ = 45° the static scattering angle, ϑ = arcsin(sin(ϕ)/n) is the corrected scattering angle (water/air interface), and ϕ is the variable scattering angle.

RESULTS

Pure DEPC membranes

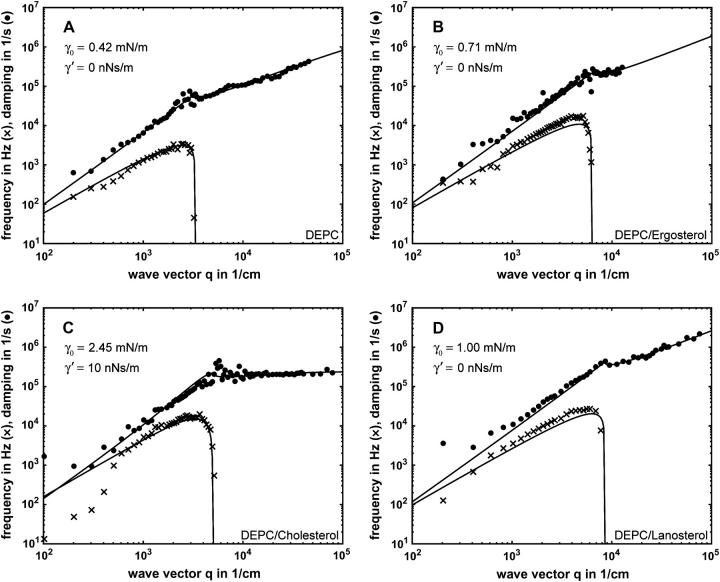
As a basic experiment a pure DEPC membrane was measured at 22°C (fluid state). Its complete dispersion curve in the range from 300 cm⁻¹ < q < 45,000 cm⁻¹ is shown in Fig. 5 A. By comparing the experimental data with best fits (solid lines) according to Eq. 1, an average lateral tension γ₀ = (0.42 ± 0.03) mN/m and a negligible shear interfacial viscosity γ′ acting in the normal direction of the membrane is obtained. Minor deviations of the frequency f₀(q) from the theory at lowest measurable q in Fig. 5 A can be ascribed to a slight time-averaged overall equilibrium deformation of the BLM, giving rise to a diminished q-resolution in the low q-range.

FIGURE 5.

Mode frequency f₀ = ω₀/2π (x, lower curve) and damping Γ (•, upper curve) versus mode wave vector q of a free planar bilayer (BLM), calculated from the experimental autocorrelation functions (examples shown in Fig. 4) measured at the corresponding q-values. The full lines represent the Kramer theory (Eq. 1) fitted to the data. The deviation from theory at low q is due to physical limitations of measurements in the vicinity of the specular spot.

Binary membrane of DEPC and ergosterol

As the first sterol, we studied ergosterol (6:4 DEPC/ergosterol) at 22°C. The dispersion curve obtained, as shown in Fig. 5 B, has a q-range of 200 cm⁻¹ < q < 1200 cm⁻¹. The reduced upper-q limit of the dispersion curve is due to the reduced lifetime of the sterol-doped BLM, since the membrane failed the long-time stability requirements (>24 h) to obtain the high q-values (the data acquisition time increases nonlinearly with q). Nevertheless, the data quality was fully sufficient to allow standard analysis, and a fit according to Eq. 1 yielded a lateral tension of the DEPC/ergosterol membrane of γ₀ = (0.71 ± 0.03) mN/m and again, as in the case of pure DEPC, a negligible shear interfacial viscosity γ′. Thus, ergosterol increased the lateral tension by a factor of 1.7 relative to the pure DEPC BLM (γ₀ = 0.42 mN/m).

Binary membrane of DEPC and cholesterol

The same experiments were carried out with cholesterol (6:4 DEPC/ergosterol) at 22°C. In contrast to ergosterol, this membrane proved to be extremely stable with a lifetime of several days, thus allowing precise measurements also in the high-q regime (200 cm⁻¹ < q < 80,000 cm⁻¹). The fit to the data (Fig. 5 C) was in excellent agreement with the theory (Eq. 1), and yielded a lateral tension γ₀ = (2.45 ± 0.05) mN/m—an increase by nearly a factor of six compared to pure DEPC, and remarkably by a factor of approximately three in comparison to the ergosterol mixture. Interestingly, fitting the cholesterol data according to Eq. 1 proved impossible without considering the surface viscosity, a parameter that was negligible for the other measurements (γ′-values below 0.1 nNs/m). Here we obtained γ′ = 10.0 nNs/m, thus an increase by at least two orders-of-magnitude (note that the lowest detectable value of the surface viscosity is 0.1 nNs/m for our setup). Even though this measurement was performed up to q-values of 80,000 cm⁻¹, contributions from κ are not expected since the κ-values of cholesterol containing membranes are on the order of 10⁻¹⁹ J (Evans and Rawicz, 1990; Duwe and Sackmann, 1990; Hofsäss et al., 2003; Henriksen et al., 2004); such contributions are thus effectively beyond the upper-q limit.

Binary membrane of DEPC and lanosterol

For lanosterol, the BLM lifetime was between that of ergosterol and cholesterol. Under similar conditions as for the other two sterols, we obtained a lateral tension of γ₀ = (1.00 ± 0.05) mN/m (Fig. 5 D). This is a factor-of-2 higher compared to the control, and distinctly higher than the value of ergosterol. Nevertheless, this increase is only one-third of that observed for cholesterol. Similar to the case of ergosterol, lanosterol did not cause any detectable alteration of the bilayer surface viscosity. As for all other measurements, no κ contributions to the dispersion curve were observed within the measured q-range.

All results of the DLS measurements are summarized in Table 1.

TABLE 1.

Dynamic light scattering results

Parameter	DEPC	DEPC/ergosterol	DEPC/lanosterol	DEPC/cholesterol
γ0 in mN/m	0.42 ± 0.03	0.71 ± 0.03	1.00 ± 0.05	2.45 ± 0.05
γ′ in nNs/m	<0.1	<0.1	<0.1	10.0 ± 0.2

Summary of the DLS results obtained at T = 22°C for pure DEPC membranes as a control and for three DEPC/sterol (6:4) mixtures, analyzed in terms of the Kramer theory (Eq. 1) giving the lateral tension γ₀ and the surface viscosity γ′, where the latter parameter is—with the exception of cholesterol—below the detectable threshold value of γ′ = 0.1 nNs/m for our DLS setup.

DISCUSSION

Major improvements of the experimental setup enabled us to study collective motions of BLMs over a wide and previously inaccessible q-range. In comparison with the first work of Crilly and Earnshaw (1983), with an upper-q limit of 1800 cm⁻¹, and our previous work (Hirn et al., 1999b) of up to 40,000 cm⁻¹, we have now extended the range to 80,000 cm⁻¹. This gives us improved confidence in determining parameters like γ₀ and γ′ according to the Kramer theory (Eq. 1). We found a strong correlation between this rather simple theoretical approach and the experimental data. Hence, all membranes studied in this work were tension-dominated and all contributions from bending energy, which can affect the dispersion curve at high q-values, were negligible. This is a significant difference from the study of membranes in closed shells (large unilamellar vesicles) whose micromechanics are generally dominated by bending energy while their lateral tension is zero. Thus, the study of BLMs represents in some ways the other limiting case. Since cell membranes can be quite extended objects that are not always tightly curved, their collective motions may exhibit aspects of both limiting cases.

Our data (Table 1) were all obtained for a fluid-state membrane (pure DEPC has a phase transition temperature at 12°C) and indicate a remarkable modulation of the collective motions of BLMs by the three sterols. Ergosterol and lanosterol, similar in their effective increase of γ₀ but still clearly distinguishable from each other by DLS, exhibited a drastic difference compared to cholesterol, both in γ₀ and γ′. The increase in γ′ caused by cholesterol is most remarkable, since none of the other sterols exhibited any increase of this parameter. This result, along with the marked increase of γ₀ induced by cholesterol, indicates the unique properties of this molecule in a lecithin bilayer. In a previous work (Endress et al., 2002a), we had studied the individual molecular motion of the three sterols in a planar bilayer stack of DPPC at the same sterol/lipid molar ratio using quasielastic neutron scattering. There we observed a significant out-of-plane motion of the cholesterol molecule (1.0-nm amplitude), which strongly suggested that this sterol can cross the bilayer midplane at a high frequency and penetrate a few Ångstroms into the opposite leaflet. Neither lanosterol nor ergosterol showed such an out-of-plane motion, indicating that they both remained confined within their leaflet. Furthermore, it was observed that cholesterol required the largest rotational radius to perform its uniaxial reorientation motion.

The DLS results presented here can be readily understood in considering the molecular motion of the sterols. Cholesterol with its large out-of-plane amplitude into the other leaflet creates a dynamically rough boundary between the both monolayers at the molecular level. As a consequence, the water molecules at the layer surface will encounter obstacles upon diffusion along the membrane interface. This is roughly equivalent to an increase in surface viscosity. Indeed, an increase of this parameter by roughly two orders of magnitude was observed by our DLS experiments (Table 1). The rough molecular interface may also increase the frictional drag between adjacent molecules for transverse shear and consequently result in higher lateral tension. The potency of cholesterol's effect becomes even more impressive, considering that an increase of surface viscosity reduces the Eigen-frequency of the membrane according to Eq. 1. This is demonstrated in Fig. 6 where we show a simulation of the dispersion curve without considering an increase in surface viscosity. In this case, the result would be physiologically unrealistic values of oscillation frequencies.

FIGURE 6.

Comparison of the fits from Fig. 5, B and C, obtained for 6:4 DEPC/ergosterol (- - -) and 6:4 DEPC/cholesterol (—) showing the different maximum frequencies near the bifurcation (arrows). In addition a simulated dispersion curve (· · ·) is shown assuming the lateral tension of DEPC/cholesterol (γ₀ = 2.45 mN/m), but with a negligible surface viscosity (γ′ < 0.1 nNs/m) as in the case of DEPC/ergosterol, thereby increasing the maximum frequency by more than one order of magnitude.

In another previous work (Endress et al., 2002b) we tested the ability of the three sterols (40 mol % sterol) to modulate the molecular order parameter of the lecithin membrane using deuterium NMR and compared it with micropipette measurements of the membrane area expansion modulus K. We found that ergosterol gave the highest value of K and showed the lowest deformation of the membrane due to an externally applied force field. Thus the response of the ergosterol BLM to an external force was less flexible, rendering this membrane more vulnerable to (bulk) compression modes acting on it. This may explain why the BLM doped with this sterol was less stable (its averaged lifetime was significantly shorter) than the other composite BLMs. Ergosterol has, like cholesterol, strong interactions between its sterol body and the lipid chains but remains—in contrast to cholesterol—confined within its leaflet of the bilayer. As a result, the retraction force for transverse shear is high, reducing the amplitude of the collective undulation while driving up its frequency. This is exactly what was observed by DLS. The significant stiffening of the membrane by ergosterol is also reflected by the finding that it gave the shortest deuterium transverse relaxation time T_2e of the lipid chains of all three sterols studied (Endress et al., 2002b). This reinforcement of the bilayer by ergosterol provides a mechanism to improve membrane stability in a static sense at the cost of a more flexible response to external forces.

Lanosterol caused an increase of the lateral tension beyond that of ergosterol but like the latter left the surface viscosity unchanged. This is again in good agreement with the results of our previous spectroscopy work (Endress et al., 2002a,b). Quasielastic neutron scattering experiments (QENS) at 20°C showed that the long-range diffusion constants of the three sterols in the out-of-plane direction increased from ergosterol to cholesterol, with lanosterol in between. Since molecular diffusion represents a dominant NMR relaxation mechanism in membranes (Martinez et al., 2002), transverse and longitudinal relaxation can be expected to exhibit a similar pattern. Indeed, a recent relaxation study of cholesterol and lanosterol in lecithin bilayers showed a good correlation with the lateral tension values determined by DLS (Martinez et al., 2004). This indicates that parameters characteristic of the molecular dynamics of the sterols in the bilayer like those extracted from QENS (diffusion correlation time) and NMR relaxation measurements (particularly T₁ measurements) manifest themselves in the lateral tension estimates obtained from our DLS experiments. In contrast, more static (i.e., longer-timescale-based) parameters extracted from micropipette experiments (e.g., the membrane expansion modulus) or NMR order parameters do not correlate well with the DLS parameters, probably because of a mismatch between the intrinsic timescales of the underlying molecular motions responsible for these parameters. Indeed, the NMR timescale relevant for order parameters can be estimated from the second moment of the spectra as 10⁻⁵ s and the membrane expansion modulus (determined by micropipettes) has an even longer timescale (in the millisecond-range). On the other hand, transverse shear is in the nanosecond-range (according to the time base of the DLS measurements), so there is a mismatch of several orders in magnitude. In contrast, the parameters extracted from QENS (nanosecond-to-picosecond range) and NMR relaxation (nanosecond range) clearly match with the DLS timescale, so a correlation between them is more likely. It is important to note, however, that the DLS experiment is sensitive for a collective mode whereas QENS (an incoherent measurement) and NMR relaxation sample individual molecular motions that may interfere with or even contribute to the collective motion like in the case of an undulation damped out by lateral diffusion of the individual membrane components (diffusion damping).

Summing up the DLS results, we have provided further experimental evidence that cholesterol has a unique effect on the microelastic properties of lecithin bilayers. It is tempting to explain this uniqueness on the basis of sterol structure. Lanosterol has three additional methyl groups rendering the α-face of its sterol body less smooth compared to the other two sterols: the dispersion force interaction between the sterol body and the lipid chains is thus weaker, owing to the larger distance imposed by the additional methyl groups. A more intriguing question is which of the differences between cholesterol and ergosterol can achieve the stiffening of the ergosterol membrane compared to the unique combination of toughness and flexibility of the cholesterol system? The crucial point is that both sterols exhibit a very similar sterol body with a flat α-face and structural differences are restricted to their alkyl chains. Here the terminus of the ergosterol chain is bulkier due to an additional methyl group. It is possible that this additional methyl group is largely responsible for the huge differences in the membrane effects of the two sterols. The ability of cholesterol to cross the bilayer midplane at a high frequency with its alkyl chain while ergosterol remains strictly within its monolayer (according to our neutron scattering results), may rely on the absence of this third methyl group. The larger projected area of the ergosterol chain may prevent its thermally driven entry into the opposite leaflet by steric and/or energetic reasons. As a result, ergosterol will have to dissipate its thermal energy in a different way than cholesterol, probably closer to the relaxation mechanism of lanosterol, which is also confined to its monolayer leaflet. This lack of out-of plane motion of ergosterol may lead to two different structures of the composite membrane: 1), For cholesterol, we can assume a dynamically interdigitated bilayer with its two leaflets effectively coupled by the high frequency cholesterol motion. This will result in a stable but highly flexible membrane since external forces can be dissipated efficiently over the whole bilayer. 2), In contrast, ergosterol and to a lesser extent lanosterol may both form a more rigid and less flexible bilayer due to the decoupling between the two monolayers (monolayer confinement). However, the different van der Waals interaction strength between their sterol bodies and the adjacent lipid chains may lead to further variations in the stiffness of the membranes at the cost of flexibility. This increased stiffness is reflected in the resistance of unilamellar vesicles doped with these two sterols with respect to external deformation force fields (Endress et al., 2002b).

From an evolutionary perspective, ergosterol is found mainly in fungi that require a very rigid membrane but do not require a very flexible response to external forces. The major sterol present in eukaryotic cells, cholesterol, may help to create soft and flexible membranes. Its evolutionary precursor, lanosterol, cannot provide these features owing to its weaker interaction with the lipid chains along with its confinement and localization within the monolayer. Moreover, cholesterol may form complexes with other lipids, the so-called rafts, which further modulate membrane micromechanics and protein function.