Abstract
Kink-turn (K-turn) motifs are asymmetric internal loops found at conserved positions in diverse RNAs, with sharp bends in phosphodiester backbones producing V-shaped structures. Explicit-solvent molecular dynamics simulations were carried out for three K-turns from 23S rRNA, i.e., Kt-38 located at the base of the A-site finger, Kt-42 located at the base of the L7/L12 stalk, and Kt-58 located in domain III, and for the K-turn of human U4 snRNA. The simulations reveal hinge-like K-turn motions on the nanosecond timescale. The first conserved A-minor interaction between the K-turn stems is entirely stable in all simulations. The angle between the helical arms of Kt-38 and Kt-42 is regulated by local variations of the second A-minor (type I) interaction between the stems. Its variability ranges from closed geometries to open ones stabilized by insertion of long-residency waters between adenine and cytosine. The simulated A-minor geometries fully agree with x-ray data. Kt-58 and Kt-U4 exhibit similar elbow-like motions caused by conformational change of the adenosine from the nominally unpaired region. Despite the observed substantial dynamics of K-turns, key tertiary interactions are stable and no sign of unfolding is seen. We suggest that some K-turns are flexible elements mediating large-scale ribosomal motions during the protein synthesis cycle.
INTRODUCTION
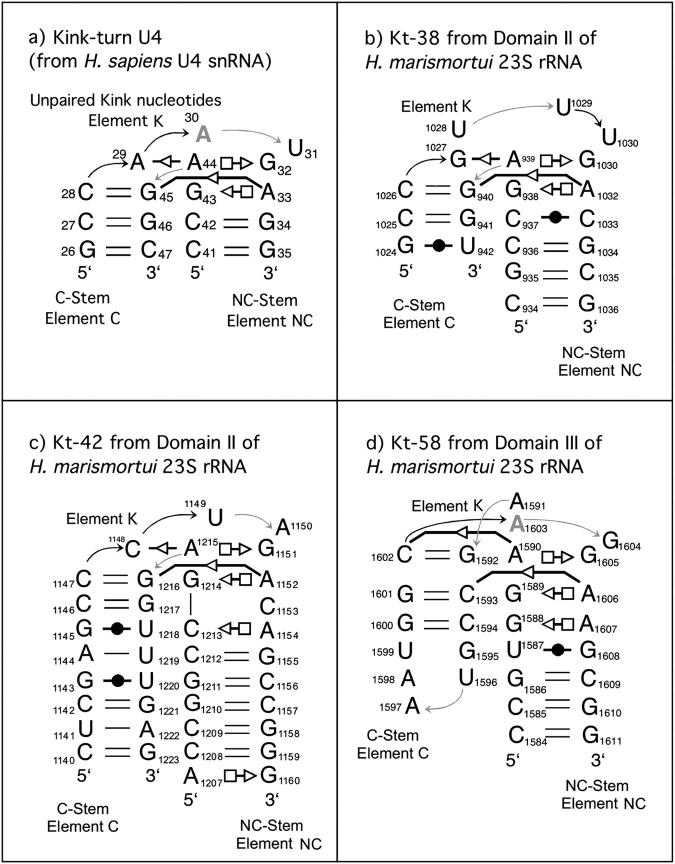
RNA kink-turn (K-turn) motifs are asymmetric internal loops characterized by a sharp bend in the phosphodiester backbone resulting in V-shaped structures. K-turns are composed of three distinct structural elements, which will be marked as NC, K, and C throughout this article (Fig. 1, and Supplementary Material, Fig. S1). NC is the noncanonical helix (NC-stem) and C represents the canonical helix (C-stem). The C- and NC-stems flank the internal loop (K), which comprises nominally unpaired nucleotides and produces a sharp bend of the RNA helix by ∼120°, leading to a V-shaped structure. K thus forms the tip of the V, with NC and C being the attached arms. For the sake of brevity, we designate as NC and C not only the two or three basepairs flanking the K region, but the whole helices attached to the kink.
FIGURE 1.
Schematic drawings of K-turn motifs with annotations to indicate non-WC basepairs (Leontis and Westhof, 2001). Circles represent WC edges, squares Hoogsteen-edges, and triangles Sugar-edges. Open symbols indicate trans pairing and closed symbols indicate cis pairing. Boldface shaded font indicates nucleotide in syn conformation and shaded arrows indicate directional changes in the sugar-phosphate backbones. (a) U4 snRNA. (b) Simulated Kt-38 from 23S rRNA of H. marismortui. (c) Simulated Kt-42 from 23S rRNA of H. marismortui. (d) Simulated Kt-58 from 23S rRNA of H. marismortui. The U4 snRNA K-turn is in full agreement with the consensus K-turn sequence (cf. Supplementary Material, Fig. S1).
The crucial interactions between NC and C are mediated through pairs of A-minor motifs (Nissen et al., 2001). A-minor motifs are key RNA tertiary interactions formed by adenosines that are usually involved in non-Watson-Crick (WC) basepairs, leaving their WC and Sugar-edges (SE) available for further interactions. These adenosines then interact with shallow grooves of WC basepairs (Fig. 2). This leads to insertion of the smooth, minor groove edges of adenines into the minor groove of neighboring helices, preferentially at C=G basepairs, where they form hydrogen bonds with one or both of the 2′-hydroxyls of those pairs. The A-minor motif is the most abundant tertiary-structure interaction in the large ribosomal subunit and apparently also in other RNAs. In 23S and 5S rRNA, 186 adenines participate in A-minor interactions, 68 of which are conserved (Nissen et al., 2001). Several types of A-minor interactions (types I, II, and 0) have been identified. The type I and type II A-minor motifs described by Nissen et al. (2001) involve direct base-base interactions and correspond to the trans SE/SE and cis SE/SE basepairs in the basepair classification of Leontis and Westhof (2001). Generally, when adenosine forms a trans SE/SE basepair with one base of a WC basepair, it also forms a cis SE/SE interaction with the other base of this basepair. In this case, the hydroxyl group of the A-minor adenosine interacts with both the hydroxyl and the YO2 or RN3 atom of its pairing partner (Fig. 2 a). Sometimes a water molecule inserts between the adenosine and its cis SE/SE pairing partner. This interaction is not described by Nissen et al. and can be considered a water-inserted, type I A-minor motif (Fig. 2 b).
FIGURE 2.
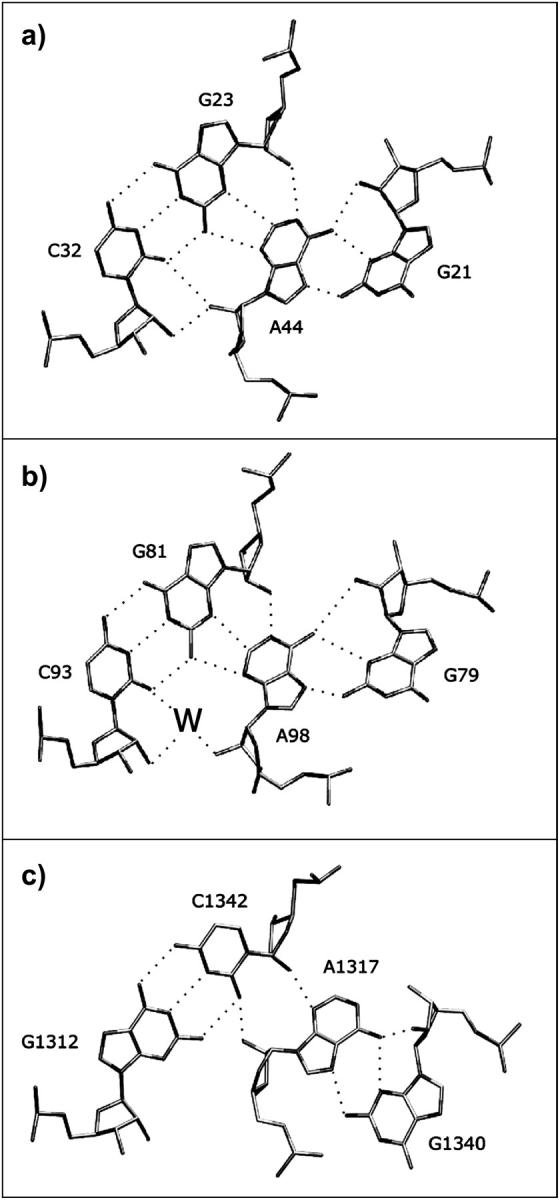
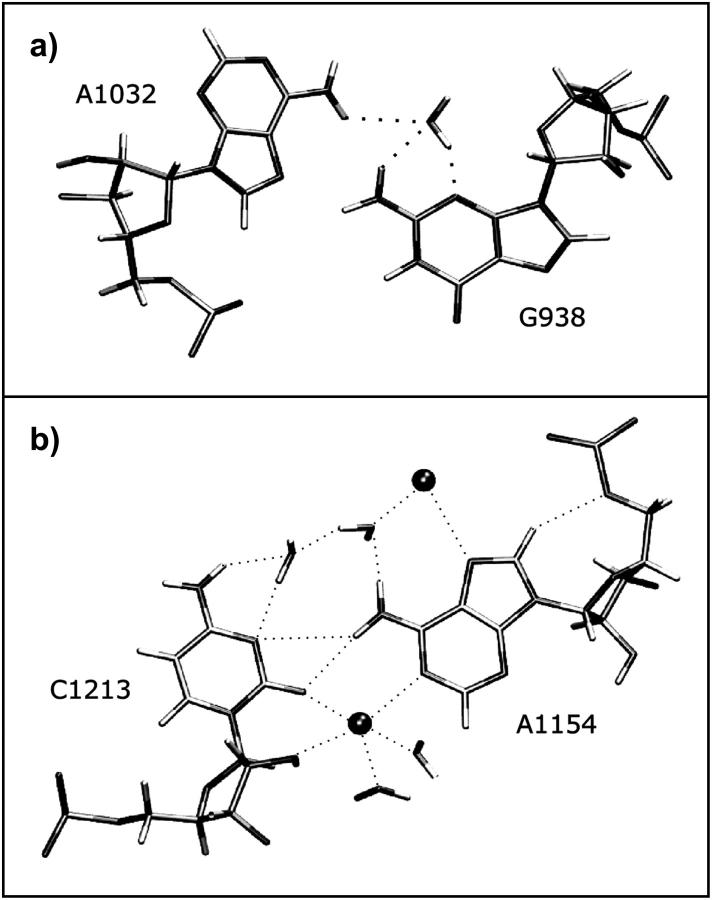
Observed variability of the second A-minor interhelical interaction in the K-turns involving the second conserved adenosine of the NC-stem and the first basepair of the C-stem. (a) Direct H-bonding A-minor type I interaction in Kt-77 from T. thermophilus 23S rRNA (Nikulin et al., 2003). (b) Water-inserted A-minor type I interaction (H. marismortui 23S rRNA, Kt-7). (c) A-minor type 0 interaction (H. marismortui 23S rRNA, Kt-46).
The K-turn RNA motif was first observed in the crystal structure of the 5′-stem loop of human U4 snRNA (Vidovic et al., 2000), whereas the K-turn secondary structure was first predicted by biochemical studies (Watkins et al., 2000). Recently, two additional x-ray structures of different K-turn sequences complexed with L7Ae protein were solved (Hamma and Ferre-D'Amare, 2004; Moore et al., 2004). However, the most extended data about the structure and diversity of K-turns emerged from crystal structures of the 30S (Schluenzen et al., 2000; Wimberly et al., 2000) and 50S (Ban et al., 2000; Harms et al., 2001) ribosomal subunits. The x-ray structures of ribosomal subunits reveal multiple K-turns present at universally conserved regions of the 16S and 23S ribosomal RNAs (Klein et al., 2001). One of these K-turns (Kt-38) occurs at the base of the so-called A-site finger (helix 38), a 100-Å-long protuberance in domain II of 23S rRNA. A second K-turn (Kt-42) occurs in domain II adjacent to the L11-binding site of 23S rRNA. The L11-binding site forms the base of the L7/L12 stalk. Together with the sarcin/ricin loop, the L11-binding site comprises the factor-binding site of the ribosome. The position of this K-turn suggests that it may act as a molecular hinge. A third and perhaps a fourth K-turn (Kt-77 and Kt-78) are found within the RNA protuberance of 23S domain V. The protuberance comprises helices 76–78 and binds ribosomal protein L1 to form the L1-stalk (Nikulin et al., 2003). This element contacts E-site bound tRNAs and must move to allow their egress from the ribosome (Yusupov et al., 2001). A composite K-turn (Kt-94/99) occurs at the base of 23S domain VI and comprises nucleotides from Helices 94 and 99. This K-turn was not reported previously. Domain VI includes the highly conserved sarcin/ricin RNA motif and elements that make contacts to other key sites of the ribosome, including Kt-42. Another K-turn of potential relevance to ribosome dynamics occurs in helix 58 of Haloarcula marismortui 23S rRNA. The terminal hairpin loop of helix 58 contacts helix 34, a small protuberance at the base of the 50S subunit. This small protuberance interacts with ribosomal protein S15 and 16S rRNA helix 20 in the 30S subunit to form intersubunit bridge B4 (Yusupov et al., 2001). Interestingly, in the lower-resolution structures of the 70S ribosome of Thermus thermophilus and the 50S subunit of Deinococcus radiodurans, the tip of H58 does not contact H34 and the motif corresponding to Kt-58 exhibits a different (more open) conformation (Harms et al., 2001; Yusupov et al., 2001). Finally, a K-turn occurs in the 30S subunit in helix 23 of 16S rRNA adjacent to the 690 loop. Helix 23 is located at the top of the platform of the 30S subunit, where major conformational changes are observed when 30S subunits bind to 50S subunits to form 70S complexes (Yusupov et al., 2001). Other K-turns occur in RNA elements that associate tightly with ribosomal proteins and mediate interactions with nearby RNA elements from the same subunit rather than with tRNA or elements of the other subunit. These do not appear to be implicated in functionally significant motions during protein synthesis, but they may play roles in RNA folding.
Recent solution studies have demonstrated that K-turns are highly flexible and unfold in the absence of the adjacent ribosomal elements. Matsumura et al. (2003) and co-workers inserted the K-turn into the hinge region of the P4–P6 domain of group I Intron RNA and analyzed the metal ion requirement of the constructs containing three different K-turn motifs using native polyacrylamide gel electrophoresis and dimethyl sulfate modification. The formation of sharply bent structures similar to the geometries seen in the ribosome crystals depends on the presence of divalent cations, although their required concentration is different for each motif. Using fluorescence resonance energy transfer, Goody et al. (2004) demonstrated that isolated K-turns in solution exhibit a dynamic equilibrium between a tightly kinked conformation and a more open unfolded structure similar to a simple bulged loop. They found that the highly kinked form is stabilized by noncooperative binding of metal ions, but a significant population of the less-kinked form is present even at relatively high concentrations of divalent metal ions. The conformation of the tightly kinked population is in agreement with the K-turn structures observed by crystallography. Thus, the tightly kinked conformation of the K-turn requires stabilization by other factors such as protein and other RNA.
We have reported a preliminary explicit-solvent molecular dynamics (MD) analysis of three ribosomal K-turns, utilizing their x-ray geometries as the starting structures (Razga et al., 2004). The simulations reveal an unprecedented dynamical flexibility of the K-turns around their x-ray geometries, making them strikingly different from other RNA motifs that are quite rigid in similar simulations. The overall behavior of the simulations suggests that the sampled geometries are essentially isoenergetic and separated by modest energy barriers. The transitions and oscillations observed in the simulations would not take place on the presently accessible simulation timescale if substantial free energy barriers and differences were involved. The nanosecond dynamics of isolated K-turns can be qualitatively considered as the motion of two rigid helical stems controlled by a flexible internal loop. This then leads to hinge-like motions between the two stems. Subtle local variations at the kink can thus produce substantial modification of the intersegment distances (up to 10 Å or more) at the ends of the flanking stems. Note that, in contrast to the solution experiments, the simulations investigated finer motions that are not accompanied by any marked destabilization of the kink region. In this article, we substantially extend the simulations to almost 200 ns and provide a detailed analysis of K-turn molecular dynamics, revealing how molecular interactions modulate shape and flexibility of this important RNA motif. The K-turns that we simulated were selected to include all three types of the second A-minor interaction between the stems (see below), as well as K-turns that may be involved in functional dynamical motions.
To understand the MD results, we need to properly relate them to the experiments. The solution experiments show that the ribosomal x-ray geometries are rather unstable when the K-turns are isolated in solution. Compared to this, the simulation timescale precludes unfolding, even in the absence of divalent cations and other stabilizing elements. Thus, the simulations characterize intrinsic conformational properties within the conformational subspace of the ribosome-like geometries, irrespective of the K-turn unfolding on a much longer timescale. Obviously, the adjacent proteins and rRNA are likely to change the dynamics of the K-turns compared with the dynamics seen in the simulations. However, even considering these factors, the simulations have a relevance to the ribosomal structures. The intrinsic mechanical properties of free K-turns highlighted in the simulations certainly affect their interactions with other molecules, including the mutual structural adaptations when forming larger biomolecular complexes. It is likely that the inherent internal flexibility of isolated K-turns affects also their behavior inside ribosomes or other functional RNAs. X-ray crystallography, solution experiments, and simulations have distinct areas of application and provide complementary views on the structure and dynamics of K-turns. Although limited by force field approximations and the timescale of the simulations, MD is capable of providing qualitative insights into RNA structure and dynamics (Auffinger et al., 1999, 2004; Auffinger and Westhof, 1998, 2000; Beveridge and McConnell, 2000; Cheatham and Kollman, 1997; Csaszar et al., 2001; Giudice and Lavery, 2002; Guo et al., 2000; Guo and Gmeiner, 2001; Hermann et al., 1998; Nagan et al., 1999, 2000; Norberg and Nilsson, 2002; Razga et al., 2004; Reblova et al., 2003a,b, 2004; Sanbonmatsu and Joseph, 2003; Sarzynska et al., 2000; Schneider et al., 2001; Schneider and Suhnel, 2000; Stagg et al., 2003; Williams and Hall, 2000; Zacharias, 2000).
During the protein synthesis cycle, tRNA occupies successive positions (A-, P- and E-sites) on the ribosome. This appears to be facilitated by coordinated conformational changes in the ribosomal subunits, the bound tRNAs, and the associated protein factors. (Frank, 2002). Most notably, there is a ratchet-like relative rotation of the two ribosomal subunits accompanying the binding of elongation factor G (EF-G) to ribosomes and subsequent guanosine 5′-triphosphate (GTP) hydrolysis (Frank and Agrawal, 2000; Valle et al., 2003b). Furthermore, the ratchet-like motion is accompanied by a 20-Å movement of the L1-stalk relative to the 50S subunit. This implies that the L1-stalk is involved in translocation of deacylated tRNAs from the P- to the E-site (Valle et al., 2003b). Based on the MD simulations discussed here, we suggest that flexible K-turns are leading structural elements allowing such motions. This is supported by the occurrence of K-turns at key conserved sites that are implicated in ribosome motions during the protein synthesis. For example, Kt-38 could provide hinge-like flexibility to the A-site finger, permitting coordinated large-scale motion to facilitate elongation. The A-site finger contacts the 30S subunit to form intersubunit bridge B1a. Cryoelectron microscopy (cryo-electron microscopy) shows that during the ratchet-like motion associated with translocation, bridge B1a moves up and down (Frank, 2003; Gabashvili et al., 2000). This implies motion of the A-site finger relative to the positions of the bound tRNAs. A 10° change in the Kt-38 interhelical angle observed in our MD simulations would therefore produce a displacement of almost 18 Å at the tip of the finger. Similarly, Kt-42 could provide hinge-like flexibility permitting large-scale motions at the factor-binding site that are necessary for EF-Tu-catalyzed A-site tRNA accommodation and EF-G-catalyzed elongation. Finally, flexibility of Kt-58 could help in formation of the functional contacts between hairpin loop H58 and H34.
METHODS
Molecular dynamics simulations were carried out using the Sander module of AMBER 6.0 (Pearlman et al., 1995) and the force field of Cornell et al. (1995). A time step of 2 fs was used for all simulations and the PME method was employed to calculate electrostatic interactions. The starting geometries of the Kt-38, Kt-42, and Kt-58 motifs were taken from the x-ray structure of the 50S subunit of H. marismortui with resolution ∼2.4 Å (Protein Data Bank (PDB) code 1JJ2) (Klein et al., 2001). The starting geometry of Kt-U4 was taken from the crystal structure of the spliceosomal protein bound to a U4 snRNA fragment. (resolution ∼2.9 Å, PDB code 1E7K) (Vidovic et al., 2000). The molecules were neutralized with Na+ monovalent cations (Ross and Hardin, 1994) initially placed using the Xleap module of AMBER. Solute molecules were solvated using a box of TIP3P water molecules with periodic boundary conditions. The initial size of the prismatic water box was 55.1 × 51.6 × 65.7 Å (4413 residues) for Kt-38, 68.2 × 69.1 × 93.8 Å (11,458 residues) for Kt-42, 53.7 × 57.9 × 65.8 Å (4687 residues) for Kt-58, and 62.3 × 58.7 × 43.8 Å (3771 residues) for Kt-U4. Equilibration was carried out in the following way. First, the RNA structures were kept rigid while only solvent molecules with counterions were allowed to move. Then the RNA structures were also allowed to relax. After full solvent and solute relaxation, the systems were heated gradually from 50 to 300 K. The simulations were initiated under periodic boundary conditions and coordinate snapshots were written to trajectory files every picosecond. The center of mass velocity was periodically removed during the production dynamics at intervals of 10 ps (Harvey et al., 1998). Trajectories were analyzed using the Carnal module of AMBER and structures were visualized using VMD (Humphrey et al., 1996). Hydration and cation distributions were calculated with the ptraj module of AMBER and graphics were prepared using the UCSF program MidasPlus (Ferrin et al., 1988). Solute-solvent contacts were monitored over the entire trajectories and analyzed in detail. We evaluated explicitly all individual significant solute-solvent and solute-cation contacts by calculating interatomic distances. A single binding event is defined as direct persistent contact between a solvent molecule (water or cation) and a given solute atom. However, picosecond-timescale fluctuations were considered insignificant and not counted as interruptions of the binding (Spackova et al., 2000). Table 1 summarizes the simulations carried out in this study, totaling ∼200 ns.
TABLE 1.
Summary of simulations carried out in this study
| Name | Length (ns) | Counterions | Nucleotides | Water molecules |
|---|---|---|---|---|
| Kt-38 | 43 | 21 Na+ | 22 | 4413 |
| Kt-42 | 37 | 36 Na+ | 38 | 11458 |
| Kt-58 | 33 | 27 Na+ | 28 | 4687 |
| Kt-U4 | 74 | 15 Na+ | 17 | 3738 |
Basepairing of the simulated K-turns is shown in Fig. 1.
Interhelical angles between C- and NC-stems were calculated as the angle defined by the centers of mass of nucleotides in the C-stem, the kink (K), and the NC-stem. For Kt-38 the first center of mass was defined using the G1024–C1026 and G940–U942 segments, the second center of mass by A939, G1027, and G1031 and the third center of mass by the G935–G938 and A1032–C1035 segments. For Kt-42 the first center of mass was defined via G1145–C1147/G1216–U1218, the second center of mass via A1215, C1148, and G1151 and the third center of mass via G1211–G1214/A1152–C1156. For Kt-58, we used the following segments for the first through third centers of mass, respectively: G1600–C1602/G1592–C1594; A1590, A1591, and G1605; and U1587–G1589/A1606–G1608. For Kt-U4, the first center of mass was defined via G26–C28/G45–C47, the second center of mass via A29, A44, and G32, and the third center of mass via C41–G43/A33–G35.
Interhelical angles for other crystal structures of K-turns (not simulated in our study) were calculated using segments as follows: for Kt-7, G76–G79/A98–C101; G94, A80, and G97; and G81–C83/G91–C93; for Kt-15, A243–G246/U265–U268; G264, A247, and A261; and G257–C260/G249–C252; for Kt-23, G683–U686/A704–C707; G700, A687, and G703; and U697–C699/G688–G690; for Kt-46, C1343–A1345/U1309–G1311; A1341, G1316, and A1313; and A1337–G1340/A1317–U1320; for Kt-77, A29–G31/C24–G26; G23, A44, and G21; and G17–G20/C45–C48; for Kt-94/99, A2827–U2830/A2910–A2913; G2826, A2914, and G2823; G2667–U2669/A2820–C2822; and for K-turn from a box C/D RNA, U3–G6/A20–A23; C16, A7, and G19; and C8–G10/A13–G15.
The interhelical torsion angle, which represents the direction of the NC-stem axis with respect to the C-stem axis, was calculated as a torsion angle defined by four centers of mass of selected base-paired nucleotide dimers in the stems. The centers of mass used for Kt-42 were as follows: the first was defined by the G1145/U1218 basepair, the second by the C1147/G1216 pair, the third by the G1214/A1152 pair, and the fourth by the G1211/C1156 pair.
Histograms were calculated from whole time traces (Table 1) of selected interatomic distances from Kt-38 and Kt-42 simulations. The time traces were smoothed with adjacent averaging procedures to reduce uninformative fluctuations, with the averaging range 500 ps. This averaging range was used to filter out the random thermal motions of the atoms and movements with time periods <500 ps, which were considered as noise for the analysis of the global dynamics. Individual histograms were calculated with bin width 0.1 Å and normalized to unit area to obtain distance distributions.
Essential dynamics analysis (EDA) was performed with modules trjconv, g_covar, and g_anaeig of the GROMACS suit of programs (Berendsen et al., 1995; Lindahl et al., 2001). EDA consists of the following steps. First, a covariance matrix is built from the atomic fluctuation in the trajectory. Only phosphate atoms (P) are included, because these atoms contain all the information needed for a reasonable description of the global dynamics. Upon matrix diagonalization, a set of eigenvalues and eigenvectors is obtained. Finally, a new trajectory containing only large correlated atomic motions is calculated from the initial trajectory by applying the most significant eigenvectors (Amadei et al., 1993). The overall translational and rotational motions were removed before EDA was carried out.
Simulated structures
The four motifs that were selected for simulations include all three types of the key second A-minor interaction between C- and NC-stems seen in the x-ray structures to date (see below). The simulated Kt-38 motif includes nucleotides 937–939 and 1027–1033 of the 23S rRNA of H. marismortui and the flanking WC basepairs C936=G1034, C1026=G940, and C1025=G941. Thus, the Kt-38 motif was simulated as two strands comprising 22 nucleotides (nt). Kt-42 occurs in helix 42, which connects the compactly folded factor-binding domain of 23S rRNA to the rest of the ribosome. The position of this K-turn at the base of the factor-binding site of 23S rRNA (Escherichia coli positions 1109–1111/1044–1050, H. marismortui positions 1213–1215/1148–1154) suggests that it may act as a molecular hinge. The Kt-42 motif was simulated as a double-stranded RNA comprising 38 nt, corresponding to positions 1140–1160 and 1207–1223. The Kt-58 motif occurs in helix 58 in domain III of 23S rRNA. Helix 58 is positioned at the base of the 50S subunit viewed from the front (30S side) near helix 34, which forms bridge B4 to the 30S subunit. The tip of H58 contacts H34 in the isolated 50S subunit of H. marismortui. In this structure, Kt-58 is in the bent conformation. The Kt-58 motif of H. marismortui 23S rRNA was simulated as a single continuous strand comprising 28 nt (corresponding to positions 1584–1611) and folding into a double-stranded structure having a hairpin loop on one end and the K-turn in its center. Finally, the Kt-U4 motif was simulated as a double-stranded RNA comprising 17 nt, corresponding to positions 26–35 and 41–47 in the crystal structure. The basepairing of the simulated K-turns is shown in Fig. 1, and a detailed description of the simulated molecules is given in Supplementary Material.
RESULTS
Closed and open conformations of the x-ray K-turn geometries
The consensus K-turn motif (Supplementary Material, Fig. S1) (Klein et al., 2001) is exemplified by the human U4 snRNA motif (shown in Fig. 1 a). One helix flanking the motif (C) is composed entirely of WC basepairs and some G/U wobble basepairs. The NC helix starts with two or three non-WC basepairs. In the U4 motif, these are the cross-strand stacked trans Hoogsteen (H)/Sugar-edge (SE) ("sheared") basepairs A33/G43 and A44/G32. In most K-turns, the NC-stem contains a third non-WC basepair at the position of G34=C42. Finally, the K region between C and NC contains unpaired bases. In the consensus motif, there are three formally unpaired nucleotides in the longer strand (A29–U31 in the U4 motif) of the K-turn. Some of the nucleotides of the C-stem form non-WC basepairs and/or interact by stacking with NC and K nucleotides. The third nucleotide of K is usually bulged out. The most common sequence variations result from insertion of nucleotides in the K region, either in the short or the long strand, and from changes in the nature of the third non-WC basepair of NC. Thus, Kt-38 has one nucleotide inserted in the long strand (Fig. 1 b), whereas Kt-58 has two inserted in the shorter strand (Fig. 1 d).
Certain nucleotides of NC and C mediate crucial tertiary interactions by forming non-WC basepairs. In the U4 snRNA K-turn motif (Fig. 1 a), the adenosine of the first trans H/SE basepair of the NC-stem (A44) forms a trans SE/SE basepair with the first nominally unpaired base of the longer strand of the K-turn (A29), i.e., the first A-minor interaction of the K-turn. A44 is universally conserved, as it participates in two important non-WC basepairs structuring the K-turn. The adenosines corresponding to A44 in the U4 motif are A939 in H. marismortui Kt-38, A1215 in Kt-42, and A1590 in Kt-58 (Fig. 1, b–d). A29, on the other hand, is not conserved, as it corresponds to G1027 in Kt-38 and C1148 in Kt-42.
The second adenosine in the tandem sheared submotif of the NC-stem (A33 in U4 motif) interacts in the minor groove of the first WC basepair of the C-stem and thus forms the second A-minor interaction. We found three variations of the second A-minor motif in the available K-turn crystal structures (Table 2, Fig. 2). The first one is a type I A-minor interaction. It has direct H-bonding between the WC and Sugar-edges of the adenosine in NC with the Sugar-edges of both bases of the first WC basepair in C. This occurs in Kt-42, Kt-77, and Kt-94/99 of the 50S subunit of H. marismortui. The second variant, which is seen in Kt-7 and Kt-38 of the 50S subunit of H. marismortui, and in Kt-23 in the 30S subunit of T. thermophilus, involves insertion of a water molecule in the cis-SE/SE A/C basepair of the type I A-minor motif. The third variant involves a lateral shift between the C- and NC-stems, converting the A-minor motif from type I to type 0 (Nissen et al., 2001). This is observed for Kt-15, Kt-46, and Kt-58 of the 50S subunit, and for the K-turn motifs in U4 and in the box C/D RNA (Moore et al., 2004).
TABLE 2.
Survey of the second A-minor interstem interactions in available K-turn crystal structures
| A-minor interaction involving second adenosine | Kink-turn motif | Interhelical angle* observed in x-ray (°) | Code in database |
|---|---|---|---|
| A-minor type I | Kt-42 (50S) | 103 | PDB code 1JJ2 |
| Directly H-bonded | Kt-94/99 (50S) | 94 | PDB code 1JJ2 |
| cis SE/SE A/C | Kt-77 (50S) | 124 | PDB code 1MZP |
| A-minor type I | Kt-7 (50S) | 98 | PDB code 1JJ2 |
| Water inserted | Kt-38 (50S) | 115 | PDB code 1JJ2 |
| cis SE/SE A/C | Kt-23 (30S) | 104 | PDB code 1J5E |
| Kt-15 (50S) | 119 | PDB code 1JJ2 | |
| A-minor | Kt-46 (50S) | 103 | PDB code 1JJ2 |
| type 0 | Kt-58 (50S) | 86 | PDB code 1JJ2 |
| Kt-U4 (snRNA) | 104 | PDB code 1E7K | |
| Kt (box C/D RNA) | 112 | PDB code 1RLG |
Interhelical angles were calculated as described in the Methods section.
In this study, the conformations of K-turns having direct H-bonding between the interacting nucleotides in the second type I A-minor motif will be called closed conformations. Those having water molecules inserted between the interacting nucleotides will be called open conformations. Note that this classification is not applicable for the A-minor type 0 interaction, in which the bases interact indirectly though their 2′-OH groups (Fig. 2). When a water molecule is inserted in the A-minor type I motif, the distance between the C- and NC-stems increases by ∼1 Å (the distance between interacting groups of bases involved in the second A-minor interaction). Despite this, we did not find a straightforward relationship between the variation of the second A-minor interaction and the highly variable interhelical angle between the C- and NC-stems in available x-ray structures (Table 2, Methods) (Klein et al., 2001). Apparently, the angle may be sequence-dependent and may be also significantly influenced by interactions (“external” deformations) of the K-turn motifs in the ribosome. Nevertheless, as shown below, for a given K-turn, the local structure of the second A-minor interaction exerts a profound effect on the angle between the C- and NC-stems. The crystal data do not allow a direct comparison of the closed and open geometries, since no data for K-turns adopting both A-minor substates is available.
MD simulations of Kt-38 and Kt-42 reveal oscillations of the second A-minor type I interaction
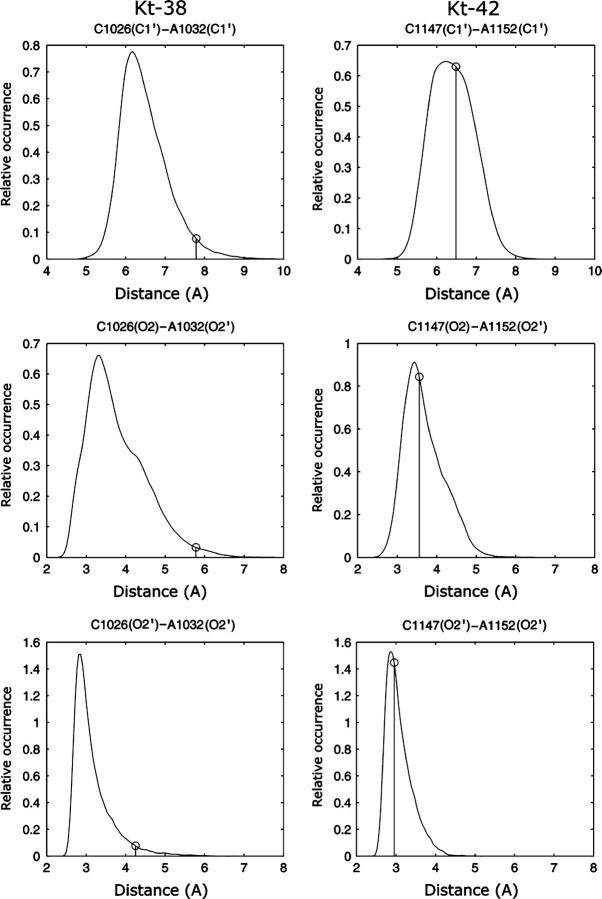
We carried out 43 ns and 37 ns of MD simulation for the Kt-38 motif and Kt-42 motif, respectively. First we analyze the dynamics of the key A-minor tertiary interactions between the NC- and C-stems. In Kt-38 these interactions include the trans SE/SE basepairs A939/G1027 and A1032/G940, and the originally water-mediated cis SE/SE C1026/A1032 basepair. Although fluctuations in H-bond distances are larger for the A939/G1027 pair than for the A1032/G940 pair, both pairs are stable throughout the simulation (see Supplementary Material, Table S1, a and b, for a complete survey of the H-bond dynamics). By contrast, the cis SE/SE C1026/A1032 interaction shows large fluctuations of the A1032(C1′)–C1026(C1′), A1032(O2)–C1026(O2′), and A1032(O2′)-C1026(O2′) distances (Fig. 3). Normalized histograms show complex distributions for the A1032(C1′)-C1026(C1′) and A1032(O2)-C1026(O2′) distances. The distribution for the A1032(O2′)-C1026(O2′) distance in Kt-38 peaks at ∼3 Å, but exhibits a long tail extending out to ∼5 Å (Fig. 3).
FIGURE 3.
Normalized histograms of interatomic distances involving the second conserved adenosine in the NC-stem and the cytosine of the first basepair of the C-stem in simulations of Kt-38 (left) and Kt-42 (right). Vertical lines indicate values in the crystal structure of the H. marismortui 50S subunit.
In Kt-42, the A1152/G1216 trans SE/SE pair is very stable, as is the corresponding pair in Kt-38. The A1215/C1148 basepair fluctuates modestly as the corresponding A939/G1027 basepair in Kt-38. Transient disruptions of the A1215(N1)-C1148(O2′) and A1215(C2)-C1148(O2) interactions occur occasionally, being coupled with a tendency for G1216 to shift toward the plane of A1215. This results in new van der Waals or H-bonding interactions, A1215(N3)-G1216(H1′) and A1215(O2′)-G1216(O4′). Nevertheless, even this pair can be considered quite stable. There are, however, large fluctuations for the A1152/C1147 interaction corresponding to A1032-C1026 in Kt-38. Fig. 3 (right panels) shows histograms for the A1152(C1′)-C1147(C1′), A1152(O2′)-C1147(O2), and A1152(O2′)-C1147(O2′) distances. The similarity between these histograms and the corresponding graphs for Kt-38 (Fig. 3, left) is striking. As for A1032-C1026 in Kt-38, a range of conformations is observed for the A1152-C1147 interaction. The median values for corresponding distances for Kt-38 and Kt-42 are nearly identical (Supplementary Material, Table S2).
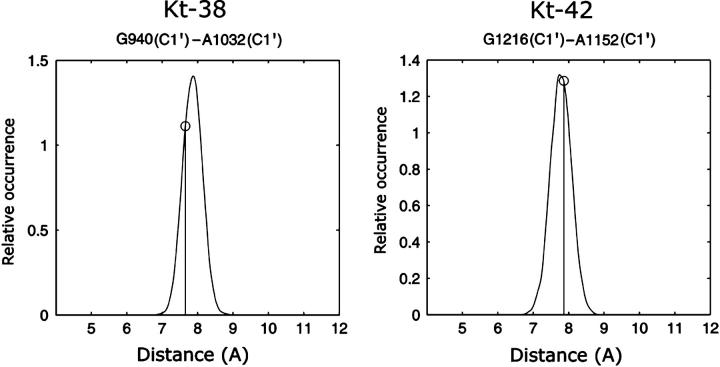
In summary, the tertiary interactions involving the first conserved adenosine are stable (A939-G1027 for Kt-38 and A1215-C1148 for Kt-42). In contrast, the tertiary interactions involving the second adenosine reveal stability of the A/G pair (A1032/G940 for Kt-38 and A1152/G1216 for Kt-42; Fig. 4) and substantial fluctuations of the A/C pair (A1032/C1026 for Kt-38 and A1152/C1147 for Kt-42; Fig. 3). This suggests a crucial role of the second A-minor interaction in K-turn dynamics.
FIGURE 4.
Normalized histograms of A/G C1′-C1′ distances in the second A-minor interaction in Kt-38 and Kt-42 simulations. The vertical lines indicate the respective x-ray values. The trans SE/SE basepairs A1032/G940 in Kt-38 and A1152/G1216 in Kt-42 are stable and act as fulcra for the motion. The pivoting motion then produces significant fluctuations in the A(O2′)-C(O2) and A(C1′)-C(C1′) distances in the second basepair of this A-minor interaction, i.e., A1032/C1026 in Kt-38 and A1152/C1147 in Kt-42 (see Fig. 3).
Long-residency hydration regulates transitions between closed and open K-turn geometries
Detailed analysis of different regions in the distance distributions of Fig. 3 reveals four main patterns of hydrogen-bonding and hydration involving the crucial A and C nucleotides at the interhelical interface (C1026/A1032 in Kt-38 and C1147/A1152 in Kt-42, see Fig. 5). In closed states, direct A(O2′)-C(O2′) and A(O2′)-C(O2) H-bonds are observed (Fig. 5 a) and the A(C1′)-C(C1′) distance is minimal. Typically, A(O2′) donates an H-bond to C(O2) and accepts an H-bond from C(O2′). In semiclosed states, a direct H-bond forms between A(O2′) and C(O2′), whereas an out-of-plane or rotated water molecule mediates the A(O2′)-C(O2) interaction. Typically, a water molecule accepts an H-bond from A(O2′) and donates an H-bond to C(O2) (Fig. 5 b). In semiopen and open states the water molecule is in the plane of the interacting groups and donates H-bonds to both A(O2′) and C(O2). In semiopen states, A(O2′) and C(O2′) are still close enough to H-bond (Fig. 5 c), whereas in fully open states a second water molecule mediates the A(O2′)-C(O2′) interaction (Fig. 5 d). The A(C1′)-C(C1′) distance increases accordingly. Thus in open states, the A1032(O2′)-C1026(O2) distance is typically >5 Å, the A1032(O2′)-C1026(O2′) distance is >4 Å and the A1032(C1′)-C1026(C1′) distance is >7 Å (Fig. 3).
FIGURE 5.
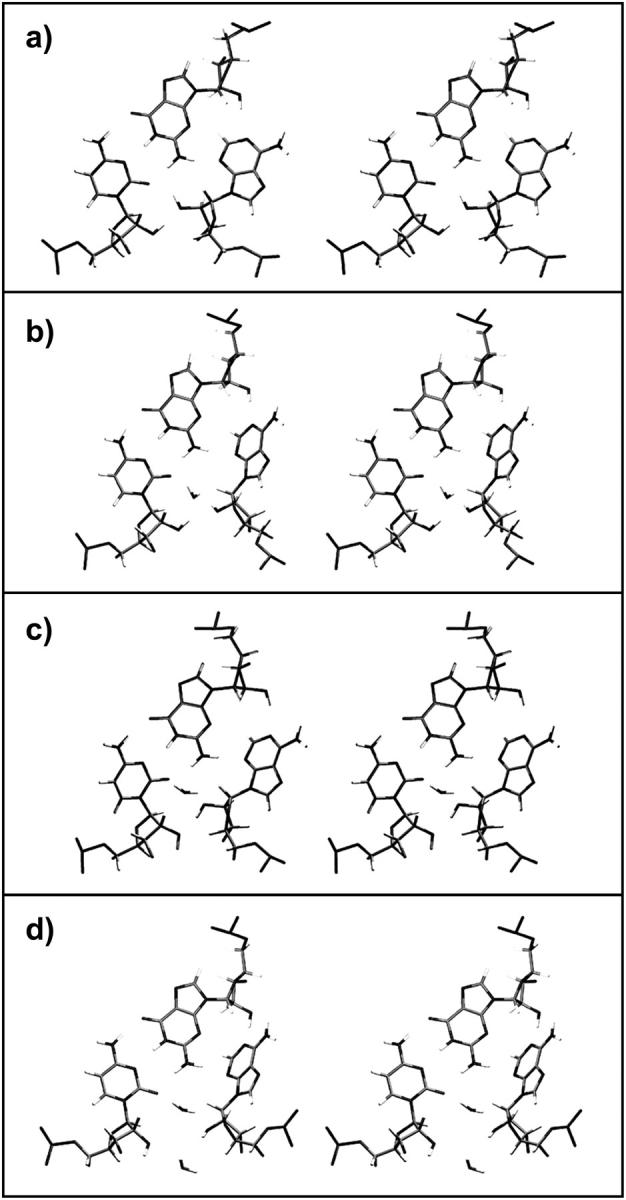
Stereo view of hydrogen-bonding and hydration patterns of the second A-minor interaction observed in simulations of Kt-38 and Kt-42. (a) Closed state: A(O2′) is directly H-bonded to C(O2) and C(O2′). (b) Semiclosed state: a long-residency water molecule donates H-bond to C(O2) and accepts an H-bond from A(O2′). (c) Semiopen state: the water molecule donates H-bonds to both C(O2) and A(O2′). (d) Open state: a second water molecule mediates the A(O2′)-C(O2′) interaction.
Transitions between closed and open states occur smoothly through intermediate semiclosed and semiopen states. The water molecule mediating the C(O2)-A(O2′) interaction changes the H-bonding pattern and moves in and out of the plane of the interacting groups. Exchange of water molecules appears to always proceed through semiclosed states in which the water molecule moves out of the plane of the bases in the direction away from the kink. The hydration site exhibits binding times for individual waters of ∼2 ns. By comparison, typical residency times for individual water molecules in common hydration sites in nucleic acids lie within the range of 0.05–0.5 ns (Auffinger and Westhof, 2000; Csaszar et al., 2001; Nagan et al., 2000; Reblova et al., 2003b; Schneider et al., 2001). The simulations thus confirm the important role of long-residency water molecules in RNA local conformational variations (Csaszar et al., 2001; Reblova et al., 2003b, 2004; Spackova et al., 2000). The largest A/C distance fluctuation occurred during the Kt-38 simulation at ∼26–29 ns, with distances A1032(O2′)-C1026(O2) ∼5.4 Å, A1032(O2′)-C1026(O2′) ∼5.0 Å, and A1032(C1′)-C1026(C1′) ∼8.4 Å. At this point of simulation two water molecules occupied the space between A1032(O2′) and C1026(O2). This salient fluctuation is largely responsible for the broader distance distributions for Kt-38. No such fluctuation occurred during the Kt-42 simulation.
The interhelical dynamics and global motions
In our preliminary report on MD simulations of rRNA K-turns, we found that nanosecond dynamics of isolated K-turns can be qualitatively considered as motion of two rigid helix stems controlled by a flexible internal loop. This leads to substantial hinge-like motions between the stems (Razga et al., 2004). In this study, we reveal that, in the case of Kt-38 and Kt-42, these global dynamics are almost completely attributable to the local variability of the A-minor motif between the C- and NC-stems. A pivotal role is played by insertion of long-residency water molecules.
To quantify the intersegment motions, interhelical (interstem) C1′-C1′ distances were analyzed for nucleotides located in the C- and NC-stems at equivalent distances (in basepairs) from the kink (Table 3). Large fluctuations were observed for the interstem distances, progressively increasing when moving further away from the apical part of the V-shaped motif. This is shown in Table 3 (mainly by the 10–90% range) and also in Supplementary Material, Fig. S2. This figure shows the bandwidths of oscillations of interstem distances as a function of distance from the kink. The linear dependence means that the stems are rigid. Normalized histograms showing distance distributions for corresponding interhelical distances in Kt-38 and Kt-42 are plotted in Supplementary Material, Figs. S3 and S4. The crystal values of the interhelical distances are above the median of each distribution for Kt-38 but below the corresponding medians for Kt-42. The only exceptions are the G940(C1′)-A1032(C1′) distribution in Kt-38 and the corresponding G1216(C1′)-A1152(C1′) distribution in Kt-42 (Fig. 4). These two distributions are narrow, with the crystal values being below the median for Kt-38 and above the median for Kt-42. As discussed above, these basepairs are very stable and the only rearrangements are small pivoting motions that decrease the G(C1′)-A(C1′) distance when the kink-turn opens and increase it when the kink-turn closes. (Note that G940 is WC-paired to C1026 in Kt-38 and G1216 is WC-paired to C1147 in Kt-42 within the C-stems (cf. Fig. 1).) In summary, the second A-minor interaction basepairs G940/A1032 in Kt-38 and G1216/A1152 in Kt-42 act as fulcra for semirigid hinge-like motions between the C- and NC-stems.
TABLE 3.
Interstem separation measured via C1′-C1′ distances (Å) in Kt-38 and Kt-42
| Kt-38 C1′-C1′ distances
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parallel strands: | X-ray | Average | Max | Min | Basepairs from hinge | 90–10% range | ||||||
| G940-A1032 | 7.7 | 7.8 | 8.7 | 6.9 | 1 | 0.71 | ||||||
| G941-C1033 | 5.5 | 4.8 | 6.7 | 3.7 | 2 | 1.36 | ||||||
| U942-G1034 | 14.7 | 13.7 | 17.0 | 11.6 | 3 | 2.08 | ||||||
| A943-C1035 | 23.6 | A943 Not simulated | ||||||||||
| G1027-A939 | 8.1 | 8.3 | 9.6 | 7.7 | 0 | 0.60 | ||||||
| C1026-G938 | 16.6 | 16.0 | 17.7 | 14.6 | 1 | 1.41 | ||||||
| C1025-C937 | 24.3 | 22.9 | 25.6 | 19.9 | 2 | 1.92 | ||||||
| G1024-C936 | 32.0 | 31.4 | 34.1 | 27.7 | 3 | 1.89 | ||||||
| Antiparallel strands | ||||||||||||
| G940-G938 | 9.2 | 9.3 | 10.3 | 8.1 | 1 | 0.96 | ||||||
| G941-C937 | 15.4 | 14.1 | 16.4 | 11.7 | 2 | 2.14 | ||||||
| U942-C936 | 24.4 | 23.3 | 25.7 | 20.1 | 3 | 1.92 | ||||||
| G1027-G1031 | 7.2 | 7.0 | 8.7 | 5.7 | 0 | 1.27 | ||||||
| C1026-A1032 | 7.8 | 6.5 | 9.5 | 4.9 | 1 | 1.47 | ||||||
| C1025-C1033 | 15.3 | 13.9 | 16.4 | 11.9 | 2 | 1.70 | ||||||
| G1024-G1034 | 23.8 | 23.3 | 26.4 | 21.1 | 3 | 1.96 | ||||||
| Kt-42 C1′-C1′ distances | ||||||||||||
| Parallel strands | X-ray | Average | Max | Min | Basepairs from hinge | 90–10% range | ||||||
| G1216-A1152 | 7.9 | 7.8 | 8.7 | 6.8 | 1 | 0.75 | ||||||
| G1217-C1153 | 5.0 | 4.5 | 5.9 | 3.5 | 2 | 0.97 | ||||||
| U1218-A1154 | 11.9 | 12.6 | 15.4 | 10.2 | 3 | 1.68 | ||||||
| U1219-G1155 | 21.4 | 22.8 | 26.2 | 19.6 | 4 | 2.20 | ||||||
| C1148-A1215 | 8.7 | 8.7 | 10.4 | 7.8 | 0 | 0.91 | ||||||
| C1147-G1214 | 16.3 | 16.3 | 18.4 | 15.2 | 1 | 1.27 | ||||||
| C1146-C1213 | 23.9 | 23.8 | 25.8 | 21.5 | 2 | 1.78 | ||||||
| G1145-C1212 | 31.4 | 32.0 | 34.6 | 29.5 | 3 | 1.92 | ||||||
| Antiparallel strands | ||||||||||||
| G1216-G1214 | 10.9 | 10.2 | 11.4 | 8.4 | 1 | 0.82 | ||||||
| G1217-C1213 | 15.4 | 15.9 | 17.6 | 14.5 | 2 | 1.19 | ||||||
| U1218-C1212 | 22.8 | 24.6 | 27.0 | 22.5 | 3 | 1.71 | ||||||
| C1148-G1151 | 8.3 | 7.5 | 10.3 | 5.6 | 0 | 2.76 | ||||||
| C1147-A1152 | 6.5 | 6.3 | 8.4 | 4.8 | 1 | 1.40 | ||||||
| C1146-C1153 | 13.1 | 13.1 | 14.9 | 10.8 | 2 | 1.41 | ||||||
| G1145-A1154 | 22.0 | 22.5 | 24.6 | 20.0 | 3 | 1.74 | ||||||
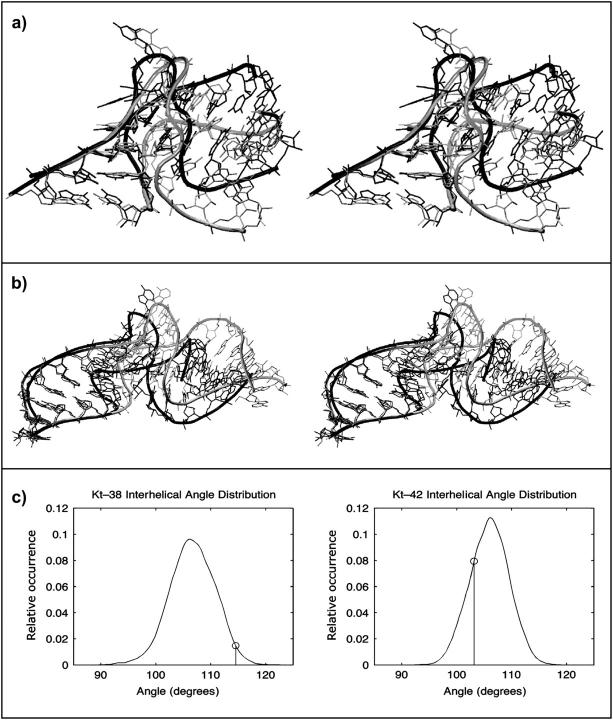
Thus, the x-ray conformations of Kt-42 and Kt-38 are in semiclosed and open states, respectively (Fig. 5). In Fig. 6, the crystal structures (black) of Kt-38 and Kt-42 are overlaid with selected structures from the simulations (shaded). The C-stems of the crystal and simulated structures are superimposed. The open crystal structure of Kt-38 is overlaid with a closed conformation from the simulation, showing that closing of the A-minor interaction reduces the interstem angle. The semiclosed crystal structure of Kt-42 is superimposed with one of the open states seen in the simulation, demonstrating that opening of the A-minor interaction leads to a marked “global” opening of the interstem angle. The interhelical angle distributions (Fig. 6 c) for Kt-38 and Kt-42, calculated as described in the Methods section, are remarkably similar, with nearly identical means (106.3° and 106.1°) and maxima (106.1° and 105.7°). Both K-turns revealed very similar dynamics regardless of their starting initial (x-ray) conformation.
FIGURE 6.
Superposition of 3D structures of closed and open structures for (a) Kt-38 and (b) Kt-42. The crystallographic structures are shown in black (open for Kt-38 and closed for Kt-42, see text) and representative simulated structures are shaded. (c) Normalized histograms of the interhelical angles calculated as described in the Methods section. The asymmetric shape of these distributions corresponds to open/closed dynamics of Kt-38 and Kt-42. The vertical lines indicate the x-ray values.
Standard basepairs are stable
Supplementary Table S1, a and b, summarize the dynamics of all basepairs in the simulations. Essentially, all standard basepairs of NC- and C-stems of Kt-38 were stable throughout the simulation, with no breathing in the duplex regions, as expected. Note that the WC pair G940=C1026 was apparently refined as a G/U pair in the crystal structure. The simulation produced average values and deviations for this pair that are typical of stable G=C pairs. The terminal pair C934=G1036 dissociated at the very end of the simulation, which is a rather common end-effect seen in simulations, with no effect on the simulation outcome. An interesting fluctuation was observed in the C936=G1034 basepair in the period 7.6–8.5 ns, when it transiently converted to a cis-WC/SE basepair. The helical stems of Kt-42 were also stable except for modest fraying at the ends of the helices (Supplementary Material, Table S1 b). Although wobble pairs G1145/U1218 and G1143/U1220 remained basepaired, G1143/U1220 underwent two temporary transitions (1.5–1.8 ns and 4.8–5.8 ns) to a cis water-inserted WC bifurcated pair. This was also observed in simulations of 5S rRNA loop E (Reblova et al., 2003b) and the beet western yellow virus pseudoknot (Csaszar et al., 2001).
Non-Watson-Crick basepairs in the NC-stems agree with the x-ray structures
Regarding Kt-38, the first trans H/SE A939/G1031 basepair remains entirely stable throughout the simulation. In the second trans H/SE basepair, A1032/G938, a water molecule mediates the A(N6)-G(N3) interaction in the x-ray structure. Remarkably, long-residency water molecules are observed at this position for most of the simulation, with maximal individual binding times up to 5 ns (Fig. 7 a). The average A1032(N6)-G938(N3) distance remains close to the crystal value (5.3 vs. 5.0 Å). The G938(N2)-A1032(O2P) H-bond fluctuates and is disrupted during most of the simulation. Large fluctuations also occurred for the water-mediated cis bifurcated C937/C1033 basepair (Supplementary Material, Table S1 a). In Kt-42, the A1215/G1151 pair was stable throughout the simulation (Supplementary Material, Table S1 b), whereas the water-inserted A1152/G1214 pair, having only one direct base-to-base H-bond, was frequently disrupted. This is reflected in the large standard deviation for the A1152(N7)-G1214(N2) distance (Supplementary Material, Table S1 b). However, disruption of this single H-bond did not have a significant structural effect due to other coupled interactions. These include H-bonding between G1214(N3/N2) and G1151(O2′) and tight binding of water between A1152(N6) and G1214(N3), with a maximal binding time of 3.3 ns. Likewise, the C1213/A1154 pair, having only a single direct H-bond is further stabilized by the C1213(N6)/A1152(O2P) H-bond. The C1213/A1154 basepair was possibly further stabilized by a three-centered C(O2)-A(N1)-C(O2′) sodium bridge with occupancy of 47% and binding times up to 4.1 ns. Six different ions visited the site. Another inner shell Na+-binding site is present at A1154(N7), with occupancy of 84% and maximal binding times up to 11.0 ns (Fig. 7 b). Unpaired C1153 remains well-stacked inside the NC-stem between A1152 and A1154 throughout the simulation. We can conclude that the simulations do not reveal any significant perturbation of the K-turn stems.
FIGURE 7.
(a) The long-residency hydration site between A1032(N6) and G938(N3). (b) Stabilization of the C1213/A1154 basepair via interaction of Na+ ions with both its groove edges.
Nominally unpaired nucleotides in the loop K
In the Kt-38 simulation, U1028, which initially is stacked on G1027 in the C-stem, shifted laterally to stack on A939 in the NC-stem (Supplementary Material, Fig. S5). This was followed by a small perpendicular shift of the C- and NC-stems. The NC-stem shifted downward, placing U1028 almost into the plane of G1027, where it could form a side-by-side cis H/SE basepair. A939, still paired to G1031, shifted down almost to the plane of the C1026=G940 basepair, where it formed a unique side-by-side cis SE/SE pair with G940. There was also a simultaneous mutual shift of the U1030 sugar with respect to the U1028 sugar. This rotation of U1028 did not include any syn-anti conversion. The unpaired base rotated with its sugars as a single rigid entity, leading to changes in the conformation of the K region through the opening of the minor groove of K. The geometry of the K region was finally stabilized after 15 ns. These observed motions of the unpaired nucleotides did not affect the global motion of Kt-38, in contrast to Kt-58 (see below). Throughout the Kt-42 simulation, U1149 remains stacked above the A1215/G1151 basepair, shifting sometimes either toward A1215 or toward its original position over G1151. Likewise, C1148 remains stacked above the C1147=G1216 basepair throughout the simulation. At those times when the interaction between C1148 and A1215 is disrupted, C1148 tends to stack primarily over C1147. These changes are transient. A1150 remains bulged out into the solution and undergoes large rotations about the glycosidic bond. In the crystal structure such motions appear to be constrained by interactions of A1150 with protein L10. In summary, the nominally unpaired K regions show modest structural changes that do not appear to affect the global geometry of the molecules and are expected in solution simulations.
Simulation of Kt-58 reveals large-scale intersegment motions primarily regulated by rearrangements of the formally unpaired nucleotides
We have carried out a 33-ns simulation for the Kt-58 motif. The x-ray structure shows that the second A-minor motif is type 0 rather than type I. The dynamics of the Kt-58 can again be described as a large-scale, hinge-like motion between the rigid C- and NC-stems regulated by molecular interactions in the apical region around K. However, in contrast to Kt-38 and Kt-42, the motion is not driven by fluctuations of the second A-minor interaction and the hydration dynamics. Instead, it originates in conformational changes directly involving the nominally unpaired region, which then induce structural change in the second A-minor interaction. Further, rather than being oscillatory, the Kt-58 motion is permanent.
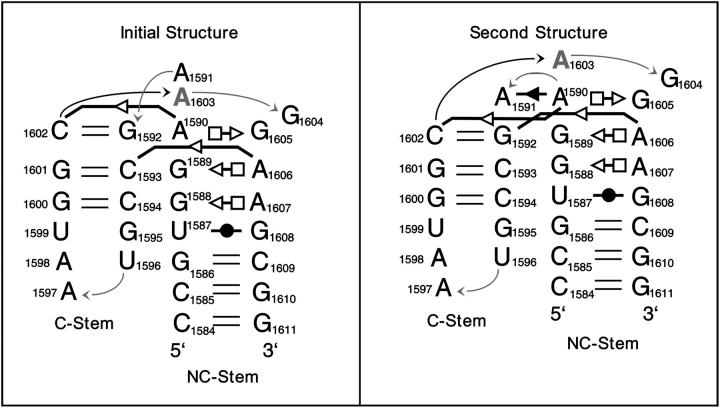
The key structural change occurred in the period 2.8–3.8 ns with all major events being completed within the first 5–6 ns (Supplementary Material, Fig. S6 a). A1591, initially stacked on A1603 (NC-stem), slowly rotated (2.8–3.8 ns) to stack with G1592 in the C-stem (Razga et al., 2004). This transition produced changes in phosphodiester torsion angles at the top of the V and resulted in an upward translation of the basepairs of the NC-stem by one base-pair step (∼3–4 Å) relative to the C-stem (Fig. 8 and Supplementary Material, Fig. S7). For example, in the starting structure, the G1600/C1594 pair lay in the plane of the G1588/A1607 pair (Fig. 8 and Supplementary Material, Fig. S7), whereas in the new structure, C1593 is shifted down to the G1588/A1607 plane. This was followed by stabilization of a new conformation with new non-WC interactions. The new geometry remains stable until the end of the simulation. A new base-sugar H-bond formed between A1591(N3) and A1590(O2′). Also, new H-bonds formed between A1591(O2P) and A1603(N6), A1591(C2) and A1590(N3), A1591(O4′) and A1590(O2′), and, finally, between A1591(N3) and A1590(O2′). This produced a new cis SE/SE basepair between A1591 and A1590.
FIGURE 8.
Schematic comparison of the initial Kt-58 structure with the second conformation formed after a few nanoseconds of simulation and persisting for the rest of the simulation. For annotations, see Fig. 1.
The A(N1)-C(O2′) H-bond distance in the conserved first A-minor trans SE/SE A1590/C1602 basepair was slightly elongated (from 2.7 Å in the x-ray to ∼3.1 Å in the simulation; see Supplementary Material, Table S1 c). We consider this a modest perturbation of the basepair. The second A-minor interaction (initially A1606/C1593) converted from the type 0 interaction to a new trans SE/SE water-mediated pair between A1606 and G1592. It actually is a water-inserted A-minor type I interaction A1606/G1592=C1062 with a direct A1606(O2′)-G1592(N2) H-bond. Long-residency water molecules occupied the A/G hydration pocket involving A1606(N3, O2′) and G1592(N2), with a maximal binding time of 3.3 ns (Supplementary Material, Fig. S8).
It is to be noted that it is not straightforward to compare the Kt-58 motif with the Kt-38 and Kt-42 motifs. In the Kt-38 and Kt-42 motifs, the first conserved adenosine interacts with unpaired bases (Kt-38, A939/G1027; Kt-42, A1215/C1148), whereas the corresponding adenosine in Kt-58 interacts with a standard basepair (A1590/C1062=G1592). It is notable that whereas the original first A-minor pair A1590/C1602 is slightly perturbed due to the conformational transition of Kt-58, a new cis SE/SE basepair is formed between the conserved A1590 and the shifted unpaired A1591. This may be considered as a strengthening of the A-minor interactions around the K region.
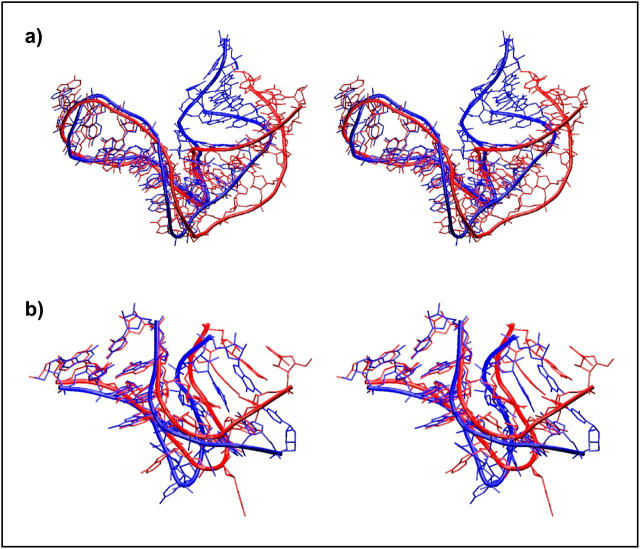
In summary, as for Kt-38 and Kt-42, the trans SE/SE tertiary interaction mediated by conserved adenosine A1590 remains basically unchanged and stabilizes the three-dimensional V shape of Kt-58. There is, however, a rather complex structural change seen in the simulation, initiated by restacking of nominally unpaired A1591 away from the NC-stem toward the C-stem and its basepairing with the conserved A1590. The structural change further involves interconversion of the initial water-mediated second A-minor type 0 interaction to final water-mediated A-minor type I interaction with the water molecule inserted between A and G. This means that the second adenosine A1606 replaces its water-mediated interaction with C1593 by a similar interaction with G1592 (Fig. 8, and Supplementary Material, Fig. S8). All these changes result in a large-scale shift of the mutual positions of the C- and NC-stems (Fig. 9 a, and Supplementary PDB files).
FIGURE 9.
Superposition of 3D structures of initial and final structures of (a) Kt-58 and (b) Kt-U4. The x-ray structures are shown in blue (more bent for Kt-58 and more open for Kt-U4) and representative final structures (averaged from MD; step, 500 ps) in red. The C-stem is overlaid. The changes from initial to final geometry were permanent in the simulated timescale (PDB files are available in Supplementary Material).
Simulation of Kt-U4 confirms the flexibility of K-turns
The 74-ns-long MD simulation of the U4 kink-turn motif, which contains the same type of second A-minor submotif like Kt-58 (A-minor type 0), revealed similar irreversible large-scale motion regulated by a shift of unpaired nucleotides as observed in the simulation of Kt-58.
Since the simulated Kt-U4, with only two short three-basepair stems, was the smallest molecule considered in this study, its conformational behavior was quite simple. After initial relaxation, the Kt-U4 molecule adapted a stable geometry, essentially similar to the starting one. The instantaneous RMSd oscillated around a value of ∼2 Å. This was followed (until 37 ns) by nonperiodical oscillations of RMSd around the value ∼2.5 Å, caused by random disruptions of the terminal C41=G35 basepair (Supplementary Material, Fig. S6 b). This basepair was then fully disrupted in the period 37–63 ns, repaired in the period 63–67 ns, and again disrupted till the end of simulation. The C41=G35 dynamics did not affect the dynamics of the kink and its interactions. We believe that the C41=G35 fluctuations should be primarily considered as common end effects sometimes seen in simulations.
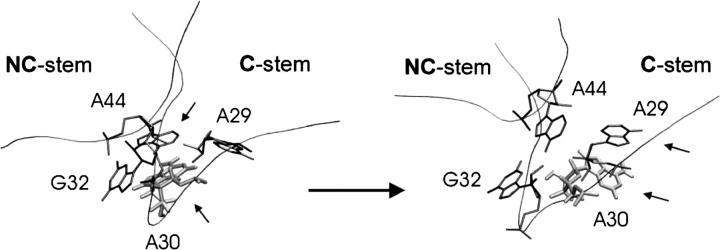
The main conformational change of the K region occurred in the last third of the simulation, slowly increasing the RMSd value to 2.5–3 Å. There was an irreversible structural transition within the period 44–51 ns. The unpaired A30 permanently changed its stacking position from the NC-stem (initially stacked on A44/G32) to the C-stem (finally stacked on A29) (Fig. 10). It caused large-scale motion of the NC- and C-stems (Fig. 9 b), resulting in a decrease of the interhelical angle by ∼10° (Supplementary Material, Fig. S9). All crucial tertiary interactions, including the first and second A-minor interaction, remained unchanged. The difference between the starting and final structures is smaller than in the case of Kt-58 due to a lack of any adaptation of the second A-minor motif. Still, the movement of a single unpaired base is sufficient to considerably affect the interhelical angle. Similar to Kt-58, the second A-minor submotif (type 0) is water-mediated. The crystal structure of Kt-U4 (PDB code 1E7K) contains no information about hydration, but the A33(N3)-G45(N3) x-ray distance, ∼5 Å, suggests that water molecules occupy this interbase region. A long-residency hydration site (revealed by MD) is formed by the A33(N3)-A33(O2′)-G45(O2′) pocket. This hydration site is stable, due to the absence of any rotation of A30, which just slides from one residue to another. In contrast, the rotation of A1591 seen in the Kt-58 simulation caused, among other things, conversion of the second A-minor type 0 submotif to type I (see above). In the Kt-U4 simulation, no such interconversion is observed (geometries of initial and final structures can be inferred from the Supplementary Material PDB files).
FIGURE 10.
Main conformational change of the kink in simulation of the Kt-U4 leading to a decrease of the interhelical angle. Initial (a) and final (b) geometry of the core nucleotides localized in the K region. Stacked residues (A30 shaded) are marked by arrows.
Note that the mobile unpaired bases (A30 in Kt-U4 and A1591 in Kt-58) do not protrude into the bulk solvent and thus are not accessible to extensive direct interactions in the ribosome. The restacking of A30 passes from G32 to A29. G32 and A29 form a base triple with the conserved A44 (the first A-minor motif) (Fig.10). Thus, A30 slides on the extended aromatic surface of this triple. Similar motion was also observed in the Kt-38 simulation, with no larger-scale structural effect. The unpaired base U1028 slid on the base triple formed by G1027, A939, and G1031 (Supplementary Material, Fig. S5), which caused some lateral shift of the helical stems (see text above). An interesting and likely related development was seen for A1591 in Kt-58. In Kt-58, the G1592=C1602 basepair interacts with the conserved A1590 to form a base quadruple, the first A-minor motif. A1591 is initially stacked on A1603, whereas the latter base is stacked on the quadruple. However, the relocations finally bring the A1591 to stack with the G1592=C1602 basepair. The slow and smooth motions of the unpaired bases suggest that the base quadruple region forms a convenient aromatic stacking surface for unpaired bases and allows them to shift without substantial energy barriers (Supplementary Material PDB files).
Hinge-like motions of Kt-42: essential dynamics analysis
In this article, we have described in a qualitative fashion the hinge-like motions seen in simulations of selected K-turns. To obtain a more quantitative description we have applied essential dynamics analysis (see Methods). The EDA fully confirms the qualitative analysis of K-turn motions given above. We illustrate the value of EDA by analyzing the open ↔ closed dynamics of Kt-42 to identify correlated atomic motions occurring during MD simulation. We identified the five largest eigenvalues (with corresponding eigenvectors) that dominated the Kt-42 dynamics. EDA illustrates the hinge-like motions and its outcome resembles the results of the trajectory analysis as described above. Thus, EDA corroborates the key conclusions reached by direct analysis of the trajectories. Additionally, EDA reveals that the motion is rather complex, and that besides the simple open ↔ closed dynamics, modest interhelical twisting also occurs, as shown in Supplementary Material (Fig. S10, a–e).
The supplementary Fig. S11 illustrates the interhelical twisting (torsion) in more detail. The interhelical torsion representing the direction of the NC-stem axis with respect to the C-stem axis oscillated with an amplitude of ∼20° in comparison to the x-ray value (Supplementary Material, Fig. S11 b). The fluctuations suggest that this type of motion may contribute to the K-turn flexibility to an extent that could be biologically important, since it gives more freedom (dimensionality) to the K-turn to act as an adaptable elbow-like element. Our preliminary results indicate a possible correlation between the opening of the kink (increasing of the interhelical angle) and the twisting (decreasing of interhelical torsion angle; see Methods section for definition). Since the results recorded here are for isolated K-turns we feel it would be premature to specifically suggest distinct roles of bending and twisting components for large-scale motions in the ribosomal context. Detailed description and analysis of correlated motions of all simulated K-turns will be published elsewhere, when additional K-turn simulations will also be available, including protein-RNA complexes. We reiterate that qualitatively the EDA analysis does not change the picture of K-turn motions presented above.
DISCUSSION
We have carried out extended explicit solvent simulations of isolated K-turn RNA motifs. Unlike other RNA molecules simulated to date, the K-turns are dynamical structural elements that sample a wide range of conformations on the multinanosecond timescale. Local conformational changes in the K-turn motifs lead to substantial hinge-like motions between their relatively rigid helical arms.
All simulated K-turn motifs reveal stability of the trans SE/SE interaction formed by the conserved adenosine (the first A-minor interaction), which is A939 in Kt-38, A1215 in Kt-42, A1590 in Kt-58, and A44 in Kt-U4. This interaction strongly stabilizes the 3D shape of these motifs.
On the other hand, the second A-minor interaction between the C- and NC-stems plays the pivotal role in the observed motions. The trans SE/SE basepairs A1032/G940 in Kt-38 and A1152/G1216 in Kt-42 are stable and act as fulcra for the motion. The pivoting motion produces small changes in the A(N6)-G(N3) H-bond but significant fluctuations in the A(O2′)-C(O2) and A(C1′)-C(C1′) distances in the A1032/C1026 basepair of Kt-38 and A1152/C1147 basepair of Kt-42. The local opening of the second A-minor motif is accompanied by insertion of a long-residency water molecule between C(O2) and A(O2′). The local motions then propagate beyond the central kink area and cause large-scale changes in the mutual positions of the adjacent helices.
The substates of the second A-minor interaction sampled in the simulations agree well with crystallographic data, including the positions of key hydration sites. The x-ray structure of Kt-38 represents an open state with a water molecule inserted between A1032 and C1026. The x-ray structure of Kt-42 represents a semiclosed state with considerably shorter distances between the corresponding A1152 and C1147 bases. Other x-ray structures of K-turns for which the second A-minor interaction is also type I reveal these two types of interaction patterns. The simulations show smooth oscillations over a wide range of geometries between and around both states for both K-turns, with a characteristic insertion of a long-residency water into the second A-minor motif when it opens. The distributions of interhelical distances and interhelical angles are nearly identical for the two kink-turns. For Kt-42 no more than one water molecule at a time was observed to bridge between C1147(O2) and A1152(O2′) during 37 ns of simulation. In the longer Kt-38 simulation the space between A1032 and C1026 opened reversibly at ∼26 ns to accommodate two water molecules. This opening correlated with increased interhelical distances and a larger interstem angle. Our study thus confirms involvement of long-residency water molecules in key sites of complex RNA structures (Csaszar et al., 2001; Reblova et al., 2003b, 2004; Spackova et al., 2000), and in this case the specific hydration is intimately involved in key dynamical motions. The simulations do not explicitly reveal whether the inserted water molecules actively drive solute structural adaptations or the water molecules are just passively inserted after the solute conformational change. Most likely, however, the changes in the solute structure and water insertion are coupled processes and neither of them is the primary event. We thus suggest that there is a competition between direct solute-solute hydrogen bonds and water-mediated bridges, resulting in a very shallow and wide overall free energy surface.
Numerous examples of type I A-minor motifs similar to those observed in K-turns are seen in the ribosome (Nissen et al., 2001). There are 51 examples in the H. marismortui 50S structure of adenosines interacting with G=C basepairs to form cis SE/SE A/C and trans SE/SE A/G basepairs. We measured the C1′-C1′ distances in these pairs and found that the A(C1′)-G(C1′) distances are narrowly distributed, just as in the simulations, with an average distance close to that in the fully hydrogen-bonded structure. On the other hand, the A(C1′)-C(C1′) distances are broadly distributed. The range and average distance are close to those calculated from the simulations. This suggests that A-minor type I motifs may be dynamic in other contexts as well. Water molecules are usually associated with these motifs in the crystal structure, either in the plane, mediating the A/C interactions, or out of the plane, as observed in the simulations for closed and semiclosed states of the kink-turns. The simulations thus agree with the x-ray data.
The complexity of the system including bound ions and long-residency waters precludes a straightforward and reliable estimation of the free energies with presently available computational tools (Srinivasan et al., 1998; Stefl et al., 2003). However, the smooth course of the transitions suggests that all the substates seen in the simulations are virtually isoenergetic. This is entirely obvious in the case of the oscillations seen for the A-minor interactions in Kt-42 and Kt-38. Such floppy systems have distinct properties compared to systems possessing well-defined free energy minima. The surrounding molecules in the ribosome can preferentially stabilize any of the substates seen in the simulations. The elbow-like mechanical properties of the K-turns could allow functionally significant changes of the positions of distal parts of the protruding RNA elements that Kt-38 and Kt-42 belong to, i.e., the A-site finger (helix 38) and the factor-binding or L11 site (helix 42–helix 44).
The simulation of Kt-58 (in contrast to Kt-38 and Kt-42) produced a geometry that differs from the initial ribosomal x-ray structure due to a substantial transition of the A1591 nucleotide in the nominally unpaired region. It cannot be ruled out that the transition is caused by some imperfection of the force field. Even in this case, however, it is fair to assume that the new geometry is in reality close in energy to the initial x-ray geometry. Albeit not perfect, the force field is unlikely to locate a geometry that is entirely irrelevant. However, the transition could also be primarily due to the lack of interactions with the other parts of the ribosome that are absent in the simulation. Then the simulation could correctly reflect the absence of these additional interactions. Notably, the key trans SE/SE tertiary contact between the C- and NC-stems remains essentially conserved in the course of the Kt-58 simulation. The main transition involves an unpaired base, which obviously is flexible in solution. There is no sign of a destabilization or unfolding of any key element of the K-turn structure on the present simulation timescale, although there is an adaptation (shift) of the second water-mediated A-minor interaction. As all key conserved interactions are preserved, we suggest that the initial and final geometries belong to a single broad free energy region, which is also supported by the very smooth, gradual transition between the two geometries. Interestingly, although the local structural rearrangements at the kink region are very different from those seen in the Kt-38 and Kt-42 simulations, they result in a similar overall hinge-like flexibility of the K-turn. We assume that this picture, when considered qualitatively, is not affected by the force-field limitations. The Kt-58 simulation, and the results from the Kt-U4 simulation, thus suggest that, besides the interrelation between the mutual positions of the C- and NC-stems and the local variations of the second A-minor interaction (see above), the K-turn geometry may also be modulated by changes in the positions of the unpaired bases. The changes of the K-turn hinge via repositioning of the unpaired bases may be sequence-specific. Further research will be needed to get broader insight into such motions. Possibly, constraining the unpaired bases via interactions with adjacent proteins and RNA elements may in some cases restrict (rigidify) the K-turn. Similarly, one can speculate that unpaired regions of some K-turns may help to absorb strains exerted on the K-turns when the mutual position of the C- and NC-stems is restrained inside the ribosome.
In the x-ray structure, the second A-minor interaction of Kt-58 (A1606/C1593=G1601, A-minor type 0) is stabilized via water molecules between A and C (x-ray waters 3119 and 5409). Although the bases are correctly oriented to form an A-minor interaction, they are too far apart to form direct H-bonds. The hydration site is reproduced in the simulation and is occupied in the initial phase of the simulation by a single long-residency water molecule for 3.6 ns. Then we observe transition of this interaction to a water-mediated A-minor type I interaction involving the adjacent G1602=C1592 basepair (Fig. 8 and Supplementary Material, Fig. S8), again with long water-binding times up to ∼4 ns. In contrast to simulations of Kt-38 and Kt-42, this new A-minor type I interaction does not reveal any substantial internal dynamics. It may be related to different topology with insertion of a water molecule in the A/G basepair of Kt-58 and in the A/C basepair of Kt-38 and Kt-42 (Supplementary Material, Fig. S8).
In assessing the biological relevance of the simulations, a few additional points need to be clarified. First, the simulation timescale precludes K-turn unfolding (seen, for example, in solution experiments) even in the absence of the divalent cations and the other stabilizing elements. All K-turns reveal stability of the first crucial tertiary interaction involving the conserved adenosines, A939/G1027 (Kt-38), A1215/C1148 (Kt-42), A1590/C1602 (Kt-58), and A44/A29 (Kt-U4). The simulations thus characterize the intrinsic conformational properties within the conformational subspace of the ribosome-like and x-ray K-turn geometries. Second, the adjacent proteins and rRNA may significantly influence the dynamics of the K-turns. Thus, their dynamics inside the ribosomal subunits may differ from the dynamics seen in the simulations. However, the intrinsic mechanical properties of free K-turns highlighted in the simulations certainly affect their interactions with the other molecular components of the ribosome, including the mutual structural adaptations of all the interacting species. It is unlikely that the inherent internal flexibility of the K-turns has no effect on their final structures and interactions inside ribosomes. The simulation technique thus complements the x-ray crystallography and solution experiments. We assume that the range of accessible K-turn geometries and possible rearrangements is still underestimated in our study, since the timescale of the simulations does not guarantee a full sampling of the relevant conformations. We suggest that, rather than actively inducing motions, the K-turns may allow smooth elbow-like adjustments of mutual positions of other molecules within the low-energy part of the folded K-turn conformational space.
K-turn motifs (as mentioned in the Introduction) can undergo metal-ion dependent conformational transitions with divalent ions being important for folding of isolated K-turns in solution. Nevertheless, we carried out our simulations in the presence of Na+ for the following reasons. First, the simulations are too short to experience the unfolding seen in solution experiments. Second, no Mg2+ ions contact the K-turns in the ribosomal x-ray structures. Thus, we are lacking proper starting geometries for initial placement of the Mg2+ ions (see below). We therefore conclude that the structural changes seen for Kt-58 are not caused by the lack of Mg2+ in the simulations. As discussed above, the Kt-58 structural adjustment reflects either a modest force-field imbalance or absence of the adjacent ribosomal components. Finally, we wish to underline that simulations with Mg2+ are inherently and considerably less accurate than simulations with monovalent ions. This is because the divalent cations are poorly represented by the simple pair-additive force field (major polarization and charge transfer effects are neglected). Further, the simulation timescale is entirely insufficient to achieve a proper sampling of divalent cations: the first-shell ligands exchange on the much longer microsecond timescale. As shown recently, improperly placed Mg2+ can cause substantial perturbations of the simulated RNA structure that are not repaired in the course of the simulation (Reblova et al., 2004). We thus suggest avoiding Mg2+ ions in simulations. As described above, there are several significant monovalent cation-binding sites seen in the K-turn simulations. However, none of the cation-binding sites appears to be crucial for the hinge-like nature of the K-turn low-energy motions. Actually, although ions are certainly important for the overall K-turn folding, the role of specific ions interacting with K-turns is smaller compared, e.g., to RNA kissing complexes and 5S rRNA loop E (Reblova et al., 2003a,b, 2004; Auffinger et al., 2004). These latter molecules contain extended cation-binding pockets, not evidenced for K-turns, which are permanently occupied by ions.
Biological significance
During the protein synthesis cycle, tRNA occupies successive positions on the ribosome: first, the A-site, as an aminoacyl-tRNA; then the P-site, as a peptidyl-tRNA, after peptide bond formation; and finally, the E-site, as a deacylated tRNA, and before leaving the ribosome. Ribosomes arrested at nearly every stage of the protein synthesis cycle have been visualized using cryo-EM with single-particle reconstruction. These studies have revealed coordinated conformational changes in the ribosomal subunits, the bound tRNAs, and the associated protein factors, at resolution approaching 10 Å (Frank, 2002). Most notably, cryo-EM revealed a ratchet-like relative rotation of the two ribosomal subunits accompanying the binding of EF-G to ribosomes and subsequent GTP hydrolysis (Frank and Agrawal, 2000; Valle et al., 2003b). Furthermore, the ratchet-like motion is accompanied by a 20-Å movement of the L1-stalk relative to the 50S subunit, implying that the L1-stalk is involved in translocation of deacylated tRNAs from the P- to the E-site (Valle et al., 2003b). We speculate that the dynamical K-turns could represent one of the structural elements that allow such motions, either within the x-ray like region of K-turn geometries sampled in our simulations or utilizing larger-scale “unfolding” motions evidenced in the solution experiments (Goody et al., 2004; Matsumura et al., 2003). This is supported by the occurrence of K-turns at key conserved sites that are implicated in ribosome motions during protein synthesis. Let us briefly comment on the possible motions that could be facilitated by K-turn dynamics.
Kt-38
As shown in supplementary Fig. S12, the A-site finger protrudes from the right side of the central protuberance of the 50S subunit (dominated by 5S rRNA, shown in orange) and crosses the interface between the ribosomal subunits directly above and parallel to the A- and P-tRNAs. So positioned, it prevents tRNAs from shifting between the A- and P-sites. The A-site finger contacts the 30S subunit to form intersubunit bridge B1a. Cryo-EM shows that during the ratchet-like motion associated with translocation, bridge B1a moves up and down (Frank, 2003; Gabashvili et al., 2000). This implies motion of the A-site finger relative to the positions of the bound tRNAs. Such motion of the A-site finger would allow A-site tRNA to slide into the 50S P-site unimpeded by the A-site finger. A distance of ∼100 Å separates the tip of the A-site finger, which contacts the 30S subunit, from kink-turn Kt-38, located near its base. A 10° change in the Kt-38 interhelical angle observed in the present MD simulations would therefore produce a displacement of almost 18 Å at the tip of the finger. Such motions require coupled motions of 5S rRNA, which contacts the A-site finger at the composite loop-E motif (H. marismortui nucleotides 953–955/1012–1014), and of protein L5, participating in bridge B1b. Thus, the function of Kt-38 could be to provide hinge-like flexibility to the A-site finger, permitting coordinated, large-scale motion to facilitate elongation.
Kt-42
EM also revealed that large displacements occur at the 50S subunit's factor-binding site (i.e., GTPase-associated center), which comprises the L7/L12 stalk and the sarcin/ricin loop. Helices 43 and 44 of 23S rRNA are connected to the rest of the ribosome by helix 42 and comprise the base of the L7/L12 stalk. Cryo-EM studies were done of the ternary complex, EF-Tu/aa-tRNA/GTP, bound to the ribosome and stalled by the antibiotic kirromycin. These studies established that the conformation and position of the aa-tRNA relative to the 50S subunit is quite different before and after decoding. During decoding, the anticodon end of the tRNA interacts with the decoding center (A-site) of the 30S subunit, whereas the elbow region of the aa-tRNA interacts with the factor-binding site, specifically helices 43 and 44 of 23S rRNA (Valle et al., 2002). In this hybrid A/T state, aa-tRNA is prevented by its interactions with the factor-binding site from prematurely “accommodating,” i.e., binding, to the A-site of the 50S subunit. Only after the codon-anticodon recognition-dependent signal is transmitted from the 30S subunit to the factor-binding site (perhaps by the cognate tRNA itself) and the GTPase activity of EF-Tu is stimulated, do the conformational changes take place. This allows for the release of EF-Tu and the full accommodation of aa-tRNA into the A-site (Valle et al., 2003a). Large-scale motion of the factor-binding site is implicated in these functions by cryo-EM studies and by x-ray crystallography. In the D. radiodurans and T. thermophilus structures, the tip of the H43/H44 domain contacts the top of helix 89 in domain V, whereas in the H. marismortui structure, the distance between these RNA elements is ∼15 Å. Analysis of the crystal structures in light of the results of our MD simulations indicates that a hinge-like opening motion localized at Kt-42 (visible in the rear view of the ribosome, Supplementary Material, Fig. S12) could displace the L7/L12 stalk away from the body of the ribosome and increase access to the 50S A-site. Likewise, a hinge-like closing motion could convert the semiclosed H. marismortui structure to the closed form and bring the H43/H44 domain into contact with helix 89. Preliminary modeling of closed and open forms of Kt-42 in the ribosome suggests that the differences between the crystal structures may be reproduced by semirigid hinge-like motions of Kt-42 observed in this study. Thus, the function of Kt-42 may be to provide hinge-like flexibility permitting the large-scale motion at the factor-binding site that is necessary for EF-Tu-catalyzed A-site tRNA accommodation and EF-G-catalyzed elongation.
Kt-58
The terminal hairpin loop of helix 58 contacts helix 34, a small protuberance at the base of the 50S subunit that interacts with ribosomal protein S15 and helix 20 in the 30S subunit to form intersubunit bridge B4 (Yusupov et al., 2001). Interestingly, in the lower-resolution structures of the 70S ribosome of T. thermophilus and the 50S subunit of D. radiodurans, the tip of H58 does not contact H34 and the motif corresponding to Kt-58 exhibits a different (more open) conformation. This indicates that K-turn flexibility could help in formation of the functional contacts between hairpin loops H58 and H34, regulated by Kt-58 conformation.
CONCLUSIONS
Molecular dynamics simulations suggest that rRNA K-turns are unique dynamical structural elements sampling a wide range of conformations on the multinanosecond timescale. Local conformational changes in the K-turn motifs lead to large-scale hinge-like motions between the relatively rigid helical arms of the K-turn motifs. In the course of the simulations, all key tertiary interactions between the C- and NC-stems are preserved, so that the simulations remain essentially within one broad substate corresponding to the tightly kinked x-ray geometries. Nonetheless, the conformational variations of the interstem geometries seen in the simulations are very significant.
The A-minor interactions between the C- and NC-stems play pivotal roles in the motions. The first A-minor interaction is stable. Regarding the second A-minor interaction, the trans SE/SE basepairs A1032/G940 in Kt-38 and A1152/G1216 in Kt-42 are stable and act as fulcra for the motion. The pivoting motion produces small changes in the A(N6)-G(N3) distance, but significant fluctuations in the A(O2′)-C(O2) and A(C1′)-C(C1′) distances in the A/C pair (A1032/C1026 and A1152/C1147) of the second A-minor type I interaction. Thus the A-minor motif oscillates in the simulations. Its local opening is accompanied by insertion of long-residency waters. The local motions then propagate beyond the central kink area and cause large-scale changes in the mutual positions of the adjacent helices. The A-minor type I substates sampled in the simulations agree well with crystallographic data, including positions of key hydration sites. The smooth course of the transitions gives very strong albeit indirect evidence that all the geometries sampled in the simulations are virtually isoenergetic.
The simulation of Kt-58 with weaker second A-minor type 0 interaction results in a new geometry, including a structural adaptation of the second A-minor interaction that is different from the initial ribosomal x-ray structure. The whole geometry change is dominated by a substantial transition of the A1591 nucleotide in the nominally unpaired region. The key trans SE/SE tertiary contact (the first A-minor interaction) between the C- and NC-stems remains conserved. Similar dynamics were seen also for Kt-U4. Thus, the K-turn geometries may also be regulated by changes of the positions of the unpaired bases. Such structural variability may be quite sequence-dependent, in contrast with the A-minor type I dynamics seen for Kt-38 and Kt-42. Also, for Kt-58 and Kt-U4 the overall behavior of the simulations suggests that the geometries sampled in the simulations are close in energy.
Viewed in light of the phylogenetic conservation and location of K-turns at the base of functionally significant protuberances in the ribosome, the dynamical results support the notion that K-turns could serve as flexible hinges to allow biologically significant motions in protein synthesis. Many K-turns are present in ribosomal positions that are implicated in dynamical motions. Moreover, the simulations provide evidence for crucial roles of long-residency water molecules in modulating the motions and stabilizing alternative conformations within a limited range of angles. Although other RNA motifs may also contribute to the conformational flexibility of RNA protuberances, K-turns appear to be the most recurrent of these motifs. Kink-turns may play a significant role in the biologically significant flexibility of the A-site finger (helix 38) and the factor-binding site (helices 42–44). Flexibility conferred by Kt-38 may allow the A-site finger to serve as a gate regulating tRNA motion between the A- and P-sites. Likewise Kt-42 appears to confer flexibility to the factor-binding site, regulating tRNA access to the A-site. Finally, flexibility of Kt-58 can help to establish functional contacts between H58 and H34.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Supplementary Material
Acknowledgments
Note added in proof: After our article was accepted, another molecular dynamics study on Kt-U4 appeared (Cojocaru, V., S. Nottrott, R. Klement, and T. M. Jovin. 2005. The snRNP 15.5K protein folds its cognate K-turn RNA: a combined theoretical and biochemical study. RNA. 11:197–209). This study deals with different aspects of K-turns, namely protein-assisted RNA folding, whereas our study aims to characterize functional K-turns involved in dynamical motions.
The authors thank Dr. Jennifer Morris of the Center for Biomolecular Modeling for her expertise in preparing the ribosome model. Our special thanks go to the Supercomputer Center, Brno, where all simulations were carried out.
This work was supported by grants MSM0021622413 from the Ministry of Education of the Czech Republic, grant GA203/05/0009 from the Grant Agency of the Czech Republic, research project AVOZ50040507 from the Ministry of Education of the Czech Republic (Institute of Biophysics), the Wellcome Trust International Senior Research Fellowship in Biomedical Science in Central Europe (GR067507), and National Institutes of Health grants 2R15 GM55898 and 3R15 GM55898.
References
- Amadei, A., A. B. M. Linssen, and H. J. C. Berendsen. 1993. Essential dynamics of proteins. Proteins. 17:412–425. [DOI] [PubMed] [Google Scholar]
- Auffinger, P., L. Bielecki, and E. Westhof. 2004. Symmetric K+ and Mg2+ ion binding sites in the 5S rRNA loop E inferred from molecular dynamics simulations. J. Mol. Biol. 335:555–571. [DOI] [PubMed] [Google Scholar]
- Auffinger, P., S. Louise-May, and E. Westhof. 1999. Molecular dynamics simulations of solvated yeast tRNA. Biophys. J. 76:50–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auffinger, P., and E. Westhof. 1998. Simulations of the molecular dynamics of nucleic acids. Curr. Opin. Struct. Biol. 8:227–236. [DOI] [PubMed] [Google Scholar]
- Auffinger, P., and E. Westhof. 2000. RNA solvation: a molecular dynamics simulation perspective. Biopolymers. 56:266–274. [DOI] [PubMed] [Google Scholar]
- Ban, N., P. Nissen, J. Hansen, P. B. Moore, and T. A. Steitz. 2000. The complete atomic structure of the large ribosomal subunit at 2.4 Å resolution. Science. 289:905–920. [DOI] [PubMed] [Google Scholar]
- Berendsen, H. J. C., D. van der Spoel, and R. van Drunen. 1995. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 91:43–56. [Google Scholar]
- Beveridge, D. L., and K. J. McConnell. 2000. Nucleic acids: theory and computer simulation, Y2K. Curr. Opin. Struct. Biol. 10:182–196. [DOI] [PubMed] [Google Scholar]
- Cheatham, III, T. E., and P. A. Kollman. 1997. Molecular dynamics simulations highlight the structural differences among DNA:DNA, RNA:RNA, and DNA:RNA hybrid duplexes. J. Am. Chem. Soc. 21:4805–4825. [Google Scholar]
- Cornell, W. D., P. Ciepak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, Jr., D. C. Spellmeyer, T. Fox, J. W. Caldwell, and P. A. Kollman. 1995. A 2nd generation force-field for the simulation of proteins, nucleic-acids, and organic-molecules. J. Am. Chem. Soc. 117:5179–5197. [Google Scholar]
- Csaszar, K., N. Spackova, R. Stefl, J. Sponer, and N. B. Leontis. 2001. Molecular dynamics of the frame-shifting pseudoknot from beet western yellow virus: The role of non-Watson-Crick base-pairing, ordered hydration, cation binding and base mutations on stability and unfolding. J. Mol. Biol. 313:1073–1091. [DOI] [PubMed] [Google Scholar]
- Ferrin, T. E., C. C. Huang, L. E. Jarvis, and R. Langridge. 1988. The MIDAS display system. J. Mol. Graph. 6:13–27. [Google Scholar]
- Frank, J. 2002. Single-particle imaging of macromolecules by cryo-electron microscopy. Annu. Rev. Biophys. Biomol. Struct. 31:303–319. [DOI] [PubMed] [Google Scholar]
- Frank, J. 2003. Electron microscopy of functional ribosome complexes. Biopolymers. 68:223–233. [DOI] [PubMed] [Google Scholar]
- Frank, J., and R. K. Agrawal. 2000. A ratchet-like inter-subunit reorganization of the ribosome during translocation. Nature. 406:318–322. [DOI] [PubMed] [Google Scholar]
- Gabashvili, I. S., R. K. Agrawal, C. M. Spahn, R. A. Grassucci, D. I. Svergun, J. Frank, and P. Penczek. 2000. Solution structure of the E. coli 70S ribosome at 11.5 A resolution. Cell. 100:537–549. [DOI] [PubMed] [Google Scholar]
- Giudice, E., and R. Lavery. 2002. Simulation of nucleic acids and their complexes. Acc. Chem. Res. 35:350–357. [DOI] [PubMed] [Google Scholar]
- Goody, T. A., S. E. Melcher, D. G. Norman, and D. M. J. Lilley. 2004. The kink-turn motif in RNA is dimorphic, and metal ion dependent. RNA. 10:254–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo, J. X., I. Daizadeh, and W. Gmeiner. 2000. Structure of the Sm binding site from human U4 snRNA derived from a 3ns PME molecular dynamics simulation. J. Biomol. Struct. Dyn. 18:335–344. [DOI] [PubMed] [Google Scholar]
- Guo, J. X., and W. H. Gmeiner. 2001. Molecular dynamics simulation of the human U2B′′ protein complex with U2 snRNA hairpin IV in aqueous solution. Biophys. J. 81:630–642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamma, T., and A. Ferre-D'Amare. 2004. Structure of protein L7Ae bound to a K-turn derived from an archaeal box H/ACA sRNA at 1.8 Å resolution. Structure. 12:893–903. [DOI] [PubMed] [Google Scholar]
- Harms, J., F. Schluenzen, R. Zarivach, A. Bashan, S. Gat, I. Agmon, H. Bartels, F. Franceschi, and A. Yonath. 2001. High resolution structure of the large ribosomal subunit from a mesophilic eubacterium. Cell. 107:679–688. [DOI] [PubMed] [Google Scholar]
- Harvey, S. C., R. K. Z. Tan, and T. E. Cheatham III. 1998. The flying ice cube: velocity rescaling in molecular dynamics leads to violation of energy equipartition. J. Comput. Chem. 19:726–740. [Google Scholar]
- Hermann, T., P. Auffinger, and E. Westhof. 1998. Molecular dynamics investigations of hammerhead ribozyme RNA. Eur. Biophys. J. 27:153–165. [DOI] [PubMed] [Google Scholar]
- Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD: visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- Klein, D. J., T. M. Schmeing, P. B. Moore, and T. A. Steitz. 2001. The kink-turn: a new RNA secondary structure motif. EMBO J. 20:4214–4221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leontis, N. B., and E. Westhof. 2001. Geometric nomenclature and classification of RNA basepairs. RNA. 7:499–512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindahl, E., B. Hess, and D. van der Spoel. 2001. GROMACS 3.0: A package for molecular simulation and trajectory analysis. J. Mol. Model. 7:306–317. [Google Scholar]
- Matsumura, S., Y. Ikawa, and T. Inoue. 2003. Biochemical characterization of the kink-turn RNA motif. Nucleic Acids Res. 31:5544–5551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore, T., Y. Zhang, M. O. Fenley, and H. Li. 2004. Molecular basis of box C/D RNA-protein interactions; cocrystal structure of archaeal L7Ae and a box C/D RNA. Structure. 12:807–818. [DOI] [PubMed] [Google Scholar]
- Nagan, M. C., P. Beuning, K. Musier-Forsyth, and C. J. Cramer. 2000. Importance of discriminator base stacking interactions: molecular dynamics analysis of A73 microhelix(Ala) variants. Nucleic Acids Res. 28:2527–2534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagan, M. C., S. S. Kerimo, K. Musier-Forsyth, and C. J. Cramer. 1999. Wild-type RNA microhelix(Ala) and 3:70 variants: Molecular dynamics analysis of local helical structure and tightly bound water. J. Am. Chem. Soc. 121:7310–7317. [Google Scholar]
- Nikulin, A., I. Eliseikina, S. Tishchenko, N. Nevskaya, N. Davydova, O. Platonova, W. Piendl, M. Selmer, A. Liljas, D. Drygin, R. Zimmermann, M. Garber, and S. Nikonov. 2003. Structure of the L1 protuberance in the ribosome. Nat. Struct. Biol. 10:104–108. [DOI] [PubMed] [Google Scholar]
- Nissen, P., J. A. Ippolito, N. Ban, P. B. Moore, and T. A. Steitz. 2001. RNA tertiary interactions in the large ribosomal subunit: the A-minor motif. Proc. Natl. Acad. Sci. USA. 98:1–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norberg, J., and L. Nilsson. 2002. Molecular dynamics applied to nucleic acids. Acc. Chem. Res. 35:465–472. [DOI] [PubMed] [Google Scholar]
- Pearlman, D. A., D. A. Case, J. W. Caldwell, W. S. Ross, T. E. Cheatham III, and S. DeBolt. 1995. AMBER, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structural and energetic properties of molecule. Comput. Phys. Commun. 91:1–41. [Google Scholar]
- Razga, F., N. Spackova, K. Reblova, J. Koca, N. B. Leontis, and J. Sponer. 2004. Ribosomal RNA kink-turn motif. A flexible molecular hinge. J. Biomol. Struct. Dyn. 22:183–194. [DOI] [PubMed] [Google Scholar]
- Reblova, K., N. Spackova, J. Koca, N.B. Leontis, and J. Sponer. 2004, Long-residency hydration, cation binding, and dynamics of loop E/helix IV rRNA-L25 protein complex. Biophys. J. 87: 3397–3412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reblova, K., N. Spackova, J. E. Sponer, J. Koca, and J. Sponer. 2003a. Molecular dynamics simulations of RNA kissing-loop motifs reveal structural dynamics and formation of cation-binding pockets. Nucleic Acids Res. 31:6942–6952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reblova, K., N. Spackova, R. Stefl, K. Csaszar, J. Koca, N. B. Leontis, J. Sponer, and J. E. Sponer. 2003b. Non-Watson-Crick basepairing and hydration in RNA motifs: molecular dynamics of 5S rRNA loop E. Biophys. J. 84:3564–3582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross, W. S., and C. C. Hardin. 1994. Ion-induced stabilization of the G-DNA quadruplex: free energy perturbation studies. J. Am. Chem. Soc. 116:6070–6080. [Google Scholar]
- Sanbonmatsu, K. Y., and S. Joseph. 2003. Understanding discrimination by the ribosome: stability testing and groove measurement of codon-anticodon pairs. J. Mol. Biol. 328:33–47. [DOI] [PubMed] [Google Scholar]
- Sarzynska, J., T. Kulinski, and L. Nilsson. 2000. Conformational dynamics of a 5S rRNA hairpin domain containing loop D and a single nucleotide bulge. Biophys. J. 79:1213–1227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schluenzen, F., A. Tocilj, R. Zarivach, J. Harms, M. Gluehmann, D. Janell, A. Bashan, H. Bartels, I. Agmon, F. Franceschi, and A. Yonath. 2000. Structure of functionally activated small ribosomal subunit at 3.3 Å resolution. Cell. 102:615–623. [DOI] [PubMed] [Google Scholar]
- Schneider, C., M. Brandl, and J. Suhnel. 2001. Molecular dynamics simulation reveals conformational switching of water- mediated uracil-cytosine base-pairs in an RNA duplex. J. Mol. Biol. 305:659–667. [DOI] [PubMed] [Google Scholar]
- Schneider, C., and J. Suhnel. 2000. A molecular dynamics simulation study of coaxial stacking in RNA. J. Biomol. Struct. Dyn. 18:345–352. [DOI] [PubMed] [Google Scholar]
- Spackova, N., I. Berger, and J. Sponer. 2000. Nanosecond molecular dynamics of zipper-like DNA duplex structures containing sheared G.A mismatch pairs. J. Am. Chem. Soc. 122:7564–7572. [Google Scholar]
- Srinivasan, J., T. E. Cheatham III, P. Cieplak, P. A. Kollman, and D. A. Case. 1998. Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate-DNA helices. J. Am. Chem. Soc. 120:9401–9409. [Google Scholar]
- Stagg, S. M., J. A. Mears, and S. C. Harvey. 2003. A structural model for the assembly of the 30 S subunit of the ribosome. J. Mol. Biol. 328:49–61. [DOI] [PubMed] [Google Scholar]
- Stefl, R., T. E. Cheatham III, N. Spackova, E. Fadrna, I. Berger, J. Koca, and J. Sponer. 2003. Formation pathways of a guanine-quadruplex DNA revealed by molecular dynamics and thermodynamic analysis of the substates. Biophys. J. 85:1787–1804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valle, M., J. Sengupta, N. K. Swami, R. A. Grassucci, N. Burkhardt, K. H. Nierhaus, R. K. Agrawal, and J. Frank. 2002. Cryo-EM reveals an active role for aminoacyl-tRNA in the accommodation process. EMBO J. 21:3557–3567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valle, M., A. Zavialov, W. Li, S. M. Stagg, J. Sengupta, R. C. Nielsen, P. Nissen, S. C. Harvey, M. Ehrenberg, and J. Frank. 2003a. Incorporation of aminoacyl-tRNA into the ribosome as seen by cryo-electron microscopy. Nat. Struct. Biol. 10:899–906. [DOI] [PubMed] [Google Scholar]
- Valle, M., A. Zavialov, J. Sengupta, U. Rawat, M. Ehrenberg, and J. Frank. 2003b. Locking and unlocking of ribosomal motions. Cell. 114:123–134. [DOI] [PubMed] [Google Scholar]
- Vidovic, I., S. Nottrott, K. Hartmuth, R. Luhrmann, and R. Ficner. 2000. Crystal structure of the spliceosomal 15.5kD protein bound to a U4 snRNA fragment. Mol. Cell. 6:1331–1342. [DOI] [PubMed] [Google Scholar]
- Watkins, N. J., V. Segault, B. Charpentier, S. Nottrott, P. Fabrizio, A. Bachi, M. Wilm, M. Rosbash, C. Branlant, and R. Luhrmann. 2000. A common core RNP structure shared between the small nucleolar box C/D RNPs and the spliceosomal U4 snRNP. Cell. 103:457–466. [DOI] [PubMed] [Google Scholar]
- Williams, D. J., and K. B. Hall. 2000. Experimental and theoretical studies of the effects of deoxyribose substitutions on the stability of the UUCG tetraloop. J. Mol. Biol. 297:251–256. [DOI] [PubMed] [Google Scholar]
- Wimberly, B. T., D. E. Brodersen, W. M. Clemons, Jr., R. J. Morgan-Warren, A. P. Carter, C. Vonrhein, T. Hartsch, and V. Ramakrishnan. 2000. Structure of the 30S ribosomal subunit. Nature. 407:327–339. [DOI] [PubMed] [Google Scholar]
- Yusupov, M. M., G. Z. Yusupova, A. Baucom, K. Lieberman, T. N. Earnest, J. H. Cate, and H. F. Noller. 2001. Crystal structure of the ribosome at 5.5 A resolution. Science. 292:883–896. [DOI] [PubMed] [Google Scholar]
- Zacharias, M. 2000. Simulation of the structure and dynamics of nonhelical RNA motifs. Curr. Opin. Struct. Biol. 10:311–317. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.