Abstract
Size distribution of dimyristoylphosphatidylcholine liposome suspensions was investigated by dynamic-light scattering (DLS) as a function of the sonication time (ts). Cumulant expansion (second- and third-order) and regularized Laplace inversion (CONTIN) of dynamic single-angle laser light-scattering data were performed. With both methods, the intensity-weighted mean hydrodynamic radius 〈r〉I depended on the investigated lengthscale. The number-weighted mean hydrodynamic radius (〈r〉N), obtained from CONTIN by modeling dimyristoylphosphatidylcholine vesicles as thin-walled hollow spheres, resulted as independent on the lengthscale. However, the 〈r〉N value obtained from cumulant expansions remained lengthscale-dependent. Therefore, the number-weighted radius distribution function is highly asymmetric. The number-weighted mean radius, the standard deviation, and the number-weighted radius at the peak 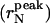 all decreased to a plateau when increasing sonication time. At ts longer than 1 h, the
all decreased to a plateau when increasing sonication time. At ts longer than 1 h, the 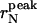 compares well with the radius of unilamellar vesicles in equilibrium with monomers predicted on a thermodynamic basis. The reliability of our analysis is proved by the comparison of experimental Rayleigh ratios with simulated ones, using the normalized number-weighted radius distribution function pN(r) determined by DLS data. A perfect agreement was obtained at longer sonication times, and the average aggregation number was determined. At lower ts values, simulations did not match experimental data, and this discrepancy was ascribed to the presence of large and floppy unilamellar vesicles with ellipsoidal shapes. Our investigation shows that, from single-angle DLS data, the radius distribution function of the vesicles can only be obtained if pN(r) is known.
compares well with the radius of unilamellar vesicles in equilibrium with monomers predicted on a thermodynamic basis. The reliability of our analysis is proved by the comparison of experimental Rayleigh ratios with simulated ones, using the normalized number-weighted radius distribution function pN(r) determined by DLS data. A perfect agreement was obtained at longer sonication times, and the average aggregation number was determined. At lower ts values, simulations did not match experimental data, and this discrepancy was ascribed to the presence of large and floppy unilamellar vesicles with ellipsoidal shapes. Our investigation shows that, from single-angle DLS data, the radius distribution function of the vesicles can only be obtained if pN(r) is known.
INTRODUCTION
Lipid vesicles are spherical shells formed from phospholipid bilayers (Cevc and Marsh, 1985), whose many technological applications include drug delivery (Gregoriadis, 1993), gene therapy (Lasic, 1997) and in the technology of adhesives, coating, ink, paint, etc. (Small, 1996). Controlling the particle-size distribution is an important morphological characteristic for the processibility and end properties of these systems (Small, 1996; Booth et al., 1997; Burak et al., 1997). The size distribution of the dissolved lipid film can be modified by mechanical stress. The relative final condition reflects both the specific protocol used and the thermodynamic conditions. But since the optimal free energy of the vesicles depends on competing contributions close to the overall thermal energy, the size distribution is inherently unstable and the vesicles spontaneously fuse, forming larger aggregates (Helfrich, 1973). Nevertheless, phenomenological theories, based on the thermodynamic equilibrium between the aggregates and the monomers, predict the presence of small unilamellar vesicles, for given thermodynamic and physicochemical conditions (Nagarajan, 1987).
Extensive investigations (Cevc and Marsh, 1985) on fully hydrated bilayers composed of a single phospholipid species show that such complexes undergo a thermotropic phase transition in which the thin wall shell, containing the lipid chains, changes from a gel state (Lβ) to a fluid or liquid-crystalline state (Lα). In addition, an intermediate phase Pβ, characterized by a rippled bilayer, is often located between the previous two (Carlson and Sethna, 1987). In dimyristoylphosphatidylcholine (DMPC), for example, the transition Pβ- Lα, called the main transition, occurs at Tm = 23.6°C, and it is characterized by a change in volume of the lipidic phase of ΔVm = 0.027 ml/g, and a variation in the bilayer thickness of Δdm = 0.8 nm (Cevc and Marsh, 1985). Depending on the storage temperature (i.e., above and below the main phase transition temperature), samples of given size-distribution undergo different evolutions in time (Helfrich, 1973).
Sonication is one of the most popular methods for producing a distribution of lipid vesicles of known size. The induced pressure stress breaks up the large and the multilamellar vesicles present in the rehydrated samples into small unilamellar vesicles, with sizes ranging from 5 to 50 nm (Small, 1996).
Despite the usefulness of knowing and controlling size-distribution of the sonicated vesicle dispersion, a detailed characterization is still lacking and a protocol to manage this type of preparation is needed. We hereby present static and dynamic light-scattering data on DMPC lipid suspensions produced by using different sonication times (ts). We provide evidence that the radius-distribution function of the vesicles in solution can be obtained from single-angle dynamic light-scattering (DLS) data only when the number-weighted radius distribution pN(r) is known.
MATERIALS AND METHODS
Preparation of sonicated vesicles
1,2-dimyristoyl-sn-glycero-3-phosphatidylcholine (DMPC) was purchased from Avanti Polar Lipids (Birmingham, AL) and used without any further purification. All other chemicals were re-agent grade. Dehydrated lipids were shipped dissolved in chloroform solvent. Chloroform was later removed by a rotary evaporation vacuum pumping. The lipid film was then dissolved and diluted in Millipore-grade water to a final concentration of 2 mg/ml. Three aliquots of the multilamellar polydisperse DMPC-H2O suspension were sonicated for different times, by using a Vibracel (Tecnochimica Sassolese, Modena, Italy) titanium-tip sonicator (Pmax = 600 W; ν = 20 KHz), above the main phase transition temperature at T = 30°C. Each sample underwent repetitive 1-Hz cycles, made of 0.4 s pulses, of power P = 150 W to control thermal effects.
Light-scattering measurements
Morphological characteristics of lipid vesicles were assessed by light scattering. Measurements of various vesicle samples were carried out with a commercial light-scattering setup ALV light-scattering spectrometer (ALV, Langen, Germany) consisting of a CGS-5000 rotating arm goniometer, an EMI-9863 photomultiplier tube, an ALV 5000 multi-Tau digital correlator, and a Coherent Innova 70 argon ion laser (Coherent Italia, Milano, Italy) operated at a wavelength of 488 nm at 100 mW. The scattering cell was immersed in a refractive index matching fluid (Toluene) maintained at 21 ± 0.1°C. For each sample, static and dynamic light-scattering data were collected simultaneously and acquired typically for a duration of 5 min for 1–3 angular runs. All the samples were investigated at six different angles, logarithmically scaled in sin(θ), where θ is the scattering angle (i.e., 66.5°, 78.4°, 88.7°, 91.4°, 108°, and 114.4°). The count rate of each acquisition was monitored to exclude runs containing artifacts due to passage through the scattering volume of dust or titanium (eventually released by the sonicator tip) particles.
LIGHT-SCATTERING ANALYSIS
The light scattered out of the incident beam is due to the presence of local fluctuations in the dielectric constant of the medium over the entire scattering volume V and, in the case of diluted suspensions, these fluctuations reflect the size and the shape of the scattering particles.
Static light scattering
When a sample can be assimilated to a solution of monodisperse particles, the Rayleigh ratio R (q) (i.e., the normalized power scattered at a given scattering wavevector is given by q = (4πn/λ)sin(ϑ/2) where θ is the scattering angle, λ the laser wavelength, and n the refractive index) can be expressed as the convolution of the single particle correlation function and the pair correlation function (Kerker, 1969). Therefore,
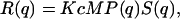 |
(1) |
where K is the optical constant given by K = (4π2/λ4NA)n2(∂n/∂c)2, with NA being the Avogadro number, c the sample concentration (g/ml), ∂n/∂c the refractive index increment of the solute (ml/g), and M the particle molar weight (g). Assuming that particles are not correlated (i.e., sufficiently diluted), their structure factor S(q) = 1. Depending on the specific shape, size, and density of the particles in solution, the form factor P(q) assumes different expressions. In the case of vesicles, the structure of the solute can be characterized by a thin-walled spherical shell (hollow sphere) of radius r and thickness δr. Therefore, the volume is given by 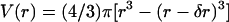 and the form factor (Kerker, 1969) by
and the form factor (Kerker, 1969) by
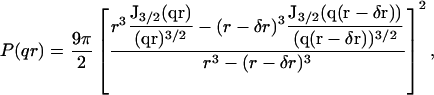 |
(2) |
where J3/2 (x) is the Bessel function of order 3/2 (Kerker, 1969). For a polydisperse sample with a continuous distribution of mass, the Rayleigh ratio can be written (Kerker, (1969) as
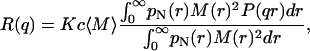 |
(3) |
where 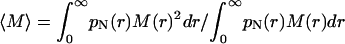 is the weight-average molecular weight, pN(r) is the normalized number-weighted radii distribution function, and M(r) is the molecular weight of the particles of given radius.
is the weight-average molecular weight, pN(r) is the normalized number-weighted radii distribution function, and M(r) is the molecular weight of the particles of given radius.
Dynamic light scattering
Dynamic light-scattering technique measures the intensity autocorrelation function g2(τ) = 〈I(t)I(t + τ)〉/〈I〉2, where τ is the lag time and the bracket represents the ensemble average. The g2(τ) can be related to the field autocorrelation function g1(τ) through the Siegert relation g2(τ) = 1 + βg12(τ), where β is an instrumental constant equal to 1 in our setup.
The mathematical form of g1(τ) depends on the physical properties of the system investigated. For a monodisperse solution of noninteracting particles, a single exponential function with decay time τ is obtained (Berne and Pecora, 2000). For a polydisperse sample, g1(τ) is no longer a single exponential. In this case, the distribution of decay rates on g1(τ) can be taken into account by introducing a weighting function,
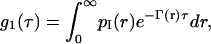 |
(4) |
where pI(r)dr is the intensity-weighted radius distribution function, describing the distribution of the fraction, in the interval dr, of the intensity scattered by a particle of hydrodynamic radius r and decay rates Γ(r) = kTq2/6πηr, with η the water viscosity and k the Boltzmann constant (Hallet et al., 1989; Pencer et al., 2001).
The classical approach for extracting the pI(r) from DLS data is based on the cumulant expansion (Koppel, 1972). In this method, the electric field autocorrelation function is expanded in terms of the distribution moments of the decay rates Γ(r),
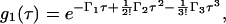 |
(5) |
where Γ1 is the intensity-weighted mean value 〈Γ(r)〉, Γ2 is the variance of the distribution, and Γ3 is its skewedness. The cumulants give just the moments but not the actual distribution function of the aggregates pI(r). Thus, in the case of large asymmetry in the size distribution, this method fails.
The value pI(r) can be otherwise obtained using the regularized Laplace inversion of the intensity autocorrelation function (CONTIN; see Provencher, 1982a,b). In this case the intensity-weighted radius distribution is obtained by a direct numerical inversion of the DLS data. The limit of this method mainly consists in the numerical difficulty of the inversion procedure for a finite number of experimental data.
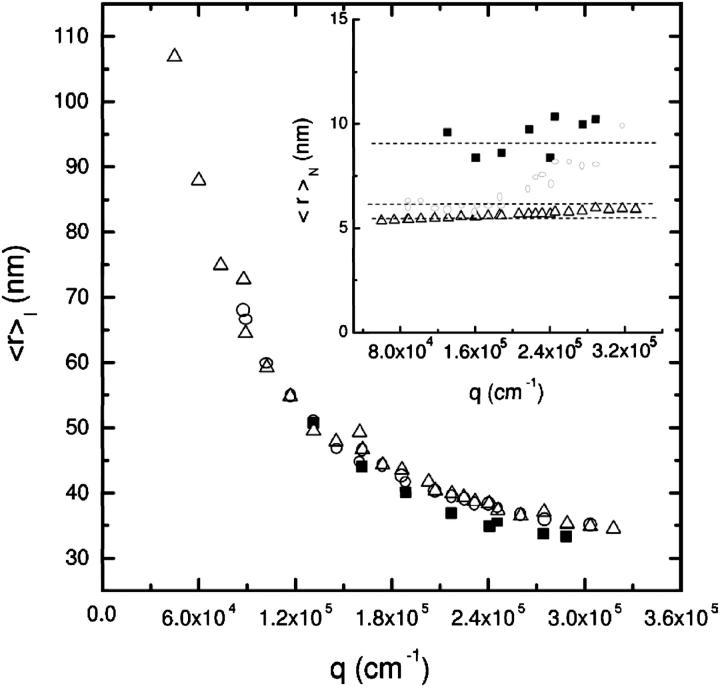
The first aim of our analysis deals with the definition of the optimal method needed to investigate vesicle size distribution. Thus we started studying the intensity-weighted mean hydrodynamic radius 〈r〉I by using both the second- and third-order cumulant expansions as well as the CONTIN inversion method. The results of the three analyses are reported in Fig. 1 for sample sonicated for 2 h, whose polydispersity is the lowest observed in our experiments. The absolute values of 〈r〉I determined with the three methods are in good agreement, suggesting that the three methods are equivalent—but a detailed analysis of the scattering data will show instead that such an equivalence is only an apparent one. The angular distribution of 〈r〉I shows a clear dependence of the mean radius on the different lengthscales investigated (q−1), independently from the method used. This q-dependence of 〈r〉I naturally arises in the presence of a large polydispersity. In this case, not only the particle volume, but also the density distribution (that is, the inner particle structure) determines 〈r〉I. The number-weighted radius distribution pN(r) essentially overcomes this problem by taking into account, for the form factor P(qr) and for the vesicle mass M(r) (Hallet et al., 1989; Pencer et al., 2001),
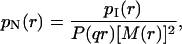 |
(6) |
where M(r) = ρV(r) with V(r) is the vesicle volume and ρ the bilayer density. By substituting the form factor (given in Eq. 2) in Eq. 6, the number-weighted radius distribution is recovered. Once pN(r) is known, it is thus easy to determine the mean hydrodynamic radius,
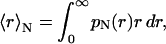 |
(7) |
and the standard deviation (SD),
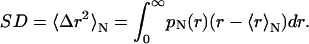 |
(8) |
In the case of cumulant analysis, we used a Gaussian distribution for the second order, whereas for the third order we used a log-normal distribution, whose skewedness is just a function of the first two moments.
FIGURE 1.
Angular dependence of the mean hydrodynamic radius calculated by using second- (▵) and third-order (○) cumulant expansion and CONTIN (▪) methods. Recovering the number-weighted radius distribution by using CONTIN to account for inner particle structure makes the mean radius independent of q (see the inset). In contrast, in using cumulant expansion, the q-dependence of the mean radius can still be seen.
With this data treatment, the 〈r〉N values do not show any further q-dependence (see inset of Fig. 1) in the case of CONTIN procedure. The second- and third-order cumulant analyses still show a q-dependence, indicating that Gaussian and log-normal distributions are not appropriate. Indeed, the skewedness calculated using experimental first and second moments in the log-normal distribution differ >10% from the skewedness observed at high q-values.
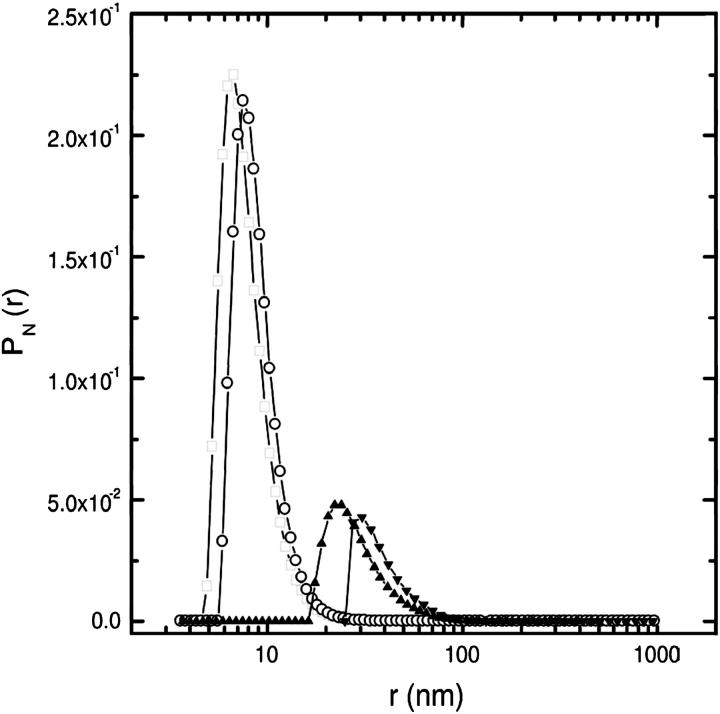
The marked difference between the 〈r〉N values obtained using CONTIN or cumulant analysis (see inset of Fig. 1), indicates that the radius-distribution function is highly asymmetric and a complete recovery of the pN(r) is needed. Indeed, upon applying the CONTIN direct-inversion method, a highly asymmetric radius distribution is found (open square in Fig. 2). In conclusion, the wide polydispersity in size, shape, and mass produces a highly asymmetric radius-distribution function for our samples; therefore, the particle form factor and the mass have to be accounted for explicitly, and the CONTIN method is indispensable.
FIGURE 2.
The number-weighted radii distribution pN shows a very asymmetric shape at all the ts investigated (2 h, □; 1 h, ○; 0.5 h, ▴; and unsonicated h, ▾). When increasing ts the particle size is drastically reduced as shown by the decreases of both the asymmetry and the peak position.
RESULTS
The main goal of this article was that of obtaining a detailed characterization of the various lipid suspensions produced by using different sonication times. We therefore analyzed DLS data to determine the intensity-weighted radius distribution pI(r) and to recover the normalized number-weighted radius distribution pN(r), the mean radius 〈r〉N, and the standard deviation SD, according to the procedures defined in the previous section.
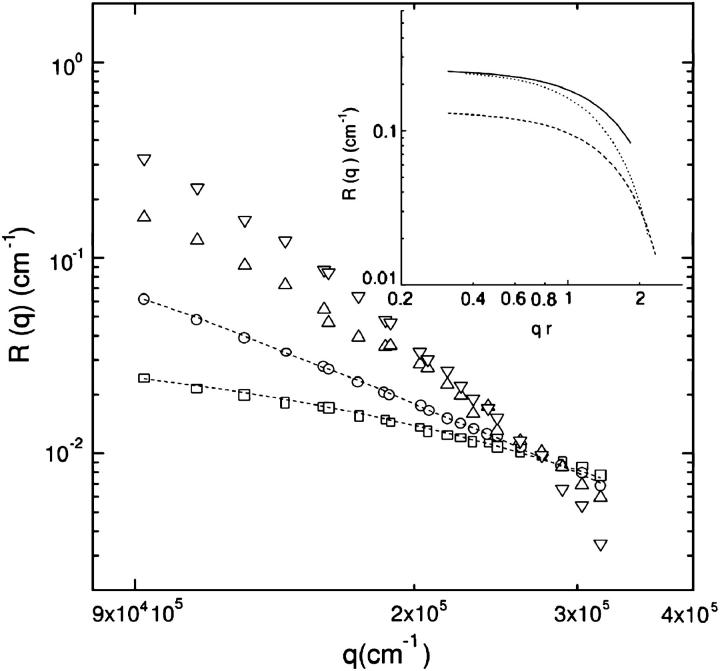
In Fig. 2 we report the normalized number-weighted radius distribution pN(r), taken at θ = 88.7. For all the ts investigated when increasing the sonication time, the distribution peaks at lower radius and the peak amplitude increases, because the vesicle volumes decrease (see Eq. 6), and the distribution width is lowered. According to Eq. 3, the pN(r) distribution could also be evaluated from a direct inversion of R(q) (Wang and Hallet, 1995), although the limited q-range and the dust-particles' related noise make this evaluation highly unsteady. Nevertheless, we were able to simulate the Rayleigh ratio by adopting all the assumptions and the parameters obtained from the DLS data. In particular we used Eq. 3 with the form factor given by Eq. 2 and the pN(r) recovered from DLS data. The optical constant K was determined by using ∂n/∂c = 0.1 ml/g, measured by differential refractometry measurements. The inversion procedure worked perfectly and the experimental Rayleigh ratio was reproduced (dashed lines in Fig. 3) in the case of samples sonicated for 1 and 2 h. Therefore, by modeling our vesicles as hollow spheres, we were able to reproduce SLS and DLS data without invoking solid spheres with an ad hoc average refractive index, as previously reported by Matsuzaki et al. (2000). For those samples that were either unsonicated, or sonicated for only 0.5 h, R(q) could not be recovered using DLS parameters. Since we modeled the vesicles as unilamellar hollow spheres, this discrepancy can only be explained by assuming 1), that the shape could be not spherical, as in the case of giant vesicles (Pencer et al., 2001; Bagatolli and Gratton, 1999); or 2), that vesicles could be multilamellar. Due to the q-dependence of R(q), it is possible to discriminate between these two possibilities. Indeed, for a given aggregation number, the form factor of ellipsoidal vesicles decays faster with q than that of spherical mono- or multilamellar vesicles. This is highlighted in the inset of Fig. 3, where the R(q) for hollow monolamellar spheres (RHMS(q)), bi-lamellar spheres (RHBS(q)), and monolamellar ellipsoids (RHME(q)) was simulated. The values RHMS(q) (dashed line) and RHBS(q) (solid line) were obtained from Eq. 1 by using the form factor given in Eq. 2 (considering radius r = 10 nm and thickness δr = 4 nm and r = 30 nm and δr = 8.3 nm, respectively). RHME(q) (dotted line) was obtained from Eq. 1 by using the form factor for hollow ellipsoids (Kerker, 1969) of axial ratio equal to 0.9, thickness δr = 4 nm, and the same aggregation number of RHBS(q). Because of the increased aggregated mass, RHBS(q), with respect to RHMS(q), upshifts without crossing it. On the contrary, RHME(q) decays with qr faster than RHBS(q) and intersects RHMS(q) at qr ∼2. Therefore, intersections of the R(q) (Fig. 3) in the high q-region of samples sonicated at different ts must be ascribed to the presence of asymmetric vesicles (Mayer et al., 1986).
FIGURE 3.
Rayleigh ratio distribution from DMPC vesicle suspensions. The sonication time has been changed from 0 to 2 h. The recovered R(q) values, obtained by adopting the form factor for a collection of polydisperse unilamellar hollow vesicles (dashed lines), of 1 (○) and 2 (□) h sonicated samples, perfectly capture experimental data. In the case of samples sonicated for a shorter time (▵, 0.5 h and ▿, 0 h) by adopting both unilamellar and multilamellar hollow spheres' form factor, it is not possible to capture the data behaviors. (Inset) The simulated R(q), for a solution of hollow bi-lamellar spheres (solid line), appears upshifted, relative to that of unilamellar spheres (dashed line). In contrast, the R(q) simulation for hollow unilamellar ellipsoids (dotted line), with the same aggregation number of the bi-lamellar hollow spheres, decays faster and intersects the R(q) of monolamellar hollow spheres. Therefore, contributions from ellipsoidal vesicles should be considered.
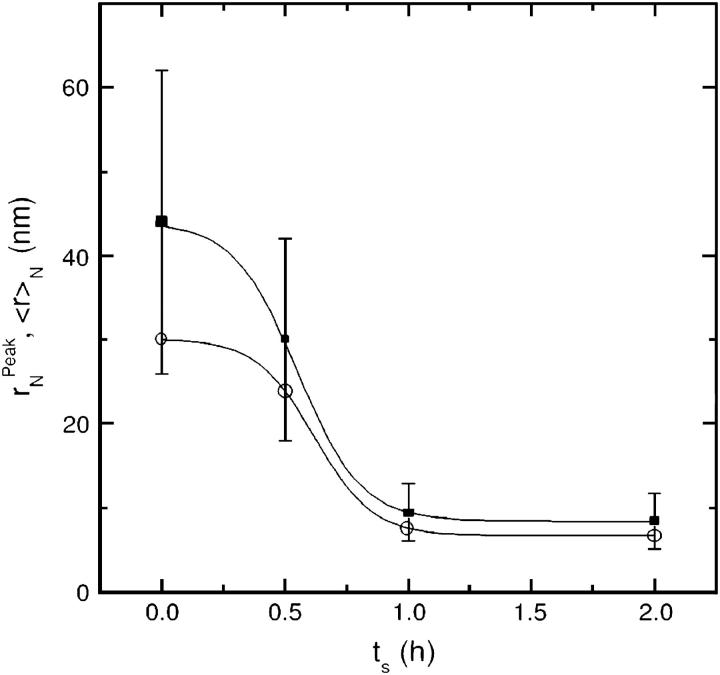
The peak and the average radius of the vesicles as a function of the sonication time are reported in Table 1 and plotted in Fig. 4. The 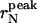 values (open circle) decreased from an initial radius of ri = 30.9 nm, to a final one of rf = 6.7 nm, while increasing ts, with the half-width being reached at
values (open circle) decreased from an initial radius of ri = 30.9 nm, to a final one of rf = 6.7 nm, while increasing ts, with the half-width being reached at 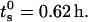 The saturation value rs well agrees with the thermodynamic prediction rtheo = 6.4 nm (Ostrowsky and Sornette, 1980). In the same figure, the 〈r〉N (solid square) with the relative SD are also reported. The polydispersity has a similar
The saturation value rs well agrees with the thermodynamic prediction rtheo = 6.4 nm (Ostrowsky and Sornette, 1980). In the same figure, the 〈r〉N (solid square) with the relative SD are also reported. The polydispersity has a similar 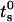 but does not reach the theoretical predicted value (SD = 0.37 against SDtheo = 0.21; see Ostrowsky and Sornette, 1980).
but does not reach the theoretical predicted value (SD = 0.37 against SDtheo = 0.21; see Ostrowsky and Sornette, 1980).
TABLE 1.
Normalized number-weighted hydrodynamic radius, and the radius at the peak position of the number-weighted radius distribution at the different ts investigated
| tsh | (〈r〉N ± SD)nm | 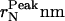 |
〈n〉 |
|---|---|---|---|
| 0 | 44 ± 18 | 30.0 | — |
| 5 | 30 ± 12 | 23.9 | — |
| 1 | 9.4 ± 3.4 | 7.6 | 3325 |
| 2 | 8.4 ± 3.3 | 6.7 | 2314 |
The average aggregation number 〈n〉, calculated from the mean hydrodynamic radius, is also reported when possible (see text).
FIGURE 4.
Dependence of the 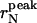 (○) and of 〈r〉N (▪) values with their relative SD, on the sonication time ts. Both
(○) and of 〈r〉N (▪) values with their relative SD, on the sonication time ts. Both 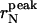 and 〈r〉N decay to a plateau (solid lines are a guide for the eye). The 〈r〉N values are slightly shifted up, reflecting the asymmetry of the radius distribution (and therefore the sonication efficiency).
and 〈r〉N decay to a plateau (solid lines are a guide for the eye). The 〈r〉N values are slightly shifted up, reflecting the asymmetry of the radius distribution (and therefore the sonication efficiency).
From pN(r) distributions (via Eq. 7), the average aggregation number 〈n〉 of lipids, each of mass m0, aggregated in a vesicle of mean radius 〈r〉N can be determined as 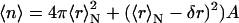 (Huang, 1969), where A is the expected area per polar head occupied by a single lipid, and equals 60 Å2 (Ostrowsky and Sornette, 1980). With this assumption, we found a decrease of the average aggregation number when increasing ts (see Table 1). The value we found at the longest ts well agrees with that previously reported for similar vesicles (〈n〉 = 2678; Huang, 1969). At the lower ts we do not evaluate 〈n〉, since the shape in no longer spherical (as discussed above).
(Huang, 1969), where A is the expected area per polar head occupied by a single lipid, and equals 60 Å2 (Ostrowsky and Sornette, 1980). With this assumption, we found a decrease of the average aggregation number when increasing ts (see Table 1). The value we found at the longest ts well agrees with that previously reported for similar vesicles (〈n〉 = 2678; Huang, 1969). At the lower ts we do not evaluate 〈n〉, since the shape in no longer spherical (as discussed above).
DISCUSSION AND CONCLUSIONS
Suspensions of DMPC vesicles prepared using different sonication times were characterized by dynamic light scattering. The intensity autocorrelation function was directly inverted by using second and third cumulant expansion and CONTIN. The intensity-weighed mean hydrodynamic radii evaluated with all these procedures superimpose, but their values show a large q-dependence. Therefore these determinations cannot be considered as reliable mean dimensions of the vesicles in solutions. From the pI(r) distribution, the relative pN(r) were recovered, modeling the vesicle as a thin hollow sphere. These distribution functions result as unimodal, due to the volume normalization. The normalized number-weighted mean hydrodynamic radii, obtained using the CONTIN method, do not show any q-dependence, whereas those from the cumulant expansion still do. This indicates that the vesicle form factor, as well as its volume and density, must be taken into account. Additionally, the size-distribution function of vesicles is strongly asymmetric, and only the direct regularized Laplace inversion gives a reliable pN(r).
To check this conclusion we compared the simulated R(q) values, using the pN(r) from DLS analysis in Eq. 3, with the experimental ones. A perfect agreement was found in the case of the samples sonicated for 1 and 2 h. At the lower ts, the simulated R(q) values no longer matched the experimental values. These Rayleigh ratios decay faster than those of mono- or multilamellar hollow spheres, revealing the presence of ellipsoidal vesicles (Mayer et al., 1986).
Our results indicate that the lipid film, upon sonication, forms large and floppy unilamellar vesicles (Bagatolli and Gratton, 1999), which then progressively reduce their size and standard deviation down to saturation values when increasing ts. At shorter ts, the total energy transferred by sonication is not sufficient to reduce multilamellar vesicles and/or giant aggregates to their optimal thermodynamical size (Ostrowsky and Sornette, 1980; Israelachvili et al., 1977). If ts is too long, the vesicles are damaged by the generated free radicals. Therefore, an optimal ts must be determined for the specific use of the vesicles.
All the radial-number distributions obtained were asymmetric and peaked. The peak positions and the distribution-width decrease on increasing ts, whereas the peak amplitude coherently increases (as expected from Eq. 6, since the vesicle mass decreases). The vesicle radius at the peak of the pN(r) corresponds to that theoretically predicted on thermodynamic grounds for those samples sonicated for 2 h. On the contrary, the pN(r)'s standard deviation resulted higher than that predicted (Nagarajan, 1987; Ostrowsky and Sornette, 1980). When considering the extruded vesicles, both the average radius and the standard deviation agreed with the thermodynamic model (Hunter and Frisken, 1998). Therefore, the size distribution must be related to the mechanisms through which sonication breaks down the solubilized lipid film, and may be associated with the Weibull distribution function, as suggested long time ago by Tenchov et al. (1985).
In conclusion, we can state that, upon sonication, the evolution of the structural properties of DMPC vesicles can be characterized by monitoring the changes of the hydrodynamic radius without accounting for shape, size, and mass polydispersity. However, a quantitative analysis needs the knowledge of the vesicle form factor and the use of a direct inversion method (CONTIN) of the intensity autocorrelation function. In this case, single-angle DLS measurements are suited for the complete characterization of the vesicle structure. When the form factor is unknown, as in the case of samples not sonicated or sonicated only for 0.5 h, the 〈r〉N and the 〈n〉 cannot be evaluated. Recovery of the pN(r) distributions is therefore the key procedure allowing single-angle DLS data analysis in the case of polydisperse solutions. Several DLS investigations on different samples with structural properties similar to those of sonicated DMPC vesicles (Matsuzaki et al., 2000; Pitcher and Huestis, 2002) are some, but not all, of the systems where the above considered data analysis should be applied to check the consistency of the evaluated particle sizes.
Acknowledgments
The authors gratefully acknowledge enlightening discussions with Prof. G.E. Martorana and Dr. R. Brunelli, and deeply thank reviewers for the many suggestions useful to improve this work.
This research was granted by Università Cattolica del Sacro Cuore.
References
- Bagatolli, L. A., and E. Gratton. 1999. Two-photon fluorescence microscopy observation of shape changes at phase transition in phospholipid giant vesicles. Biophys. J. 77:2090–2101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berne, B. J., and R. Pecora. 2000. Dynamic Light Scattering. Dover Publications, Mineola, New York.
- Booth, P. J., M. L. Riley, S. L. Flitsch, R. H. Templer, A. Farooq, A. R. Curran, N. Chadborn, and P. Wright. 1997. Evidence that bilayer bending rigidity affect membrane protein folding. Biochemistry. 36:197–203. [DOI] [PubMed] [Google Scholar]
- Burak, W. R., A. R. G. Dibble, M. M. Allieta, and R. L. Biltonen. 1997. Change in vesicles morphology induced by lateral phase separation modulate phospholipase a2 activity. Biochemistry. 36:10551–10557. [DOI] [PubMed] [Google Scholar]
- Carlson, J. M., and J. P. Sethna. 1987. Theory of ripple phase in hydrated phospholipid bilayers. Phys. Rev. E. 36:3359–3374. [DOI] [PubMed] [Google Scholar]
- Cevc, G., and D. Marsh. 1985. Phospholipid Bilayers: Physical Principles and Models. John Wiley & Sons, New York.
- Gregoriadis, G. 1993. Liposome Technology. CRC Press, Boca Raton, FL.
- Hallet, F. R., T. Craig, J. Marsh, and B. Nickel. 1989. Particle size analysis: number distributions by dynamic light scattering. Can. J. Spectr. 34:63–70. [Google Scholar]
- Helfrich, W. 1973. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. 28:357–362. [DOI] [PubMed] [Google Scholar]
- Huang, H. 1969. Studies on phosphatidylcholine vesicles: formation and physical characteristics. Biochemistry. 8:344–352. [DOI] [PubMed] [Google Scholar]
- Hunter, D. G., and B. J. Frisken. 1998. Effect of extrusion pressure and lipid properties on the size and polydispersity of lipid vesicles. Biophys. J. 74:2996–3002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Israelachvili, J. N., D. J. Mitchell, and B. W. Ninham. 1977. Theory of self-assembly of lipid bilayers and vesicles. Biochim. Biophys. Acta. 470:185–201. [DOI] [PubMed] [Google Scholar]
- Kerker, M. 1969. The Scattering of Light and Other Electromagnetic Radiation. Academic Press, New York.
- Koppel, D. E. 1972. Analysis of macromolecular polydispersity in intensity correlation spectroscopy: the method of cumulants. J. Chem. Phys. 57:4814–4820. [Google Scholar]
- Lasic, D. D. 1997. Liposomes in Gene Delivery. CRC Press, Boca Raton, FL.
- Matsuzaki, K., O. Murase, K. Sugishita, S. Yoneyama, K. Akada, N. Ueha, A. Nakamura, and S. Kobayashi. 2000. Optical characterization of liposomes by right-angle light scattering and turbidity measurement. Biochim. Biophys. Acta.. 1467:219–226. [DOI] [PubMed] [Google Scholar]
- Mayer, L., M. Hope, and P. Cullis. 1986. Vesicles of variable sizes produced by a rapid extrusion procedure. Biochim. Biophys. Acta. 858:161–168. [DOI] [PubMed] [Google Scholar]
- Nagarajan, R. 1987. Self-assembly of bola-amphiphiles. Chem. Eng. Comm. 55:251–273. [Google Scholar]
- Ostrowsky, N., and D. Sornette. 1980. Stability and fusion of vesicles. In Light Scattering in Liquids and Macromolecular Solutions. V. Degiorgio, M. Corti, and M. Giglio, editors. Plenum Press, New York. 125–137.
- Pencer, J., G. White, and F. R. Hallet. 2001. Osmotically induced shape changes of large unilamellar vesicles measured by dynamic light scattering. Biophys. J. 81:2716–2726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitcher, W. H., and W. H. Huestis. 2002. Preparation and analysis of small unilamellar phospholipid vesicles of a uniform size. Biochem. Biophys. Res. Comm. 296:1352–1355. [DOI] [PubMed] [Google Scholar]
- Provencher, S. 1982a. CONTIN: a general purpose constrained regularization program for inverting noisy linear algebraic and integral equations. Comp. Phys. Comm. 27:229–242. [Google Scholar]
- Provencher, S. 1982b. A constrained regularization method for inverting data represented by linear algebraic or integral equations. Comp. Phys. Comm. 27:213–227. [Google Scholar]
- Small, D. 1996. Handbook of Lipid Research. Plenum Press, New York.
- Tenchov, B., T. Yanev, M. Tihova, and R. Koynova. 1985. A probability concept about size distributions of sonicated lipid vesicles. Biochim. Biophys. Acta. 816:122–130. [DOI] [PubMed] [Google Scholar]
- Wang, J., and F. R. Hallet. 1995. Vesicle sizing by static light scattering: a Fourier cosine transform approach. Appl. Opt. 34:5010–5015. [DOI] [PubMed] [Google Scholar]