New Fluorescence Correlation Spectroscopy Enabling Direct Observation of Spatiotemporal Dependence of Diffusion Constants as an Evidence of Anomalous Transport in Extracellular Matrices

Abstract

The potential of fluorescence correlation spectroscopy (FCS) is extended to enable the direct observation of anomalous subdiffusion (ASD) in inhomogeneous media that are of great importance particularly in many biological systems, such as membranes, cytoplasm, and extracellular matrices (ECMs). Because ASD can be confirmed by monitoring the spatiotemporal dependence of observable diffusion coefficients (D_obs), the size of the effective confocal volume (V_eff) for FCS sampling (sampling volume) was continuously changed on a scale of 300–500 nm using a motorized variable beam expander through which an illuminating laser beam passes. This new method, namely, sampling-volume-controlled (SVC)-FCS, was applied to the analysis of hyaluronan (HA) aqueous solutions where the D_obs of light-emitting solute (Alexa 488) markedly changed, corresponding to the change in V_eff (220–340 nm in the half-axis), because the network structure of HA of 7–33 nm (nanostructure) interferes with the material transport within it. The results indicate that moderate ASD may occur even in the presence of a small amount (∼0.1 wt %) of HA in ECM. Because the change in D_obs along with the traveling distance (the mean-square displacement) can be identified even in systems with no deformation of the autocorrelation function, this technique has a great potential for general applications to many biological systems in which ASD shows complex time and space dependences.

INTRODUCTION

Molecular diffusion in a heterogeneous medium has a close association with a wide variety of phenomena in biological systems that are of great importance in sustaining life. For example, the diffusive behavior of signaling substances plays a crucial role in determining the activity and apoptosis of cells (Bianchi and Manfredi, 2004; Cao and Shoichet, 2001; Gurdon et al., 1994; McDowell et al., 1997). In heterogeneous systems such as membranes, cytoplasm, and extracellular matrices (ECMs), the effect of anomalous subdiffusion (ASD) has been reported (Bacia and Schwille, 2003; Wachsmuth et al., 2000) whereas the diffusive migration of such molecules and other larger particles, such as cells and viruses, is spontaneous and stochastic, and probably can be described by Brownian motion, driven by the collision of water molecules in a sufficiently short time (Bouchaud and Georges, 1988; Saxton, 1996).

ASD is generally accounted for by the phenomenon that the mean-square displacement, 〈r²〉, of diffusing particles is nonlinear with time, i.e., 〈r²〉 ∝ t^α with 0 < α < 1 where no conventional diffusion coefficient (diffusion constant) can be specified. Instead, observable diffusion coefficient (D_obs) decreases with sampling duration (Netz and Dorfmüller, 1997; Saxton, 1989, 1994), i.e., D_obs ∝ 〈r²〉 / t ∝ t^α−1, and as a result, D_obs depends on the observation duration of each applied methodology. Throughout this article, we call the dependence of D_obs on the observation time the time dependence of diffusion coefficient.

We previously reported the D_obs values measured by a photochemical technique and pulsed-field gradient NMR, which have characteristic observation times of 300–400 ns and 10–100 ms, respectively (Masuda et al., 2001, 2004). The D_obs of cytochrome c (cytc) significantly depends on observation time in an aqueous solution of hyaluronan (hyaluronic acid (HA)), which is one of the most important substances in ECM (Abatangelo and Weigel, 2000; Evered and Whelan, 1989; Laurent, 1998). Around each of these two measurement points, observation time could be converted to 〈r²〉 expressing the real distance of diffusion that can be related to the mesh size formed in HA solution because the linear dependence of 〈r²〉 on time is sustained and the diffusion process can be described as normal diffusion. We also call the dependence of D_obs on diffusion distance the space dependence of diffusion coefficient. The time and space dependences of D_obs are two different faces of the same characteristic of inhomogeneous diffusion and are mutually converted by the relation, t ∝ 〈r²〉 / D_obs where 〈 〉 denotes the statistically averaged values in some ensembles that are defined by sampling methods or those obtained from experiments.

HA, which is the target ECM material in this study, is a polysaccharide with an anionic group (-COO⁻) on each disaccharide unit. The occupation of a large volume with a low content of HA, the main chain of which is moderately straightened and with a high hydrophilicity, confers a viscous, gel-like property and a loose meshwork structure in its aqueous solution even at very dilute concentrations, lower than 2–3 wt % (Laurent, 1998). The physiological consequence of HA within ECM is caused by this hydrated meshwork structure that surrounds cells as the protector against physical damage and modulates the diffusion of various factors to maintain cell functions. Growth factor proteins, for example, may be locally concentrated in the HA meshwork inside ECM. This local increase in the number of the growth factor proteins may regulate signal transactions in cells and may control ECM's responses to the signal coming from the cell. The question is how molecular diffusion can be controlled in dilute solutions of HA, that is, typical HA contents in ECM of 2–4 mg/ml (Abatangelo and Weigel, 2000; Laurent, 1998). Therefore we also aim in this study to clarify the role of ECM, which frequently contains a small amount of saccharides, in sustaining life through the control of material transport.

In this article, the principle and equipment used in sampling-volume-controlled fluorescence correlation spectroscopy (SVC-FCS) are reported, and the results of the application of SVC-FCS to the investigation of material transport in HA aqueous solutions are shown.

The principle of SVC-FCS

In our previous study on the space dependence of D_obs of cytc (Masuda et al., 2001, 2004), only two extreme cases, i.e., fast diffusion over a short distance (<15–18 nm) and slow diffusion over a long distance (∼3–9 μm), were observed in the aqueous HA solution where the estimated mesh size is 7–10 nm at 1 wt %. The results showed that D_obs decreased rapidly in a relatively narrow region at ∼10–100 nm. We concluded that this decrease in D_obs with distance plays a role as a barrier to the dissipation of substances in ECM.

In the sequence of our previous studies, we attempted to develop a new method of handling the space dependence of D_obs for ASD in a direct manner by a single methodology. Fluorescence correlation spectroscopy (FCS) was improved to have a variable confocal volume (sampling volume) holding the Gaussian distribution of illuminating laser beam. This method was called the sampling-volume-controlled (SVC)-FCS. The D_obs of a dye molecule gradually decreased with increasing diffusion distance in aqueous HA solution reflecting the heterogeneous meshwork structure of HA.

Recently, a similar approach in FCS to change the size of confocal volume has been presented independently (Masuda et al., 2003) by Marguet and his co-workers (Wawrezinieck et al., 2004). Their method is different from this method because they break the Gaussian intensity distribution of illuminating laser on the focal plane. Such situation may bring difficulty in use of a normal autocorrelation function in the analyses of FCS.

FCS is an established method of measuring fluorescence intensity fluctuations in a small open volume element in solution defined by a laser beam and a confocal geometry (Rigler and Elson, 2001). The major sources of the fluctuations within the confocal volume are molecular diffusion by Brownian motion, convection, and chemical reaction that change fluorescence yield. The parameters of molecular dynamics can then be extracted by the analysis of the time correlation function of fluorescence fluctuations. In recent years, FCS has been extensively applied to the analysis of various interactions among biomolecules and of transport processes in cells using a confocal optical microscope (Bacia and Schwille, 2003; Schwille, 2001).

FCS can simply extract D_obs resulting from one ensemble average over a large number of molecular events depending on the size and shape of the confocal volume, (V_eff), for fluorescence sampling. Therefore, conventional FCS has problems in the systematic treatment of the time and/or space dependence observed in ASD that appears as a deviation from normal correlation curves. In many previous cases of treating this deviation, the autocorrelation function of fluorescence fluctuations is analyzed using the fractional parameter, α, introduced in the term of correlation time τ substituting into τ^α (Schwille et al., 1999); α has been considered to be the index for the heterogeneity of the system. In some cases, however, alternative expression is possible if more than one diffusing component is assumed in the autocorrelation function, for example, by the temporary trapping of diffusive molecules (Saxton, 1996; Wachsmuth et al., 2000). It is difficult to distinguish which factor is dominant, ASD or multiple components with different diffusion coefficients.

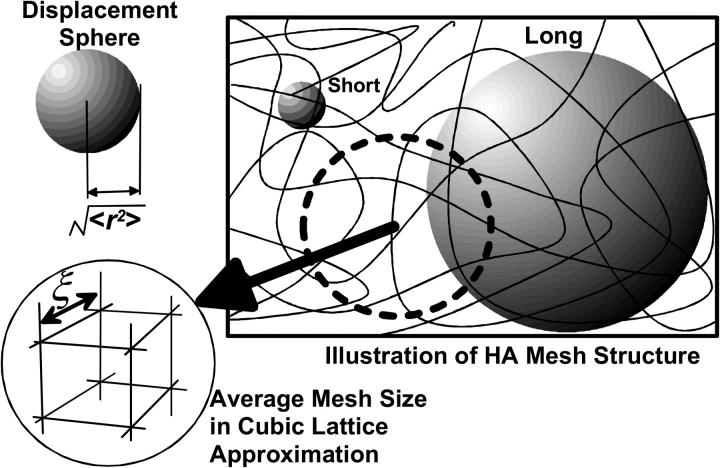
The general situation of the diffusive migration of particles in HA solution with random mesh structures is depicted in Fig. 1. One straightforward spatial expression for the mean-square displacement of normal diffusion is to draw a sphere with the radius of 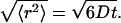This sphere (herein referred to as the “displacement sphere”) shows the probability with which particles in an object reach some position at time t after starting from the origin at the center without being hindered by polymers. The roughness of the random mesh in HA solution is characterized by the size ξ in cubic lattice approximation, which we use throughout this article. This characterization is often adopted in describing gels because any real pictures of a moving mesh of HA cannot be detected at typical magnitudes of ξ at 1–100 nm, which are lower than the optical resolution limit. The size relation between 〈r²〉 and ξ (〈r²〉 ≫ ξ, 〈r²〉 > ξ, 〈r²〉 ∼ ξ, etc.) is the primary reason the space dependence of D_obs emerges in HA solution, and probably, in general ECMs. In diffusion over a sufficiently long distance expressed by a large displacement sphere, almost all traveling particles are hindered by polymer chains occasionally. However, particles traveling a short distance, for example, a distance shorter than the mesh size, have fewer opportunities to make contact with the surrounding mesh.

FIGURE 1.

Illustration of hyaluronan aqueous solutions containing random and mobile mesh structures. The mesh size of the random structure is characterized by ξ assuming the cubic lattice approximation shown in the figure. The normal diffusion of a single particle is expressed by a sphere (displacement sphere) whose radius is the mean-square displacement, 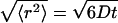(see text). The diffusion over a short distance observed for a short duration corresponds to the small displacement sphere, and long-distance diffusion obtained by long-time observation is expressed by the large displacement sphere. The relation between the size of displacement spheres and random mesh generate the space dependence of D_obs.

Our SVC-FCS, in which we vary the radius of the effective confocal volume (V_eff) using an additional beam expander, has the function of changing the size of the sampling space of diffusion measurement in which we statistically collect the displacement sphere of each particle. Moreover, the Gaussian distribution of laser illumination is held and the total amount of introduced laser power is constant in changing the confocal volume. The optics is suitably designed for the normal analyses with an autocorrelation function. This method is quite efficient in handling the space dependence of D_obs, quantitatively.

The application of an approach similar to our SVC-FCS method to changing the observation volume by fluorescence recovery after photobleaching (FRAP) was previously reported (Lopez et al., 1988; Salomé et al., 1998; Yechiel and Edidin, 1987). FRAP is very similar to FCS in both theoretical and experimental approaches to the observation of molecular motions such as diffusion. The fundamental difference between FRAP and FCS is that FRAP measures relaxation from an initial off-equilibrium state produced by photobleaching fluorescent molecules, whereas FCS measures stochastic fluctuations that occur even in a system resting in equilibrium. The spot sizes of photobleaching can be changed using objectives of different magnifications and numerical apertures. Yechiel et al. measured the lateral diffusion of lipids and protein molecules in a plasma membrane within several discrete spot sizes (Yechiel and Edidin, 1987). However, they did not discuss the spatiotemporal dependence of D_obs itself, but investigated the distribution of D_obs depending on spot size to elucidate the domain structure of organized plasma membranes. Basically, our SVC-FCS method can change confocal volume continuously with the use of one objective, which can be applied to more general targets, and FCS is superior to FRAP in terms of time resolution and molecular sensitivity.

MATERIALS AND METHODS

Materials and sample preparation

Rhodamine 123 (Sigma-Aldrich, St. Louis, MO) and Alexa Fluor 488 (Molecular Probes, Eugene, OR) were purchased and used without further purification. A biosynthetic HA-labeled molecular weight, 300 kDa, was obtained from DENKA (Denki Kagaku Kogyo K. K., Tokyo, Japan). HA was dissolved in phosphate buffer (20 mM phosphate and 80 mM NaCl, pH 7, Wako Pure Chemicals Industries, Osaka, Japan). The sample preparation for the HA solution was the same as that described previously (Kluge et al., 1998, 2000; Masuda et al., 2001, 2004).

SVC-FCS equipment

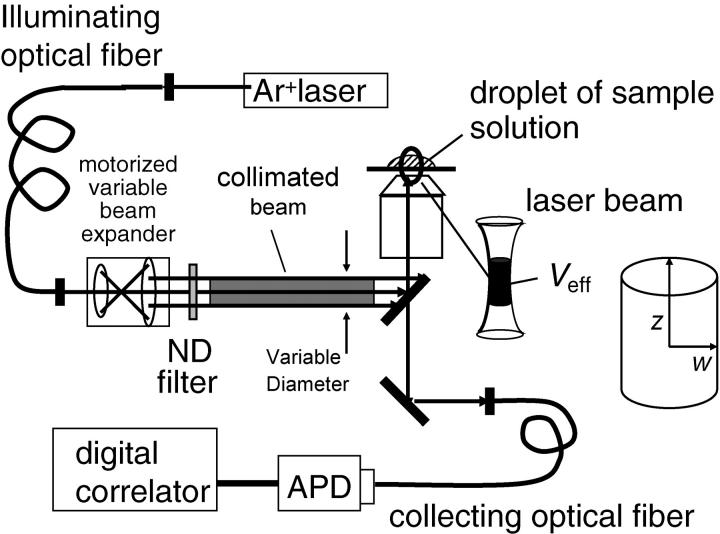
The schematic of the modified spectrometer used to perform SVC-FCS having variable laser-illuminated volume is shown in Fig. 2. A motorized variable beam expander consisting of a lens (f₁ = 8 mm; YF4A-2, Fuji Photo Optical, Tokyo, Japan) and a motorized zoom lens (f₂ = 8 ∼ 96 mm, D12 × 8A-YE2, Fuji Photo Optical, Japan) was inserted before the light-injection port of the microscope (Olympus IX71, Olympus, Japan). The radius of the collimated beam, d, was magnified proportional to the focal length, f₂, of the zoom lens. The radius d was changed continuously from 0.6 to 4.3 mm, which was measured at the end of the zoom lens (marked with an asterisk in Fig. 2) assuming Gaussian beam approximation. The objective lens is of water-immersion type (Olympus UPlan Apo, Tokyo, Japan; 60×, 1.20 N.A.).

FIGURE 2.

Diagram of new FCS spectrometer designed for our SVS-FCS measurement.

We used three multimode fibers with different core diameters, namely, 50, 100, and 200 μm, for collecting fluorescence. The aperture of the fiber was precisely placed on the image plane, which is the site confocal to the illuminated focal point. The V_eff of the confocal microscope depends on both illumination volume, V_i, and detection volume, V_d, which is given by the convolution of the objective point-spread function with the fiber aperture image. The V_i depends on the beam diameter, d, of the incident light into the objective. Therefore, the V_eff of FCS can be controlled by adjusting the f₂ of the zoom lens and the core diameter of the collection fiber (see details in the Results section). The zoom lens was controlled by a computer and f₂ was determined using a potentiometer attached to the lens.

The validness of the Gaussian confocal volume approximation is known to be influenced by the relationship between the sizes of the back aperture of objective lens and the fiber aperture for detection located at the confocal plane (Hess and Webb, 2002) The back aperture size of our objective lens was 7.2 mm in diameter and overfilling of laser beam may occur with small 1/f. However, if the fiber aperture is sufficiently small, V_eff can be satisfactorily regarded as a Gaussian confocal volume. Although the optics may show slight overfilling behavior when 1/f < 16 m⁻¹, the V_eff still can be regarded as Gaussian with the small aperture of the fibers (50, 100, 200 μm) for detection. When 1/f > 16 m⁻¹, the condition seems safely involved in the underfilling condition.

A small fraction (50–300 μW) of 488 nm light from a CW Ar ion laser (Coherent INNOVA 90, Coherent, Santa Clara, CA) was used for excitation in all the experiments. Photon signals were collected using an avalanche photodiode (SPCM-100 from RCA Electro Optics, Fremont, CA) the response time of which is ∼20 ns and accumulated on a multiple-tau digital correlator board (ALV-5000E from ALV-Laser Vertriebsgesellschaft m.b.H., Langen, Germany). The samples were held in a Lab-Tek 8 chamber (Nalge Nunc International, Rochester, NY) on the stage of the microscope.

We also performed FCS using a commercial laser microscope (LSM-510/ConfoCor II from Zeiss, Jena, Germany) in which the optimized and fixed alignments of optical elements enable the realization of the smallest V_eff in this study.

RESULTS AND DISCUSSION

Control of observation volume to realize SVC-FCS method

In FCS experiments, the fluorescence emitted from V_eff, which is an optically well-defined tiny space containing an extremely small number of molecules, is monitored as a function of time. The intensity fluctuations of fluorescence δF(t) approximately the time average 〈F(t)〉 is determined from the optical profile of both laser illumination and detection by sensors together with the concentration fluctuations (Hess and Webb, 2002) as

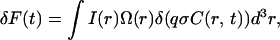(1)

where I(r) is the illumination intensity profile, Ω(r) is the collection efficiency profile, r is the position in the objective space, and q, σ, and C(r,t) are the effective quantum yield, extinction coefficient, and concentration of light-emitting molecules, respectively. Intensity fluctuations are considered to reflect the change in the total number of molecules involved in V_eff, however, only diffusion will contribute to the results in this experiment using small dye molecules dissolved in neat buffer or aqueous HA solution. Therefore, the autocorrelation function G(τ) can be calculated with Green's function Γ(r, τ) for the diffusion equation

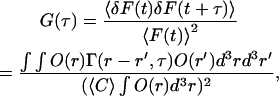(2)

where O(r) is the confocal volume profile defined as 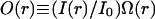with the amplitude of illumination, I₀.

Equation 2 can be solved analytically by assuming a three-dimensional (3D) Gaussian observation volume for O(r) (Rigler and Elson, 2001).

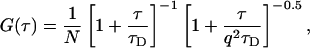(3a)

where q is a structure parameter defined by q = z / w (z and w are the axial and radial radii of the V_eff, respectively). N is the average number of molecules in the V_eff. τ_D is the diffusion time and is defined as lateral diffusion time for a molecule through V_eff: 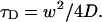In this study, because the 3D Gaussian intensity distribution in the radial direction is held in illuminating volume, experimental data can be fitted to a practical autocorrelation function containing the additional term of the triplet state of the dyes used

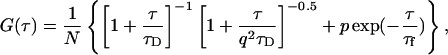(3b)

where p is the fraction of the contribution of the triplet state and τ_f is the lifetime of the triplet state.

There are two means of controlling the size of the V_eff because it depends on both the illumination and detection profiles as described in the experimental section: 1), V_i is continuously changed by increasing the incident beam radius, d, using the zoom lens shown in Fig. 2; 2), the detection volume V_d can take three sizes using three types of collecting optical fiber with different core diameters (50, 100, and 200 μm). The size of the V_eff can be controlled by the combination of two parameters. Gaussian optics theory predicts the relation between the lateral radius (w_i) of V_i and d to be 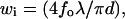where f_o is the focal length of the objective lens and λ is the wavelength of the incident laser. Then, the simple relation 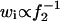is approved because the focal length of the zoom lens f₂ is in proportion to d. When a constant V_d is assumed for one collecting fiber, the values of w = z/q in Eqs. 3a and 3b reflect the variation in w_i.

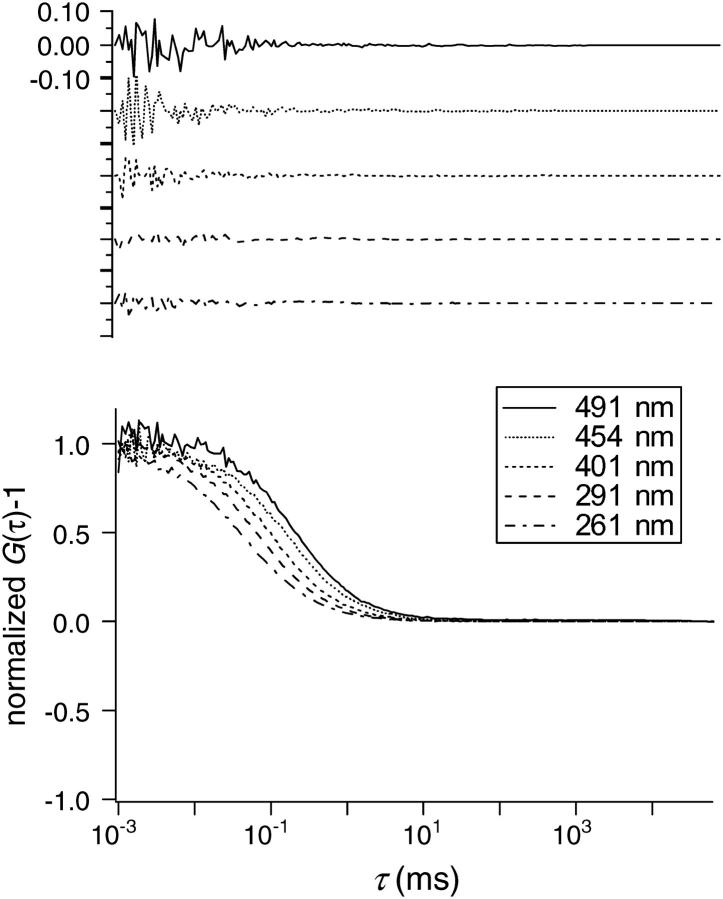
To confirm the performance of our SVC-FCS system, we carried out a standard measurement for the correlation functions of aqueous Rhodamine 123 (R123) solution whose diffusion coefficient is known (3.0 × 10⁻¹⁰ m² s⁻¹). When f₂ was increased, the values of w were evaluated using τ_D values obtained for the R123 solution and the relation, w = (4Dτ_D)^0.5. Fig. 3 illustrates the results of SVC-FCS measurements performed at various V_eff characterized by w. These correlation curves were normalized by G(0) for convenience in comparing the curves. As shown in Fig. 3, diffusion time seemed to increase linearly with the increase in w. In any cases measured here, the correlation curves can be fitted by the autocorrelation function of Eq. 3b without any significant discrepancies, and examples of the residues after fitting by Eq. 3b are depicted in the upper insert of Fig. 3. As the V_eff increased, a slight decrease in signal/noise ratio was observed due to the increase in the number of molecules inside the V_eff.

FIGURE 3.

The FCS autocorrelation functions plotted against correlation time, τ for Rhodamine 123 in water with various sizes of V_eff (w = 261, 291, 401, 454, and 491 nm). (Top panel) Examples of residues after fitting using Eq. 3b.

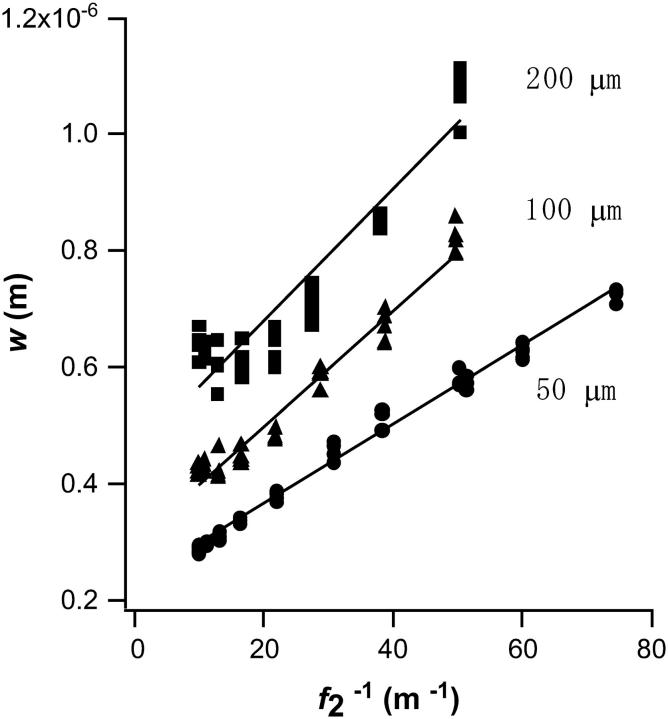
The evaluated values of w are plotted against 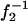in Fig. 4 for three types of collecting optical fiber. These linear plots clearly show that V_eff is effectively increased by the use of the additional zoom lens except in the smaller 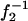region with the larger (100 or 200 μm) core fiber. This deviation may be attributed to the large projection of the fiber aperture on the focal plane, the projection of which obscures the variation in w_i induced by the zoom lens. When the detection volume is much larger than V_i (1 / f₂ → 0, then w → 0), the relative contribution of secondary emission or light scattering from the outer space of V_i is not negligible because its magnitude relative to the desired emission should be approximately proportional to 1/w²z. Another possibility is the contribution of slight overfilling effect as described in the experimental section especially for the fiber with a large diameter (Hess and Webb, 2002).

FIGURE 4.

Dependence of calculated half-axis of V_eff on 1/ f₂ (f₂, focal length of the zoom lens) obtained for Rhodamine 123 aqueous solution. Three types of detection optical fiber were used with diameters of 50, 100, and 200 μm.

The result of this measurement is proof that we can continuously control the V_eff size simply by changing the f₂ of the zoom lens as long as we use a detecting fiber of 50–200 μm diameter. The size change of the collecting fiber provides a shift of and an increase in the area of the variable region for w. At the same time, this result enables the calibration of the absolute size of V_eff (Schwille, 2001).

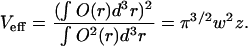(4)

The fitting result of q gradually increased with increasing w, but q → ∞ when w > 400 nm. This denotes that the shape of V_eff becomes cylindrical in the large w limit and that Eq. 3b is reduced to

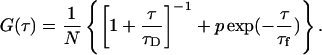(5)

Molecular diffusion in HA aqueous solution

We applied the SVC-FCS measurement to the analysis of an inhomogeneous fluid system, that is, a diffusing (probe) molecule (Alexa 488) dissolved in HA aqueous solution. The mesh size ξ of the HA network was estimated to be 33 nm for a 0.1 wt % solution where HA random coils already fill up the entire solution (Laurent, 1998). The diameter of Alexa 488 is ∼1.4 nm assuming a spherical molecule. Because w is available from the data of R123 in Fig. 4, D_obs for each w is estimated using

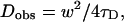(6)

with the τ_D obtained from the fitting of the observed correlation curve using Eq. 3b.

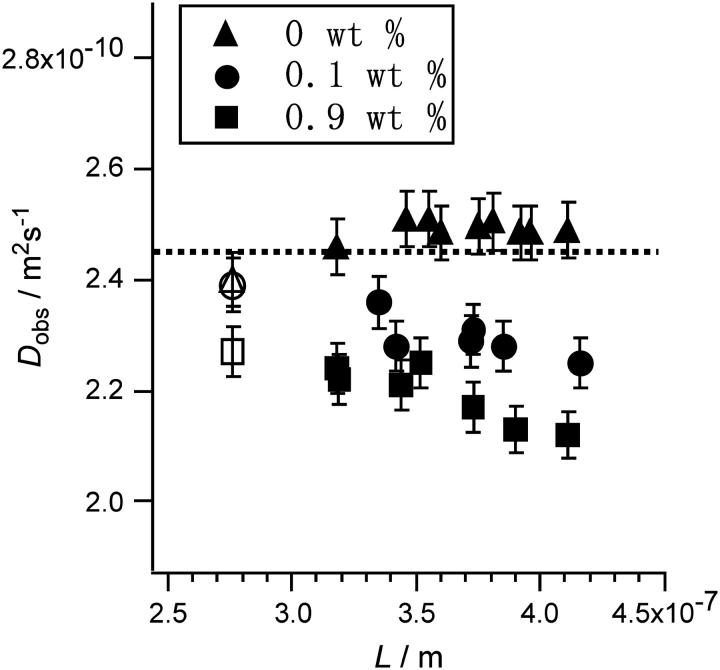
In this step, we defined a diffusion distance, L, as (6D_obsτ_D)^0.5. The obtained D_obs of Alexa with and without HA was plotted against L in Fig. 5. A gradual reduction in D_obs was observed in the presence of HA. The magnitude of the reduction increased with increasing HA concentration. The points are smoothly associated with the D_obs values for the smallest L obtained by the commercial instrument (LSM-510). This 10–20% reduction in D_obs occurred in a very narrow area of L = 270–410 nm for Alexa 488. We conclude that this variation is not an artifact of the measurement system, because Alexa 488 seems to diffuse freely with a constant D_obs that is independent of V_eff size in the absence of HA, as also shown in Fig. 5.

FIGURE 5.

Plot of observed diffusion coefficient (D_obs) versus diffusion distance (L) observed for aqueous solution of Alexa 488 with (0.1 and 0.9 wt %) and without hyaluronan. Two points for the smallest L (L = 270 nm; open symbols) were obtained with a commercial instrument (see text).

The ratio of the molecular numbers with and without HA was constant for any size of V_eff in Fig. 5. This result proves that the confocal volumes are the same with and without HA in the solution. This is also supported by the fact that the change of refractive index on HA addition is extremely small The literature values are dn/dc = 0.155 mL/g (Praest et al., 1997) or the increase of 4.08 × 10⁻⁴ for 0.25% HA solution (Barrett, 1978).

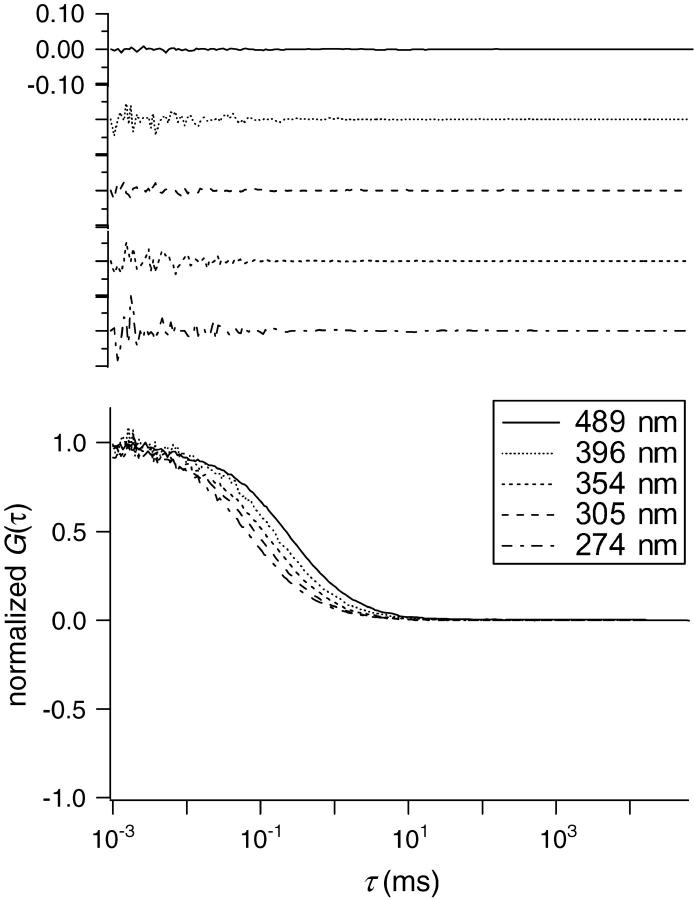
It should be noted that no significant deviation was observed in the fittings of observed autocorrelation curves using Eq. 3b for all the points in Fig. 5. Some examples of fitting results are shown in Fig. 6. The results show that the diffusion of Alexa in individual measurement with a fixed V_eff can be analyzed using the normal theory assuming a diffusion coefficient D_obs as if the heterogeneity of the HA meshwork was averaged to disappear. However, only the obtained D_obs decreased with the expansion of V_eff, which is evidence of inhomogeneous diffusion, or probably of ASD. Because the main component of the solution is water, this should be attributed to the facts that the HA meshwork contains water-filled pathway for Alexa 488 and that the heterogeneity of HA solution is too low to be detected. Instead, D_obs decreases with diffusion time and/or distance in all measurements at each different ensemble average.

FIGURE 6.

The FCS autocorrelation functions plotted against τ for Alexa 488 in HA aqueous solution ([HA] = 0.1 wt %) with various sizes of V_eff (w = 274, 305, 354, 396, and 489 nm). (Top panel) Examples of residues after fitting using Eq. 3b.

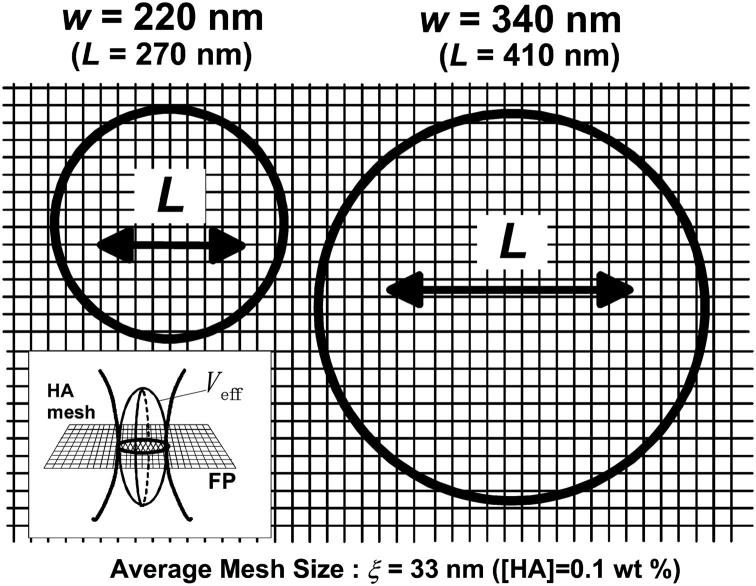
Fig. 7 shows the comparison of the horizontal cross section of V_eff at the focal plane with the averaged mesh size of HA ([HA] = 0.1 wt %, ξ = 33 nm) on a common scale for the minimum (270 nm) and maximum (410 nm) L values in Fig. 5. Even for L = 270 nm, where only a small reduction in D_obs was identified, the value of the mean-square displacement is approximately seven times larger than the average mesh size. This indicates that the local heterogeneity of the matrix is insignificant so that we could not detect any serious deviation from the normal autocorrelation function (Eq. 3b). Some researchers previously reported the deviation of the autocorrelation function in FCS measurements for biological systems where severe heterogeneity and complexity may induce remarkable ASD. In contrast, our case shows the existence of ASD without any deformation of Eq. 3b but with changes in D_obs.

FIGURE 7.

Comparison of average mesh size ξ = 33 nm in 0.1 wt % HA aqueous solution with the horizontal cut of V_eff (see insertion) for the minimum (w = 220 nm) and maximum (w = 340 nm) sizes in Fig. 5. The figure shows a projection on the focal plane (FP) drawn on a common scale; the mean-square displacements for each measurement are also shown.

This result is supported by recent numerical calculation of Seki et al. (2005). They assumed a step function taking two extreme values for the distance dependence of the diffusion coefficient and obtained an analytical solution for the modified autocorrelation function instead of Eq. 3b. On introduction of practical parameters obtained from this study, no severe deformation of the autocorrelation function was predicted but gradual change of D_obs values analyzed from Eq. 3b was identified.

In our previous research, the diffusion of cytc was free over several tens of nanometers but was prevented over several micrometers in the HA solution. The D_obs of cytc decreased by >30% in 2.0 wt % HA solution. Our recent FCS measurement showed that cytc is hindered by the HA chain even with a diffusion distance of hundreds of nanometers (L = 240 nm) (A. Masuda and K. Ushida, unpublished data). Therefore, a critical boundary for cytc is considered to exist in the relatively narrow area (L = 10–100 nm) between the slow- and fast-diffusion modes. The spatiotemporal scale of the network structure of HA is responsible for the position of this boundary; material transport is probably affected both dynamically and statistically by the local nano-microstructure of HA.

For Alexa 488, whose particles are smaller than those of cytc (diameter = 3.4 nm) and have a larger diffusion coefficient, the critical boundary of D_obs is expected to shift to a larger L than that of cytc, and the effect of HA mesh should appear after a longer travel in the solution. Therefore, it is reasonable that the boundary was just covered by the variable confocal volume of this SVC-FCS and that the transient behavior of D_obs between the short and long diffusion was successfully observed. Consistently, the transient area seemed to move to a lower position of L in a smaller mesh ([HA] = 0.9 wt %), as shown in Fig. 5. Therefore, we satisfactorily conclude that the observed gradual reduction in D_obs is also caused by the obstruction effect of the HA mesh, which is similar to that found for cytc. The profile of the reduction in transient D_obs provides useful information on the interactions between solutes and the HA chain, their fluctuations, and their dynamics. For example, the difference of the position of L, where the reduction of D_obs appears, for various molecular size may endow the HA solution with the ability to act as a molecular sieve that controls substance diffusion inside ECM. This effect emerges, for example, as the gradient of concentrations of signaling factors secreted from cell surfaces forming in the ECM space in contact with plasma membranes.

Fig. 7 also shows that ASD occurs even in a dilute HA solution ([HA] = 0.1 wt %) as observed under physiological conditions. It is suggested that the small amount of HA in ECM, sometimes coexisting with other materials such as collagen, has the ability to control molecular diffusion and concentrate substances. This large effect on material transport promoted by a small amount of additional sugars, i.e., HA and other saccharides, may play a crucial role in sustaining various biological activities although the concentration of these sugars may be negligible in material analysis or spectroscopic observations. The importance of this high-performance effect on various transports with only a small amount of molecules should also be justified as a rational strategy of life possessing limited abilities of syntheses and secretions. Therefore, a quick response is possible with minimum number of synthesized materials inducing a large influence on transport phenomena. We also expect similar effects of sugars on intracellular organisms in controlling material transport although evidence is difficult to obtain in highly complex real biological systems.

CONCLUSIONS

For the application of FCS to complex systems such as ECM, the time dependence of D_obs should be considered in the analysis of the correlation data in FCS. In this SVC-FCS method, by continuous varying V_eff size, we were able to directly observe the transient behavior of D_obs as a function of time and space. The results of molecular diffusion in HA solution demonstrated the high potential of SVC-FCS for determining the molecular mobility parameters of heterogeneous biomaterials such as cellular compartments.