How Many States Can the Motor Molecule, Prestin, Assume in an Electric Field?

Abstract

By using an analogy between the magnetization of a paramagnetic material in an external magnetic field and the electric polarization of the lateral wall of outer hair cells in response to the transmembrane potential, we show that, based on experimental data on the charge transfer across the membrane, it is impossible to make a statement about the number of possible conformational states of the motor molecule, prestin. Although the choice of model affects the values of derived parameters, such as total charge and motor charge, this is frequently overlooked in the literature.

Outer hair cell (OHC) electromotility (1) is likely caused by the concerted action of molecular motor complexes, an essential component of which appears to be the prestin molecule (2,3), in conjunction with small cytoplasmic anions (4). Prestin is the only protein known to produce electromechanical force up to at least 70 kHz (5). The notion prevails in the literature that the motor complex occupies just two conformational states, where a transition between states is associated with voltage-dependent charge transfer across the lateral cell membrane (6–11). An exception is the work of Iwasa (12), who also considers three states. An alternative to the motor hypothesis is the membrane flexo-electricity model of Raphael et al. (13), which assumes a continuously varying polarization of the membrane.

Here, we argue that, based on the experimentally determined steady-state and transient charge transferred as a function of the transmembrane voltage, it is not yet possible to distinguish between systems of two or more states. Consequently, it is currently not clear how many states prestin occupies in the transmembrane electric field or if the motor charge moves continuously.

To demonstrate this, an analogy between the OHC motor mechanism and a paramagnetic material is employed. Such a material contains permanent microscopic magnetic moments whose orientations in the absence of an external magnetic field are randomly distributed (if their mutual interaction is neglected). In a magnetic field, however, the energy levels of differently oriented moments split, because alignment of a moment with the field is energetically favorable. In equilibrium, the occupation of these levels (and thus orientation of magnetic moments) then becomes Boltzmann distributed, which leads to a net macroscopic magnetic moment of the material—the magnetization.

In the case of OHCs, the microscopic moments can be electrical mono- and/or dipole moments associated with a prestin molecule. These sense the electric field caused by the potential gradient across the lateral membrane. Different positions of a monopole and different orientations of a dipole in the field, caused either by a conformational change (deformation) or by dislocation/rotation of the molecule, correspond to different energy levels. Variation of the field leads to shifting of the levels and, consequently, to a redistribution of the occupation numbers. The latter corresponds to a charge movement across the membrane and to a change of its macroscopic electric polarization.

It is well known (14) that the Brillouin function B_J quantum mechanically describes the dependency of the magnetization M of a paramagnet on the external magnetic field and the quantum number J of the microscopic magnetic moments of the material. Their component parallel to the field can assume 2J + 1 values. B_J is derived by calculating the expected value of an ensemble of magnetic moments in an external magnetic field. If the external field is represented by the energy E of the as-much-as-possible aligned moment within the field (in units of k_BT, where k_B is Botzmann's constant and T is temperature), then the Brillouin function is

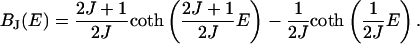(1)

B_J ranges from −1 to 1. In the classical limit, the moments can be aligned continuously with the field and J → ∞. In this case, B_J becomes the Langevin function

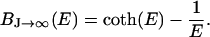(2)

This case was assumed by Raphael et al. (13) for the flexo-electricity model of OHC motility. Notice also that

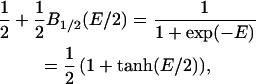(3)

so that for a two-state system, the (shifted and scaled) Brillouin function reduces to a first-order Boltzmann function. The equivalence of the exponential and hyperbolic-tangent expressions in Eq. 3 was pointed out by Weiss and Leong (15).

When quantifying OHC electromechanical data, the total transferred charge and the charge valence are usually free parameters in the numerical fitting procedure (6,7,9,10). Consequently, the energy is a free parameter. For the purpose of showing the similarities among descriptions with a different number of states, it is necessary to scale the B_J and E axes. This is achieved by multiplying these variables with Q_M and ɛ, respectively, so that the function that is to be fitted is

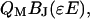(4)

where Q_M is the normalized total charge and ɛ the relative energy of the moment within the field. These are free-fitting parameters.

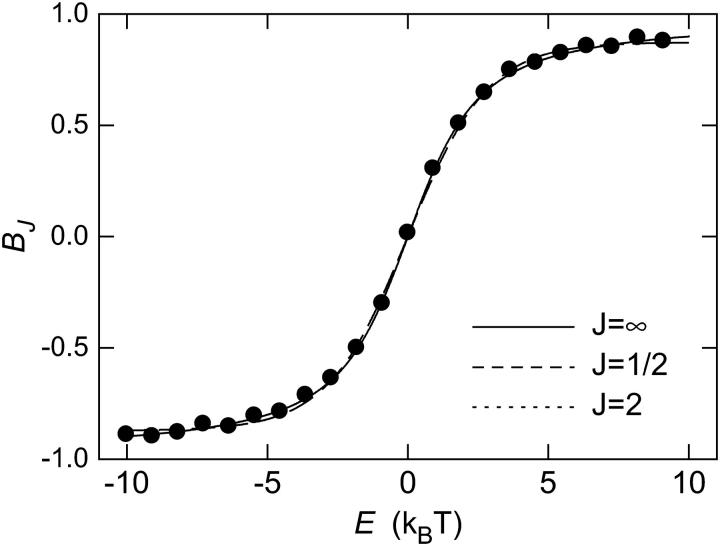
Fig. 1 shows that Brillouin functions for different numbers of states (different 2J + 1) can be fitted to match each other almost perfectly over at least 90% of their range, provided the energy level and a global scaling factor are fit parameters (as in the case of OHCs) and the range of energies is limited to ±10 k_BT. The latter constraint is justified by the fact that in the asymptotic cases, where all the motors are in either contracted or elongated states, mechanical and/or electrical constraints could play a role and deviations from the Brillouin (or Boltzmann) characteristics could occur (e.g., (8,10)). Thus, in equilibrium, a two-state system can have the same dependency on the transmembrane voltage as a continuous system if the energy of the moment in the field is reduced to 35% and the total transferred charge is reduced to 87% (see Fig. 1 caption). Consequently, the motor charge might be about three times higher than the 0.7–0.9 e⁻ obtained from the two-state model (6,7,9,10). Because the number of motors can be roughly estimated from the ratio of total to motor charges (6–8), the number is reduced to 40% in the continuous case compared to a two-state system.

FIGURE 1.

The symbols show a set of data artificially generated by adding 1% uniformly distributed random error to a Brillouin function (Eq. 1) with J = ∞; that is, the data represent a classical dipole. E is proportional to transmembrane voltage. Fitted to the data is the scaled Brillouin function (Eq. 4) with J = 1/2 (two states, Q_M = 0.873 ± 0.007, ɛ = 0.350 ± 0.009), J = 2 (five states, Q_M = 0.897 ± 0.005, ɛ = 0.724 ± 0.015), and J = ∞ (classical limit, Q_M = 0.996 ± 0.006, ɛ = 1.021 ± 0.020). Obviously, the fitted lines are almost indistinguishable.

Because electric field strength within the membrane and motor charge valence are a priori unknown (the latter is derived from data fitting), and because it is unknown whether the total available motor charge is actually moved all the way through the electric field, nothing can be confidently asserted from the steady-state data about the scaling of E and B_J.

Transient charge movement, e.g., the current in response to a voltage step, could reveal several time constants, indicative of a number of different transition rates. However, from patch-clamp recordings, to date, only one time constant is apparent. A possible reason, why a system with potentially many states could still exhibit only one time constant in these recordings, is that if the transition rates are sufficiently fast (>5 kHz, which is quite likely considering the broad frequency response of OHC electromotility (5)), their detection would be compromised by the limited bandwidth of the patch-clamp amplifier.

Hence, we conclude that neither steady-state nor transient charge data available at the moment are suitable to extract the number of states of prestin, and that the values of total charge and motor charge obtained from the two-state model should be interpreted with this uncertainty in mind. The underlying problem is that both electromotility and capacitance measurements detect an ensemble average. An answer to the title question presumably requires the observation of single prestin molecules or the ability to force a number of these molecules into the same state.