Fluctuation Correlation Spectroscopy with a Laser-Scanning Microscope: Exploiting the Hidden Time Structure

Abstract

Images obtained with a laser-scanning microscope contain a time structure that can be exploited to measure fast dynamics of molecules in solution and in cells. The spatial correlation approach provides a simple algorithm to extract this information. We describe the analysis used to process laser-scanning images of solutions and cells to obtain molecular diffusion constant in the microsecond to second timescale.

As our understanding of cellular organization increases, there is a need for methodologies to ascertain molecular concentration, dynamics, and organization at high temporal and spatial resolution. A common approach to study cellular dynamics uses fluorescently tagged molecules that can be observed by fluorescence wide field, total internal reflection fluorescence (TIRF), or confocal microscopy. Single-point fluorescence correlation spectroscopy (FCS) originally developed by Magde et al. for solutions (1) and more recently by Berland et al. for cells (2), provides high temporal resolution information about protein concentrations and dynamics within a small volume (<1 fL) of the cell. However, the limitations of this technique include a lack of spatial information, restricted information about processes that involve slower protein dynamics within large slowly moving structures, and lack of simultaneous cell imaging. Image correlation spectroscopy (ICS) as originally developed by Petersen et al. (3,4) provides the concentration, degree of aggregation of proteins, and the average number of aggregates in the cell membrane. In a recent variation, ICS was expanded to measure temporal correlations between images collected in a time sequence (5) and to determine spatial correlations due to flow and other cellular processes (6). The ICS theory was developed with the assumption that nothing moves on the timescale of the frame acquisition. To date it has been applied to fixed samples or slowly moving transmembrane or cytoskeleton associated proteins (6). Overall, ICS provides a powerful method for systematically analyzing images for dynamic processes and molecular aggregation. The main idea of the ICS method is to calculate the image spatial autocorrelation function and to extract the number and size of aggregates from the analysis of the spatial power spectrum. For the time correlation in ICS, the autocorrelation function is calculated from stack of successive images.

We propose a novel approach to probe spatial correlations and previously inaccessible temporal windows. We exploit the time structure present in images obtained with a laser confocal microscope to spatially correlate adjacent pixels that are a fraction of a micron and a few microseconds apart along a line and a few milliseconds apart in successive lines. By exploiting this time structure we measure dynamic processes such as molecular diffusion in the microseconds to second timescale. We demonstrate this data analysis by measuring the diffusion of fluorescent beads, enhanced green fluorescent protein (EGFP) in solution, and EGFP inside the cytoplasm of live cells using raster scan images. This new analysis, termed raster image correlation spectroscopy (RICS), now allows one to bridge the timescales of FCS and ICS and provide spatially resolved information in the microsecond to seconds time range. To date, expensive and specialized instruments have been used for FCS experiments. A drawback of these instruments, when used for cell work, is that the correlation measurements and imaging are done at two different times. Because laser-scanning confocal microscopes are readily available in almost all life science labs, our method opens up scanning correlation microscopy to the general microscope user. In fact, we used an analog system (Olympus Fluoview 300, Melville, NY) with excellent results in a forthcoming article.

We consider signal fluctuations due to the diffusion of particles in a homogenous medium. In addition to translational diffusion, other processes at the molecular level such as conformational transitions, quenching associated with aggregation and molecular rotations can also cause fluorescence fluctuations. We focus on diffusion; as this is a common mode of transport of molecules from one location to another in the cell. The change in concentration of particles as a function of time due to diffusion in a uniform medium is described by the following relationship:

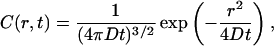[1]

where C(r,t), concentration, is proportional to the probability of finding particles characterized by a diffusion coefficient D at position r at time t when the particles were at the origin (r = 0) at time t = 0. There are two parts of this equation, a temporal part and a spatial Gaussian term. If a particle was at the origin at t = 0, it can be found at a distance r from the origin with a Gaussian distributed probability where the variance depends on time and on the diffusion coefficient of the particle. If the concentration is sampled at one position, (single-point FCS) the autocorrelation function of the fluorescence decays with a characteristic time that depends on the diffusion constant and the size of the illumination volume. Alternatively, the concentration can be sampled at different spatial locations. The spatial autocorrelation function decays with a characteristic length that depends on the diffusion constant and the size of the illumination volume.

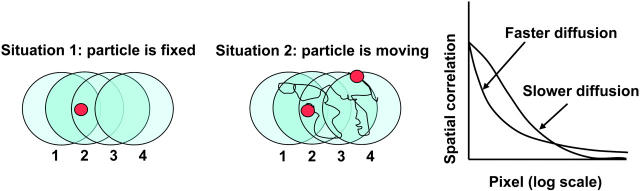
If particles are either not moving or are moving very slowly, as we sample different locations in a raster scan image, the intensity at one point is correlated to the intensity of the adjacent points if there is superposition of the point spread function (PSF) at the adjacent points (Fig. 1, situation 1). In this case the two-dimensional (2-D) spatial correlation of an image just reflects the extent of superposition of the PSF in the adjacent points. To explain spatial correlation for fast-moving particles, consider two points separated by a given distance r. If this distance is less than the width of the PSF then there may be some correlation of the fluorescence between the two points (Fig. 1, situation 2) but the spatial correlation will be less than that for immobile particles. However, for points that are not superimposed by the PSF, there could be some correlation due to the diffusion of the particle to these points.

FIGURE 1.

Raster scan images contain temporal information because pixels are recorded sequentially. (Situation 1) if a particle is not moving or slowly moving, a signal will be detected at position 1, 2, and 3 but not at 4 during the scan. The correlation of the fluorescence at different pixels depends on the extent of the PSF. (Situation 2) if the particle is moving quickly, there is a chance to get some signal even at location 4. The spatial extent of the correlation increases due to diffusion.

We derive expressions for the spatial autocorrelation function assuming that the intensity fluctuation is due to diffusion of a particle that is small compared to the PSF. In the temporal domain, the particle performs a random motion with an end-to-end distance that depends on the square root of time. In the spatial domain, the particle has a probability to be found at a distance from the original position that is described by a three-dimensional Gaussian with a variance that is related to the diffusion constant in (1). We express the scanning part of the correlation function S(x,y) (x and y are the horizontal and vertical coordinates, respectively) in terms of the pixel size, δr (in the range 0.1–0.2 μm), the pixel residence time, τ (in the range 5–100 μs), and the pixel sequence number n. For points along a line n is 1. For points in different lines, n is equal to the number of pixels in a line (256 or 512) plus an equivalent number of pixels corresponding to retracing time (typically 64–128).

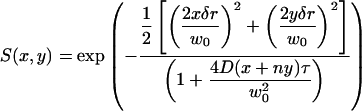[2]

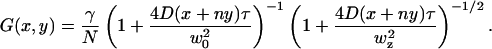[3]

The overall correlation function is given by 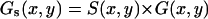. For raster scan pattern the correlation of a series of images appears on three different timescales. Along the horizontal axis adjacent pixels are separated by microseconds, along the vertical axis pixels are milliseconds apart and pixels from successive image frames are typically seconds apart. We have performed extensive simulations of particles diffusing in a three-dimensional grid to test the validity of the expressions used to fit the spatial autocorrelation functions. These results are not reported in this letter due to space restrictions. We systematically varied the values of the diffusion coefficient, number of particles, pixel size, beam waist, and the other parameters of the experiments. In all cases the recovered parameters from the fit matched the simulated parameters.

For the measurements described in this letter we used the two-photon excitation scanning fluorescence microscope previously described (2). Excitation wavelengths were 780 nm (for 10-nm polystyrene beads from Molecular Probes, Eugene, OR) and 910 nm (for EGFP). Due to the possible variation in the laser alignment from day to day, the beam waist w₀ was calibrated before each day's measurement by measuring the autocorrelation curve for 10 nM fluorescein in 0.01 M NaOH, and was fit using a diffusion constant of 300 μm²/s. Data were collected at a pixel rate of 16 μs/pixel for the solution experiments and 32 μs/pixel for the CHOK1 cell. For solution and cell experiments the scanning area was 128 × 128 pixels corresponding to a 14-μm square. For the solution measurements 2000 frames were collected whereas 790 frames were collected for the CHOK1 cells expressing EGFP experiments. Although only one image is sufficient theoretically to obtain the autocorrelation function and the diffusion coefficient of freely diffusing particles, in practice we average the information of many frames to improve statistics. For the samples in solution each sample was also measured in two different modalities, point FCS and raster scan pattern. The diffusion coefficient recovered from the fit of the single-point FCS matched the parameters recovered from the fit of the 2-D spatial correlation. Fig. 2 shows experimental data for the solution systems investigated.

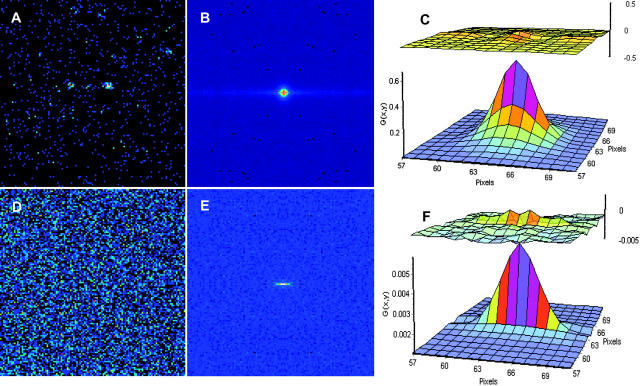
FIGURE 2.

(A) Image of 10-nm beads in solution. (B) Spatial autocorrelation. (C) Fit of the spatial autocorrelation function using equations [2] and [3] D = 5 ± 1 μm²/s. (D) Image of EGFP in solution. (E) Spatial autocorrelation. (F) Fit of the spatial autocorrelation function using equations [2] and [3] D = 91 ± 10 μm²/s. The upper images in panels C and F are the residues of the fit.

When measuring cells, there are often immobile structures in the image. Immobile features per se give a dominant correlation pattern within which the fast-diffusing particles are difficult to see. We propose a method to select only the high-frequency component of the image effectively filtering out the fixed or slowly moving structures. This is done by averaging all of the images of the stack and subtracting this average image from each frame. However, the autocorrelation function tends to oscillate widely because denominator is near zero. To avoid this effect, we add a quantity equal to the mean of the average image. After performing this operation we calculate the 2-D spatial correlation. The result is a full cancellation of the autocorrelation due to fixed structures. Of course, the size of the correlation function, i.e., the G(0,0) term is affected by this subtraction operation. In Fig. 3 we apply the subtraction algorithm to images from a CHOK1 cell transfected with cytoplasmic EGFP. The subtraction algorithm gives a pattern for the spatial correlation that is lacking the features due to the particular shape of the cell (compare Fig. 3, C and D). To prove our point, we selected different parts of the cell that give different shape of the spatial correlation when the subtraction method is not applied. When the subtraction method is applied, the remaining pattern due to the mobile protein is relatively constant across the cell. We obtain a diffusion value of 21 ± 5 μm²/s for EGFP in the cytoplasm of live cells that is in agreement with the published literature (7).

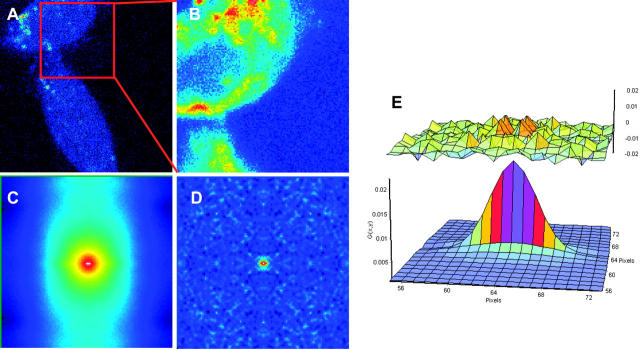
FIGURE 3.

(A) Image of a CHOK1 cells expressing EGFP. (B) A region (128 × 128 pixels) of the cell in panel A. (C) Spatial correlation before subtraction of the average image. (D) After subtraction of the average image. (E) Fit of the spatial correlation D = 21 ± 5 μm²/s. The upper image in panel E represents the residues of the fit.

In conclusion we presented RICS, an analysis method that exploits the time structure of raster scan images to recover the values of the diffusion of particles in solution. RICS can be used to obtain information on the timescale of diffusion motion of proteins in solution and of course for the slower dynamics in cells. Our method is similar to the original ICS idea. However, it is not limited to slow dynamics inherent in the original ICS method. Our algorithm introduces a new powerful tool for measuring fast cellular process using a standard confocal microscope.