Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2005 Mar 18;88(6):3822–3828. doi: 10.1529/biophysj.104.057703

Lipid Bilayer Perturbations around a Transmembrane Nanotube: A Coarse Grain Molecular Dynamics Study

Steve O Nielsen *, Bernd Ensing *, Vanessa Ortiz †, Preston B Moore ‡, Michael L Klein *
PMCID: PMC1305616  PMID: 15778436

Abstract

The perturbations induced in a lipid bilayer by the presence of a transmembrane nanotube are investigated using coarse grained molecular dynamics. Meniscus formation by the lipids and tilting of the nanotube occur in response to hydrophobic mismatch, although these two effects do not compensate completely for the total mismatch. The lipid head-to-tail vector field is examined and shows strong ordering in the membrane plane regardless of the nanotube length. Molecular layering at the lipid-nanotube interface is reported. This study extends previous theoretical approaches to a more realistic setting.

INTRODUCTION

A common theme in membrane protein structure studies is the occurrence of homooligomeric ion channels (Torres et al., 2001). Many of these channels must assemble from the separate monomers since they are not synthesized in the membrane (Fernandez-Lopez et al., 2001; Park et al., 2003). Very little is known about the factors which control the assembly of the monomers into a biologically active oligomeric state. This is because the time and length scales of the self-assembly process, as well as the complex hydrated membrane environment, place it outside the range of study possible with either experimental techniques or fully atomistic computer simulations.

There are many aspects which make such a study formidable; for example the presence of floppy cytoplasmic and extracellular domains and the fact that the secondary and tertiary structures of the monomers in water and in the membrane are often different due to the different environments.

Direct interactions between the monomers are important at short range (Torres et al., 2005) but at long range the forces are membrane mediated and are largely determined by the membrane perturbations around the separate monomers. A large body of theoretical work exists using simplified models which emphasize the lipid bilayer perturbations caused by the monomers. Some of the models used are based on membrane elasticity theory (Dan et al., 1993), in which the membrane is represented as a continuum; chain packing theory (May and Ben-Shaul, 2000), in which the conformational freedom of individual lipid chains is taken into account; integral equation theory (Lagüe et al., 2000), which incorporates some static atomistic properties; and the director model (Bohinc et al., 2003), in which the lipid is simply represented by a vector. These studies are valuable in elucidating and testing the basic physical concepts controlling the membrane-mediated aggregation of monomers into a channel. The restriction is made to the barrel-stave model of ion channel formation in which the monomers, represented as rigid cylinders of a fixed radius and length, insert in a transmembrane orientation and then aggregate. The two principal concepts which have emerged from these studies are the stiff volume-excluding nature of the monomers and the phenomenon of hydrophobic matching. The latter occurs when the lipid tails adjust their extension length along the direction perpendicular to the membrane plane to solvate the hydrophobic domain of the (assumed) transmembrane monomer (Dumas et al., 1999; Harroun et al., 1999a).

In this work, the barrel-stave restriction is maintained and, within it, we ask what the origins of the forces responsible for aggregation are. Our aim is to stay within the conceptual framework of prior modeling studies, and see how the picture which emerges from these studies is altered in the more realistic setting provided by coarse grained molecular dynamics. In doing so, we hope to retain the conceptual advantages inherent to a simple description while removing some of the less desirable restrictions that accompany these models. In particular, we remove the need to impose boundary conditions at the cylinder-lipid interface (required to solve models employing Euler-Lagrange differential equations), and we allow the cylinder to tilt in response to the lipids.

Recently, a study in the coarse grain molecular dynamics framework reported a minimal model for a stable transmembrane cylindrical nanotube (Lopez et al., 2004). In this work, we focus on the membrane perturbations induced by a similar nanotube and point out the differences and similarities with previous work.

METHODS

Model for lipid, water, and nanotube

The coarse grained model for lipids and water has been extensively discussed in previous work (Nielsen et al., 2004; Shelley et al., 2001); the lipid used here is a 13-site representation of DMPC. The nanotube is constructed from a number (8–12) of either 8- (narrow) or 18-site (wide) rings that are stacked vertically and linked with all possible bonds and bends between proximal sites. All the bonds and bends are harmonic with force constants of 10,000 K Å−2 and 10,000 K rad−2, respectively (10,000 K = 83.15 kJ/mol). The bonds have an equilibrium distance of 4.65Å. For the 10-ring narrow nanotube, which consists of 80 atoms, the construction is as follows: the individual rings have bonds (80 total) and bends (80 total, 135° equilibrium) in the plane of the ring. Adjacent rings are connected by 144 bonds, and 432 bends with an equilibrium angle of 60°. There are 288 bends involving adjacent rings with an equilibrium angle of 120°. Finally, there are 256 bends connecting three rings with equilibrium angles of 120° or 180°, depending on whether the outside two atoms are aligned or offset.

Nanotube-lipid interactions

The nonbonded interactions between the nanotube and the lipid and water particles are parameterized by using a very general method which was recently developed for modeling surfactant adsorption on hydrophobic surfaces (Nielsen et al., 2005). Although the parameterization could have been performed by modeling the nanotube directly as a cylinder, with parameters derived in a manner similar to the lipid parameters, a more general method was used. Unfortunately for this purpose, a full exposition of the procedure is too involved to be presented here. A few details will be given along with some comments which will hopefully capture the flavor of the method.

The route to coarse graining the interaction between a liquid and a solid goes through an intermediate step in which the solid/liquid interface is assumed to be flat. However, this is merely a computational device and the assumption about flatness is removed at the end of the calculation. Let us give some details about this aspect by first recalling that it is common in atomistic simulations to, for a flat solid/liquid interface, sum over all of the solid particles by approximating the surface as a continuum with number density ρ that occupies the semiinfinite region z ≤ 0. An atom belonging to the liquid phase at a height z > 0 interacts with the surface via (Hill, 1986; Lee and Rossky, 1994; Shelley and Patey, 1996)

graphic file with name M1.gif (1)

where for the last expression the Lennard-Jones potential u(r) = 4ε [(σ/r)12 − (σ/r)6], between an individual atom in the surface and an atom in the liquid phase, has been used. The great advantage of this expression, from the point of view of coarse graining, is that the solid has, in some sense, been removed from the problem. We will proceed with the coarse graining shortly, but first we would like to demonstrate why we can reverse this flatness assumption later on in the procedure. The key is to realize that Eq. 1, which we restate here as Inline graphic can be reversed simply by taking two derivatives to yield

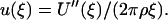graphic file with name M3.gif (2)

Furthermore, the parameter ρ appearing in this expression represents the level of coarse graining of the surface. For example, let us assume that we are presented with the surface potential given at the end of Eq. 1. In recovering the explicit potential by the use of Eq. 2, let us assume we choose to use a value for ρ, which is one half of the value used in obtaining the surface potential in the first place. Namely, pretending we don't know what value of ρ was used to get the expression in Eq. 1 because we are just given the function numerically, we happen to choose ρ in Eq. 2 as one half of the density that went into yielding the surface potential U(z). Carrying out the math, these choices yield the reconstructed explicit potential as u(r) = 8ε[(σ/r)12 − (σ/r)6], which is exactly double the Lennard-Jones potential we began with. So what has happened? To recover the surface potential U(z) with an assumed site-density of only one half of the actual value, we discover that we need twice the u(r) potential. In other words, with only half as many sites (which can be thought of as a coarse graining by a factor of 2) we need a stronger potential to recover the same U(z). This is perfectly reasonable and justifies our claim that not only can the flatness assumption be removed, but the solid can also be coarse grained by an appropriate choice of ρ in Eq. 2.

Now that we have established a way both of undoing the flatness assumption and of coarse graining the solid, we turn to the problem of coarse graining the liquid. This is done by replacing a group of atoms in the liquid phase by their center of mass (COM) and calculating the effective interaction between the COM and the surface. The task is (relatively) easy because the surface has already been removed from the problem. To achieve this, the interactions are described, not in terms of potential energies, but in terms of probability distributions. The probability and the potential are related by 𝒫=e−βU, where β is the inverse of Boltzmann's constant times the temperature. The details are not given here. After this step, the coarse grained site-site potentials between a liquid site and a solid site are recovered using Eq. 2. The solid sites can then be arranged in any geometry we desire, in this case a cylinder.

For the hydrophilic nanotube sites, the same procedure was followed with the additional contribution of a surface dipole interacting with the partial charges on the atomistic liquid sites. When the surface is restored to an explicit representation these electrostatic contributions are subsumed into an effective nonbonded potential.

Simulation systems

The outer two nanotube rings on each end are hydrophilic, whereas the inner (remaining) rings are hydrophobic. For the lipid bilayer systems, 256 lipids and 2560 water sites (representing 7680 water molecules) are used along with one nanotube in each of 10 different systems—the 10 systems being distinguished by the nanotube: 8, 9, 10, 11, and 12 eight-site rings and 8, 9, 10, 11, and 12 18-site rings to have two different radii nanotubes and a range of lengths. A snapshot of the 10 eight-ring nanotube system is shown in Fig. 1. In addition the 10 18-ring nanotube was used in a simulation with 2560 water sites and 512 pentadecane molecules arranged in an oil/water slab geometry (bilayer mimetic). Finally, a pure hydrated bilayer was simulated as a reference. A constant temperature (303 K) and pressure (membrane plane (x and y box sides constrained to change in the same proportion) and membrane normal (z) pressures separately set to 1 atm) ensemble was used with Nosé-Hoover chains of length three. The simulation unit cell thus fluctuates but has an average size of ∼97 Å × 97 Å × 58 Å. For each simulation, 10,000 frames were collected at an interval of 450 fs. For analysis purposes, the position of the lipid headgroup is defined as the center of mass of the first three lipid sites, and two lipid head-to-tail vectors are defined for each lipid from the headgroup center of mass to each of the two terminal tail sites. The radii of the narrow and wide nanotubes are 6.06 Å and 13.31 Å, respectively. The resulting area occupied by the nanotubes in the plane of the membrane corresponds to ∼1.5 and 8 times the area per lipid, respectively. The approximate van der Waals radius for the nanotube-lipid interactions is 4.9 Å, resulting in the “contact distance” being 10.9 Å for the narrow nanotube and 18.2 Å for the wide nanotube.

FIGURE 1.

FIGURE 1

Open in a new tab

Snapshots, from the top and the side, of the simulation unit cell consisting of 256 DMPC lipids, 2560 coarse grain water sites representing 7680 water molecules, and one 10-ring narrow transmembrane nanotube. The six inner hydrophobic nanotube rings are colored white whereas the hydrophilic rings are colored blue. The lipid tails are shown in yellow and the headgroups in red, purple, and green. The water, which is suppressed in the top view, is colored in blue.

RESULTS

The simulated systems have been tailor-made to study hydrophobic matching (or mismatch). All of the necessary ingredients are present and the model is sufficiently general to serve as a conceptual testing ground, free of system-specific competing effects such as aromatic peptide capping groups (de Planque et al., 2003). The height of the lipid headgroup center of mass, averaged over the two leaflets, as a function of its radial distance from the nanotube, is shown in Fig. 2. Three regimes are apparent. Far from the nanotube, the membrane is unperturbed. This is expected for a fluidic system and should be realized by using a sufficiently large unit cell. It appears (see Fig. 2 B) that the system size is slightly too small; however, we feel that the results have not been adversely affected by this deficiency. At an intermediate distance from the nanotube, the bilayer thickens regardless of its width at contact with the nanotube. This thickening has been reported by Bohinc et al. (2003) under zero hydrophobic mismatch conditions using a director model and was attributed to the lipid head-to-tail vectors being tilted away from the nanotube. Our calculations support this view and the lipid head-to-tail vector field is discussed below. In the immediate vicinity of the nanotube, the bilayer thins as it approaches contact with the nanotube, and its width at contact is clearly dependent on the nanotube length. The bilayer thickness at contact with the nanotube is shown in Fig. 3 as a function of the nanotube length, along with the best linear fit to the data. The fit is almost perfect for the wide nanotube (correlation coefficient 0.9996), whereas the data for the narrow nanotube shows some deviation from linearity (correlation coefficient 0.9926). It will be shown below that this behavior can be explained by the tilting capacity of the nanotube. The slopes are far from unity: this is of great significance since it removes the perfect hydrophobic matching boundary condition imposed in membrane inclusion studies (Owicki and McConnell, 1979; Fattal and Ben-Shaul, 1993; Aranda-Espinoza et al., 1996; Harroun et al., 1999b; Sens and Safran, 2000; Bohinc et al., 2003; Partenskii et al., 2004) where the bilayer fully adjusts to a change in nanotube length giving a slope of one. A notable exception to these studies is the theoretical work of Duque et al. (2002) in which a phenomenological free energy expression is avoided, resulting in only a partial response to mismatch attributed to nanotube tilting and entropic effects. Experimentally, it is clear that only a partial response to mismatch is achieved: de Planque et al. (1998) report that even the maximal possible changes in first-shell lipid length were relatively small and represented only a partial response to mismatch. The actual values of the linear fits reported here are not important because they are model-dependent. What is important is that in using a coarse grain molecular dynamics model, the artificial boundary conditions that hinder theoretical modeling efforts are removed. This hindrance is highlighted in the recent work of Partenskii et al. (2004), which is exclusively devoted to another boundary condition—the membrane slope along the curve where the nanotube borders the membrane surface. This slope could also be estimated from our data, although the statistics are poor because of the small number of lipids in contact with the nanotube. The lipids respond to mismatch and adjust their height more for the wide (radius) nanotube than the narrow one. This simply reflects the greater number of lipids in contact with the wide nanotube due to its larger circumference and smaller curvature as compared to the narrow nanotube. Atomistic simulations by Tieleman et al. (1998) also demonstrate that the effect of larger proteins on the local membrane thickness is more pronounced.

FIGURE 2.

FIGURE 2

Open in a new tab

Lipid bilayer meniscus around a transmembrane nanotube. Shown is the lipid headgroup height (averaged over the two leaflets) as a function of its radial distance from the nanotube, starting from the contact distance. Data for the narrow nanotube is shown in panel A, and for the wide nanotube in panel B.

FIGURE 3.

FIGURE 3

Open in a new tab

Extent of hydrophobic matching. The lipid headgroup height at contact (see Fig. 2) is plotted against the nanotube length. The best linear fit to the data is also shown. A slope of one would represent full matching in which a change in the hydrophobic length of the nanotube induces an equal change in the width of the lipid bilayer in contact with the nanotube. Length-dependent tilting of the nanotube long axis with respect to the membrane normal affects the linearity of the data for the narrow nanotube (see Fig. 5).

The hydrophobic matching effect leads to the expected change in the angle that the lipid head-to-tail vector makes with the bilayer normal as shown in Fig. 4. A short transmembrane nanotube induces the bilayer to thin in its vicinity, resulting in the nearby lipid tails having a narrower vertical region to inhabit. This causes the affected lipids to acquire an average head-to-tail vector angle with the membrane normal which is larger than the equilibrium, unperturbed value. Conversely, a long transmembrane nanotube induces the bilayer to thicken in its vicinity, causing the lipid tails to stretch out more along the vertical direction, reducing the average lipid head-to-tail vector angle with the membrane normal in the vicinity of the nanotube. Again, the perturbation from the absence of a transmembrane nanotube is more pronounced for the wide nanotube systems, reflecting its greater interaction energy with the bilayer. Although not directly related, lipid ordering has been reported around the gramicidin A channel, due to a reduced fraction of gauche conformations (Woolf and Roux, 1996).

FIGURE 4.

FIGURE 4

Open in a new tab

Shown is the lipid head-to-tail vector angle from the membrane normal, as a function of the lipid's radial distance from the nanotube. Data for the narrow nanotube is shown in panel A, and for the wide nanotube in panel B. Data for a bilayer in the absence of any membrane inclusions is shown for comparison.

There is, however, another aspect of hydrophobic mismatch which should be mentioned: its effect on the nanotube. In most modeling studies this aspect is ignored and the nanotube is fixed in space. Once again, molecular simulations offer the advantage of allowing the system to access more energetically favorable states. It is known experimentally that increasing mismatch reduces the fraction of nanotubes inserting into the lipid bilayer (de Planque et al., 2001). Less drastically, the nanotube may choose to adjust its tilt angle to better accommodate itself in the membrane. The nanotube tilt distributions are shown in Fig. 5. The expected result of wide short nanotubes tilting less than narrow long nanotubes agrees with the recent mesoscopic simulations of Venturoli et al. (2005). It is apparent from Fig. 5 that in the case of the wide nanotube the energetics are such that the tilt distribution remains virtually unchanged across the spectrum of lengths (Fig. 5 B). For the narrow nanotube, however, the tilt distribution changes dramatically as the nanotube lengthens (Fig. 5 A). This can be explained by the fact that the tilting of a wide nanotube, although removing the meniscus, would cause a large deformation in the surrounding membrane (see also Duque et al., 2002). This geometry is of higher free energy than a vertical nanotube orientation with its accompanying partial meniscus.

FIGURE 5.

FIGURE 5

Open in a new tab

Nanotube tilt distribution. The nanotube (data for the narrow nanotube shown in panel A, wide nanotube shown in panel B) long axis tilts from the bilayer normal as shown. Narrow nanotubes tilt more as their length increases, although the distributions also acquire a bimodal character as discussed in the text. Wide nanotubes are stable and their tilt distribution is independent of length over the range of lengths used in this study.

For the two longest nanotubes studied, the distribution appears to acquire a bimodal character representing a vertical orientation supporting a pronounced meniscus and a tilted orientation in which the meniscus is suppressed. Going back to Fig. 3, the length-dependent nanotube tilting causes the hydrophobic matching curve to deviate from a straight line. This effect explains why the wide nanotube data is fit much more accurately to a line than the data for the narrow nanotube. This observation leads us to predict that as the ratio of the nanotube radius to length decreases, tilting will become more pronounced.

We return now to the intermediate regime in Fig. 2 mentioned above, in which the membrane thickening was attributed to the tendency of the lipid head-to-tail vectors to point away from the nanotube. Fig. 6 quantifies this tendency by showing the correlation function between two vectors, one being the lipid head-to-tail vector projected into the membrane plane, and the other being the projection in the membrane plane of the vector from the nanotube center of mass to the lipid center of mass. This correlation function is plotted as a function of the magnitude of the second vector, namely the radial distance between the nanotube and the lipid. The resulting correlation function quantifies the extent to which lipid head-to-tail vectors are oriented radially outwards from the nanotube. For the eight-ring narrow nanotube shown in Fig. 6 A, a graphical representation of the lipid vector field is shown in Fig. 7. In accordance with all the other plots, the data in Fig. 6 has a clear, monotone dependence on the length of the nanotube. The correlation extends a significant distance from the nanotube and is stronger for shorter tube lengths. The later point is explained by the tilting in the bilayer normal direction shown in Fig. 4. The shorter the nanotube, the more the lipid head-to-tail vector tilts away from the bilayer normal, increasing its projected length in the bilayer plane. The region of negative correlation seen for long nanotubes in Fig. 6 is attributed to a depletion effect discussed in detail by Venturoli et al. (2005): the long nanotubes induce a significant positive meniscus (see Fig. 2) in their vicinity; this can result in a void at an intermediate distance from the nanotube which is filled in by lipid tails in a manner such as to cause an inward orientation.

FIGURE 6.

FIGURE 6

Open in a new tab

Lipid ordering around a transmembrane nanotube. Shown is the correlation function between the lipid head-to-tail vector projected into the membrane plane and the vector from the nanotube center of mass to the lipid center of mass, also projected into the membrane plane. Data for the narrow nanotube is shown in panel A, and for the wide nanotube in panel B.

FIGURE 7.

FIGURE 7

Open in a new tab

Lipid ordering around a transmembrane nanotube. Shown is the vector field of lipid head-to-tail vectors projected into the membrane plane around an eight-ring narrow nanotube. The color of the arrows indicates their intensity, from blue for high intensity to red for low intensity. This image was prepared using VMD (Humphrey et al., 1996). This figure is another representation of the data shown for the eight-ring nanotube in Fig. 6 A.

Although the nanotube is allowed to flex naturally within the molecular dynamics framework, the bonds and bends holding the nanotube sites in its cylindrical geometry are stiff compared to the lipid bonds and bends. The nanotube thus presents a rigid boundary which restricts the conformational freedom of the lipids in its vicinity. Indeed, we should expect the well understood phenomenon of molecular layering to occur in the liquid at this “solid-liquid” interface (Yu et al., 2000). Fig. 8 clearly demonstrates this effect, which consists of the solid inducing ordering of the liquid in the form of density oscillations normal to the interface. The data shown in Fig. 8 corresponds to two-dimensional radial distribution functions (equivalent to radially averaged density; Lagüe et al., 2000) in the membrane plane for different depths in the membrane. The plot shows data for both a hydrated lipid bilayer and an oil/water slab system in the presence of a 10-ring wide transmembrane nanotube. The initial value of the curves gives the vertical location of the membrane slice being probed. The lipid tails are flexible and, despite some tilting (see Figs. 4 and 6), tend to be oriented along the membrane normal. This results in the strong density oscillations seen deep inside the bilayer in Fig. 8.

FIGURE 8.

FIGURE 8

Open in a new tab

Two-dimensional radial distribution functions in the membrane plane as a function of depth for both a hydrated lipid bilayer and an oil/water slab in the presence of a 10-ring wide transmembrane nanotube. The initial value of the curves gives the vertical location of the membrane slice being probed. The curves are normalized to asymptotically approach a value of one plus their initial value.

For comparison we simulated an oil slab; the middle of the oil slab is also flexible and experiences an attractive (hydrophobic-hydrophobic) interaction with the nanotube. The density modulations in this part of the oil slab are strikingly similar to that of the lipid bilayer—the existence of this similarity was pointed out by Venable et al. (1993) in a different context, and by Woolf and Roux (1996) who suggested that the local packing of the hydrocarbon chains around the gramicidin A channel should be viewed as more similar to that of free methylene groups rather than rigid lipid molecules. Near the membrane/water interface the nature of the density modulations change. For the oil slab, its interactions with the nanotube are now unfavorable since it sees the hydrophilic caps. This leads to an unstructured density rise from zero inside the nanotube to one far from the nanotube. The lipid density modulations undergo two changes as the membrane/water interface is approached. Firstly, the oscillations are not as long-ranged as in the membrane interior, and secondly the minimum between the first two density peaks disappears. The first effect is due to the decreased flexibility of the lipid headgroups compared to the lipid tails, which is an inherent property of bilayers. The second effect results from the tendency of the headgroup dipoles to lie nearly flat, parallel to the bilayer plane. Since the measured density modulations are restricted to an in-plane membrane slice, the resulting two-dimensional radial averaging conceals the one-dimensional in-plane headgroup bond ordering.

CONCLUSIONS

A coarse grain molecular dynamics study of the perturbations induced in a lipid bilayer by the presence of a transmembrane nanotube was presented. The model also allows the nanotube to respond to the lipid bilayer. It was seen, in accordance with experimental knowledge, that the system only partially adjusts to situations of hydrophobic mismatch. These two phenomena, namely nanotube response to the lipids and incomplete hydrophobic matching, along with the full consideration of lipid perturbations afforded by the molecular dynamics framework, represent a significantly more realistic scenario than the phenomenological free energy theoretical modeling in which the nanotube does not respond to the lipids and the lipid perturbations are idealized and truncated at linear or quadratic order with limited coupling between them. Nonetheless, some of the observed bilayer perturbations, such as ordering of the lipid head-to-tail vectors in the membrane plane and lipid tail density modulations due to molecular layering at the lipid-nanotube interface, are qualitatively similar to existing theoretical models.

The use of a more realistic description is imperative for the study of nanotube aggregation in membranes because it is the quantitative details of the perturbations which sensitively determine whether two such nanotubes experience an attractive or repulsive membrane-mediated interaction at a given separation (Lagüe et al., 2000). Indeed, the forces responsible for aggregation arise from the overlap of the lipid perturbations induced by the individual nanotubes. A study along these lines is currently being pursued; the results presented here serve as a foundation for further study.

Acknowledgments

This work was supported in part by a grant from the National Institutes of Health.

References

  1. Aranda-Espinoza, H., A. Berman, N. Dan, P. Pincus, and S. Safran. 1996. Interaction between inclusions embedded in membranes. Biophys. J. 71:648–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bohinc, K., V. Kralj-Igliè, and S. May. 2003. Interaction between two cylindrical inclusions in a symmetric lipid bilayer. J. Chem. Phys. 119:7435–7444. [Google Scholar]
  3. Dan, N., P. Pincus, and S. A. Safran. 1993. Membrane-induced interactions between inclusions. Langmuir. 9:2768–2771. [Google Scholar]
  4. de Planque, M. R. R., B. B. Bonev, J. A. A. Demmers, D. V. Greathouse, R. E. Koeppe, F. Separovic, A. Watts, and J. A. Killian. 2003. Interfacial anchor properties of tryptophan residues in transmembrane peptides can dominate over hydrophobic matching effects in peptide-lipid interactions. Biochemistry. 42:5341–5348. [DOI] [PubMed] [Google Scholar]
  5. de Planque, M. R. R., E. Goormaghtigh, D. V. Greathouse, R. E. Koeppe II, J. A. W. Kruijtzer, R. M. J. Liskamp, B. de Kruijff, and J. A. Killian. 2001. Sensitivity of single membrane-spanning α-helical peptides to hydrophobic mismatch with a lipid bilayer: effects on backbone structure, orientation, and extent of membrane incorporation. Biochemistry. 40:5000–5010. [DOI] [PubMed] [Google Scholar]
  6. de Planque, M. R. R., D. V. Greathouse, R. E. Koeppe II, H. Schäfer, D. Marsh, and J. A. Killian. 1998. Influence of lipid/peptide hydrophobic mismatch on the thickness of diacylphosphatidylcholine bilayers. A 2H NMR and ESR study using designed transmembrane α-helical peptides and gramicidin A. Biochemistry. 37:9333–9345. [DOI] [PubMed] [Google Scholar]
  7. Dumas, F., M. C. Lebrun, and J.-F. Tocanne. 1999. Is the protein/lipid hydrophobic matching principle relevant to membrane organization and functions? FEBS Lett. 458:271–277. [DOI] [PubMed] [Google Scholar]
  8. Duque, D., X. Li, K. Katsov, and M. Schick. 2002. Molecular theory of hydrophobic mismatch between lipids and peptides. J. Chem. Phys. 116:10478–10484. [Google Scholar]
  9. Fattal, D. R., and A. Ben-Shaul. 1993. A molecular model for lipid-protein interaction in membranes: the role of hydrophobic mismatch. Biophys. J. 65:1795–1809. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Fernandez-Lopez, S., H.-S. Kim, E. C. Choi, M. Delgado, J. R. Granja, A. Khasanov, K. Kraehenbuehl, G. Long, D. A. Weinberger, K. M. Wilcoxen, and M. R. Ghadiri. 2001. Antibacterial agents based on the cyclic D,L-α-peptide architecture. Nature. 412:452–455. [DOI] [PubMed] [Google Scholar]
  11. Harroun, T. A., W. T. Heller, T. M. Weiss, L. Yang, and H. W. Huang. 1999a. Experimental evidence for hydrophobic matching and membrane-mediated interactions in lipid bilayers containing gramicidin. Biophys. J. 76:937–945. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Harroun, T. A., W. T. Heller, T. M. Weiss, L. Yang, and H. W. Huang. 1999b. Theoretical analysis of hydrophobic matching and membrane-mediated interactions in lipid bilayers containing gramicidin. Biophys. J. 76:3176–3185. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hill, T. L. 1986. An Introduction to Statistical Thermodynamics. Dover Publications, Mineola, NY.
  14. Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD: visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
  15. Lagüe, P., M. J. Zuckermann, and B. Roux. 2000. Lipid-mediated interactions between intrinsic membrane proteins: a theoretical study based on integral equations. Biophys. J. 79:2867–2879. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Lee, S. H., and P. J. Rossky. 1994. A comparison of the structure and dynamics of liquid water at hydrophobic and hydrophilic surfaces—a molecular-dynamics simulation study. J. Chem. Phys. 100:3334–3345. [Google Scholar]
  17. Lopez, C. F., S. O. Nielsen, P. B. Moore, and M. L. Klein. 2004. Understanding nature's design for a nanosyringe. Proc. Natl. Acad. Sci. USA. 101:4431–4434. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. May, S., and A. Ben-Shaul. 2000. A molecular model for lipid-mediated interaction between proteins in membranes. Phys. Chem. Chem. Phys. 2:4494–4502. [Google Scholar]
  19. Nielsen, S. O., C. F. Lopez, G. Srinivas, and M. L. Klein. 2004. Coarse grain models and the computer simulation of soft materials. J. Phys. Condens. Matter. 16:R481–R512. [Google Scholar]
  20. Nielsen, S. O., G. Srinivas, C. F. Lopez, and M. L. Klein. 2005. Modeling surfactant adsorption on hydrophobic surfaces. Phys. Rev. Lett. n press. [DOI] [PubMed]
  21. Owicki, J. C., and H. M. McConnell. 1979. Theory of protein-lipid and protein-protein interactions in bilayer membranes. Proc. Natl. Acad. Sci. USA. 76:4750–4754. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Park, S. H., A. A. Mrse, A. A. Nevzorov, M. F. Mesleh, M. Oblatt-Montal, M. Montal, and S. J. Opella. 2003. Three-dimensional structure of the channel-forming trans-membrane domain of virus protein “u” (Vpu) from HIV-1. J. Mol. Biol. 333:409–424. [DOI] [PubMed] [Google Scholar]
  23. Partenskii, M. B., G. V. Miloshevsky, and P. C. Jordan. 2004. Membrane inclusions as coupled harmonic oscillators: effects due to anisotropic membrane slope relaxation. J. Chem. Phys. 120:7183–7193. [DOI] [PubMed] [Google Scholar]
  24. Sens, P., and S. A. Safran. 2000. Inclusions induced phase separation in mixed lipid film. Eur. Phys. J. E. 1:237–248. [Google Scholar]
  25. Shelley, J. C., and G. N. Patey. 1996. Boundary condition effects in simulations of water confined between planar walls. Mol. Phys. 88:385–398. [Google Scholar]
  26. Shelley, J. C., M. Y. Shelley, R. C. Reeder, S. Bandyopadhyay, and M. L. Klein. 2001. A coarse grain model for phospholipid simulations. J. Phys. Chem. B. 105:4464–4470. [Google Scholar]
  27. Tieleman, D. P., L. R. Forrest, M. S. P. Sansom, and H. J. C. Berendsen. 1998. Lipid properties and the orientation of aromatic residues in OmpF, influenza M2, and alamethicin systems: molecular dynamics simulations. Biochemistry. 37:17554–17561. [DOI] [PubMed] [Google Scholar]
  28. Torres, J., A. Kukol, and I. Arkin. 2001. Mapping the energy surface of transmembrane helix-helix interactions. Biophys. J. 81:2681–2692. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Torres, J., J. Wang, K. Parthasarathy, and D. X. Liu. 2005. the transmembrane oligomers of coronavirus protein E. Biophys. J. 88:1283–1290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Venable, R. M., Y. H. Zhang, B. J. Hardy, and R. W. Pastor. 1993. Molecular-dynamics simulations of a lipid bilayer and of hexadecane - an investigation of membrane fluidity. Science. 262:223–226. [DOI] [PubMed] [Google Scholar]
  31. Venturoli, M., B. Smit, and M. M. Sperotto. 2005. Simulation studies of protein-induced bilayer deformations, and lipid-induced protein tilting, on a mesoscopic model for lipid bilayers with embedded proteins. Biophys. J. 88:1778–1798. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Woolf, T. B., and B. Roux. 1996. Structure, energetics, and dynamics of lipid-protein interactions: a molecular dynamics study of the gramicidin A channel in a DMPC bilayer. Proteins. 24:92–114. [DOI] [PubMed] [Google Scholar]
  33. Yu, C.-J., A. G. Richter, A. Datta, M. K. Durbin, and P. Dutta. 2000. Molecular layering in a liquid on a solid substrate: an X-ray reflectivity study. Physica B. 283:27–31. [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES