Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2005 Apr 1;88(6):3954–3965. doi: 10.1529/biophysj.104.050229

Normal Mode Analysis Suggests a Quaternary Twist Model for the Nicotinic Receptor Gating Mechanism

Antoine Taly *, Marc Delarue †, Thomas Grutter *, Michael Nilges ‡, Nicolas Le Novère §, Pierre-Jean Corringer *, Jean-Pierre Changeux *
PMCID: PMC1305627  PMID: 15805177

Abstract

We present a three-dimensional model of the homopentameric α7 nicotinic acetylcholine receptor (nAChR), that includes the extracellular and membrane domains, developed by comparative modeling on the basis of: 1), the x-ray crystal structure of the snail acetylcholine binding protein, an homolog of the extracellular domain of nAChRs; and 2), cryo-electron microscopy data of the membrane domain collected on Torpedo marmorata nAChRs. We performed normal mode analysis on the complete three-dimensional model to explore protein flexibility. Among the first 10 lowest frequency modes, only the first mode produces a structural reorganization compatible with channel gating: a wide opening of the channel pore caused by a concerted symmetrical quaternary twist motion of the protein with opposing rotations of the upper (extracellular) and lower (transmembrane) domains. Still, significant reorganizations are observed within each subunit, that involve their bending at the domain interface, an increase of angle between the two β-sheets composing the extracellular domain, the internal β-sheet being significantly correlated to the movement of the M2 α-helical segment. This global symmetrical twist motion of the pentameric protein complex, which resembles the opening transition of other multimeric ion channels, reasonably accounts for the available experimental data and thus likely describes the nAChR gating process.

INTRODUCTION

nAChRs are hetero- or homopentameric integral membrane proteins with a fivefold axis of pseudo-symmetry perpendicular to the membrane plane. Each subunit can be subdivided into three domains: extracellular, transmembrane, and intracellular. The extracellular domain carries the ACh binding sites at the boundary between subunits, and the transmembrane domain delineates an axial cation-specific channel (Corringer et al., 2000; Wilson and Karlin, 2001). These domains are functionally coupled to each other. Therefore, nAChRs possess all the structural elements necessary to convert a chemical signal, typically an increase of extracellular ACh concentration, into an electrical signal generated by the opening of the ion channel.

Electrophysiological analysis of nAChRs shows that rapid delivery of ACh promotes the transient opening of the channel, whereas prolonged application results in a slow decrease of the response amplitude or “desensitization”. Several kinetic models have been proposed for the processes of activation and desensitization (Katz and Thesleff, 1957) and the structural transitions related to general mechanisms of allosteric transitions known to mediate signal transmission (see Changeux and Edelstein, 1998, and Perutz, 1989). Within this framework, the concerted Monod-Wyman-Changeux (MWC) model (Monod et al., 1965) was extended to the nAChR and the receptor protein assumed to exist, spontaneously, in thermal reversible equilibrium between a basal state (B), an active open channel state (A) stabilized by ACh and the nicotinic agonists, and one or several high affinity desensitized state(s) (D) with a closed channel (see Changeux and Edelstein, 1998).

So far, attempts to grow three-dimensional crystals of nAChRs have achieved limited success (Paas et al., 2003) because of technical difficulties inherent to transmembrane proteins. From sequence analysis, it is known that nAChRs are constituted of large N-terminal extracellular domain, mainly composed of β-sheets, a transmembrane domain composed of four helical segments (M1–M4) that cross the membrane, and of a cytoplasmic domain, inserted between M3 and M4 segments, composed of two amphipathic helices joined by a hypervariable peptide segment (Le Novere et al., 1999). Recent x-ray crystallography and electron microscopy studies provide for the first time the opportunity to develop experimentally based three-dimensional models of both the extracellular and the membrane domains. Indeed, the three-dimensional structure of a protein homologous to the extracellular domain of nAChRs (acetylcholine binding protein from Limnea stagnalis, AChBP) has been obtained by x-ray crystallography at 2.7 Å resolution (Brejc et al., 2001), yielding three-dimensional models of the extracellular domain of nAChR (Fuchs et al., 2003; Le Novere et al., 2002; Schapira et al., 2002; Sixma and Smit, 2003) by comparative modeling. Second, electron microscopy data at 4 Å collected with Torpedo marmorata receptor-rich membranes revealed that transmembrane segments are α-helical (Miyazawa et al., 2003), thus providing a template for this domain of the receptor molecule.

We present molecular modeling data of the nAChR molecule including both its transmembrane and extracellular domains. Indeed, affinity labeling and site-directed mutagenesis experiments support the idea that both domains carry the essential structural elements required for the chemo-electrical signal transduction. In particular, we note the ACh binding sites that are located at the subunit interface within the extracellular domain, the ion channel that is bordered by the M2 segments from the transmembrane domain, and the gating elements between both functional sites at the extracellular-transmembrane domain interface (Kash et al., 2004, 2003). The homomeric α7 receptor was selected as a prototypic nAChR because of its fivefold symmetry. We studied the accessible conformational transitions by normal mode analysis (see Brooks and Karplus, 1983 and Go et al., 1983, for early examples), which is based on a physical description of the protein (the force field that describes the interactions between the atoms) and allows the flexibility to be decomposed into discrete deformations (i.e., the modes; for a review of normal modes with the models used here, see Tama, 2003; see also recent developments, Bahar et al., 1997; Durand et al., 1994; Hinsen, 1998; Hinsen et al., 1999; Li and Cui, 2002; Marques and Sanejouand, 1995; Mouawad and Perahia, 1993; Tama et al., 2000). It was previously shown that most protein conformational transitions documented in the protein data bank can be accounted for by a few low-frequency normal modes (Krebs et al., 2002; Tama and Sanejouand, 2001). Recently, normal mode analysis has been used to efficiently analyze the conformational transition of the mechanosensitive channel (Valadie et al., 2003). Here, we deformed the initial model along the 10 modes with the highest amplitudes (lowest frequencies) to produce new structures and challenged them with the available experimental results. It is shown that the first mode accounts well for the opening of the channel. Detailed analysis of the conformational transition of the gating mechanism suggests that it primarily consists of a global symmetrical twist of the quaternary structure of the receptor pentamer with opposing rotations for the upper and lower domains.

METHODS

Model building

Sequence alignment

The multiple sequence alignment was performed with the program CLUSTALX (Thompson et al., 1997).

Comparative modeling

The template was built using the structures 1I9B (AChBP) and 1OED (membrane domain). We positioned by hand the two structures at a distance compatible with the formation of a peptide bond between the C-terminal glycine residues of AChBP (that correspond to the last residue solved within the crystal structure) and the N-terminal proline residues of the α1, β, γ, and δ Torpedo transmembrane domains. The template was used to construct the initial model with the program MODELLER (Sali and Blundell, 1993).

Minimization

The minimization was performed with the program CHARMM (Brooks et al., 1983; MacKerell et al., 1998) using the param22 parameter set (all-atom). The solvent was represented implicitly with a distance-dependent dielectric constant. The minimization protocol is performed as follows: The model was first fivefold-averaged; a minimization was then performed with a decreasing harmonic potential on the position of the backbone; and finally, the fivefold symmetry was checked. The cycle was repeated until the root mean-square displacement (RMSD) between Cα carbons of different subunits was ≪1.5 Å. This procedure yielded RMSD between pair of subunits from 0.91 to 1.32 Å.

Normal mode analysis

Normal mode analysis has been performed using the elastic-network model (Tirion, 1996) within which the protein is represented by a network of atoms linked by springs if (and only if) their mutual distance is less than a given threshold,

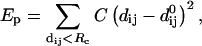graphic file with name M1.gif

where dij is the distance between atoms i and j, 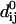Inline graphic being the distance between these two atoms in the structure. C, the strength of the potential, is a phenomenological constant assumed to be the same for all interacting pairs. The value of C has been arbitrarily set to 1000 kcal/Å2 mol and used throughout this work. Rc is an arbitrary cutoff parameter above which the interactions are not considered. As discussed in Tirion (1996), the cutoff parameter mainly influences the higher-frequency modes. Here, Rc was set to 10 Å.

We used a simplified version of the model where the protein is represented only by its Cα carbons (Bahar et al., 1997; Hinsen, 1998). The code used was that distributed freely by Y.-H. Sanejouand (see http://ecole.modelisation.free.fr), described in Tama and Sanejouand (2001) and Delarue and Sanejouand (2002) and recently successfully used in the study of the mechanosensitive channel (Valadie et al., 2003).

Reconstruction of all atoms models

After modification of the positions of the α-carbons along normal modes, the positions of the backbone and side-chain atoms were adjusted by energy minimization using decreasing harmonic potentials with the program CHARMM (Brooks et al., 1983; MacKerell et al., 1998).

Analysis of the angle indicating the displacement of the internal β-sheet

To compute the angles between the two β-sheets in our structures, the structure was split in two parts; the internal β-sheet was defined as residues 1–87 and 94–125, and the external β-sheet was considered together with the rest of the protein (residues 126–340).

The analysis of the angle between the two β-sheets was carried out using CHARMM. The tested structure was superposed to the template structure (not minimized, i.e., the closest possible to AChBP). For each subunit an RMSD fit was performed successively on each β-sheet. This is done using the command “coor orient” that centers the atoms at the origin and rotates the atoms to align the principal axes. The angle necessary to move the tested structure from one fit to the other was taken as the internal β-sheet displacement-angle. In the case of the structure 0 (after minimization) the angle was ∼2–3°, depending on the subunit. This test shows that the variation on the angle due to the minimization is negligible.

Analysis of the coupling between M2 helix and the internal β-sheet

We analyzed the tertiary deformation of the subunits at the level of the secondary structure elements using an RMSD-fit procedure. The secondary structure elements were defined as internal β-sheet from residues 1 to 87 and 94 to 125; external β-sheet from residues 126 to 205; and M2 from residues 238 to 265 where the numbers are those of the residues in our model (Fig. 1).

FIGURE 1.

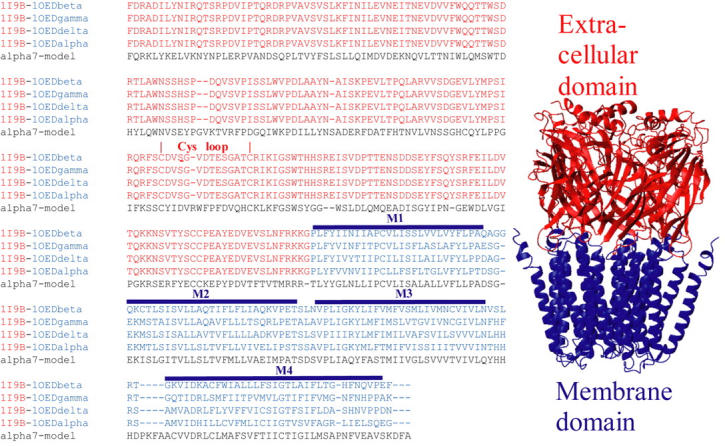
FIGURE 1

Open in a new tab

(Left) Alignment between human α7 sequence and the chimerical AChBP-Torpedo marmorata subunits. The residues from α7 intracellular loop were removed. The residues of AChBP and Torpedo marmorata membrane domain are represented in red and blue, respectively. The positions of the Cys-loop (loop 7) and of α-helices are highlighted. (Right) Structure 0: model α7 receptor obtained after energy minimization of a preliminary structure obtained using comparative modeling. The extracellular and membrane domains are represented in red and blue, respectively.

The RMSD-fitting (superposition of structures to minimize RMSD) procedure to determine which β-sheet was more closely coupled to M2 involved the following steps: Two sets were defined (M2 and either the internal or the external β-sheet) for which an RMSD-fit was performed.

Analysis of the size of the pore

The size of the pore was measured at several locations:

  1. We identified visually the atom that is the closest to the axis of the pore, thus defining a ring of five homologous atoms that constitute the most constricted region of the pore.

  2. We measured the distance between each of these atoms and their neighbors of the adjacent subunits.

  3. The geometry was approximated to be that of a regular pentagon, characterized by an edge equal to the mean of the previously calculated edges.

  4. The distance from the axis of the pore was calculated, from which the Van der Waals radius of the atom (taken from CHARMM parameters) was subtracted.

RESULTS AND DISCUSSION

A structural model of α7 nAChR

AChBP-Torpedo nAChR chimeric template construction

The first step consisted in the fusion of the known structures of both the extracellular and transmembrane domains into a single structural template. To this aim we fused the three-dimensional structure of the homomeric AChBP from Lymnea stagnalis obtained by x-ray crystallography (Brejc et al., 2001) with the model of the transmembrane domain of the heteromeric Torpedo marmorata receptor based on cryo-electron microscopy (Miyazawa et al., 2003). We positioned by hand the two structures at a distance compatible with the formation of a peptide bond between the C-terminal glycine residues of AChBP (that correspond to the last residue solved within the crystal structure) and the N-terminal proline residues of the α1, β, γ, and δ Torpedo transmembrane domains. It is possible to maintain this distance simultaneously for the five subunits, thus making this operation unambiguous. It should be mentioned, however, that a few clashes of side chains were observed. Yet no clashes of the backbone were ever observed and this makes the template suitable for comparative modeling. The primary sequence of the resulting chimeric subunits is given in Fig. 1.

α7 model construction

To build an α7 model by comparative modeling, we first performed a sequence alignment between the AChBP/Torpedo chimeric subunits and the human α7 subunits in which the cytoplasmic domain was ignored, using CLUSTALX (Fig. 1). This alignment shows that the chimeric subunits carry an additional glycine residue at the junction between the extracellular and the transmembrane domains, as compared to α7. This supernumerary glycine residue was removed as the structure was generated using the program MODELLER. We therefore obtained a model of the human α7 receptor that includes the extracellular and transmembrane domains.

We observed that both before and after the Simulated Annealing refinement performed by MODELLER (the procedure in which the stereochemical properties of the structure are improved), the structure of the membrane domain was found to be asymmetric (RMSD between pairs of subunits >2 Å). The extent of the asymmetry appeared to exceed the effect of thermal fluctuations, and was due to the fact that we used a chimeric template that was derived from the membrane domain of the heteropentameric Torpedo receptor. We thus decided to skip the Simulated Annealing step and rather to impose fivefold symmetry during an additional minimization step performed with the molecular modeling program CHARMM (see Methods). This procedure yielded an initial structural model, called structure 0, characterized by a fivefold symmetry compatible with a homomeric protein (RMSD between pairs of subunits in the range of 0.91–1.32 Å).

Structure 0 is presented in Fig. 1. The two domains closely resemble the structures used to build the template. The minimization does not cause any significant global modification of the structure. The RMSD computed (for the α-carbons) for the complete receptor, the extracellular and the membrane domain, before and after the minimization/symmetrization procedure, are 3.49, 2.83, and 3.29 Å, respectively. The size of the pore is neither increased nor decreased by the minimization/symmetrization: the RMSD for the α-carbons of the M2 segment is 2.01 Å.

At the interface between the two domains, we note that:

  1. The M2–M3 loop of the membrane domain is surrounded by loop 2 (β1–β2 loop) and loop 7 (Cys loop) of the extracellular domain. During the minimization/symmetrization procedure, loops 2 and 7 moved away slightly, improving the interaction with the M2–M3 loop.

  2. Loop 7 is inserted in the middle of the four α-helices and establishes contact with all of them.

  3. Interactions exist between residues in the extracellular portion of M4 and residues in the extracellular domain.

In the Torpedo original model of the membrane domain, the M4 segment was found separated from the other segments, and even “makes no extensive van-der-Waals contacts with either M1 or M3, suggesting that it is mainly separated from these helices by water filled space” (Miyazawa et al., 2003). During the minimization/symmetrization procedure on α7, the relative positions of the transmembrane helices changed drastically, generating a more compact structure: M3 came in closer contact to both M2 and M1; M4 came in contact with the other transmembrane segments and increased its contacts with residues in loop 7.

Exploring normal modes space

The conformational transitions of the α7 receptor model were investigated by normal mode analysis. This method approximates the surface of the conformational landscape and gives a decomposition of the movements into discrete modes. It takes advantage of a simplified but physically meaningful representation of the interaction between the atoms, based on simple springs connecting close pairs of atoms in the native structure. Both the quadratic approximation of the landscape and the crude representation of the protein lead to the loss of the fine details of the dynamics. However, this method leads to a time-independent equation that can be solved in closed form analytically (at variance to molecular dynamics), and therefore allows studying slow (biologically relevant) and collective conformational transitions.

On a database of proteins for which experimental structures of different conformations were known, it has been shown that only a handful of the very first modes (usually one or two) are usually enough to describe the transitions (Krebs et al., 2002).

Normal mode analysis was performed using the elastic-network model of Tirion (1996) as simplified by Hinsen (1998), who showed that it was possible to use C-α atoms only. To further simplify the calculations for the 1700 amino-acids α7 receptor, we used this simplified version of the model (Hinsen, 1998). Normal mode analysis using this approximation was shown to give a fair description of protein flexibility (Bahar, 1999; Tama and Brooks, 2002), and it is the same as that used by Krebs et al. (2002) in their survey of all conformational transitions documented in the PDB.

Altogether, the flexibility study presented here includes some approximations (e.g., normal-mode analysis, absence of water/membrane, simplified force field restricted to α-carbons). These approximations imply that some of the structures obtained may include deviations in the precise positioning of atoms. As a consequence, although the general trends are anticipated to be correct, the structures should not be analyzed at the atomic level.

We computed the first 100 lowest-frequency modes and selected the first 10, where each mode was explored in its two opposite directions thus resulting in two structures. The magnitude of the amplification of each mode is one of the variables of the study. For each mode the energy applied was adjusted such that the two structures would have an RMSD of ∼2 Å. This arbitrary RMSD value was chosen because it produced realistic structures with all modes and the changes were large enough to be extensively and easily analyzed by visual inspection of the end points. Higher RMSD was possible only with the first mode, while still maintaining stereochemically acceptable structures (see below). After amplification, the new positions of the α-carbons were applied to structure 0 and the energy of the resulting structure was minimized with decreasing harmonic potentials on the positions of the α-carbons, i.e., the structure was relaxed with constraints on the position of the α-carbons. This step was performed using the program CHARMM (Brooks et al., 1983; MacKerell et al., 1998).

We then performed a systematic analysis of the pairs of structures. In particular we investigated whether each mode would reproduce some key modifications associated with gating events, in particular: 1), an opening of the pore (and/or tilt, rotation, or bending of M2); or, 2), distributed changes in both the membrane and the extracellular domains, indicative of a coupling between the ACh binding site and the ion channel. Interestingly, both criteria pointed only toward the first mode (described in detail in the next section). We therefore present only a brief description of the other modes.

Modes 3 and 4

Modes 3 and 4 are degenerated modes (mixed during the process of modes calculation). The fivefold symmetry is responsible for that degeneracy as they are found to display a high degree of overlap in their eigenvectors when the symmetry is taken into account (data not shown). Degenerated modes are not independent and should therefore be analyzed together. Both modes show a strongly asymmetric hinge-bending motion of the whole protein in opposite directions, with the hinge point located at the junction of the extracellular and membrane domains. Furthermore, in both modes the size of the pore was found constant.

Modes 2 and 5–10

Within these modes, the region having the highest movement amplitude was consistently M4. In the initial model, M4 protrudes from the membrane by ∼10 Å, and these modes mainly result in a tilt and/or kink of the entire M4 helix, thus bringing the C-terminal tail close to the membrane level. The C-terminal segment of M4 is hydrophilic and therefore its diving into the membrane would be energetically unfavorable. The remainder of the protein was unchanged or involved only local conformational changes. These modes do not display an opening of the pore.

Test case

To evaluate the influence of the fine three-dimensional structure on the normal mode analysis, we performed an identical normal mode analysis on the α7 model generated after homology modeling but before the minimization/symmetrization procedure. This structure retains two characteristic features of the structure obtained on the Torpedo receptor: asymmetry and an empty space between M4 and the rest of the domain. The different modes are the same, although appearing in a different order. Interestingly, the first mode described below appears as the third mode in the test case, with identical eigenvectors. The two modes have been compared by computing a normalized correlation coefficient between the eigenvectors for each α-carbon, i.e., the cosine of the angle between the two sets of vectors. The expected value of this cosine is therefore expected to be close to 1 (or −1) when two modes are highly correlated and to 0 when the modes are unrelated. Here the value is 0.944, showing that both modes describe the same movement. The first and second modes of the test case correspond to large fluctuations of the C-terminus of M4 and are therefore not relevant to our study because they concern neither the agonist binding site nor the ion channel.

Description of the first mode

At variance with the other modes, it was possible to induce a larger conformational change of structure 0 according to this mode without generating any unrealistic distortion of the molecule. This allowed the generation of two models (Fig. 2), called 1C (closed) and 1O (open) that had a RMSD of 6 Å (each model was chosen with an RMSD of 3 Å as compared to structure 0). This normal mode yields symmetrical deformations of the structure primarily at the quaternary level but also at the tertiary level (see below), and is associated with a ∼3 A opening of the pore in the 1O conformation (Fig. 2).

FIGURE 2.

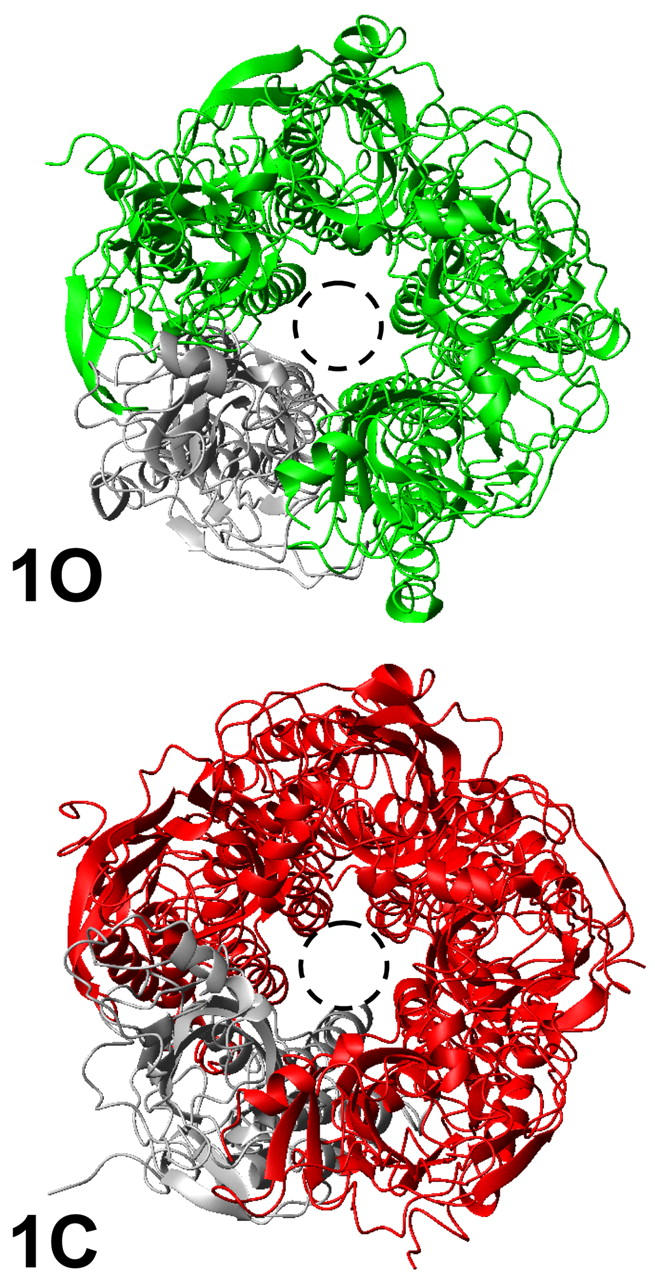
FIGURE 2

Open in a new tab

Models 1O and 1C. View from the synaptic cleft. One subunit is represented in gray for clarity. The dashed circle allows for comparing the size of the pore in both structures, which illustrates the larger pore of the structure 1O.

Quaternary reorganization

This mode, illustrated by the 1C → 1O transition, is characterized by a strong reorganization of the quaternary structure, with a symmetrical tilt of ∼15° of each subunit around an axis perpendicular to the membrane as illustrated in Fig. 3. This axis goes through the extracellular/transmembrane domain interface and intercepts the fivefold axis of symmetry. Therefore, the interface between the two domains is located at the position where the relative movement is of minimal amplitude. If the conformational change from 1C to 1O is viewed from the extracellular side, the top of each subunit rotates in an anticlockwise manner around the fivefold axis of symmetry. At the same time the bottom of each subunit rotates in a clockwise manner around the fivefold axis of symmetry. In other words, the quaternary deformation can be described by a global twist movement with opposing rotations of the top and bottom domains. Two movies (provided as Supplementary Material) illustrate the conformational transition from the structure 1C to the structure 1O, as viewed from the synaptic cleft and laterally. They have been prepared by generating 96 intermediates along the mode, reconstructing the position of all atoms of the residues from the α-carbons coordinates using extensive minimization with decreasing harmonic potential. They are proposed in MPEG format (viewed, for example, with QUICKTIME).

FIGURE 3.

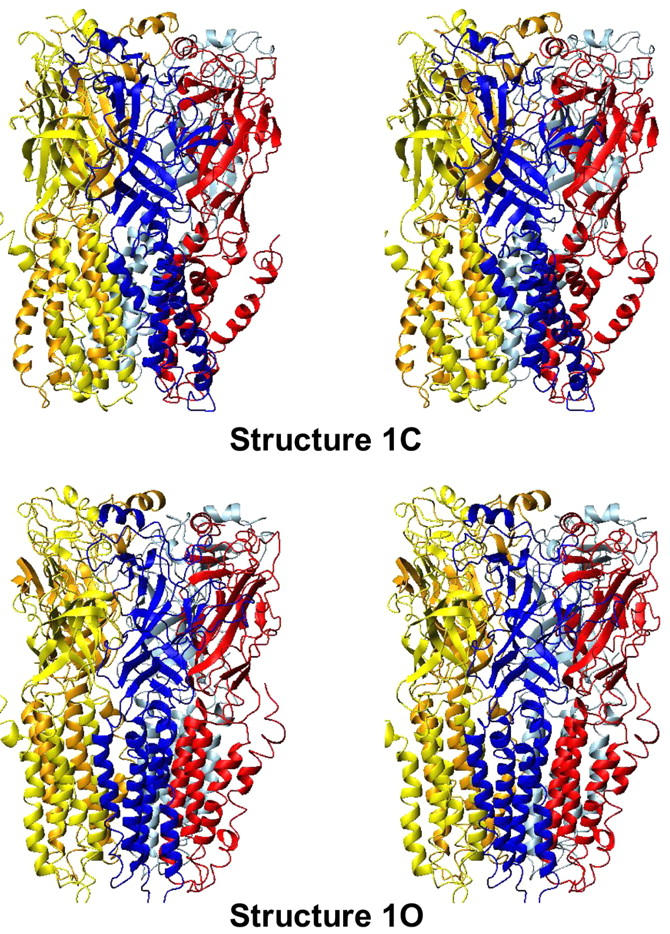
FIGURE 3

Open in a new tab

Models 1C and 1O; lateral view.

Tertiary reorganization

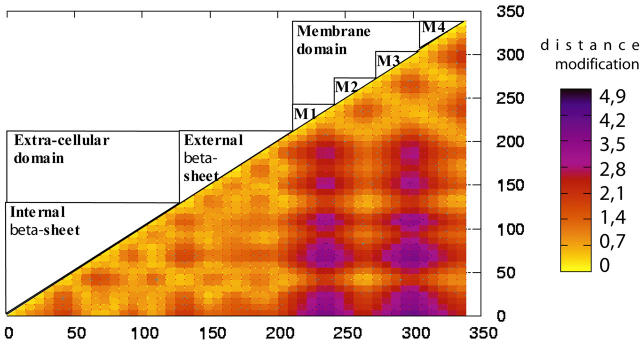
To dissect the internal motions occurring in the various subunits, we searched for rigid bodies motions (block of residues that move in a concerted manner). We first used a method that can be conducted without any a priori hypotheses. We first compared the relative movement of all residues within the subunits using a procedure inspired from that described in Valadie et al. (2003). For each subunit, a square matrix was constructed in which all distances between pairs of α-carbons were reported. Then, the difference between the matrices derived from structures 1C and 1O was calculated. The matrices of the subunits were found very similar (data not shown), further indicating a symmetrical motion of the protein. Fig. 4 shows the average matrix of the five subunits that represents the distance variation between pairs of residues associated with mode 1.

FIGURE 4.

FIGURE 4

Open in a new tab

Matrix representation of the relative movement in the protein between structures 1C and 1O. The distances between pairs of atoms are computed for the 1C and 1O structures and the difference is plotted as a matrix using the numbers of the residues in the model. The positions of the helices and β-sheets are represented in the upper-left half of the matrix.

Visual inspection of the matrix reveals two major tertiary reorganizations:

  1. It highlights two regions within which the pairs of α-carbon distances vary <2 Å between 1C and 1O. Strikingly, these regions perfectly match the extracellular and transmembrane domains, indicating a bending of the subunits at the domain interface, with comparative weak internal flexibility within the domains. This bending is well illustrated by the lower-right square of the matrix that represents the relative motions between the two domains, where α-carbon distances are modified by up to 5 Å.

  2. Yet, within this lower-right square, the distance pattern is found to be different for the four transmembrane α-helices: the motions of M1 and M3 segments relative to the extracellular domain are much larger than those of the M2 and M4 segments, pointing to a significant reorganization within the membrane domain. Interestingly, the matrix shows that the relative motions between the M2 helix and the extracellular domain are weak, suggesting that both structural elements would move in a concerted manner.

These observations are illustrated in Fig. 5, which shows a single subunit in its 1C and 1O conformations. It highlights that the 1C → 1O transition involves a bending of the subunit at the domain interface, with the transmembrane domain, as a whole, tilting within the membrane. In addition, the M2 helix tilts to a much lower extent, but bends in its upper part.

FIGURE 5.

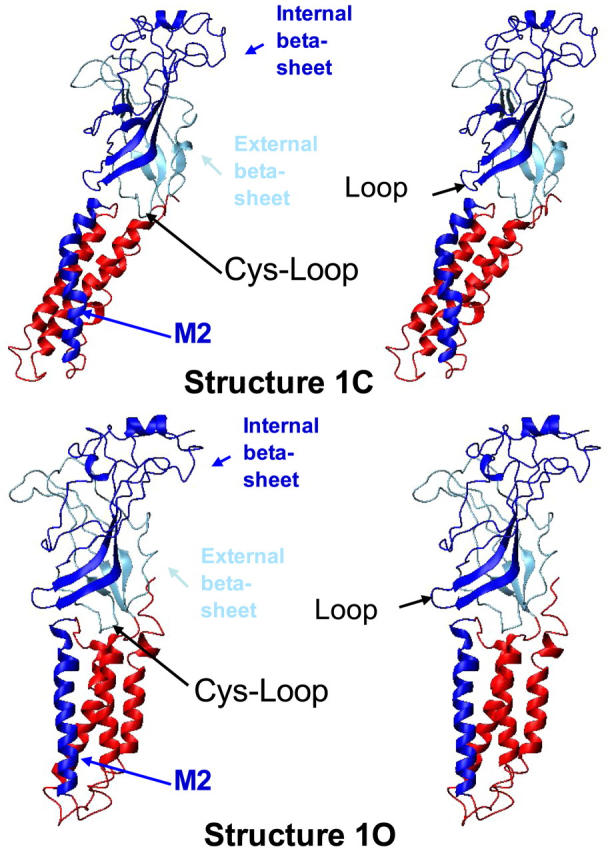
FIGURE 5

Open in a new tab

Conformational change between structures 1C and 1O at the tertiary structure level. Only one subunit is represented. The internal β-sheet and M2 helix are represented in blue, the external β-sheet is represented in light blue and the rest of the protein is displayed in red.

To investigate more subtle tertiary reorganizations, we developed complementary methods that were primarily designed to study the relative motions of the two β-sheets composing the sandwich of the extracellular domain. We found that the 1C → 1O transition was associated with a significant change in the inter-β-sheet angle (calculated as described in Methods), from ∼3 to 13°. The same calculation performed on the other modes showed no relative movement of the internal β-sheets, with a calculated angle always smaller than 3°. Finally, to search for concerted motions between the extracellular and membrane domains, we analyzed the relative movements of each β-sheet as compared to the transmembrane helices. We find that the movement of the internal β-sheet is more coupled to the M2 (RMSD = 2.41 Å) than to the M1 (RMSD = 4.33 Å), M3 (RMSD = 3.8 Å) or M4 (RMSD = 4.57 Å) helices, whereas the external β-sheet consistently showed higher RMSD with the four membrane segments. To further test how strong was the correlation between the internal β-sheet and M2, we computed the RMSD of the internal β-sheet, of the M2 helix, or of both between the structures 1C and 1O. The RMSD are in the range of 1.8 Å when the elements are analyzed separately, and of 2.41 Å when analyzed together, compared to the value of 3.95 Å obtained with the RMSD of the entire subunit. This comparison of the RMSD values shows that the movement of the internal β-sheet and M2 helix are significantly correlated (Fig. 5).

Altogether, the 1C→1O conformational reorganization consists mainly of a quaternary twist of the whole protein. Still, significant reorganizations are observed at the tertiary level, and involve a bending of the subunits at the domain interface. An increase of angle between the two β-sheets of the extracellular domain also occurs, and the movement of the internal β-sheet is significantly correlated to the movement of the M2 segment.

Pore size reorganization

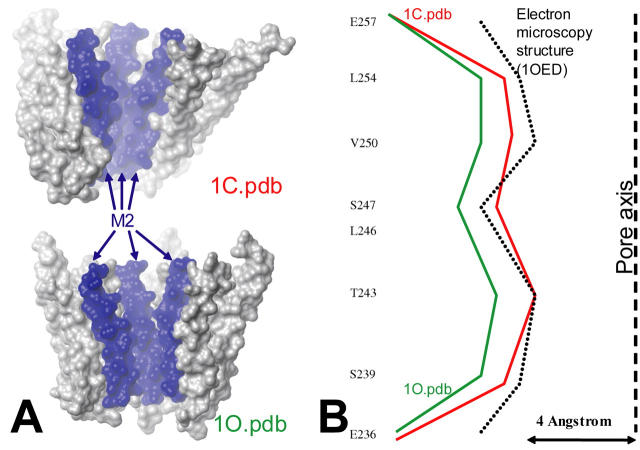
The global quaternary twist movement of the protein governs the diameter of the central pore, with a smaller diameter when subunits are tilted with respect to the principal axis (model 1C and structure 0), as compared to a larger diameter when subunits are parallel to the principal axis (model 1O). The pore size has been calculated at different level as described in Methods (Fig. 5). The minimum size increased from ∼6.7 Å in the structure 1C to ∼9.6 Å in the structure 1O (∼5.7 Å in the structure 0). It should be noticed, however, that the diameter of a cation with its first hydration sphere is ∼8 Å, which makes the structure 1O the only one wide enough to allow the translocation of cations through the channel. The structural modification included in the first mode is such that the size of the pore was increased uniformly (i.e., not at a single level) in the structure 1O (Fig. 6). In addition, the tilt of the subunit does not involve any significant rotation of the M2 helix, leading the same residues to face the pore in the 1C and 1O conformations.

FIGURE 6.

FIGURE 6

Open in a new tab

(A) Models 1C and 1O including side chains. Only the membrane domain is represented in a space-filling representation. Slab mode is used in order to see the pore. (B) Radius of the pore at different levels for the structure 1C (red) 1O (green), and the structure derived from electron microscopy studies (dotted line). The axis of the pore is represented as a dashed line.

COMPARISON WITH EXPERIMENTAL DATA

Comparison of the initial structure (structures 0) with experimental data

Comparison with the original AChBP structure and electron microscopy densities

The overall shape of the structure 0 is consistent with the structures of AChBP and of the membrane domains from Torpedo receptors. Yet, our minimization protocol significantly modified the organization of the transmembrane α-helices that tended to move closer to each other generating a more compact domain. The largest movement was that of M4. This is not surprising, since 1), the structure of the transmembrane segment M4 is probably the least accurate, because this part of the receptor is associated with a lower electron density; and 2), M4 may have been partially influenced by our fivefold averaging procedure because it is the most asymmetric part of the membrane domain (Miyazawa et al., 2003). However, the membrane domain does not undergo any significant global modification of the structure, such as tilt or bending of the helices, which could be attributed to a conformational change. Therefore it remains consistent with the experimentally derived structure.

The presence of water-filled space between the helices was inferred from electron microscopy experiments. In agreement with that finding, a site for general anesthetics has been identified in an homologous position in GABA receptors (Chang et al., 2003; Chou, 2004; Husain et al., 2003; Rudolph and Mohler, 2004). However, the presence of a hydrophilic pocket remained questionable since M1, M3, and M4 are not amphiphilic. Therefore, we did not impose constraints to reproduce this aspect. In our minimization protocol no explicit water was present, which led the helices to come in contact with each other and the empty space between them to disappear. However, the test case performed with the original structure of the membrane domain (in which the M4 helix remained fixed) gave similar results (see above), also identifying the first mode as important for understanding of the dynamics of the protein; this shows that the movement of M4 observed here does not interfere with our results.

Analysis of the interface between the extracellular and the transmembrane domains

The most critical part of our model is the interface between the extracellular and transmembrane domains. We found that the original structures of AChBP and the transmembrane domain of the Torpedo receptor snugly fit together when assembled. This structural complementarity probably results from the method used to produce the structure of the transmembrane domain in which the determination of the position of the atoms was made in the presence of the atoms of the structure 1I9B (AChBP).

So far, few structural data have been collected at the interface between the two domains. Experiments on the GABA-A receptor α1 and β2 subunits have identified pairs of residues that are sufficiently close to each other, when mutated to cysteine, to allow a disulfide bond with the oxidizing agent Cu:phenantroline (Kash et al., 2003), suggesting that they are distant of <15 Å in the three-dimensional structure (Careaga and Falke, 1992). These reactions preserved a functional channel, and occurred both in the presence and absence of the agonist GABA. The identified pairs were α1D57/α1H2797, β2D56/β2K274, β2D139/β2K274, and β2D146/β2K274 (homologous to α7 N45/A261, V47/A261, D128/A261, and D133/A261; Kash et al., 2004, 2003). Investigation of these different pairs of residues within our model (Fig. 7 A) showed a pattern of distances (12.5, 14.5, 16, and 13.5 Å, respectively; see Fig. 7 A) that are consistent with the formation of disulfide bonds. Given the phylogenic distance between the GABA-A and nAChRs, our model thus reasonably accounts for these disulfide cysteine experiments.

FIGURE 7.

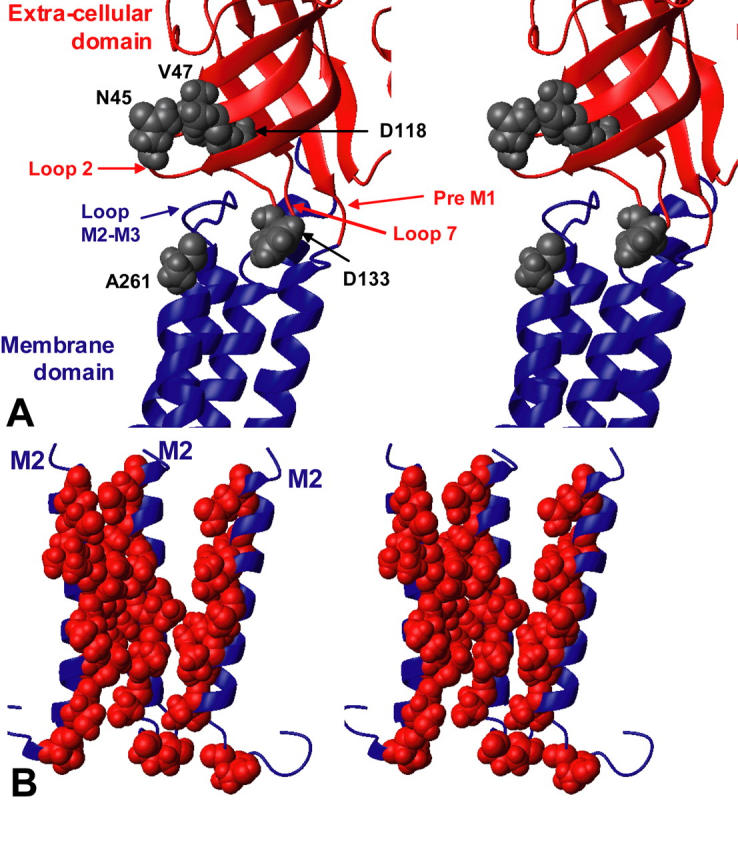
FIGURE 7

Open in a new tab

(A) Coupling zone between the extracellular and the membrane domains. The residues homologous to those identified on the GABA-A receptor (Kash et al., 2004, 2003) are represented in gray. (B) Three M2 segments on which the residues exposed to the solvent (262, 258, 255, 251, 248, 244, and 241) as identified by SCAM (Wilson and Karlin, 2001) and affinity labeling (Corringer et al., 2000) experiments are represented in red.

Analysis of the transmembrane domains

Since our model does not involve any dramatic reorganization of the transmembrane domain, it accounts for the wealth of biochemical data previously reviewed by the authors of the original model (Miyazawa et al., 2003). Noticeably, 1), the protein-lipid interface is mainly contributed by the M3 and M4 segments, but also by a portion of the M1 segment (Blanton and Cohen, 1994); and 2), the ion channel is contributed by one side of the five M2 transmembrane helices (Giraudat et al., 1986). The solvent-accessible residues as highlighted by SCAM (Wilson and Karlin, 2001) and affinity labeling (Corringer et al., 2000) experiments are shown on the structure of M2 segment that surround the channel pore (Fig. 7 B). In our model, as expected, these residues are also exposed to the channel.

Comparison of the conformational changes from the first mode with experimental data

Having established a reasonable model of the extracellular and transmembrane domains of the α7 receptor, the aim of our study was to provide insights into the gating mechanism. Our approach is based on the assumption that the regions easily deformed within the model are likely to contribute to the gating mechanisms in the presence of agonists, a feature that has been extensively documented for other proteins. Among the first 10 normal modes, only that of the lowest frequency produces realistic deformations. We point out that the lowest-frequency normal mode is the one associated with the largest possible amplitude leading to the largest possible rearrangement, because, at a given temperature, the amplitude of each mode is inversely proportional to its frequency. Furthermore, this mode is also found in the normal mode analysis on an asymmetric version of structure 0 (which is closer to the templates used to build the model), indicating that the structural flexibility associated with this mode is independent of the fine structural details of the model.

To analyze this mode, we generated two structures, called 1C (closed) and 1O (open), each displaying a RMSD of 3 Å from structure 0. These structures are therefore not aimed at representing a particular allosteric conformation of the receptor, but were built to highlight the structural reorganizations associated with mode 1. This mode accounts for an opening of the pore caused by a global conformational reorganization of the protein, providing new insights into the regions of the protein which are able to participate in the gating mechanism. In this section, we will confront the first mode to the main experimental data that were published on the conformational reorganization of the protein.

Extracellular domain

The structural reorganizations underlying the opening transition were previously followed by electron microscopy of the Torpedo receptor. Using fast application of a high concentration of ACh followed by rapid freeze-trapping of the protein, electron density maps at 9 Å resolution were recorded for the open conformation, and compared to those obtained in the absence of ACh (Unwin, 1995). Later, a rigid body fitting of AChBP was performed in the electron microscopy density maps obtained in the absence or presence of acetylcholine (Unwin et al., 2002). Within the extracellular domain, strong asymmetry was observed for the closed conformation, and the two α-subunits underwent a major structural reorganization upon activation, which mainly consists of a 15° tilt of the inner β-sheet that renders the protein more symmetric.

A common feature of mode 1 and the electron microscopy experiments is a similar increase in the angle between the internal and external β-sheets in the course of activation, although the transition is symmetrical in our homomeric receptor, unlike the one reported on the heteromeric Torpedo receptor. Another difference is that the first mode mobilizes the entire extracellular domain (in fact, the entire receptor), whereas the transition described in Unwin (1993) includes only local changes in the internal β-sheet. In the structure 1O, the angle between both β-sheets was ∼13 degrees, very close to the 15° value found by Unwin et al. ( 2002). It should be noted that this result depends on the amplitude of the mode amplification. Because our model satisfactorily reproduces this experimental result, the amplitude of the mode amplification is reasonable.

Membrane domain

The structural reorganization associated with the first mode accounts for major features for the channel opening investigated using affinity labeling and site-directed mutagenesis. In particular, the 1C→1O transition is not associated with any dramatic change in the orientation of the M2 helix relative to the ion channel, as deduced from affinity labeling and SCAM experiments (Corringer et al., 2000; Wilson and Karlin, 2001). In addition, a particular residue from the M1 segment has been suggested to line the pore. Indeed, the reaction of a mutated cysteine at this position with a positively charged reagent was dependent on the membrane potential. The reaction occurred in the presence of ACh, suggesting that it is accessible to the pore only in the open state of the channel. This residue is positioned at the extracellular end of M1 (Val-229 of the muscle β-subunit homologous to Leu-213 in our model; Zhang and Karlin, 1997). Interestingly, our models nicely reproduce these data, since this residue faces the pore in the 1O conformation, whereas it is inaccessible in the 1C conformation.

In contrast, the interpretation of the electron microscopy experiments is still a matter of controversy. The analysis of the electron densities maps of the Torpedo receptor obtained in the absence and presence of ACh have indeed been interpreted in terms of a symmetrical reorganization, but either a single rigid body rotation of M2 (Unwin, 1995), or a twist motion of the M2 segment as been proposed (Sansom, 1995). In any case, using an RMS-fit procedure, we identified a set of residues involved in a collective movement composed of the internal β-sheet of the extracellular domain and the M2 helix of the membrane domain. This idea is thus in agreement with the proposal that the M2 helix moves independently from the other helices and is coupled to the movement of the internal β-sheet (Unwin, 2003).

Symmetry of the movement

The conformational transition associated with the first mode has been found to concern all subunits together, to be all-or-none and thus preserve the symmetry of the molecule. Given the amplitude and the direction of the movement described here, it is difficult to imagine how one subunit could make the transition alone. This feature contrasts with the conclusions of the analysis of the electron microscopy data collected in the presence or absence of ACh with Torpedo nAChRs, which point to an asymmetric motion within the extracellular domain (Unwin et al., 2002). Such an asymmetry has also been suggested from mutagenesis studies on heteromeric nAChR (Mitra et al., 2004; Chakrapani et al., 2004) and GABA-A (Kash et al., 2004). Therefore, it is possible that the heteromeric nature of the Torpedo receptor causes a significantly different structural reorganization than homomeric receptor, especially at the level of the asymmetrically distributed ACh binding sites.

It is noteworthy that symmetrical reorganizations has been consistently observed for the opening mechanism of several ion channels. First, the pentameric mechanosensitive channel MscL, using the same normal mode analysis as described here in Methods, opens through a symmetrical reorganization consisting of an irislike movement involving both twist and tilt rotation (Valadie et al., 2003). Second, in the case of the potassium channel KcsA, a symmetrical kink of the internal helix at the level of a conserved Gly residue has been suggested to produce channel opening (MacKinnon, 2003).

The normal-mode analysis study presented here was performed in the absence of ligand. Yet, the nicotinic ligands, which are small, are not anticipated to significantly modify the force field and therefore the results of normal mode analysis. The gating mechanism might therefore be an intrinsic property of the protein architecture rather than induced by the presence of ligand (see Xu et al., 2003, for a similar result obtained on hemoglobin). This suggests that the mechanism is compatible with the MWC theory. Therefore, our theoretical work matches experimental evidences from multiple sources showing that equilibrium of pre-existing states is more realistic than sequential induced fit (see Goh et al., 2004, for a review on the topic).

CONCLUSION AND PERSPECTIVE

We present in this article a three-dimensional model of the α7 nicotinic acetylcholine receptor obtained by comparative modeling. Yet, the model structure obtained cannot be of higher quality than the structures used as templates for the comparative modeling (2.7 and 4 Å, respectively). It has not reached an atomic resolution, which prevents, at this stage, performing calculations that require high quality structures (electrostatics interactions and/or surface complementarity for docking, for example).

To explore its conformational space, the model was subjected to normal mode analysis based on a highly simplified representation of proteins that has proved very efficient in other studies of the same kind (Krebs et al., 2002, Valadie et al., 2003). A wide opening of the channel pore was observed in the first mode. This mode associates tertiary and quaternary changes, leading to a macroscopic quaternary twist movement of the protein. These results have shown good agreement with experimental data from cysteine accessibility, affinity labeling, and electron microscopy experiments.

Further studies are needed, in particular to test the model structures and predictions described above. Studies measuring the proximity of various residues as a function of the state of the receptor, such as those performed on the GABA receptor, would probably allow further testing for the details of the conformational changes. Site-directed mutagenesis experiments probing the ability of substituted cysteines/histidines to bind metals should also help to test the surface of the receptor at various levels and lead to the refinement of the models, as very recently shown on the μ-opioid receptor (Fowler et al., 2004). Further modeling will be performed using novel structures of AChBP in the presence of ligands recently released in the Protein DataBank (Celie et al., 2004), or that should be released in the future. It might also be of interest to fit the models directly in the electron densities maps derived from electron microscopy.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Supplementary Material

[Supplemental File]
biophysj_104.050229_index.html (877B, html)

Acknowledgments

We thank Dr. Stuart Edelstein and Brian Molles for careful reading of the manuscript and Nicolas Maubourguet for his help with the calculation of the distance-differences matrices.

A.T. is the recipient of a fellowship from the Association Française contre les Myopathies. This work was supported by the Collège de France, the Commission of the European Communities, the Association pour la Recherche sur le Cancer, and the Association Française contre les Myopathies.

References

  1. Bahar, I. 1999. Dynamics of proteins and biomolecular complexes: inferring functional motions from structure. Rev. Chem. Eng. 15:319–349. [Google Scholar]
  2. Bahar, I., A. R. Atilgan, and B. Erman. 1997. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 2:173–181. [DOI] [PubMed] [Google Scholar]
  3. Blanton, M. P., and J. B. Cohen. 1994. Identifying the lipid-protein interface of the Torpedo nicotinic acetylcholine receptor: secondary structure implications. Biochemistry. 33:2859–2872. [DOI] [PubMed] [Google Scholar]
  4. Brejc, K., W. J. van Dijk, R. V. Klaassen, M. Schuurmans, J. van Der Oost, A. B. Smit, and T. K. Sixma. 2001. Crystal structure of an ACh-binding protein reveals the ligand-binding domain of nicotinic receptors. Nature. 411:269–276. [DOI] [PubMed] [Google Scholar]
  5. Brooks, B., and M. Karplus. 1983. Harmonic dynamics of proteins: normal modes and fluctuations in bovine pancreatic trypsin inhibitor. Proc. Natl. Acad. Sci. USA. 80:6571–6575. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
  7. Careaga, C. L., and J. J. Falke. 1992. Thermal motions of surface α-helices in the D-galactose chemosensory receptor. Detection by disulfide trapping. J. Mol. Biol. 226:1219–1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Celie, P. H., S. E. van Rossum-Fikkert, W. J. van Dijk, K. Brejc, A. B. Smit, and T. K. Sixma. 2004. Nicotine and carbamylcholine binding to nicotinic acetylcholine receptors as studied in AChBP crystal structures. Neuron. 41:907–914. [DOI] [PubMed] [Google Scholar]
  9. Chang, C. S., R. Olcese, and R. W. Olsen. 2003. A single M1 residue in the β2 subunit alters channel gating of GABAA receptor in anesthetic modulation and direct activation. J. Biol. Chem. 278:42821–42828. [DOI] [PubMed] [Google Scholar]
  10. Changeux, J. P., and S. J. Edelstein. 1998. Allosteric receptors after 30 years. Neuron. 21:959–980. [DOI] [PubMed] [Google Scholar]
  11. Chakrapani, S., T. D. Bailey, and A. Auerbach. 2004. Gating dynamics of the acetylcholine receptor extracellular domain. J. Gen. Physiol. 123:341–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Chou, K. C. 2004. Modelling extracellular domains of GABA-A receptors: subtypes 1, 2, 3, and 5. Biochem. Biophys. Res. Commun. 316:636–642. [DOI] [PubMed] [Google Scholar]
  13. Corringer, P. J., N. Le Novere, and J. P. Changeux. 2000. Nicotinic receptors at the amino acid level. Annu. Rev. Pharmacol. Toxicol. 40:431–458. [DOI] [PubMed] [Google Scholar]
  14. Delarue, M., and Y. H. Sanejouand. 2002. Simplified normal mode analysis of conformational transitions in DNA-dependent polymerases: the elastic network model. J. Mol. Biol. 320:1011–1024. [DOI] [PubMed] [Google Scholar]
  15. Durand, P., G. Trinquier, and Y. H. Sanejouand. 1994. A new approach for determining low-frequency normal modes in macromolecules. Biopolymers. 34:759. [DOI] [PubMed] [Google Scholar]
  16. Fowler, C. B., I. D. Pogozheva, H. Levine 3rd, and H. I. Mosberg. 2004. Refinement of a homology model of the μ-opioid receptor using distance constraints from intrinsic and engineered zinc-binding sites. Biochemistry. 43:8700–8710. [DOI] [PubMed] [Google Scholar]
  17. Fuchs, S., R. Kasher, M. Balass, T. Scherf, M. Harel, M. Fridkin, J. L. Sussman, and E. Katchalski-Katzir. 2003. The binding site of acetylcholine receptor: from synthetic peptides to solution and crystal structure. Ann. NY Acad. Sci. 998:93–100. [DOI] [PubMed] [Google Scholar]
  18. Giraudat, J., M. Dennis, T. Heidmann, J. Y. Chang, and J. P. Changeux. 1986. Structure of the high-affinity binding site for noncompetitive blockers of the acetylcholine receptor: Serine-262 of the δ-subunit is labeled by [3H]chlorpromazine. Proc. Natl. Acad. Sci. USA. 83:2719–2723. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Go, N., T. Noguti, and T. Nishikawa. 1983. Dynamics of a small globular protein in terms of low-frequency vibrational modes. Proc. Natl. Acad. Sci. USA. 80:3696–3700. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Goh, C. S., D. Milburn, and M. Gerstein. 2004. Conformational changes associated with protein-protein interactions. Curr. Opin. Struct. Biol. 14:104–109. [DOI] [PubMed] [Google Scholar]
  21. Hinsen, K. 1998. Analysis of domain motions by approximate normal mode calculations. Proteins. 33:417–429. [DOI] [PubMed] [Google Scholar]
  22. Hinsen, K., A. Thomas, and M. J. Field. 1999. Analysis of domain motions in large proteins. Proteins. 34:369–382. [PubMed] [Google Scholar]
  23. Husain, S. S., M. R. Ziebell, D. Ruesch, F. Hong, E. Arevalo, J. A. Kosterlitz, R. W. Olsen, S. A. Forman, J. B. Cohen, and K. W. Miller. 2003. 2-(3-Methyl-3H-diaziren-3-yl)ethyl 1-(1-phenylethyl)-1H-imidazole-5-carboxylate: a derivative of the stereoselective v for photolabeling ligand-gated ion channels. J. Med. Chem. 46:1257–1265. [DOI] [PubMed] [Google Scholar]
  24. Kash, T. L., M. J. Dizon, J. R. Trudell, and N. L. Harrison. 2004. Charged residues in the β2 subunit involved in GABAA receptor activation. J. Biol. Chem. 279:4887–4893. [DOI] [PubMed] [Google Scholar]
  25. Kash, T. L., A. Jenkins, J. C. Kelley, J. R. Trudell, and N. L. Harrison. 2003. Coupling of agonist binding to channel gating in the GABA(A) receptor. Nature. 421:272–275. [DOI] [PubMed] [Google Scholar]
  26. Katz, B., and S. Thesleff. 1957. A study of the desensitization produced by acetylcholine at the motor end-plate. J. Physiol. 138:63–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Krebs, W. G., V. Alexandrov, C. A. Wilson, N. Echols, H. Yu, and M. Gerstein. 2002. Normal mode analysis of macromolecular motions in a database framework: developing mode concentration as a useful classifying statistic. Proteins. 48:682–695. [DOI] [PubMed] [Google Scholar]
  28. Le Novere, N., P. J. Corringer, and J. P. Changeux. 1999. Improved secondary structure predictions for a nicotinic receptor subunit: incorporation of solvent accessibility and experimental data into a two-dimensional representation. Biophys. J. 76:2329–2345. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Le Novere, N., T. Grutter, and J. P. Changeux. 2002. Models of the extracellular domain of the nicotinic receptors and of agonist- and Ca2+-binding sites. Proc. Natl. Acad. Sci. USA. 99:3210–3215. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Li, G., and Q. Cui. 2002. A coarse-grained normal mode approach for macromolecules: an efficient implementation and application to Ca2+-ATPase. Biophys. J. 83:2457–2474. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. MacKerell, A. D. J., B. Brooks, C. L. I. Brooks, L. Nilsson, B. Roux, Y. Won, and M. Karplus. 1998. CHARMM: the energy function and its parameterization with an overview of the program. In The Encyclopedia of Computational Chemistry. John Wiley & Sons, Chichester, UK. 271–277.
  32. MacKinnon, R. 2003. Potassium channels. FEBS Lett. 555:62–65. [DOI] [PubMed] [Google Scholar]
  33. Marques, O., and Y. H. Sanejouand. 1995. Hinge-bending motion in citrate synthase arising from normal mode calculations. Proteins. 23:557–560. [DOI] [PubMed] [Google Scholar]
  34. Mitra, A., T. D. Bailey, and A. L. Auerbach. 2004. Structural dynamics of the M4 transmembrane segment during acetylcholine receptor gating. Structure. 12:1909–1918. [DOI] [PubMed] [Google Scholar]
  35. Miyazawa, A., Y. Fujiyoshi, and N. Unwin. 2003. Structure and gating mechanism of the acetylcholine receptor pore. Nature. 423:949–955. [DOI] [PubMed] [Google Scholar]
  36. Monod, J., J. Wyman, and J. P. Changeux. 1965. On the nature of allosteric transitions: a plausible model. J. Mol. Biol. 12:88–118. [DOI] [PubMed] [Google Scholar]
  37. Mouawad, L., and D. Perahia. 1993. DIMB: diagonalization in a mixed basis: a method to compute low-frequency normal modes for large macromolecules. Biopolymers. 33:569–611. [Google Scholar]
  38. Paas, Y., J. Cartaud, M. Recouvreur, R. Grailhe, V. Dufresne, E. Pebay-Peyroula, E. M. Landau, and J. P. Changeux. 2003. Electron microscopic evidence for nucleation and growth of three-dimensional acetylcholine receptor microcrystals in structured lipid-detergent matrices. Proc. Natl. Acad. Sci. USA. 100:11309–11314. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Perutz, M. F. 1989. Mechanisms of cooperativity and allosteric regulation in proteins. Q. Rev. Biophys. 22:139–237. [DOI] [PubMed] [Google Scholar]
  40. Rudolph, U., and H. Mohler. 2004. Analysis of GABAA receptor function and dissection of the pharmacology of benzodiazepines and general anesthetics through mouse genetics. Annu. Rev. Pharmacol. Toxicol. 44:475–498. [DOI] [PubMed] [Google Scholar]
  41. Sali, A., and T. L. Blundell. 1993. Comparative protein modelling by satisfaction of spatial restraints. J. Mol. Biol. 234:779–815. [DOI] [PubMed] [Google Scholar]
  42. Sansom, M. S. 1995. Ion-channel gating. Twist to open. Curr. Biol. 5:373–375. [DOI] [PubMed] [Google Scholar]
  43. Schapira, M., R. Abagyan, and M. Totrov. 2002. Structural model of nicotinic acetylcholine receptor isotypes bound to acetylcholine and nicotine. BMC Struct. Biol. 2002;2(1):1. Epub 2002 Jan 18. [DOI] [PMC free article] [PubMed]
  44. Sixma, T. K., and A. B. Smit. 2003. Acetylcholine binding protein (AChBP): a secreted glial protein that provides a high-resolution model for the extracellular domain of pentameric ligand-gated ion channels. Annu. Rev. Biophys. Biomol. Struct. 32:311–334. [DOI] [PubMed] [Google Scholar]
  45. Tama, F. 2003. Normal mode analysis with simplified models to investigate the global dynamics of biological systems. Protein Pept. Lett. 10:119–132. [DOI] [PubMed] [Google Scholar]
  46. Tama, F., and C. L. Brooks, III. 2002. The mechanism and pathway of pH-induced swelling in Cowpea Chlorotic Mottle virus. J. Mol. Biol. 318:733–747. [DOI] [PubMed] [Google Scholar]
  47. Tama, F., F. X. Gadea, O. Marques, and Y. H. Sanejouand. 2000. Building-block approach for determining low-frequency normal modes of macromolecules. Proteins. 41:1–7. [DOI] [PubMed] [Google Scholar]
  48. Tama, F., and Y. H. Sanejouand. 2001. Conformational change of proteins arising from normal mode calculations. Protein Eng. 14:1–6. [DOI] [PubMed] [Google Scholar]
  49. Thompson, J. D., T. J. Gibson, F. Plewniak, F. Jeanmougin, and D. G. Higgins. 1997. The CLUSTAL_X WINDOWS interface: flexible strategies for multiple sequence alignment aided by quality analysis tools. Nucleic Acids Res. 25:4876–4882. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Tirion, M. M. 1996. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 77:1905–1908. [DOI] [PubMed] [Google Scholar]
  51. Unwin, N. 1993. Nicotinic acetylcholine receptor at 9 Å resolution. J. Mol. Biol. 229:1101–1124. [DOI] [PubMed] [Google Scholar]
  52. Unwin, N. 1995. Acetylcholine receptor channel imaged in the open state. Nature. 373:37–43. [DOI] [PubMed] [Google Scholar]
  53. Unwin, N. 2003. Structure and action of the nicotinic acetylcholine receptor explored by electron microscopy. FEBS Lett. 555:91–95. [DOI] [PubMed] [Google Scholar]
  54. Unwin, N., A. Miyazawa, J. Li, and Y. Fujiyoshi. 2002. Activation of the nicotinic acetylcholine receptor involves a switch in conformation of the α-subunits. J. Mol. Biol. 319:1165–1176. [DOI] [PubMed] [Google Scholar]
  55. Valadie, H., J. J. Lacapere, Y. H. Sanejouand, and C. Etchebest. 2003. Dynamical properties of the MscL of Escherichia coli: a normal mode analysis. J. Mol. Biol. 332:657–674. [DOI] [PubMed] [Google Scholar]
  56. Wilson, G., and A. Karlin. 2001. Acetylcholine receptor channel structure in the resting, open, and desensitized states probed with the substituted-cysteine-accessibility method. Proc. Natl. Acad. Sci. USA. 98:1241–1248. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Xu, C., D. Tobi, and I. Bahar. 2003. Allosteric changes in protein structure computed by a simple mechanical model: hemoglobin T<→R2 transition. J. Mol. Biol. 333:153–168. [DOI] [PubMed] [Google Scholar]
  58. Zhang, H., and A. Karlin. 1997. Identification of acetylcholine receptor channel-lining residues in the M1 segment of the β-subunit. Biochemistry. 36:15856–15864. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplemental File]
biophysj_104.050229_index.html (877B, html)
Download video file (4.1MB, mpg)
Download video file (3.2MB, mpg)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES