The Kinetics of Phase Separation in Asymmetric Membranes

Abstract

Phase separation in a model asymmetric membrane is studied using Monte Carlo techniques. The membrane comprises two species of particles, which mimic different lipids in lipid bilayers and separately possess either zero or non-zero spontaneous curvatures. We study the influence of phase separation on membrane shape and the influence of the coupling of composition and height dynamics on phase separation and domain growth, via both the degree of shape asymmetry and relative kinetic coefficients for height relaxation.

INTRODUCTION

There is an increasing amount of evidence that the plasma membrane of many cells is heterogeneous (Friedrichson and Kurzchalia, 1998; Harder et al., 1998; Pralle et al., 2000; Varma and Mayor, 1998). One type of membrane heterogeneity, termed “rafts,” are enriched in cholesterol, saturated lipids such as sphingomyelin and glycosphingolipids, and certain membrane proteins (Simons and Ikonen, 1997; Simons and Toomre, 2000). They have putative roles in regulating many cell functions, including signaling, endocytosis, apoptosis, protein organization, and lipid regulation (Anderson and Jacobson, 2002; de Jong et al., 1997; Edidin, 2001; Simons and Ikonen, 1997; Thomas et al., 1994).

Raft formation in plasma membranes is a complex issue. Not only is the composition of the plasma membrane of living eukaryotic cells extremely complex, consisting of up to 500 different lipid species and numerous proteins, but the plasma membrane is also structurally and dynamically coupled to the extracellular matrix and the cytoskeleton network (Mayor and Rao, 2004). However, raft formation can be driven by lipid-lipid interactions. Evidence for this comes from model membrane studies in which a mixture of a saturated lipid, an unsaturated lipid, and cholesterol can exhibit phase coexistence (Dietrich et al., 2001; Lawrence et al., 2003; Veatch and Keller, 2003). In this case the unsaturated lipid assumes the role of nonraft lipids, because the nonraft region of a membrane is enriched in phosphatidylcholine, which typically has a saturated and an unsaturated acyl chain (Barenholz and Thompson, 1999; Shinitzky, 1984). The unsaturated acyl chain contains one or more double bonds of the cis configuration (Barenholz and Thompson, 1999; Shinitzky, 1984), which produces “kinks” and prevents the lipids from close packing. Lipids in membrane rafts, on the other hand, are more ordered owing to their saturated acyl chains facilitating close packing. The saturated nature of raft lipids is thought to promote their interaction with cholesterol (Brown and London, 1998). The ordered (raft) phase can range in size from the nanometer to the micron scale (Silvius, 2003).

There is no current agreement on the size of rafts in living cells (Devaux and Morris, 2004), but the consensus is that their sizes are smaller than the optical diffraction limit (250 nm) (Kusumi et al., 2004). For example, clusters of specific proteins thought to be raft components have been estimated to be <70 nm in size (Friedrichson and Kurzchalia, 1998; Varma and Mayor, 1998). However, Gaus et al. (2003) observed that domains of higher acyl-chain alignment in living cell macrophages appeared to be of the order of micrometers. They propose that either individual rafts could be clustering together or that raft sizes in macrophages has been previously underestimated. It is well known that the plasma membrane of eukaryotic cells is asymmetric, with phosphatidylserine and phosphatidylethanolamine predominantly found on the inner leaflet, and phosphatidylcholine, sphingomyelin, and glycosphingolipids predominantly, if not exclusively, found on the outer leaflet (Devaux, 1991). Hence, membrane components in rafts in biological membranes are likely to be asymmetrically distributed across the bilayer. Furthermore, sphingolipid headgroups occupy larger areas in the plane of the outer leaflet than their predominantly saturated acyl chains (Simons and Ikonen, 1997). This leads to these lipids packing as a truncated cone (Israelachvili, 1998). Given that there is a likely asymmetric distribution of membrane components across the bilayer of rafts and the geometries of the components facilitate membrane bending, it is reasonable to assume that rafts have a spontaneous curvature. A recent two-photon microscopy experiment performed on living cells indeed suggests that membrane domains do have curvature (Gaus et al., 2003). This spontaneous curvature sets a length scale for domains given by the radius of curvature. Therefore it is possible that the spontaneous curvature of rafts may limit their size in living cells. However, model membranes tend to have a symmetric distribution of membrane components across the bilayer (Devaux and Morris, 2004), and so, theoretically, the maximum length scale of a domain is set by the system size. In practice, however, the domain size in this case is limited by slow coarsening.

There have been many studies in the past decade of the influence of bending and spontaneous curvature on the morphology of membranes. Lipowsky (1992) in particular studied budding in a simple model of a domain of spontaneously curved material in a flat matrix. He showed that the instability to budding is governed by the competition between line tension of the domain edge and the bending energy of the domain, where an increase in line tension leads to a more budded domain. However, surprisingly, this work did not consider the effect of frame tension on domain morphology. Jülicher and Lipowsky (1993, 1996) later studied the energetics and shapes of budding of single or few domains on vesicles in much detail. Experiments performed around the same time include work by Kas and Sackmann (1991) and Döbereiner et al. (1993). They observed rich shape-transition behavior, including domain-induced budding, in multicomponent lipid bilayer membranes. Recently Baumgart et al. (2003) visualized coexisting liquid phases in giant unilamellar vesicles via fluorescence imaging. They used two dyes that preferentially labeled different fluid phases in a ternary system, comprising sphingomyelin, dioleoylphosphatidylcholine, and cholesterol, hence providing a correlation between domain composition and curvature. They followed the model of Jülicher and Lipowsky (1996) to extract the line tension between coexisting liquid domains in the absence of spontaneous curvature. They observed domain ordering over the entire vesicle that corresponded to the curvature pattern of the domains. If these domains were in a fluid phase and were surrounded by a gel matrix, then one possible mechanism for domain curvature is that the more flexible fluid phase will bend. However, in that study, the bending moduli of the domains were approximately equal; and since there was no spontaneous curvature, bending energy must not be responsible for domain curvature.

The static morphology of domains in the high concentration limit has been well studied, and a variety of striped and hexagonal structures have been predicted as a function of composition, degree of segregation, and different elastic constants of the separate phases (Andelman et al., 1992; Gozdz and Gompper, 2001; Guttman and Andelman, 1993; Harden and MacKintosh, 1994; Kawakatsu et al., 1993; Taniguchi et al., 1994). More recently, the dynamics of multicomponent membranes has been explored. Kumar and Rao (1998) introduced an off-lattice kinetic Monte Carlo technique for studying the dynamics of multicomponent membranes in vesicle form. More recently, Chen (2004) studied membrane shape instabilities in active membranes. Hansen et al. (1998) addressed the effects of intermonolayer coupling both on the lateral ordering processes and the conformational behavior of the bilayer membrane. The intermonolayer coupling was represented by a term that incorporates the spontaneous curvature. They show a variety of phase diagrams including both symmetric and transversely asymmetric phase-separated states with different degrees of bilayer undulation. Laradji and Kumar (2004) recently studied domain coarsening in multicomponent bilayer fluid vesicles via dissipative particle dynamics in the absence of spontaneous curvature. Their study is novel since it considers hydrodynamic effects and area/volume constraints. They found that flat circular domains form initially regardless of the area/volume ratio. At later times, budding that leads to vesiculation was observed when there is excess area, in order to reduce line tension. For the case where there was no excess area, coarsening proceeded mainly via coalescence of flat circular patches.

In this article we study how the spontaneous curvature and associated bending (curvature) of phase-separated domains under an applied frame tension control both their morphology and evolution. We represent a membrane as a binary mixture of U and S particles, respectively representing unsaturated and saturated lipids. To implicitly treat a bilayer, a particle represents an assumed local compositional difference between two leaflets of a bilayer, and hence we assume locked monolayers. This single layer model corresponds to a quench into the transversely asymmetric HO2 state in the work by Hansen et al. (1998). Our approximation is expected to fail for short times because of interlayer friction, and one can, in principle, have much richer dynamics in which phase separation within the two monolayers is either coupled or uncoupled, depending on the lipid environments of the two monolayers. We leave these complications for the future, but see recent work by Sens (2004) addressing budding induced by adding excess lipids to one leaflet, which leads to a competition between bending and intermonolayer diffusion. To model the spontaneous curvature of the domains, the membrane is assumed to have a local spontaneous curvature proportional to the area fraction of S particles. Note that in reality, however, either saturated or unsaturated lipids can induce a spontaneous curvature in a membrane since this merely reflects the degree of asymmetry across the bilayer, which is determined by the local environment of the two leaflets.

The summary of this article is as follows. In Morphology of Domains, we use a simple analytic model of a spherical cap in a background matrix to study the expected transition to budding and raftlike (nonbudded domains) as a function of frame tension, line tension, and bending energy. This complements and duplicates more detailed recent (largely numerical) work on budding in homogeneously phase-separated domains (Gozdz and Gompper, 2001; Harden and MacKintosh, 1994; Kumar et al., 2001), and also sets the scene for the relevant parameter range to be explored numerically. In this section we also simulate the morphology and membrane shapes as a function of different degrees of phase separation, both coarsening extent and composition difference between phases. Then, in Continuum Theory for Coarsening of Domains, we study the evolution of height and composition degrees of freedom within a continuum model, following the classical theories of spinodal decomposition coupled to height fluctuations. We compare membranes that relax by either permeable or impermeable dynamics, and explore how height fluctuations can speed up coarsening and influence the length scales. We then present our Conclusions.

MORPHOLOGY OF DOMAINS

Macroscopic model

Initially we study how the competition between the energetic features within a membrane control the shape of domains. To do this we use a macroscopic model. The free energy G of the membrane comprises three terms: the line energy, the bending energy, and the frame energy. The line energy is given by

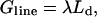(1)

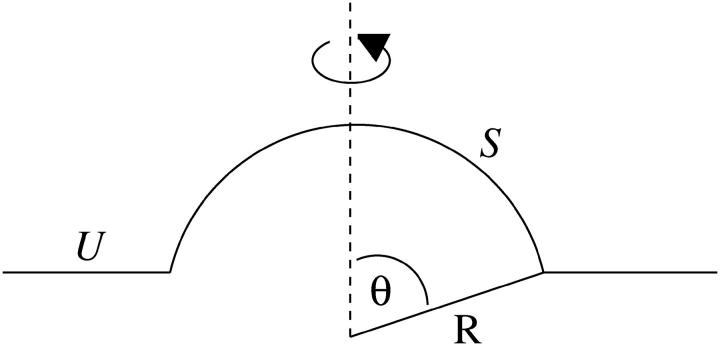
where λ is the line tension and L_d is the length of the domain edge. For a flat circular domain, the length of the domain edge is given by 2πR, where R is the radius. However, this does not correspond to the lowest line energy since it can be reduced through the domain becoming budded (Lipowsky, 1992); see Fig. 1.

FIGURE 1.

Possible domain shapes.

Such domain shapes shown in Fig. 1 can incur a bending energy, given by

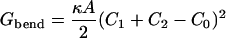(2)

(Boal, 2002), where κ is the bending rigidity, A is the surface area of the domain, C₁ and C₂ are the principal curvatures of the domain, and C₀ is the domain's spontaneous curvature. The domain has a minimal bending energy if its curvature is equal to the spontaneous curvature. We have neglected the Gaussian bending energy, which would give rise to an effective shape-dependent line tension at the interface between domains, proportional to the difference in Gaussian curvature moduli. However, we are interested in how the spontaneous curvature influences the morphology and evolution of domains, and thus consider identical curvature moduli in both phases.

Finally, frame tension in the membrane suppresses membrane deviations from the flat state. Frame tension arises because the membrane is assumed to be part of a larger system, i.e., a vesicle or a cell. The work done against the frame tension is given by

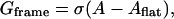(3)

where σ is the frame tension and A_flat is the projected area of the S domain onto the flat plane.

We define the dimensionless quantities,

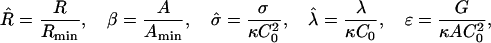(4)

where G = G_line + G_bend + G_frame, and R_min = 2/C₀ and 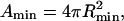are the domain radius and area, respectively, that minimize the bending energy. With this notation, the total energy now has the form

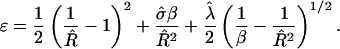(5)

We now calculate the shape of a domain of S particles within a U membrane as a function of 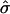and β. We assume an ideal spherically curved S domain and a flat U domain (Fig. 2), and neglect thermal fluctuations and the elastic interactions between the U and S domains. This will give a lower limit on the domain free energy, since a physical system will relax the sharp interface between phases. More precise shapes have been calculated previously (Harden and MacKintosh, 1994; Lipowsky, 1992), but this calculation gives a serviceable estimate of the boundaries between different shapes.

FIGURE 2.

Spherically curved raftlike domain comprising S particles within a flat U membrane.

Minimizing Eq. 5 with respect to gives

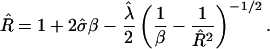(6)

A fully formed bud occurs when cos θ = – 1, where cos θ is given by

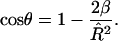(7)

Hence the condition for a bud is 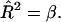Substituting this into Eq. 6 gives

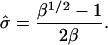(8)

Therefore, the maximum value of 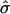allowable to form a bud is 0.125. Substituting average values for the lateral tension (∼10⁻⁴ m Nm⁻¹) and the bending modulus (∼10⁻¹⁹ J) from Baumgart et al. (2003) into the expression for 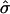shown in Eq. 4 leads to a minimum value of spontaneous curvature required to form a bud of 2.83 μm⁻¹. In this particular case, domains that have a flat radius R_domain > 2.83 μm will form a bud, using the expression for β in Eq. 4 and given that R_min = 2/C₀.

For a raft, cos θ ≥ 0, giving the condition 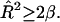Substituting this into Eq. 6 gives

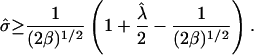(9)

Eqs. 8 and 9 define the shape of the S domain as a function of 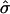and β (Fig. 3).

FIGURE 3.

Shape diagram illustrating bud, budding, and raft regimes for an S domain within a flat U membrane as a function of reduced area β and frame tension for different reduced line tension 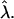Raft line (solid); bud line (dotted).

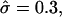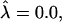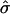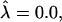For β = 4, and a domain would be in the raft regime. Reducing at constant β causes the domain to bud, and eventually leave the membrane. Similarly, for β = 0.5, and a domain would be in the raft regime. Increasing β at constant 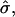i.e., due to coarsening after a quench into the phase coexistence region, causes the domain to enter the budding regime before re-entering the raft regime. This re-entry into the raft regime arises because the bending energy per unit area A of a domain is independent of A and the applied frame energy per unit area is linear in A (Eq. 5). Therefore for small A the bending energy dominates and the system favors a curvature approximately equal to C₀. As A increases, the tension term dominates, which reduces the height of the domain. Upon increasing the raft line shifts toward higher and lower β. Hence, the length of the domain boundary decreases in order to reduce the line energy. This causes the domain to approach or enter the budding regime. Whether the re-entrant regime would be reached during coarsening depends on the relative kinetics of height growth and coarsening; in all likelihood the budding regime would intervene kinetically. The bud line does not depend on 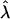since this is where the length of the domain edge becomes zero. Our study is consistent with Lipowsky's study of domain budding (Lipowsky, 1992) in the zero frame tension limit, but the re-entry behavior at finite frame tension is new.

Mesoscopic model

We now investigate how the competition among the bending energy, the frame energy, and the interaction energy between the U and S particles leads to different morphological domains for a mesoscopic model. We model the bilayer as a two-dimensional lattice with sides of length L. Each lattice site is occupied by one of the two types of particles, U or S, of equal area a². The particles have two degrees of freedom; they can laterally exchange positions with neighboring particles, and can change their height h(x, y). We adopt the Monge representation of a single-valued height h(x, y), which prohibits overhangs. All energies are measured in units of k_BT and all lengths are measured in units of the lattice spacing a. Particle height changes are selected randomly between ±0.13a since this gave rise to acceptance percentages of order 20%. Particles positioned at the edges of the membrane have zero height.

The lipid-lipid interaction energy is given by

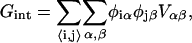(10)

where 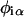is the composition of species α at lattice site i, where α can be U or S. The value V_αβ is the contact energy of nearest neighbors. The physical contribution to V_αβ is from electrostatic, van der Waals, and hydrophobic interactions between the lipids. This term can lead to phase separation if the strength of the energetic interaction between U and S particles (V_US) relative to their self-interactions (V_UU, V_SS), χ, given by

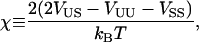(11)

satisfies χ > χ_MF = 2 within mean field theory (Jones, 2002), or χ > χ_c = 3.526 in a physical system incorporating critical fluctuations (Ising model) (Huang, 1987). Hence, for V_UU = V_SS = 1, phase separation occurs if V_US > 1.88.

The bending energy is given by

(12)

where the summation is over all lattice sites. We assume κ_S = κ_U ≡ κ for simplicity. The local mean curvature H_ij at site i, j is given by

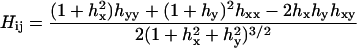(13)

(Boal, 2002), where h_x ≡ ∂_xh(i, j), h_xy ≡ ∂_x∂_yh(i, j), etc., and all derivatives are computed discretely at each lattice site i, j from height values averaged over nearest neighbors. To reduce possible lattice symmetry effects, the mean curvature was computed as an average of that calculated in x−y and x′−y′ coordinate systems, where the x′−y′ axes are rotated with respect to the x−y axes by 45°.

The spontaneous curvature C_0ij is given by

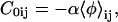(14)

where the local composition 〈φ〉_ij is averaged over, typically, N = 25 lattice sites centered at i, j, so that the spontaneous curvature varies smoothly. The spontaneous curvature factor α implicitly contains both geometrical information about the particle shapes (e.g., tail length, head size, and nature of packing) and their asymmetric distribution across the bilayer. The character α ranges from no spontaneous curvature, α = 0, to a maximum value typically of order α ∼1, when the height difference between a central particle and its neighbors is equal to one lattice spacing. The frame energy is given by

(15)

where h_ij is the height of the particle at site i, j.

The simulations were evolved from an initial state by accepting or rejecting trial configurations according to the Metropolis criterion (Metropolis et al., 1953). A series of such steps allowed the membrane to approach equilibrium. One Monte Carlo cycle is defined as the number of steps required for each lattice site to have the opportunity to change its configuration.

Exploration of shape diagram from simulations

Simulations for a system comprising a central circular domain of S particles within a U membrane were performed to explore the shape diagram shown in Fig. 3 (Fig. 4). This diagram is expected to be a mean field description of the problem, since no thermal fluctuations were included in the estimates above. Note that the effect of 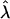could not be explored since the particles were only allowed to move in the vertical direction.

FIGURE 4.

Membrane cross sections at L/2 for a circular domain of radius 12. (a) Varying 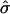by changing σ. (From left to right, σ = 6, 15, 25, 50, and 100; α = 0.3 and κ = 100.) (b) Changing α and σ to vary β and maintain fixed 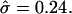(From left to right, α = 1, σ = 240; α = 0.5, σ = 60; α = 0.3, σ = 27; α = 0.24, σ = 13; α = 0.1, and σ = 2.6.) (c) Varying σ and κ while maintaining β = 2.3 and 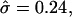with α = 0.5. The thick solid line corresponds to the location of the S domain. 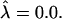Note that the vertical scale is magnified compared to the horizontal scale, and the small slope limit ∂h/∂r ≪ 1 is well satisfied in all cases.

As anticipated, an increase in 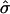at constant β leads to a flatter membrane domain as it is forced further into the raft regime (Fig. 4 a). Reducing β at constant leads to a higher membrane domain (Fig. 4 b). For this range of β, re-entry into the raft regime should be observed according to Fig. 3. However, the effect of elasticity at the interface between the domain and the surrounding membrane was not considered in the simple analytical model: an abrupt change in curvature from the flat U domain to the spherically curved S domain is energetically unfavorable, and continuity and boundary conditions lead to a smooth deformation away from the idealized cap morphology. Note that κ was set equal to 1000 in Fig. 4 b for reasons of clarity since, for larger values of κ, thermal fluctuations have a smaller effect. However, similar trends are observed for smaller values of κ. Fig. 4 c shows membrane cross sections for simulations having the same value of 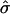and β but differing values of σ and κ. As expected by comparison with the shape diagram (Fig. 3), these cross sections look very similar, with changes in the detailed shape and degree of thermal fluctuations for lower values of σ and κ.

Effect of composition on curvature

Simulations were then performed to analyze the effect of varying the composition of the central circular domain on the domain curvature (Fig. 5).

FIGURE 5.

Effect of composition on curvature. (a) Varying compositions of a central domain within an all U membrane. (From left to right, φ = 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0.) U, solid; S, open. (b) Membrane cross sections at L/2. S, (•);

Using Eq. 6 and the definition for 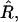where R_min = 2/α〈φ〉, the estimated domain radii R are ∞, 41.6, 20.8, 13.9, 10.4, and 8.3 for a domain of φ equal to 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0, respectively. The curvature radii of the domains was calculated by inscribing a circle at the apex of the curved domain, from Fig. 5 b. These radii are approximately equal to ∞, 11.9, 9.5, 9.0, 7.6, and 6.2 for a domain of φ equal to 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0, respectively. Differences between the analytical estimates and the simulation data are due to the simple analytical model used, in particular due to the neglect of smooth elastic deformation. Note that in Fig. 5 b the membrane immediately surrounding the S domain does not have zero height, but is pulled up by the domain. This effect is more pronounced for higher φ. This buckling up would lead to the smaller observed R. In either case (simple model or calculation), the domain radii decreases (i.e., the curvature increases) with increasing φ, because this leads to an increased asymmetry across the domain bilayer.

Next we analyze how a phase-separated state influences the bending of the membrane. A membrane that was held flat was quenched from a high-temperature mixed state into the phase coexistence region (Fig. 6 a) and coarsening allowed us to proceed with the membrane held flat. Once phase separation had been achieved, the composition was held fixed while the height evolved, until the shapes seen in Fig. 6 developed. As expected, peaks in the membrane cross sections correspond to the location of S particles (Fig. 6, b–d). Moreover, increasing α leads to higher and more highly curved domains, corresponding to the local spontaneous curvature. The range from α = 0.2 to α = 0.5 remains within the raft regime noted in the shape diagram, Fig. 3.

FIGURE 6.

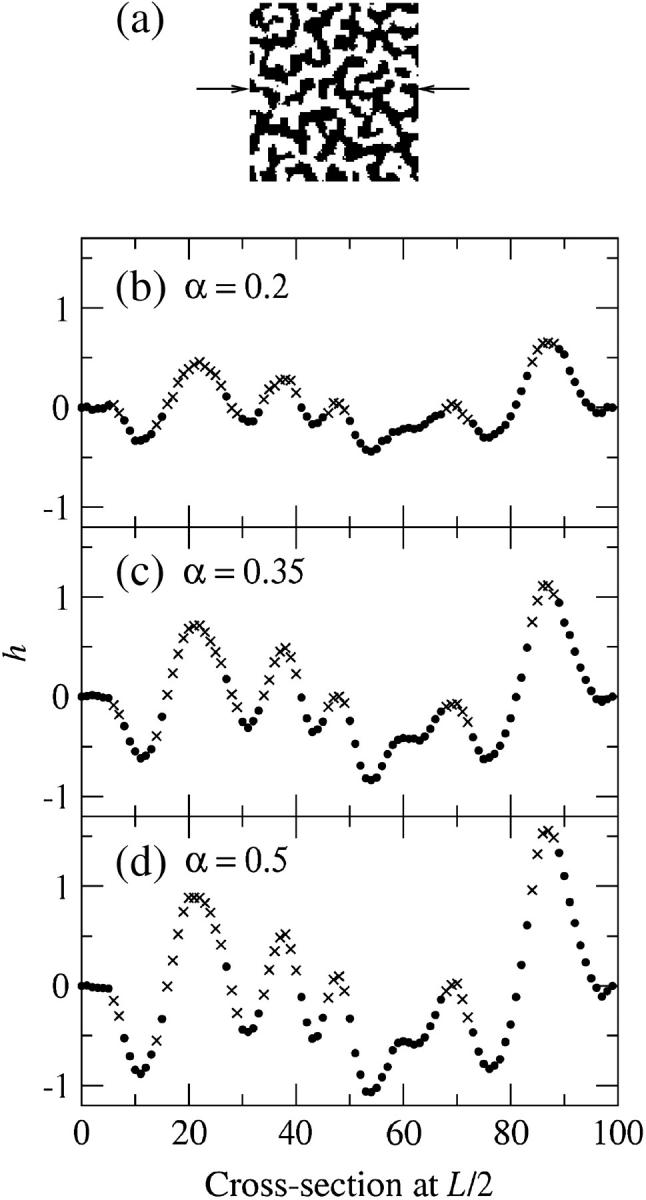
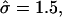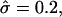Coupling of curvature to composition and degree of asymmetry for a membrane that was quenched into the phase coexistence region. (a) Top view of the final membrane configuration indicating the L/2 position. χ = 8. U, solid; S, open. Membrane cross sections for simulations having σ = 60, κ = 1000; (b) α = 0.2, and β = 0.1; (c) α = 0.35, and β = 0.3; and (d) α = 0.5, and β = 0.6. U, (•); S, ×. 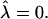β was determined as β = πℓ²/A_min, where ℓ6 is the characteristic length scale of the phase-separated pattern.

CONTINUUM THEORY FOR COARSENING OF DOMAINS

We next study the evolution of composition and height after a quench into the phase-separated regime, using a continuum model to describe the emergence of long wavelength structure. In this work we only study the initial stages of growth, in which the deviations of composition from the mean and of the height from a flat state are both linear. The free energy of a membrane comprising line energy, bending energy, and frame energy can be written, in the Monge gauge and to second order in height fluctuations, as

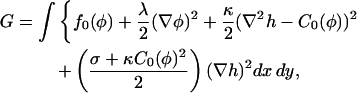(16)

where f₀(φ) is the free energy density for a uniform mixture of composition φ, and C₀(φ) is the spontaneous curvature for a membrane of composition φ. The final term above proportional to 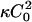arises from expanding the area measure dA = dx dy (1 + (∇h)²)^1/2 to second order in h (Gozdz and Gompper, 2001).

Phase separation and domain coarsening

The local composition variable φ (typically area fraction) obeys the continuity equation (mass conservation),

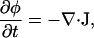(17)

where the flux J of material is given by Fick's law,

(18)

(Jones, 2002), where M is the particle lateral mobility and μ ≡ δG/δφ is the chemical potential. Upon combining with Eqs. 17 and 18, we can expand the composition dynamics to linear order in deviations of composition and height. We use a Fourier expansion,

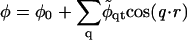(19)

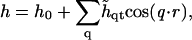(20)

where φ₀ and h₀ = 0 are the constant composition and height, respectively.

To linear order in the q ≠ 0 modes, we find

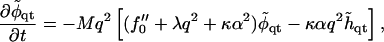(21)

where

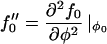and we have used the relation C₀ = – α〈φ〉, Eq. 14.

Neglecting height changes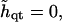

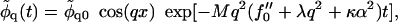(22)

where the exponential term governs the evolution of composition fluctuations. Inside the spinodal line, f″₀ < 0 and composition fluctuations grow for wavevectors q that satisfy Mq²f″₀ > Mq⁴λ + Mq²κα². Hence the bending energy, according to Mq²κα², acts to suppress phase separation. Indeed, as can be seen from Eq. 21, the coupling to bending effectively increases the critical χ for demixing by χ_c → χ_c + κα², within mean field theory.

We now compare with simulations. A flat membrane comprising φ = 0.5 was quenched from a high-energy mixed state into the phase coexistence region. In the absence of coupling to curvature, the characteristic domain length scale ℓ grows as ℓ ∼ t^1/3, as expected for coarsening due to diffusive growth (Jones, 2002). Fig. 7 shows the effect of coupling to curvature on domain coarsening as a function of varying the interaction parameter χ, the bending rigidity κ, and the spontaneous curvature factor α.

FIGURE 7.

Effect of varying (a) χ, (b) κ, and (c) α on a flat membrane. Particle configurations were obtained after 1750 Monte Carlo cycles. L = 100, φ = 0.5. U, solid; S, open. The simulations marked with an asterisk had the same value of κα².

For χ equal to 3 or 4 (Fig. 7 a), the membrane is not in the phase-separation regime. Increasing χ from 5 to 8 leads to purer phase-separated domains that grow more slowly as the energy cost of a U–S contact becomes higher. Increasing both κ and α suppresses phase separation, since the bending energy of a large S domain will be high because the membrane cannot deviate from the flat state. This trend agrees with the theory, since an increase in the κα² term leads to a reduction in the exponential growth of composition fluctuations (Eq. 22). Hence, κα² increases the effective critical χ of the mixing-demixing transition. Two of the simulations performed had the same value of κα² (marked with an asterisk). The particle configurations are similar, as expected in this case (Eq. 22). The simulations having κ = 65 (Fig. 7 b) and α = 0.4 (Fig. 7 c) are not in the phase-separation regime. Interestingly, increasing the depth of the quench into the phase coexistence region via increasing χ leads to slower coarsening since there is a reduction in particle lateral mobility. However, increasing the depth of the quench via reducing either κ or α speeds up coarsening, since these quenches do not increase the local incompatibility of different monomer species.

Height growth

The height evolution for a porous membrane is given by

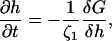(23)

where the friction coefficient ζ₁ is due to dissipation within and solvent flow through the pores (Leng et al., 2001; Marlow and Olmsted, 2002). Using Eqs. 23 and 16 and ignoring edge effects, we find

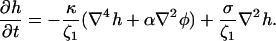(24)

In Fourier space, this is given by

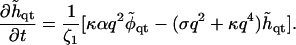(25)

For an impermeable membrane, this equation becomes

(26)

(Brochard and Lennon, 1975; Messager et al., 1990), where qζ₂ is due to dissipation incurred in the velocity field set up by moving membranes in the surrounding solvent (Brochard and Lennon, 1975).

Equation 24 implies that a sharper interface will speed up the initial height growth of the membrane. To study this in the simulations, the height was evolved from a flat membrane with a straight U stripe of varying width, which spanned the system placed in the center (∇²h = ∇⁴h = 0), so that

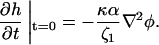(27)

Since 〈φ_ij〉 drives the height evolution (Eq. 14), where the average is taken over 25 sites centered at site (i, j), an effectively sharper interface is formed for increasing stripe-width w until saturation for w = 5 lattice sites. This then increases ∇²φ, which speeds up the height growth of the surrounding membrane (Fig. 8).

FIGURE 8.

Effect of a straight U stripe in the center of the membrane, with widths w = 0, 1, 2, 3, 4, 5, and 6 lattice sites. The mean-square height 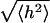was calculated over a central strip having a width of eight lattice sites.

Equation 27 also predicts the form of the initial height growth of a domain. The local composition on the U (C₀ = 0) side of the interface between the U and S domains obeys ∇²φ > 0, so the local height should decrease with time; similarly, ∇²φ < 0 on the S side, where the local height should initially increase with time. In the center of the domain, ∇²φ = 0 since the composition is uniform, and the center is initially stationary (Fig. 9 a). Hence growth should propagate in from the edges of the domain, as found in the simulations (Fig. 9 b).

FIGURE 9.

(a) Schematic early-time behavior for a membrane comprising a central circular S domain; a smooth profile is shown because an average over neighboring sites is used to define the local spontaneous curvature. (b) Cross sections at L/2 after various times, for α = 0.5, κ = 1000, and σ = 60.

Coupled composition and height growth

Finally, we consider simultaneous composition and height evolution after a quench. This problem has recently been addressed firstly by Kumar and Rao (1998), who studied the same problem in the absence of a tension and omitted the contribution 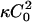in Eq. 16, and secondly by Chen (2004), who studied active membranes. Equations 21 and 25 can be written as

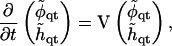(28)

where

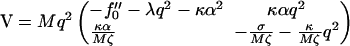(29)

and

(30)

Hence, κα controls the strength of the coupling between composition and height growth, and 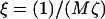controls the dynamic coupling. For ξ ≪ 1 the diffusive coarsening is faster than height growth, whereas for ξ ≪ 1 the height evolves faster than diffusive coarsening.

Assuming the solutions

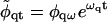(31)

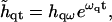(32)

we have

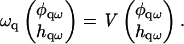(33)

Hence, the eigenvalues (Λ₁, Λ₂) of the matrix V yield the rates ω_q, which govern the growth of composition and height fluctuations. Because the second eigenvalue Λ₂ was stable in the entire q-range for the parameters we consider, we will focus on the effect of Λ₁ on domain growth. Fig. 10 shows the growth rate ω_q ≡ Λ₁ as a function of q for a porous membrane, for different degrees of dynamic coupling ξ and static coupling α.

FIGURE 10.

Growth rate ω_q for curvature couplings α = 0.4, 0.5, and 0.6 for a porous membrane (dynamic coupling 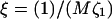). ξ = 0.001 (solid); ξ = 0.1 (dotted); and ξ = 10 (dashed). σ = 1, κ = 2, 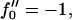and λ = 1.

As ξ increases, corresponding to faster height growth, the range of unstable q values is the same, i.e., ω_q = 0 is independent of system kinetics. However, some modes are significantly less stable, and the dominant growing wavevector q* increases, corresponding to a smaller characteristic length scale (Fig. 11 a). Additionally, the magnitude of ω_q that leads to growth also increases upon an increase in ξ. Hence, the ability of the membrane to buckle reduces the effective resistance to coarsening, allowing faster coarsening, and presumably the presence of a characteristic length scale (spontaneous curvature) leads to a smaller characteristic coarsening length scale.

FIGURE 11.

(a) Most unstable wavevector q* as a function of the dynamic coupling ratio ξ; (b) cos ψ versus wavevector q for static coupling α = 0.4; and (c) cos ψ _q* versus ξ. All results are for a porous membrane (dynamic coupling 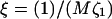). σ = 1, κ = 2, and λ = 1.

As the strength of the energetic coupling between composition and height growth α increases, the range of unstable q decreases, with a loss of the growth of the shorter length-scale domains. Also, growth proceeds more slowly at the most unstable wavenumber. As mentioned earlier, this is because κα² increases the effective critical χ (decreases the critical temperature) of the demixing transition. For an increase in coupling strength between the composition and height growth the critical wavenumber q* decreases (Fig. 11 a). This effect is particularly noticeable for small ξ.

The projection of the eigenvector corresponding to the unstable growing eigenvalue Λ₁ onto the composition component of the eigenvector defines an angle ψ, which parameterizes how height evolution contributes to the initial growth. For cos ψ = 1 the growth is purely compositional, whereas for cos ψ = 0 only the height evolves. Fig. 11 b shows cos ψ versus q for various ξ-values for α = 0.4. For ξ = 0.001, cos ψ = 1 for small q, whereas for larger q the projection cos ψ decreases, implying that height growth contributes to the evolution on these shorter length scales. As ξ increases, cos ψ < 1 for the entire q-range, whereas for ξ = 10, there is a reversal in trend, with height evolution dominating at long length scales (small q) and composition at shorter length scales. The growth mode at the most unstable wavenumber q* as a function of dynamic coupling ξ is shown in Fig. 11 c; growth is purely compositional for all α for low values of ξ. For log(ξ) ≥ 1 height evolution contributes, with a greater value for larger α, but of course compositional growth always dominates. Similar trends were observed for an impermeable membrane, with the only substantial difference, for the parameter range we have considered, being an enhancement of the contribution of height motion to the low wavenumber unstable modes (Fig. 12); this follows directly from the coupling of long wavelength modes to the solvent hydrodynamics, which is more effective in relaxing the instability to phase separation than is pure diffusion. It would be of interest to extend this work to examine the competition between diffusion and buckling after an unstable quench in the nonlinear regime, similar to the study of asymmetry relaxation by Sens (2004). However, we leave this issue to the future.

FIGURE 12.

Comparison between a permeable and impermeable membrane. (a) Growth rate ω_q versus q for α = 0.5 and ξ = 0.1; (b) cos ψ versus q for α = 0.5 and ξ = 0.1.

CONCLUSIONS

In this article we have studied how the competition among the bending energy of a domain, the line tension of the domain edge, and the applied frame tension leads to different-shaped domains. We first studied the energy-minimized shape of a domain as a function of the reduced area and reduced frame tension for different values of reduced line tension, using the simple spherical cap on a flat membrane estimate introduced by Lipowsky (1992) to study budding. A shape diagram spanned by the reduced tension 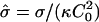and the ratio β of membrane area to the area of an ideal spherical bud, as a function of reduced line tension 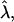is sufficient to describe the shape diagrams. Interestingly, at finite frame tension, a large line tension stabilizes a wide re-entrant raft regime whereby larger domains are stable against strong deformations. This mean field estimate ignores fluctuations and the smooth elastic deformation that would result from the full minimization of the exact elastic problem (Harden and MacKintosh, 1994; Jülicher and Lipowsky, 1996).

To study fluctuation effects and the effect of various composition patterns on membrane height, we introduced a mesoscopic Monte Carlo-based model in which particles, representing a small lipid-sized patch of bilayer with local spontaneous curvature due to the local composition, can phase-separate and fluctuate in height within a Monge gauge (no overhangs) approximation. The approximation of a shape diagram spanned by the reduced variables frame tension 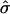and area ratio β works well, except for the presence of fluctuation effects. Note that the cap-on-a-plane approximation actually missed a rather large amount of the flat phase that is entrained by the elastic energy, as can be seen in the “skirt” drawn up around the domains in Fig. 4. Interestingly, a fairly flat raftlike domain, with curvature present mainly at the domain edges rather than at the domain center, results for high area ratio 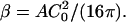This is thought to occur as follows. The boundary obtains the locally preferred curvature first because height growth is initiated from the boundary of a domain. For the center of the domain to subsequently evolve toward its preferred curvature the edges must become less highly curved, and the resulting elastic cost stabilizes the domain against further growth. Decreasing β at fixed reduced tension via decreasing α (Fig. 4 b) leads to a higher domain, in accord with the cap-on-plane model, but re-entry into the raft regime at very low β was not observed.

Domain coarsening was then studied for a flat membrane. The most striking effect of incorporating a composition-dependent spontaneous curvature is an increase in the critical χ (or decrease in the critical temperature) for phase separation proportional to κα². This is relevant for phase separation of asymmetric membranes in situations where the height is fixed by a strong external field, e.g., atomic force microscopy observations of phase separation within a supported bilayer, where membrane-surface interactions induce strong membrane adsorption. The growth of a domain is also enhanced by a sharper interface (Fig. 8). This implies, for example, that for phase-separated domains of equal size and bulk compositions (which would lead, in the main, to similar morphologies), the state with the sharper interface width would grow faster.

We finally investigated, analytically, the initial domain evolution when composition and height growth are coupled, as a function of the dynamic coupling ξ, which parameterizes the ratio of height to composition mobilities. We found that the unstable range of q-values is independent of ξ. However, for increasing ξ, i.e., for reduced particle lateral mobility, the dominant unstable wavenumber q* increases, or equivalently the initial domain size decreases. Additionally, the membrane becomes more unstable. This is due to the availability of the membrane buckling channel to help relax the instability toward phase separation before diffusion on the membrane can occur. Upon increasing the energetic coupling between the composition and height growth, i.e., α, the most unstable wavenumber q* decreases, leading to larger initial domains. This is mainly because increasing α decreases the effective temperature, which places a given quench closer to the critical point and thus leads to larger fluctuations.

There is evidently much more to study in this rich system. The development of asymmetry, which in the bilayer case would be effectively due to different environments on either side of the membrane that comprises two locked monolayers, should actually be treated in terms of two separate interacting monolayers. A step toward this complicated procedure was taken recently by Sens (2004), and can be studied analytically within the formalism of Seifert and Langer (1993, 1994). Full simulations of bilayers, even with united atom or mesoscopic models, are far from full phase separation, but may be capable in the near future of providing a numerical tool for studying these effects. Accurate modeling of the morphology of domains within bilayers must also account for detailed changes in membrane thickness due to the details of different tail length, degree of saturation, and different headgroups. Finally the very important, but still poorly understood, non-equilibrium nature of membranes, surely has a larger influence on the purely relaxational effects we have studied: pumps and embedded proteins provide point-forces acting within the membranes (Chen, 2004; Prost et al., 1998), contact with external proteins such as the cytoskeleton provides external constraints, and the constant transport of materials to and from membranes provides sources and sinks of both different compositions of lipids and force perturbations.