Abstract
Skeletal muscle contraction is a canonical example of motor-driven force generation. Despite the long history of research in this topic, a mechanistic explanation of the collective myosin force generation is lacking. We present a theoretical model of muscle contraction based on the conformational movements of individual myosins and experimentally measured chemical rate constants. Detailed mechanics of the myosin motor and the geometry of the sarcomere are taken into account. Two possible scenarios of force generation are examined. We find only one of the scenarios can give rise to a plausible contraction mechanism. We propose that the synchrony in muscle contraction is due to a force-dependent ADP release step. Computational results of a half sarcomere with 150 myosin heads can explain the experimentally measured force-velocity relationship and efficiency data. We predict that the number of working myosin motors increases as the load force is increased, thus showing synchrony among myosin motors during muscle contraction. We also find that titin molecules anchoring the thick filament are passive force generators in assisting muscle contraction.
INTRODUCTION
The mechanism of skeletal muscle fiber contraction has been a topic of investigation since antiquity. The major force-generating element in the muscle is the motor protein myosin II (Huxley and Niedergerke, 1954; Huxley and Simmons, 1971; Cooke, 1986; Rayment et al., 1993; Piazzesi et al., 2002; Reconditi et al., 2004). A large body of work has been devoted to the mechanochemistry of myosin (Huxley and Simmons, 1971; Reedy et al., 1965; Rayment et al., 1993; Gulick and Rayment, 1997; Conibear et al., 2003; Pate et al., 1993; Siemankowski et al., 1985; Greene and Eisenberg, 1990, 1980; Clark et al., 2003; Kurzawa et al., 1997; Lymn and Taylor, 1971). Single-molecule measurements can now detect the motion of myosins interacting with actin (Rayment et al., 1993; Milligan et al., 1990; Howard, 1994; Conibear et al., 2003). Combined with detailed x-ray structures of myosins in different conformations (Gulick and Rayment, 1997; Conibear et al., 2003), a plausible mechanism is emerging for the working cycle of individual myosin motors. In this article, we attempt to connect the dynamics of individual myosins with the observed behavior of muscle contraction. We will show that there are important collective effects in skeletal muscle dynamics. The geometrical organization of the sarcomere and the kinematics of the constitutive parts play an important role. We will provide an explanation for the observed synchrony in muscle contraction and show how an increasing load force leads to an increasing number of myosins working on actin. We show that a force-dependent ADP release step can explain the dynamics of skeletal muscle contraction.
Proteins of the myosin family are integral components in several cellular activities. Even among the skeletal muscle myosins, there is a rich diversity of observed behavior (Pate et al., 1993; Bagshaw, 1993). In the present work, we focus on the fast skeletal muscle of the rabbit. However, there are universal features common among the myosins. For instance, the powerstroke of the myosin motor occurs after phosphate release (Cooke, 1986; Spudich, 2001; Howard, 2001). In addition, a force-dependent ADP release step responsible for synchrony in muscle contraction is also responsible for the unidirectional motion of myosin-V on actin (Lan and Sun, 2005). Therefore, the myosin motors generate force in a similar manner; how the forces are utilized lead to different observed behavior.
From known skeletal myosin kinetics with purified proteins, the actin binding step is quite slow. In fact, it is energetically unfavorable, by ∼2.3 kBT, for myosin to bind to actin (Greene and Eisenberg, 1980; Howard, 2001). Yet, the force-velocity curve shows a rather large stall force, indicating that many myosin heads must be working under load (Pate et al., 1994; Howard, 2001). However, at low load conditions, if there are many bound working heads, they must mechanically oppose each other. Thus, synchrony must exist among the motors and the number of actin-bound motors must change as a function of the external load. Electron micrographs of muscle under tension show increasing order in the cross-bridge arrangement as a function of load force. These measurements are consistent with the notion of synchrony among the motors. In our model, we show how synchrony is achieved during muscle contraction.
The work of Duke established the basic framework of understanding muscle contraction (Duke, 1999; Vilfan and Duke, 2003). Duke's model is also based on the swinging cross-bridge mechanism of Huxley and Simmons (1971), which now is widely accepted as the basic explanation of the role of the myosin in muscle contraction. The model presented in this article builds upon Duke's and Huxley's earlier works. We show how the thin filament movement is connected with the conformational change in the myosin motors. Duke's work treated the chemical rate constants as fitting parameters. He contends that synchrony in muscle contraction is due to a slow phosphate (Pi) release step. Forces from other myosin motors can assist Pi release (Duke, 1999). Biochemical studies, however, suggest that Pi release is rapid (Siemankowski et al., 1985; Howard, 2001). In our current work, experimentally measured chemical rate constants are used. Realistic geometrical arrangement of the mechanical elements in the sarcomere is included. Thus, the number of unknown parameters is limited to the mechanical constants of the myosin motor during its chemical cycle and the elastic modulus of the stalk protruding out of the thick filament.
SARCOMERE ULTRA-STRUCTURE
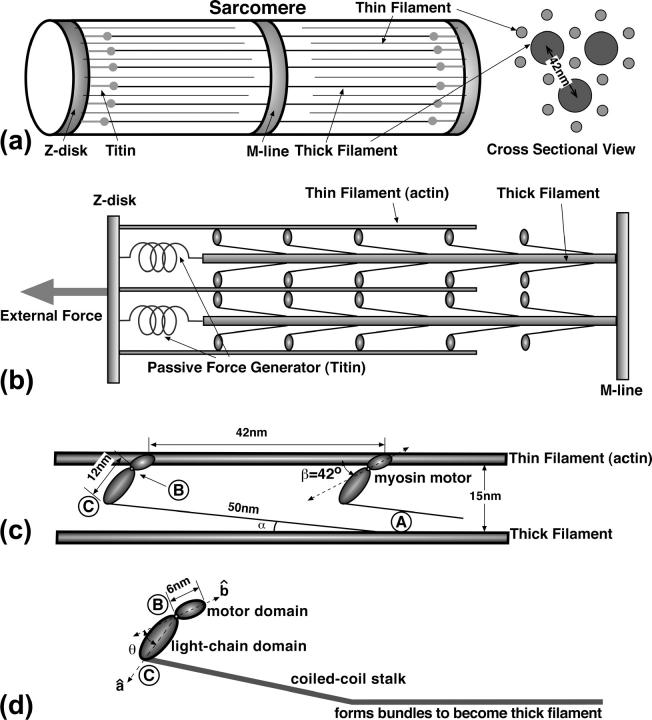
The basic arrangement of the sarcomere is shown in Fig. 1. Each thick filament, comprised of a bundle of myosin stalks, is surrounding by a hexagonal arrangement of thin filaments (actin). The thin filaments are anchored to the Z-disk (Huxley and Hanson, 1954). The thick filaments are anchored to the M-line (Reedy et al., 1965). The thick filaments are also connected to the Z-disk via an elastic element made of titin (Linke et al., 1996, 1998; Linke, 2000; Li et al., 2002). In the experiments that we shall attempt to explain, an external load force is applied to the Z-disk in the x direction (Reedy et al., 1965). All of the actin filaments are under tension, as well as the titin elastic elements. The elastic elements are passive force generators (Minajeva et al., 2002; Linke, 2000); the myosin motors along the thick filament are active force generators.
FIGURE 1.
The ultra-structure of a sarcomere. (a) The rough arrangement of the thick and thin filaments between the Z-disk and the M-line. (b) The detailed side-view of the sarcomere. The myosin motors are arranged all along the thick filament. The thick filament is connected to the Z-disk via the elastic titin molecules. The titin molecules restrain the movement of the Z-disk away from the thick filament, thus they are passive force generators. (c) The rough geometry of the actin-myosin interaction. The myosin motors are spaced 42-nm apart. The stalk domain protruding from the thick filament is ∼50 nm in length and is elastic. The angle α is actually quite close to zero. Here, the figure is exaggerated to show the stalk. (d) The myosin motor consists of three domains. The angle, θ, between the motor domain and the light-chain domain (LCD) changes during the powerstroke. The stalk, which consists of a coiled-coil motif, actually continues into the thick filament. A bend is thought to occur in the light-chain, angling it upward to actin.
The gross structural features of the myosin motor are also shown in Fig. 1. The myosin domains are labeled as the motor domain, the light-chain domain (LCD), and the stalk. During muscle contraction, a myosin motor binds to the actin filament and undergoes a conformational change (Cooke, 1986; Rayment et al., 1993). The conformation change, or powerstroke, is coupled to the ATP hydrolysis cycle (Rayment et al., 1993; Finer et al., 1994; Lymn and Taylor, 1971). Given the three domains, we defined unit vectors, 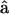 and
and  oriented along the motor domain and the LCD, respectively.
oriented along the motor domain and the LCD, respectively.  and
and 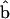 define an angle, θ, at point B. The powerstroke motion is a rotation in θ. Changes in θ are translated to the movement of the thin filament in the x direction. In Energy Transduction within the Skeletal Muscle: Two Scenarios, the kinematics of this movement is discussed in more detail.
define an angle, θ, at point B. The powerstroke motion is a rotation in θ. Changes in θ are translated to the movement of the thin filament in the x direction. In Energy Transduction within the Skeletal Muscle: Two Scenarios, the kinematics of this movement is discussed in more detail.
There are ∼150 myosin motors interacting with the hexagonal thin filaments. When an external load force is applied to the Z-disk, all six actin filaments are under the same amount of mechanical tension. If we simplify the problem and assume that the Z-disk can only move in the x direction, then it is equivalent to model 150 myosin motors interacting with a single actin filament. If the Z-disk is always held perpendicular to the x axis by other tissue, then the current assumption is a valid one.
The dimensions of the actin-myosin system are important for kinematic considerations. The distance between the centers of the thick filaments is ∼42 nm. The distance between the centers of the thick and thin filaments is 24 nm. The radii of the thick and thin filaments are 6 nm and 3 nm, respectively (Epstein and Herzog, 1998). Thus, the distance between the surfaces of the thick and thin filaments is 15 nm. High resolution structures are available for the motor domain and a part of the LCD. Cryo-electron micrographs of muscle under tension show a cross-bridge connecting the thick and thin filaments. Since the motor domain is 6 nm in length and approximately the same size as the thin filament, we estimate that the observed cross-bridge is mostly the LCD which is ∼12–15 nm in length. The stalk, which protrudes slightly out of the thick filament, is known to be elastic and semiflexible. The persistence length, lp, of the stalk is estimated to be ∼100 nm (Uyeda et al., 1996) and the length of the stalk is ∼50 nm (Cooke, 1986; Bagshaw, 1993). Therefore, bending of the stalk is perhaps important. The effect of stalk elasticity will be extensively discussed in Energy Transduction within the Skeletal Muscle: Two Scenarios.
High resolution x-ray structures of myosin bound to actin are currently not available. However, fitting of myosin structures to cryo-EM shapes indicates that the myosin motor domain contacts actin with an angle β = ∼42° (Milligan et al., 1990). It is not known whether the contact angle between actin and myosin changes if the catalytic site of myosin changes occupancy. In our model, we have assumed that this angle is fixed. The exact structural change within the myosin domain during the powerstroke is also unknown. Instead, we postulate that there is a conformation energy as a function of θ that is ultimately derived from the underlying atomic level interactions. In absence of atomic-scale details, kinetic measurements and structural considerations are used to parameterize our model.
MECHANICAL ENERGY TRANSDUCTION IN A SINGLE MYOSIN
The dynamics of molecular motors can be described by the coupled Langevin equations
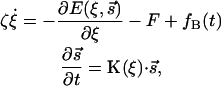 |
(1) |
where ξ is a dynamical observable of interest. The value ζ is the friction due to the surrounding medium. The value F is an external load force and fB(t) is the Brownian random force obeying the fluctuation dissipation theorem. The value s is the chemical state of the molecular motor and E(ξ, s) is the elastic energy of the motor as a function of the dynamical observable and the chemical state. K is a matrix of kinetic transition rates describing the chemical reactions in the motor catalytic site. K is, in principle, a function of ξ also.
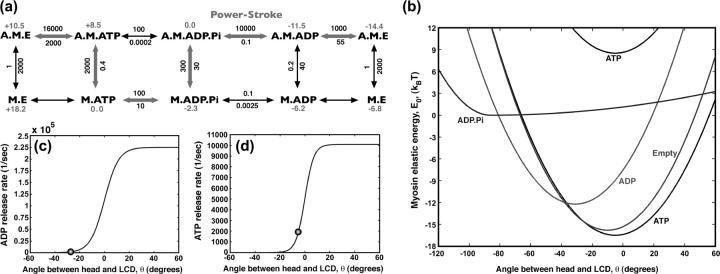
A single myosin motor binds and hydrolyzes ATP to generate force. The binding and hydrolysis is also coupled to myosin's affinity for actin (Conibear et al., 2003; Greene and Eisenberg, 1980; Lymn and Taylor, 1971). The chemical cycle in a single skeletal muscle myosin is shown in Fig. 2. The actin-bound myosin states are labeled A.M.E, A.M.T, A.M.DP, and A.M.D, corresponding to empty, ATP, ADP.Pi, and ADP occupancies in the catalytic site. The actin-free myosin states are similarly labeled, but without the A designation. The overall free-energy change after the hydrolysis of one ATP at normal cellular conditions is ∼25 kBT.
FIGURE 2.
The mechanochemistry of a single myosin motor. (a) The kinetic cycle is shown along with the measured rate constants for the reactions 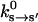 in s−1. The relative free energies of the states are also displayed. The most probable kinetic pathway is shown in heavy arrows, although no particular pathway is assumed in our model. All of the observed states are included. (b) The myosin motor energy as a function of the angle θ, defined in Fig. 1. The free energy differences between equilibrium conformations are given by the kinetic constants. The M.* states have the exactly the same shape as the corresponding A.M.* states except for additive constants. (c) The kinetic rate constant as a function of θ for ADP release from A.M.D and (d) ATP release from A.M.T. The functions have a sigmoidal shape, as explained in the text. At the equilibrium conformation, θ0 (indicated as spheres), the rate constants correspond to the experimental values with purified proteins.
in s−1. The relative free energies of the states are also displayed. The most probable kinetic pathway is shown in heavy arrows, although no particular pathway is assumed in our model. All of the observed states are included. (b) The myosin motor energy as a function of the angle θ, defined in Fig. 1. The free energy differences between equilibrium conformations are given by the kinetic constants. The M.* states have the exactly the same shape as the corresponding A.M.* states except for additive constants. (c) The kinetic rate constant as a function of θ for ADP release from A.M.D and (d) ATP release from A.M.T. The functions have a sigmoidal shape, as explained in the text. At the equilibrium conformation, θ0 (indicated as spheres), the rate constants correspond to the experimental values with purified proteins.
Myosin conformational energy
Changes in the chemical state are coupled to conformational changes in the myosin motor domain. We propose that θ is a dynamical variable under the influence of the protein conformational energy. The equilibrium value of θ, θ0 is a function of the chemical state, s. Thus, for most of the chemical states, we write the elastic energy of myosin motor as a function of θ as
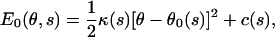 |
(2) |
where θ0(s) is the preferred angle (conformation) of the myosin motor domain and κ(s) is the force constant. The value c(s) is an additive constant that specifies the relative height of the energies. For the *.M.DP states, a slightly different E0 is used, as
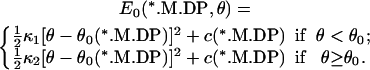 |
(3) |
The functional form of E0 is currently unknown. In principle, it can be obtained from experiments or computer simulations. For most of the chemical states, we have chosen the simplest function possible to describe the energy. However, the harmonic form of Eq. 2 is inadequate for the s = M.DP state. For ATP hydrolysis to proceed, the *.M.DP state should always be lower in energy than the *.M.ATP state. The alternative function of Eq. 3 satisfies this constraint.
The energetic constant, c(s), can be computed from experimental kinetic measures of unstrained purified myosins. The detailed balanced condition states that
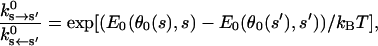 |
(4) |
where  is an experimentally measured kinetic rate constant with purified proteins. This allows us to compute c(s) unambiguously. The constants used in the present model are summarized in Table 1. Fig. 2 b displays E0(θ, s) used in our model.
is an experimentally measured kinetic rate constant with purified proteins. This allows us to compute c(s) unambiguously. The constants used in the present model are summarized in Table 1. Fig. 2 b displays E0(θ, s) used in our model.
TABLE 1.
Parameters used in the definitions of E0(θ, s)
| si | Identity | κ(si)(kBT/rad2) | θ0(si) (degrees) | c(si)(kBT) |
|---|---|---|---|---|
| 1 | M.E | 32.0 | −10 | −5.1 |
| 2 | M.ATP | 29.0 | −5 | 0.0 (−25.0) |
| 3 | M.ADP.Pi | 36.0 (1.0) | −86 | −2.0 |
| 4 | M.ADP | 32 | −31 | −8.7 |
| 5 | A.M.E | 32.0 | −10 | −18.1 |
| 6 | A.M.ATP | 29.0 | −5 | 0.2 |
| 7 | A.M.ADP.Pi | 36.0 (1.0) | −86 | −7.8 |
| 8 | A.M.ADP | 32 | −31 | −20.5 |
The differences in the c(si) are the measured free energy differences between chemical states. For *.M.DPi states, the two constants, κ1(κ2), are given.
Myosin chemical kinetics
The kinetic rate constants describing the chemical changes in the catalytic site are functions of the conformational variable, ks→s′(θ). Experiments have measured the rate constants with purified proteins (Pate et al., 1993; Siemankowski et al., 1985; Greene and Eisenberg, 1990, 1980; Bagshaw, 1993). The experimental rate constants, 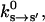 represent the rate constants at conformational equilibrium:
represent the rate constants at conformational equilibrium:
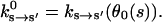 |
(5) |
In addition, detailed balance must be satisfied, as
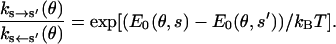 |
(6) |
With these constraints, we have devised the following set of functions for ks→s′(θ):
Binding to actin. The value kM.*→A.M.* is independent of θ. Therefore, binding can occur regardless of the motor conformation.
Hydrolysis and Pi release. The values kA.M.T→A.M.DP and kA.M.DP→A.M.D are independent of θ and are set to
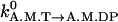 and
and 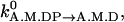 respectively.
respectively.Reverse hydrolysis and Pi binding. The values kA.M.DP→A.M.T and kA.M.D→A.M.DP are given by the detailed balance condition of Eq. 6 and our choice of kA.M.T→A.M.DP and kA.M.DP→A.M.D.
-
ADP release. An important postulate of our model is that ADP release, kA.M.D→A.M.E, is a strong function of the conformation. Thus, the ADP release rate is given by
where the constants are αD = 5.0, Δ = 31°. The value k0 is the equilibrium ADP release rate measured in kinetic experiments. The parameters are chosen so that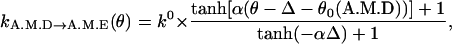
(7)
This function is plotted in Fig. 2. A similar function was also used to explain the processivity of myosin-V (Lan and Sun, 2005). We propose that the angular position of the light-chain is coupled to the geometry of the catalytic site. If the angle swings past the equilibrium value, the binding site becomes more open, and ADP release is enhanced. If the angle is forced to be smaller than the equilibrium value, the catalytic site is closed and ADP release rate is exponentially smaller.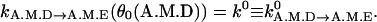
(8) Notice that our choice for kA.M.D→A.M.E is equivalent to the notion of torque-enhanced ADP release (Veigel et al., 2001). If an external torque is applied to the light-chain, then we expect that the torque will cause some conformational change in the catalytic site. Therefore, the ADP release rate should be modified to
where τ is the applied torque and Δθp is the strain developed in the binding pocket. The value Δθp is an unknown parameter. The rate expression of Eq. 9 is equivalent to the our rate expression near θ0(A.M.D). Our functional form is a sigmoid, indicated that there is an upper bound to the ADP release rate.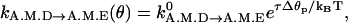
(9) ATP release. For reasons similar to those for the ADP release, the ATP release rate should also depend on the conformation. Since the lever-arm position is correlated with the openness of the binding pocket, we expect larger release rates when the lever-arm swings past the equilibrium position. Thus, the same functional form of Eq. 7 is used for kA.M.T→A.M.E, where α = 8.0, Δ = 5°. The value k0 is now the measured ATP release rate.
- ATP and ADP binding. ATP and ADP binding are determined using the detailed balance condition of Eq. 6. For instance.
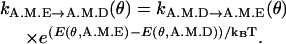
(10) -
Chemistry when detached from actin. For all the chemical rates, ks→s′, where s and s′ are both detached from actin, the rate constants are all independent of θ:
Fig. 2 shows the experimentally estimated myosin rate constants at conformational equilibrium. We have used simplest assumptions in modeling the θ-dependence of the kinetic rates. Aside from the conformation-dependent ADP and ATP release rate, no other assumptions are made. Whenever possible, experimental values are used to parameterize the model.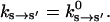
(11) Thus, we have completely specified the energy transduction mechanism in a single myosin motor. Pi release leads to a powerstroke that changes the preferred angle of the light-chain. But how does this motion translate to muscle movement? Here, we will examine two possible scenarios. These are depicted in Fig. 3. If the shape of the stalk is described by the function R(s), the angle ψ is defined as the angle formed between and the tangent vector t(L) of the stalk at point C:
and the tangent vector t(L) of the stalk at point C: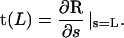
(12)
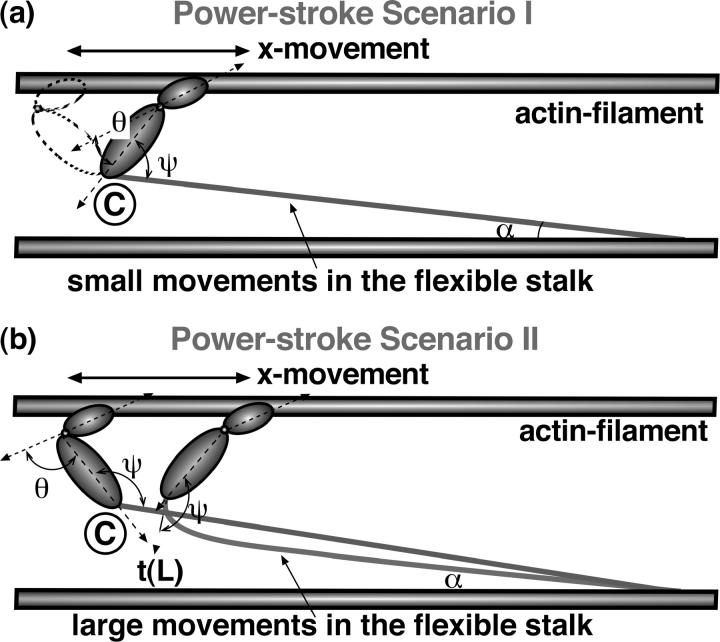
FIGURE 3.
Two powerstroke scenarios. (a, scenario I) Myosin motor rotates with respect to point C. The angles, ψ and θ, change during the powerstroke. The light-chain filament is largely undeformed during the powerstroke, except for a small deflection when the myosin motor is almost perpendicular to the actin filament. This deflection energy is accounted for in our model. (b, scenario II) In the second scenario, the angle ψ is fixed during the powerstroke. The motion is achieved through bending the stalk domain, and the subsequent relaxation of the bending energy drives the thin filament forward.
In scenario I, the myosin motor simply rotates around point C, creating a powerstroke in the x direction. The value ψ is allowed to change during the powerstroke. To a first approximation, we treat ψ as completely flexible. In addition to this motion, a slight bend occurs in the stalk. (Actin is much more rigid than the light-chain filament, and therefore is treated as undeformable.)
In scenario II, we assume the opposite extreme and treat ψ as completely fixed. The powerstroke distorts the stalk domain. The subsequent relaxation of the stalk leads to the x movement. Both scenarios will now be examined in detail.
ENERGY TRANSDUCTION WITHIN THE SKELETAL MUSCLE: TWO SCENARIOS
Scenario I
If the angle ψ is completely flexible, then the conformational change in θ can be mapped to a movement in x using the relationship
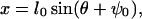 |
(13) |
where l0 is the length of the light-chain domain and ψ0 = π/2 − β. Using this relationship, E0(θ, s) can be directly mapped to the energy E0(x, s). In addition, when the myosin head rotates, a strain is developed in the light-chain filament that is proportional to the vertical displacement,
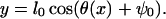 |
(14) |
Therefore, the total energy of the actin filament per myosin motor is
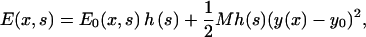 |
(15) |
where y0 is the equilibrium length in the y direction and h(s) is a function that is 1 if s = (A.M.*) and 0 if the head is detached from actin. The second part of the elastic energy is the small deflection energy of a straight filament. The value M is not a free parameter, but related to the bending stiffness of the filament, lp. In Appendix B, we give an expression for M as a function of the persistence length of the stalk. The value M is essentially 0 for the present case.
We note that single molecule experiments have measured the size of the myosin powerstroke (Finer et al., 1994). The value l0 is obtained from the myosin structure and is not a fitting parameter. Thus, for given l0 and known powerstroke size (10 nm) (Huxley and Simmons, 1971; Cooke, 1986; Pate et al., 1993; Finer et al., 1994) θ0(s) specifying E0(θ, s) is in fact fixed. The only possible freedom is in choosing κ(s).
The total energy of actin depends on the number of bound myosin heads,
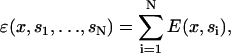 |
(16) |
where N is the total number of myosin heads and E(x, si) appears in Eq. 15. The movements of the actin filament can be computed using the Langevin equation of Eq. 1, or the Fokker-Planck equation explained in Muscle Dynamics using Non-Equilibrium Statistical Mechanics. The chemical transitions of each myosin motor are largely unmodified except for myosin unbinding from actin. Due to the vertical elastic energy, the unbinding rates become
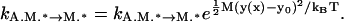 |
(17) |
This modification preserves detailed balance between the bound and unbound states.
Scenario II
If the contact angle, ψ, between the myosin head and the actin filament is fixed, then powerstroke can only occur by flexing the myosin stalk. The total elastic energy of the myosin and the stalk is therefore
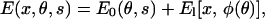 |
(18) |
where φ(θ) is the angle of the tangent vector, t(L). The value φ is a function of the myosin conformation, θ. The exact relationship is made explicit in Appendix A. The value x is the location of the bound myosin head with respect to point A. The value El(x, θ) is the elastic energy of the stalk domain that depends on the geometry of the filament but not the chemical state. The way we compute El(x, s) is given in Appendix A. Because the stalk is very close to the thick filament, when the stalk bends, it can impinge on the thick filament. We approximate El is a sum of two contributions,
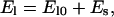 |
(19) |
where El0 is the energy of pure bending and Es is the interaction energy between the stalk and the thick filament. Note that El should be larger than El0 and Es is always positive.
After E(x, θ, s) is computed, the powerstroke motion can be obtained from comparing E(x, θ, A.M.DP) and E(x, θ, A.M.D). Since θ relaxes much more quickly than x, the work delivered in the x direction can be found by minimizing θ for each x, i.e.,
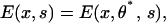 |
(20) |
where θ* is the value that minimizes E for fixed x.
In Fig. 4, we plot the work delivered in the x direction and the powerstroke size for each myosin motor using scenario II. The energy surface E(x, θ, A.M.D) is also shown. Here, to simplify the presentation, we have set Es = 0. Single molecule experiments have established that the powerstroke size of a single myosin II motor is ∼10 nm. Thus, θ0(A.M.DP) − θ0(A.M.D) is not an adjustable parameter. The only adjustable parameters are the stiffness constants, κ(s), determining E0(θ, s). Since El is close to 0 immediately after myosin binds to actin, κ(A.M.DP) is relatively unimportant. The important parameter determining the magnitude of the powerstroke is κ(A.M.D). We see that, although the size of the powerstroke is 10 nm, the work delivered in the x direction is, at most, 10 kBT—far below the work delivered using scenario I. Thus, without the inclusion of Es, the work delivered suggests that the stall force in scenario II is substantially smaller. With the inclusion of Es, our calculations show that the powerstroke size is substantially smaller (<5 nm). The work delivered in the x direction is also smaller. The combined results suggest that the efficiency and the stall forces using scenario II must be much smaller than scenario I. This conclusion is also confirmed by computations not reported here.
FIGURE 4.
The origin of the powerstroke in scenario II. (a) The contour plot of E(x, θ, A.M.D) without contributions from Es, i.e., El = El0. The energetic minimum of E(x, θ, A.M.DP) is at (x′, θ′), labeled A. The energetic minimum of E(x, θ, A.M.D) is at (x*, θ*), labeled C. After Pi release, the system first drops to the A.M.D surface at (x′, θ′). The subsequent change in x, from B to C, is the powerstroke. (Here, the powerstroke goes from the right to left.) In the inset, a representative shape, R(s), of the stalk is shown. In this case, the stalk actually impinges upon the thick filament. (b) The powerstroke as a function of κ(A.M.D), again without contributions from Es. κ(A.M.D) is the only adjustable parameter in this problem. The powerstroke size (whose scale is on the right, in nm) is given by the dotted line. The energy of the powerstroke is given by the red line (scale at left, in kBT). For all possible values of κ(A.M.D), the powerstroke size never exceeds 10 nm. More importantly, the powerstroke energy is never greater than 10 kBT.
MUSCLE DYNAMICS USING NON-EQUILIBRIUM STATISTICAL MECHANICS
Given the overall energy of the actin filament as a function of x and the chemical states of the myosin motors, we now can solve for the dynamics of the muscle contraction using scenario I. If an external load force, F, is applied to the Z-disk, the overall energy is modified to
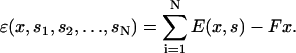 |
(21) |
To obtain the mean contraction velocity, we solve a Fokker-Planck equation for the actin position probability, P(x,s1,s2,…,sN),
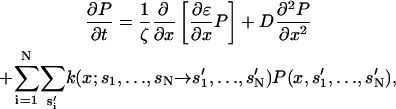 |
(22) |
where ζ is the friction acting on the actin filament and the Z-disk. The chemical transition rates, k(x;s1,…,sN→s′1,…,s′N), have been specified in Mechanical Energy Transduction in a Single Myosin. Due to the large number of myosin motors (N = 150), the dimension of the energy surface is quite large. A more natural way to solve the equation is by using Monte Carlo trajectories. We discretize x and describe the changes in x and the chemical states as a set of Markov equations:
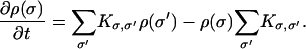 |
(23) |
Here, if the actin filament is at the ith position along x, then σ labels the composite state of the system
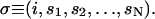 |
(24) |
The transition probability matrix, Kσ, σ′, is given by
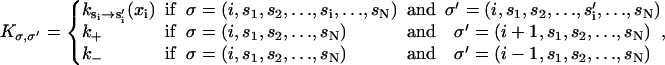 |
(25) |
where
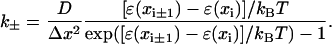 |
(26) |
The Markov equations obtained after discretization are good approximations to the Fokker-Planck equation if Δx = xi − xi−1 is not too large (Wang et al., 2003). A trajectory in this multidimensional space is a sequence of jumps among the states. A method to sample this ensemble in trajectory space was first proposed by Bortz et al. (1975). Given the current state of the system, σ, the time to leave the current state, Δt, is given by e−Δt/τ where
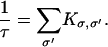 |
(27) |
A random number is chosen according to e−Δt/τ to obtain Δt. Another random number is chosen from 0 to 1/τ to determine the identity of the destination state. In this fashion, a sequence of jump times between the states is generated according to the probability distribution of the trajectories. An observable such as the average speed of actin movement is given by
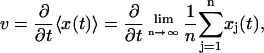 |
(28) |
where xj(t) is the position as a function of time for the jth trajectory and n is the total number of trajectories.
RESULTS
Using 150 myosin motors, we have computed the force versus velocity curve for muscle contraction. This is shown in Fig. 5. The computational results are slightly different from the experimental data at large load forces. We argue that this is not surprising. In the experimental situation, the contraction is not only due to the myosin motors working along actin, but also due to the contraction of the passive force generator, titin. Thus a fraction of the applied force is balanced by titin, and the force along the actin filament is lower than the total applied force. Titin is also a nonlinear elastic object. At high load forces, the resorting force generated by titin can be quite substantial. Independent measurements of titin elasticity suggest that titin is responsible for ∼20% of the contractile force (Minajeva et al., 2001, 2002; Linke, 2000; Linke et al., 1996, 1998). Thus, our computational results are consistent with experimental measurements.
FIGURE 5.
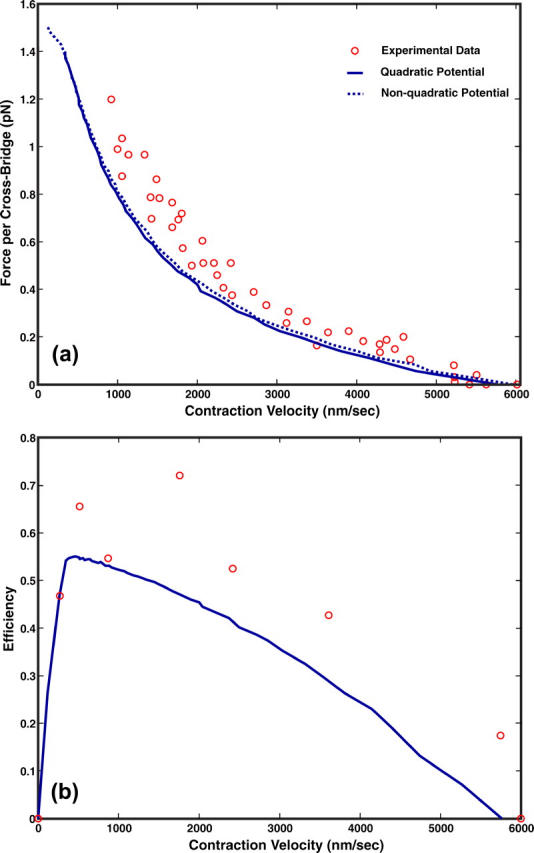
(a) The force versus velocity curve for the skeletal muscle of rabbit. The theoretical results are shown as the solid line and experimental measurements are shown as circles. There are 150 cross-bridges in the computation. (b) The efficiency versus velocity for muscle contraction. The experimental results are shown as the open circles.
To explore the dependence of our force-velocity relationship on the shape of the myosin conformational energy, E0, we used a more complicated nonharmonic function to model E0(θ, A.M.D). The function is similar to what we used for myosin-V, as
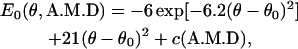 |
(29) |
and gives a slightly larger force near θ ≈ θ0. However, the force-velocity relationship is insensitive to this change. Thus, our result is robust with respect to different forms of E0.
The efficiency, ɛ, of the muscle, is defined as
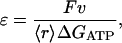 |
(30) |
where ΔGATP = 25 kBT and 〈r〉 is the average rate of overall ATP hydrolysis. Our results shown in Fig. 5 display a similar trend. The measured efficiency is always slightly higher. Again, due to the titin restoring force, the actual force applied to actin is smaller by ∼20%. Therefore, our result is in good agreement with the measurements.
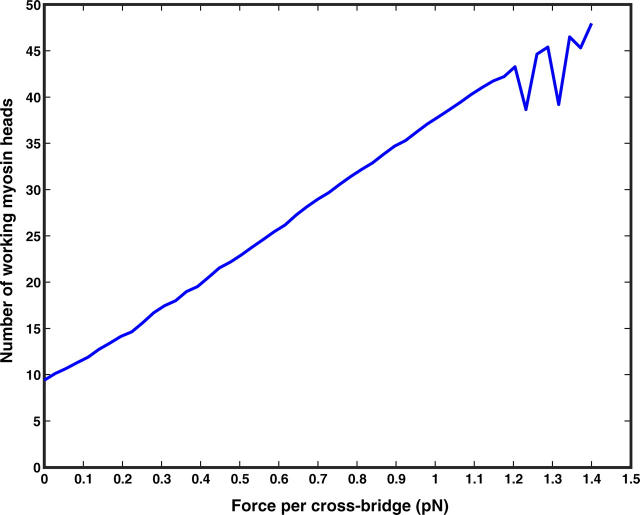
In Fig. 6, we plot the average number of working heads as a function of F. We see that the number of working heads is very low when the load force is small. As the load force increases, the number of working heads increases gradually. The explanation of this result can be seen from Fig. 2. When the load force is small, the rate-limiting step is actin binding. After a myosin head is bound, it quickly releases Pi and makes a powerstroke to reach the equilibrium conformation of the A.M.D state. At this equilibrium conformation, the ADP release rate is quick and the kinetic cycle proceeds without hindrance. If the load force is high, then the myosin head cannot complete its powerstroke. The conformation is stuck in the ADP state before the equilibrium value. At this position, ADP release is slow and rate-limiting. Thus, the kinetic cycle is stopped until another myosin head binds to actin and makes a powerstroke. If there are enough heads bound, the collective powerstroke can overcome the load force and reach the equilibrium conformation. Thus, the conformation-dependent ADP release step is the explanation for synchrony in muscle contraction.
FIGURE 6.
The average number of attached myosin heads as a function of the externally applied force. The increasing number of attached heads is our explanation of synchrony in muscle contraction.
Note in Fig. 6, when the applied force is large, the number of attached heads shows an oscillatory behavior. In this regime, the system is unstable and exhibits a dynamical phase transition (Badoual et al., 2002).
DISCUSSION AND CONCLUSIONS
In the present work, we have presented a comprehensive model for skeletal muscle contraction. We have considered two scenarios of force generation by the myosin motors. We have shown that scenario I, where only small deformations occur in the stalk domain, is the most likely force-generation mechanism. Scenario II generates a smaller powerstroke with a lower efficiency. Experimentally measured rate constants for the various chemical steps are used to parameterize our model. Because the actin binding step is slow and energetically unfavorable, the number of working heads is quite low. When the load force is increased, the myosin motors are stuck at the conformation where they cannot release ADP. The only way the kinetic cycle can proceed is to bind more myosin motors. This leads to synchrony observed in muscle contraction.
Using generic parameters, we are able to explain the experimentally measured force versus velocity curves. We found that the elasticity of titin plays an important role in the overall contractile force. The load force experienced by the thin filament is likely to be lower than the overall applied force. The efficiency of the myosin motors is also lower than expected. Thus, further experiments with isolated sarcomere without titin are desirable.
In a model such as our work, there are a set of unknown parameters; several of them are summarized in Table 2. We emphasize that we have taken very generic functional dependences to parameterize our model. For instance, simple quadratic and sigmoidal functions are used to parameterize E0(x, s) and ks→s′(x). Experimentally measured rates further constrain our model. Whenever possible, parameters are computed from known elastic properties of the components. There is likely some dependence of our results on the parameters. However, the behavior we observe and mechanism we propose are generic and stable with respect to small changes in the parameters.
TABLE 2.
Table of constants used in our model
| Constants | Value |
|---|---|
| Stiffness of the stalk, lp. | 100 nm |
| Angle between the stalk and thick filament, α. | ≈2° |
| Length of the LCD, l0. | 12 nm |
| Length of the stalk, L. | 50 nm |
| Distance between the thin and thick filaments, d0. | 15 nm |
| Force constant for light-chain deflection, M. See Appendix B. | 0.002 kBT/nm2 |
These values are taken from estimates based on experiments. None of these values are fitted parameters.
The conformational dependent ADP release step should be examined in more detail in experiments. Laser trap experiments with a single myosin have shown a force-dependent ADP release (Veigel et al., 2001). Thus, some of the assumptions of the model are already justified. The quantitative dependence of the ADP release rate on θ is unavailable. Perhaps molecular dynamics simulations or detailed experiments can answer this question.
We note that the computed results in this article are for muscle movement near steady state. The transient, nonequilibrium behavior of muscle contraction is also interesting (Huxley and Simmons, 1971; Piazzesi et al., 2002; Reconditi et al., 2004). For instance, a bistable behavior is observed near stall. The discussion of the transient aspects, and further elaborations on the role of titin will be the subjects of a forthcoming article.
Acknowledgments
G.L. and S.X.S. are supported by the Whitaker Biomedical Engineering Leadership award and the Whiting School of Engineering at Johns Hopkins University.
APPENDIX A: ELASTIC ENERGY OF THE STALK
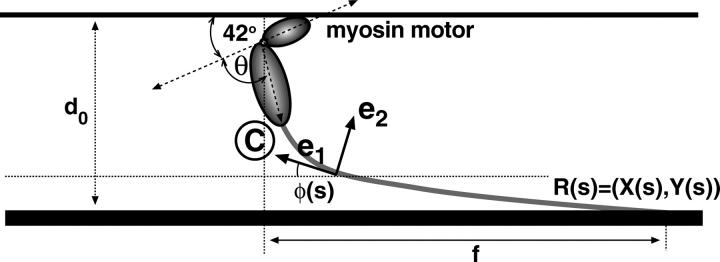
The geometry and energy of an elastic filament are completely specified by its boundary conditions (see Fig. 7). The shape of the filament is given by a two-component function R(s) = (X(s), Y(s)) in the x,y plane. We start with the force and torque balance conditions,
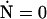 |
(A1) |
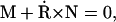 |
(A2) |
where N is the total force per unit length along the filament and M is the torque per unit length. The dot notation represents a derivative with respect to the arc-length, e.g.,  We also define a body fixed frame, (e1(s), e2(s)), where
We also define a body fixed frame, (e1(s), e2(s)), where 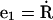 and
and
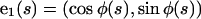 |
(A3) |
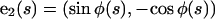 |
(A4) |
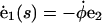 |
(A5) |
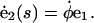 |
(A6) |
FIGURE 7.
The geometry of the light-chain filament. The myosin motor changes the boundary condition of the filament at s = L. The subsequent relaxation of the filament produces the powerstroke.
Written in component form, we have
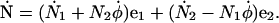 |
(A7) |
This implies
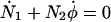 |
(A8) |
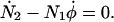 |
(A9) |
The torque is
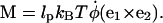 |
(A10) |
Combining with the torque balance condition of Eq. A2, we obtain
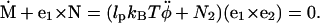 |
(A11) |
This implies 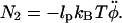 We finally arrive at four coupled equations describing the filament geometry:
We finally arrive at four coupled equations describing the filament geometry:
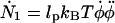 |
(A12) |
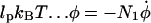 |
(A13) |
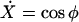 |
(A14) |
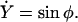 |
(A15) |
The elastic energy in the filament is then given by
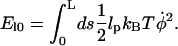 |
(A16) |
To solve the elastic equations, six boundary conditions, i.e., X(0), Y(0), X(L), Y(L), φ(0), and φ(L), are required. We have
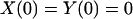 |
(A17) |
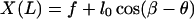 |
(A18) |
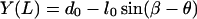 |
(A19) |
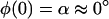 |
(A20) |
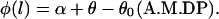 |
(A21) |
The endpoint (X(L), Y(L)) is related to the filament position x by the relationship
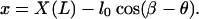 |
(A22) |
By varying θ and X(L), we obtain El0(x,θ).
APPENDIX B: THE RELATIONSHIP BETWEEN M AND LP
During the powerstroke in scenario I, the vertical displacement of the stalk is small compared to its overall length. Thus, small deflection approximation is excellent in describing the overall change in elastic energy. The shape of the filament is given by the function, y(x). The elastic energy in this case is
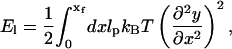 |
(B1) |
where xf = L cos α. The Euler-Lagrange equation minimizing the filament geometry is therefore
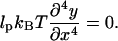 |
(B2) |
The solution is a polynomial, y = ax3 + bx2 + cx + d. The boundary conditions are
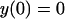 |
(B3) |
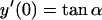 |
(B4) |
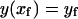 |
(B5) |
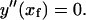 |
(B6) |
Therefore,
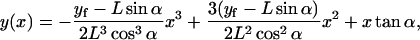 |
(B7) |
and
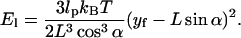 |
(B8) |
Since the undeformed filament height is y0 = L sin α, El is in the form of
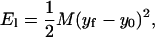 |
(B9) |
where
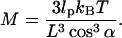 |
(B10) |
If lp = 100 nm, L = 50 nm, and α = 2°, then M ≈ 0.002 kBT/nm2, or essentially negligible.
References
- Badoual, M., F. Julicher, and J. Prost. 2002. Bidirectional cooperative motion of molecular motors. Proc. Natl. Acad. Sci. USA. 99:6696–6701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bagshaw, C. R. 1993. Muscle Contraction, 2nd Ed. Chapman and Hall, London, UK.
- Bortz, A., M. Kalos, and J. Lebowitz. 1975. A new algorithm for Monte Carlo simulation of Ising spin systems. J. Comput. Phys. 17:10–18. [Google Scholar]
- Clark, R. J., M. Nyitrai, M. R. Webb, and M. A. Geeves. 2003. Probing nucleotide dissociation from myosin in vitro using microgram quantities of myosin. J. Muscle Res. Cell Motil. 24:315–321. [PubMed] [Google Scholar]
- Conibear, P. B., C. R. Bagshaw, P. G. Fajer, M. Kovacs, and A. Malnasi-Csizmadia. 2003. Myosin cleft movement and its coupling to actomyosin dissociation. Nature Struct. Bio. 10:831–835. [DOI] [PubMed] [Google Scholar]
- Cooke, R. 1986. The mechanism of muscle contraction. CRC Crit. Rev. Biochem. 21:53–118. [DOI] [PubMed] [Google Scholar]
- Duke, T. A. J. 1999. Molecular model of muscle contraction. Proc. Natl. Acad. Sci. USA. 96:2770–2775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein, M., and W. Herzog. 1998. Theoretical Models of Skeletal Muscle. John Wiley and Sons, London, UK.
- Finer, J. T., R. M. Simmons, and J. A. Spudich. 1994. Single myosin molecule mechanics: picoNewton forces and nanometre steps. Nature. 368:113–119. [DOI] [PubMed] [Google Scholar]
- Greene, L. E., and E. Eisenberg. 1980. Dissociation of the actin subfragment 1 complex by adenyl-5′-yl imidodiphosphate, ADP, and PPi. J. Biol. Chem. 255:543–548. [PubMed] [Google Scholar]
- Greene, L. E., and E. Eisenberg. 1990. Dissociation of clathrin from coated vesicles by the uncoating ATPase. J. Biol. Chem. 12:6682–6687. [PubMed] [Google Scholar]
- Gulick, A. M., and I. Rayment. 1997. Structural studies on myosin II: communication between distant protein domains. Bioessays. 19:561–569. [DOI] [PubMed] [Google Scholar]
- Howard, J. 1994. Clamping down on myosin. Nature. 368:98–99. [DOI] [PubMed] [Google Scholar]
- Howard, J. 2001. Mechanics of Motor Proteins and the Cytoskeleton. Sinauer Associates, Sunderland, MA.
- Huxley, A. F., and R. M. Simmons. 1971. Proposed mechanism of force generation in striated muscle. Nature. 233:533–538. [DOI] [PubMed] [Google Scholar]
- Huxley, A. F., and R. Niedergerke. 1954. Structural changes in muscle during contraction. Nature. 173:971–973. [DOI] [PubMed] [Google Scholar]
- Huxley, H., and J. Hanson. 1954. Changes in the cross-striations of muscle during contraction and stretch and their structural interpretation. Nature. 173:973–976. [DOI] [PubMed] [Google Scholar]
- Kurzawa, S. E., D. J. Manstein, and M. A. Geeves. 1997. Dictyostelium discoideum myosin II: characterization of functional myosin motor fragments. Biochemistry. 36:317–323. [DOI] [PubMed] [Google Scholar]
- Lan, G. H., and S. X. Sun. 2005. Dynamics of myosin-V processivity. Biophys. J. 88:999–1008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, H., W. A. Linke, A. F. Oberhauser, M. Carrion-Vazquez, J. G. Kerkvliet, H. Lu, P. E. Marszalek, and J. M. Fernandez. 2002. Reverse engineering of the giant muscle protein titin. Nature. 418:998–1002. [DOI] [PubMed] [Google Scholar]
- Linke, W. A. 2000. Stretching molecular springs: elasticity of titin filaments in vertebrate striated muscle. Cell. Mol. Biol. 15:799–811. [DOI] [PubMed] [Google Scholar]
- Linke, W. A., M. Ivemeyer, N. Olivieri, B. Kolmerer, J. C. Ruegg, and S. Labeit. 1996. Towards a molecular understanding of the elasticity of titin. J. Mol. Biol. 261:62–71. [DOI] [PubMed] [Google Scholar]
- Linke, W. A., M. Ivemeyer, P. Mundel, M. R. Stockmeier, and B. Kolmerer. 1998. Nature of peak titin elasticity in skeletal muscle. Proc. Natl. Acad. Sci. USA. 95:8052–8057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lymn, R. W., and E. W. Taylor. 1971. Mechanism of adenosine triphosphate hydrolysis by actomyosin. Biochemistry. 10:4617–4624. [DOI] [PubMed] [Google Scholar]
- Milligan, R. A., M. Whittaker, and D. Safer. 1990. Molecular structure of F-actin and location of surface binding sites. Nature. 348:217–221. [DOI] [PubMed] [Google Scholar]
- Minajeva, A., M. Kulke, J. M. Fernandez, and W. A. Linke. 2001. Unfolding of titin domains explains the viscoelastic behavior of skeletal myofibrils. Biophys. J. 80:1442–1451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minajeva, A., C. Neagoe, M. Kulke, and W. A. Linke. 2002. Titin-based contribution to shortening velocity of rabbit skeletal myofibrils. J. Physiol. 540:177–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pate, E., G. J. Wilson, M. Bhimani, and R. Cooke. 1994. Temperature dependence of the inhibitory effects of orthovanadate on shortening velocity in fast skeletal muscle. Biophys. J. 66:1554–1562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pate, E., H. White, and R. Cooke. 1993. Determination of the myosin step size from mechanical and kinetic data. Proc. Natl. Acad. Sci. USA. 90:2451–2455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piazzesi, G., M. Reconditi, M. Linari, L. Lucii, Y. B. Sun, T. Narayanan, P. Boesecke, V. Lombardi, and M. Irving. 2002. Mechanism of force generation by myosin heads in skeletal muscle. Nature. 415:659–662. [DOI] [PubMed] [Google Scholar]
- Rayment, I., H. M. Holden, M. Whittaker, C. B. Yohn, M. Lorenz, K. C. Holmes, and R. A. Milligan. 1993. Structure of the actin-myosin complex and its implications for muscle contraction. Science. 261:58–65. [DOI] [PubMed] [Google Scholar]
- Reconditi, M., M. Linari, L. Lucii, A. Stewart, Y. B. Sun, P. Boesecke, T. Narayanan, R. F. Fischetti, T. Irving, G. Piazzesi, M. Irving, and V. Lombardi. 2004. The myosin motor in muscle generates a smaller and slower working stroke at higher load. Nature. 428:578–581. [DOI] [PubMed] [Google Scholar]
- Reedy, M. K., K. C. Holmes, and R. T. Tregear. 1965. Induced changes in orientation of the cross-bridges of glycerinated insect flight muscle. Nature. 207:1276–1280. [DOI] [PubMed] [Google Scholar]
- Siemankowski, R. F., M. O. Wiseman, and H. D. White. 1985. ADP dissociation from actomyosin subfragment 1 is sufficiently slow to limit the unloaded shortening velocity in vertebrate muscle. Proc. Natl. Acad. Sci. USA. 82:658–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spudich, J. A. 2001. The myosin swinging cross-bridge model. Nat. Rev. Mol. Cell Biol. 2:387–392. [DOI] [PubMed] [Google Scholar]
- Uyeda, T. O. P., P. D. Abramson, and J. A. Spudich. 1996. The neck region of the myosin motor domain acts as a lever arm to generate movement. Proc. Natl. Acad. Sci. USA. 93:4459–4464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veigel, C., F. Wang, M. Bartoo, J. Sellers, and J. Molloy. 2001. The gated gait of the processive molecular motor, myosin-V. Nat. Cell Biol. 4:59–65. [DOI] [PubMed] [Google Scholar]
- Vilfan, A., and T. A. Duke. 2003. Instabilities in the transient response of muscle. Biophys. J. 85:818–827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, H., C. S. Peskin, and T. C. Elston. 2003. A robust numerical algorithm for studying biomolecular transport processes. J. Theor. Biol. 221:491–511. [DOI] [PubMed] [Google Scholar]