Metapopulation dynamics and spatial heterogeneity in cancer

Abstract

With the advent of drugs targeting specific molecular defects in cancerous cells [Gorre, M. E., et al. (2001) Science 293, 876–880], it is important to understand the degree of genetic heterogeneity present in tumor cell populations and the rules that govern microdiversity in human cancer. Here, we first show that populations with different genotypes in genes influencing cell growth and programmed cell death coexist in advanced malignant tumors of the colon, exhibiting microsatellite instability. Detailed, physical mapping of the diverse populations shows them to be arranged in small, intermingling areas, resulting in a variegated pattern of diversity. Using computational modeling of the experimental data, we find that the coexistence between similar competitors is enhanced, instead of deterred, by spatial dynamics [Hanski, I. (1999) Metapopulation Dynamics (Oxford Univ. Press, New York)]. The model suggests a simple and plausible scenario for the generation of spatial heterogeneity during tumor progression. The emergence and persistence of the patterns of diversity encountered in the tumors can be generated without a need to invoke differences in mutation rates, neutrality of interactions, or separated time scales. We posit that the rules that apply to spatial ecology and explain the maintenance of diversity are also at work in tumors and may underlie tumor microheterogeneity.

The standard model invoked to explain tumor progression, the increase of biological malignancy with time, is clonal evolution, first proposed by Nowell in 1976 (1). Successive acquisition of mutations generates diverse clones, and it is postulated that the emergence of a dominant clone underlies the biological and clinical properties of a tumor at a point in its natural history (2). The study of structural genetic alterations found in human tumors provides further support for the clonal evolution model (3, 4), and limited observations suggest that the tempo of tumor progression may follow a punctuated pattern with long periods of stasis and periods of rapid genetic change in the tumor cells (5). In contrast to the concept of the emergence of a dominant clone, it is becoming increasingly apparent not only that microheterogeneity of tumor cells can be demonstrated at the phenotypic level, but that genetic heterogeneity is present in many advanced tumor types. Recent reports demonstrating genetic diversity within loci that play a key mechanistic role in tumor formation [e.g., K-ras, p53, transforming growth factor-βRII (TGFβRII), and BAX] present a paradox (6–8). How can the prolonged coexistence of genetically diverse populations and the concomitant lack of dominance be explained? After studying microdiversity in tumors exhibiting a microsatellite instability (MSI), we present a possible answer to this question. In silico modeling of the geography of clonal diversity suggests that the same fundamental principles that explain lack of dominance in complex ecosystems underlie the maintenance of clonal diversity in human tumors.

Materials and Methods

Human Tissues and Microdissection.

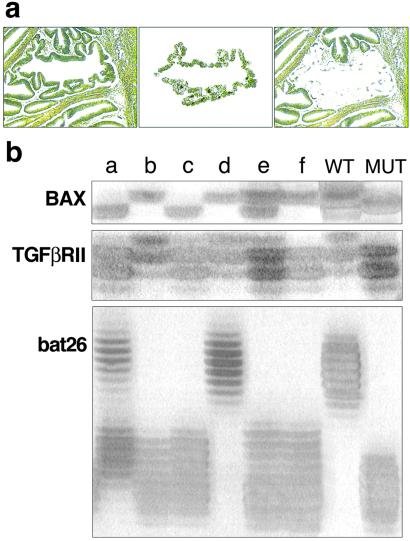
Annotated, anonimized tissues were obtained after approval by the human investigations committee at the Ciutat Sanitària i Universitària de Bellvitge, Barcelona. The six tumors were part of a group of colorectal neoplasms previously studied for MSI (9). All were adenocarcinomas with variable amounts of mucin production. Four tumors were staged as Duke's B (T-2, T-3, T-5, and T-6), and two tumors belonged to the Duke's C with visceral metastases (T-1 and T-4). For microdissection, archival paraffin tissue blocks were cut at a thickness of 6 μm and stained with methyl green. Microdissection was carried out by laser capture (PixCell; Arcturus Engineering, Mountain View, CA), by using a ×40 lens and paying attention to the exclusion of stromal cells. Intraepithelial lymphocytes in tumor glands were not identified. The micrographs in Fig. 1a show how a tumoral glandular structure is acquired: from the field shown at Left, a single structure is lifted from the tissue (Center). The result (Right) verifies the purity of the microdissected cell population. Each pool of cells analyzed represents the population of tumor cells enclosed in a contiguous surface of 100 μm².

Figure 1.

(a) The micrographs show how a tumoral glandular structure is acquired: from the field (Left), a single structure is lifted from the tissue (Center). The result (Right) verifies the purity of the microdissected cell population. Each pool of cells analyzed represents the population of tumor cells enclosed in a contiguous surface of 100 μm². (b) The results of the genetic analysis can be interpreted easily for each of the selected areas. Lane e shows a BAX^+/−; TGFβRII^+/−; bat26^−/−. Heterozygosity is not caused by contamination of normal cell elements because the DNA extracted from a single area often shows a mut/mut genotype for one of the three loci examined. The 27 possible genotypes for any given area make it unlikely that heterozygosity would be caused by an equal mixture of +/+ and −/− cells.

Genotyping.

DNA extraction with proteinase K, as manufacturers recommend, was followed by PCR amplification by using 40 cycles of three loci: bat26 (a 26 A tract within an intron of hMSH2) (10), a G8 repeat (codons 38–41) within BAX (11), and an A10 tract (nucleotides 709–718) within TGFβRII. The 100-bp fragment of TGFβRII was amplified from ≈200 pg of DNA by using 40 cycles of 94°C for 30 s, 60°C for 45 s, and 72°C for 45 s with the primers as described (12). Detection of mutations was performed by electrophoresis in sequencing gels and silver staining. The results of the genetic analysis (Fig. 1b) can be interpreted easily for each of the selected areas. Lane e in Fig. 1b shows a BAX^+/−; TGFβRII^+/−; bat26^−/−. Heterozygosity is not caused by contamination of normal cell elements because the DNA extracted from a single area often shows a mutation/mutation genotype for one of the three loci examined. The 27 possible genotypes for any given area make it unlikely that heterozygosity would be caused by an equal mixture of +/+ and −/− cells. To ascertain that allele dropout was not a source of artifact, we performed triplicate PCRs by using serial dilutions of the input DNA. Each original reaction was performed with 200 pg of DNA. Allele drop-out emerged (one of three replicates) at 2 pg. To verify the results of the TGFβRII genotyping, especially in the case of heterozygosity, we have pooled three samples and verified that the genotype remains the same after 35 cycles. In addition, 30 samples were chosen randomly and the genotyping for TGFβRII was repeated. In all instances, the genotypes were confirmed.

In Silico Model.

Our model is a simple, stochastic, cellular automaton (voter-like) model on a 3D grid Ω with N×N×N sites and zero-flux boundary conditions (13–16). Here, we use n = 45. The spatial position of each site is given by r = (i, j, k) with 1 ≤ i, j, k ≤ N. Cell types are indicated by means of an integer variable S(r) ∈ Σ = {0,1,2}. These three states correspond to empty [S(r) = 0], normal epithelium [S(r) = 1], and cells with MSI [S(r) = 2], respectively. Each cell with MSI will be characterized by two additional values, b(r), t(r) ∈ {0,1,2}, indicating the number of mutated alleles in BAX and TGFβRII, respectively. Each run of in silico tumor growth involves, at the beginning, eight cells (located at the center of the lattice Ω). These cells are in state 1 (i.e., normal epithelium), and the rest of the lattice is empty (state 0).

Three rules define the dynamics of this cellular automaton. (i) Cell death: any given cell can die with probability P_d = D_kδ, where δ is the basal probability of death per cell per replication round and k = b(r). Here, D₀ = 1, and 0 < D₁, D₂ < 1 multiplicative factors that decrease apoptosis (cell death) depend on b(r). (ii) Cell replication: a given cell can replicate to any of its six nearest grid sites, with probability P_r= R_kρ, where k = t(r) and ρ is the basal replication probability (here this is fixed to ρ = 0.05). Now R₀ = 1 and R₁, R₂ > 1. An additional constraint to this rule would restrict cell proliferation to the presence of available empty sites. Under this approach, dominant clones expand at a rate that essentially is defined by the die-off of less dominant cell populations. This additional constraint does not modify our final conclusions, but it is computationally expensive. (iii) Mutation: once replication takes place, mutations in BAX and TGFβRII also can occur in cells with MSI. Each gene can independently add a mutation with fixed probability μ, i.e., t (m) → t(m) + 1 and/or b(m) → b(m) + 1.

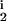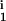We use a simple algorithm (17) to search over the six-dimensional parameter space T = (δ, μ, D₁, D₂, R₁, R₂). Using the rules specified above, a set of M = 10² candidate solutions defined as 6-tuples C_i = (δⁱ, μⁱ, D, D, R, R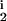); i = (1, …,M) is created by randomly generating the parameters, with δⁱ, μⁱ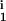, D, D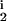 ∈ [0, 0.25] and 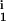R, R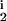 ɛ [1, 3]. This defines the G = 0 generation in the algorithm. For each of these vectors, in silico tumor growth occurs over T = 200 steps, and this is repeated over 20 replicas. At the end of each replica, the cell populations with different frequencies of mutations in BAX and TGFβRII are computed, and the distance F_i between the ith simulation average and the experimental data are stored (here, this distance will play a role of inverse fitness in the algorithm). Once all M runs are finished, the average distance F = Σ_i F_i/M is computed, and those solutions such that F_i > F are eliminated. The eliminated solutions are replaced by new ones derived from the survivors after small changes (within 5% of their current values) in the parental parameters.

Results

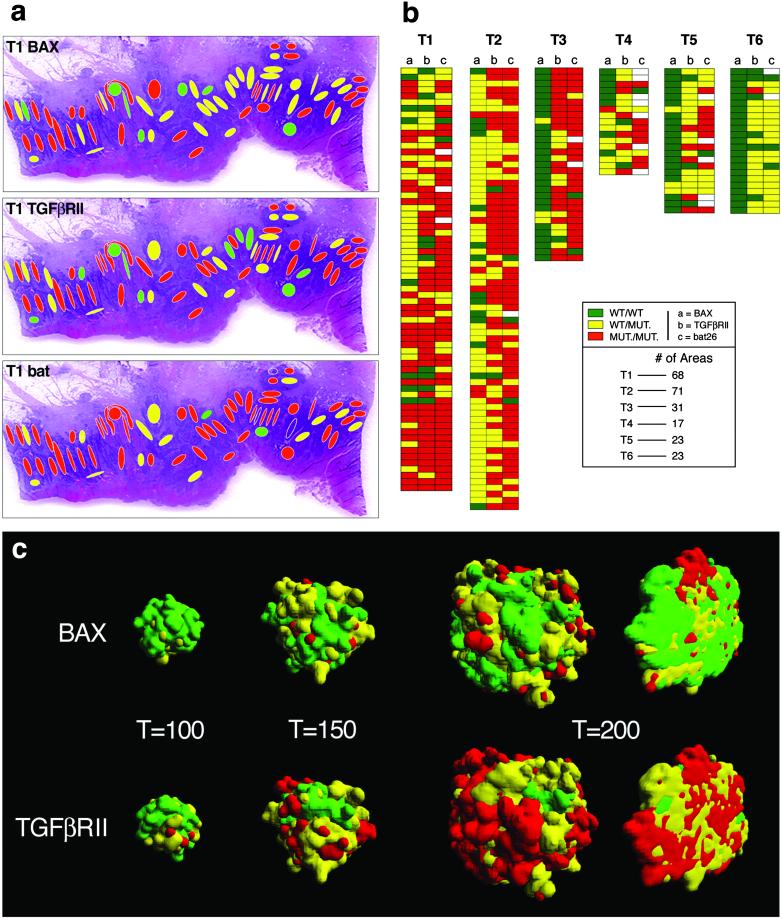
We began by constructing a detailed, 2D diversity map of six sporadic, advanced colonic carcinomas exhibiting MSI (18). We used laser-assisted microdissection to acquire distinct tumor cell populations occupying an average area of 100 μm² each (Fig. 1a). For each of the 233 populations examined, we determined the length of three microsatellite sequences located in an intronic region of hMSH2 (bat26) and within exons of TGFβRII and BAX (10–12) (Fig. 1b). The prevalence of mutations in the 233 zones was as follows: bat26 heterozygous, 26%, homozygous, 68%; TGFβRII heterozygous, 42%, homozygous, 48%; BAX heterozygous, 41%, homozygous, 16%. The heterozygous patterns are unlikely to be due to contamination by nontumoral cells with normal genotypes because in 77% of the samples, at least one of the loci examined exhibited a homozygously mutated pattern (Fig. 2b). The results showing coexistence in the same sample of a homozygously mutated locus with a WT genotype also argue against contamination as an explanation for the results obtained. The possibility of allele dropout also was ruled out by ascertaining that exclusion of one allele did not occur with the conditions used (see Materials and Methods). Mutations in two of these three genes, TGFβRII and BAX, are functionally significant in terms of cell growth and cell death and play a role in the pathogenesis of colonic carcinomas with MSI (19, 20). We classified each of the 233 distinct areas into 27 possible genotypes (+/+, WT; +/−, heterozygous mutation; −/−, homozygous mutation in three loci). The degree and scale of heterogeneity present in the six tumors we analyzed are depicted in Fig. 2 a and b. Fig. 2a illustrates the high degree of intermingling of clones with diverse genotype seen in one of the tumors. The geographical distribution of genotypes in advanced tumors indicates that clones with homozygous loss of TGFβRII and hemizygous for BAX are unable to take over the space occupied by a TGFβRII-hemizygous/BAX-WT neighbor. The lack of dominance is even more strikingly demonstrated by the presence of isolated tumor clones that are WT for one or the other of the tumor genes analyzed or even for both (Fig. 2b). The abnormal morphology of the cells sampled and the demonstration of a bat26^−/− genotype indicate that these populations lacking shortening of the microsatellite sequences in TGFβRII and BAX indeed are tumoral. The possibility that the WT pattern (normal length of the repeat) could be produced by shortening of a previously mutated (lengthened) microsatellite locus is unlikely in view of the data presented by Ionov et al. (20). Table 1 gives the frequency of TGFβRII and BAX genotypes in the totality of tumor areas sampled. The most prevalent genotype is [TGFβRII^−/−;BAX^+/−], followed by [TGFβRII^+/−;BAX^+/+]. As is evident from the schematic representation of the results found for each individual tumor (Fig. 2b), BAX^+/+ predominates in the less cellular, mucin-rich tumors for which the total number of areas sampled is smaller.

Figure 2.

(a) The dappled pattern of heterogeneity is shown for one of the tumors studied. Note the diversity of genotypes generated when three loci are referred to a single area. The micrograph of the tumor also illustrates the advanced stage of the tumor growth, which penetrates the entire thickness of the intestinal wall. (b) Summary of results for the six tumors studied. Each gene is represented in a column, with each file through the three columns representing an independently sampled area of the tumor. In many instances, an area that contains cells with two mutated alleles (e.g., TGFβRII and bat26) and a WT BAX can be seen. Tumors are arranged from the most cellular to the least cellular because of large mucin pools. The mucinous tumors, although in the same size category, yielded less cellular areas for genotypic characterization. (c) The geographical distribution of clones in the model indicates that the parameters found by the algorithm are close to the experimental data. The optional parameters found by the search algorithm were: δ = 0.01, μ = 0.0021, D₁ = 0.760, D₂ = 0.376, R₁ = 1.399, R₂ = 1.413. A cross-section of the 3D representation generated by the model shows the intermingling of clones with diverse genotypes to be close to the experimental findings.

Table 1.

Percentage of TGFβRII/BAX genotypes obtained experimentally/in silico

BAX	TGFβRII
	WT/WT	WT/MUT.	MUT./MUT.
WT/WT	6.44/5.08	20.17 /21.53	16.31 /20.17
WT/MUT.	3.00/2.98	16.73 /16.00	21.03 /19.33
MUT./MUT.	0.86/0.38	4.72 /5.21	10.73 /9.28

MUT., mutation. 

To gain insight and explore possible explanations for the striking lack of dominance we observed, we used a simple in silico model of tumor growth and progression. Of the three loci we studied, the model involves the two genes with functional significance, TGFβRII and BAX. We used an evolutionary algorithm (17) to search for the parameter values that would yield results closest to the maps obtained experimentally. The parameters are rates of replication, death, and mutation. Mono- or biallelic mutations in both genes lead to corresponding changes in the rates of division and death and, thus, explicitly include selective advantages (see Materials and Methods). Each generation or step of the algorithm creates 100 tumors, each characterized by a different and specific set of parameters, and selects those closest to the experimentally observed distribution of mutations. For each step, the solutions laying below the average distance to the experimental data are retained for a subsequent step of selection. At the end of each step, the extinct solutions are replaced by slightly altered replicas of the survivors (see Materials and Methods). Each step in the algorithm involves the growth of 100 virtual tumors. The robustness of the model (Fig. 3) is indicated by the fact that executing the algorithm 100 times (thus, growing 10,000 tumors) always provides the same optimal sets and no alternative solutions are found. An example of the close fit of the solutions to the experimental data is given in Table 1, and Fig. 2c shows that the geographical distribution of the virtual tumor cell populations reproduces the variegated spatial distribution observed in the human tumors (Fig. 2c).

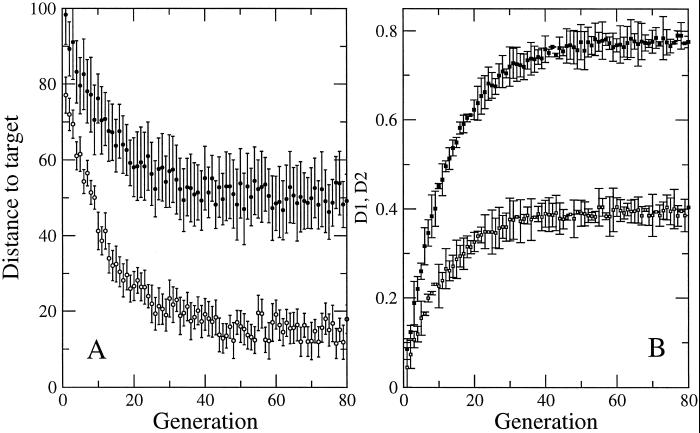
Figure 3.

The robustness of the search algorithm is shown. (A) The average distance (●) and the distance to the target for the optimal solution (○) is shown (the SDs are obtained over 10 different runs of the search algorithm). After ≈40 generations, near-optimal solutions already are obtained. (B) An example of the optimal values obtained for the parameters controlling apoptosis: D₁ (■) and D₂ (□) (see model description). The SD is shown (under the same conditions as in A). The curves show that different runs of the search algorithm reach basically the same parameter values.

Discussion

Genetic tumor cell heterogeneity in tumors showing MSI has been observed previously, and different explanations have been proposed. These explanations include: (i) mutations occur at different points in the history of the tumor, (ii) different rates of mutation exist for different loci in the same tumor, and (iii) mutations that show diversity are irrelevant for progression (7, 8). The model was designed to explain the maintenance rather than the origin of diversity. The spatial resolution of our model, at this point, does not match the spatial resolution of the experimental results. The scenario generated by the model we have used suggests an alternative, simple, and plausible explanation for the generation of spatial heterogeneity. The algorithm finds a solution that does not require differences in mutation rates, neutrality of interactions, or separated time scales for the emergence and persistence of diversity during tumor growth. It suggests that the coexistence of small clusters of cells with diverse genotype can be explained through the spatial dynamics resulting from the growth of two populations of similar competitors (14, 15). Under the local constraints imposed by explicit space, competitive exclusion requires extremely long times (more than 10⁴ generations), and, thus, spatial diversity is maintained. The model we present is actually close to the so-called voter model (15) in which coexistence between similar competitors is enhanced (instead of deterred) by spatial dynamics. This is illustrated clearly in Fig. 2c Lower, where we can see a rapid and simultaneous development of yellow (TGFβRII^+/−) and red (TGFβRII^−/−) domains that coexist. In biological tumors, this scenario would be enhanced by the high mortality rates that are expected to occur in cells generating thousands of mutations (21) and would provide a further source of diversity through recruitment limitation (22) as it occurs in complex ecosystems. Mutations in BAX spread at a slower pace (as shown by the predominance of green areas in Fig. 2b). This is not surprising because mutations in BAX, although important, have a smaller effect on fitness, here defined as the effective replication rate, f (i,j) = (1 − D_i δ) R_j ρ (see Materials and Methods). The fitness values for the mutated cells in the optimal solution are very similar, with 0.069 < f (i,j) < 0.070. This explains the differences in the spatial distribution between BAX and TGFβRII and their shape. Both in the model and the tumor clusters, TGFβRII cells tend to coalesce because of their increase in proliferative capacity, whereas groups of BAX-mutated cells persist and occupy their space. The model is also consistent with experiments with spatially extended microbial ecosystems (23, 24) and provides a strong indication that the rules that apply to spatial ecology are also at work in tumor dynamics. When we remove spatial constraints from the rules, homogeneity is achieved rapidly and consistently (data not shown).

Under the conditions defined by the search algorithm, the model gives support to the spatially dependent mechanism for the maintenance of diversity and also makes certain predictions regarding the fitness value of mono- or biallelic loss of function. The model indicates that a mutation in one allele of the BAX gene modifies cell death rate by 0.760 and by a factor of 0.376 when the mutation is homozygous. The proportionality of these effects is consistent with experimental studies in genetically modified mice that assessed the functional impact of hemi- and nullizygosity for BAX (25). With respect to TGFβRII, the model predicts that mutation in a single allele increases fitness by a factor of 1.399 and mutations leading to homozygosity increase fitness by a factor of 1.413. This prediction indicates that the second mutation in TGFβRII contributes little to the fitness as defined in silico and suggests that haplo-insufficiency for TGFβRII is of biological significance and an important determinant of tumorigenicity. The available experimental evidence in this regard is not inconsistent with this hypothesis (26, 27), and the prediction presented here should serve as rationale for studies that directly address this question.

The results we present offer a limited view of tumor cell diversity because it takes three loci under consideration (two functional and one neutral) and examines a single tumor type caused by a specific mechanism. Nevertheless, three arguments suggest that the general explanation we propose for a lack of clonal dominance, and thus diversity, is likely to be applicable to many forms of cancer and preneoplasia. First, similar genetic heterogeneity patterns have been found in colonic carcinomas without MSI (6); second, genetic heterogeneity has been documented in tumors of a variety of histological types (28, 29); and, third, a common principle may underlie the geography of diversity throughout biology. The development of highly specific therapeutic agents targeting the products of abnormal cancer genes gives urgency to the definition and understanding of tumor microheterogeneity. Indeed, in silico therapeutic experiments with the model we describe demonstrate that restitution of the function of TGFβRII has a very different impact on tumor growth and phenotype than restitution of BAX function (data not shown). Thus, it is likely that validated tumor models that closely replicate the biology of human tumors may play an important role in the selection of therapeutic targets and, thus, be relevant to the treatment and prevention of cancer.

Abbreviations

MSI

microsatellite instability

TGFβRII

transforming growth factor-βRII