Fast synaptic inhibition promotes synchronized gamma oscillations in hippocampal interneuron networks

Abstract

Networks of GABAergic interneurons are of critical importance for the generation of gamma frequency oscillations in the brain. To examine the underlying synaptic mechanisms, we made paired recordings from “basket cells” (BCs) in different subfields of hippocampal slices, using transgenic mice that express enhanced green fluorescent protein (EGFP) under the control of the parvalbumin promoter. Unitary inhibitory postsynaptic currents (IPSCs) showed large amplitude and fast time course with mean amplitude-weighted decay time constants of 2.5, 1.2, and 1.8 ms in the dentate gyrus, and the cornu ammonis area 3 (CA3) and 1 (CA1), respectively (33–34°C). The decay of unitary IPSCs at BC–BC synapses was significantly faster than that at BC–principal cell synapses, indicating target cell-specific differences in IPSC kinetics. In addition, electrical coupling was found in a subset of BC–BC pairs. To examine whether an interneuron network with fast inhibitory synapses can act as a gamma frequency oscillator, we developed an interneuron network model based on experimentally determined properties. In comparison to previous interneuron network models, our model was able to generate oscillatory activity with higher coherence over a broad range of frequencies (20–110 Hz). In this model, high coherence and flexibility in frequency control emerge from the combination of synaptic properties, network structure, and electrical coupling.

Gamma frequency oscillations are thought to be of key importance for higher brain functions, such as feature binding and temporal encoding of information (1–5). Experimental and theoretical evidence suggests that local networks of synaptically connected GABAergic interneurons are critically involved in the generation of these oscillations (6–19). First, perisomatic inhibitory interneurons (basket cells) fire action potentials at high frequency during gamma activity in vivo, with single spikes phase-locked to the oscillations of the field potential (6, 7). Second, pharmacologically isolated networks of inhibitory interneurons in vitro can oscillate at gamma frequency in response to metabotropic glutamate receptor activation (8). Finally, models of mutually connected interneurons generate coherent action potential activity in the gamma frequency range in the presence of a tonic excitatory drive (9–19).

The mechanisms leading to the generation of coherent gamma oscillations in interneuron networks, however, have remained unclear. Although gamma frequency oscillations can be generated in interneuron network models, coherence is fragile against variation in amplitude and time course of the inhibitory postsynaptic conductance, against heterogeneity of the tonic excitatory drive, and against sparseness of connectivity (11–14). The mechanisms contributing to the control of network frequency are also poorly understood. It is thought that the time course of the inhibitory synaptic conductance change is a major factor (8–14), but the significance of other parameters remains undetermined. Some models suggest that coherent oscillations can be generated only in a relatively narrow frequency band around 40 Hz (e.g., ref. 12), whereas others indicate that frequency is regulated over a wider range by synaptic kinetics, synaptic strength, and tonic excitatory drive (e.g., ref. 11).

Although the inhibitory postsynaptic conductance change is a key determinant of both coherence and frequency of oscillations, synapses between interneurons have remained largely uncharacterized. Unitary inhibitory postsynaptic currents (IPSCs) at interneuron–interneuron synapses in the dentate gyrus (DG) show unexpectedly fast kinetics, with a mean decay time constant of 2.5 ms at near-physiological temperature (16). However, it is unknown whether the rapid time course of IPSCs at interneuron–interneuron synapses is a general principle that also applies to other cortical regions. Furthermore, it is unclear how the properties of interneuron–interneuron synapses in DG, and the cornu ammonis area 3 (CA3) and 1 (CA1) of the hippocampus relate to the differences in power and preferred frequency of gamma oscillations in vivo (6) and in vitro (8, 20–24).

To address these questions, we made paired recordings from synaptically connected perisomatic inhibitory interneurons in the hippocampal CA3 and CA1 region, using transgenic mice that express enhanced GFP (EGFP) under the control of the parvalbumin promoter. Based on these results, we developed a realistic interneuron network model and examined its oscillatory properties. This combined experimental and computational approach allowed us to examine the mechanisms of one form of gamma oscillation that is generated in isolated interneuron networks (8).

Methods

Paired Recordings from Synaptically Connected Basket Cells (BCs) in Transgenic Mice.

Transgenic mice expressing EGFP under the control of the parvalbumin promoter were generated using bacterial artificial chromosome (BAC) techniques (25), as described in detail elsewhere (26). In brief, a mouse BAC library was screened with a parvalbumin probe, clone 450D23 that contained the largest genomic insert (180 kb) was selected, and an EGFP coding sequence was inserted at the translation start site. The BAC DNA was linearized and injected into the pronuclei of B6D2F2 mouse zygotes. Transgenic mice were crossed with wild-type (C57BL/6) mice, and the expression of the transgene in the offspring was monitored by UV body illumination (26). To ensure specificity of EGFP expression, a mouse line with a single integrated copy of the transgene was used.

Transverse hippocampal slices (300 μm thickness) were cut from brains of 20- to 25-day-old mice by using a vibratome (DTK-1000, Dosaka, Kyoto). Animals were killed by decapitation, in accordance with national and institutional guidelines. EGFP-expressing interneurons were visually identified using epifluorescence illumination. Recordings from selected neurons were made under visual control (infrared-differential interference contrast videomicroscopy). Patch pipettes were pulled from borosilicate glass tubing (2 mm outer diameter, 1 mm inner diameter). The resistance of the pipettes after filling with intracellular solution was 1.8–2.5 MΩ. The recording temperature was 33–34°C.

Two Axopatch 200B amplifiers (Axon Instruments, Foster City, CA) were used for current- and voltage-clamp recording. Recordings with initial resting potentials more positive than −55 mV for BCs and −65 mV for principal neurons were discarded. Spiking patterns were tested at the beginning of the experiment by using 500-ms or 1-s depolarizing pulses. In paired recordings, the presynaptic neuron was held in the current-clamp mode and stimulated at a frequency of 0.1–0.2 Hz, unless specified differently. Action potentials were initiated by brief current pulses (duration 2 ms, amplitude 1–1.4 nA). The postsynaptic cell was held in the voltage-clamp mode (holding potential −70 mV) with series resistance compensation enabled (70–95%, lag 10–35 μs; resistance before compensation 5–10 MΩ), unless specified differently. Pre- and postsynaptic signals were filtered at 5 kHz by using the four-pole low-pass Bessel filters of the amplifiers, and digitized at ≥10 kHz by using a 1401plus laboratory interface (Cambridge Electronic Design, Cambridge, U.K.) connected to a Pentium PC.

Data Analysis.

Rise time (20–80%), peak current, and latency of unitary IPSCs were determined using averages of 8–50 traces as described (16). The decay of the IPSCs was fitted with the sum of two exponentials [A₁ exp(−t/τ₁) + A₂ exp(−t/τ₂)], using a nonlinear least-squares fit algorithm. The amplitude-weighted mean decay time constant was obtained as τ_w = (A₁ τ₁ + A₂ τ₂)/(A₁ + A₂). Paired-pulse depression (PPD) was determined from average traces (including failures), measuring the peak amplitudes of IPSCs from the preceding baselines. Values are given as mean ± SEM. The statistical significance of differences was assessed by a two-sided Mann–Whitney U test or a Kruskal–Wallis test at the significance level (P) indicated.

Solutions and Chemicals.

The physiological extracellular solution contained 125 mM NaCl, 25 mM NaHCO₃, 25 mM glucose, 2.5 mM KCl, 1.25 mM NaH₂PO₄, 2 mM CaCl₂, and 1 mM MgCl₂ (equilibrated with 95% O₂/5% CO₂ gas mixture). Ten micromolar 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX; Tocris Bristol, U.K.) or 2 mM kynurenic acid (Sigma; in three paired recordings) was added to the bath solution to block excitatory postsynaptic currents. The intracellular solution contained 110 mM K-gluconate, 40 mM KCl, 0.1 mM EGTA, 2 mM MgCl₂, 2 mM Na₂ATP, and 10 mM Hepes; the pH was adjusted to 7.2 with KOH and the osmolarity was 310–315 mOsm; 0.1% biocytin (Molecular Probes) was added for intracellular labeling. Other chemicals were from Merck, Sigma, Riedel-de Haën (Seelze, Germany), or Gerbu (Gaiberg, Germany).

Morphological Analysis.

Biocytin-filled neurons were visualized using either avidin conjugated with 7-amino-4-methylcoumarin-3-acetic acid (AMCA, Vector Laboratories; ref. 27) or avidin-biotinylated peroxidase complex and 3,3′-diaminobenzidine (DAB) as chromogen (16, 27). Parvalbumin immunoreactivity was tested using a mouse monoclonal antibody against parvalbumin (diluted 1:5,000; Swant, Belinzona, Switzerland) and a Cy3-conjugated goat antibody against mouse IgG.

Development of an Interneuron Network Model.

Networks of fast-spiking inhibitory interneurons were modeled using NEURON 5.1 (28), running on a Pentium PC under Linux. Neurons were represented as single compartments. The specific leak conductance was 0.1 mS⋅cm⁻². Active conductances were modeled using modified Hodgkin and Huxley equations (12, 16). The time of an action potential was determined as the first point in the rising phase that exceeded 0 mV.

Chemical synapses were simulated as a postsynaptic conductance with exponential rise (rise time constant 0.16 ms) and biexponential decay [decay time constants 1.2 ms (amplitude contribution 90%) and 8 ms (10%); see Table 1, which is published as supporting information on the PNAS web site, www.pnas.org], unless specified differently. The unitary postsynaptic peak conductance (g_GABA) was varied from 0.001 to 1 mS⋅cm⁻², and the reversal potential was assumed as −75 mV. Synaptic latency consisted of a component of conduction and a component of synaptic delay (0.5 ms). Electrical synapses were implemented as a transcellular conductance of 0.01 mS⋅cm⁻², unless specified differently. Exp2Syn processes were used for implementation of chemical synapses (one or two per connection for monoexponential and biexponential decay, respectively). GAPS.MOD processes were used for implementation of electrical synapses (example file of the NEURON package).

A structured interneuron network was assembled from 200 neurons arranged on the circumference of a ring with 50 μm spacing, a simple representation that avoids edge effects. Each neuron was randomly connected to its 100 nearest neighbors by chemical synapses; the connection probability was given by a Gaussian function with a standard deviation of 24 cell–cell distances and an average connection probability of 0.57. This connectivity was consistent with published anatomical data (ref. 29; see also ref. 12). The conduction time was calculated from the distance between pre- and postsynaptic cells along the circumference. The conduction velocity was assumed to be 0.25 m⋅s⁻¹, unless specified differently, leading to conduction delays of 0.2–10 ms. This delay was consistent with the measured IPSC latency in pairs, given that recordings were preferentially made between closely spaced cells. Furthermore, each neuron was randomly connected to its eight nearest neighbors by electrical synapses with a connection probability of 0.5.

Network Simulations.

Neurons were initialized to a resting membrane potential of −65 mV. To initiate activity in the network, tonic driving currents (representing, for example, metabotropic glutamate receptor or kainate receptor activation) with amplitudes randomly chosen from a normal distribution (with mean I_μ and standard deviation I_σ) were applied to the neurons. I_μ ranged from 0.5–5 μA⋅cm⁻², and I_σ/I_μ was 0.1. To examine the development of synchronization from a disordered initial condition (simulation type 1; Fig. 3, Fig. 4 A–D), step-like driving currents were applied to individual neurons with randomized onset times taken from a uniform distribution in the range −150 ms ≤ t < −100 ms. Chemical and electrical synapses were inactive at −150 ms ≤ t < 0 and enabled for t ≥ 0. To examine the response of the network to a synchronous excitatory stimulus (simulation type 2; Fig. 4E), chemical and electrical synapses were enabled throughout the simulation, and a step-like excitatory drive was applied simultaneously to all or a subset of cells at t = 0 (with I_μ and I_σ, see above). In all simulations, the time step was 10 μs.

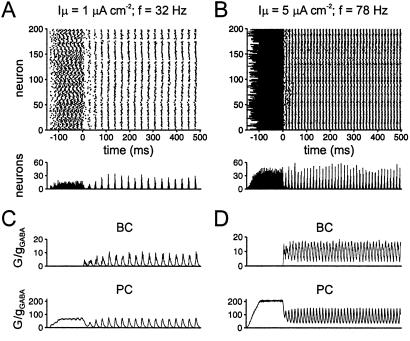
Figure 3.

A “realistic” interneuron network model with fast inhibitory synapses generates coherent activity over the entire gamma frequency range. (A and B) Network activity with standard parameters and unitary postsynaptic peak conductance g_GABA = 0.025 mS⋅cm⁻². Upper graphs are raster plots, with time on the horizontal axis, and index of the neuron in the network on the vertical axis. Each point represents an action potential. Lower graphs in A and B represent spike frequency histograms for the network; bin width 1 ms. (C and D) Analysis of inhibitory conductances during oscillations. Upper graphs represent the normalized total inhibitory conductance in a single interneuron (cell #1, G/g_GABA). The half-duration of the compound conductance changes determined from the last five oscillation cycles was 6.3 ms (C) and 8.1 ms (D), substantially slower than that of the unitary inhibitory conductance (1.4 ms). Lower graphs represent the synaptic output of the interneuron network simulated in a model principal neuron receiving convergent input from all interneurons [synaptic latency, 0.6 ms; decay time constants of unitary conductance, 1.2 ms (60% amplitude contribution) and 7.3 ms (40%), which was the typical inhibitory synaptic conductance change at BC–principal neuron synapses in CA1; see Table 1]. Tonic excitatory drive was applied at random time points −150 ms ≤ t < −100 ms, and chemical and electrical synapses were enabled at t ≥ 0 (type 1 simulation).

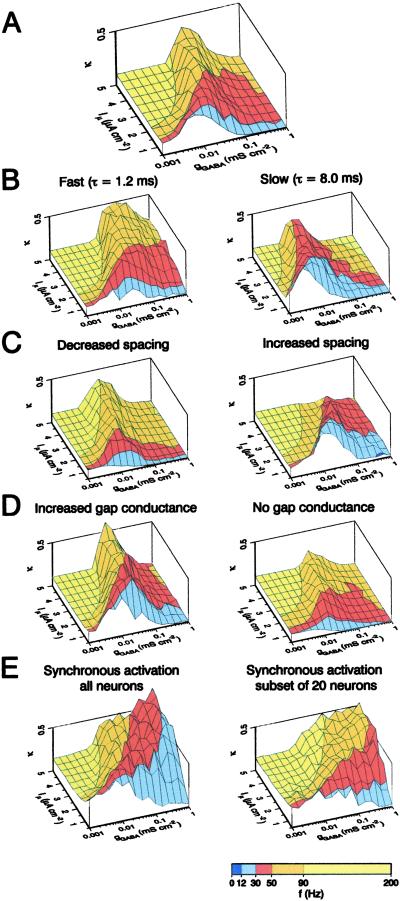
Figure 4.

Parameters that determine coherence and frequency in the interneuron network model. All graphs show coherence (κ) plotted against the amplitude of the unitary postsynaptic peak conductance (g_GABA) and excitatory drive (I_μ). Action potential frequency in the network is shown by superimposed color code (see scale bar at bottom). (A) Simulations with standard settings. Chemical and electrical synapses; biexponential synaptic conductance with decay time constants of 1.2 ms (90% amplitude contribution) and 8 ms (10%); 50 μm spacing; gap junction conductance 0.01 mS⋅cm⁻². (B) Influence of the decay kinetics of the inhibitory postsynaptic conductance. (Left) Fast monoexponential decay (decay time constant 1.2 ms). (Right) Slow monoexponential decay (decay time constant 8 ms). (C) Effects of spacing of neurons. (Left) Decrease in cell-cell distance by a factor of 2 (25 μm). (Right) Increase by a factor of 1.5 (75 μm). (D) Impact of electrical synapses. (Left) Increased gap junction conductance (0.02 mS⋅cm⁻²). (Right) Block of gap junctions. In all simulations (A–D) step-like driving currents were applied to individual neurons with randomized onset times of −150 ms ≤ t < −100 ms. Chemical and electrical synapses were inactive at −150 ms ≤ t < 0 and enabled for t ≥ 0 (type 1 simulation). Coherence was calculated for the time interval 400 ≤ t < 500 ms. (E) Effects of synchronous application of drive to the entire network (Left) or to a subset of 20 adjacent cells (10% of the population; Right). Chemical and electrical synapses were enabled throughout the simulation, and a step-like excitatory drive was applied simultaneously to all or a subset of cells at t = 0 (type 2 simulation). Coherence was calculated for the time interval 0 ≤ t < 100 ms.

Frequency and coherence of network activity were analyzed in 100-ms epochs (400 ms ≤ t < 500 ms and 0 ≤ t < 100 ms for type 1 and type 2 simulations, respectively). Average firing frequency (f) was determined from the mean interspike interval. To determine coherence, action potential patterns were represented in a binary format (with 0 when no action potential occurred and 1 if action potentials were generated in a given time interval). To account for differences in firing frequency, the time interval for the calculation of coherence was set to 0.1/f (12, 16). A cross-correlation-based population coherence measure κ was calculated as described (12, 16). Plots in Fig. 4 represent averages of five runs obtained with different random number generator seeds.

Results

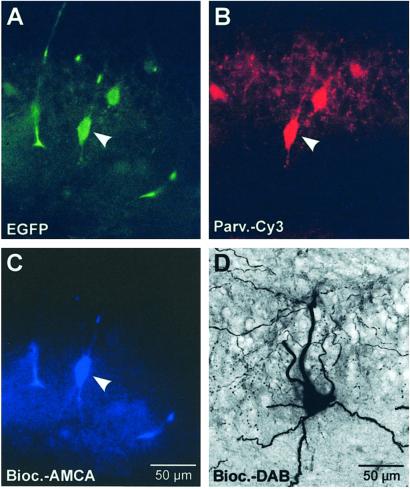
To examine the functional properties of inhibitory synaptic transmission in hippocampal interneuron networks, we focused on the parvalbumin-positive BC, a major type of interneuron that participates in nested theta-gamma oscillations (6, 7). To obtain recordings from pairs of synaptically connected BCs in slices, we made use of transgenic mice that expressed EGFP under the control of the parvalbumin promoter (Fig. 1; ref. 26). In hippocampal slices from these mice, several EGFP-labeled somata were observed in or close to the principal neuron layers under epifluorescence illumination (Fig. 1A). Double labeling confirmed that >80% of EGFP-positive cells were immunoreactive for the Ca²⁺-binding protein parvalbumin (Fig. 1B). Intracellular biocytin filling (Fig. 1C and D) revealed that their axons mainly arborized in the principal cell layers (11 of 11 EGFP-positive neurons; Fig. 1D). In whole-cell recordings, these cells generated high-frequency trains of action potentials during long depolarizing current pulses (mean action potential frequency 287 ± 18 Hz, range 110–420 Hz; 22 cells). In conclusion, these results demonstrate selective labeling of parvalbumin-positive fast-spiking BCs in hippocampal slices, ensuring reliable identification under experimental conditions.

Figure 1.

Identification of parvalbumin-expressing BCs in slices of transgenic mice. (A) EGFP labeling, (B) parvalbumin immunoreactivity probed with anti-parvalbumin antibody and Cy3-conjugated secondary antibody, and (C) biocytin labeling with AMCA-conjugated avidin. Images were taken from the same cell in the CA1 pyramidal cell layer (arrowheads). (D) Light-microscopic image of a biocytin-labeled interneuron (EGFP-positive) in the CA3 region visualized using DAB as a chromogen. Note axonal arborization in the pyramidal cell layer.

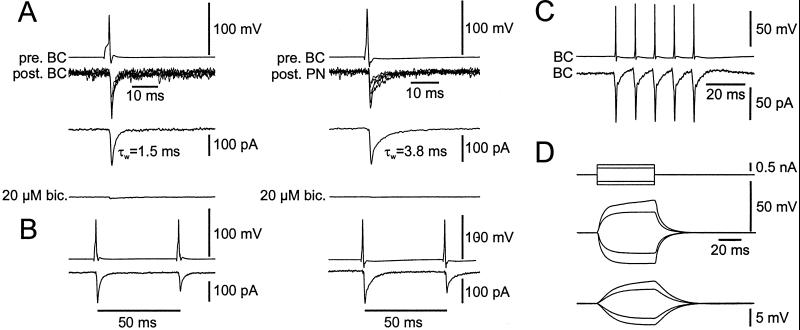
Recordings from pairs of EGFP-positive cells in DG, CA3, and CA1 revealed that BCs were coupled by both chemical and electrical synapses (Fig. 2). The key properties of chemical synaptic transmission were as follows (Fig. 2 A and B). First, unitary IPSCs showed very fast kinetics. The amplitude-weighted decay time constant obtained from a biexponential fit of the decay phase of average unitary IPSCs was 1.2–2.5 ms, with significant differences among regions (CA3 < CA1 < DG; P < 0.05; Fig. 2A Left; see Table 1). This fast IPSC decay time constant was a specific property of BC–BC synapses, because IPSCs generated at BC–principal neuron synapses in the same regions exhibited a slower decay (P < 0.05; Fig. 2A Right). Second, the IPSC peak amplitude was very large, particularly in CA3 and CA1 (93–208 pA; see Table 1). Third, IPSCs were blocked by bicuculline methiodide, a competitive antagonist of GABA_ARs (Fig. 2A Bottom; ref. 30). Finally, unitary IPSCs showed PPD during a pair of presynaptic action potentials (Fig. 2B Left; refs. 16, 31, and 32). PPD appeared to be independent of the type of target cell, because the extent of PPD was similar at BC–BC synapses and BC–principal neuron synapses in all three regions (P > 0.05; Fig. 2B Right). In contrast, slight differences in PPD were observed for BC–BC synapses among hippocampal subfields (CA3 > CA1 > DG; P < 0.05).

Figure 2.

Fast chemical and electrical transmission at BC–BC synapses in the hippocampus. (A) Unitary IPSCs in a pair of EGFP-labeled BCs (Left) and a pair of an EGFP-positive BC and an EGFP-negative principal cell (Right) in the CA1 subfield. Presynaptic action potentials are shown on top, unitary IPSCs (seven each) are shown superimposed in the center, and average unitary IPSCs (from 20 sweeps) are depicted below. Unitary IPSCs were almost completely blocked by the GABA_A receptor antagonist bicuculline methiodide (20 μM; Bottom traces). Note difference in the IPSC decay time constant between the two synapses. (B) PPD of unitary IPSCs in a pair of EGFP-labeled BCs (Left) and a pair of an EGFP-positive BC and an EGFP-negative principal cell (Right) in the CA1 subfield. Action potentials with a 50-ms interpulse interval are shown on top, corresponding average IPSCs (from 30 sweeps) are depicted at the bottom. Note similarity of PPD between the two synapses. Same pairs as those shown in A. (C and D) Electrical coupling in a pair of EGFP-labeled neurons in the DG. In C, the presynaptic cell was held in current-clamp, and the postsynaptic cell was held in voltage-clamp configuration. Lower traces are averages from 31 sweeps. Note that electrical PSCs mirrored presynaptic action potentials. In D, both cells were held in the current-clamp mode, and long de- or hyperpolarizing current pulses were applied. Traces are averages from 15 sweeps. The coupling ratio determined from pre- and postsynaptic voltage changes was 0.2.

In a subset of BC–BC pairs, presynaptic spikes evoked fast electrical PSCs (33–35), which were characterized by minimal latency, invariant peak amplitude (Fig. 2C), and bidirectionality (not illustrated). Furthermore, application of long current pulses to one cell resulted in correlated voltage changes in the other cell, which unequivocally demonstrates the electrical nature of the coupling (Fig. 2D). The mean coupling ratio for long current pulses, determined from pre- and postsynaptic voltages, was 0.11 ± 0.01 (three BC–BC pairs in DG). Electrical coupling was never observed between BCs and principal cells.

Our results show that the presence of fast and strong inhibitory synapses in networks of parvalbumin-positive perisomatic inhibitory interneurons is a general principle of synaptic organization of the hippocampus. The observed properties of BC–BC synapses challenged several assumptions of existing models of interneuron gamma oscillations (e.g., refs. 11–14). We therefore developed an interneuron network model based on realistic assumptions about synaptic properties and network structure, using the experimentally determined parameters from the CA1 region, and examined its oscillatory properties in the presence of a tonic excitatory drive (see Methods). With the realistic time course of the inhibitory synaptic conductance [τ₁ = 1.2 ms (90%), τ₂ = 8.0 ms (10%)] and a heterogeneity of the tonic excitatory drive (I_σ/I_μ) of 0.1, coherent oscillations emerged in the network model when chemical and electrical synapses were activated (Fig. 3). Synchronized activity was evident in the raster plots (Fig. 3 A and B Upper) and the corresponding spike frequency histograms (Fig. 3 A and B Lower). Synchronized activity was also apparent in the total inhibitory conductance in a given interneuron (Fig. 3 C and D Upper) and the inhibitory output simulated in a principal cell (Fig. 3 C and D Lower). Thus the model showed coherent activity over a wide range of tonic excitatory drive (Fig. 3 A and B).

To understand why the interneuron network model based on realistic assumptions was a robust gamma frequency oscillator, we varied individual network parameters and examined the effects on coherence and frequency (Fig. 4; see legend for explanation of the color code for frequency). We first ran simulations in which both tonic drive (I_μ) and unitary postsynaptic peak conductance (g_GABA) were varied systematically (Fig. 4A). With a heterogeneity I_σ/I_μ of 0.1, our model produced coherent oscillations in a large part of the parameter space corresponding to a broad range of frequencies (24–74 Hz for half-maximal κ). The maximum of coherence was close to the experimentally determined g_GABA [≈0.04 mS⋅cm⁻², estimated from a peak current of 208 pA (see Table 1), and a somatodendritic surface area of approximately 12,000 μm² (16)], suggesting that synaptic strength in the network is optimized for maximizing synchronization.

We then varied the synaptic decay time constant, the structural properties of the network, and the gap junction coupling conductance (Fig. 4 B–D). The synaptic decay time constant influenced both coherence and frequency of the oscillations (Fig. 4B). If the synaptic decay time constant was set to the value of the fast component, high coherence was mainly reached with high excitatory drive and large g_GABA, which corresponded to the upper gamma frequency band (37–79 Hz for half-maximal κ; Fig. 4B Left). Conversely, if the decay time constant was set to the value of the slow component, high coherence was mainly reached with low drive and small g_GABA, which corresponded to the lower gamma frequency band (18–55 Hz for half-maximal κ; Fig. 4B Right). The “realistic” network (Fig. 4A) appeared to inherit properties of both networks (Fig. 4B), resulting in flexible frequency control.

In contrast, structural properties of the network primarily affected the frequency, and to a smaller extent the coherence of the oscillations (Fig. 4C). Decreased spacing between neurons in the network (i.e., decreased conduction delay) increased the frequency (Fig. 4C Left), whereas increased spacing reduced it (Fig. 4C Right). Unexpectedly, both decreased and increased spacing reduced the average coherence value, indicating that an intermediate spacing (i.e., intermediate conduction delay) maximizes synchronization in the gamma frequency range (Fig. 4A). Finally, changes in gap junction conductance affected coherence selectively, with only minimal effects on frequency (Fig. 4D). An increase in gap junction conductance increased coherence (Fig. 4D Left), whereas a block of gap junctions reduced it (Fig. 4D Right). Thus the robustness of coherence appears to emerge from the combined effects of synaptic properties, network structure, and gap junction coupling.

In several types of oscillatory activity in vivo (e.g., during nested theta-gamma activity) the excitatory drive is nonstationary, unlike in the simulations shown (Fig. 4 A–D). To examine how the temporal–spatial structure of the excitatory drive affected coherence and frequency, we used a step-like excitatory drive applied to either all cells or to a subpopulation of neurons (Fig. 4E). If a drive with synchronized onset was applied to all cells, the network oscillated with higher coherence, but at approximately the same frequency (22–78 Hz for half-maximal κ; Fig. 4E Left) in comparison to the network subjected to an asynchronous excitatory drive (Fig. 4A). In contrast, if the synchronized drive was applied to a cluster of 20 adjacent interneurons, coherent oscillations were generated at markedly higher frequencies (30–110 Hz for half-maximal κ; Fig. 4E Right). In conclusion, the temporal–spatial structure of the stimulus critically shapes the oscillatory properties of the interneuron network. Our interneuron network model, if stimulated synchronously and focally, may explain “fast” (>90 Hz) gamma oscillations in the hippocampal CA1 region in vivo (36).

Discussion

Using transgenic mice that express EGFP under the control of the parvalbumin promoter, we found that unitary IPSCs at hippocampal BC–BC synapses showed rapid time course and large amplitude. Electrical coupling occurred in a subset of pairs. Both the fast kinetics of unitary IPSCs and the presence of gap junction coupling were target cell-specific, but region-independent properties. Thus, interneurons selectively express an extensive repertoire of fast signaling mechanisms (27, 37–42).

The experimentally observed properties of BC–BC synapses were not consistent with assumptions of prevailing models of interneuron gamma oscillations (e.g., refs. 11–14). First, the decay time constant was markedly faster than assumed in existing models (typically 10 ms). Second, inhibitory coupling appeared to be stronger than previously thought. The estimated specific unitary postsynaptic conductance change is 0.04 mS⋅cm⁻² in the CA1 region, larger than suggested previously (e.g., 0.001–0.002 mS⋅cm⁻²; ref. 12). Third, electrical coupling was abundant, but was not considered in many earlier simulation studies (refs. 11–14; but see ref. 17).

We therefore developed an interneuron network model that incorporated both realistic synaptic properties (using the experimentally determined parameters from the CA1 region) and a spatial structure with conduction delays. In comparison to the model proposed by Wang and Buzsáki (12), our model showed higher maximal coherence, despite a higher heterogeneity in the tonic excitatory drive (I_σ/I_μ = 0.1 vs. 0.03). Furthermore, it generated highly coherent oscillations over a broad range of tonic excitatory drive, corresponding to a wide range of frequencies (20–110 Hz). Finally, it showed highly coherent oscillations at physiologically relevant values of the unitary postsynaptic conductance change (≈0.04 mS⋅cm⁻²). In conclusion, our model generates coherent oscillations very robustly, but allows for flexibility in the control of network frequency.

Why is the new model able to generate coherent oscillations more robustly than previous models? Our simulation results (Fig. 4) suggest that high coherence is an emerging property that arises from the combination of several factors. Specifically, it is the combination of fast inhibitory conductance, high synaptic strength, and the presence of conduction delays in a structured network that appears to be favorable for establishing and maintaining synchrony. This conclusion differs from the previous view that slow/weak synapses are optimal for synchronization in the absence of conduction delays (refs. 12–14; see refs. 43 and 44). Intuitively, however, a rapid inhibitory signal generated with a certain delay is a very effective synchronizing signal. In contrast, a slow inhibitory signal without delay is not as effective, because recovery from inhibition is temporarily less well defined. In addition, we find that gap junctions enhance coherent oscillatory activity. However, the effects (Fig. 4D) are smaller than reported previously (17). This difference may be interpreted as partial functional redundancy generated by the coexpression of two fast signaling mechanisms.

In contrast to our initial expectations, differences in the decay time course of the inhibitory postsynaptic conductance did not explain the different oscillatory properties of the hippocampal subfields. In the intact rat a high-frequency gamma oscillator (80 Hz) in the DG predominates, whereas after entorhinal lesion a lower frequency oscillator (40–60 Hz) in CA1 emerges (6). Similarly, in the in vitro slice preparation, the preferred oscillation frequency is higher in the DG than in CA1 under similar conditions [DG: 60–70 Hz (20, 21); CA1: 30–50 Hz (8, 11, 22–24)]. This trend is opposite to the observed differences in the kinetics of the postsynaptic conductance, which were slower in the DG than in CA1 (see Table 1). However, our results suggest several alternative mechanisms of frequency tuning (see ref. 11). Different preferred frequencies could be explained by the differences in g_GABA, as observed experimentally (see Table 1; CA1 > CA3 ≫ DG; Fig. 4A), a higher tonic excitatory drive in the DG, presumably generated by the perforant path input (6), and differences in network structure, such as spacing between synaptically connected interneurons (Fig. 4C). Finally, the oscillation frequency depends on the temporal and spatial structure of the stimulus. Intuitively, the higher frequency of the oscillations in a subnetwork of clustered cells (Fig. 4E) could be understood as the result of reduced average conduction delay and decreased total inhibition on individual neurons.

In conclusion, we have shown that an interneuron network model based on realistic assumptions generates highly coherent oscillations over a wide range of frequencies (20–110 Hz). The model may provide an adequate representation of certain forms of hippocampal gamma oscillations, such as pharmacologically isolated interneuron network gamma in vitro (8, 11) and nested theta-gamma oscillations in vivo (6, 7), in which the activity is markedly higher in interneurons than in principal cells. Whether our model can be applied to gamma oscillations in the neocortex, however, remains to be established.

We thank Drs. J. Bischofberger, M. Heckmann, and R. Traub for critically reading the manuscript. This work was supported by Deutsche Forschungsgemeinschaft Grants SFB 505/C5 (to P.J.) and SFB 505/C6 (to M.F. and P.J.), Human Frontiers Science Program Organization Grant RG0017/1998-B (to P.J.), and grants from the Alexander-von-Humboldt Foundation (to P.J. and M.F.), the Schilling Foundation (to H.M.), and Novartis (to H.M.).

Abbreviations

EGFP

enhanced GFP

IPSC

inhibitory postsynaptic current

PPD

paired-pulse depression

DG

dentate gyrus

CA3

cornu ammonis area 3

CA1

cornu ammonis area 1

BC

basket cell