Modeling dynamic and network heterogeneities in the spread of sexually transmitted diseases

Abstract

A wide range of communicable human diseases can be considered as spreading through a network of possible transmission routes. The implied network structure is vital in determining disease dynamics, especially when the average number of connections per individual is small as is the case for many sexually transmitted diseases (STDs). Here we develop an intuitive mathematical framework to deal with the heterogeneities implicit within contact networks and those that arise because of the infection process. These models are compared with full stochastic simulations and show excellent agreement across a wide range of parameters. We show how such models can be used to estimate parameters of epidemiological importance, and how they can be extended to examine the effectiveness of various control strategies, in particular screening programs and contact tracing.

Sexually transmitted diseases (STDs) are an important and increasing public-health problem throughout the world, causing widespread mortality and morbidity and having immense social and economic consequences (1–4). The progress and dynamics of these infections within a population must be understood so that treatment and interventions can be most effectively targeted. Here we present a mechanism to predict the spread of infection through a network of contacts. This work bridges the gap between full simulations, which are difficult to parameterize, and risk-structured mean-field models, which ignore the strong effects attributable to partnerships.

The localized spread of infectious diseases has been successfully captured with a variety of spatial models (5–10). Such approaches recognize that the predominantly local nature of disease transmission leads to a high degree of spatial segregation and means that the population is not uniformly well mixed. An alternative and often more realistic strategy is to consider the spread of infection across a network of contacts. This approach is necessary for STDs because proximity in space is no longer the determining risk factor for transmission. The resulting sexual mixing network contains all of the information on potential pathways of infection and as such has proved vital in understanding STD spread (11–18).

The sexual mixing network focuses on one of the central issues of epidemiology: who can acquire infection from whom (19–22). Such networks represent each individual within a population as a node, with connecting edges denoting relationships that could lead to the transmission of infection (Fig. 1). For many of the common airborne infections it may be difficult to define which contacts form an edge (23); for STDs, however, edges are more precisely defined and correspond to sexual partnerships. We note that the network is disease dependent, with STD networks contained within the networks of more readily transmitted infections.

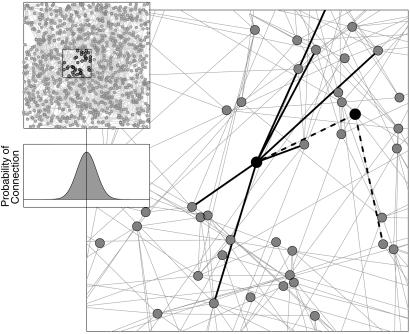
Figure 1.

An example of the full computer-generated contact network (Upper Inset) and a magnified section (main graph). Individuals are placed at random within the environment at an average density of one per unit area. The probability kernel determining the connection of two nodes (shown at the same scale as the full network in the Lower Inset) is the sum of a localized Gaussian (whose height and breadth may be specified) and a fixed probability representing global connections. Hence, the probability of connection between nodes a distance d apart is P(d) = U + μe^−d2/2σ2, where U, μ, and σ may be varied. The majority of the neighbors of a node are close by, with a smaller number of long-distance edges. To indicate the heterogeneities present in the network structure, two connected nodes are highlighted on the main figure. One node has only two relatively local neighbors, whereas the other possesses seven local and one longer range (out of shot) connection. Throughout the paper U = 0.0025, μ = 0.21, and σ = 2.5.

The initial spread and long-term behavior of any infectious disease are determined by both its epidemiological characteristics and the graph theoretical properties of the network—such as the average number of neighbors, degree of clustering, and the path length between nodes (24–26). One of the important dynamical features of infection taking place within the constraints of a network is the rapid build-up of correlations in the infection status of connected individuals (27–29); for example, most infected nodes have infected neighbors, by whom they were infected or to whom they have transmitted infection. This aggregation reduces the average number of susceptible partners per infected individual and consequently slows the propagation of an epidemic. Standard epidemiological models (19) ignore this powerful correlation; this simplification has the greatest impact when the number of neighbors is low, which is generally the case for STDs in the vast majority of the population.

Because of the large number of individuals involved, the personal nature of the contact information, and the biases that are frequently present, it is very difficult to accurately reconstruct the entire network of sexual contacts (30–32). However, work carried out by genito-urinary medicine (GUM) clinics provides some data about the local properties of the network. To limit further spread, the GUM clinic attempts to trace the sexual partners of any index case or subsequently discovered infectious individual. Ideally, we would like to reconstruct the entire mixing network by using this or similar approaches (11–14, 33, 34), but in practice this is rarely possible as the chains of transmission detected are seldom more than a few people long (31, 35). This limitation identifies the need for a modeling approach that utilizes the available detailed information about the network characteristics, but does not require the complete network to be reconstructed.

We present a model formulation that utilizes the essential characteristics of the mixing network. It captures both the build-up of correlations within the population and the effects of heterogeneities already present in the network structure. This capability is achieved by modeling partnerships as dynamic variables, developing a set of differential equations for the various types of connected pairs within the network. This is a significant step toward a more individual-based understanding of the dynamics of STDs; unlike computer simulations of the full network, these models are easily parameterizable through the use of readily attainable contact tracing data, and they retain a high degree of generality.

The next section describes the basic formulation of the pair-wise network equations and introduces a simplifying approximation that dramatically eases computation. The section after that tests these new equations and other standard approaches for modeling STDs against full stochastic simulations of disease transmission on computer-generated networks, which can provide complete comprehensive information. Finally, we show how our model can be used to estimate important individual-level epidemiological parameters from available data and to determine the effects of both random screening and contact tracing, which cannot be achieved with the usual model formulation.

Pair-Wise Network Model

Standard models for the dynamics of diseases classify individuals in terms of their infection history. In general, such models consider the proportion of individuals in each class and ignore network or spatial structure. Commonly, individuals can be in one of three states; they are susceptible (S) and can catch the disease, infectious (I) and can spread the disease, or recovered (R) and immune (19). For STDs there is generally little or no immunity, so individuals return to the susceptible state on recovery; therefore we restrict our focus primarily to such SIS dynamics.

Model Formulation.

One obvious risk factor for contracting an STD is the number of sexual partners (in network terms, the number of neighbors) (16, 36). However, the risk also depends on the characteristics of the neighbors, in particular the likelihood that they are infected. Hence, to model STD dynamics accurately it is necessary to know not only the disease status and activity level of each individual as included in risk-structured models (19) but also the status of their sexual partners; thus information about partnerships is vitally important (20–22, 24, 37–39).

The model developed here considers partnerships as the fundamental variables (40–43), modeling the edges on the mixing network rather than just the nodes. Only by treating partnerships within their network context can the correlations between neighboring individuals be captured. This model extends the recent work on pair-wise models (27–29, 44, 45) by introducing heterogeneities into the network structure (46). In this model all partnerships are considered to be active and hence concurrent (26, 40, 43), which may be a realistic approximation for highly promiscuous subpopulations although not for a general population over a long time period. Using the standard compartmental approach and following the notation of Keeling et al. (27), we label individuals as S or I, and include superscripts to denote their number of partners in the network. For example, [Iⁿ] denotes the number of infected individuals with n partners, and [SⁿI^m] is the number of partnerships between a susceptible with n partners and an infected with m (Table 1 gives the notation used in more detail). It is only through such partnerships, between a susceptible and an infected individual, that infection can be transmitted.

Table 1.

Notation used in model formulation

Term	Meaning
τ	The rate at which infection is spread through a contact
g	Recovery rate
[S], [I]	No. of susceptible, infected individuals
[Sn], [In]	No. of susceptible, infected individuals with n partners
[n]	No. of individuals with n partners
[SnIm]	No. of partnerships between an Sn and an Im
[nm]	No. of partnerships between individuals with n and m partners
[SnI] = ∑m[SnIm]	Total no. of infected partners of all Sns
[SI] = ∑m,n[SnIm]	Total no. of partnerships between an S and an I
[BnCmDp]	No. of triples with Cm having both Bn and Dp as partners

Considering the dynamics of infectious individuals two basic events can occur. Either recovery, which is assumed to occur at rate g, or a susceptible individual can be infected by an infectious partner—this leads to the inclusion of partnership information in an equation for individuals:

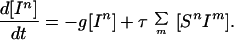1

In more detail, the term ∑_m [SⁿI^m] refers to the total number of infected partners of all Sⁿ, each of whom transmits infection at rate τ. If we make the standard assumption and ignore partnerships but use the contact data to estimate mixing between classes we could approximate this term by using

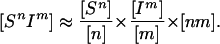2

Although this equation includes risk-structured heterogeneities, such a mean-field approach ignores the correlations in infection status that emerge between connected individuals. More accurately, a further set of equations can be constructed to model the dynamics of pairs, for example,

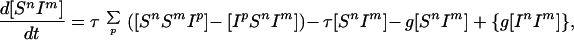3

the last term being absent in the SIR model. The terms in Eq. 3 refer to creation of the [SⁿI^m] pair caused by infection of an S^m within an [SⁿS^m] pair, loss of the pair caused by infection of the Sⁿ either from outside or from within the partnership, loss of the pair because of recovery of the infected individual, or in the SIS framework creation of the pair attributable to an Iⁿ recovering. In a similar manner, by considering the possible events that can occur we construct equations for all types of pairs (see Appendix A). This process could in theory be extrapolated, modeling triples, such as [SⁿS^mI^p], in terms of quadruples and so on; however, not only does the system rapidly become more complicated but the amount of data available to characterize triples is limited. We therefore make a moment closure approximation (27–29, 47), estimating the number of triples in terms of the number of pairs (see Appendix A), which closes the system, enabling us to calculate the behavior of individuals and pairs.

A Refining Approximation.

For the pair-wise network model above, the number of equations grows quadratically with the maximum number of neighbors allowed, and quickly becomes computationally intense. We thus look for a simplifying approximation that can reduce the number of the equations without losing the partnership representation or network structure aspects of the model.

From Eq. 1 we observe that the number of new infections is proportional to ∑_m [SⁿI^m], and hence the network properties of the infected neighbors are irrelevant at this scale. This observation motivates us to ignore the full set of pairs and use variables of the form [AⁿB] (= ∑_m [AⁿB^m]) to capture the behavior (Appendix B and Appendix C, which is published as supporting information on the PNAS web site, www.pnas.org). The network structure (i.e., the number of [nm] pairs) still enters into the equations for pairs, hence much of the network heterogeneity is retained, but it is now treated as independent of the infection status of the individuals concerned. The size of this approximate set of equations grows only linearly with the maximum number of neighbors, making it far more computationally efficient.

Comparison to Full Network Simulations

We now wish to test the accuracy of both the pair-wise network model and the approximation in comparison to the more standard risk-structured models (which ignore correlations) and the k-regular pair-wise model (which includes correlations, but ignores network structure by assuming all individuals have exactly k neighbors). We compare all four of these models with the results of a true stochastic infection process occurring on a fully connected computer-generated network (Fig. 1). This procedure has two advantages. First, the computer simulations and networks can be tightly controlled to simulate many different scenarios. Second, the simulations provide very precise and detailed information without any of the usual biases that may be present in real data.

Incidence of Infection.

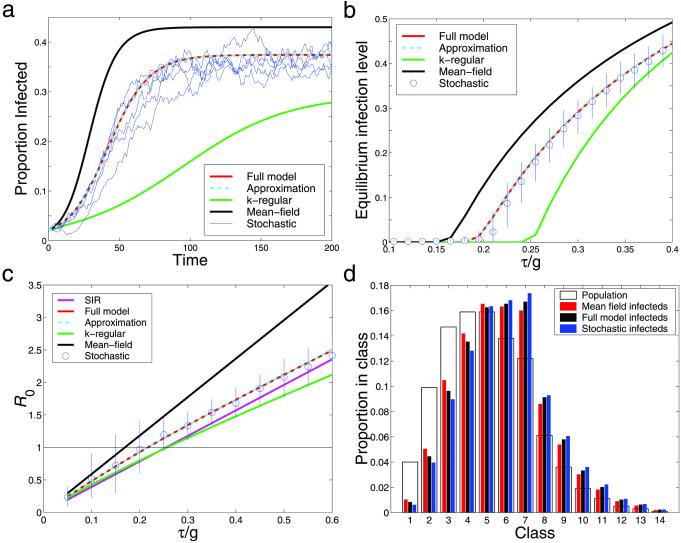
Fig. 2a shows the numbers of infectious cases, comparing the four deterministic models with the results of typical stochastic simulations. Neither the mean-field nor the k-regular pair-wise model satisfactorily predicts the equilibrium level of infection, whereas both the full and approximate pair-wise models perform well. Thus both correlations and risk structure appear to be important. This finding is further demonstrated in Fig. 2b, which shows the equilibrium levels of infection over a range of the dimensionless infection parameter τ/g, which is the normalized infectivity across a partnership. Not only do the equilibrium levels vary greatly between models, but so does the persistence threshold at which the disease can invade.

Figure 2.

The graphs show stochastic iterations (blue) and four deterministic models carried out on the same computer-generated network: the full pair-wise model (Eq. 6) (red) and the approximation (Eq. 8) (cyan), as well as a mean-field model (Eq. 2) (black) and a k-regular pair-wise model (green) where all individuals are assumed to have the same, mean, number of neighbors k. (a) Typical time series with infection parameter τ/g = 0.35. (b) Equilibrium levels of infection over a range of the parameter τ/g including the mean and 90% confidence intervals from 200 stochastic iterations. (c) The basic reproductive ratio, R₀, over a range of the parameter τ/g; also included is the analytic value for an SIR type infection (mauve); the difference between the SIS and SIR approaches is evident. The stochastic R₀ is estimated by using the distribution of infection when the epidemic has reached the (low) level of infection at which, in the full model, growth rate hits its early-stage equilibrium. (d) The equilibrium distribution of infected individuals throughout the population compared with the distribution of all individuals, for τ/g = 0.27; more highly connected nodes, representing increasingly promiscuous individuals, are at a greater risk of infection.

For low levels of the infection parameter τ/g, the k-regular pair-wise model underestimates incidence because it does not include the highly sexually active, highly connected core-group vital to maintaining infection at low levels (14, 18, 21, 37, 48). In contrast, at very high parameter values (not shown in Fig. 2) this model overestimates prevalence because of a lack of poorly connected individuals that are shielded from disease. The mean-field model consistently overestimates the level of infection, because the correlations that naturally limit transmission are ignored. The failure of these two forms of model emphasizes the importance of integrating the pair-wise and network approaches, such that both forms of heterogeneity are included.

The full pair-wise model and the approximation both perform extremely well for a global network where sexual connections are made largely at random; however for a more local network when triangular connections are more frequent and path lengths between individuals are longer these models produce slight overestimates. Although sexual networks are likely to be significantly clustered, it seems that there are sufficient long-range links such that spatial segregation is less influential than for many infections (11, 34, 49, 50). The recent work on small-world networks has indicated that even a low density of long-range connections can reduce the influence of such segregation (51, 52), and in such cases our model is likely to perform well.

R₀ and Early Growth Rates.

The basic reproductive ratio, R₀, is defined as the average number of secondary cases produced by an average infectious individual in a totally susceptible population. When R₀ is greater than 1 a disease can invade and increase within a virgin population, whereas when R₀ is less than 1 any invasion is doomed to deterministic extinction (although stochastic effects can make a difference, especially close to the R₀ = 1 boundary). Hence, R₀ is a fundamental quantity in epidemiology and disease control (19, 53–55).

In practice R₀ is calculated from the initial growth rate of an infinitesimal infection in an otherwise susceptible population. However, when the population is structured, the growth rate may depend on which class of individual is infected. We therefore allow the level of infection to equilibrate between the classes (such that high-risk individuals are more likely to be infected), before calculating the number of secondary cases. Correspondingly, for network models, R₀ should be calculated only once the early spatial correlations (which develop within a couple of generations) have formed (29).

For the SIR version of the pair-wise network model (Appendix A) the basic reproductive ratio is given by

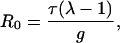4

where λ is the dominant eigenvalue of the matrix M given by

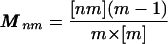5

(see Appendix D, which is published as supporting information on the PNAS web site). This matrix M is therefore a useful means of quantifying the connectedness of contact networks. We note that M is a modified version of the standard contact matrix given by [nm], which contains all of the information about the types of partnerships present in the network.

The strong correlations between the infection statuses of neighboring individuals play two roles. First, the negative correlation between susceptible and infectious individuals acts to damp the epidemic spread and therefore reduces R₀. Second, in standard mean-field models, which ignore partnerships and correlations, R₀ is the same for both SIS and SIR formulations. However for a pair-wise version of the SIR epidemic, infectious individuals have a high proportion of recovered (and therefore immune) individuals in their neighborhood, which limits the spread of the disease. This limitation does not occur in the SIS formulation, and consequently epidemic growth is more rapid, as can be seen from Fig. 2c. R₀ cannot be given in a simple closed form for the SIS case (see Appendix D in supporting information), but Eq. 4 provides a lower bound.

Fig. 2c shows how R₀ and therefore the initial growth rates differ between the various models. Where there is no straightforward analytic solution, R₀ is calculated from the early growth rate of the epidemic, once the local spatial structure has equilibrated. The importance of taking partnerships into account is underlined by the degree to which the mean-field model overestimates initial epidemic spread.

Core Groups.

Fig. 2d considers how infection is distributed between the classes; as expected, those individuals with more neighbors are more likely to be infected, and this bias becomes more pronounced as the infection level decreases (48). There is little substantial difference between the results of the two models and simulations, as the distribution across cases is dependent primarily on the risk-level heterogeneities, which are the same in all formulations. Both the full and mean-field models underestimate, to some extent, the degree to which infection is skewed toward higher activity classes, the mean-field model in particular failing to represent the sheltering that the network can provide for the less active groups. The heterogeneities between classes are therefore vital for understanding the persistence, spread, and invasion of STDs. A control policy focused on the high-risk individuals (those with large numbers of contacts), taking advantage of the heterogeneities present in the network, is likely to be more successful than one applied at random (19). The high-risk classes are even more important when public health agencies are close to eradicating the disease, as they can act as both a reservoir of infection and a potential invasion route for new infections. Hence as an intervention policy achieves success it becomes increasingly important to target those individuals most central to disease spread.

Applications to Sexual Network Data

To illustrate the utility of this approach, we shall apply it to a network of sexual relationships in Manitoba, Canada, shown in Wylie and Jolly (11). These network data are unusual in that they contain the sexual partnerships between 82 connected individuals together with the presence of chlamydia and gonorrhea infection, and as such represent the results of a large volume of research by many public health workers. We now consider the invasion parameters and control of these two diseases on such a highly connected subpopulation.

Parameter Estimation.

The information on partnerships was used to parameterize the mixing matrix used by pair-wise and mean-field models. In contrast to the previous section, which assumed the same individual-level parameters for each model, here we use the level of prevalence to estimate the model specific infection parameter, τ/g (Fig. 3a and Table 2). It is clear that the mean-field model requires lower values of the infection parameter to achieve the same levels of prevalence, as it ignores the damping effects of partnerships and hence correlations. By using these parameters, it is possible to calculate R₀ in each case, providing a network-specific measure of the invasiveness of each disease (Table 2). The significantly higher value of R₀ obtained by using the mean-field model illustrates the differences between the approaches, even when controlling for prevalence. (The k-regular model, in contrast, lacking the highly active individuals, shows a much slower growth of infection.) The significantly larger value of R₀ calculated for the mean-field model implies that invasion occurs more slowly in practice than predicted by standard models. However, as shown below, this does not necessarily mean that the disease is easier to control.

Figure 3.

(a) Estimation of τ/g by using the prevalence of infection on a network taken from Wylie and Jolly (11), for chlamydia and gonorrhea and three different models: the full pair-wise, the mean-field, and the k-regular. (b) For the same network, evaluation of the effectiveness of control strategies by using the pair-wise network model. The equilibrium infection prevalence is shown as the two control methods are varied. One is the infection parameter τ/g relative to the estimated value; this is a measure of the change in infectivity attributable to random screening or public awareness. The other is the contact tracing efficiency, the proportion of infected partners who are successfully traced and treated once an index case is identified. The dashed red line shows the corresponding extinction threshold for the mean-field model, which is unaffected by contact tracing.

Table 2.

Estimation of parameters

STD	τ/g			R0
	Pairwise	Mean-field	k- regular	Pairwise	Mean-field	k- regular
Chlamydia	1.03	0.76	1.32	2.11	2.76	1.22
Gonorrhea	1.38	1.06	1.52	2.84	3.81	1.34

Control of STDs.

Attempts to combat any infectious disease take two main forms: screening and contact tracing. Screening programs act at the individual level by testing and treating a random sample of the population, or a subpopulation of high-risk individuals. Such programs lead to a more rapid detection and recovery of infected individuals and, as such, act in a similar manner to public awareness campaigns. By contrast, contact tracing focuses on the partners of infected individuals (once they have been identified) and hence utilizes the network structure associated with transmission. Here we compare these two strategies using the pair-wise network equations and the parameters derived from Wylie and Jolly (11). Contact tracing cannot be realistically modeled by a mean-field approach because information on partnerships has been neglected.

The level of screening (or public awareness) is reflected by a reduction in the infection parameter (τ/g) relative to its estimated value; screening alone results in individuals recovering back into the susceptible class while their partners are unaffected. Contact tracing is modeled by additionally treating a proportion of the partners of an identified index case—this proportion is referred to as the tracing efficiency. In practice this procedure would follow the chains of transmission, but for simplicity we truncate the tracing at secondary cases (see Appendix E in supporting information on the PNAS web site). Fig. 3b shows the prevalence of infection as the levels of the two control measures vary. Clearly, the level of screening has to be sufficiently high so that index cases can be detected—contact tracing alone is unlikely to be effective. Contact tracing also has little effect when the incidence of infection is high. However, as screening/awareness improves and the incidence of infection decreases contact tracing becomes a more efficient way of searching for infection. This observation suggests that a combined policy is generally the optimal approach to achieve eradication. We note that a more targeted screening campaign, focusing on high-risk individuals, is likely to be far more successful.

Discussion

Sexual mixing networks demonstrate the interlinked pattern of sexual interactions, and are conceptually important in modeling STDs. The clearly defined nature of sexual partnerships and the restricted number of partners of each individual mean that the population cannot be considered well mixed; rather, infection status in neighboring individuals is highly correlated. For both STDs and other infections the accurate determination of the complete networks is rarely feasible, but local information such as the distribution of number of partners is often available.

We have presented a model that requires only local information to produce a highly accurate description of the disease dynamics. This model treats the partnerships between individuals as its variables, and as such can include both the heterogeneities within the network structure and the heterogeneities that develop because of the disease dynamics. This model proved far more accurate than either the standard (mean-field) risk-structured models (20, 21) or the k-regular pair-wise models (27–29), agreeing closely with stochastic simulation on a computer-generated network. This result shows that both heterogeneities in behavior and correlations at the partnership level must be included in any predictive scheme. The full pair-wise model developed here, however, suffers from requiring a vast number of variables to capture the state of the network (the system is high-dimensional); this complexity motivated the formulation of an approximation, which performs as well as the full model, but has a much lower number of variables and is far more computationally efficient.

Having demonstrated the accuracy of this approach against computer simulations, we use some of the available network data (11) to consider some more applied aspects. The prevalence level of infection can be used to estimate the individual-level parameters for that subpopulation by using any given model. The pair-wise model consistently predicts higher partner-to-partner transmission rates, but a lower basic reproductive ratio, R₀. However, because of the nonlinear behavior of R₀ as the infection parameter changes (Fig. 2c) this does not simply translate into an extinction threshold. Instead, for random disease control the standard models underestimate the difficulty of eradication. The pair-wise model can also be used to evaluate the impact of contact tracing—a form of targeted control that utilizes the network structure. This extension of the pair-wise model shows that an integrated strategy using both random screening/prevention and contact tracing is likely to be the most successful, because contact tracing has the biggest effect when the prevalence of infection is already low. In contrast, standard mean-field models predict that the eradication threshold is not affected by contact-tracing because they ignore the essential information on partnerships.

The modeling approach developed here does have two potential flaws, however. First, it is deterministic, essentially assuming a vast population size, and therefore cannot reproduce the variability seen in the stochastic simulations or the chance localized extinctions of infection that can occasionally occur. Second, the model loses some of its accuracy if the partnerships are formed predominantly with nearby individuals—i.e., when there is a strong spatial element in the network. Although sexual networks contain primarily local interactions with most partners residing in the same village, town, or city region, the presence of a significant proportion of out-of-town, long-range, links (11, 34, 49, 50) may mean that they are more like small-world than exclusively local networks. Hence for real-world networks and for large populations the model is expected to perform well.

The complexities and complications of real sexual networks and STD transmission can never be fully captured by simple models. However, the approach shown here, which can accurately decompose the detailed structure of a mixing network into a system of relatively simple equations, has been demonstrated to provide a robust and reliable framework. The techniques and methodologies can be simply adapted to match a variety of disease dynamics and network characteristics, and as such provide a practical tool for understanding and predicting the presence, progression, and prevention of STDs.

Abbreviation

STDs

sexually transmitted diseases

The Pair-Wise Network Equations

Because infection can be transmitted only via edges in the mixing network, for the purposes of disease spread only partnerships consisting of an infected and a susceptible individual need be considered. Hence the full SIS model is described by the following set of equations:

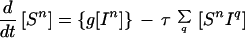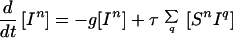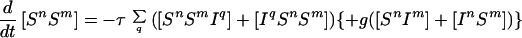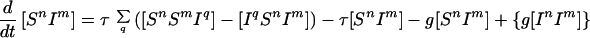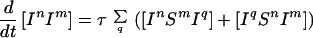6

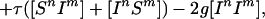where the triples are evaluated by using the moment closure approximation:

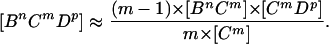7

This expression itself can be refined when there are triangles (loops containing three individuals) in the population to take into account the partnership between the Bⁿ and the D^p (27, 29). However, for many STD networks, the proportion of triangles compared with triples is likely to be very low (in heterosexual networks triangles are absent), hence for simplicity these will be ignored.

Diseases with SIR-type dynamics follow a similar set of differential equations, with the terms in brackets ({·}) absent.

The Approximated Pair-Wise Equations

From the form of the individual equations, we have been motivated to use variables of the form [AⁿB] = ∑_m [AⁿB^m] instead of the full set of all possible pairs. This can be achieved by summing the full pair-wise equations over all possible m values. Where necessary we use the approximation:

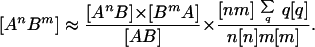8

The first term takes into account the partnership types (finding an Aⁿ next to a B and a B^m next to an A), and the second term accounts for the neighborhood structure (finding an n–m pair). This leads to a smaller but more complex set of equations (see Appendix C in supporting information).