The natural center of chromaticity space is not always achromatic: A new look at color induction

Abstract

Although current theories of color vision differ in many respects, they all assume the existence of a uniquely defined neutral point in chromaticity space. It generally is assumed that this point satisfies several criteria simultaneously. One of these criteria is that it is perceived as achromatic. A further criterion shared by most theories is the structural assumption that lines in chromaticity space of constant hue converge on the neutral point. The basic assumption that these two criteria coincide is clearly true for isolated spots of light presented in darkness, and it usually is taken for granted that this coincidence generalizes to more complex visual stimuli. Here, we show that this is not the case. Our experiments with infields in chromatic surrounds revealed that the point in chromaticity space that appears gray is clearly different from the point on which lines of constant hue converge. A plausible interpretation of this apparently paradoxical finding in terms of color scission is proposed.

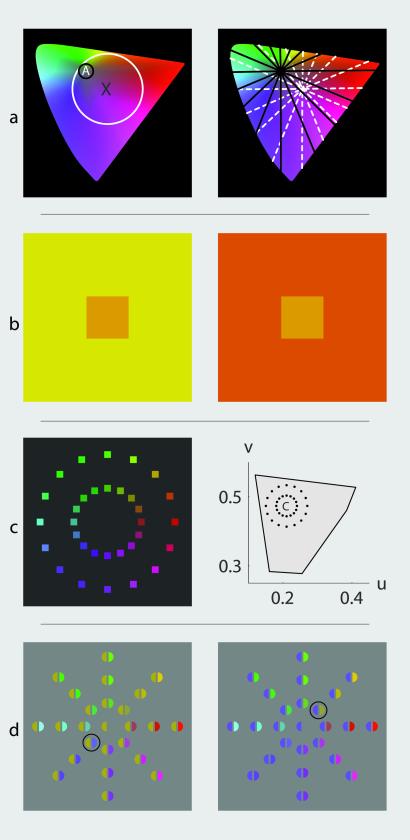
A familiar example of the special role attributed to achromatic colors can be found in the description of three-dimensional color space along the dimensions of hue, saturation, and brightness: in any plane of equal brightness, the achromatic point is assumed to correspond to a natural center, which can be defined alternatively by purely structural criteria. For instance, it is the only point of zero saturation, any closed path around this point contains all possible hues (enclosure criterion; see Fig. 1a Left), and it is the convergence point of all lines of constant hue (convergence criterion; see Fig. 1a Right). The special role of achromatic colors also is acknowledged by the opponent-colors theory (1, 2), which assumes that an achromatic color is perceived when both the yellow–blue and the red–green opponent mechanisms are in equilibrium. The above-mentioned structural criteria are assumed to hold also within this theoretical framework.

Figure 1.

(a) Two properties of the achromatic point shown in the uv chromaticity space. (Left) If the small, black circle around achromatic point A is the smallest circle around this point containing all hues (albeit at low saturation), then the larger, white circle is the smallest circle around the chromaticity X that contains all hues, because, if it is made smaller, the greens will be missing. (Right) The straight lines emanating from the achromatic point are of approximately constant hue with increasing saturation. The straight lines emanating from any other point, such as the white, dashed ones, cannot all be of constant hue. (b) Simultaneous color contrast. Although the two small rectangles are physically identical, they look different because of the different inducing effects of the surrounds. The effect is even stronger when center-surround stimuli are viewed in a surround of complete darkness. (c Left) Schematic picture of the display used in experiment 1 with a black surround. The surrounds in the experiment were chromatic and equiluminant to the patches. (Right) Chromaticities of the patches for a center C, which, in this case is equal energy white, and an inner circle radius of 0.03. The polygon is the border of the monitor gamut at the luminance used in our experiments. (d) Schematic illustration of the scission account of our results outlined in Discussion. Left and Right correspond to the situation of a yellow and a blue surround, respectively. The left half of each disk represents the color of the common background component, and the right half represents the color of the “contrast component.” A feature that is not clear from this figure is that the salience of the background component increases as the infield chromaticity approaches that of the surround. The figure illustrates the impossibility of making true achromatic settings and the best alternative choice (black rings).

These concepts concerning the structure of color space and its relation to perceptual variables ultimately have their roots in an experimental paradigm that studies isolated light spots surrounded by complete darkness (3). In this simple case, any light corresponds uniquely to a point in three-dimensional color space. However, it is well known that the perceived color of a light spot may change radically if it is surrounded by a colored region (4, 5) (see Fig. 1b). The effect of introducing neighboring stimuli usually is modeled as a context-dependent transformation of the coordinates of the isolated light (6–8). This transformation is thought to preserve both the three-dimensionality and the above-mentioned structural properties of color space. Because the intuition behind this assumption is that the effect of the surround is, in essence, to relocate attributes of color appearance within a tristimulus space, we will refer to it as the “relocation assumption.” Restricting attention to infields of some fixed luminance presented in a given surround, this ubiquitous assumption implies that the achromatic point and the point of convergence for lines of constant hue also should coincide in this case. We investigated whether, in fact, this is the case. Our results strongly suggest that it is not.

General Methods

In all experiments, the stimuli consisted of one or more square infields embedded in a homogeneous rectangular surround. All colors in the display were equiluminant at 10 cd/m². The stimuli were presented on a cathode ray tube screen (resolution, 1,024 × 768 pixel; 75-Hz frame rate) in a completely dark chamber. The monitor was controlled by a graphics card with a color depth of 8 bits per red–green–blue channel. This setup was colorimetrically calibrated by means of a colorimeter (LMT Lichtmesstechnik, Berlin; C1210), following a standard procedure described by Brainard (9). All chromaticities are given in uv coordinates (CIE 1976 uniform chromaticity space, ref. 3).

Experiment 1

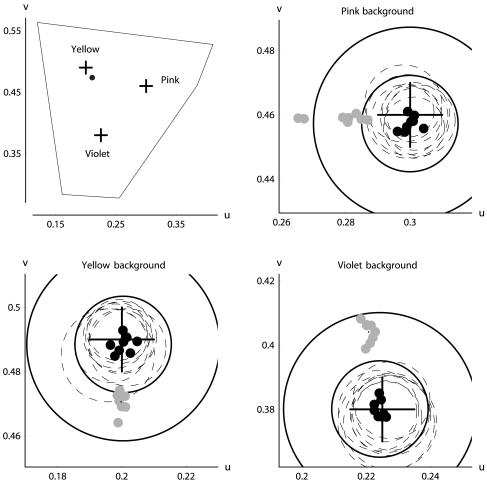
Experiment 1 consisted of three parts. In experiment 1a, we let subjects set the chromaticity of an infield (width, 0.66° visual angle) to achieve an achromatic appearance in three different, fixed, homogeneous, chromatic surrounds (width, 14.25°; height, 10°). The surrounds, which appeared approximately yellow, pink, and violet, had the uv coordinates (0.2, 0.49), (0.3, 0.46), and (0.225, 0.38), respectively. As is to be expected from the results of previous experiments of a similar kind (6, 7), the settings were shifted—relative to the achromatic point for isolated spots of light—in the direction of the chromaticity of the surround (see Fig. 2).

Figure 2.

Typical results from experiment 1 (subject VE). (Upper Left) The crosses represent the three background chromaticities investigated. The black point represents the chromaticity of equal energy white. The surrounding polygon is the monitor gamut at the luminance used in our experiments (10 cd/m²). The other graphics represent scaled-up portions of this space. (Background chromaticity crosses are scaled correspondingly in size.) The gray dots represent the achromatic settings (experiment 1a), and the black dots represent the settings made in experiment 1b. Around the mean of these settings, two black, solid circles are drawn with the fixed radii used. Each of the dotted circles represents one single setting from experiment 1c.

In experiment 1b, we used a previously undescribed method, inspired by an informal demonstration described by Whittle (4), to determine the neutral point indirectly by employing the above-mentioned structural criteria of enclosure and convergence: two sets of 16 colored patches (width, 0.33° each) arranged on two circles (“spatial circles”; radii, 1.38° and 2.06°) were displayed in the same surrounds as in experiment 1a (see Fig. 1c Left). The chromaticities of these patches were equally spaced on two concentric circles (“chromaticity circles”) in the CIE uniform chromaticity space (3). The radius of the inner chromaticity circle was set at a relatively small value (0.015 Euclidean distance in the uv plane). The outer chromaticity circle had the same center as the inner one, its radius being twice as large (see Fig. 1c Right). The chromaticity of each patch on the screen was set to that point of the chromaticity circles that corresponds to its location on the spatial circles (see Fig. 1c). If one rigidly translates the two chromaticity circles in chromaticity space (i.e., the relative positions of all infield chromaticities are unchanged), one finds a uniquely defined setting in which each pair of patches on the screen with the same angular position appear to be of the same hue. Furthermore, the otherwise almost uniform collection of colors unfurl rather impressively into a set of colors spanning a full gamut of hues as soon as this particular point is reached (4). According to the enclosure and the convergence criterion, this is exactly what one would expect to happen when the circles of infield chromaticities are centered around the neutral point. The task of the subjects in this part of the experiment was to find this point.

In experiment 1c, only one circle of patches was presented in the surround. Thus, subjects could not rely on the convergence criterion and had to rely on the enclosure criterion only. The only difference in procedure compared with experiment 1b was that the subjects also controlled the radius of the circle of chromaticities. The task of the subjects was to find the point that enabled the perception of a full hue circle§ with the smallest possible radius setting.

The results from all three parts of experiment 1 are plotted in Fig. 2. It can be seen that the cluster of the achromatic settings is clearly distinct from that of the settings made when using the structural criteria. Furthermore, the means of the latter settings for each surround coincide almost perfectly with the surround chromaticities. This result suggests that, in simple infield-surround stimuli, the lines of constant hue converge not on the achromatic point but, instead, on the background chromaticity.

Because this finding challenges a basic assumption of most color theories, it is natural to ask whether the above result may be due to artifact. Indeed, it may be argued that the settings for the achromatic point cannot be compared with the hue convergence settings: the first were made with only one single infield, whereas the latter were made effectively with 32 infields, and, thus, the observed difference of the settings may be due to a difference in the complexity of the stimulus. Our second experiment was designed to address this issue.

Experiment 2

In experiment 2, subjects matched the hue of only two infields (width, 0.66°; center-to-center distance, 1.38°) in the same surround (width, 14.25°; height, 10°). The chromaticity of one of these patches was fixed to 1 of 16 equidistant points on a circle in uv chromaticity space. The chromaticity of the second infield could be adjusted continuously along a smaller concentric circle in chromaticity space in the search for the hue match. The center of both chromaticity circles was located at the point halfway between the background chromaticity and the achromatic point, which was determined experimentally by using the same procedure as in the first part of experiment 1. The radii of these chromaticity circles were 1.5 times and 3 times the distance between these two points, respectively (see Fig. 3). Because the radii of the chromaticity circles depend on the gray settings of the subject, it often happened that the outer chromaticity circle extended beyond the monitor gamut. In these cases, the surround colors, which initially were set to the same values as in experiment 1, were made slightly less saturated and the entire procedure was repeated.

Figure 3.

Typical results from experiment 2 in uv chromaticity coordinates (subject GW). Row 1 is for the pink background, row 2 is for the violet background, and row 3 is for the yellow background. The results of three additional subjects were almost identical. In the left column, the data are plotted together with lines predicted by the hypothesis that lines of constant hue converge on the achromatic point (black filled circle). Shorter lines are drawn from the chromaticities of the fixed patches (small white dots on the outer circle) to the corresponding mean settings (small white dots on the inner circle), and the angular deviation from the predicted lines is in black. The white ring represents the best-fitting point of convergence, and the black cross represents the background chromaticity. In the right column, the same data are plotted, except that the lines predicted by the hypothesis that lines of constant hue converge on the background chromaticities are given.

The convergence criterion implies that straight lines drawn through the standard infield chromaticity and the chromaticity of the hue match intersect at the neutral point of chromaticity space. Because both the achromatic point and the background chromaticity were located symmetrically with respect to the center of the inner chromaticity circle and well within it (see Fig. 3), it was a priori equally possible for the lines of constant hue to converge on either of these points.

Typical results from this experiment are presented in Fig. 3. To estimate the neutral point for a subject and a given surround, we searched for the chromaticity X that minimized the mean absolute angular deviation between the line from fixed chromaticity to the subjects' settings and the line from the fixed chromaticity to the neutral point X. It can be seen that the estimated neutral points lie very close to the background chromaticity and much farther away from the mean achromatic settings. Thus, the results from experiment 1 also can be confirmed in this more rigorous test.

Experiment 3

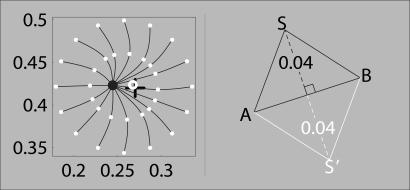
A central assumption underlying our use of the convergence criterion in the above experiments is that lines of constant hue are approximately straight. If, however, contrary to this assumption, the lines were strongly curved, for instance, as depicted in Fig. 4 Left, the results of experiment 2 may be compatible with the standard assumption that lines of equal hue converge on the achromatic point. Although only relatively small deviations from linearity have been reported (3), the possibility that large deviations may occur under the present experimental conditions cannot be ruled out a priori. Therefore, we conducted a third experiment in which we addressed this possibility explicitly.

Figure 4.

(Left) A possible alternative interpretation of the data in experiment 2 (here for the pink background; compare with Fig. 3, row 1) in terms of curved lines of constant hue. (Right) Illustration of the choice of infield chromaticities in experiment 3 (see text for details). The black and white lines correspond to two different conditions used for each surround.

The results of experiment 2 show that if lines of equal hue were curved and thus still may converge on the achromatic point, some of them should have the strongest curvature (see Fig. 4 left), and we focused on these cases. We used a method with fixed stimuli instead of the adjustment procedure used in experiment 2. The subjects viewed two infields (width, 1.27°; center-to-center distance, 2.64°) in a common surround (width, 27.6°; height, 19.2°). The surrounds, which may be described roughly as yellow, pink, and violet, had the uv coordinates (0.2, 0.53), (0.3, 0.46), and (0.22, 0.35), respectively. In a four-alternative, forced-choice procedure, the subjects were asked to indicate whether the left (test) infield (i) had the same hue as the right (standard) infield, (ii) had a hue different from that of the standard, (iii) was invisible against the surround, or (iv) appeared achromatic. They were instructed to use a strict criterion for a hue match.

For each surround, the chromaticities for the test infield were chosen from a triangular region in uv space spanned by the chromaticities A, B, and S of the achromatic point, the surround, and the standard infield, respectively. All different chromaticities inside this triangle realizable at 8-bit color resolution were used for the test infields. The achromatic point—just as in experiment 2—was determined for each subject in a preliminary experiment. The individually determined mean A over eight achromatic settings for a surround together with the surround chromaticity B defines a line AB in chromaticity space. For the standard infield, we used a chromaticity S that (in uv chromaticity space) had a Euclidean distance of 0.04 units from this line and was equally far away from A and B (see Fig. 4 Right).

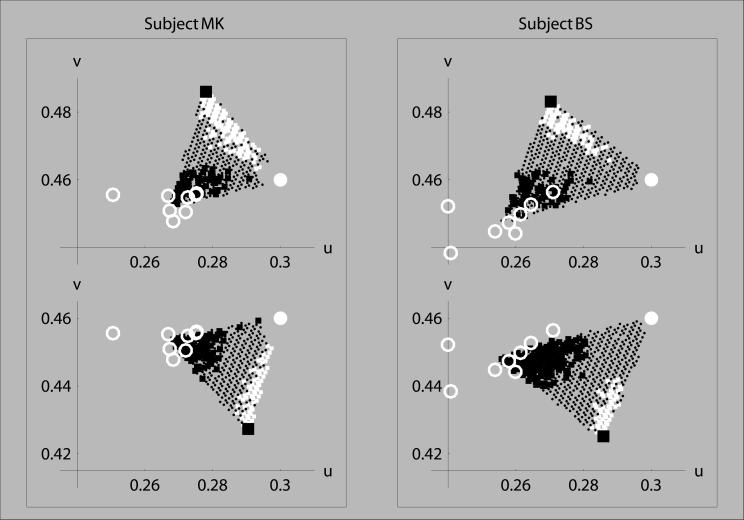
The results for one of the surrounds are plotted for two subjects in Fig. 5 (the results of an additional subject were similar to those of subject MK and are not shown). It can be seen clearly that the equal hue lines for subject MK, which extend all the way down to threshold detectability of the infield against the surround, are approximately straight and converge on the surround chromaticity. This equal hue line and the achromatic locus are separated by an extended region that is classified neither as achromatic nor as a hue match. The equal hue lines of observer BS look like “amputated” versions of those of subject MK. After the experiment, subject BS reported that he had experienced a pronounced impression of transparency when the infield was similar to the background and that he, in view of the instruction to apply a strict criterion, had not classified these cases as hue matches. Similar reports of perceptual transparency also were made by the other subjects (see Discussion). The general pattern of results apparent in Fig. 5 is equally clear in the data for the other surrounds (not shown).

Figure 5.

Typical results from experiment 3 in uv chromaticity coordinates. Solid white circle, background chromaticity; open white circles, gray settings from preliminary experiment; large black square, standard infield chromaticity. Each point within the triangle represents one of the test chromaticities. Points plotted as white squares represent test infields that appear equal in hue to the standard infield, those plotted as small black squares represent test infields that appear achromatic, and those plotted as small black dots represent test chromaticities that are judged to be neither achromatic nor a hue match. Chromaticity points for those test infields that appeared indistinguishable from the surround are omitted in the plot, yielding an empty region close to the white filled circle.

The results of experiment 3 clearly rule out nonlinearities of equal hue loci as a possible explanation for the dissociation of the achromatic point and the convergence point for lines of equal hues observed in experiments 1 and 2. Furthermore, because in this experiment judgments of achromaticity and hue equality were made under the same conditions, any artifact resulting from slight differences in context also can be ruled out.

Discussion

The results of all three experiments support the conclusion that there is a dissociation between the perceptual criterion of achromaticity and the structural definition of the neutral point in chromaticity space in terms of the convergence criterion. Lines of equal hue converge on the background chromaticity and not on the achromatic point. Therefore, contrary to common intuitions, the chromaticity of the background should be regarded as a more natural center of chromaticity space than the achromatic point. Interestingly, a similar dissociation of the achromatic point and a functionally relevant neutral point has been found in a study (10, 11) on contrast adaptation. Here, the experimentally determined center of contraction in contrast adaptation was not the achromatic point but the mean of a temporally modulated, adapting stimulus.

The present finding appears paradoxical if one tries to understand it in terms of classical notions of color space with three dimensions such as hue, saturation, and brightness (12). In this view, if brightness and hue are constant, the only variable attribute of color is saturation, whereby desaturation is taken to mean a (perceptual) mixture with white. Consequently, lines of constant hue should converge on white. This should not change if a chromatic surround is introduced, because according to the relocation assumption, only the position of the white point should move.

Contrary to this, the results of our experiments show that lines of constant hue converge on a chromatic color, namely, that of the background. This means that colors on this line must contain, in addition to the hue that should be matched, varying amounts of the background color, which seems to be at odds with the fact that the subject found it easy and natural to make complete hue matches and was never uncertain about which point to choose. A parsimonious way to resolve this apparent paradox is to assume that the visual system performs a decomposition of the proximal stimulus into two simultaneously perceived color components—a common background component and a contrast component (4) defined relative to the background (see Fig. 1d). The critical assumption one has to make is that even though both are perceived simultaneously, the subjects base their hue matches in an immediate and effortless way only on the contrast component and can—in this regard—be said to discount the common background component. This interpretation makes the observations that lines of equal hue converge on the background chromaticity and that the smallest possible full color circle encloses the background chromaticity intelligible.

Interestingly, however, the above account of our results in terms of color scission suggests that true achromatic settings actually should be impossible to make, because in this case as well, two chromatic color components should be perceived simultaneously. Indeed, it already has been observed by others that it is impossible to find gray infields in different surrounds that appear truly identical (13). According to the scission account, this could be explained by assuming that in such a situation the two color components present are both faint and that the background component can be balanced—but not canceled—by a complementary contrast component such that the total impression is close—but not identical—to a true gray (see Fig. 1d).

The scission interpretation outlined above is supported not only by our data but also by the phenomenological observation that, especially at low chromatic contrast, the contrast II color component of the infield seems to be covered by a “veil” that has the same color as the background. The perceptual impression is reminiscent of perceptual transparency (14–16). Hence, Hering's description of “desaturation” as a “veiling with white” (1) seems to be appropriate in a literal sense provided that “white” is replaced by “background color.”

In more complex stimuli, similar phenomena of “laminar segmentation” (17) or “scission” (18) of color, such as the simultaneous perception of illumination and surface color (19), or of background color and a transparent overlay are well known. Our findings strongly suggest that such a dual coding of color occurs even in simple infield-surround stimuli, albeit in an embryonic form (8, 17).