Assessment of Multiple Sclerosis Lesions with Spherical Harmonics: Comparison of MR Imaging and Pathologic Findings

Abstract

Spherical harmonics (SH) were used to approximate the volume and three-dimensional geometry of multiple sclerosis (MS) lesions in deceased patients. The institutional ethical committee does not require its approval for studies involving pathologic specimens. Pathologic findings were used as the reference standard. In addition, lesion volume was measured with cylindrical approximation (CA). Volumetric comparisons of biases were based on summary statistics, Spearman correlation, Wilcoxon test, and two-way analysis of variance. Shape comparison metrics included mean distance and Dice similarity coefficient (DSC). Eight of 11 lesions had smaller biases with SH method (P < .001). Median biases with SH and CA did not differ significantly, as compared with pathologic findings (r = 1.00 vs 0.99, respectively). Variances of the biases were significantly smaller for SH (P =.04). Ranges of normalized distance and DSC were 0.1%–2.5% and 75%–96%, respectively. Mean DSC was significantly higher than 70% (P < .001). SH method provided unbiased lesion volume and added geometric information that may enable a better understanding of the pathogenesis and lesion evolution over time.

Magnetic resonance (MR) imaging of the brain is the preferable paraclinical test for the diagnosis and assessment of disease progression in patients with multiple sclerosis (MS). MR imaging provides a direct measure of the extent of pathologic changes compared with clinical symptoms, enables detection of subclinical activity, and is sensitive to the long-term accumulation of disease burden within the brain. However, it remains difficult to correlate the exact relationship between the evolution of MS lesions on MR images and the details of pathologic findings. Kirshner et al (1) found that MR imaging can help visualize lesions as small as 3 mm in diameter and that the extent of lesions detected with MR imaging was similar to the extent seen in pathologic examinations. Another comparative study reported that even when extensive areas of abnormal MR imaging signal intensity were observed, only small periventricular plaques were found at dissection (2). De Groot et al (3) found that 44% of the MR imaging–detectable abnormalities were neither visible nor palpable macroscopically. They also found that the size and shape of the lesions in different brain samples derived from the same patient were homogeneous, thus suggesting a patient-specific lesion formation.

A modeling approach has been developed to assess brain lesions in patients with MS by using spherical harmonics (SH) (4). SH can quantitatively define and calculate complicated three-dimensional (3D) geometric features to assess the shape of MS lesions. Moreover, with SH, it is possible to obtain the morphometric measurements of the lesions, as well as an analytic description of the shape, yielding accurate estimations of its features. Consequently, it is possible to quantitatively compare the change in 3D lesions and monitor differences over time. The geometry of the studied lesions can be characterized by indices derived from SH, which are invariant to space rotation (5), enabling the reduction of errors resulting from inaccurate patient repositioning during MR imaging examinations.

As a limitation, however, in the previous investigation (4), only artificial MS lesions were simulated to perform statistical validations of the volume approximation with SH. Furthermore, the shape approximation was visually inspected only artificially and in vivo (4). Therefore, in the present study, our purpose was to evaluate SH to measure volume and approximate the 3D geometry of MS lesions in comparison to pathologic findings, which were used as the reference standard.

Materials and Methods

Specimens and MR Images

Imaging data were obtained from two pathologic specimens. A half of the brain from each of two deceased patients with MS was obtained. The brains were fixed and preserved in formaldehyde and were donated externally by the Multiple Sclerosis Human Neurospecimen Bank, Los Angeles, Calif. The postmortem specimens we received had been obtained with authorization from the next of kin or an appropriate legal representative for use for research proposes. The ethical (Helsinki) committee at the Multiple Sclerosis Center of Sheba Medical Center does not require its approval for studies involving pathologic specimens.

MR images were acquired with a 2-T imager (Prestige; Elscint, Haifa, Israel) by using a clinically existing T1-weighted protocol (repetition time msec/echo time msec of 550/20, field of view of 24 cm, and matrix size of 256 × 256 pixels). Images were acquired in the coronal plane, with a 2-mm section thickness and no gap between sections, yielding a voxel size of approximately 2 mm³; 61 and 69 image sections were obtained for the two brains.

MR Image Analysis

To determine the presence of MS lesions, the acquired images were analyzed by two readers (D.G.Z. and A.A., with 7 and 10 years of experience in brain MR imaging, respectively) by means of consensus.

The identified MS lesions were segmented by one reader (D.G.Z.) by using either an adaptive threshold algorithm (6) or mouse tracking when lesions appeared near the cortical sulci. By using the segmented contours of the identified MS lesions, 3D shapes were approximated with SH. For additional comparison, the volume of each lesion was measured with the commonly used technique of section stacking, referred to herein as cylindrical approximation (CA), which is done by segmenting the lesions from the two-dimensional MR images and then multiplying the area of each segment by the section thickness.

SH Technique

SH quantitatively defines a complicated 3D surface in terms of a small number of parameters, which are the coefficients of the corresponding SH expansion functions on the unit sphere (see mathematic details in Appendix A). The resulting analytically defined surface closely approximates the desired target surface as the number of coefficients is increased. Finally, irregular and even more complicated 3D shapes can easily be approximated in analytic terms by using SH. This method has also been employed to approximate and analyze complicated anatomic shapes, such as brain ventricles and brain caudates (7,8). An example of the potential of SH to reconstruct irregular surfaces is shown in Figure 1.

Figure 1.

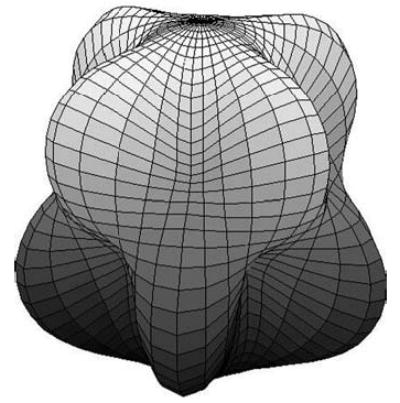
An example of an irregular surface reconstruction with the SH method.

Characterization of 3D Lesion Geometry with SH

The characterization of 3D lesion geometry is based on several sets of MS lesion contours taken from segmented MR images. To obtain the same number of points in all contours, each outline was interpolated and resampled. Subsequently, the points of each contour were rearranged in such a way that the first point on each contour was the most extreme point on the right-hand side. The rest of the points were then registered in a counterclockwise direction. The application and/or optimization procedures of the interpolation and arrangement are explained with more detail elsewhere (4). Because only coronal sections were acquired, a transverse and a sagittal contour were also added by applying the Akima interpolation method (9) to data points located on these planes and two additional points extrapolated from the contour center of gravity. These two contours were used to constrain the solution along the direction perpendicular to the coronal plane. The final sets of contours obtained for each lesion were arranged according to their respective spatial orientation, yielding a 3D cluster of points.

By using this cluster of points, the 3D geometry and the corresponding SH polynomial representation of each individual lesion were estimated. The center of gravity of the cluster of points was used as the center of the spherical coordinate system; consequently, the SH approximation is invariant to translation. Additionally, it was noted that the choice of the number of harmonics (n) must be set according to the ratio of lesion size to image resolution to avoid distortions in the estimated 3D surface. Therefore, n was set to be equal to the number of coronal contours when two or more transverse contours were used for the approximation. A value of n = 2 was selected when only one coronal contour was used for the approximation to prevent the final 3D shape from becoming spherical.

As a result of the uneven distribution of the data points and the lack of information about the lesion surface in the intersection space, the choice of a higher n value can cause distortions to the final surface. By using the sets of points expressed in spherical coordinates, the corresponding SH functions Y_lm (Eq [A1] in Appendix A) were calculated to estimate the coefficients r_lm (Eq [A2] in Appendix A), which define the estimated regression radii R (Eq [A2] in Appendix A). A new set of points that covers the entire 3D space (ie, θ in the range 0–π and φin the range 0 –2π) was obtained, and the corresponding SH functions were again estimated. Finally, R was recalculated by using the previously estimated coefficients r_lm. Consequently, a complete 3D lesion surface was obtained.

Pathologic Findings

After MR imaging, the brain halves were cut into 5-mm-thick coronal slices (10). Each pathologic slice was independently examined macroscopically for the presence of MS lesions by two pathologists (B.S. and D.N., with 5 and 15 years of experience in brain pathology, respectively). The dimensions of each lesion were measured, particularly focusing on the thickness, by obtaining 2-mm consecutive slices at the lesion area. From each selected region, a tissue block was fixed in 4% formalin and embedded in paraffin. Five microscopic millimeter-thick sections of each block were stained with hematoxylineosin, luxol fast blue, and Bielschowsky stains to ascertain the presence of MS lesions (Fig 2).

Figure 2.

Photomicrographs show histologic evidence of an MS lesion. (a) Hematoxylineosin stain demonstrates hypocellularity with reduction in myelinated fibers and axons (original magnification, ×40), (b) which is confirmed with luxol fast blue stain for myelin (original magnification, ×40) and (c) Bielschowsky stain for axons (original magnification, ×40).

Photographs of the brain slices (original magnification, ×40) were scanned into a computer. The area of each lesion was determined by contouring the edge of the lesions by using mouse tracking (D.G.Z.) and by applying Green’s theorem in the plane (6) (see mathematic details and reasons for using this theorem in Appendix B). Lesion volume was calculated by multiplying its area by the 2-mm thickness according to macroscopic examination. Pathologic findings were considered the reference standard conventionally used in image validation and comparison, as in other prospective multicenter clinical trials (11–13). The macroscopically detected lesions were then compared with the corresponding MR imaging sections to match as many lesions as possible.

MR Imaging Features versus Pathologic Findings

To match each of the identified lesions at MR imaging with its corresponding pathologic lesion, the following five-step procedure was implemented: (a) For the sets of MR images, the most anterior and the most posterior sections were considered to be the first and the last sections, respectively; (b) the approximated location of each lesion at MR imaging was determined by taking the number of the MR sections in which each lesion appeared and multiplying it by the section thickness; (c) the brains were cut in an anterior-posterior direction (B.S.); (d) the pathologic lesions were sought one at a time in the four pathologic slices closer to their corresponding location determined in the second step; and (e) correspondence between the pathologically identified lesions and the lesions identified on MR images was determined by three readers (D.G.Z., A.A., and B.S. [who had 5 years of experience in brain pathology]) by means of consensus. The readers compared each pathologic slice in which lesions were identified with the corresponding MR imaging sections.

Hypotheses Tested

Two main hypotheses were tested (D.G.Z., K.H.Z.): first, that the SH method would show improvement over the CA method in 3D volumetric measurement, as correlated with the pathologic reference standard; and second, that the SH method would follow closely the shape of the image-segmented contour.

Detailed statistical methods are elaborated on later for each of these two hypotheses. Analytic and statistical software programs used included Matlab 6.0 (www.mathworks.com), S-Plus 6 (www.insightful.com), and Excel 2000 (www.microsoft.com).

Statistical Volumetric Comparisons: SH and CA versus Pathologic Findings

1. For each of the volumetric variables, summary statistics, including range, median, mean, and standard deviations, were computed. Furthermore, a z test of normality of the distributions of the data was conducted for each continuous variable (14,15). Thus, we chose the appropriate subsequent statistical hypothesis tests, either by means of ln (a natural log with a base of e) transformation of the data for symmetrization and normalization or on the basis of nonparametric statistical tools. The ln transformation is necessary because the distribution of volume tends to be skewed and have a restricted range. It is often employed in statistical analysis (17). In addition, lesion-specific percentage bias (B) of each approximation method was determined by standardizing the approximated volume (V_SH and V_CA) against the pathologic volume (V_Path): B(V_SH) = [(V_SH − V_Path)/V_Path]× 100%, and similarly to compute B(V_CA) for the CA method. Furthermore, absolute biases were also calculated.

2. Because the volumetric distribution (in cubic millimeters) is nonnormal, nonparametric methods and Spearman rank correlation coefficient were used to evaluate the correlation between the volumetric data of each approximation method and the pathologic reference standard (16,17). The Wilcoxon signed-rank test for paired data was conducted to compare the underlying median biases (16).

3. To compare the underlying means of the percentage biases between the two approximation methods, two-way analysis of variance was performed, where the two factors were the lesions versus the methods. The equivalence of variances of the percentage biases by these methods was also tested by using an F test. Similar analyses were conducted for comparing the means and variances of the absolute biases after log transformation. Because absolute biases were often not normally distributed, these hypotheses tests were conducted on the absolute biases under a log transformation, with normality verified by using a z test of normality (14,15).

4. To visually compare the magnitude of the standardized absolute biases of SH versus CA, a scatterplot was created for all lesions, along with a 45° line through the origin with a slope of 1. The Spearman rank correlation coefficient of these standardized absolute biases between these two methods was computed.

5. The coefficient of variation, calculated by dividing the standard deviation by the mean and then multiplying the result by 100%, was compared for the absolute bias of each method.

Statistical Shape Representation of SH against Segmented Contour

1. The reconstructed surface lying close to the segmented contour in the same coordinate system was recut along the coronal plane into discrete slices. A shape comparison between the segmented contour and its corresponding contours from the recut surface was performed.

2. For each lesion, the shape representation of the SH method was assessed against the segmented contour contour-wise. Euclidian distance was computed between these two corresponding points of the contours. Furthermore, because of the size variability, we only reported percentage normalized distance according to area of the corresponding segmented contour. Lesion-specific minimum, mean, and maximum values of the mean normalized distance were graphed for all lesions. The hypothesis that the median distance is 0 was tested by using a one-sided Wilcoxon rank-sum test, and the correlation between the distance and the pathologic volume of the lesions was assessed by using a Spearman rank correlation coefficient.

3. Because the traditional distance-based metrics might be influenced by variable underlying lesion volume, Dice similarity coefficient (DSC) was also used as an additional validation metric of spatial shape representation according to SH against segmented contour (SC), where DSC is defined as DSC(SH,SC) = 2(SH ∩ SC)/(SH + SC), where ∩ represents intersection. The value of this coefficient ranges from 0 to 1, indicating no overlap to complete overlap (18,19). A DSC of 70% was interpreted as satisfactory spatial overlap according to the literature (19). Lesion-specific minimum, mean, and maximum DSC values were graphed for all lesions. The underlying mean of the logit-transformed mean DSCs was tested at 70% by using a Student t test after applying the z test of normality (14,15), where logit(DSC) = ln[DSC/(1 − DSC)]. The correlation between DSC and the pathologic volume of the lesions was also computed by using a Spearman rank correlation coefficient.

Results

MR Imaging Features versus Pathologic Findings

Nineteen lesions were identified macroscopically by the pathologists and were confirmed to be MS lesions. Most of them were chronic according to histologic examination. Of these 19 identified MS lesions, 11 (58%) were matched with the T1-weighted MR imaging sections. On in vivo T1-weighted MR images, MS lesions and cerebrospinal fluid appear as areas of hypointensity. In our study, because of the relaxation time shortening inherent with formalin fixation, the lesions and the cerebrospinal fluid appeared as areas of hyperintensity. These lesions were then represented by SH and CA methods, along with the segmented contour method. MR imaging–detectable abnormalities were neither visible nor palpable macroscopically in the remaining eight (42%) lesions.

Statistical Volumetric Comparisons: SH, CA, and Pathologic Findings

The actual volumetric measurements and biases (in cubic millimeters) of the 11 lesions varied from lesion to lesion (Table 1, with the lesions listed in increasing order of pathologic volume). The summary statistics were the following, according to pathologic volume: range of 10.7–2409.2, with a median of 56.1; according to SH, range of 12.1–2132.5 with a median of 53.6; and according to CA, range of 15.7–2117.3 with a median of 51.8. The volume data were significantly nonnormal on the basis of the z test of normality (P =.001, P =.002, and P < .001, according to pathologic, SH, and CA volumes, respectively).

TABLE 1.

Volumetric Measurements and Biases of Matched Lesions according to SH and CA Methods

Lesion No.	Pathologic Volume (mm3)	SH Volume (mm3)	Bias of SH (%)	CA Volume (mm3)	Bias of CA (%)
1	10.7	12.1	13.1	15.7	46.7
2	33.2	34.5	3.9	39.1	17.8
3	34.4	36.6	6.4	36.0	4.7
4	37.6	38.7	2.9	40.4	7.4
5	40.0	45.1	12.8	46.6	16.5
6	56.1	53.3	−5.0	51.8	−7.7
7	116.6	123.8	6.2	125.9	8.0
8	214.4	225.3	5.1	230.0	7.3
9	335.9	385.0	14.6	308.2	−8.2
10	1512.0	1358.3	−10.2	1519.2	0.5
11	2409.2	2132.5	−12.2	2117.3	−12.1

Note.—Data are correlated with the pathologic standard of reference and are presented in increasing order of the pathologic volumes. Spearman rank correlation coefficient was r = 1.00 between SH and pathologic volumes and r = 0.99 between CA and pathologic volumes.

By using the ln transformation, we normalized the distribution of the data (P = .19, P = .21, and P = .12 for ln-transformed pathologic, SH, and CA volumes, respectively). After applying the ln transformation of the volume measurements, the two-way analysis of variance test of the mean volumes did not show significant differences among pathologic, SH, and CA volumes (P =.25). However, there was a significant lesion-to-lesion effect on the basis of the same test (P < .001).

Nonparametric rank correlation analysis showed that both SH and CA volumes were highly correlated with pathologic volume (Spearman rank correlation, r = 1.00 and 0.99, respectively).

In Table 2, the summary statistics of the percentage biases were the following: for SH, range of −11.5% to 15.3%, median of 6.3%, and mean ± standard deviation of 4.0% ± 9.0; for CA, range of −12.1% to 46.7%, median of 7.3%, and mean of 7.4% ± 16.3. The summary statistics of the percentage absolute biases were the following: for SH, range of 3.5%–15.3%, median of 7.3%, and mean of 8.7% ± 4.1; for CA, range of 0.5%–46.7%, median of 8.0%, and mean of 12.4% ± 12.4.

TABLE 2.

Summary Statistics of Biases and Absolute Biases of SH and CA Methods

Measure and Summary Statistics	SH	CA
Bias (%)
Range	−11.5 to 15.3	−12.1 to 46.7
Median	6.3	7.3
Mean ± SD*	4.0 ± 9.0	7.4 ± 16.3
Absolute bias (%)
Range	3.5 to 15.3	0.5 to 46.7
Median	7.3	8.0
Mean ± SD*	8.7 ± 4.1	12.4 ± 12.4

Note.—SD ± standard deviation.

^*P = .04 and P = .001 from the test of equal variances of the biases and absolute biases of the SH and CA methods, respectively.

Both SH and CA methods were shown to be unbiased: By testing the mean percentage biases at 0 for SH and CA methods separately, we found that neither method was biased statistically. In addition, the log-transformed absolute biases satisfied the normality assumption, as verified by the z test (P = .68 and .12 for SH and CA, respectively), and the mean absolute percentage biases were not statistically different from 0 for each method. However, results of the F test of the variances of the percentage biases were significantly smaller for SH than for CA (P =.04), as well as for the variances of the absolute percentage biases (P =.001), suggesting that SH was more robust for different lesions than was CA. The coefficient of variation of the ln-transformed absolute bias was only 0.25 for SH, in comparison with 0.53 for CA.

The absolute percentage biases showed that eight (ie, lesions 1, 2, 4, 5, 7, 8, 10, and 11) of the 11 lesions (73%) had biases smaller for SH than for CA, as these points lie below the 45° diagonal line (Fig 3). However, Spearman rank correlation was r = 0.33 between the paired standardized absolute biases of these two methods, suggesting a slightly positive correlation. In other words, while the bias in CA increases, this scatterplot suggests that the bias in SH increases only slightly, but overall, SH performed better than CA.

Figure 3.

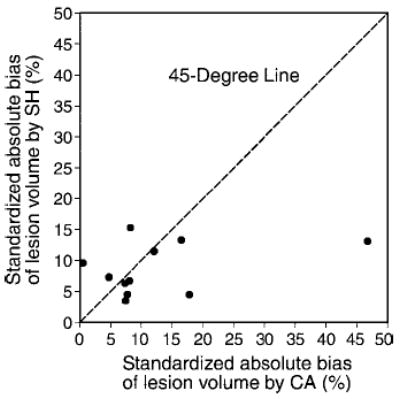
Scatterplot of percentage absolute bias of lesion volume according to SH, against percentage absolute bias of lesion volume according to CA, each standardized according to pathologic volume. Eight (ie, lesions 1, 2, 4, 5, 7, 8, 10, and 11) of the 11 lesions had smaller absolute biases with the SH method than with the CA method, with data points lying under the 45° line.

Statistical Shape Representation of SH against Segmented Contour

The shape of each MR imaging–identified lesion was approximated by using SH. Figures 4 and 5 demonstrate two different examples of MS lesions, showing the brain slice (Figs 4a, 5a) on the corresponding MR imaging section in Figures 4b and 5b and the approximated 3D shape of the lesion according to SH in Figures 4c and 5c. Figures 4b and 5b are examples of periventricular white matter lesions that were extended into two and three MR imaging sections, respectively. Visual comparisons of each of the contours of these lesions outlined during the segmentation process with their corresponding contours extracted from the 3D SH-reconstructed shape are shown in Figures 4d, 4e, 5d, 5e, and 5f. The lesion shape in Figure 4c is similar to the classical elliptically shaped MS lesions, while the shape obtained in Figure 5c is similar to a pyramidal shape.

Figure 4.

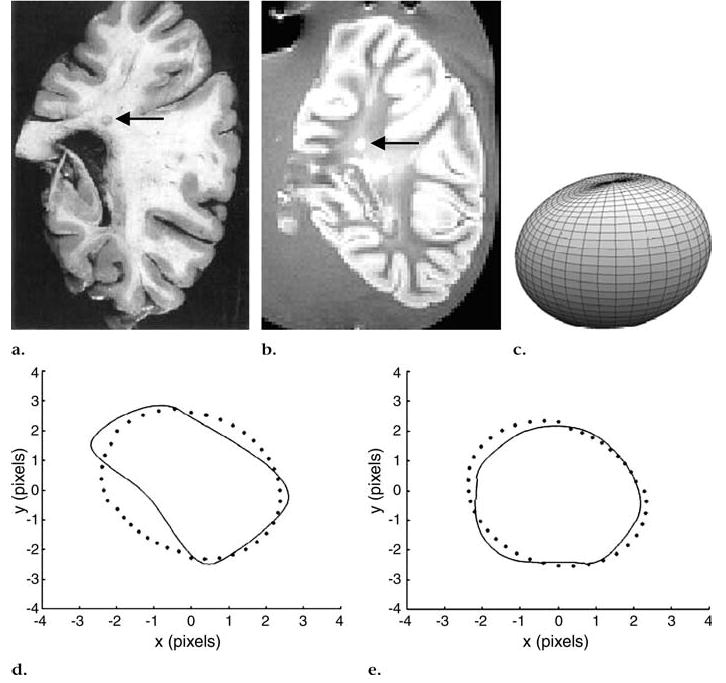
Periventricular lesion (arrow) that extended into two coronal MR sections (550/20, field of view of 24 cm, matrix size of 256 × 256 pixels). (a) Pathologic slice, (b) one of two MR sections, and (c) approximated 3D lesion shape obtained with SH method show that lesion is similar to classical elliptically shaped MS lesion. (d, e) Segmented axial contours (solid line) versus corresponding contours obtained from 3D-reconstructed shape with SH method (dotted line).

Figure 5.

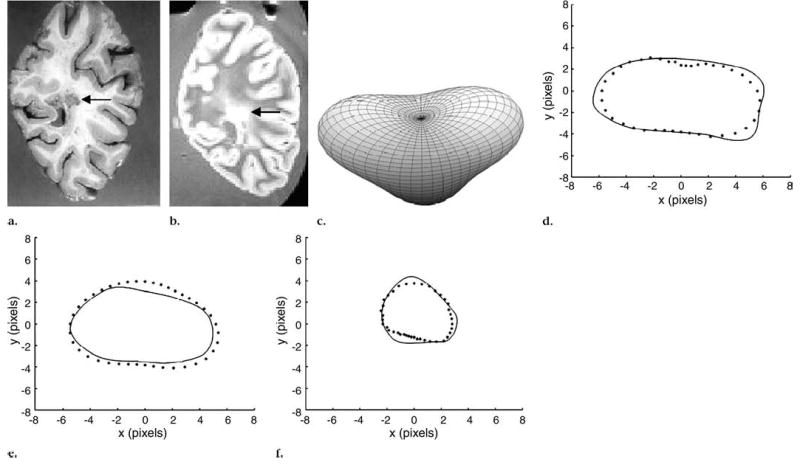
Periventricular lesion (arrow) that extended into three coronal MR sections (550/20, field of view of 24 cm, and matrix size of 256 × 256 pixels). (a) Pathologic slice, (b) one of three MR sections, and (c) approximated 3D lesion shape obtained with SH method show pyramidal shape of lesion. (d–f) Segmented axial contours (solid line) versus corresponding contours from 3D-reconstructed shape with SH method (dotted line).

The results of the statistical comparisons are as follows:

1. The number of contours per lesion is given in Table 3. In Figure 6, the normalized distance measures (percentages), standardized according to the sum of pathologic and SH areas (analogous to the calculation of DSC described later), are displayed with regard to individual lesions in increasing order of pathologic volumes. The overall range of the normalized distance was 0.1%–2.5%. The mean distance was slightly negatively correlated with lesion size (r = −0.38), suggesting that the normalized distance was smaller for larger lesions with a larger normalizing lesion area.

2. Figure 7 shows the DSC versus the individual lesions, also displayed in increasing order of pathologic volume. The overall range of the DSC was 75%–96%. The logit (a function of the ln) transformation significantly improved normality, as the z test of normality showed P = .004 and P = .61 before and after logit transformation, respectively.

TABLE 3.

Ranges of Normalized Mean Distance and DSC Measured between Contours according to SH and Segmented Contours Methods

Lesion No.	No. of Contours	Range of Normalized Mean Distance (%)	Range of DSC (%)
1	1	0.8–0.8	88.0–88.0
2	1	0.4–0.4	93.9–93.9
3	2	1.0–1.6	80.0–82.8
4	2	0.6–0.7	86.7–90.9
5	2	0.6–0.9	85.7–91.4
6	2	0.7–1.4	81.1–87.8
7	3	0.5–1.0	75.4–92.9
8	3	0.2–0.4	91.3–94.1
9	3	0.4–1.2	75.6–86.3
10	10	0.1–1.2	82.5–95.5
11	14	0.1–2.5	74.6–95.1

Note.—The mean DSC is significantly above 0.7 (P < .001).

Figure 6.

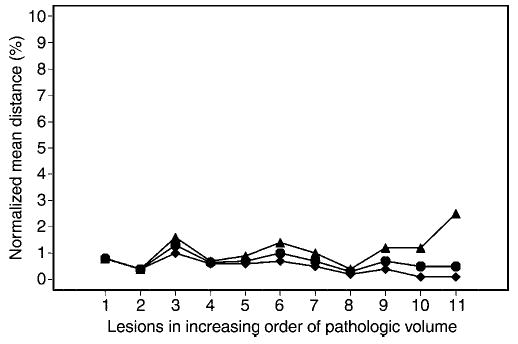
Graph shows lesion-specific percentage normalized mean distance, with individual lesions presented in increasing order of pathologic volume. Overall range of the normalized distance was less than 2.5%. Normalized distance tended to be smaller for larger lesions with larger normalizing lesion area. ▴ = Maximum of mean distances over all contours per lesion. • = Average of mean distances over all contours per lesion. ♦ = Minimum of mean distances over all contours per lesion.

Figure 7.

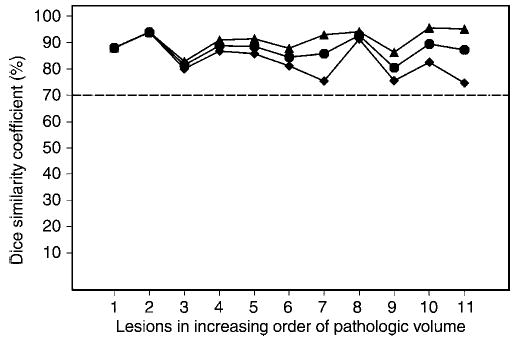
Lesion-specific DSC, with individual lesions presented in increasing order of pathologic volume. Mean DSCs are significantly greater than 70% (dotted line). All DSC values were greater than 70%, the threshold found in the literature, suggesting satisfactory spatial overlap. Mean DSC was not correlated with lesion size, suggesting that SH were robust with respect to lesion size. ▴ = Maximum of DSCs over all contours per lesion. • = Mean of DSCs over all contours per lesion. ♦ = Minimum of DSCs over all contours per lesion.

The underlying mean of the logit-tranformed DSC values was significantly above logit (0.70) (P < .001) but was not significantly correlated with lesion size (r = 0.08). Thus, on the basis of DSC as a validation metric, SH was robust with respect to lesion size.

Discussion

In previous pathologic studies of MS lesions (20–24), investigators found that the number, pattern of distribution, and size of lesions varied considerably between and within patients; furthermore, lesions can occur in all areas of the central nervous system. In an extensive study of postmortem brains (21), it was established that lesions had different shapes—for example, spherical, egg-shaped, ring-shaped, or conical, with the long axis oriented in the same direction as the long communicating venules. Polyhedral or bizarre ramifying shapes were also present (20). The spherical and elliptical shapes appear most frequently in the white matter and are attributed to a perivascular extension of the inflammatory and demyelinating process along straight venules (24).

Because MR imaging is an important tool for detecting and monitoring MS lesions, further assessment of the geometry of the lesions could contribute to better understanding of their evolution over time. Moreover, such information can assist examination of several clinical variables, such as rate of progression to disability and response to drug treatments. In a couple of studies (25,26), investigators have also underlined the importance of MR imaging in the diagnosis of suspected MS and in predicting the future conversion of the diagnosis to clinically definite MS.

It is apparent that although great improvement has been achieved so far, specific aspects related to MR imaging technology, section thickness, or variations in lesion load measurements are still not standardized, and thus, it is extremely difficult to compare findings between patients or between studies. The development of analytic methods, such as the SH technique for assessment of MS lesion volume and geometry, is crucial for future studies and will enable early diagnosis and sensitive monitoring of disease activity.

It was reported that lesion size and shape of different lesions within the same patient were often similar (3). However, this homogeneity was not observed in our study; instead, significantly different MS lesion patterns, with high variations in size and shape in the same patient, were demonstrated on the basis of two-way analysis of variance.

SH is an analytic modeling approach that provides accurate measurements of MS lesion volumes, yields 3D shape information (4), and enables monitoring of temporal changes in lesion geometry (5). In the present study, as well as in a previous study (4), on the basis of the fact that most MS lesions manifest a spherical or elliptical shape, the center of gravity of the data points was used as that of the spherical coordinate system. Thus, one and only one pair of values for the elevation and azimuth angles (θ and φ, respectively) can represent each point on the lesion’s surface. For more irregular lesions with a half-moon (known as Dawson fingers in MS), star-like, or other shape, this parameterization (ie, assigning a pair of θ and φ values to each point on the lesion’s surface) may be limited. This is due to the possibility that more than one pair of θ and φ values could represent some of the points on the lesion’s surface. For those cases, a more sophisticated procedure to parameterize the data is needed. Those complex problems are usually solved by flattening and conformal mapping to map the data to a unitary sphere (27–29).

In the present study, we have applied and validated this method on the basis of brain MS lesions with known pathologic findings used as the reference standard. Our investigation was mainly devoted to volume assessment, since the evaluation of shape parameters was investigated previously (5). Since the goal of the current investigation was not comparison of section thickness and partial volume averaging, we tried to get the same 2-mm thickness of the MR imaging sections for the pathologic examination, the findings of which were used as the reference standard. Because of the manual pathologic slicing process, however, the achieved slice thickness was inaccurate. We found that the pathologic lesions appeared in only one slice, and then we estimated their volumes according to the CA method after measuring the individual thickness for each particular pathologic slice. The decision to use CA for measuring the pathologic volumes of the lesions was based on a previous, more extended analysis (4), which shows that on average, CA is slightly better than SH when only one contour per lesion is available for estimating the volume. The fact that only one pathologic slice was available for estimating the volumetric reference standard could be a cause of measurement uncertainties. As stated earlier, however, for this kind of situation, where only one contour per lesion is available, CA yields a good approximation of the lesion volume (4).

Our volumetric analysis confirmed that SH closely correlated with the pathologic lesion volume with no significant bias. In addition, SH yielded significantly reduced variability in the bias with regard to CA (P = .04), even for significantly different lesion types and sizes (P = .001). The lesion volume assessed according to SH highly correlated with pathologic volume (r = 1.00).

The main difference in the proposed method and the previously used CA method was in the variances of the biases for the volume measurement in comparison to the pathologic volume. Thus, SH was found to be closer to histologic measurements. Even though the deviation from the pathologic volume seems normally distributed with all measurements, for small lesions (<50 mm³), the volume measured according to SH or CA is consistently larger than that at pathologic examination. This may suggest that there was systematic measurement error in one or all lesions, which was beyond the scope of the correlation analysis when considering pathologic findings as the “practical” standard of reference by convention. However, the fact that the SH measurement was closer to the pathologic measurement might not have guaranteed that the SH was a better measurement than the CA method. One of the possible causes for small lesion volume at pathologic measurement may be shrinking of samples during fixation.

Next, in our shape analysis, both the distance and DSC as spatial validation metrics showed negligible shape differences between the image-segmented contours and the corresponding contours derived from SH. The range of the mean distance was only 0.1%–2.5%, and the range of the DSC was 75%–96%. The mean DSC was also statistically significantly above 70%, a cutoff value for satisfactory spatial overlap (P < .001) (19). Both the normalized distance and DSC were robust with respect to lesion size and shape.

This study had several limitations. First, only 11 lesions were available in two brain halves with confirmed pathologic findings obtained externally for statistical validation purposes. This limited sample size was due to two possible factors—first, the relative inaccuracy of the slicing process, and second, the uncertainties introduced by the fact that only one pathologic slice per lesion was available. Next, there were the difficulties in corresponding all brain slices with a precisely corresponding MR image. These difficulties result from different imaging plane and thickness (30) and the lack of topographic landmarks (3). Better MR imaging techniques may yield improved visualization of the MS lesions; as a result of higher spatial resolution of images (eg, 1-mm section thickness or less) and more automated MR imaging segmentation techniques, MS lesion volume and shape will be better estimated by using SH. Another limitation was the existing MR imaging acquisition protocol used in our clinical practice, as alluded to earlier. T1-weighted multisection MR imaging was used in the study. In the future, a 3D acquisition protocol may be considered as an alternative, since thinner sections can be obtained, even with isotopic voxels, which allows a better quantification of volume and irregular shape of lesions. Finally, the voxel size was approximately 2 mm³, which may introduce additional uncertainty when dealing with small lesions. An attempt to identify such uncertainty was done by using computerized simulations of MS lesions (4), and additional attempts will be made in the future.

In summary, SH provided unbiased lesion volume and smaller variable biases, along with 3D shape information. The demonstration of its utility in the sense of providing diagnostic information may require a wider scope of evaluation, which is beyond the scope of this work. However, we suggest including SH as an additional tool for assessing MS lesions, which may enable better understanding of the pathogenesis, as well as lesion evolution and progression over time.

Appendix A

SH are orthonormal functions over the unit sphere used to describe complicated surfaces in 3D space. These functions are defined by the following equation (31):

$$\begin{array}{l}{Y}_{lm}(\theta ,\varphi )\\ =\sqrt{\frac{2l+1}{4\pi }\frac{(l-m)!}{(l+m)!}}{P}_l^m(\text{cos\hspace{0.28em}}\theta )\mathrm{\hspace{0.17em} }\text{exp}(im\varphi ),\end{array}$$ (A1)

where Y_lm(θ,φ) is the corresponding SH function defined in a spherical coordinate system (R,θ,φ), $P_l^m(\text{cos}\theta )$ is the associated Legendre polynomial, the parameter l (function’s degree) is zero or a positive integer, and the integer m (function’s order) can have only the values of −l, − (l – 1), . . . , 0, . . . , (l – 1), l.

For a spherical coordinate system (ie, R,θ,φ), the surface radii R can be presented discretely with the following equation:

$$R(\theta ,\varphi )=\sum _{l=0}^n\sum _{m=-l}^l{r}_{lm}{Y}_{lm}(\theta ,\varphi ),$$ (A2)

where r_lm are the amplitudes of the corresponding SH functions (represented by complex numbers, with l running from 0 to the selected number of harmonics “n”).

Equation (A2) can be represented as a multiple linear regression model. Thus, by using a least squares approximation, an MS lesion can be described analytically by calculating the corresponding r_lm coefficients. The term r₀₀ is the general average radius of the approximated surface. Hence, r₀₀ represents the size or volume of the shape. Unlike r₀₀, which represents a global measure (ie, size or volume), the terms r_lmY_lm(θ,φ)[z]wbo_l,m>0 contain more local information of the 3D SH surface shape.

Appendix B

A cross-sectional area bounded by a closed contour can be estimated by Green’s theorem in the plane:

$$\text{Area}=\frac{1}{2}\oint xdy-ydx.$$ (B1)

The integral can be calculated by integrating over each contour segment and summing the results. By using a summation notation and substituting Δ_x = x_i – x_i–1 for dx and Δ_y = y_i – y_i–1 for dy, the formula is given thus:

$$\text{Area}=\frac{1}{2}\sum _{i=1}^N[x_i(y_i-y_{i-1})-y_i(x_i-x_{i-1})],$$ (B2)

where N is the number of points in the contour, x_i and y_i are the coordinates of each contour point, and x₀ and y₀ are also the coordinates of the last contour points x_N and y_N, respectively.