The relationship between FRQ-protein stability and temperature compensation in the Neurospora circadian clock

Abstract

Temperature compensation is an important property of all biological clocks. In Neurospora crassa, negative-feedback regulation on the frequency (frq) gene's transcription by the FRQ protein plays a central role in the organism's circadian pacemaker. Earlier model calculations predicted that the stability of FRQ should determine the period length of Neurospora's circadian rhythm as well as the rhythm's temperature compensation. Here, we report experimental FRQ protein stabilities in frq mutants at 20°C and 25°C, and estimates of overall activation energies for mutant FRQ protein degradation. The results are consistent with earlier model predictions, i.e., temperature compensation of Neurospora's circadian rhythm is a highly regulated process where the stability of FRQ is an important factor in determining Neurospora's circadian period as well as the clock's temperature compensation. The partial loss of temperature compensation in frq⁷ and frq^S513I mutants can be described by a simple negative-feedback model (the Goodwin oscillator) when the experimentally obtained activation energies of FRQ degradation for theses mutants are incorporated into the model.

Circadian clocks are physiological oscillators, which are important in the daily and seasonal adaptation of organisms to their environment (1–4). A characteristic property of circadian clocks is the ability to keep the period length approximately constant despite changes in ambient environmental conditions (5). Temperature compensation, the approximate constancy of the period at different constant temperatures, is one of the best known examples of circadian period homeostasis. Despite the relative insensitivity of the circadian period to temperature, the underlying physiological component processes are generally quite dependent on temperature, with Q₁₀ values of 2 or even higher. The mechanisms behind temperature compensation are not well understood, although a general theory applicable to reaction kinetic oscillator models (6–22) can be formulated (23–28).

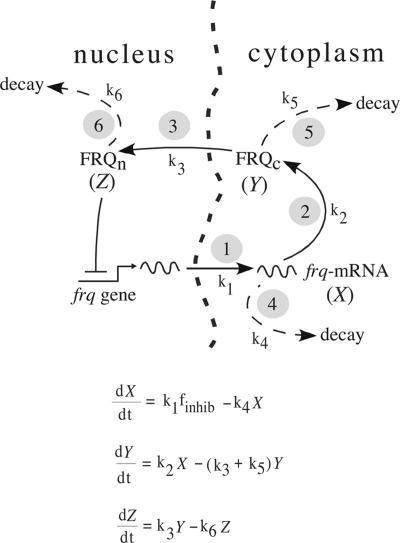
In the model organism Neurospora crassa, the frequency (frq) gene has a central role in generating a circadian conidiation rhythm by means of a transcriptional and translational negative-feedback loop (29–32). This negative-feedback loop is considered to be part of a central oscillator that controls a variety of rhythmic output genes, so-called clock-controlled genes (30, 31). We have taken the negative-feedback loop in its simplest manifestation [Fig. 1 Upper (compare with refs. 30 and 31)] and cast it as a Goodwin-type model [Fig. 1 Lower (33)]. As implemented, the model assumes that kinetically important rate constants involve the transcription yielding frq mRNA, its translation, and the net nuclear import of FRQ, as well as the decay of these species. Events associated with the processing of frq primary transcripts, their export to the cytoplasm, and their assembly onto ribosomes are subsumed under rate 1, and as a first approximation, the impact of FRQ in inhibiting its own gene's expression is taken to be an immediate function of its nuclear concentration. Despite these approximations, simulation calculations with the Goodwin model showed that the dynamics of the frq negative-feedback loop are in good agreement with experimental phase-resetting kinetics (16, 17, 34, 35). The model's predictions were that the stability of the FRQ protein not only should have a major influence on the clock's period length but that a regulated thermal stability of FRQ is required to maintain temperature compensation (35, 36). These predictions were partly confirmed by experiments, where the stability of the FRQ protein was altered by replacing the phosphorylation site serine 513 by isoleucine (37). These results were supported by another study where a PEST-like sequence was removed from FRQ (38), which also resulted in a more stable FRQ-protein (compared with frq⁺) and an increased period length.

Fig. 1.

The model. (Upper) Negative-feedback loop of the Neurospora circadian clock (30, 31). Encircled numbers (“i”) correspond to processes R_i with rate constants k_i: 1, export of primary frq transcript into cytoplasm and assembly onto ribosomes; 2, translation to FRQ protein; 3, import of cytosolic FRQ into nucleus; 4, degradation of transcript; 5 and 6, degradation of cytosolic and nuclear forms of FRQ, respectively. (Lower) Goodwin-type equations that were used in the calculations. The variables are X ≡ frq-mRNA, Y ≡ FRQ_c (cytosolic FRQ), and Z ≡ FRQ_n (nuclear FRQ). For rate-constant values and initial concentrations, see Table 1.

Guided by the model predictions, the aim of this study was to obtain estimates for the thermal stability of FRQ in frq mutants by measuring the overall activation energies of FRQ degradation and correlating the stability data with the mutant rhythms' temperature sensitivities. The results show that the partial loss of temperature compensation in frq⁷ and frq^S513I mutants is related to an increase in FRQ's stability (causing a larger period length) and an increase in the activation energy of FRQ degradation (causing a more temperature-sensitive period). By incorporating the experimentally determined activation energies of FRQ degradation into the Goodwin model (Fig. 1), we were able to consistently describe the periods and the occurrence/loss of temperature compensation in frq⁺, frq¹, frq⁷, and frq^S513I mutants.

A Theory of Temperature Compensation

When describing the time evolution of a physiological system by reaction kinetics, the system is broken down into a set of component reactions R_i, which are translated into chemical rate equations (39). The influence of temperature on an individual process R_i is described by the Arrhenius equation (Eq. 1)

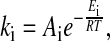[1]

where k_i is the rate constant of process R_i. Symbols E_i, R, T, and A_i denote the activation energy, gas constant, temperature, and collision factor, respectively (40). The activation energy, E_i, is a measure of how sensitive process R_i is toward variations in temperature.

For a chemical/metabolic oscillator, the period P depends on the individual processes R_i and their corresponding rate constants k_i, i.e.,

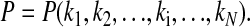[2]

Temperature compensation requires that the period P is independent of temperature, which leads to the condition (see Appendix):

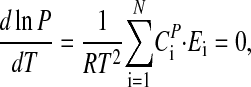[3]

where the C^P_i (control coefficients) obey the summation theorem (41, 42):

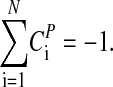[4]

Because activation energies E_i are positive, Eq. 3 requires that the C^P_i must have positive and negative values. This is equivalent to the presence of an “antagonistic balance” of opposing reactions (23) that resemble the compensation mechanisms in mechanical and electronic clocks (27). In fact, almost 50 years ago, Hastings and Sweeney (43) suggested that opposing reactions may lead to temperature compensation in circadian rhythms. Interestingly, for physicochemical oscillators, the presence of positive and negative C^P_i values appears to be closely related to the presence of positive- and negative-feedback loops as a necessary part of the rhythm generator (23, 44). We are not aware of any reaction kinetic oscillator model that has only negative C^P_i values (note that such an oscillator could not have temperature compensation). Thus, any reaction kinetic oscillator should in principle be able to show temperature compensation when suitable activation energy combinations (Eq. 3) are chosen.

By integrating Eq. 3, and assuming that 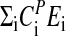is temperature independent, the following expression for P can be obtained:

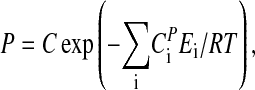[5]

where C is a constant (see Appendix).

Once the rate constants are defined for a given reference temperature, T_ref, concentrations and the control coefficients can be calculated for a given temperature, T.

Table 1 shows the frq⁺ rate constants used and the model's C^P_i values. Slight modifications of the present model compared with the earlier version (34) include thresholds for inhibition and start of frq transcription, respectively (Table 1). This allows for an extended parameter space for which oscillations can be observed (35). The different frq mutants are represented in the model by different values for the FRQ degradation rate constants k₅, k₆ and activation energies E₅, E₆. Because in the experiments total FRQ (i.e., cytosolic and nuclear FRQ) is measured, and for the sake of simplicity, we assumed that k₅ = k₆ and E₅ = E₆ (Table 1).

Table 1. Rate constants, control coefficients, and activation energies used in the model calculations.

Reaction i	Rate constant ki, h-1	CiP (15% variation of the kis)	Ei, kJ/mol	CiPEi, kJ/mol
1	0.3	0.131	190	24.9
2	0.3	0.093	190	17.7
3	0.3	-0.040	190	-7.6
4	0.27	-0.470	30	-14.1
5	0.2*	-0.131	30†	-3.9
6	0.2*	-0.628	30†	-18.8
		ΣiCiP = -1.045		ΣiCiPEi = -1.8

The given rate constant values are defined for T_ref = 292 K. Rate constants k₅ and k₆ (with asterisk) differ for the various frq mutants. Initial concentrations (a.u.) used in all calculations: X = 6.124 × 10^-2, Y = 8.452 × 10^-2, Z = 5.245 × 10^-1. Threshold for frq transcription inhibition, Z_max = 0.1 a.u.; threshold for reactivating frq transcription, Z_min = 0.05 a.u. (used in all calculations).

^*k₅, k₆ values for frq⁺ at T_ref = 292 K. The following k₅, k₆ values (defined at T_ref = 292 K) have been used in the calculations for the other mutants: frq¹, 0.320 h^-1; frq⁷, 0.124 h^-1; frq^S5131, 0.080 h^-1.

^†E₅ and E₆ values for frq⁺. The following E₅, E₆ values (E₅ = E₆) have been used in the calculations for the other mutants (see also Table 2): frq¹, 29 kJ/mol; frq⁷, 46 kJ/mol; frq^S5131, 59 kJ/mol.

The negative control coefficients C^P₅, C^P₆ (Table 1) indicate that when temperature compensation in the model is lost because of increased E₅, E₆ values (leading to decreased k₅, k₆ values), the period should decrease with increasing temperature leading (as in the frq⁷ mutant) to negative dlnP/dT values (Eq. 3). Although experimental results with the frq^S513I and frq^ΔPEST-1 mutants (37, 38) indeed confirmed that a more stable FRQ protein leads to larger period lengths, the question of which properties of FRQ relate to changes in temperature compensation were so far not considered. Here, we show that variations in the overall experimental activation energies of FRQ degradation are consistent with the dynamics of a Goodwin oscillator and can account for the various degrees of temperature compensation in the frq mutant alleles.

Materials and Methods

Model Calculations. The model calculations with the Goodwin oscillator (Fig. 1 and Table 1) were done by using the FORTRAN subroutine LSODE (Livermore Solver of Ordinary Differential Equations) (45).

Growth-Tube Experiments. Growth tubes were prepared as described in ref. 46 with 1× Vogel's medium, 0.2% glucose, 0.17% arginine, and 1.5% agar. The tubes were inoculated with conidia and transferred to incubators (darkness) directly after inoculation at different but constant temperatures (±0.5°C). Measuring the distance between two distant conidiation peaks and dividing the distance by the growth speed and the number of cycles between the peaks determined the average period length. In general, six growth tube replicates were run in parallel per experiment.

Shaking Cultures. Twenty-five milliliters of LL medium (2% sucrose in 1× Vogel's medium) was added to Erlenmeyer flasks. The solution was inoculated with a 200-μl conidial suspension (≈10⁸ conidia per liter) of the mutant strain in question. The cultures were shaken under continuous light (LL) conditions. After 22 h (20°C) or 32 h (25°C), the lights were turned off, and mycelium was harvested in 2-h intervals for periods up to 16 h.

Western Blotting Analysis. The mycelium was ground in liquid nitrogen and extracts, and blots were made as described in ref. 47. Densitometric analysis of scanned films was performed with nih image (National Institutes of Health; http://rsb.info.nih.gov/nihimage).

Experimental and Computational Results

FRQ degradation rate constants k (i.e., k = k₅ = k₆) for frq¹, frq⁺, frq⁷, and frq^S513I mutants were estimated at 20°C and 25°C by measuring the amount of FRQ at different times after a light (LL) to dark (DD) transition. In light (LL), frq transcription is increased and FRQ is not able to inhibit its own transcription (48, 49). After a transfer from light (LL) to darkness (DD), FRQ becomes capable of inhibiting its own transcription with the result that within the time interval before the circadian rhythm onset, FRQ is degraded without being produced. The FRQ levels, which were determined during that period, are fitted to first-order decay kinetics (Eq. 6)

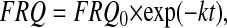[6]

where FRQ represents FRQ levels, k is the degradation rate constant (Table 2), and t is the time after the transfer of cultures from LL to DD. From the determined k value, the FRQ half-life, t_1/2, is calculated as

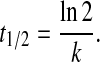[7]

This method was previously used to estimate FRQ protein stabilities (37, 38). We have chosen not to use cycloheximide in the determination of k, because cycloheximide can dramatically decrease protein degradation (16, 50).

Table 2. Experimental (Exp) and theoretical (Theor) FRQ degradation rate constant values at 20°C and 25°C.

	FRQ1		FRQ+		FRQ7		FRQS5131
	Exp	Theor	Exp	Theor	Exp	Theor	Exp	Theor
k (20°C)*, h-1	0.27	0.33	0.22	0.21	0.16	0.13	0.08	0.09
k (25°C)*, h-1	0.33	0.41	0.27	0.26	0.22	0.18	0.12	0.13
Ea (kJ/mol)	29		30		46		59

^*The theoretical k values at 20°C and 25°C are calculated from the (theoretical) k₅ (=k₆) FRQ degradation rate constants given in Table 1 by using the experimentally determined activation energies E_a and Eq. 1.

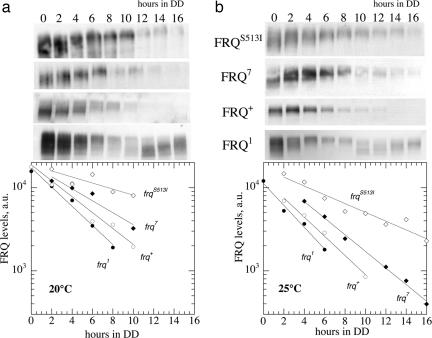
Fig. 2 shows measured levels of FRQ¹, FRQ⁺, FRQ⁷, and FRQ^S513I at 20°C (Fig. 2a) and 25°C (Fig. 2b) observed after the LL-to-DD transfer. The fits to Eq. 6 are shown as straight lines in the semilogarithmic plots. The obtained k values are shown in Table 2 (“Exp” columns) from which the activation energies, E_a, were calculated by Eq. 8 (Table 2, last row):

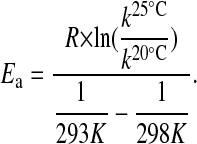[8]

From the experimental activation energies and the initial set of rate constants (Table 1), rate-constant values that were used in the model calculations were determined by Eq. 1 as a function of temperature (Table 2).

Fig. 2.

Western blots for FRQ in frq¹, frq⁺, frq⁷, and frq^S513I mutants at 20°C (a) and 25°C (b) after a LL-to-DD transition. One representative experiment of two is shown. Densitometric results are shown as semilogarithmic plots below. Straight lines show exponential fits to the data. First-order degradation rate constants from the exponential fits are given in Table 2 (“exp” columns).

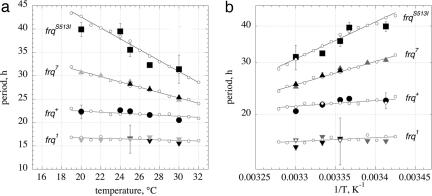
Fig. 3a shows experimental and calculated period lengths for the frq mutants as a function of temperature. For the frq^S513I mutant, the period length at 25°C was found to be in excellent agreement with those previously reported (37). Fig. 3b shows the preferred representation of period–temperature data, i.e., a semilogarithmic Arrhenius-like plot between the period length and 1/T (Eq. 5). By means of the slopes in Fig. 3b, the balance equation (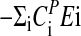) is determined. In agreement with the experimental activation energies of FRQ⁷ and FRQ^S513I degradation, the 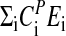for these mutants show increased negative values (compared with FRQ⁺) leading to increased positive slopes.

Fig. 3.

Period–temperature relationships in frq mutants. (a) Plot showing periods as a function of temperature. Solid black symbols with error bars are experimental growth tube results from this study (n = 6). Gray solid symbols are the results from Gardner and Feldman (52). Small open circles represent computational results with linear regressions (solid lines). (b) Arrhenius-like plot showing periods as a function of 1/T for the data of a. The exponential fits to the computational results are shown as solid lines. The slope gives the “balance equation” – 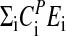, with the following numerical values: frq, –2.5 kJ/mol, frq⁺, –3.7 kJ/mol; frq⁷, –15.2 kJ/mol; frq^S513I, –24.2 kJ/mol. Negative signs indicate that the period decreases with increasing temperature.

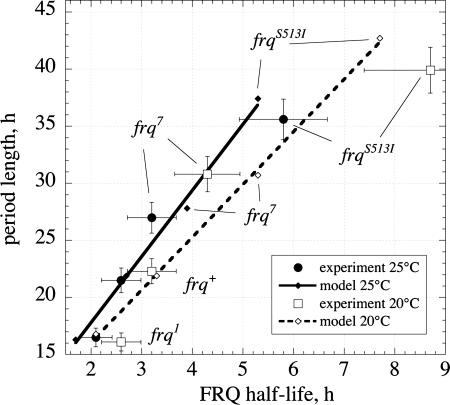
Fig. 4 shows the experimentally determined period lengths at 20°C and 25°C as a function of the experimental FRQ half-lives, t_1/2, together with the corresponding set of calculated data. Whereas the model indicates a linear relationship between period length and FRQ half-life, the experimental results seem to indicate a more curved relationship. However, because of the relative large experimental uncertainties, it is difficult to make a clear distinction. Fig. 4 also shows that there is no “unique” relationship between period length and FRQ half-life, i.e., frq mutants with the same FRQ half-lives may still have different period lengths at different temperatures.

Fig. 4.

Experimental and model calculated period lengths of frq mutants as a function of FRQ half-lives at 20°C and 25°C. Note that only for a given temperature (“isotherm”) is there a correspondence between period length and FRQ half-life. The uncertainties in FRQ half-lives are calculated from a 15% variation in the determination of the degradation rate constant k (Eq. 8). From growth-tube experiments, the uncertainties in the period is shown as an average variation of ≈5%.

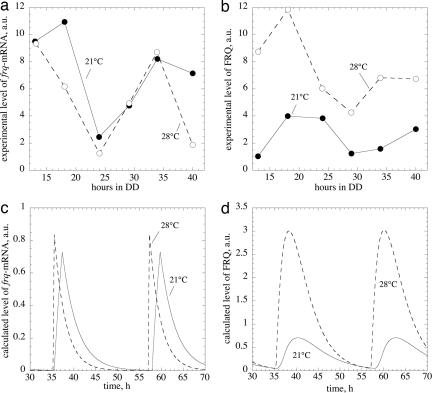
We also tested the model's amplitude behavior as a function of temperature. Earlier experiments (51) suggested that the amplitude/magnitude of FRQ⁺ oscillations might increase with increasing temperature, while frq⁺-mRNA levels show only small changes (Figs. 5 a and b). This behavior is clearly observed in the temperature-compensated model (Figs. 5 c and d), suggesting that a single negative-feedback representation of the Neurospora circadian clock with FRQ as a central component may be able to correctly describe the temperature regulation of the clock core components' amplitudes and the clock's period.

Fig. 5.

Temperature behavior of frq⁺-mRNA and FRQ⁺ amplitudes. a and b show earlier experimentally determined frq⁺-mRNA and FRQ⁺ levels measured at 21°C (solid lines) and 28°C (dashed lines). The data are replotted from Liu et al. (51). c and d show calculated concentration profiles of frq⁺-mRNA and FRQ⁺ protein in the temperature compensated Goodwin model (Fig. 1 and Table 1) at 21°C (solid lines) and 28°C (dashed lines). Because in the experiment (b) total (i.e., nuclear and cytosolic) FRQ was measured, calculated FRQ levels are represented by the sum of variables Y (cytosolic form of FRQ) and Z (nuclear form of FRQ; see Fig. 1).

Discussion

The stability of FRQ is of importance in determining Neurospora's circadian period length (35, 37, 38) and, as shown here, for the clock's temperature compensation. All investigated frq mutants have altered FRQ stabilities due to point mutations, which correlate with period lengths (Fig. 4).

The influence of temperature on any reaction kinetic oscillator's period is described by Eq. 3. When 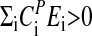, the period increases with increasing temperature, whereas when 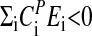, the period decreases with increasing temperature as observed for some of the frq mutants. Temperature compensation occurs when 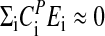, but generally only within a certain temperature range, which is often considered to be physiologically of importance. In Neurospora, temperature compensation ceases abruptly when temperatures increase to 30–34°C (52) with an estimated change of Q₁₀ from ≈1 (average for 20–30°C) to ≈1.8–2 (30–34°C). It appears that this abrupt disappearance of temperature compensation is related to a sudden change of certain properties within the balancing process, which can no longer be maintained at higher temperatures. Interestingly, this strong temperature dependence of Neurospora's period length above 30°C resembles closely what is observed for most chemical oscillatory reactions (see discussion below).

There exist strains of Neurospora that affect temperature compensation by mutations in genes other than frq. In particular, prd-4 has a short period but is defective in temperature compensation by decreasing its period with increasing temperature (52). Our model suggests that prd-4 should have an increased FRQ turnover compared with prd-4⁺, leading to shorter period lengths. In addition, the activation energy of FRQ degradation should also be increased in prd-4, leading to a negative balance equation, , and resulting in decreasing periods with increasing temperature. PRD-4 is a cell cycle kinase that, when mutated, leads to premature phosphorylation of FRQ (A. Pregueiro, J.C.D., and J.J.L., unpublished work) and possibly to an increased degradation rate of FRQ.

Temperature compensation likely emerged through an evolutionary process with the adaptation of reaction sensitivities and activation energies such that 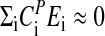. FRQ is a central clock element, and its stability is highly regulated through a variety of means including PEST-like sequences and multiple phosphorylation sites, which are part of Neurospora's temperature-compensation mechanism. Both CKII and CAMK-1 along with the phosphatase PP1 have been identified as determining FRQ's stability and being essential for the normal operation of Neurospora's circadian clock (53–56). There is also evidence that FRQ degradation requires FWD1, an F-box/WD-40 repeat-containing protein, which is considered to be necessary for the ubiquitination of FRQ and its degradation via the ubiquitin-proteasome pathway (50). More indirectly, FRQ turnover is also regulated by the COP9 signalosome that controls the FWD1 ubiquitin ligase complex (57).

Contrary to the evidence presented above that temperature compensation in Neurospora's circadian clock is a highly regulated process, the majority of chemical oscillators depend rather heavily on temperature. In these oscillators, the frequency generally obeys Van't Hoff's rule with Q₁₀ values of ≈2–3. Because in chemical oscillators component processes are “evolutionary unrelated,” one can assume that component processes obey Van't Hoff's rule with Q₁₀ values of 2–3. At 25°C, this would correspond to an average activation energy, 〈E_a 〉, of the frequency of ≈50–85 kJ/mol. By making this assumption and replacing the E_i in Eq. 3 by 〈E_a 〉, the balance equation reduces with help of Eq. 4 to

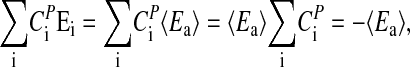[9]

which, when inserted into Eq. 5, leads to

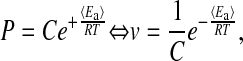[10]

showing why the periods P (or frequencies ν) depend exponentially on temperature with 〈E_a 〉 values between 50 and 85 kJ/mol. For example, in the Belousov–Zhabotinsky reaction, which is one of the most studied chemical oscillators (58), the period follows Eq. 10 over a large temperature range, indicating that 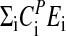is approximately independent of temperature (59). As seen in Fig. 3b, this is also the case for the various frq mutants, at least for the temperature window in which temperature compensation is generally observed.

The data in Fig. 4 show that there is a correspondence between period length and FRQ half-life. However, it should be noted that this correspondence is temperature-dependent because, depending on the temperature, different period lengths can be observed for the same FRQ half-life.

Despite its simplicity, the Goodwin oscillator has previously been shown to simulate many circadian clock properties (16, 17, 34, 36). The temperature-compensated model presented here is able to provide a consistent, almost quantitative description of the temperature dependence of frq-mRNA and FRQ amplitudes and its period length, thereby showing that temperature compensation in the Neurospora circadian clock can be understood as part of the FRQ negative-feedback loop and pointing to a central role for FRQ. Many of the processes described by the equations in Fig. 1 are formulated as first-order reactions but are clearly more complex— as, for example, the degradation of FRQ, which appears to be degraded by the ubiquitin-proteasome pathway (50). As more detailed quantitative experimental data on various component processes become available, an amplified version of the model will be required to do quantitative simulations.

The approach taken here, i.e., combining experiments with theoretic principles and model calculations, appears to be useful for developing a quantitative picture of the regulatory elements, including temperature compensation, within the clockwork of circadian rhythms (27).

Appendix

Derivation of Eq. 3. Applying the chain rule on Eq. 3 leads to

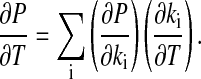[11]

The last term in Eq. 11 can be explicitly calculated from the Arrhenius equation (Eq. 1), which gives

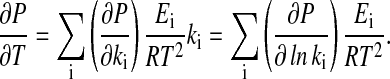[12]

Multiplying Eq. 12 by 1/P and observing that ∂ P/P = ∂lnP, Eq. 12 can be written as

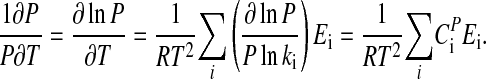[13]

Derivation of Eq. 5. Making the assumption that 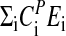is independent of temperature, Eq. 13 can be integrated

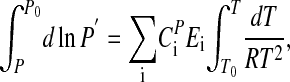[14]

leading to

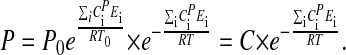[15]