Breaking the diffraction barrier in fluorescence microscopy at low light intensities by using reversibly photoswitchable proteins

Abstract

Fluorescence microscopy is indispensable in many areas of science, but until recently, diffraction has limited the resolution of its lens-based variant. The diffraction barrier has been broken by a saturated depletion of the marker's fluorescent state by stimulated emission, but this approach requires picosecond laser pulses of GW/cm² intensity. Here, we demonstrate the surpassing of the diffraction barrier in fluorescence microscopy with illumination intensities that are eight orders of magnitude smaller. The subdiffraction resolution results from reversible photoswitching of a marker protein between a fluorescence-activated and a nonactivated state, whereby one of the transitions is accomplished by means of a spatial intensity distribution featuring a zero. After characterizing the switching kinetics of the used marker protein asFP595, we demonstrate the current capability of this RESOLFT (reversible saturable optical fluorescence transitions) type of concept to resolve 50–100 nm in the focal plane. The observed resolution is limited only by the photokinetics of the protein and the perfection of the zero. Our results underscore the potential to finally achieve molecular resolution in fluorescence microscopy by technical optimization.

Owing to its specificity and sensitivity, fluorescence microscopy would be extremely powerful for biological imaging (1, 2) if diffraction (3) did not pose a limit on the minimal distance Δx at which similarly marked objects can be discerned. In the focal plane, Δx is well approximated by Abbe's equation, Δx ≥ λ/(2nsinα), where λ is the wavelength of light and nsinα is the numerical aperture of the lens (3). With typical values of nsinα < 1.5, it follows that Δx will never be smaller than λ/3. However, in an emerging family of microscopes using reversible saturable optical fluorescence transitions (RESOLFT) between two marker states (A and B), the resolution is governed by

[1]

with ζ denoting the saturation factor of the saturated transition. In a RESOLFT microscope, ζ → ∞ yields Δx → 0, meaning that the resolution is no longer limited by diffraction (4, 5).

The simplest variant of RESOLFT microscopy is readily explained as follows. If we illuminate with a (diffraction-limited) intensity I(x) that features a point x₀ with I(x₀) = 0 and I(x₀ ± ε) > 0, to induce A → B, this transition will occur everywhere except at x₀. Saturating A → B by increasing max[I(x)] creates narrow regions of state A delimited by x₀ ± Δx/2, even though I(x) is limited by diffraction. For example, if the state A is a fluorescent state, the fluorescence will be possible only in this narrow region around x₀ whose extent Δx can be squeezed down to the molecular scale. Images can now be obtained by moving the intensity zero across the specimen and subsequently reading out the fluorescence for each coordinate. This concept is not restricted to a single zero but can be extended to include many zero points or lines, in which case, one can use a camera for sequential read-out and image buildup (4–6).

With σ denoting the cross section of A → B, the rate k_AB is given by σI(x). In a RESOLFT microscope, the resolution and the effective spot size Δx depend on the rate of possible competing processes that may counteract the saturation of A → B. If the competing process is, for example, a (spontaneous) transition B → A occurring at rate k_BA, this rate must be outperformed (k_AB >> k_BA) by applying I(x) >> k_BA/σ ≡ I_sat. The saturation intensity I_sat thus classifies the intensity magnitude required to prepare small Δx. For a given form of I(x), Δx merely depends on max[I(x)] ≡ ζ I_sat. Calculation shows that for ζ >> 1, the state A is confined to Δx as given by Eq. 1 (4, 5).

Stimulated emission depletion (STED) microscopy is a RESOLFT type of microscopy, where the fluorescent molecular state (A) is deexcited to the ground state (B) by stimulated emission (6, 7). Because the saturation of stimulated emission (typical σ ≈ 10^–17 cm²) is opposed by the nanosecond fluorescent decay k_fl ≈ (1 ns)^–1, STED necessitates I_sat = k_fl/σ ≈ 100 MW/cm². Although the potential of this method to resolve λ/50 (16 nm) has been confirmed, as has Eq. 1 (8), a disadvantage of STED is the requirement for intense (picosecond) pulses tending to boost multiphoton-induced bleaching of the dye (9, 10). Here, we break the diffraction barrier by using ultralow levels of light by employing a saturable transition between two conformational states of a fluorescent protein. The weak spontaneous interstate conversion results in weak competing rates and hence low I_sat.

Photochromic fluorescent proteins have recently become a target of research because of their ability to visualize protein tracking (11–16). In this study, we use asFP595 (11) from Anemonia sulcata, featuring a fluorescence-activated metastable “on” state (state A) and a fluorescence-inhibited metastable “off” state (state B), between which the protein can be “switched” by using blue (on → off) and yellow (off → on) light. After characterizing the transition rates of asFP595, we prove the breaking of the diffraction barrier with a few nanowatts of light.

Materials and Methods

The plasmid pQE30-asFP595 was a kind gift from K. Lukyanov (Bioorganic Chemistry, Russian Academy of Sciences, Moscow). After expression in the bacteria Escherichia coli Bl21CodonPlus (Stratagene), the proteins were purified by affinity chromatography applying standard procedures on a Ni-nitrilotriacetic acid column and by subsequent size-exclusion chromatography on a Superdex 200 pg column (Amersham Pharmacia). The purity of the protein fractions was verified by polyacrylamide gel electrophoresis.

Photoswitching across a 1 × 1-mm² area of E. coli colonies expressing asFP595 was performed with an epifluorescence microscope featuring two mercury lamps with separate excitation filters (blue 450FS40-50 and yellow 550FS40-50 from LOT-Oriel, Darmstadt, Germany) inhibiting and eliciting fluorescence, respectively. The asFP595 fluorescence peaks at 605 nm (17). Photoswitching with sharply focused spots as well as subdiffraction imaging experiments were performed with a stage-scanning microscope employing two single wavelengths, 568 nm (yellow) and 458 nm (blue), from a continuous wave, linearly polarized argon-krypton laser. The oil immersion lens that was used (1.4 numerical aperture, Leica) featured α = 68°. The fluorescence was projected onto a detector with a removable aperture of size corresponding to 0.8 times the magnified Airy disk of the fluorescence spot. The intensity point-spread functions (PSFs) were probed by a gold bead of 80-nm diameter. The applied intensities were determined from their full width at half maximum (FWHM), 2r₀, in the focal plane and the power P transmitted by the lens, I = P/(π r²₀). All images were smoothed by using a Lagrangian interpolation of third order. The protein was dissolved in PBS buffer (3 μg/μl, pH 7) and thinly spread on a microscope cover glass, such that adsorption of asFP595 produced a layer <0.5 μm.

Phase plates for shifting the phase of the blue light by π were made by coating half of a glass plate with a 0.6-μm layer of MgF₂. A focal spot with a central line-shaped zero bordered by two peaks was produced by inserting a phase plate such that the dividing line of the halves was parallel to the linear polarization of the beams. The intensity of the blue light in the two peaks was calculated as max(I_b) = 0.45P_b/(π r²₀) = 0.45I_b.

Results

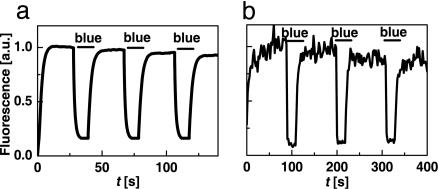
Photoswitching of asFP595 Fluorescence. Fig. 1a demonstrates the control of the fluorescence of E. coli colonies in an epifluorescence microscope. The fluorescence was generated by yellow light of intensity I_y = 2 W/cm². Addition of blue intensity I_b = 0.1 W/cm² reduced it to 15% of its initial value. Fig. 1b shows the analogue experiment on a spot (r₀ = 155 nm) of a purified asFP595 layer. Switching off and on was performed by I_y = 4.4 W/cm² and I_b = 3.6 W/cm², respectively. Generating these intensities required a continuous wave power of just P_y = 3.3 nW and P_b = 2.2 nW, respectively. The intensity required for attaining the same inhibition with STED is eight orders of magnitudes larger (6–8).

Fig. 1.

Wide-field photoswitching of asFP595 fluorescence from an E. coli colony (a) and on a 0.3-μm-diameter focal spot of an ultrathin asFP595 layer (b). The fluorescence is elicited by 10 mW (a) and 3.3 nW (b) of continuous wave irradiation with yellow light. Inhibition results from addition of 0.3 mW (a) and 2.2 nW (b) of blue light.

Interrupting the blue light recovers the fluorescence. In contrast to STED, the settling occurs on a millisecond time scale (Fig. 1b). Increasing I_b and I_y can, in principle, cut down the fluorescence settling time to that of the actual molecular switch [i.e., ≈100 ps (18, 19)], but at the low intensities used in our study, the observed fluorescence settling time reflects the population kinetics of the states. Four challenges in using asFP595 become apparent: (i) the signal is rather noisy because of the <1% fluorescence quantum yield of asFP595 (19); (ii) switching off by blue light is incomplete; (iii) repeated cycling is accompanied with photobleaching; (iv) in an imaging system, the applied intensities have to be adapted to the pixel recording time because they determine the fluorescence settling.

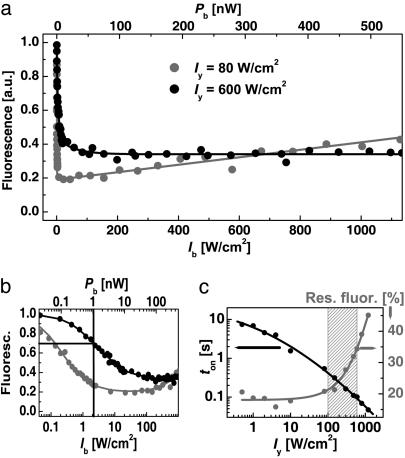
We therefore explored the optimal I_y and I_b for inhibiting the asFP595 fluorescence. Fig. 2a displays the inhibition as a function of I_b, revealing a steep decline at ultralow I_b, turning into a residual value. These curves are the counterpart to the depletion curves describing STED (7). Contrary to STED, I_b ≈ 1 W/cm² is sufficient to reduce the signal markedly (Fig. 2b).

Fig. 2.

Characterization of asFP595 photoswitching. (a) Inhibition of fluorescence as a function of the blue intensity I_b for the yellow intensities I_y = 80 W/cm² (black circles) and 600 W/cm² (gray circles). (b) Same data on a semilogarithmic plot to disclose I_sat.(c) Effect of I_y on the time t_on needed for settling the fluorescence level (black circles) as well as on the minimal residual fluorescence after inhibition (gray circles).

However, the I_y not only elicits fluorescence of on-state asFP595 (A → A*) but also switches off-state proteins on (B → A). Therefore, we measured the inhibition at I_y = 80 and 600 W/cm², obtained by focusing P_y = 65 and 500 nW, respectively. We found a residual fluorescence level of 20% at I_y = 80 W/cm² and of 30% at I_y = 600 W/cm² (Fig. 2a). Inhibition obviously works better when the light for fluorescence generation is less intense. If we regard the residual level as a baseline, we can locate the I_sat at the 50% value of the inhibition range. In the case of I_y = 600 W/cm², I_sat = I_b ≈ 1W/cm² is found at the 65% notch; it is produced by ≈1 nW of continuous wave power (Fig. 2b).

Interestingly, there is a maximal applicable I_b stemming from the fact that I_b can also elicit fluorescence. Responsible for the residual fluorescence, this action cross-talk can be inferred from Fig. 2a, where, for the case of I_y = 80 W/cm², the quenched fluorescence level slightly increases toward larger I_b. To quantify the action cross-talk, we have measured the inhibition as a function of both I_y and I_b. Within the investigated range, the intensity inhibiting best scales as ; the depth of the minimum itself scales as shown in Fig. 2c. The strongest depth (15%) was obtained for I_y < 100 W/cm², meaning that a larger I_y counteracts the inhibition. In consequence, (i) the activation (B → A) cannot be arbitrarily accelerated by I_y, and the fluorescence flux cannot be arbitrarily raised; (ii) there is an upper limit to the intensity of the blue inhibition light, limiting the applicable saturation factor ζ; and, above all, (iii) a time span t_on has to be allowed for building up the population of on-state asFP595.

The values obtained for t_on are shown in Fig. 2c for a three-orders-of-magnitude range of I_y; they are based on an exponential fit to the fluorescence settling (Fig. 1b). For imaging, it is important to choose an I_y that provides strong inhibition but also a small t_on. Fig. 2c shows that these requirements are reconciled for I_y = (100–600) W/cm².

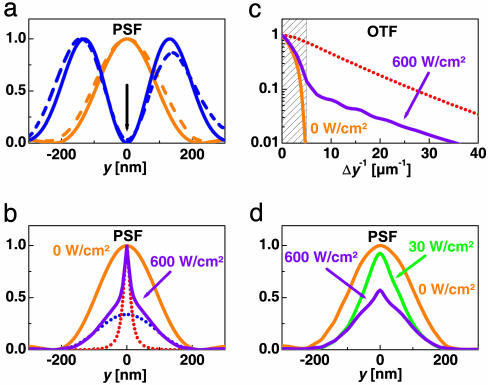
Subdiffraction Fluorescence Focal Spots with asFP595. Whereas the yellow light was focused to a regular spot, the blue light was prepared to render an x-oriented zero-intensity line bordered by two y-offset peaks. Fig. 3a shows the calculated and the measured y profile of this double peak, referred to as the inhibition PSF (In-PSF). The calculations were performed for the 568-nm and 458-nm wavelengths, using a vectorial diffraction theory (20). The measured In-PSF (dashed line) is similar to its theoretical counterpart, except that the central minimum is not zero but 1.5% of the peak level. The In-PSF is expected to photoswitch the asFP595 molecules into the off state such that the spot in which fluorescence is possible is squeezed to subdiffraction dimensions along the y axis. The resulting fluorescent spot gives the effective PSF (E-PSF) of the microscope.

Fig. 3.

Subdiffraction point spread and transfer function by asFP595 photoswitching. (a) Measured and calculated In-PSF (blue) with the PSF for fluorescence generation (yellow). Solid lines are calculated, and dashed lines are experimental. (b) E-PSF calculated for I_y = 600 W/cm² and different intensities I_b = 600 W/cm² (violet) and I_b = 0 (yellow). In the former case, the E-PSF consists of a diffraction-limited PSF_diff (blue dots) plus a subdiffraction PSF_RESOLFT counterpart (red dots) (ε = 0.3, Eq. 2). PSF_RESOLFT is attained as well when disregarding the action cross-talk of blue light within the calculations. (c) The associated modulus of the effective OTF (violet) and OTF_RESOLFT (red) quantifies the gain in spatial frequency bandwidth over the diffraction limit (shaded) or reference OTF for I_b = 0 (yellow). (d) E-PSFs calculated in the same way as in b but employing the experimental In-PSFs.

Fig. 3b shows the E-PSF calculated from the measured inhibition curves of Fig. 2 assuming the theoretical In-PSF of Fig. 3a. Fig. 2 actually gives the fluorescence for any combination of yellow and blue intensity. Fig. 3b shows the simulated narrowing of the E-PSF for I_y = I_b = 600 W/cm². The initial spot size of 195-nm FWHM (yellow) is squeezed to 40-nm FWHM (violet). The incomplete inhibition of fluorescence stemming from the action cross-talk is also noticeable at the periphery of the spot. If it were absent, the E-PSF would be a solitary peak of 20 nm FWHM (Fig. 3b, dotted red line).

The resolution gained by photoswitching is always beyond diffraction, because the E-PSF features a subdiffraction top. In good approximation, the E-PSF can be decomposed into a diffraction-limited (PSF_diff) and a subdiffraction (PSF_RESOLFT) counterpart,

[2]

with 0 < ε < 1 and with all functions normalized to unity. This decomposition is exemplified in Fig. 3b for ε = 0.3; the blue dotted line marks the PSF_diff, and the red dotted line marks the PSF_RESOLFT. Note the ≈10-fold FWHM decrease predicted in this simulation.

The resolution is also evident from the magnitude of the effective optical transfer function (E-OTF) of the microscope describing the relative magnitude of the spatial frequencies transferred to the image (Fig. 3c). Again, the diffraction barrier is surpassed upon application of the In-PSF. Contrary to a standard microscope, the bandwidth of a RESOLFT microscope is unlimited per se, but for large I_b, the high frequencies are markedly raised. If we consider the bandwidth up to the 1% threshold, applying I_b = 600 MW/cm² expands the bandwidth ≈7.8-fold. As with the E-PSF, the E-OTF can be decomposed correspondingly: E-OTF = εOTF_diff + (1 – ε)OTF_RESOLFT. Given the 1% criterion, the OTF_RESOLFT of our simulations displays a bandwidth enlargement over OTF_diff by ≈13-fold.

Provided that PSF_diff and OTF_diff do not swamp the subdiffraction frequencies by noise, the latter can be strengthened in the image by multiplication in the Fourier space. A still more straightforward solution relies on the fact that the image B is given by the convolution of the object function O with the E-PSF; i.e.,

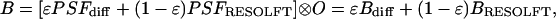[3]

with B_diff and B_RESOLFT denoting a diffraction-limited and a subdiffraction image, respectively. Hence, B_RESOLFT can be calculated by also recording B_diff and subsequent subtraction.

In Fig. 3d, we have calculated the E-PSF resulting from the measured In-PSFs of Fig. 3a featuring the 1.5% minimum. Applying I_b = 30 W/cm² is expected to squeeze the spot from 210-nm to 120-nm FWHM. However, when applying I_b = 600 W/cm², the residual intensity in the minimum is predicted to attenuate the contribution of the PSF_RESOLFT. Thus, the resolution gain is restricted at higher I_b, consequently impeding the implementation of large saturation factors with asFP595. Nonetheless, at I_b ≈ 30 W/cm², the E-PSF is still anticipated to be sharpened 1.7-fold down to ≈120-nm FWHM. Taking advantage of Eq. 2 gives a factor of 2.3, thus yielding 90 nm.

Subdiffraction Fluorescence Microscopy with asFP595. The protein currently exists only as a tetramer, which restricts its use as a marker. Nonetheless, the operation of this RESOLFT microscope can be validated with test structures. To this end, we used custom-prepared glass slides featuring parallel grooves produced by focused ion beam milling (Fraunhofer Institute IISB, Erlangen, Germany) that were ≈10 μm long, 0.5–1 μm deep, and ≈100 nm wide. The distance between the grooves was ≈500 nm. To label this structure, the glass slide was immersed in a buffered solution of asFP595 filling the grooves by adsorption. Nonadsorbed proteins were rinsed away. After coaligning the yellow and the blue In-PSF and lining up the grooves in the y direction, we scanned the sample with a 20-nm pixel size in the y direction and with a pixel dwell time of 50 ms, applying I_y = 600 W/cm² and I_b = 30 W/cm².

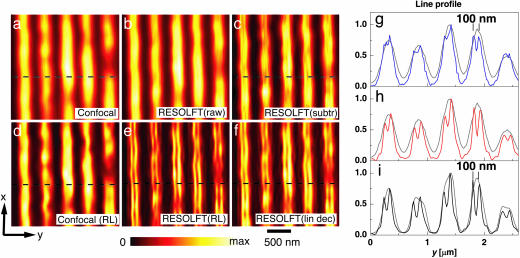
Fig. 4 displays images of the same sample region that were consecutively recorded without (a) and with (b) the In-PSF. The staining makes the grooves visible as bright lines. Comparison of the images confirms a modestly higher y-resolution in b. The reason for the modest improvement is the fact that the raw image data of b contains contributions from PSF_diff, masking the details in the image. Therefore, we applied Eq. 3 using the value ε = 0.3 extracted from Fig. 2a. The resulting image (c) now exhibits structures that are barely visible in b but not in a. The improvement is also visible in the profile of g, proving that the application of the In-PSF reveals sharp peaks at 100-nm distance. The presence of peaks at the margins indicates that the protein aggregates at the edges of the grooves.

Fig. 4.

Subdiffraction fluorescence microscopy with asFP595. Nanofabricated grooves stained with asFP595 and imaged without (a) and with (b) the blue In-PSF. c shows the weighted subtraction of a from b. d exhibits the restored data of a; e is its counterpart based on b. f shows the linearly deconvolved image of b. g compares line profiles from the images a and c, extracted at the dashed horizontal line, in gray and blue, respectively. h shows the analogous comparison for a and f; i compares the profiles for d and e. The 35% depth of the 100-nm distant peaks of the linearly deconvolved data in h enable an extrapolation of resolution of distances <100 nm. The sharp peaks are a hallmark of the saturation process and of RESOLFT microscopy in general.

More efficient than subtraction is a single-step linear deconvolution (Fig. 4 f and h). The resolution is even further augmented by a nonlinear iterative Richardson–Lucy restoration (Fig. 4e) (21). For fair comparison, we have subjected both the data of Fig. 4a and the raw data of Fig. 4b to this restoration. Displayed in d and e, the restored images reconfirm the improvement. Fig. 4i displays line profiles extracted from the dashed lines of d and e. The restoration alone is not able to resolve the structure, whereas the restored RESOLFT data separate structures at 100-nm distance with a modulation depth of 60%.

We also performed two negative controls. First, we removed the asF595 from the grooved coverslip and stained it with an aqueous organic fluorophore solution (Atto 532, Atto-Tec, Siegen, Germany) featuring a similar emission spectrum as asF595. The images obtained by 568-nm excitation were virtually identical to Fig. 4a. In the second control, we converted the In-PSF to a normal PSF. We observed no gain in resolution. All data thus indicate that the resolution increase stems from the saturated transition of asFP595 from its on state to its off state.

Discussion, Conclusion, and Outlook

We have shown that the reversible photoswitching of a fluorescent protein between two conformational states breaks the diffraction barrier of fluorescence microscopy. The resolution gain, observed as an improved separation of protein clusters, is found to be in agreement with simulations combining diffraction theory and the measured protein photokinetics. Importantly, a few W/cm² of light is sufficient to provide enough saturation to surpass the diffraction barrier.

The reason for the low intensities is that, unlike with multiphoton processes, the nonlinearity induced by saturation is not based on the concomitant action of multiple photons but on the population kinetics of the marker. Saturated transitions allow for creating an unlimited optical bandwidth at optical intensities that readily lend themselves to imaging. This basic tenet of RESOLFT microscopy is corroborated in Fig. 2a, showing that the fluorescence steeply falls off by applying only a few W/cm² of inhibition light.

Although such low intensities are readily obtained by focusing on a spot, our work by no means implies the requirement for single spot scanning. On the contrary, Fig. 2a suggests parallelization with an array of zeros or lines, which greatly reduces the image acquisition time. Parallelized imaging onto a camera is simple if the zeros are farther apart than Abbe's barrier, because then the diffraction-blurred spots or lines on the camera can be readily assigned to their sharp counterparts in the focal plane. If they are slightly closer, which is usually favorable, one has to resort to deconvolution for cross-talk removal. In any case, the pattern has to be scanned across the specimen and the camera read out for each position of the pattern. Scanning with line patterns in conjunction with deconvolution has been shown to enhance the lateral resolution by up to 2-fold over conventional microscopy (22, 23). However, the fundamental advantage of a (similarly parallelized) RESOLFT type of microscope over the latter is the fact that, in the RESOLFT case, the resolution increase is not limited by diffraction.

Instead of saturating the inhibition, one could also saturate the fluorescence generation B → A → A*. In this case, the saturation creates ultrasharp, dark “holes” or “valleys” of off-state (B) fluorophores. Because the image information is hidden in steep valleys bordered by bright slopes, the image can be obtained only by deconvolution, which is prone to noise issues.

In Fig. 4 g–i, photoswitching of asFP595 has evidenced a separation of ≈100 nm. The actual resolution surpasses this value, because in the linearly deconvolved data of Fig. 4h, the peaks are separated by a 35% modulation depth. Using these data, we can extrapolate a depth of ≈15%, 10%, and 7% for distances of 60, 50, and 40 nm, respectively. The valley disappears at a separation of 20 nm. This extrapolation confirms the potential of protein switching for attaining nanoscale resolution. Fig. 3d shows that resolution potential would have been higher if the central “zero” of the In-PSF had been <<1.5%. A remedy is to perfect the In-PSF by active wavefront control.

The low quantum yield (1%) of asFP595 necessitated a rather high protein concentration to provide an acceptable image contrast. Proteins with higher quantum yield will decrease the required concentration or the recording time, accordingly. Eq. 1 and the gain in resolution are based on specific protein characteristics (i.e., on the saturation of a specific protein transition). Yet the resolution does not depend on the spatial distribution of the protein in the sample, because the role of the (inhibition) light is to transiently prepare photophysical conditions under which fluorescence is allowed. At a given spatial coordinate, this condition is in place regardless of the presence of the protein. Therefore, the resolution of the microscope depends neither on the local concentration of the protein marker nor on the specific structure of the sample.

An advantage of STED over protein photoswitching is the ultrafast (200 ps) settling of the involved fluorophore populations and hence of the fluorescence level. When applying STED, the fluorescence inhibition occurs within the lifetime of the excited state. Therefore, STED does not inherently impose a minimal pixel dwell time in imaging. In contrast, the specific properties of asFP595, in particular, the minimization of the action cross-talk (Fig. 2), called for pixel exposure times of milliseconds for settling the fluorescence level. Although such pixel dwell times are not an issue with fixed samples, millisecond pixel times may be too long for moving or diffusing objects, because a fraction of the protein markers may have moved out of the focal volume before having switched to the other conformational state. Likewise, they may have diffused away before having contributed with photons to the signal. The preferred solution is to resort to proteins that allow for a faster population transfer, as well as proteins with negligible action cross-talks. The fastest imaginable population buildup is the time needed for the actual conformational switch of the molecule (typically <<1 ns). Therefore, with suitable proteins gained by mutagenesis, the fluorescence settling time and the concomitant illumination intensity can, in principle, be selected within a many-orders-of-magnitude range. By adjusting the settling time to 1–10 μs, one can accommodate diffusion through a subdiffraction-sized spot (50 μs) at reasonably low intensities of a few kW/cm². In this case, one can also apply an In-PSF of inhibition light for squeezing the focal volume in three dimensions (7). The smaller probing volumes by fast reversible protein switching would enable fluorescence fluctuation spectroscopy at higher concentrations than what is currently allowed by diffraction-limited spots (7, 24). However, the effect of diffusion should not be overestimated. A light microscope retaining the ease of use and the specificity of fluorescence imaging but with a resolution of a few nanometers (in largely static samples) should have a significant impact in biology.

Most of the challenges discussed herein can be addressed by protein mutagenesis. The new proteins have to be optimized toward minimal cross-talk, high quantum yield, and large cycling numbers. Another protein that holds promise for implementing RESOLFT microscopy is dronpa (14, 16). In dronpa, both switching on and switching off can be implemented as saturable transitions. Thus, our results indicate that the key to establishing nanoscale imaging by protein photoswitching is the protein itself.

In conclusion, we demonstrated the breaking of the diffraction barrier in fluorescence microscopy with ultralow intensities of light. Relying on photoswitchable proteins, this version of RESOLFT microscopy opens up the fascinating prospect of nanoscale imaging of (living) cells with conventional illumination by using innate properties of the cell.