On the Role of Attention in Naturally Occurring Matching Relations

Abstract

Prior researchers have evaluated the efficacy of using the matching law to describe naturally occurring behavior–environment interactions. However, spurious matching could be obtained if the response and environmental event were correlated, even if the event did not reinforce the response. To assess the likelihood of obtaining spurious matching when relating attention and problem behavior, we evaluated the problem behavior of 3 participants for whom attention did not serve as a reinforcer for problem behavior in a functional analysis. Both the simple and generalized matching equations were used to examine matching relations extracted from descriptive observations that were conducted in the participants' classrooms. The results of aggregated matching analyses showed that the proportional rate of responding approximately matched the proportional rate of contiguous adult attention. Matching analyses conducted for all participants showed correlations between attention and problem behavior. These results demonstrate that spurious matching can be obtained, and they highlight the role of functional analyses in the analysis of naturally occurring matching relations.

Descriptive analyses are often conducted to infer the operant function of problem behavior (e.g., Anderson & Long, 2002). If it is accepted that a functional analysis is most appropriate for identifying the operant function of behavior, then a different application of descriptive methodology becomes available. Once a reinforcer is identified via functional analysis, descriptive data can be used to learn more about how behavior and reinforcers interact in natural environments. That is, descriptive observations can be used as an assay instead of as an assessment tool. Borrero and Vollmer (2002) used this approach to investigate the phenomenon of matching. They showed that stimulus events that functioned as reinforcers in a functional analysis were related to aberrant behavior in ways predicted by the matching law.

The matching law is a quantitative formulation stating that the relative rate of responding should approximately equal, or match, the relative rate of reinforcement provided for those responses (Herrnstein, 1961). The simple matching equation can be expressed as follows:

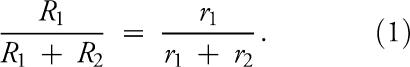In this equation, R₁ represents the rate of responding for Response 1, R₂ represents the rate of responding for Response 2, r₁ represents the rate of reinforcement obtained for Response 1, and r₂ represents the rate of reinforcement obtained for Response 2. This equation can be transformed to yield the generalized matching equation, which is expressed as follows:

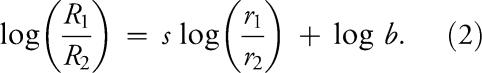Thus, the generalized matching equation expresses the relation between the logarithms of the ratios. Again, R₁ and R₂ represent the rates of responding for Responses 1 and 2, and r₁ and r₂ are the rates of obtained reinforcement for those responses. The equation also includes two fitted parameters, s and b, that permit the fitting of a straight line to the obtained data. These fitted parameters have been conceptualized as representing sensitivity (s) to the schedules and bias (b) toward one of the responses (Baum, 1974). A third form, referred to as the single-response matching equation, can also be derived from the simple matching equation. The single-response matching equation can predict the rate of responding for a single response based on the rate of reinforcement for that response in relation to the rate of reinforcement for all other responses.

As stated above, researchers have tested predictions made by the matching equation in natural (uncontrolled) environments. Matching research has been conducted in natural environments to confirm that relations obtained in laboratory experiments are similar to response–reinforcer relations in natural settings. This research has typically involved collecting data on responses and naturally occurring reinforcers in home or classroom environments, then subjecting those data to matching analyses. McDowell (1981), for example, reevaluated data collected for a previous publication (Carr & McDowell, 1980) using the single-response matching equation to relate 1 boy's self-injurious scratching to the rate of parental reprimands for that behavior. Reprimands had been shown to function as a reinforcer in a reversal design. The single-response matching equation accounted for 99.7% of the variance in the rate of scratching.

Martens and Houk (1989) also used the single-response matching equation to relate 1 girl's on- and off-task behavior to the attention provided by a teacher and a classroom aide. Although no functional analysis was conducted to determine if attention was a reinforcer, the line predicted by the single-response matching equation approximated the obtained data points. The generalized matching equation accounted for up to 86.5% of the variance in the rate of responding. Martens and Houk concluded that this was evidence of a reinforcement relation between attention and disruptive classroom behavior.

More recently, functional analyses have been used as a means of determining environmental events that function as reinforcers prior to conducting matching analyses of descriptive observations. Oliver, Hall, and Nixon (1999) used the simple and generalized matching equations to relate problem and appropriate behavior to escape (negative reinforcement) following these responses. The experimenters first conducted descriptive observations in the participant's school and then manipulated antecedent events, including a demand condition and an attention deprivation condition. Although consequences were not manipulated in this analysis, the highest rates of problem behavior were observed in a condition in which demands were presented. The matching analysis showed that the relative rates of problem behavior generally matched the relative rates of reinforcement.

Borrero and Vollmer (2002) conducted descriptive observations of 4 participants' problem and appropriate behavior in the participants' homes or in the living area of a hospital unit. Next, they conducted functional analyses similar to those described by Iwata, Dorsey, Slifer, Bauman, and Richman (1982/1994). Data from the descriptive analysis were analyzed with the simple and generalized matching equations, using the reinforcers identified in the functional analysis. The matching equations provided excellent fits to the obtained data, accounting for up to 99.7% of the variability in the relative rate of responding by comparing it to the relative rate of reinforcement. This research extended the previous literature in several ways. First, reinforcers were identified through the experimental manipulation of consequent events. Prior research had either not tested the reinforcing efficacy of consequences (Martens & Houk, 1989; Oliver et al., 1999) or had tested only one putative reinforcer (McDowell, 1981). Second, some participants' behavior was multiply controlled; for these participants, all reinforcers were included in the matching analysis. Third, the authors provided some evidence that response rate may drive reinforcer rate, which would cause spurious matching.

One potential limitation of the Borrero and Vollmer (2002) study was that they did not evaluate the extent to which matching relations could be obtained spuriously. Spurious matching may occur between child problem behavior and caregiver attention. Thompson and Iwata (2001) showed that attention was the most prevalent consequence of problem behavior. Because attention occurs so frequently in the natural environment, examining matching relations using attention as the putative reinforcer may be especially likely to yield spurious matching. For example, a caregiver may provide a reprimand each time the client engages in self-injurious behavior (SIB). Although the reprimand may not influence the rate of SIB (i.e., it may not serve as a reinforcer), matching might be obtained when relating the rate of problem behavior to the rate of caregiver attention. Such spurious matching relations could lead to erroneous conclusions about the generality of the matching law in natural settings.

Spurious matching requires further analysis, because much of the prior matching literature using descriptive observations has focused on the relation between attention and some form of problem behavior. One way this issue has been addressed is to conduct a functional analysis. However, when functional analyses have not identified attention as a reinforcer, it is unknown whether a matching analysis would yield a matching relation between attention and target responses nonetheless (i.e., even though attention is not a reinforcer). Given that prior research has already shown matching relations when attention is known to be a reinforcer, the purpose of the current investigation was to examine the relation between attention and problem behavior that was not reinforced by attention in a functional analysis. Although the primary purpose of this study was exploratory in nature (i.e., to investigate naturally occurring matching phenomena), there may be some indirect clinical utility. Specifically, although correlation does not equate to causation, numerous examples exist in recent literature using correlation to infer possible functional relations in descriptive observations (e.g., Anderson & Long, 2002; Freeman, Anderson, & Scotti, 2000). Thus, this study may be useful for identifying boundaries when making inferences about the matching law in human behavior and may provide empirical support for caution in inferring behavioral function from correlational data.

Method

Participants

Three students with varying degrees of developmental disabilities participated. All participants had been referred for the study because they displayed problem behavior in a school setting. Target responses for each individual were chosen based on direct observations and because these responses were viewed as problematic by parents, teachers, and school administrators.

Greg was a 16-year-old boy who had been diagnosed with Down syndrome and profound mental retardation. He had been referred for inappropriate vocalizations and various topographies of SIB, including head hitting and chin hitting. Amy was a 14-year-old girl who had been diagnosed with mental retardation. Her primary target responses were topographies of SIB including self-choking, chin hitting, nose hitting, and head hitting. Paul was a 19-year-old man who had been diagnosed with cerebral palsy and mental retardation. Paul's target behavior was placing his hands down his pants.

Descriptive Analysis

Matching relations were evaluated from data collected during descriptive observations conducted on the playground and in each participant's classroom. More specifically, participants were observed in the classroom during structured instructional time, free play, and lunch. Teachers, aides, and other students were present during all observations. Although each classroom was equipped differently, all included chairs, desks, a television, and instructional materials.

Descriptive analyses were conducted using the methods described by Vollmer, Borrero, Wright, Van Camp, and Lalli (2001). Individual observations lasted from 0.5 hr to 3 hr, depending on the class and observers' schedules. Total observation time was 440 min for Greg, 150 min for Amy, and 240 min for Paul. Observations were conducted until at least 400 instances or 50 min of problem behavior topographies were recorded. In some cases, observations continued beyond this point because the individual was not yet able to enter a treatment program. Observers collected data using handheld computers equipped with a real-time data-collection program that used continuous recording. During descriptive observations, observers recorded the behavior of the participant and the teachers, aides, or peers who interacted with the participant. Data were collected on each participant's target behavior and potential reinforcers (attention, delivery of tangible items, and escape from demands). Operational definitions and measurement systems are listed in Table 1. The three reinforcers recorded were not mutually exclusive and could precede or follow the target behavior in any combination. For the purposes of this study, the most important potential reinforcer in the observations was attention.

Table 1. Operational Definitions and Measurement Systems.

Participant	Response	Definition	Measurement
Greg	Vocalizations	Repetitive, nonsensical vocal sounds	Number
Greg	Head hitting	Forceful contact between the palm or fist and any region of the head above the eyes	Number
Greg and Amy	Chin hitting	Forceful contact between the palm or fist and the chin	Number
Amy	Nose hitting	Forceful contact between the palm or fist and the nose	Number
Paul	Hands down pants	Any portion of the hand passing inside the waistband of the pants	Duration
All	General attentiona	Questions or statements directed at the participant, or physically touching the participant	Duration
All	Tangible delivery	Participant has access to tangible items, including toys, food, TV, or music	Duration

^aGeneral attention included negative statements or reprimands directed at the participant (such as “don't do that”). Reprimands were scored using a rate measure. However, for the purposes of data analysis, reprimands were combined with other forms of attention, including a duration measure of general attention, as part of the general attention category.

Observers were undergraduate or graduate students in behavior analysis, who had achieved high interobserver agreement scores (three consecutive sessions above 90% for 2 different participants) with previously trained observers. Observers were seated in the corner of the classroom. Descriptive observations were a typical component of the behavioral services provided for the participants and their fellow students, so the presence of observers was not unusual.

Functional Analysis

Functional analyses were conducted using procedures similar to those described by Iwata et al. (1982/1994). Trained graduate students conducted all functional analysis sessions in a vacant classroom containing tables, chairs, and toys. A portion of the room was sectioned off for the sessions; observers sat outside this area. Four test conditions and a control condition were alternated in a multielement design. Sessions were conducted 1 to 3 days per week, with one to four sessions conducted per day. All functional analysis sessions were 10 min.

During the attention condition, the participant had access to toys but did not receive attention until he or she engaged in problem behavior. At the start of the session, the therapist diverted his or her attention from the participant and said, “I can't talk to you right now.” Problem behavior resulted in a brief (3- to 5-s) statement that mimicked those observed during the descriptive analysis, such as “Cut that out, you'll hurt yourself.” This condition tested for reinforcing effects of adult attention.

During the escape condition, participants were asked to complete tasks; tasks were chosen based on those presented during the descriptive observations. Tasks included sitting in various chairs around the room or completing self-care tasks, such as hair brushing or face washing. Therapists delivered instructions every 15 s using a three-prompt sequence (Horner & Keilitz, 1975). When problem behavior occurred, the task materials were removed and a 30-s escape period ensued. This condition tested for reinforcement by escape from demands.

During the no-consequence or alone sessions, the participants were observed in an austere environment. The therapist did not provide any programmed consequences for problem behavior during these sessions. This condition tested for behavioral maintenance via automatic reinforcement.

During the control condition, the participants had access to preferred items, attention was continuously available (Greg and Paul) or provided on a fixed-time (FT) 30-s schedule (Amy), and no demands were presented. The therapist did not provide any programmed consequences for problem behavior during this condition.

Only Amy and Greg were exposed to the tangible condition. Paul was not exposed to the tangible condition because no evidence of access to tangible items following problem behavior was observed during descriptive observations. During this condition, the participants were allowed to briefly sample preferred tangible items before the items were withheld. The therapist provided either FT 30-s attention (Amy) or continuous attention (Greg). Problem behavior resulted in 30-s access to preferred toys for Amy or 3-s access to juice for Greg. These items were selected because they had been observed to occasionally follow problem behavior in the descriptive analysis and were shown to be preferred during a preference assessment similar to the one described by Roane, Vollmer, Ringdahl, and Marcus (1998). This condition tested for reinforcement by access to tangible items.

Interobserver Agreement

Interobserver agreement was obtained by having a second independent observer collect data on all responses during the descriptive and functional analyses. Interobserver agreement was calculated by dividing each observation into 10-s bins and dividing the smaller number of observed responses by the larger number. For duration measures, the smaller duration for each 10-s bin was divided by the larger. The obtained values for each bin were averaged for the entire observation session. Interobserver agreement percentages were then averaged across sessions to obtain a mean interobserver agreement score. Interobserver agreement was obtained during 23% of descriptive analysis sessions and 34% of functional analysis sessions.

Because descriptive observations varied in length, each 10-min block of observation time was evaluated as a separate session. Agreement scores averaged 97% (range, 85% to 100%) for Greg's chin hitting and 89% (range, 77% to 100%) for his vocalizations. Average agreement was 91% (range, 80% to 97%) for Amy's nose hitting, 84% (range, 44% to 100%) for her chin hitting, and 98% (range, 96% to 100%) for Paul's behavior of placing his hands down his pants. During the descriptive analysis, interobserver agreement averaged 88% (range, 61% to 100%) for attention across all observations. Agreement scores for attention averaged 92% for Greg (range, 67% to 100%), 87% for Amy (range, 61% to 98%), and 84% for Paul (range, 64% to 100%).

During the functional analysis, interobserver agreement averaged 97% (range, 93% to 100%) for Greg's chin hitting and 87% (range, 78% to 100%) for his vocalizations. Agreement scores averaged 90% (range, 66% to 100%) for Amy's nose hitting and 93% (range, 76% to 100%) for her chin hitting. Agreement for Paul placing his hands down his pants averaged 88% (range, 70% to 100%).

Matching Analysis

All response rates and reinforcement rates used in the matching analyses were calculated from the descriptive observation data. Descriptive observations were partitioned into 10-min blocks for data analysis, yielding 44 blocks for Greg, 15 blocks for Amy, and 24 blocks for Paul. The rate of problem behavior and the rate of attention that occurred contiguous with problem behavior were calculated for each block. Attention was considered contiguous if it occurred within 10 s after the target problem behavior. Although 10 s was a largely arbitrary value, other research on matching relations has used this value in analysis and showed good matching relations (e.g., Borrero & Vollmer, 2002). Also, we examined larger time windows and found similar results. For Greg and Amy, the rate of problem behavior was calculated by dividing the number of instances of problem behavior by the session time (10 min). For instance, if problem behavior occurred twice in any one session, the rate of responding for that session would be 0.2 responses per min. For Paul, placing his hands down his pants was recorded as a duration measure. This measure was converted to a rate-like statistic by dividing the total number of seconds that the behavior occurred by the total session time (10 min); in essence, we counted each second that Paul's hands were down his pants as an instance of problem behavior. For example, if Paul had his hands in his pants for 100 s in any session, the rate of responding for that session would be 10 responses per minute. For all participants, the rate of contiguous attention was calculated by dividing the number of times that problem behavior was followed by attention within 10 s by the total session time. If one instance of problem behavior was followed by attention within 10 s, the rate of contiguous attention would be 0.1 per minute.

Target topographies of problem behavior were chosen for the matching analysis based on the rates of responding observed during the descriptive observations. If participants engaged in more than two topographies of problem behavior, the two topographies occurring most frequently were chosen for the matching analysis (chin hitting as Response 1 and nose hitting as Response 2 for Amy; chin hitting as Response 1 and vocalizations as Response 2 for Greg). Paul engaged in only one topography of problem behavior (placing his hands down his pants). Therefore, we used only that behavior for the matching analyses.

Both aggregated and individual analyses were conducted. For the aggregated analysis, the mean rate of responding and mean rate of contiguous attention were calculated across sessions. The means for all participants were then analyzed using the simple matching equation (Equation 1) and the generalized matching equation (Equation 2). For the individual analysis, the rate of responding and rate of contiguous attention for each 10-min block was included in a participant-by-participant matching analysis using the simple and generalized matching equations. Observation blocks that did not contain at least one instance of problem behavior that was followed by contiguous attention were excluded from the simple matching analysis, because the results of the matching equation cannot be calculated when the denominator is zero. Similarly, blocks that did not include at least one instance of problem behavior were excluded from the generalized matching analysis, because the results of the generalized matching equation cannot be calculated when the dividend equals zero. (Because differing numbers of observations were excluded, the graphs displayed in Figure 2 have different numbers of data points within a participant's data.)

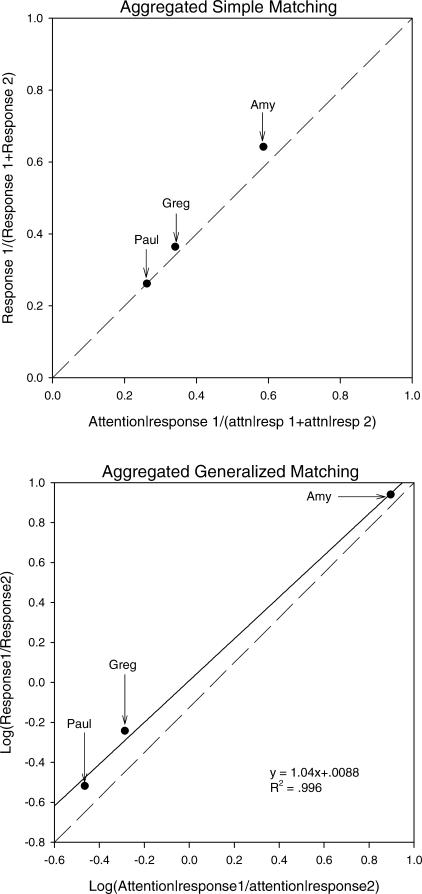
Figure 2. Scatter plots of the predicted and observed allocation of problem behavior for all participants.

Aggregated data were analyzed using the simple matching equation (top) and the generalized matching equation (bottom). Aggregated data for each participant is represented by a single data point. In both panels, the dashed line depicts the allocation predicted by the equation. In the lower panel, the solid line is the best fitting line through the data points, with the slope and bias depicted in the linear equation.

Below are examples of matching calculations completed in this study. For the aggregated matching calculations, the response rate was averaged across sessions and the reinforcer rate was averaged across sessions. For example, Greg engaged in an average of 0.77 chin hits per minute and 1.35 vocalizations per minute during the descriptive analysis. The rate of attention following these responses within 10 s was 0.16 and 0.31, respectively. For the simple matching analysis, the proportion of chin hits was calculated by dividing 0.77 by 2.12, yielding 0.36. The proportion of attention following these responses was obtained by dividing 0.16 by 0.47, yielding 0.34. The proportional numbers were then plotted. For the generalized matching analysis, the ratio of chin hits to vocalizations was calculated by dividing 0.77 by 1.35, yielding 0.57. The ratio of attention following chin hits to attention following vocalizations was calculated by dividing 0.16 by 0.31. The quotients were then logged to obtain the plotted −0.243 (logged response ratio) and −0.287 (logged ratio of contiguous attention). Similar calculations were completed for the other 2 participants.

For the individualized matching analyses, the calculations were completed for each 10 min observation block. For example, in one 10-min block, Amy engaged in 0.5 chin hits per minute and 0.1 nose hits per minute. The rate of attention following these responses was 0.4 and 0.1, respectively. These rates yielded a proportional rate of responding of 0.83 and a proportional rate of contiguous attention of 0.8 for the simple matching analysis. For the generalized analysis, the same observation block yielded a logged ratio of responses of 0.69 and a logged ratio of contiguous attention of 0.60, which were then plotted.

Paul's matching analyses were conducted slightly differently because only one response topography was included. For his matching analyses, the number of seconds that his hands were down his pants was used as the first response. This number was subtracted from 600 (the duration of the observation block in seconds) to obtain the number of seconds that his hands were not down his pants. For example, in one observation block, Paul had his hands down his pants for 421 s. The rate of attention following Paul's placing his hands down his pants was 37.6, and was 10.7 following instances of Paul not having his hands down his pants. To calculate simple matching, 421 was divided by 600, yielding 0.7 as the proportional rate of having hands in pants. Then, the proportional rate of attention was calculated by dividing 37.6 by 48.3, yielding 0.78. These numbers represent the x-axis and y-axis values for a single data point in Paul's simple matching analysis.

Results

Functional Analysis

Figure 1 depicts the functional analysis results for all participants. Recall that the purpose of the functional analysis was to demonstrate that problem behavior was not reinforced by attention. Any person whose functional analysis showed a reinforcement effect in the attention condition would have been excluded from the study, because prior research has shown that matching can be obtained between attention and problem behavior when attention serves as a reinforcer (Borrero & Vollmer, 2002; McDowell, 1981).

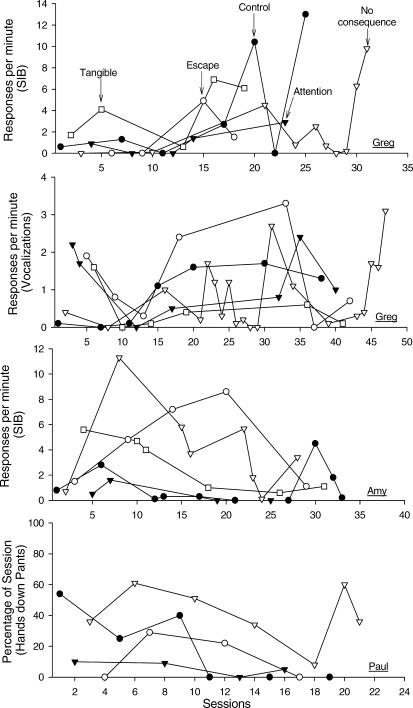
Figure 1. Functional analysis results for Greg's self-injury, Greg's vocalizations, Amy's SIB, and Paul's problem behavior.

Two functional analyses were conducted with Greg; each analysis focused on a separate group of topographies—self-injury and vocalizations. During the functional analysis of self-injury (first panel), consequences were provided for chin hitting, head hitting, or head banging. No one topography of behavior occurred more frequently in any condition, and rates of overall self-injury were undifferentiated across conditions. However, self-injury was on an upward trend during repeated alone sessions. In addition, the rate of responding during the attention condition was consistently lower than the rate during the control condition. During Greg's functional analysis of inappropriate vocalizations (second panel), rates of responding were undifferentiated across all conditions. Rates of vocalizations also increased during repeated alone sessions, and rates during the attention condition were lower than during the control condition. These data suggest that Greg's self-injury and vocalizations were automatically reinforced, or at least not reinforced by attention.

During Amy's functional analysis (Figure 1), consequences were provided for nose hitting, chin hitting, and self-choking. Amy engaged in high rates of self-injury in the escape and no-consequence sessions. Amy also engaged in low but consistent rates of self-injury during the tangible condition. On the other hand, she engaged in low, and often zero or near-zero, rates of self-injury during the control and attention conditions. No single topography of behavior occurred more frequently in any condition. These results suggest that Amy's self-injury may have been multiply controlled or automatically reinforced. In either case, self-injury was not reinforced by attention during the functional analysis.

Paul's functional analysis (Figure 1) showed the highest levels of problem behavior in the alone condition, with variable levels occurring during the control, attention, and escape conditions. Although the function was not clear, this pattern of responding suggests that Paul's problem behavior was automatically reinforced, or at least not reinforced by attention, given that the duration of problem behavior in the attention condition was consistently less than or equal to the duration in the control condition.

Matching Analysis

Figure 2 shows the aggregated descriptive data analyzed with the simple matching equation (Equation 1) and generalized matching equation (Equation 2). Each participant's data are represented by a single data point. For all 3 participants, the mean proportional rate of responding approximately equaled, or matched, the proportional rate of contiguous attention provided for that response, even though attention did not function as a reinforcer for any of the target responses (as demonstrated via the functional analysis). For Paul, the proportional rate of responding exactly matched the proportional rate of contiguous attention for that response. Greg and Amy allocated slightly more of their responding toward Response 1 than would be predicted by the simple matching equation.

The lower panel of Figure 2 depicts the log of the mean ratios of the rates of Response 1 to rates of Response 2 against the log of the mean rates of contiguous attention for those responses. Again, each data point represents the data for a single participant. The dashed line represents perfect matching as predicted by the generalized matching equation. The solid line is the best fitting line through the data points and was fitted using simple linear regression. The solid line closely approximates the dashed line, suggesting a close approximation to matching. In addition, the equation accounts for 99.6% of the variability in the rate of responding by relating it to the rate of contiguous attention.

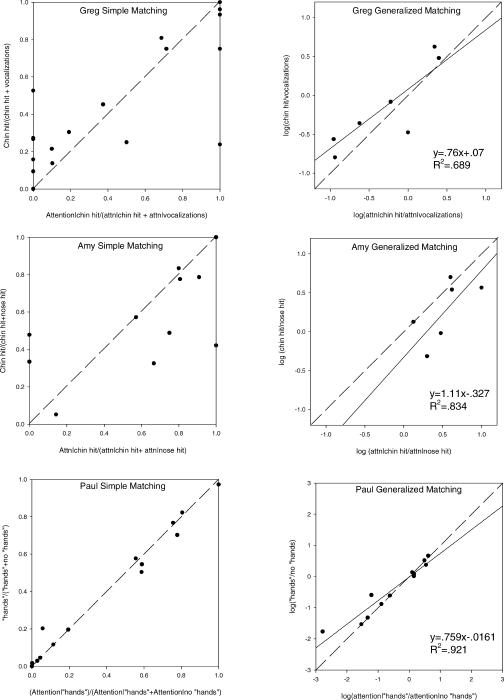
Individual analyses also were conducted for each participant (Figure 3). The upper left panel shows Greg's proportion of chin hitting over chin hitting and vocalizations against the proportional rate of reinforcement provided for those responses. Considerable variability was observed in Greg's simple matching analysis, and the data points do not fall close to the dashed line. The upper right panel shows the log ratio of chin hitting to vocalizations against the log ratio of contiguous attention provided for those responses. The solid line shows the best fitting line using simple linear regression, and the dashed line represents perfect matching as predicted by the generalized matching equation. The solid line approximates the dashed line, and the equation accounted for 68.9% of the variance in the rate of responding by relating it to the rate of reinforcement. These results suggest that there was a correlation between Greg's problem behavior and an adult's attention in the classroom.

Figure 3. Results of simple and generalized matching equations for Greg, Amy, and Paul.

Each data point represents one 10-min descriptive observation block. In the left panels, the dashed line shows perfect matching, as predicted by the simple matching equation. The right panels show the results of the generalized matching equation (Equation 2). The dashed line depicts the allocation as predicted by the matching equation. The solid line is the best fitting line through the actual data points. Slope and bias are depicted in the linear equation.

The middle panels of Figure 3 depict Amy's data. The results using the simple matching equation (left) showed that Amy engaged in less chin hitting than would be predicted by the matching equation. The right panel depicts the results of the generalized matching analysis. The solid line again approximates the dashed line. The generalized matching equation accounted for 83.4% of the variance in responding by relating it to contiguous attention, suggesting that a relation exists between those two variables, even though attention did not reinforce problem behavior in the functional analysis.

The lower left panel of Figure 3 shows the proportion of seconds that Paul engaged in hands-in-pants behavior over total observation time against the proportion of contiguous attention provided for those responses. All of the data points fall closely to the dashed line, suggesting matching. For Paul, attention seemed to follow placing his hands down his pants, even though attention did not reinforce that response. The results of the generalized matching analysis are depicted in the lower right panel of Figure 3. As in the aggregated analysis, the solid line closely approximates the dashed line, and the equation accounted for 92.1% of the rate of responding by relating it to the rate of contiguous attention.

Discussion

We used the simple and generalized matching equations to assess the relation between adult attention and child problem behavior that was not reinforced by attention. Results from aggregated matching analyses suggested matching, with the relative rate of responding approximately equaling the relative rate of attention for all 3 participants. An examination of matching for individual participants suggested correlations between adult attention and child problem behavior. These results, in combination, provide evidence for the possibility of spurious matching in descriptive observations.

Spurious matching between problem behavior and attention could result from two distinct phenomena. First, the rate of problem behavior could influence the rate of attention. This type of spurious matching would occur if the problem behavior tended to provoke verbal or physical attention from caregivers. A second possibility is that matching would occur by chance—that is, the rate of problem behavior did not increase the rate of ongoing attention but rather contacted response-independent attention due to the high frequency of problem behavior. Although it was not a focus of the current study, the conditional and unconditional probabilities of attention were calculated for each participant. For all participants and target responses, the conditional probability was calculated by dividing the number of responses that were followed by attention within 10 s by the total number of responses. The unconditional probability was calculated by dividing each second that was followed by attention within 10 s by the total number of seconds in the session (Vollmer et al., 2001). The results of this analysis showed that, for all participants, the conditional and unconditional probabilities of attention were similar (results available from the authors). These results suggest that the spurious matching obtained in this study was due to increased rates of responding simply contacting ongoing, response-independent attention. This finding is further supported by an examination of the rate of responding and the rate of attention during the descriptive observations. In many cases, attention occurred at a very high rate and duration throughout the observation period. However, because only attention following problem behavior was used in the matching analysis, spurious matching was obtained because the increased response rates resulted in higher rates of contact with attention.

Regardless of the cause, the possibility of correlations between behavior and attention underscores the need for functional analyses when examining behavior in natural environments. Because attention did not serve as a reinforcer for problem behavior for any of the participants in this study, matching between adult attention and child problem behavior would not be expected. However, spurious matching was obtained, to varying degrees, for all participants. Through functional analyses, researchers and clinicians can be more confident that a response and reinforcer are not simply correlated. In addition, the results leave open the possibility that matching relations seen in other studies, even those that included a functional analysis, may not represent the same sort of phenomenon observed in laboratory matching experiments. That is, if matching is obtained when attention is not a reinforcer, the direction of causation between behavior and attention is questionable. It is likely that problem behavior produces attention as easily as attention might reinforce problem behavior. We are currently conducting studies designed to tease apart, via experimental manipulations, the reinforcing effects of attention on problem behavior and the antecedent effects of problem behavior on attention. It should also be considered that attention might become a reinforcer for problem behavior if it consistently follows that behavior.

The results also suggest that conducting matching analyses on an individual level is important because less spurious matching was observed in the individual analyses relative to the aggregated analyses. In this study, almost perfect matching was obtained in the aggregated analyses similar to those conducted by Borrero and Vollmer (2002). However, nearly perfect matching was found for only 1 participant during the individual analyses. Therefore, the probability of obtaining spurious matching appears to be lower with more molecular matching analyses.

Although the purpose of the descriptive analysis in the current study was not to identify the operant function of behavior problems in this study, many researchers and clinicians do use descriptive analyses for that purpose. Our data show that the methods used to analyze descriptive data may lead to different inferences regarding behavioral function. The conditional probability analysis discussed above did not imply that a positive contingency existed between problem behavior and attention, whereas the matching analyses suggested an attention function for the problem behavior of all participants. The difference in conclusion between the probability analysis and the matching analysis could be due to the number of 10-min blocks excluded from the matching analysis because no contiguous attention occurred. Nevertheless, some analyses of descriptive observations may lead to what looks like a reinforcement effect, especially for attention when one watches high-rate behavior that is frequently reprimanded. Therefore, caution is warranted for using descriptive observations for making inferences regarding operant function.

Some limitations of this study should be noted. First, attention from any adult was scored using a single measure. A teacher and several aides were present in all of the participants' classrooms; prior research has shown that different matching relations are obtained when relating either teacher or aide attention to child problem behavior using the single-response matching equation (Martens & Houk, 1989). Therefore, it is possible that different results would be obtained when the attention provided by the classroom teacher and aides is separated.

Second, the functional analyses conducted in this study did not assess the extent to which the teachers' attention functioned as a reinforcer for the participants. Because experimenters conducted all functional analysis sessions, it is possible that attention from the teachers functioned as a reinforcer for the participants' behavior, even though the experimenter's attention did not. There were multiple other differences between the contexts in which the functional analysis and descriptive observations were conducted. For instance, the classroom setting included teacher's aides, other children, a different configuration of furniture and equipment, and different items to manipulate than the experimental setting. This limitation should be addressed in future research. However, the approach to functional analysis used here was similar to that used in prior matching studies (e.g., Borrero & Vollmer, 2002).

Finally, Paul's analyses differed from Greg's and Amy's in that the second response was categorized as anything but having his hands in his pants. This type of response classification is often used in the single-response matching equation, which is another possible way to analyze Paul's data. However, to remain consistent with both prior research and the other participants in this study, we used only the simple and generalized matching equations. Further research may be required to determine if similar spurious matching relations are obtained when the single-response matching equation is used.

Future research should also examine other situations in which spurious matching may be obtained. The current study evaluated only one contiguous environmental event—adult attention. However, spurious matching could be obtained when relating problem behavior to other putative reinforcers, such as access to tangible items or escape from demands. We chose to evaluate attention in this study because prior research has shown that attention was the most prevalent consequence for problem behavior (Thompson & Iwata, 2001) and therefore was the event for which spurious matching was most likely to be obtained. In addition, most prior research on matching in natural environments has included attention as a reinforcer, sometimes to the exclusion of other variables.

The data from this study suggest that spurious matching relations can be obtained when relating problem behavior and adult attention. These results highlight the need for functional analyses when conducting quantitative analyses of descriptive data. Our data also show that the generality and applicability of the matching law, as well as its limitations, require further exploration and experimentation.