Slow growth rates of Amazonian trees: Consequences for carbon cycling

Abstract

Quantifying age structure and tree growth rate of Amazonian forests is essential for understanding their role in the carbon cycle. Here, we use radiocarbon dating and direct measurement of diameter increment to document unexpectedly slow growth rates for trees from three locations spanning the Brazilian Amazon basin. Central Amazon trees, averaging only ≈1mm/year diameter increment, grow half as fast as those from areas with more seasonal rainfall to the east and west. Slow growth rates mean that trees can attain great ages; across our sites we estimate 17-50% of trees with diameter >10 cm have ages exceeding 300 years. Whereas a few emergent trees that make up a large portion of the biomass grow faster, small trees that are more abundant grow slowly and attain ages of hundreds of years. The mean age of carbon in living trees (60-110 years) is within the range of or slightly longer than the mean residence time calculated from C inventory divided by annual C allocation to wood growth (40-100 years). Faster C turnover is observed in stands with overall higher rates of diameter increment and a larger fraction of the biomass in large, fast-growing trees. As a consequence, forests can recover biomass relatively quickly after disturbance, whereas recovering species composition may take many centuries. Carbon cycle models that apply a single turnover time for carbon in forest biomass do not account for variations in life strategy and therefore may overestimate the carbon sequestration potential of Amazon forests.

Tropical forests have the world's most diverse tree communities (1) and store ≈40% of the carbon in terrestrial biomass (2, 3). The largest tropical rain forest lies in the Amazon River basin, covering >3.6 million square km. Because of its continental scale, this vast forest spans variation in climatic regime, topography, geography, and consequently forest structure.

Old-growth Amazonian forests play a fundamental role in the global climate and carbon cycle. They cycle ≈20% of the planet's fresh water and 30% of carbon contained in land vegetation. The conversion of old-growth tropical forests to other land uses, such as pasture or agriculture, contributes significantly to the accumulation of CO₂ in the atmosphere and leads to important changes in the hydrologic cycle, locally, regionally, and globally (4). The annual rate of deforestation between August 2002 and August 2003 was 23,750 km², the second highest recorded by the Brazilian Space Agency-Instituto Nacional de Pesquisas Espaciais. With these growing deforestation rates there is an increased need for studying the role of land-atmosphere interactions in the Amazon.

Living trees and soil organic matter constitute the largest carbon stocks in tropical forests. Whereas much of the carbon in soil organic matter exists in forms that are stabilized on mineral surfaces and are hundreds to thousands of years old (5), most carbon cycle models currently assume that carbon resides in living tree biomass for only a few decades (6). However, few data are available to constrain these estimates. To comprehend the role of the Amazon region in the global carbon budget and global climate system, in particular, the influence of old-growth forests as sources or sinks of energy, moisture, and carbon caused by changes in climate or atmospheric composition, it is critical to understand the dynamics of carbon in trees of the terra firme (or well drained), mature forests that contain ≈74% of the basin's terrestrial biomass.

Although there is increasing information on the variation of productivity and biomass across the Amazon basin (7-9), information is still lacking on the age structure of tropical forest stands. Many upland tropical forest trees do not have annual growth rings, so estimates of tree age largely come from extrapolation of growth rates derived from permanent plot surveys (10-12). Errors associated with these estimates are usually considered large because of uncertainties inherent in applying observations of growth over a few years to the entire lifetime of the tree (13).

Radiocarbon dating provides another method for determining tree ages and long-term growth rates in tropical forests. Previous studies applying radiocarbon to date tropical trees have selected only the largest trees (14), single species (15), or recently downed individuals (16). Ages for individual trees or single species do not necessarily permit extrapolation to a tropical forest stand. Although large trees (>60 cm in diameter) may represent the majority of forest biomass (17) they are relatively rare, representing <5% of individuals (18) with diameter >10 cm. Recently downed, large trees similarly are not necessarily representative of the population age structure of the forest. If mortality is not random, ages of downed individuals will be biased compared with living trees. Species-specific growth rates, even of more common species, are not representative of a tropical forest stand in forests with high biodiversity.

Here, we expand the use of radiocarbon to determine ages and growth rates of tropical trees on a more systematic basis, so as to represent the age structure of the forest and a community of individuals of varying size and life history.

Materials and Methods

Site Description. We chose to work in forests representing a range in biomass, species diversity, and canopy structure (18). Dendrometer data and radiocarbon samples were collected in permanent inventory plots established at three study sites in the Amazon basin, Brazil: (i) in central Amazonia, the EEST-Experimental Station of the Forest Management (frequently called ZF-2) operated by Brazil's National Institute for Amazon Research, located ≈90 km north of Manaus (60°11′W, 2°58′S); (ii) in western Amazonia, the Catuaba Experimental Farm of Universidade Federal do Acre; located ≈30 km from the city of Rio Branco (67°62′W, 10°07′S); and (iii) in eastern Amazônia, the Tapajós National Forest (Flona Tapajós): near km 67 (54°58′W, 2°51′S) and km 83 (54°56′W, 3°3′S) of the Santarém-Cuiabá highway (BR-163), which runs along the eastern edge of the Tapajós National Forest (Flona Tapajós). The Flona Tapajós is located on the Eastern side of the Tapajós River and extends from 50 to 150 km south of the city of Santarém, Pará State, at the confluence of the Tapajós and Amazon rivers.

Mean annual rainfall in Manaus, Rio Branco, and Santarém is 2,285 mm (averaged 1961-1990), 1,940 mm (1969-1990), and 1,909 mm (1967-1990), respectively (18). Average temperatures at the three sites are similar (26.7°C, 24.5°C, and 25.0°C, respectively) (18), and relative humidity averages ≈85% at all three sites. The major climatic difference among the sites is seasonality in the distribution of rainfall (length of dry season) as a result of annual movement of the intertropical convergence zone across the Amazon basin (19). The length of the dry season here is calculated as the number of months with rainfall averaging <100 mm·month^-1. Manaus experiences the shortest dry season (3 months, July-September) followed by Rio Branco with 4 months (June-September) and Santarém with 5 months (July-November).

Soils at the Manaus, Rio Branco, and Santarém sites are nutrient-poor clay Oxisols with low organic C content, low pH, low effective cation exchange capacity, and high aluminum saturation (5, 20-23).

The vegetation in Manaus and Santarém sites is dense terra firme (upland) tropical moist forest (24, 25), and in Rio Branco (Catuaba Experimental Farm) the vegetation is a mosaic with small patches of dense forest within a large matrix of smaller-stature, open forest with bamboo [Guadua. Weberbaueri Pilger (23)]. The forest canopy height is a relatively homogeneous ≈35 m in Manaus, with few emergent trees that can reach up to 40 m. The canopy structure in Rio Branco and Santarém is more stratified, with large emergent trees up to 45 m in height in Rio Branco and 55 m in Santarém, and a closed canopy at ≈30 m and ≈40 m in Rio Branco and Santarém, respectively; there are few indications of recent anthropogenic disturbance other than hunting trails in Manaus and Santarém. The large logs, abundant epiphytes, and emergent trees qualify the Manaus and Santarém sites as mature, or “old growth.” The Santarém site is characterized by a larger number of gaps and vines than the Manaus site. In Rio Branco, the Catuaba Experimental Farm is an extractive reserve where there are small trails to support extractive use of trees for rubber and Brazilian nut products. The relief varies among the sites we sampled at all sites in upland (terra firme) forest, with slopes of <10%. Water tables are deep in Manaus and Santarém (up to 30 and 100 m deep, respectively), but can reach ≈5 m below the surface in the wet season in Rio Branco.

Permanent Plots. To determine the forest structure and estimate the biomass we used data from permanent plots already established at the sites (18, 26, 27) but with different areas and layout. In Manaus, forest inventory data are derived from three plots totaling 3 hectare (ha) [The Biomass and Nutrient Experiment (BIONTE) project] where all stems ≥10 cm in diameter at breast height (DBH) were tagged and mapped, and diameters were measured. In Rio Branco we used data from 160 contiguous permanent plots (25 × 25 m) totaling 10 ha (200 × 500 m), where all stems ≥35 cm DBH were tagged, mapped, and measured. A subset of 16 plots (1 ha) was randomly selected, and all stems ranging from 10 to 35 cm were tagged. In Santarém, we surveyed 20 ha of forest in four 1-km-long transects. All trees >35 cm DBH were inventoried, as were all trees >10 cm DBH on subplots comprising 4 ha. At all areas the DBH was converted to tree carbon by using an allometric equation adjusted for wood density differences as reported in Vieira et al. (18) and assumed 50% of the biomass for a tree was carbon. The data are available from the authors on request.

Diameter Increment Analysis. We used data from other studies (18, 26, 27) to determine the annual tree-diameter increment in three DBH size class (10-30, 30-50, and >50 cm) at our three sites. In Manaus we used three years of monthly dendrometry data from two transect plots [20 × 2,500 m (5 ha) each; 79 of these trees were in terra firme forest]. This transect is part of the Jacaranda Project (28). In Santarém and Rio Branco dendrometer bands were fitted to ≈300 trees (100 stems in each DBH size class, randomly selected) in the permanent plots we established.

Changes in stem circumference were measured with electronic calipers [precision of ± 0.02 mm (29)]. Changes in tree diameter were calculated as the change in the circumference divided by π in each measurement period; periodic measurements were combined to determine wood increment in each year; we have used the mean of 2-3 years. We have made no correction to the data for seasonal variation in stem water content and its potential effect on our measured growth rates. We assume that, averaged over the course of an entire year, the changes in stem water content will be zero.

Tree Age Measurements (Radiocarbon). At the Catuaba permanent plot sites, we randomly selected approximately 10 trees in each diameter size class (10-30 cm DBH, 30-50 cm DBH, and >50 cm DBH) and sampled these trees by coring. At the Manaus and Santarém sites, we took advantage of tree harvests in plots located within 1-2 km of our permanent plots (at sites with the same soil type, forest structure, slope, and drainage) to obtain cross-sectional disks of trees that allowed for easy identification of the trees' centers. In Manaus the trees were harvested according to our random sampling design among three diameter classes, but in the Tapajós National Forest, we were limited to selecting trees randomly from those cut for commercial harvest. At the Santarém site we augmented tree harvest samples with tree cores from the permanent plot sites. However, most of the trees we determined ages for in the Santarém site fall within a single size class.

We used radiocarbon to determine age and mean diameter increment for a total of 97 individual trees. Samples of ≈5 mg wood were taken at intervals along the radius defined by the core or along the mean radius observed in a cut slab. Holocellulose was purified from wood and combusted, and the resulting CO₂ purified was then reduced to a graphite target for accelerator MS measurement of ¹⁴C at the Keck Carbon Cycle Accelerator Mass Spectrometry facility at the University of California, Irvine (30).

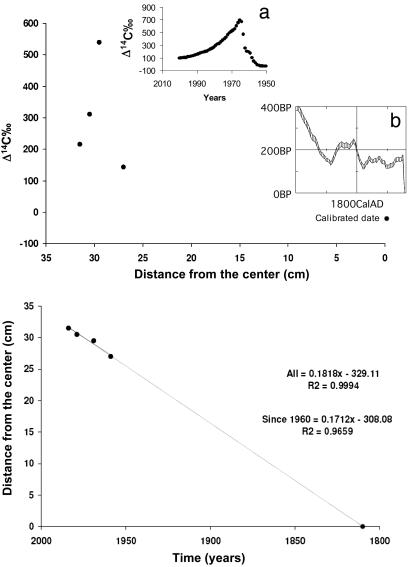
To estimate the age of woody tissue sampled, we matched our measured radiocarbon values against a time series of atmospheric radiocarbon. Radiocarbon can be used in two ways to determine the age of trees: (i) comparing the sample with positive Δ¹⁴C and recent (after 1950) atmosphere Δ¹⁴C (Fig. 1a) or (ii) using existing tree-ring based calibration curves to estimate the age of a sample with negative Δ¹⁴C (Fig. 1b). For each tree, we first measured the radiocarbon age of the center portion of the tree and used the program oxcal 3.0 (31, 32) to determine the calibrated ages for wood grown before 1950 by using the calibration curve shcal02 for the southern hemisphere (33). A calibration data set is necessary to convert conventional radiocarbon ages into calibrated years, because specific activity of the ¹⁴C in the atmospheric CO₂ is not constant. oxcal used the ¹⁴C ages from the samples against the reference curve itself to find all possible points of intersection between the measurements and reference curve. The program calculates the relative probabilities for each match. We saved these probability distributions, summing separately to 95.4% of all probable dates (2-σ errors; P < 0.05) for each sample.

Fig. 1.

Distribution of Δ¹⁴C at different distances along a tree core and resulting estimated growth rate (before and after 1960) and estimated age of Hymenaea courbaril L. (DBH = 64.0), Catuaba Experimental Farm, acre. (a) The Δ¹⁴C distribution in atmosphere between 1950 and 2000. (b) The calibration curve to radiocarbon age. Southern hemisphere data from ref. 33.

It is well known that radiocarbon dating is problematic when calibrated ages fall between ≈1650 (350 years old) and 1950 (50 years old), because of variation in cosmogenic production of ¹⁴C. For the tree ages that fell into this category (about half of our samples), we used one of the following approaches: (i) we reported the center of the calibrated age range and used the oldest and youngest calendar ages as the stated error in this estimate, or (ii) we extrapolated the tree age from more recent rates of diameter increment determined by using the history of radiocarbon in atmospheric CO₂ since 1950 (34, 35). Large changes in the ¹⁴C of atmospheric CO₂ caused by nuclear weapons testing allow us to calculate the age of holocellulose to within 1-2 years over the 1963-2004 period. To determine diameter increment rates, we measured ¹⁴C in about four to eight samples taken along the radius of the tree and used the relationship between growth year since 1964 and radial distance (transformed to DBH) to define a linear trend (in all 31 cases where we performed this analysis, the r² values were >0.85). The total tree diameter was divided by this slope to yield an estimate of tree age. An example of this procedure is shown in Fig. 1.

Radiocarbon-based mean annual diameter increment rates were calculated as the measured or estimated age of the tree divided by the DBH; these represent the mean diameter increment rate averaged over the lifetime of the tree, or, for those where we extrapolated the ages, the averaged rate over the past 40 years. All original radiocarbon data and plots showing how growth rates were calculated are available in Table 2, which is published as supporting information on the PNAS web site.

Age Structure. Our goal in using radiocarbon in this study was to obtain estimates of diameter increment rates that could be compared with short-term diameter increment rates that were obtained by using dendrometers. Because both methods yielded similar rates, we could use the distribution of dendrometer-based rates to estimate how long it took the trees in our forests to reach the diameter they had attained at the time of our study. We estimated the age of the living tree population (per ha) by using a Monte Carlo model based on dividing the observed diameters of individual trees in each of our permanent plot sites by diameter increment rates that were randomly selected from a lognormal distribution fit to the dendrometer diameter increment rate data for each diameter class (36). We reduced the standard deviation of the lognormal distribution to 2/3 of the value calculated from the curve fit. This reduction is based on the idea that as more data accumulate over many years of dendrometer measurements the tailing of the distribution will decrease. If the randomly selected diameter increment rate fell below 0.02 cm·yr^-1, which was the minimum rate estimated from radiocarbon data, we replaced it with this minimum. We estimate the age of each tree as the time it would take to grow to its present diameter; i.e., by dividing the tree diameter by the randomly generated growth rates for each size class. We ran the simulation 400 times and report the average and standard deviation of those runs by size class.

Uncertainties for the Monte Carlo model are largest for the 10- to 30-cm size class, which represents most of the individuals in the forest, and which was undersampled by our approach of identifying 100 individuals per size class for dendrometry studies. We performed two sensitivity tests for the Monte Carlo approach to see the effect of model assumptions on forest age structure. In the first, we relaxed the assumption that reduced the standard deviation of the lognormally distributed growth rates and used the actual value obtained by fitting the data. In the second, we changed the minimum allowed growth rate from 0.02 to 0.04 cm/yr.

Age of Biomass. We estimated the age of biomass in standing trees as

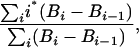[1]

where i is the year of growth, B_i is the biomass in year i determined from tree diameter by the equation of Chambers et al. (36), and the difference in biomass from one year to the next (B_i - B_i-1) is determined by the growth rate assigned in the Monte Carlo model. Using this formulation, and assuming that the growth rate is constant over the life of the tree (see Results and Discussion), the mean age of biomass is less than half the age of the tree, because biomass is a function of the square of diameter, whereas age is a linear function. We report the mean age of biomass for the whole stand by using the Monte Carlo model described above, and determining the biomass (C) age for each individual tree in each of the three size classes.

Statistical Analyses. Data distribution was evaluated by the Kolmogorov-Smirnoff test (37) for normality. When the data were not normally distributed, they were first transformed to log scale and then parametric tests and Pearson correlations were applied. Student's t test was used to assess differences between growth rate by radiocarbon and dendrometer comparisons. ANOVA followed by a post hoc Tukey HSD was used to determine differences when more than two parameters were being analyzed. All statistical analyses were performed with the software statistica (38). Differences at the 0.05 level were reported as significant.

Results and Discussion

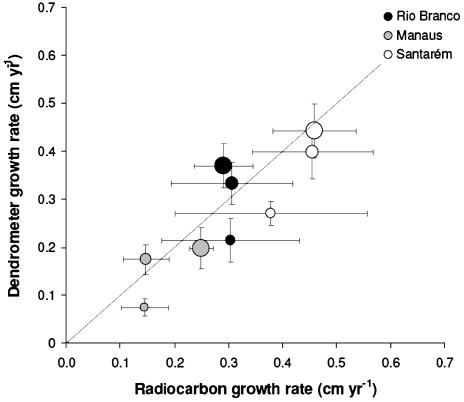
The mean growth rates determined by using radiocarbon for trees averaged by size class were not distinguishable (P < 0.005) from mean growth rates calculated from dendrometer bands for the same size classes (Fig. 2), although we sampled far fewer trees for radiocarbon measurement. Individuals with ages >300 years were common for all sites and size classes (Table 2). Some of the data in Table 2 are based on single radiocarbon determinations for which (because of the cost of the ¹⁴C analyses) we have data only for the oldest part of the tree and report the center of the range identified in the calibration of the radiocarbon age. We measured only five individuals >700 years of age, but because of our sampling strategy we did not necessarily expect to find the oldest trees in a stand, which may occur as fewer than one individual per ha (10, 14, 39). For example, ages >1,000 years previously reported for selected large (>150 cm) individuals in the Manaus region (14) were consistent with the mean growth rates (0.1-0.3 mm·yr^-1) observed for trees at the Manaus site (Fig. 2).

Fig. 2.

Mean tree growth rates (cm·yr^-1) in three size classes derived from radiocarbon [(diameter divided by radiocarbon-derived age; ≈ 10) and annual dendrometer increment (average of 2-3 years of data; n ≈ 100 (18) except to Manaus (18)]. Circles of increasing size represent size classes of 10-30, 30-50, and >50 cm, respectively. The error bar in each case represents the SEM. Larger errors are associated with radiocarbon-based growth rates because fewer analyses were available.

Despite diameter increment rates that were highly variable within all stands, we found that on average growth rates obtained by dendrometer bands in Manaus were roughly half of those in Santarém and Rio Branco (P < 0.001) (18). As a consequence, trees of the same diameter are on average older in Manaus than in the other two sites. The annual diameter increments measured in Amazon forests were smaller than those reported (albeit for individual species) in tropical forests of Costa Rica (16, 25), Panamá (40), and Venezuela (15). Higher growth rates in Central American forests may derive from greater soil fertility compared with our sites in Amazônia or caused by the difference in species composition and canopy structure among areas.

As has been shown in other studies (14, 25), larger trees, which tend to be canopy emergents with greater access to sunlight, grow faster than smaller trees, which may remain in the subcanopy their entire lives (Fig. 2). Indeed, radiocarbon data show that a number of trees <30 cm DBH can attain ages of several centuries across all of the sites we measured (Table 2). Because of the diversity of tropical forests, and the large variability of growth rates, the species that are growing slowly in the <30-cm-diameter size class are not necessarily the same ones that grow more rapidly and pass quickly to the greater diameter size classes. This supposition is supported by the fact that we, like others (15), see no consistent evidence for changes in growth rates for individual trees during their lifetimes, and by the correspondence of radiocarbon-based growth rates, which average over the lifetime of the tree, with those obtained by dendrometer measurements over the past 3 years (Fig. 2; see ref. 18).

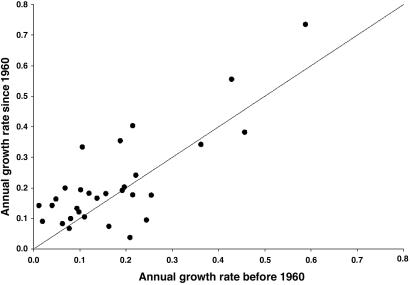
The overall correspondence of mean diameter increment rates from dendrometers that average over the last few years, and radiocarbon, which averages over the last 30 years or the entire lifetime of the tree, suggest that growth rates are indistinguishable within the limits of error of the techniques and are roughly constant when averaged over the size class. If this is true, we can use a randomly selected, but constant, diameter increment rate in our Monte Carlo model to estimate tree age distributions given the size of trees in our permanent plots. A further check on how reasonable it is to assume that diameter increment rates for individual trees are approximately constant over time was obtained by comparing estimated diameter increment rates for 30 individual trees for which we have data for the age at the center and can interpolate a diameter increment rate by using the “bomb” radiocarbon method (Fig. 3). Although there is some scatter in Fig. 3, the data show overall correspondence of diameter increment rates averaged over the past 30 years with those that average over the lifetime of the tree. A T test shows there is no significant tendency for more recent growth rates to be faster or slower than the longer-term averaged growth rates.

Fig. 3.

Annual growth rate before and after 1960 calculated by radiocarbon for the same tree.

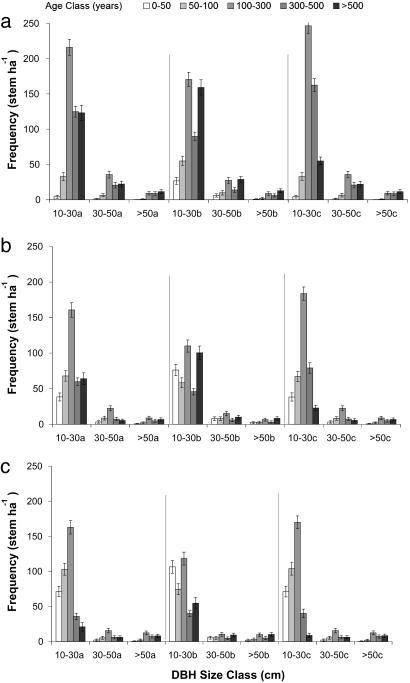
Using averages from 300 Monte Carlo model simulations, we estimate the mean age of individuals to be ≈380 years in Manaus but ≈200-280 years in the other two areas (Fig. 4). Because we sampled equal numbers in all size classes, whereas the number of individuals in a given stand decreases roughly exponentially with size (Fig. 4), our estimates of mean tree age for smaller diameter classes have larger associated uncertainty than those for larger trees. For all sites we estimate that 17-50% of the individuals per ha are >300 years old, with the largest percentage of old trees in Manaus.

Fig. 4.

Distribution of tree ages (stem·ha^-1 ± SD) in permanent plots in Manaus (a), Santarém (c), and Rio Branco (b). Ages are based on the Monte Carlo extrapolation of dendrometer-based growth rates for the three different size classes used: 0.65 times the standard deviation of the lognormal distribution when randomly assigning growth rates, minimum growth rate cutoff was 0.02 cm·yr^-1 (a); 1.0 times the standard deviation of the lognormal distribution when randomly assigning growth rates, minimum growth rate cutoff was 0.02 cm·yr^-1 (b); and 0.65 times the standard deviation of the lognormal distribution, minimum growth rate cutoff was 0.04 cm·yr^-1 (c).

The Monte Carlo simulations assume a constant mean diameter increment rate over the life of the tree. Clearly, diameter increment rates for individual trees can vary both interannually (27, 41) and over the lifetime of a tree (13), but (unlike many temperate forests) there are not necessarily negative relationships between diameter increment and DBH (12, 42-47). Further, comparison of diameter increment rates for the last 40 years and the lifetime of the tree (Fig. 3) shows no common trends across individuals. In this case, we based our estimates on tree age by using the complete variability observed in the diameter increment rate data within a size class, assuming the error in random increases in growth caused by gap formation is included. This approach also factors in issues such as trees of the same species that may experience different rates of diameter increment because of differences in their local environmental conditions. Although it is clear that some small trees that on average have slower diameter increment rates ultimately become emergents, with on average higher diameter increment rates, this can happen to only a small fraction (<5%) of individuals. In any case our approach would underestimate the age of these individuals if we assume constant, higher diameter increment rates apply over their entire lifetimes. Although the majority of individuals in the subcanopy can be released from growth suppression temporarily once the canopy closes again, such growth spurts will be short-lived. The radiocarbon data tell us that for the overall forest this is not such a bad assumption, because diameter increment rates averaged over long time periods give us the same result for trees in the same size classes (Fig. 3). Any given individual may have a variable diameter increment rate within that period, but for the age structure of the forest, we have averaged over that variability by using the Monte Carlo method.

The sensitivity of our estimates of forest age structure to various assumptions used in our Monte Carlo models are given in Table 1. Assuming that the diameter increment rate distribution has a larger standard deviation (i.e., more of the randomly selected points will fall toward the tail of the distribution) tends to yield overall older forests and biomass. Changing the minimum growth rate from 0.02 to 0.04 cm/yr results in overall younger forests. However, the basic differences between the three forests we investigated here remain.

Table 1. Stand carbon dynamics above ground wood in trees >10 cm DBH, for the three sites.

Sites	Stem frequency, stem·ha–1	Biomass C, Mg·ha–1	C added through annual diameter increment at stand level, Mg·ha–1·year–1	Mean residence time, years	Mean biomass (C) age, years			Mean tree age, years			Percent of trees >300 years old
Manaus	626	180	1.9	95	109*	119†	92‡	381*	422†	297‡	50*	50†	45‡
Rio Branco	466	95	2.6	37	89*	103†	76‡	279*	332†	219‡	32*	38†	27‡
Santarém	460	141	2.6	54	63*	80†	59‡	195*	255†	153‡	18*	27†	17‡

From biomass/C storage rate.

^*Used 0.65 times the standard deviation of the lognormal distribution (as in ref. 39) when randomly assigning growth rates; minimum growth rate cutoff was 0.02 cm·yr^–1

^†Used 1.0 times the standard deviation of the lognormal distribution when randomly assigning growth rates; minimum growth rate cutoff was 0.02 cm·yr^–1

^‡Used 0.65 times the standard deviation of the lognormal distribution; minimum growth rate cutoff was 0.04 cm·yr^–1

We estimated ages and diameter increment rates for some commercially harvested tree species as part of our data set (see Table 2). Some of these, including Bertholletia excelsa H.B.K, Carapa guianensis Aubl., Manilkara huberi (Ducke) A.Chev., and Dipteryx odorata (Aubl.) Willd, were among the older, slow-growing trees we measured. Improved knowledge of the age and diameter increment rates of these harvested trees can be useful to estimate the time it would take to replace them with a new tree of the same size.

These findings have important implications for the carbon cycling in Amazonian forests. Most individuals in the forest are in the smallest size class, so the mean age of trees reflects the dynamics of slower growing individuals. However, most of the biomass (and therefore carbon) is in faster-growing, larger-size classes (18). Hence the mean age of trees can be largely decoupled from the mean age of carbon in the forest. Although forests regrowing after disturbance can regain much of their biomass within a century (39, 48), the slow growth rates of individuals (mostly in the subcanopy) indicate that recovery of the stand in terms of structure (stem by size class and floristic composition) will take much more time. Because biomass depends on the square of diameter, whereas age varies linearly with diameter, the age of trees is much greater than the age of the carbon in them (Table 1).

Because most of the biomass, especially in Rio Branco and Santarém, is in larger individuals, which are increasing faster in diameter, the biomass-weighted age of C in the forest has a smaller range across sites than the tree ages (Table 1). The mean age of C in all stands is obtained by simply dividing the total biomass C by the rate of C allocation to new wood (Table 1), overlaps, or is shorter than the mean age of C in standing biomass estimated by the Monte Carlo model. Possible reasons for differences in the mean residence time of C and the mean age of C in standing biomass may include nonrandom mortality (with larger or faster growing trees contributing more to the dead wood pool), or (in Santarém and Rio Branco especially) the possibility that the forests are not at steady state and are accumulating biomass after disturbance. The mean age of C in dying tropical forest trees is assumed in many global C cycle models to be 40-50 years (49), which matches the residence times we estimate for forests in Rio Branco, but not those in Santarém or Manaus. Models that currently assume all forest trees, and all forest types, respond equally to factors like CO₂ fertilization will thus overestimate short-term (decadal) C sequestration potential of the forest as a whole.

In conclusion, the greater species diversity of tropical forests involves multiple life strategies for trees, which is reflected in the size and age distribution of trees within tropical forests. Failure to account for the diversity of tree C residence times in global C cycle models can significantly bias estimates of tropical forests to sequester or release C under scenarios of climate or nutrient change. The ability to estimate age and growth for commercially harvested tropical trees can yield information useful for planning harvest frequency.