Genetically indistinguishable SNPs and their influence on inferring the location of disease-associated variants

Abstract

As part of a recent high-density linkage disequilibrium (LD) study of chromosome 20, we obtained genotypes for ∼30,000 SNPs at a density of 1 SNP/2 kb on four different population samples (47 CEPH founders; 91 UK unrelateds [unrelated white individuals of western European ancestry]; 97 African Americans; 42 East Asians). We observed that ∼50% of SNPs had at least one genetically indistinguishable partner; i.e., for every individual considered, their genotype at the first locus was identical to their genotype at the second locus, or in LD terms, the SNPs were in “perfect” LD (r² = 1.0). These “genetically indistinguishable SNPs” (giSNPs) formed into clusters of varying size. The larger the cluster, the greater the tendency to be located within genes and to overlap with giSNP clusters in other population samples. As might be expected for this map density, many giSNPs were located close to one another, thus reflecting local regions of undetected recombination or haplotype blocks. However, ∼1/3 of giSNP clusters had intermingled, non-indistinguishable SNPs with incomplete LD (D′ and r² <1), sometimes spanning hundreds of kilobases, comprising up to 70 indistinguishable markers and overlapping multiple haplotype blocks. These long-range, nonconsecutive giSNPs have implications for disease gene localization by allelic association as evidence for association at one locus will be indistinguishable from that at another locus, even though both loci may be situated far apart. We describe the distribution of giSNPs on this map of chromosome 20 and illustrate the potential impact they can have on association mapping.

The International HapMap Project aims to characterize the patterns of LD throughout the entire human genome (The International HapMap Consortium 2003, 2004). The rationale behind the project is that because of the existence of LD, it should be possible to genotype a smaller set of variants that will capture most of the common patterns of variation in the genome. In this way, it should be possible to perform genome-wide tests of association with a limited number of “tag” SNPs (Johnson et al. 2001; Goldstein et al. 2003; Ke and Cardon 2003; Weale et al. 2003; Carlson et al. 2004b; Halldorsson et al. 2004; Ke et al. 2004a).

A key question in the tagging/association paradigm concerns the composition of the markers initially screened. If these represent the true genomic patterns in the population of interest, then their correlated tag proxies should as well; but if they do not, then neither would a subset of them. Focusing on high-frequency variants is a clear deviation from genomic representation (Kruglyak and Nickerson 2001), which is recognized, but argued to have limited adverse effects under the common-disease, common-variant hypothesis (Lohmueller et al. 2003). Another key feature of genomic representation concerns marker density. Many of the initial large-scale LD studies used relatively sparse marker densities (Patil et al. 2001; Reich et al. 2001; Dawson et al. 2002; Gabriel et al. 2002; Phillips et al. 2003). However, a number of recent studies have demonstrated the importance of high marker density (Carlson et al. 2003; Ke et al. 2004b; Hinds et al. 2005), as it deepens genomic coverage, allows better selection of tagSNPs, and elucidates the local structure of recombination hotspots. In recognition of the importance of marker density, the International HapMap Consortium has undertaken a follow-on genotyping phase to increase the average marker density from 1 SNP/5 kb to 1 SNP/600 bp on average.

Regions of high LD in fine-scale maps can often be indicative of SNPs that are in “perfect” LD with one another (Carlson et al. 2004a,b). In classical LD terms, this means that they have an r² coefficient of 1.0, or, equivalently, that only two of the four possible haplotypes are observed in a pair of di-allelic markers (Weir 1996). Barring genomic rearrangements such as gene conversion between the SNPs, this means that they are ancestrally nonrecombinant. In the practical context of trait association studies, it means that the two SNPs are “genotypically indistinguishable”, i.e., for every individual considered, their genotype at the first locus is identical to their genotype at the second locus. We term such sites “genetically indistinguishable SNPs” (giSNPs). These identities are present in all individuals in the sample and may occur at any positions (i.e., even at nonadjacent sites).

GiSNPs will naturally yield identical evidence for association with any trait, as they are indistinguishable from one another. This raises the importance of marker selection and association localization in haplotype tagging; the primary aim of haplotype tagging is to minimize genotyping by selecting nonredundant markers, and as giSNPs are entirely redundant, they are the first to be eliminated. But genotyping only one member of a cluster of indistinguishable markers distributed across a wide region could lead to errors of inference in disease-gene localization. Often giSNPs are in regions of high LD or “haplotype blocks” where they are of little concern since localization is difficult in such regions anyway. However, they are not always in contiguous LD regions, and even when they are, they can span hundreds of kilobases, encompass many genes, and involve a very large number of markers.

In terms of tagging efficiency, there is no a priori reason to choose one giSNP over another, yet this choice may dictate the subsequent attribution of etiological importance to specific genes/variants. If all SNPs were genotyped in the initial screening study, this would simply be a matter of annotation, whereby investigators could maintain a catalog of all indistinguishable variants. However, this is implausible because the location of all markers is unknown for any single population, so they cannot all be genotyped. Consequently, in the absence of external information, any association study has the potential for incorrect localization inference.

Here we describe the frequency of giSNPs and their distribution across chromosome 20 at a density of one marker/2 kb (Ke et al. 2004b). We show that giSNPs can essentially form three types of cluster with either “perfect,” “complete,” or “incomplete” LD (Fig. 1). We use these data and two of the ENCODE regions of the HapMap to extrapolate the densities and frequencies of SNPs to the genome at large. We also assess the importance of sample size by regenotyping giSNPs in a larger set of Western European samples and evaluating the extent to which they remain indistinguishable.

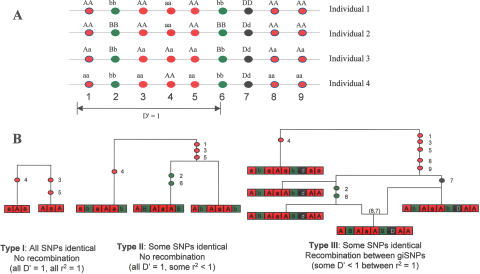
Figure 1.

Schematic representations of the three different types of giSNP cluster. (A) Genotype representation of the categories for nine SNPs genotyped on four illustrative individuals. Category 1 giSNP clusters (red SNPs 3, 4, and 5) do not have any intervening SNPs that are nonindistinguishable. Category 2 clusters (green SNPs 2 and 6) have intervening SNPs, but there is no evidence of recombination throughout the cluster (i.e., all SNPs in the region are D′ = 1). Category 3 clusters (red SNPs 1, 3, 4, 5, 8, and 9) contain intervening SNPs that are nonindistinguishable, as well as evidence for a recombination event in the region (i.e., some pairs of SNPs are D′ < 1). (B) Bifurcating genealogical trees (Type I and Type II) and ancestral recombination graph (Type III) describing formation of the three types of giSNP cluster. Each graph describes the ancestral events giving rise to a giSNP cluster. Colored circles in the graph represent an ancestral mutation with the number indicating the SNP involved. The (6,7) in the graph of the Type III giSNP cluster refers to an ancestral recombination event between SNPs 6 and 7. The boxes at the base of the figure refer to the multilocus haplotype present in the population sample, with each box representing a single SNP with alleles coded as a capital vs. lower case letter for each cluster. Since genotypes are formed through the pairing of haplotypes, a pair of loci will be genetically indistinguishable when only two pair-wise conformations are present in the population (i.e., aa and AA are the only pair-wise combinations present among all haplotypes; or alternatively, aA and Aa are the only combinations present in the population). In the case of the Type I cluster, all SNPs are genetically indistinguishable. In the Type II cluster, all SNPs have D′ = 1 with each other. SNPs 2 and 6 are genetically indistinguishable, but are separated by the Type I subcluster consisting of SNPs 3, 4, and 5. In the Type III cluster, SNPs 1, 3, 4, 5, 8, and 9 are genetically indistinguishable, but are separated by SNP 7, which is different from any other SNP, and forms all four possible haplotypes with any other SNP in the cluster. Note that in this example the Type I cluster is part of a larger Type III cluster. These would not be listed as separate in this study and are shown separately in this figure for descriptive purposes only.

Results

Distribution of giSNPs

The frequency of giSNPs on the 2-kb map of chromosome 20 suggests that they are not a rare phenomenon, but rather a ubiquitous feature of the human genome. Fifty-five percent of the SNPs assayed on the UK unrelateds sample have at least one genetically indistinguishable partner. The figure is slightly higher in the smaller sized Asian and CEPH samples and much lower in the African American sample (see Table 1), probably reflecting the lower levels of LD seen in Africans compared with European and Asian populations (Reich et al. 2001; Shifman et al. 2003; Stumpf and McVean 2003; Ke et al. 2004b; Evans and Cardon 2005). Consistent with this observation, the average number of SNPs in a cluster is smaller on average in African Americans than in the Asian, CEPH, or UK unrelateds samples. Clusters also extend over shorter distances on average in African Americans (Table 1).

Table 1.

GiSNP statistics for SNPs genotyped across Chromosome 20 in four population samples

Population	African American	Asian	CEPH	UK Unrelateds
Sample size	97	42	47 Founders	91
Total SNPs	33,206	25,719	28,223	28,460
Total giSNPs	10,081	16,506	17,464	15,680
% of all SNPs that are giSNPs	30.3%	64.2%	61.9%	55.1%
Total giSNP clusters	3527	4060	4527	4313
Mean giSNP cluster length	11.6 kb	14.8 kb	15.3 kb	13.7 kb
Median giSNP cluster length	3.5 kb	5.5 kb	5.7 kb	5.1 kb
Mean number of giSNPs per cluster	2.9	4.1	3.9	3.6
MAF 0-10% giSNPs	2473 (24.5%)	2704 (16.4%)	3108 (17.8%)	3423 (21.8%)
MAF 10-20% giSNPs	2376 (23.6%)	3764 (22.8%)	3883 (22.2%)	3125 (19.9%)
MAF 20-30% giSNPs	1994 (19.8%)	3571 (21.6%)	3848 (22.0%)	3248 (20.7%)
MAF 30-40% giSNPs	1736 (17.2%)	3571 (21.6%)	3607 (20.7%)	2983 (19.0%)
MAF 40-50% giSNPs	1499 (14.9%)	2894 (17.5%)	3018 (17.3%)	2901 (18.5%)

SNPs with only one or two heterozygotes were removed from the analysis, resulting in lowered levels of MAF <10% SNPs.

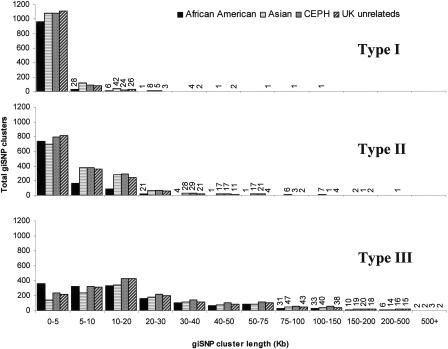
Figure 2 shows that while the majority of clusters are relatively short in length (i.e., <20 kb), a significant number involve SNPs that extend across large genomic distances. The vast majority of the longer clusters (>50 kb) are made up of Type III clusters, whereas the Type I and Type II clusters rarely extend past 30 or 50 kb, respectively. The relationship between cluster size and length does not seem to be related to the MAF of common variants (Supplemental Figs. 1 and 2), although there is an overrepresentation of clusters with lower MAFs (<10%) that extend across large distances. We observed very little change in our results when SNPs with only one or two heterozygotes were included in the analysis (Supplemental Figs. 3 and 4).

Figure 2.

Relationship between giSNP cluster length (kb) and cluster type in the four population samples. GiSNP clusters >200 kb were almost entirely made up of Type III clusters and had a tendency toward lower MAF, though a sizeable proportion had MAF >10%. The figure shows the bias of Type I and Type II clusters toward shorter clusters, whereas Type III clusters have much more widespread lengths.

GiSNP clusters by definition are composed of only two haplotypes. These two haplotypes are always “yin–yang” or mirror images of each other, as only this combination can produce giSNPs. Zhang et al. (2003) noted numerous yin–yang haplotypes covering large sections (75%–85%) of the genomic regions studied, which fits well with our observation of numerous and widespread giSNP clusters.

We assessed whether the distribution and density of giSNPs on chromosome 20 was expected under standard coalescent theory or whether the distribution of giSNPs is unusual and implies the action of additional mechanisms (e.g., gene conversion events, recombination hotspots, population bottlenecks, selection, etc.). The standard coalescent does not reflect the bias in SNP ascertainment to common alleles in the public database and does not allow for variability in recombination rates that will affect the distribution of LD, and hence, giSNP cluster formation. Our simulations revealed that the expected frequency and size of giSNP clusters increased with marker density, but decreased with sample size. Most importantly, the coalescent simulations did not reflect the high observed percentage of SNPs that were part of clusters in the Asian, CEPH, and UK unrelateds group (at a density of one SNP every 2.5 kb, ∼30% of SNPs are expected to be genetically indistinguishable). In addition, the simulations indicated that clusters consisting of seven or more giSNPs were extremely rare (i.e., <1% chance of seeing a cluster consisting of more than seven SNPs at the previous density). These results imply that the parameters in the standard coalescent model do not approximate the data well and that additional mechanisms are necessary to explain both the frequency and length of the giSNP clusters observed on chromosome 20.

GiSNPs and haplotype blocks

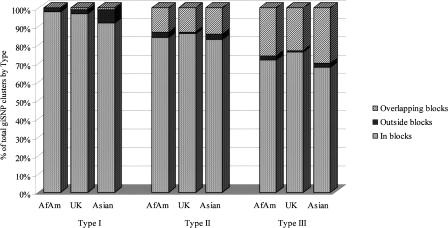
GiSNPs that are adjacent or separated by other loci in complete LD (Type I or Type II) are not especially surprising, as they fit well with observations of local variation in recombination rates (McVean et al. 2004). Figure 1B illustrates the interplay between ancestral recombination and mutation events in the formation of Type III giSNPs and the subsequent erosion of the resulting LD. For example, giSNPs may occur over relatively long distances, despite the presence of recombination in the region (e.g., SNPs 1 and 9), although we would then expect them to have occurred as a result of relatively recent mutation or low-frequency recombination events. It is important to emphasize that Type III giSNP clusters may be qualitatively different from haplotype blocks, depending on the block definition used. Most definitions of haplotype blocks are based upon pair-wise measures of LD, on measures of haplotype diversity, or some combination of the two (Daly et al. 2001; Patil et al. 2001; Dawson et al. 2002; Gabriel et al. 2002; Zhang et al. 2002; Cardon and Abecasis 2003; Wall and Pritchard 2003). Thus, a Type III cluster would span several haplotype blocks under the four gamete test (Hudson and Kaplan 1985; Wang et al. 2002). In contrast, the pair-wise block approach of Gabriel et al. (2002) appears to provide a closer correspondence between giSNPs, particularly in the case of Type I and Type II classifications (Fig. 3). Type III clusters also correspond to Gabriel blocks more often than not, but less consistently than Type I or Type II clusters. In the UK unrelateds sample, 84% of Type III giSNP clusters spanned only one haplotype block (15% spanned two or more haplotype blocks). In the African-American and Asian samples, 81% and 80%, respectively, of the clusters were found within Gabriel blocks. Thus, although detectable ancestral recombination had occurred within the Type III clusters, it was limited, and in most cases, the clusters still met the Gabriel et al. (2002) definition of a single haplotype block. Still, it is inappropriate to assume SNP pairs with r² = 1 will always fall within common haplotype blocks.

Figure 3.

Percentage of Type I, Type II, and Type III giSNP clusters falling within, outside, or across Gabriel-defined haplotype blocks.

Illustrative cluster and cross-population giSNPs

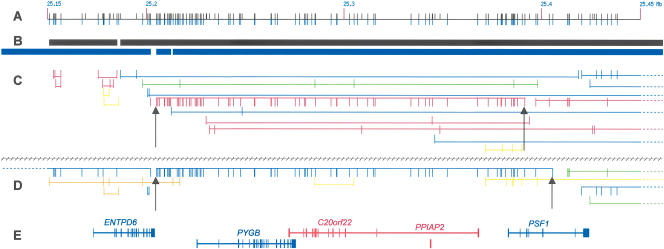
Figure 4 displays a region on chromosome 20p11.21 that contains the largest observed cluster in the UK unrelated sample. The figure shows the complicated nature of giSNP clusters, where many clusters of varying MAF can overlap and interlace with one another. It also demonstrates some of the features of giSNP clusters including large clusters overlapping with genes and regions of high LD, and the tendency for giSNPs to occur across populations. The largest cluster in the UK unrelateds sample consists of 72 giSNPs (MAF = 47%), is almost 200 kb in length, and overlaps almost perfectly with a 76-giSNP cluster in the Asian sample (MAF = 8%). Large clusters are also present in the same region in the other two population samples. Almost all of the giSNPs in the Asian cluster are also genetically indistinguishable in the UK unrelateds sample (70 SNPs were present in both the Asian and UK unrelateds clusters). Indeed, this seemed to be the case for chromosome 20 as a whole—giSNPs in one population sample are likely to be genetically indistinguishable in other population samples. In fact, 63% of giSNPs observed in African, Asian, or UK unrelateds samples were found in two or all three populations (Supplemental Fig. 5). These pan-ethnic clusters tend to have higher MAF than clusters specific to one population or SNPs that are not genetically indistinguishable (Supplemental Fig. 6).

Figure 4.

The 20p11.21 region of chromosome 20 that contains large 72 and 76 giSNP clusters in the UK unrelateds and Asian samples, respectively. From top to bottom: (A) SNP location of all SNPs genotyped and present in each population; (B) Gabriel et al. (2002) defined haplotype blocks for UK unrelateds (black) and Asians (blue); (C,D) giSNP clusters from UK unrelateds (above black-hashed line) and Asian (below black-hashed line) populations, respectively. GiSNPs in the same cluster are connected by a horizontal bar and MAF is represented by color (MAF: <10, blue; 10–20, green; 20–30, yellow; 30–40, orange; 40+, red). The horizontal bar between the giSNP ticks represents the number of SNPs per cluster. The higher the bar, the greater the number of giSNPs per cluster (bar height maximum, 15 giSNPs). The start and finish points of the 72- and 76-member giSNP clusters are indicated by black arrows; (E) gene locations.

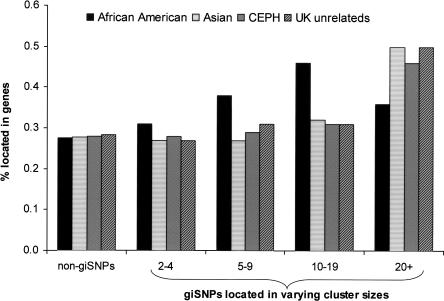
These results suggest that giSNPs do not occur independently across populations, but rather concentrate in particular areas. Why this is the case is unclear, but it may relate to conserved regions of high LD, selection, or some physical feature of the genome. For example, there is increasing evidence that recombination hotspots occur in similar genomic locations even in different human populations (Crawford et al. 2004; McVean et al. 2004; Evans and Cardon 2005). We therefore investigated whether the distribution of giSNPs might be influenced by the composition of the region. Figure 5 shows that giSNPs are only slightly more likely to be located within genes (exons or introns) than SNPs that are not genetically indistinguishable (30% vs. 28%). However, giSNPs belonging to large clusters are far more likely to be located within genes than giSNPs from smaller clusters (Supplemental Fig. 7).

Figure 5.

Percentage of non-giSNPs and giSNPs located within genes on chromosome 20. Percentages were calculated by scoring each SNP as either outside or inside genes from each SNP category (i.e., non-giSNPs, giSNPs from clusters containing 2–4, 5–9, 10–19, and ≥20 giSNPs).

Sample size effects

We observed a greater proportion of genetically indistinguishable SNPs in the smaller CEPH founder sample (47 individuals) than in the larger UK unrelateds sample (91 individuals). As association studies often involve many hundreds of individuals, we wanted to see what effect increasing sample size would have on larger giSNP clusters. We regenotyped 216 SNPs (from four of the largest clusters observed in the original UK unrelateds sample) using DNA from 360 unrelated UK individuals, all from the same Porton Down repository. After removal of poorly genotyped SNPs, we were able to analyze 171 SNPs from the original four giSNP clusters.

Of the 171 SNPs analyzed, we observed that 125 (73%) remained as a giSNP, with at least one other SNP within their original cluster (Supplemental Table 1). All four clusters broke up into smaller giSNP groupings as expected, though the cluster with lowest MAF was least affected. Despite the decrease in giSNP numbers, the average r² values between SNPs in the four clusters remained very high (mean r² = 0.95). Given the small initial sample size, the 95% confidence interval includes 3/42 discrepant individuals by sampling alone. When allowing for two or three genotype mismatches in the larger sample (which could represent genotyping error), virtually all of the SNPs (164 of 171) would have an “indistinguishable” partner (see Supplemental Table 2). These results suggest that increasing sample sizes will fragment large, long giSNP clusters to a certain extent, but r² values will probably remain very high even with large sample sizes.

SNP density effects

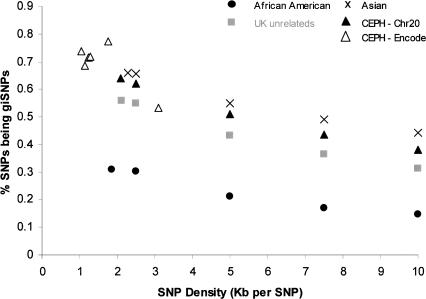
In this study we were able to analyze giSNPs at a maximum density of one SNP per 1.9–2.3 kb. To evaluate what proportion and number of giSNPs we might expect at higher SNP densities, we examined the HapMap Encode data (one SNP/1 kb). Figure 6 displays the number of giSNPs observed at varying SNP densities within our chromosome 20 study and the Encode chromosome 2, 4, and 7 regions (CEPH only). To measure giSNPs between densities of one SNP per 2 kb and 10 kb, we randomly selected sets of SNPs at the respective densities from our chromosome 20 data for each of the African American, Asian, CEPH, and UK unrelateds samples. The results suggest that at SNP densities of one SNP per kilobase or greater, we might expect to see 70% of SNPs having at least one indistinguishable partner in Asian or European origin samples of ∼50 individuals. Increasing SNP density cannot break up giSNP clusters, but could increase existing cluster sizes in addition to potentially converting Type I and Type II clusters into Type III clusters.

Figure 6.

Percentage of giSNPs observed at varying SNP densities using data from Encode (chromosomes 2, 4, and 7) and chromosome 20 (Sanger). Encode only contained data for CEPH families and is represented by hollow triangles (▵); all other data points are from the chromosome 20 study. Plots are shown for each sample using all available data points from a maximum density of one SNP per kilobase (Encode region 4) to a minimum density of one SNP per 10 kb (Chromosome 20). Percentage of giSNPs at 2.5, 5, 7.5, and 10 kb densities were calculated from randomly selected SNPs that were present in all four population samples.

Trait-association example

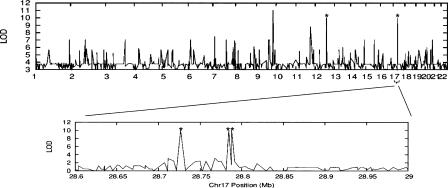
Type I and Type II clusters of giSNPs should pose few difficulties for association mapping inference apart from reflecting regions in which delineation of causal variants from indirect SNPs in strong LD will be difficult. However, Type III clusters may pose greater challenges. To explore this further, we examined the gene-expression data described by Morley et al. (2004) since a subset of the individuals for whom these “eQTL” phenotypes have been assayed have also been genotyped in the HapMap project as part of the CEPH family collection. Although the number of SNPs genotyped and publicly available is very high (>1 million SNPs; www.hapmap.org), the sample size is very small (42 founders), and thus, this example should just be considered as illustrative of the potential problems that can arise. One of the eQTL phenotypes described by Morley et al. (2004) was DDX17, which is located on chromosome 22q13.1 and linked to the same chromosome. We conducted allelic association tests for this phenotype by regression analysis of the expression level on genotypes coded additively for each HapMap marker. Figure 7 illustrates the effects of Type III giSNPs on allelic association inference. On chromosome 9, there are two close giSNPs that reveal identical evidence for trait-association. On chromosome 17, there is a giSNP cluster with three members spanning over 80 kb and another member spaced on an entirely different chromosome (12). We do not know which, if any (or all), of these are etiological, but from the primary association evidence we are left with several different genomic regions associated with indistinguishable genetic variants. The pattern of discrepant localization in Figure 7 would not be particularly troublesome if all giSNP clusters were known and annotated. However, for any population it is presently impossible to know all genetic variants in the genome, so the problem that emerges relates to unknown giSNP members. This is particularly worrisome for rare allele markers, as (1) they are underrepresented in the current public repositories (Carlson et al. 2003) and thus have a higher chance of being unknown; and (2) they are more likely to comprise giSNP clusters (Table 1).

Figure 7.

Caution with location inference. Example of SNP associations to expression levels of DDX17 in 42 CEPH individuals. LOD scores calculated for association using all SNPs including those with r² = 1. An enlarged section of chromosome 17 is shown to highlight three giSNPs that are within 70 kb of each other. The peaks indicated by asterisks are giSNPS with MAF 5%. The chromosome 9 SNPs that are identical in the Morley samples are rs1556220 and rs2274750. The chromosome 17 giSNPs include rs1552472, rs6505172, and rs8081598 clustered together with rs10506772 on chromosome 12.

Discussion

Using a dense map of one SNP every 2.5 kb across chromosome 20, we observe that over 50% of SNPs have indistinguishable partners (r² = 1.0) in Asian, CEPH, and UK unrelateds samples. GiSNPs can form large clusters containing tens of markers and can span tens to hundreds of kilobases. Large clusters are relatively rare compared with the numerous, small giSNP clusters but are almost twice as likely to be located within genes. The longer clusters often span the genomic location of ancestral recombination events, which could pose problems for locating disease loci via association studies.

GiSNP clusters have similarities to the r² bins described in Hinds et al. (2005), but reflect the extreme case of exact matching rather than high, but incomplete correlation. Like giSNP clusters, the Hinds et al. (2005) bins are able to overlap with each other, though SNPs can be present in multiple bins, whereas giSNPs are specific to their defined cluster. GiSNPs can therefore be viewed as bins of SNPs that have a stringent threshold of r² = 1. As most giSNP clusters are in regions of high LD they tend to align well with haplotype blocks, but not always.

The fact that not all giSNP clusters fit neatly into haplotype blocks highlights potential difficulties for fine-mapping studies using tagSNPs (unless the cluster is relatively short). The primary aim of the HapMap is to select tagSNPs that will capture as much LD as possible across the genome, while reducing the number of SNPs required for association studies (Johnson et al. 2001; The International HapMap Consortium 2003). One way to select tagSNPs is to take one SNP from two or more markers with very high pair-wise r² (Carlson et al. 2004b). In the case of large giSNP clusters, this method could result in SNPs located many kilobases from the selected or tagSNP being excluded. If a tagSNP revealed positive association, it would then be difficult to know whether it was the directly associated trait locus or if one of its distal, indistinguishable partners was actually the correct locus. If indistinguishable partners to tagSNPs are known and highlighted in the HapMap data, then giSNPs should become less problematic. The bigger issue concerns unknown or “hidden” SNPs (Carlson et al. 2003; Evans et al. 2004) that are not present in the HapMap. We have shown that as SNP density increases, so does the proportion of SNPs with indistinguishable partners (see Fig. 7). This implies that there will be many “hidden” giSNPs uncovered as coverage increases.

The sample sizes used in this study and the HapMap are small compared with those required for well-designed association studies (Cardon and Bell 2001; Zondervan et al. 2002; Zondervan and Cardon 2004). It is possible that the HapMap results, based on small samples, may not generalize to the larger samples required for trait applications. Here we have shown that increasing sample size does indeed break up large giSNP clusters, although the pair-wise r² values remain very high between SNPs in the original cluster. Large sample sizes, therefore, might not eradicate all long-range, high r² values between SNPs. There is future scope to use lower r² thresholds (e.g., r² > 0.8) to calculate giSNP clusters, as this could account for occasional genotyping errors that might make giSNPs non-indistinguishable and highlight closely associated markers which are almost indistinguishable.

In this study we describe several aspects of giSNPs. There is scope for further analysis with both larger sample sizes and SNP densities to clarify their effects on association mapping. The gene resequencing projects such as the Environmental Gene Project (EGP) (Livingston et al. 2004) or SeattleSNP Program for Genomic Applications (PGA) (SeattleSNPs, http://pga.gs.washington.edu) could help resolve the SNP density issue. GiSNPs highlight the unpredictable and complicated nature of fine-scale LD and imply that the location of positive association results should be interpreted with caution.

Methods

Sample populations

The following panels were used in the giSNP analysis: 97 unrelated African Americans (HD100AA, Coriell Cell Repositories); 47 founders from 12 × 3 generation CEPH/Utah families; 42 unrelated East Asians (consisting of 32 Japanese [22 from the American Diabetes Association] and 10 Chinese); and 91 UK unrelateds (from the Human Random Control [HRC] panel 1). Original panels selected for African American, CEPH, and UK unrelateds were slightly larger. Some members (three African Americans, five UK unrelateds, and one CEPH) were removed due to failing quality control (QC).

SNP selection, genotyping, and quality control

SNPs were genotyped by a combination of Illumina and Sequenom platforms at the Wellcome Trust Sanger Institute, extending the 10-Mb region described earlier (Ke et al. 2004b). After initial SNP quality/confidence checking, we removed SNPs with zero heterozygosity and/or <80% genotype success. SNPs that violated Hardy Weinberg equilibrium (HWE) were only removed if they did not have both heterozygotes and homozygotes present. The final number of SNPs analyzed for each sample were as follows: 33,694 SNPs in the African American sample, 27,397 SNPs in the Asian sample, 29,405 SNPs in the UK unrelateds sample, and 29,964 SNPs in the CEPH sample.

Extra UK unrelateds genotyping of giSNP clusters

We selected 219 SNPs from four of the largest UK unrelateds' giSNP clusters to be regenotyped in 360 UK unrelateds from the Porton Down repository (see Supplemental Table 1 for details). One individual had an extremely low genotype success rate (<50%) and was removed from analysis. Assays were successfully designed for 216 of the 219 selected SNPs with 195 of these producing genotypes on the Sequenom platform (all SNPs were originally genotyped in the 91 UK unrelateds using the Illumina platform). Of the SNPs genotyped, 145 SNPs passed our original QC threshold of ≥80% genotyping success. This threshold was lowered to 70%, as we found it made no difference in the percentage of SNPs remaining as giSNPs, while allowing a greater number (174 SNPs) to be analyzed. Three markers were removed due to excessive HWE departures (χ² > 50) resulting in 171 SNPs having analyzable genotypes. It should also be noted that due to some genotyping failure, the effective population sample size per SNP was on average around 290. We calculated pair-wise r² and D′ for each SNP pair in addition to calculating giSNP clusters as described below.

GiSNP measurements

We compared genotypes between each SNP pair along the entire length of chromosome 20. Any SNPs with all matching genotypes (r² = 1) in a given sample were grouped together into giSNP clusters. Any missing data in either SNP was skipped; i.e., treated as a match. A giSNP cannot exist in two or more separate clusters, so in the presence of missing data we placed these giSNPs in the groups with the most members. If the number of SNPs in the clusters was the same, we placed these “multicluster SNPs” in the nearest of the matching clusters. We also carried out duplicate analysis using either (1) all SNPs including those with only one or two heterozygotes, or (2) only SNPs with at least three heterozygotes within the specified sample. By using only SNPs with at least three heterozygotes, we should remove the possibility of SNPs being indistinguishable by chance alone. Unless stated, the results presented in this study use only SNPs with three or more heterozygotes. SNPs with only one or two heterozygotes in one population sample were not excluded from other samples if those samples contained three or more heterozygotes.

GiSNP categories

In order to facilitate description of giSNPs, we divide the giSNP clusters into three categories based upon the presence/absence of intervening SNPs and LD patterns (Fig. 1) as follows:

1. Type I cluster: All successive SNPs in a cluster are indistinguishable, with no intervening non-giSNPs. In this case, only two multilocus haplotypes are present, since all sites in the cluster are r² =1.

2. Type II cluster: The cluster is interspersed with SNPs that are in complete, but imperfect LD (D′ =1, r² < 1). The interspersed SNPs may form their own giSNP cluster, but are not in perfect LD with the others. In this case, three of four of the multilocus haplotypes are present in the population.

3. Type III cluster: The cluster is interspersed with at least one SNP showing D′ < 1 and r² < 1 with the SNPs in the cluster. That is, multiple SNPs which appear nonrecombinant (giSNPs) have intervening SNPs that are obligate recombinant.

Figure 1B depicts the formation of the three types of giSNP cluster in the context of the ancestry of sampled haplotypes. Type I and Type II clusters can only be formed in the absence of ancestral recombination, where the ancestry of sampled haplotypes can be represented by means of a bifurcating genealogical tree. The distinct sampled haplotypes correspond to the “leaves” at the foot of the tree.

Type II clusters consist of overlapping sets of Type I clusters of giSNPs formed from mutation in the absence of recombination. Under the standard coalescent process (Kingman 1982), the oldest lineages of the genealogy are expected to be the longest. Thus, clusters of this type may not be particularly rare.

The ancestry of Type III clusters requires at least one recombination event and can be conveniently represented by means of an ancestral recombination graph (Griffiths and Marjoram 1996, 1997).

Coalescent simulations

We ran a series of coalescent simulations to investigate the effect of several parameters on the expected distribution of giSNPs. The 1-MB sequences were generated under the standard coalescent with uniform recombination as implemented in the program MS (Hudson 2002). We assumed a per base mutation rate of μ = 10^–8 per generation and a uniform recombination rate of 1 cM/Mb per generation corresponding to a scaled recombination rate of ρ = 400 and a scaled mutation rate of θ = 400 for an effective population size of 10,000 individuals. These sequences were then randomly paired together to form the requisite number of individuals. We examined the effect of marker density (i.e., one SNP per kb, one SNP per 2.5 kb, one SNP per 5 kb, one SNP per 7.5 kb, and one SNP per 10 kb) and sample size (50, 96, 250, or 500 individuals) on the frequency and distribution of giSNPs (10,000 replications for each condition).