Sequence features in regions of weak and strong linkage disequilibrium

Albert V Smith; Daryl J Thomas; Heather M Munro; Gonçalo R Abecasis

doi:10.1101/gr.4421405

letter

. 2005 Nov;15(11):1519–1534. doi: 10.1101/gr.4421405

Sequence features in regions of weak and strong linkage disequilibrium

Albert V Smith ^1,^2,⁵, Daryl J Thomas ^3,^5,⁶, Heather M Munro ⁴, Gonçalo R Abecasis ⁴

PMCID: PMC1310640 PMID: 16251462

Abstract

We use genotype data generated by the International HapMap Project to dissect the relationship between sequence features and the degree of linkage disequilibrium in the genome. We show that variation in linkage disequilibrium is broadly similar across populations and examine sequence landscape in regions of strong and weak disequilibrium. Linkage disequilibrium is generally low within ∼15 Mb of the telomeres of each chromosome and noticeably elevated in large, duplicated regions of the genome as well as within ∼5 Mb of centromeres and other heterochromatic regions. At a broad scale (100–1000 kb resolution), our results show that regions of strong linkage disequilibrium are typically GC poor and have reduced polymorphism. In addition, these regions are enriched for LINE repeats, but have fewer SINE, DNA, and simple repeats than the rest of the genome. At a fine scale, we examine the sequence composition of “hotspots” for the rapid breakdown of linkage disequilibrium and show that they are enriched in SINEs, in simple repeats, and in sequences that are conserved between species. Regions of high and low linkage disequilibrium (the top and bottom quartiles of the genome) have a higher density of genes and coding bases than the rest of the genome. Closer examination of the data shows that whereas some types of genes (including genes involved in immune response and sensory perception) are typically located in regions of low linkage disequilibrium, other genes (including those involved in DNA and RNA metabolism, response to DNA damage, and the cell cycle) are preferentially located in regions of strong linkage disequilibrium. Our results provide a detailed analysis of the relationship between sequence features and linkage disequilibrium and suggest an evolutionary justification for the heterogeneity in linkage disequilibrium in the genome.

Large-scale data sets providing information on linkage disequilibrium for >1 million markers are now available (The International HapMap Consortium 2003; Hinds et al. 2005). These data sets will aid in the design and interpretation of genome-wide association studies and facilitate the identification of alleles underlying susceptibility to complex disease (Cardon and Abecasis 2003; Hirschhorn and Daly 2005). An example of the utility of these resources is the recent positional cloning of a susceptibility gene for age-related macular degeneration (Edwards et al. 2005; Haines et al. 2005; Klein et al. 2005; Zareparsi et al. 2005).

In addition to facilitating genome-wide association studies, these data sets also provide us with the best opportunity yet to explore the relationship between local sequence features and patterns of linkage disequilibrium (Abecasis et al. 2005). Although this relationship has been examined in several previous studies (for examples, see Eisenbarth et al. 2000; Yu et al. 2001; Dawson et al. 2002), these have focused on relatively small amounts of data. The results of these initial studies show that linkage disequilibrium is strongly influenced by the local recombination rate (Dawson et al. 2002) and correlated with other factors that are associated with local recombination rates, such as GC content, gene density, and the presence of SINE or Alu repeats (Fullerton et al. 2001; Yu et al. 2001; Dawson et al. 2002). New large-scale data sets will enable us to more precisely characterize and quantify the relationship between these types of sequence features and linkage disequilibrium, thus furthering our understanding of genome architecture.

The effects of population history on linkage disequilibrium have been extensively studied analytically (for examples, see Ohta and Kimura 1969; Nei and Li 1973), through simulation studies (Hudson 1990; Kruglyak 1999) and in data sets that include genotype data collected in multiple populations (Tishkoff et al. 1996; Gabriel et al. 2002). Many of these effects are now well understood—for example, it is generally accepted that whereas population bottlenecks, geographic subdivision, and natural selection can increase the extent of linkage disequilibrium, population growth and random mating tend to decrease the extent of linkage disequilibrium in a genome.

In addition to these population genetic factors, the extent of linkage disequilibrium in a particular genomic region can also be influenced by the physical characteristics of the surrounding DNA sequence (Abecasis et al. 2005; Nordborg and Tavare 2005). In principle, local sequence features can affect linkage disequilibrium in several different ways, both directly and indirectly. For example, some types of sequences (such as GC-rich sequences) (see Fullerton et al. 2001) may be associated with higher rates of recombination and/or mutation, two phenomena that could directly lower surrounding levels of linkage disequilibrium. In other types of sequences (such as protein-coding sequences), changes brought about by recombination or mutation might be more likely to affect the fitness of an individual—and these sequences could be indirectly associated with unique patterns of linkage disequilibrium as a consequence of natural selection.

Here, we use data from the International HapMap Consortium (2003) to characterize the relationship between local sequence features and patterns of linkage disequilibrium in the genome in three different populations. Our results show that regions of weak and strong linkage disequilibrium are remarkably consistent across populations and suggest that GC content, DNA polymorphism, and repeat content are strongly associated with the local extent of linkage disequilibrium. Additionally, we find that genes and coding sequences are enriched in regions of high and low disequilibrium compared with the rest of the genome. We use the Gene Ontology database to aggregate genes according to their functional roles, and we show that different types of genes locate preferentially in regions of high and low disequilibrium.

Results

Genotype data

Variation in linkage disequilibrium in the genome

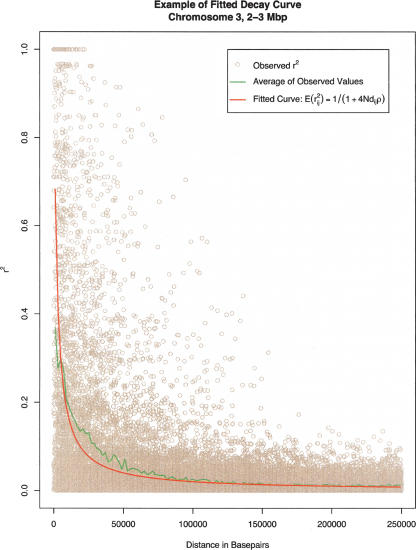
We fitted curves to model the decay of r² within sliding windows distributed throughout the genome. Our approach is based on the simple model of Ohta and Kimura (1969), which predicts that the expected disequilibrium between alleles at any two loci i and j is E(r²_ij) = 1/(1 + R_ij). In this model, the population recombination rate, R_ij = 4Nc_ij, is a function of N, the effective population size, and c_ij, the recombination fraction between markers i and j. As detailed in the Methods, we fitted a parameter corresponding to the per base-pair population recombination rate within each genomic window and used it to model disequilibrium for all pairs of markers within the window. The fitted parameter defines a curve for the decay of linkage disequilibrium in each window and provides a means to compare degree of disequilibrium in any two windows of the genome. Here, our comparisons are simply based on examining the fitted values for marker pairs separated by an arbitrary distance (for this model, examining the fitted values at any other distance would result in the same ordering of regions). Disequilibrium coefficients for an exemplar region, a decay curve generated by taking the average of observed disequilibrium coefficients, and the fitted curve using the model of Ohta and Kimura (1969) are presented in Figure 1.

Figure 1. — Pairwise disequilibrium coefficients (r²) for one window in the genome. Tan circles denote the observed values. Green line denotes the average of observed values. Red line denotes the curve resulting from the fitted model, which models the decay of linkage disequilibrium as a function of the per base-pair population recombination rate, 4Nρ, and the distance between markers *d_ij* (see Methods). The example refers to marker pairs in the window from 2–3 Mb on chromosome 3.

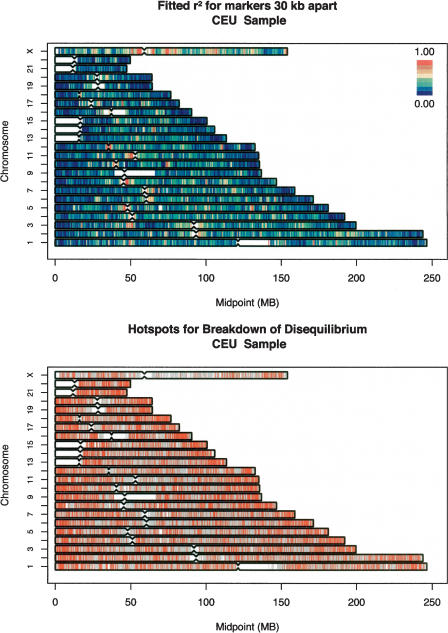
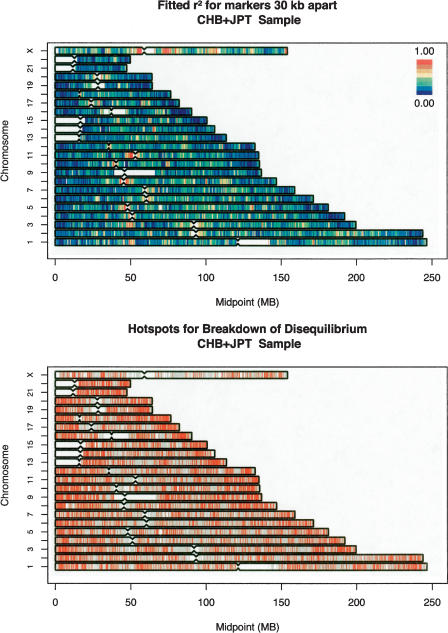
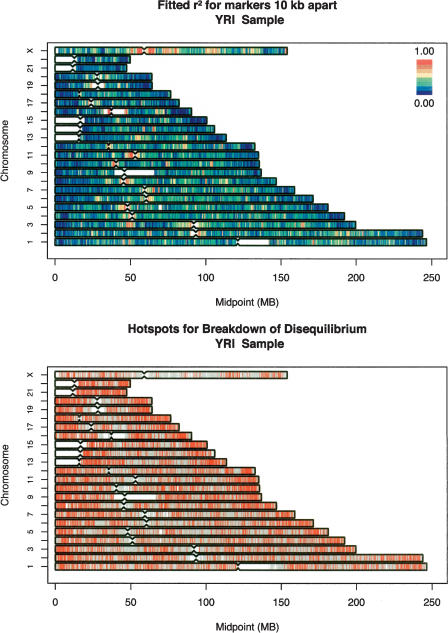
The top panels in Figures 2 (CEU sample), 3 (YRI sample), and 4 (CHB+JPT samples) summarize the properties of the fitted curves for the entire genome (divided into 100,000-bp windows) by plotting fitted r² value for markers separated by 30,000 bp (for the CEU sample and for the combined CHB+JPT samples) or markers separated by 10,000 bp (for the YRI sample, which shows much less linkage disequilibrium overall). Using these 100,000-bp windows, the model explained 34.2% of the variance in pairwise linkage disequilibrium coefficients in the CEU sample, 19.6% of the variance in the YRI sample, and 37.5% of the variance in the CHB+JPT samples. Part of the difference in the proportion of variance explained is due to the fact that the CHB+JPT and CEU samples exhibit higher levels of disequilibrium, whereas the YRI samples exhibit much lower disequilibrium. When linkage disequilibrium is lower (as in the YRI samples), a model predicting that linkage disequilibrium decays with distance will only be able to explain less of the observed variation because many more of the coefficients will be near background levels, and stochastic variation will play a proportionately larger role in determining observed levels of disequilibrium. The proportion of the variance in pairwise linkage disequilibrium explained decreased when we used larger 1000-kb windows, to 29.6% in the CEU samples, 17.3% in the YRI samples, and 32.8% in the CHB+JPT samples.

Figure 2. — Genome-wide summary of fitted linkage disequilibrium values and identified “hotspots” for the rapid breakdown of linkage disequilibrium. (*Top*) The fitted disequilibrium coefficients for markers separated by 30 kb. Disequilibrium coefficients were calculated within 100-kb windows distributed throughout the genome. (*Bottom*) Intermarker intervals (in red), where linkage disequilibrium decays very rapidly, such that disequilibrium between spanning marker pairs is generally low (for details, see text). Evaluated intervals where disequilibrium did not appear to decay very rapidly are marked in light blue.

Figure 3. — Genome-wide summary of fitted linkage disequilibrium values and identified “hotspots” for the rapid breakdown of linkage disequilibrium. (*Top*) The fitted disequilibrium coefficients for markers separated by 30 kb. Disequilibrium coefficients were calculated within 100-kb windows distributed throughout the genome. (*Bottom*) Intermarker intervals (in red), where linkage disequilibrium decays very rapidly, such that disequilibrium between spanning marker pairs is generally low (for details, see text). Evaluated intervals where disequilibrium did not appear to decay very rapidly are marked in light blue.

Figure 4. — Genome-wide summary of fitted linkage disequilibrium values and identified “hotspots” for the rapid breakdown of linkage disequilibrium. (*Top*) The fitted disequilibrium coefficients for markers separated by 10 kb. Disequilibrium coefficients were calculated within 100-kb windows distributed throughout the genome. (*Bottom*) Intermarker intervals (in red), where linkage disequilibrium decays very rapidly, such that disequilibrium between spanning marker pairs is generally low (for details, see text). Evaluated intervals where disequilibrium did not appear to decay very rapidly are marked in light blue.

The genome-wide view of linkage disequilibrium in the top panels of Figures 2, 3, 4 highlights several important patterns. First, the degree of linkage disequilibrium is much greater in the CEU and CHB+JPT samples than in the YRI sample (in fact, the degree of disequilibrium for markers separated by ∼30 kb in the CEU and CHB+JPT samples is similar to the degree of disequilibrium between markers separated ∼10 kb in the YRI samples). This is in agreement with results for other comparisons of samples of African descent with samples of European or Asian descent (Gabriel et al. 2002; Ke et al. 2004; Liu et al. 2004), all of which show much less linkage disequilibrium in African-descent samples. Second, the relative degree of linkage disequilibrium is broadly similar across populations—regions that exhibit above-average linkage disequilibrium in any one sample typically also exhibit above-average linkage disequilibrium in the other samples. Examples of this include a region centered at ∼50 Mb on chromosome 3, which shows strong disequilibrium in all samples and regions of very strong disequilibrium surrounding the centromeres of chromosomes 5, 8, 11, 12, 16, and X in all three populations (cf. Figs. 2, 3, 4). However, note that we refer to the overall degree of linkage disequilibrium in a region rather than to specific combinations of associated alleles—which can differ between populations both in regions of strong and weak disequilibrium. As expected (Schaffner 2004), linkage disequilibrium in all populations was generally higher on the X chromosome—which has a smaller effective population size, since males only carry one copy—than in the autosomes.

Several genomic patterns are apparent in the distribution of linkage disequilibrium. For example, linkage disequilibrium is generally weak near chromosome ends, probably due to the high recombination rate of these regions in male meiosis, and stronger around centromeres and other internal portions of each chromosome, where recombination rates are lower on average (Weissenbach et al. 1992; Broman et al. 1998; Yu et al. 2001; Kong et al. 2002). In further agreement with recombination rate maps of the genome, linkage disequilibrium is generally stronger in the large chromosomes—which have a lower sex-averaged recombination rate—and weaker in the small chromosomes—which have a higher sex-averaged recombination rate.

Correlation of linkage disequilibrium with sequence features

In order to characterize the relationship between linkage disequilibrium and genomic sequence characteristics, we first calculated the Spearman rank correlation coefficient between a series of sequence features and the estimated degree of linkage disequilibrium in each region. The Spearman correlation coefficient is robust to non-normality of the variables being examined and appropriate for these types of data, where some features have highly skewed distributions. The results for each population and for three different window sizes (100, 500, and 1000 kb) are summarized in Tables 1 and 2. In Table 1, it is clear that the strongest correlations are observed when linkage disequilibrium levels in two populations are compared.

Table 1.

Spearman rank correlation between disequilibrium and sequence features in windows of 100, 500, and 1000 kb

	CEU sample			YRI sample			CHB+JPT sample
	100 kb	500 kb	1000 kb	100 kb	500 kb	1000 kb	100 kb	500 kb	1000 kb
LD in other populations
CEU	1.00^*	1.00^*	1.00^*	0.81^*	0.86^*	0.89^*	0.86^*	0.89^*	0.90^*
YRI	0.81^*	0.86^*	0.88^*	1.00^*	1.00^*	1.00^*	0.80^*	0.85^*	0.88^*
CHB+JPT	0.84^*	0.88^*	0.89^*	0.79^*	0.84^*	0.87^*	1.00^*	1.00^*	1.00^*
Basic sequence features
GC content	-0.33^*	-0.33^*	-0.33^*	-0.34^*	-0.34^*	-0.35^*	-0.33^*	-0.33^*	-0.33^*
CpG Islands	-0.07^*	-0.13^*	-0.17^*	-0.06^*	-0.13^*	-0.18^*	-0.07^*	-0.12^*	-0.16^*
Polymorphism (π)	-0.38^*	-0.43^*	-0.42^*	-0.37^*	-0.40^*	-0.39^*	-0.36^*	-0.41^*	-0.41^*
Genes and related features
Gene count	0.01	-0.04^*	-0.08^*	0.01	-0.05^*	-0.08^*	0.01	-0.04^*	-0.07^*
Genic bases (intron, exon, UTR)	0.05^*	0.00	-0.03	0.05^*	-0.01	-0.05^*	0.05^*	0.00	-0.03
Coding bases	0.03^*	-0.02	-0.06^*	0.03^*	-0.02	-0.06^*	0.03^*	-0.02	-0.05
Exonic bases	0.01	-0.04^*	-0.08^*	0.01	-0.04^*	-0.09^*	0.01	-0.04	-0.07^*
Intronic bases	0.05^*	0.00	-0.03	0.04^*	-0.01	-0.05^*	0.05^*	0.00	-0.03
UTR (3′ and 5′)	-0.01	-0.06^*	-0.10^*	-0.01	-0.06^*	-0.11^*	-0.01	-0.06^*	-0.09^*
Other features
Bases in transcription factor binding sites	-0.10^*	-0.10^*	-0.09^*	-0.11^*	-0.11^*	-0.10^*	-0.10^*	-0.10^*	-0.09^*
Bases in transcribed fragments^a	-0.03^*	-0.03	-0.03	-0.03^*	-0.02	-0.02	-0.03^*	-0.02	-0.02
Predictions of conserved elements (phastCons)	-0.09^*	-0.08^*	-0.07^*	-0.09^*	-0.09^*	-0.09^*	-0.09^*	-0.08^*	-0.07^*
Identical base in alignment with M. musculus	-0.19^*	-0.19^*	-0.17^*	-0.20^*	-0.20^*	-0.19^*	-0.19^*	-0.19^*	-0.17^*
Conserved noncoding sequence	-0.16^*	-0.14^*	-0.12^*	-0.17^*	-0.15^*	-0.13^*	-0.16^*	-0.14^*	-0.12^*
Identical base in alignment with R. norvegicus	-0.18^*	-0.18^*	-0.17^*	-0.19^*	-0.20^*	-0.18^*	-0.18^*	-0.19^*	-0.17^*
Repeat content
Total bases in repeats	0.25^*	0.34^*	0.35^*	0.26^*	0.36^*	0.37^*	0.25^*	0.33^*	0.34^*
Bases in LINE repeats	0.27^*	0.34^*	0.36^*	0.27^*	0.34^*	0.37^*	0.27^*	0.33^*	0.36^*
Bases in SINE repeats	-0.12^*	-0.15^*	-0.18^*	-0.11^*	-0.15^*	-0.19^*	-0.12^*	-0.14^*	-0.17^*
Bases in LTR repeats	0.00	0.06^*	0.09^*	-0.01	0.08^*	0.11^*	0.00	0.06^*	0.08^*
Bases in DNA repeats	-0.03^*	-0.08^*	-0.12^*	-0.03^*	-0.09^*	-0.13^*	-0.03^*	-0.08^*	-0.11^*
Bases in simple repeats	-0.21^*	-0.28^*	-0.31^*	-0.21^*	-0.26^*	-0.29^*	-0.20^*	-0.27^*	-0.30^*
Bases in low complexity repeats	0.04^*	0.04^*	0.03	0.05^*	0.07^*	0.06^*	0.05^*	0.06^*	0.04
Bases in satellite repeats	0.03^*	0.02	0.04	0.02^*	0.02	0.04	0.02^*	0.03	0.04
Bases in other repeats	0.05^*	0.07^*	0.08^*	0.06^*	0.08^*	0.08^*	0.05^*	0.08^*	0.09^*

Open in a new tab

Correlation is significant at P < 0.0001 level.

Only applies to chromosomes 6, 7, 13, 14, 18, 19, 20, 21, 22, and X.

Table 2.

Correlation between chromosomal organization and linkage disequilibrium in windows of 100, 500, and 1000 kb

	CEU sample			YRI sample			CHB+JPT sample
Chromosome organization	100 kb	500 kb	1000 kb	100 kb	500 kb	1000 kb	100 kb	500 kb	1000 kb
Within 5 Mb of centromere	0.13^*	0.16^*	0.17^*	0.13^*	0.17^*	0.19^*	0.12^*	0.15^*	0.17^*
Within 10 Mb of centromere	0.10^*	0.12^*	0.14^*	0.11^*	0.14^*	0.16^*	0.09^*	0.11^*	0.13^*
Within 15 Mb of centromere	0.08^*	0.10^*	0.12^*	0.09^*	0.12^*	0.14^*	0.07^*	0.09^*	0.11^*
Within 5 Mb of telomere	-0.15^*	-0.19^*	-0.21^*	-0.14^*	-0.18^*	-0.21^*	-0.14^*	-0.17^*	-0.20^*
Within 10 Mb of telomere	-0.21^*	-0.26^*	-0.29^*	-0.20^*	-0.26^*	-0.29^*	-0.19^*	-0.25^*	-0.27^*
Within 15 Mb of telomere	-0.23^*	-0.29^*	-0.32^*	-0.22^*	-0.28^*	-0.32^*	-0.22^*	-0.27^*	-0.31^*
Within 5 Mb of heterochromatin	0.09^*	0.11^*	0.12^*	0.09^*	0.12^*	0.14^*	0.09^*	0.11^*	0.13^*
Within 10 Mb of heterochromatin	0.08^*	0.09^*	0.11^*	0.08^*	0.10^*	0.13^*	0.08^*	0.10^*	0.12^*
Within 15 Mb of heterochromatin	0.05^*	0.06^*	0.07^*	0.06^*	0.08^*	0.10^*	0.05^*	0.06^*	0.08^*
Large genomic duplications	0.07^*	0.07^*	0.06^*	0.07^*	0.06^*	0.05	0.07^*	0.07^*	0.06^*
Large genomic duplications (cis)	0.05^*	0.04^*	0.03	0.06^*	0.03	0.01	0.04^*	0.03	0.02
Large genomic duplications (trans)	0.06^*	0.10^*	0.09^*	0.07^*	0.09^*	0.09^*	0.07^*	0.10^*	0.10^*

Open in a new tab

Correlation is significant at P < 0.0001 level

Nevertheless, several other interesting patterns emerge. Increased GC content is strongly associated with lower levels of disequilibrium (r ≈ –0.33) and the strength of the association appears similar for various window sizes. Sequence polymorphism, which we quantified using the per base-pair nucleotide diversity (π, see Methods), is also strongly associated with lower levels of disequilibrium (r ≈ –0.40) across the various window sizes. In contrast, genes and related features (introns, exons, and coding bases) are weakly associated with increased linkage disequilibrium levels when windows of 100 kb are considered (r ≈ 0.01–0.05) but associated with decreased disequilibrium when larger 1000-kb windows are considered (r ≈ –0.03 to –0.08). Given the large sample size, these differences are significant—and may reflect that while genes themselves exhibit a high degree of disequilibrium (because of reduced recombination rates or because alleles are undergoing natural selection), there might be increased recombination and therefore decreased linkage disequilibrium in the regions between and around genes. The presence of transcription factor binding sites (r ≈ –0.10), conserved noncoding sequences (r ≈ –0.14), sequences that were conserved in multispecies alignments (r ≈ –0.09), and the presence of sequences that are conserved in pairwise comparisons between the completed human genome sequence and the rat (r ≈ –0.18) (Gibbs et al. 2004) or mouse genomes (r ≈ –0.19) (Waterston et al. 2002) were all associated with decreased levels of linkage disequilibrium. Finally, the repeat composition of each region was strongly associated with the observed levels of linkage disequilibrium, and these correlations appeared to significantly increase in strength when larger genomic windows were considered. The total repeat content of a region and the presence of LINE repeats was associated with increasing levels of linkage disequilibrium (r ≈ 0.26 for 100-kb windows and r ≈ 0.36 for 1000-kb windows), whereas some other repeat types, especially SINE repeats (mostly Alu repeats, r ≈ –0.18 for 1000-kb windows) and simple repeats (r ≈ –0.31), were strongly associated with decreased levels of linkage disequilibrium.

Table 2 shows the relationship between chromosomal location and linkage disequilibrium levels. As expected from prior knowledge of recombination rate variation in humans (Yu et al. 2001; Kong et al. 2002), proximity to telomeres is strongly associated with decreased levels of linkage disequilibrium (r ≈ –0.32 for 1000-kb windows within 15 Mb of a telomere), whereas proximity to centromeres is associated with increased levels of linkage disequilibrium (r ≈ 0.17 for regions within 5 Mb of a centromere). In addition, we note increased levels of linkage disequilibrium surrounding regions of heterochromatin (r ≈ 0.12 for regions within 5 Mb of heterochromatic sequence) and in large duplicated regions of the genome. These results suggest that in addition to centromeres, heterochromatin and large genomic duplications are also associated with reduced recombination rates. To evaluate whether these large chromosomal features could explain the associations presented in Table 1, we repeated our correlation analysis excluding 15 Mb of sequence surrounding telomeres, centromeres, and heterochromatin. Our results did not change substantially, except for the correlation between disequilibrium and satellite repeats, which disappeared (it appears that satellite repeats are associated with linkage disequilibrium mainly because they are preferentially located near centromeres, and there is no evidence for an association between satellite repeats and recombination when the rest of the genome is considered alone).

One limitation of the analyses presented in Tables 1 and 2 is that they do not explicitly account for the similarities between sequence feature profiles and the degree of linkage disequilibrium in consecutive genomic windows. While these similarities should not bias estimates of the correlation coefficients, they can affect significance tests for these coefficients—since these tests typically assume that all observations are independent. For each population and window size, we repeated our analysis by selecting a series of 280 windows spaced 10 Mb apart along the genome and that thus were nearly independent. Although this analysis discards much of the available data, it produced correlation coefficients similar to those reported in Tables 1 and 2, and all coefficients with absolute value >0.15 remained significant (P < 0.05).

Base composition in regions of high and low linkage disequilibrium

To further characterize the relationship between linkage disequilibrium and sequence variation in the genome, we divided the genome into quartiles according to the estimated level of linkage disequilibrium in each 100-kb window. Regions not genotyped by the HapMap project were left unclassified. Initially, we carried out the analysis in each population separately, but since results were similar, we averaged the ranking for each window across populations for our final analysis. To ensure that this organization of the genome into quartiles was not an artifact of differences in SNP ascertainment across the genome, we calculated the average minor allele frequency (MAF) of SNPs in each of the four quartiles. Frequencies of the SNPs used to estimate linkage disequilibrium levels (all with MAF >0.05) were very similar in regions of high, low, and intermediate levels of linkage disequilibrium in both the CEU (average MAF of 0.268 in Q1, 0.270 in Q2, 0.269 in Q3, and 0.274 in Q4), the CHB+JPT (0.269 in Q1, 0.272 in Q2, 0.271 in Q3, and 0.270 in Q4) and in the YRI (0.257 in Q1, 0.260 in Q2, 0.257 in Q3, and 0.261 in Q4) samples.

Within each quartile, we calculated the proportion of base pairs contained within genes and related features, within transcription factor binding sites and other conserved sequences, and also within different types of repeats. The results are summarized in Table 3, which tabulates the number of bases (per 10,000) present in each of several categories for the different quartiles. For all of the features summarized in Table 3, the differences in base composition between the different genomic quartiles are highly significant (P <10^–4) when an F-test is used to compare composition of the 100-kb windows.

Table 3.

Sequence composition of quartiles of the genome, defined according to the extent of linkage disequilibrium

	Genome covered by HapMap		Genome quantiles, defined using LD
	Mean	(±S.E.)	(Low LD) Q1	Q2	Q3	(High LD) Q4	Trend
Basic sequence features
GC bases	4080.3	(±2.3)	4349.6	4102.3	3964.8	3904.6	Decreases with LD
Bases in CpG islands	72.0	(±0.7)	93.8	72.8	63.4	57.9	Decreases with LD
Polymorphism (π)	10.1	(±0.02)	11.9	10.6	9.6	8.3	Decreases with LD
Genes and related features
Known genes (per 1000 kb)	6.4	(±0.4)	6.6	6.1	6.2	6.7	U shaped
Genic bases (exon, intron, UTR)	3854.7	(±16.9)	3764.8	3456.9	3603.1	4594.0	U shaped
Coding bases	116.2	(±0.8)	112.4	104.1	112.0	136.2	U shaped
Exonic bases	222.1	(±1.5)	225.8	204.2	214.6	243.9	U shaped
Intronic bases	3678.0	(±16.6)	3584.5	3293.5	3432.5	4401.5	U shaped
UTR (3′ and 5′)	105.9	(±0.8)	113.4	100.1	102.6	107.7	U shaped
Other features
Bases in transcription factor binding sites	101.7	(±0.3)	110.1	107.1	98.7	90.8	Decreases with LD
Bases in transcribed fragments^a	251.3	(±2.4)	290.9	258.0	232.9	223.3	Decreases with LD
Predictions of conserved elements (phastCons)	485.0	(±1.5)	520.5	499.1	465.9	454.5	Decreases with LD
Conserved noncoding sequence	139.1	(±0.6)	164.6	154.3	132.1	105.7	Decreases with LD
Identical base in alignment with M. musculus	2531.5	(±4.7)	2768.9	2678.6	2466.2	2212.2	Decreases with LD
Identical base in alignment with R. norvegicus	2454.0	(±4.8)	2679.8	2600.5	2395.5	2140.4	Decreases with LD
Repeat content
Total bases in repeats	4787.2	(±5.0)	4421.4	4642.0	4858.8	5226.7	Increases with LD
Bases in LINE repeats	2090.7	(±4.6)	1649.7	1988.4	2235.9	2488.9	Increases with LD
Bases in SINE repeats	1359.7	(±3.9)	1474.0	1307.8	1261.6	1395.3	U shaped
Bases in LTR repeats	851.2	(±2.4)	808.3	872.1	895.0	829.2	∩ shaped
Bases in DNA repeats	302.6	(±0.7)	306.9	305.2	301.0	297.3	Decreases with LD
Bases in simple repeats	89.0	(±0.3)	109.3	91.2	82.1	73.4	Decreases with LD
Bases in low complexity repeats	57.6	(±0.1)	56.1	56.8	58.9	58.5	Increases with LD
Bases in satellite repeats	20.8	(±1.3)	5.4	6.9	8.4	62.5	Increases with LD
Bases in other repeats	14.0	(±0.2)	10.4	12.0	14.3	19.4	Increases with LD

Open in a new tab

Only applies to chromosomes 6, 7, 13, 14, 18, 19, 20, 21, 22, and X.

Average base counts (per 10,000 bases) and standard errors are presented for each feature.

Most of the differences in base composition are consistent with the correlation results presented in Table 1. For example, it is clear that CG content decreases gradually as linkage disequilibrium increases (from 4349 CG nucleotides per 10,000 bases in the quartile of the genome with the lowest disequilibrium to 3904 CG nucleotides per 10,000 bases in the quartile of the genome with the highest disequilibrium). However, an interesting pattern emerged when we examined the distribution of genes and related features in different sections of the genome. We found there were significantly more genes (about 10% more) in the quartiles of the genome with the highest and lowest LD than in the two quartiles with intermediate levels of linkage disequilibrium. Specifically, we found ∼6.7 genes per Mb in the two extreme quartiles and only ∼6.1 genes per Mb in the two middle quartiles. In a similar fashion, we found more coding bases, exonic bases, and intronic bases in the two extreme quartiles than in the two middle quartiles. This result is interesting because it suggests that whereas for some genes it might be advantageous to locate in regions of strong linkage disequilibrium where fewer allelic combinations exist, for other genes, the greater sequence and haplotype diversity present in regions of low disequilibrium might be favored.

When we examined the proportion of bases in large duplicated regions or near telomeres, centromeres, and heterochromatin, our results were again as predicted from the observed correlations (Table 4). For example, we found that regions within 15 Mb of telomeres accounted for 24% of bases (2407 of every 10,000 bases) in the quartile of the genome with the lowest disequilibrium, but only 4% of bases (430 of every 10,000 bases) in the quartile with high disequilibrium. In contrast, bases in genomic duplications or surrounding centromeres and heterochromatin were enriched in the fraction of the genome exhibiting high levels of linkage disequilibrium.

Table 4.

Chromosomal organization and quartiles of the genome, defined according to extent of linkage disequilibrium

	Genome covered by HapMap		Genome quartiles, defined using LD
Chromosome organization	Mean	(±S.E.)	(Low LD) Q1	Q2	Q3	(High LD) Q4	Trend
Within 5 Mb of centromere	555.4	(±9.7)	311.7	355.5	480.5	1074.0	Increases with LD
Within 10 Mb of centromere	1227.0	(±13.9)	973.7	993.8	1138.3	1802.1	Increases with LD
Within 15 Mb of centromere	1919.1	(±16.7)	1670.1	1699.7	1850.0	2456.8	Increases with LD
Within 5 Mb of telomere	392.5	(±8.2)	861.8	367.9	232.4	108.1	Decreases with LD
Within 10 Mb of telomere	806.7	(±11.5)	1721.1	797.5	487.8	220.4	Decreases with LD
Within 15 Mb of telomere	1220.6	(±13.9)	2407.8	1247.8	796.3	430.2	Decreases with LD
Within 5 Mb of heterochromatin	323.2	(±7.5)	180.6	229.2	282.8	600.2	Increases with LD
Within 10 Mb of heterochromatin	760.3	(±11.2)	553.6	644.7	717.3	1125.7	Increases with LD
Within 15 Mb of heterochromatin	1205.7	(±13.8)	1013.4	1167.0	1168.0	1474.3	Increases with LD
Large genomic duplications	365.9	(±6.4)	237.3	283.6	415.1	527.5	Increases with LD
Large genomic duplications (cis)	265.5	(±5.5)	153.5	191.4	307.9	409.1	Increases with LD
Large genomic duplications (trans)	159.8	(±3.9)	118.7	136.2	182.2	201.9	Increases with LD

Open in a new tab

Proportion of bases in each category (per 10,000 bases) is presented for each genomic quartile.

Gene categorization in regions of high and low linkage disequilibrium

In order to examine the differences between genes in regions of high and low linkage disequilibrium, we used curated gene annotations from the Gene Ontology database (Ashburner et al. 2000), excluding annotations that were inferred from electronic annotation only, as these are considered less reliable (Harris et al. 2004). We then classified each gene, depending on whether it overlapped with the quartile of the genome with high disequilibrium or whether it overlapped with the quartile of the genome with lowest disequilibrium. Genes that overlapped neither quartile, that overlapped both of the extreme quartiles, or that mapped to a region of the genome where insufficient data was available were left unclassified. The results are summarized in Table 5 for a subset of gene ontology categories.

Table 5.

Distribution of genes across regions of high and low linkage disequilibrium

		Assigned to region of
Gene function (GO Term)	Annotated genes	Low LD	High LD	High-Low Ratio	χ²	P-value
Amine metabolism	167	51	45	0.88	0.14	—
Biological process unknown	648	165	190	1.15	10.45	—
Biosynthesis	447	130	129	0.99	2.43	—
Carbohydrate metabolism	212	74	70	0.95	0.76	—
Catabolism	357	112	90	0.80	0.02	—
Cell adhesion	335	110	78	0.71	0.93	—
Cell cycle	493	119	177	1.49	26.24	<.00001
Cell differentiation	182	70	38	0.54	4.19	.04
Cell motility	180	69	44	0.64	1.67	—
Cell organization and biogenesis	545	138	178	1.29	16.43	.00005
Cell proliferation	876	254	267	1.05	8.25	.004
Cell surface receptor linked signal transduction	670	256	149	0.58	10.99	.0009
Cell-cell signaling	474	181	93	0.51	13.50	.0002
Cellular lipid metabolism	253	87	60	0.69	1.03	—
DNA metabolism	366	74	139	1.88	35.37	<.00001
Immune response	622	232	94	0.41	34.36	<.00001
Includes: humoral immune response	154	54	19	0.35	10.60	.001
Includes: inflammatory response	161	66	18	0.27	18.84	.00001
Intracellular signaling cascade	604	212	150	0.71	1.84	—
Intracellular transport	263	56	95	1.70	19.61	<.00001
Ion transport	213	81	42	0.52	5.84	.02
Lipid metabolism	351	121	87	0.72	0.84	—
Neurogenesis	366	132	67	0.51	10.30	.001
Neurophysiological process	384	149	78	0.52	10.35	.001
Includes: sensory perception	191	82	41	0.50	6.75	.009
Organelle organization and biogenesis	444	107	152	1.42	19.65	<.00001
Organic acid metabolism	226	70	55	0.79	0.05	—
Organogenesis	805	294	162	0.55	16.49	.00005
Phosphorus metabolism	368	99	120	1.21	8.51	.004
Programmed cell death	350	111	85	0.77	0.21	—
Protein localization	174	39	60	1.54	9.76	.002
Protein metabolism	1193	318	375	1.18	23.33	<.00001
Protein transport	159	38	55	1.45	7.53	.006
Reproduction	171	44	43	0.98	0.69	—
Response to stimulus	1346	472	290	0.61	14.78	.0001
Includes: response to DNA damage	154	35	54	1.54	8.85	.003
Includes: response to external biotic stimulus	431	158	56	0.35	30.62	<.00001
Includes: response to external stimulus	825	303	154	0.51	23.53	<.00001
Includes: response to pest, pathogen or parasite	415	154	53	0.34	31.42	<.00001
RNA metabolism	208	41	71	1.73	15.33	.00009
Vesicle-mediated transport	203	61	64	1.05	1.95	—
All SWISS-PROT Entries Examined	7520	2305	2045	0.89	—	—

Open in a new tab

For most functional categories, genes are approximately equally distributed between the regions showing high and low linkage disequilibrium. However, a few categories show a skew that is quite different from the overall observed ratio of ∼0.89: 1.00 (last row in Table 5). For example, genes associated with immune response (including both genes involved in humoral and inflammatory immune responses, as well as genes involved in response to pathogens and parasites), neurogenesis, and neurophysiological processes (including sensory perception) are often located in regions of low linkage disequilibrium. In contrast, genes associated with response to DNA damage, the cell cycle, or DNA and RNA metabolism appear to be more often located in regions of strong linkage disequilibrium. It is tempting to speculate that immune response genes and other genes in regions of low linkage disequilibrium might represent genes for which great allelic diversity is advantageous to the species and individuals, whereas DNA repair genes and other genes in regions of strong linkage disequilibrium are genes that represent conserved biological processes where recombination and mutation are likely to result in deleterious haplotypes that are removed from the population by natural selection.

Genes in the same functional category are often clustered along the genome, and this clustering could contribute to an observed skew of particular gene categories in regions of high and low linkage disequilibrium. To investigate this possibility, we flipped gene positions along each chromosome—a process that preserves the original clustering but should destroy much of the association between genes and regions of high and low disequilibrium. We then repeated our analysis for this flipped data set. In the flipped data set, we observed no gene categories with a significant skew at P < 0.001 compared with 18 skewed categories in the original data. Thus, it appears that the preferential localization of categories in regions of high and low disequilibrium is not simply a result of chance clustering.

Hotspots for the breakdown of linkage disequilibrium

The analyses in the previous sections examine variation in linkage disequilibrium at a very broad scale (100,000s to 1,000,000s of base pairs). In order to better characterize fine-scale variation in linkage disequilibrium, we identified hotspots for the breakdown of linkage disequilibrium (Jeffreys et al. 2001; McVean et al. 2004). Initially, we defined hotspots as segments of <10 kb where r² between any two flanking markers did not exceed 0.10. In each sample, the maximum spanning r² for the intervals we evaluated was >0.70 on average, and our threshold of 0.10 selected 2%–3% of all intervals. Inspection of the results revealed that this definition favored regions with slightly lower marker density and greater distance between markers. Thus, we refined our definition to (1) select all intervals defined by pairs of consecutive markers separated by <10 kb; (2) for each interval, identify the flanking pair of markers and select five equally spaced markers covering 40 kb on each side of the interval (for a total of 12 markers); (3) calculate the maximum spanning r² across the interval, using the two consecutive markers and the five flanking markers on either side (that is, by examining 36 pairings of markers); (4) organize intervals into 100-bp bins according to the distance between flanking markers and, in each bin, label the 2% of intervals with the smallest spanning r² as regions of rapid breakdown of disequilibrium. The distribution of the resulting hotspots is summarized in the bottom panels of Figures 2 (CEU), 3 (YRI), and 4 (CHB+JPT). Again, we observe great variation in the distribution of these hotspots across every chromosome, but good consistency across samples. Each chromosome includes both regions that are densely covered in hotspots and regions of several megabases without any such hotspots.

In total, we identified 14,524 such hotspots covering 44,760,378 bp in the CEU sample (2.0% of examined intervals, 2.0% of examined bases), 15,622 hotspots covering 47,246,212 bp in the YRI sample (2.0% of intervals, 2.0% of bases), and 12,606 hotspots covering 40,420,681 bp in the CHB+JPT sample (2.0% of intervals, 2.0% of bases). Overall, the maximum spanning r² for these intervals was 0.065, 0.060, and 0.061 on average, for the CEU, YRI, and CHB+JPT samples, respectively. However, the thresholds used to define an interval varied slightly between populations and by interval size. For example, in the CEU sample, intervals of 900–1000 bp were classified as hotspots if the maximum spanning r² was <0.15, but a stricter threshold requiring the maximum spanning r² <0.07 was applied for intervals of 9900–10,000 bp. Regions classified as hotspots in one population typically exhibited rapid decay of linkage disequilibrium in the other populations too. For example, in the CEU samples, the average maximum spanning r² was 0.77 for all 716,624 intervals we examined, but only 0.30 for regions that were identified as hotspots in the YRI samples and 0.20 for regions that were identified as hotspots in the CHB+JPT samples. Among the 44,760,378 bp classified as being in hotspots in the CEU sample, 10,736,096 bp (24%) were also classified as hotspots in the YRI sample and 15,128,014 (34%) were also classified as hotspots in the CHB+JPT sample. Hotspots that overlapped between populations did not appear to be “hotter” than those that did not overlap—that is, they did not exhibit significantly lower values for the maximum spanning r² statistic.

Other strategies have been proposed to identify hotspots for the breakdown of linkage disequilibrium (e.g., Li and Stephens 2003; McVean et al. 2004). One of these definitions (McVean et al. 2004) has recently been used to construct a recombination rate map of the whole genome (submitted to Nature by the International HapMap Consortium). We compared recombination rates in hotspots identified through our model and in the remainder of the genomic sequence using the recombination rate estimates of McVean and colleagues for the 10 HapMap ENCODE regions (Supplemental Table 1). The average recombination rate was 16.4 * 10^–8 per base pair per generation for the CEU hotspots, 18.8 * 10^–8 for the CHB+JPT hotspots, and 9.6 * 10^–8 for the YRI hotspots. For the remainder of the ENCODE sequence, recombination rates were estimated at 1.03 * 10^–8 (CEU), 0.92 * 10^–8 (CHB+JPT), and 0.93 * 10^–8 (YRI). Thus, we expect that the 2% of the sequence we classified as hotspots for the breakdown of linkage disequilibrium accounts for ∼17%–29% of recombination events (Supplemental Table 1).

Sequence features of recombination hotspots

We compared the sequence composition of potential recombination hotspots with the sequence composition of other genomic intervals for which we calculated the maximum spanning r². Our results are summarized in Tables 6 and 7. Note that because the HapMap project preferentially targeted genes and coding polymorphisms, the average sequence composition in Tables 6 and 7 is slightly different from that in Tables 3 and 4. For example, the intervals we evaluated when searching for hotspots are enriched for genes and surrounding features (with about 130 coding bases per 10,000, see Table 6) compared with our analysis of all 100-kb sliding windows covered by the HapMap (which have about 115 coding bases per 10,000). This difference occurs because the average is calculated on a per-interval basis, giving greater weight to regions with slightly higher marker density and therefore more intervals defined by consecutive markers.

Table 6.

Sequence composition in hotspots for the rapid breakdown of linkage disequilibrium and other intervals

	CEU sample		YRI sample		CHB+JPT sample
	Hotspots	Other intervals	Hotspots	Other intervals	Hotspots	Other intervals
Number of intervals	14,525	702,099	15,623	750,857	12,607	610,826
Basic sequence features
GC content	4379	4056^**	4404	4052^**	4395	4067^**
CpG islands	72	58	68	56	78	60^*
Polymorphism (π)	13.49	12.33^**	13.68	12.15^**	13.85	12.49^**
Genes and related features
Genic bases (exon, intron, UTR)	3608	3862^**	3543	3835^**	3787	3916
Coding bases	135	131	126	128	143	141
Exonic bases	273	248	255	240	295	261
Intronic bases	3385	3663^**	3341	3643^**	3556	3707^*
UTR (3′ and 5′)	138	117	129	112	152	120^*
Other features
Bases in transcription factor binding sites	124	114^**	122	113^*	128	115^**
Bases in transcribed fragments^a	292	280	296	269	290	289
Predictions of conserved elements (phastCons)	579	532^**	560	528^*	594	537^**
Identical base in alignment with M. musculus	3112	2889^**	3141	2908^**	3050	2874^**
Identical base in alignment with R. norvegicus	2999	2803^**	3036	2823^**	2957	2787^**
Conserved noncoding sequence	183	157^**	180	157^**	193	157^**
Repeat content
Total bases in repeats	3717	4113^**	3732	4142^**	3667	4086^**
Bases in LINE repeats	1237	1716^**	1249	1741^**	1224	1703^**
Bases in SINE repeats	1295	1161^**	1281	1160^**	1277	1155^**
Bases in LTR repeats	741	774	744	783	722	771^*
Bases in DNA repeats	287	303	294	304	289	302
Bases in simple repeats	93	79^**	93	78^**	92	80^*
Bases in low complexity repeats	57	56	56	56	56	56
Bases in satellite repeats	4	14^**	7	10	2	12^**
Bases in other repeats	3	7^**	5	7	3	7^**

Open in a new tab

Only applies to chromosomes 6, 7, 13, 14, 18, 19, 20, 21, 22, and X.

Hotspots and other intervals differ significantly at P < 0.001 level.

^**

Hotspots and other intervals differ significantly at P < 0.000001 level.

Average sequence composition (per 10,000 bases) is presented for hotspots and control intervals.

Table 7.

Relationship between hotspots for the rapid breakdown of linkage disequilibrium and chromosomal organization

	CEU sample		YRI sample		CHB+JPT sample
	Hotspots	Other intervals	Hotspots	Other intervals	Hotspots	Other intervals
Number of intervals	14,525	702,099	15,623	750,857	12,607	610,826
Chromosome organization
Within 5 Mb of centromere	325	471^**	324	460^**	282	464^**
Within 10 Mb of centromere	965	1124^**	942	1127^**	933	1115^**
Within 15 Mb of centromere	1715	1804	1647	1816^**	1685	1798^*
Within 5 Mb of telomere	795	352^**	879	336^**	766	347^**
Within 10 Mb of telomere	1642	773^**	1793	746^**	1635	765^**
Within 15 Mb of telomere	2219	1179^**	2425	1138^**	2273	1170^**
Within 5 Mb of heterochromatin	195	271^**	202	273^**	182	269^**
Within 10 Mb of heterochromatin	553	694^**	575	700^**	558	700^**
Within 15 Mb of heterochromatin	1057	1153^*	1041	1159^*	1077	1160
Large genomic duplications	85	137^**	107	133^*	78	129^**
Large genomic duplications (cis)	41	81^**	53	78^*	43	75^**
Large genomic duplications (trans)	47	67^*	62	65	40	62^*

Open in a new tab

Hotspots and other intervals differ significantly at P < 0.001 level.

^**

Hotspots and other intervals differ significantly at P < 0.000001 level.

Overall, we again observe a strong enrichment for GC nucleotides (which constitute about 44% of hotspot sequences, but only 40% of other intervals) and an increase in the rate of sequence polymorphism within these intervals. Interestingly, although the overall proportion of genic sequences appeared to decrease in hotspots, we did not see a similar decrease in the proportion of exons and coding bases (in fact, the proportion of coding bases and other bases in exons did not differ significantly between hotspots and other intervals). In agreement with results we observed for windows of the genome showing lower linkage disequilibrium, hotspots were enriched for transcription factor binding sites and sequences conserved across species, as well as Alu repeats and simple repeats, but had fewer bases in repeats overall and fewer bases in LINE repeats.

Multivariate analysis

The genomic sequence features examined here correlate not only with linkage disequilibrium, but also with each other. For example, genes and coding sequences are typically concentrated in GC-rich regions of the genome. In order to build a parsimonious model for the relationship between linkage disequilibrium and genomic sequence features, we used the forward-selection model building approach. First, we used quantile normalization to transform observed linkage disequilibrium values and the number of bases associated with each feature within a particular genomic window into a normally distributed z-score. Quantile normalization converts the percentile rank of a particular observation into a normally distributed variable and can be used to convert a wide range of continuous distributions to normality.

All of the sequence features listed in Tables 1 and 2 were considered as candidates for inclusion in a model predicting the relative degree of linkage disequilibrium within each window of the genome. Analyses were initially carried out in each population and gave similar results. The results summarized in Table 8 refer to linkage disequilibrium values averaged across populations. For all of the window sizes examined, polymorphism, GC content, and the total number of bases within repeats were the features most strongly associated with local linkage disequilibrium levels. Whereas increasing sequence polymorphism and GC content were associated with decreased linkage disequilibrium, the total number of bases in repeats was associated with increased linkage disequilibrium. Similar results were observed for untransformed data (Supplemental Table 2), but the proportion of variance explained was slightly lower—since the data are noisier due to the presence of outliers both in the distribution of linkage disequilibrium values and in the distribution of sequence features across each window.

Table 8.

Results of model fitting to describe decay of linkage disequilibrium

Round of selection	Feature added to model	Variance explained	Fitted model
		Models for extent of linkage disequilibrium within 100-kb windows
1	Polymorphism (π)	0.140	E(z_LD) = -0.38 z_π
2	GC	0.240	E(z_LD) = -0.36 z_π - 0.32 z_GC
3	Total repeats	0.316	E(z_LD) = -0.38 z_π - 0.29 z_GC + 0.28 z_{Total repeats}
4	Known gene codons	0.349	E(z_LD) = -0.34 z_π - 0.39 z_GC + 0.30 z_{Total repeats} + 0.24 z_codons
5	Centromere (5 Mb)	0.364	E(z_LD) = -0.34 z_π - 0.39 z_GC + 0.29 z_{Total repeats} + 0.24 z_codons + 0.27 z_{centromere(5 Mb)}
		Models for extent of linkage disequilibrium within 500-kb windows
1	Polymorphism (π)	0.174	E(z_LD) = -0.42 z_π
2	Total repeats	0.327	E(z_LD) = -0.44 z_π + 0.39 z_{Total repeats}
3	GC	0.413	E(z_LD) = -0.45 z_π + 0.35 z_{Total repeats} - 0.30 z_GC
4	Known gene codons	0.442	E(z_LD) = -0.42 z_π + 0.34 z_{Total repeats} - 0.45 z_GC + 0.24 z_codons
5	Centromere (5 Mb)	0.462	E(z_LD) = -0.41 z_π + 0.32 z_{Total repeats} - 0.46 z_GC + 0.25 z_codons + 0.30 z_{centromere(5 Mb)}
		Models for extent of linkage disequilibrium within 1000-kb windows
1	Polymorphism (π)	0.168	E(z_LD) = -0.42 z_π
2	Total repeats	0.326	E(z_LD) = -0.44 z_π + 0.40 z_{Total repeats}
3	GC	0.433	E(z_LD) = -0.47 z_π + 0.36 z_{Total repeats} - 0.33 z_GC
4	Known gene codons	0.457	E(z_LD) = -0.44 z_π + 0.34 z_{Total repeats} - 0.49 z_GC + 0.23 z_codons
5	Centromere (5 Mb)	0.482	E(z_LD) = -0.43 z_π + 0.32 z_{Total repeats} - 0.50 z_GC + 0.25 z_codons + 0.33 z_{centromere(5 Mb)}

Open in a new tab

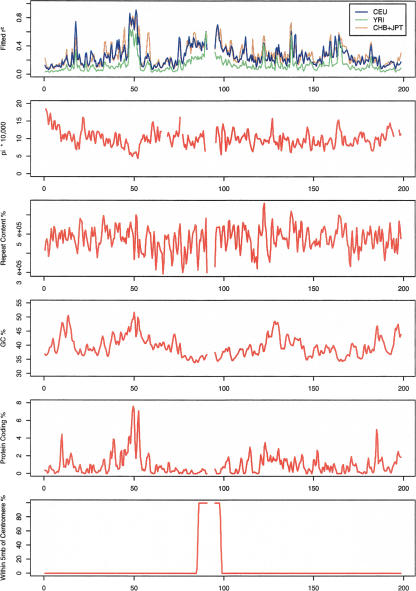
Interestingly, when these three features were included in the model, the proportion of protein-coding base pairs was the next most significant predictor of linkage disequilibrium and was associated with increased disequilibrium. Proximity to the centromeres was the final variable selected for inclusion in our models. When the models were further refined to include six or more variables, no single variable could explain more than 1.5% of the remaining variance in disequilibrium values (whatever the window size). In Figure 5, variation in linkage disequilibrium along chromosome 3 is compared with variation in the five selected features (polymorphism, GC content, repeat content, proportion of coding bases, and proximity to the centromeres). Note, for example, that the region at ∼50 Mb that exhibits strong disequilibrium in all populations also shows much reduced polymorphism (∼6 × 10^–4 vs. ∼6 × 10^–4 for the genome covered by HapMap), very high GC content (∼50% vs. ∼40%), and a high proportion of genic transcripts (∼7% vs. ∼1.2%).

Figure 5. — Variation of fitted linkage disequilibrium values (for markers separated by 30,000 bp) across the three groups of samples and of selected sequence features including sequence polymorphism, total repeat content, GC content, proportion of coding bases, and proximity to the centromeres. Results refer to 1000-kb windows across chromosome 3.

When we repeated our analysis, excluding regions on the X chromosome from consideration, results did not change substantially and the same set of five features was selected for all window sizes (data not shown). When we excluded total repeat content from the model fitting procedure, the proportion of bases in LINEs and in simple repeats as well as the proportion of identical bases in the alignment with the Mus musculus genome were selected into the model instead. Whereas the proportion of bases in LINE elements was associated with increased disequilibrium, simple repeats and sequences conserved in the comparison with the M. musculus genome were associated with reduced disequilibrium in this alternative model.

Discussion

Across different populations we observe substantial agreement in regions classified as having high or low linkage disequilibrium. We were intrigued by the possibility that regional similarities in linkage disequilibrium values across populations resulted not only from a shared history between populations, but also because phenomena that modulate linkage disequilibrium (such as recombination and mutation rates and natural selection) could be influenced by local sequence features. Here, we provide a summary of the observed relationship between linkage disequilibrium and local sequence features.

At a very broad scale, we find that whereas centromeres are associated with increased disequilibrium, telomeric regions of chromosomes typically show little disequilibrium. In addition, we observed more disequilibrium in the larger chromosomes than in smaller chromosomes. These observations are compatible with current recombination rate maps of the genome (Yu et al. 2001; Kong et al. 2002). Large genomic duplications are associated with higher linkage disequilibrium. Since recombination events between duplicated regions are associated with human disease (Lupski 1998), the deleterious effects of these events could favor low recombination rates for these regions, accounting for the high observed levels of linkage disequilibrium.

At a finer scale, we found that GC content and sequence polymorphism were both strongly associated with the degree of linkage disequilibrium. We observed this correlation both when we divided the genome into windows of 100–1000 kb and also when we compared sequence characteristics of “hotspots” for the breakdown of linkage disequilibrium and other genomic regions. GC content has previously been associated with recombination rate and linkage disequilibrium (Eisenbarth et al. 2000; Yu et al. 2001), and the association could occur either because GC-rich sequences are more prone to recombination or because recombination leads to mutation from A/T to G/C base pairings more often than to mutations in the opposite direction (Huang et al. 2005). The association between sequence polymorphism and linkage disequilibrium could occur because recombination events are mutagenic, because regions of lower linkage disequilibrium are likely to descend from a more distant ancestor so that they have undergone more rounds of both mutation and recombination, or even because some regions of strong disequilibrium result from selective sweeps and show limited diversity (Hudson 1990; Nachman et al. 1998). A correlation between recombination rates and nucleotide diversity has also been reported in Drosophila (Begun and Aquadro 1992).

We observed that repeat content is strongly associated with increasing levels of linkage disequilibrium. Interestingly, the direction and strength of association was not uniform for different repeat types. Whereas LINE elements were associated with increased levels of disequilibrium, SINE elements (mainly Alus) were associated with decreased levels of disequilibrium. One possibility for the low levels of disequilibrium associated with SINEs is that these elements contain sequences that promote recombination, a possibility that is compatible with the observation of a relatively high rate of recombination events between SINE elements in the genome (Prak and Kazazian Jr. 2000; Deininger and Batzer 2002). The mechanism through which LINEs are associated with increased disequilibrium is less clear—one possibility is that they might displace functional sequences that are typically associated with increased recombination and another possibility is that, when in a polymorphic state, LINE insertions actually inhibit recombination.

Intriguingly, we found that over short distances (genomic windows of 100 kb), genes were associated with slightly increased levels of linkage disequilibrium, but over longer distances (500- or 1000-kb windows), they were associated with decreased levels of linkage disequilibrium. The Hill-Robertson effect (Hill and Robertson 1966), which postulates that increased recombination between genes is advantageous because it allows natural selection to focus on individual alleles, provides an attractive explanation for this discrepancy. In this manner, when natural selection increases linkage disequilibrium around a particular allele, the increased disequilibrium will be rapidly eroded by the high-recombination rates surrounding genes and will not extend far.

We compared the proportion of genes in different quartiles of the genome defined according to the degree of linkage disequilibrium they exhibit. Our results show that both the genomic quartile with the strongest linkage disequilibrium and the genomic quartile with the weakest linkage disequilibrium have a greater density of genes and coding bases than the rest of the genome. Comparison of linkage disequilibrium data with functional annotation from the Gene Ontology database (Ashburner et al. 2000), showed that whereas some types of genes (including those involved in immune response and sensory perception) are preferentially located in regions of weak linkage disequilibrium, other types of genes (including those involved in DNA and RNA metabolism, response to DNA damage, and in the cell cycle) are more often located in regions of weak linkage disequilibrium.

We speculate that it is advantageous for some genes to be located in regions of weak linkage disequilibrium, where greater allelic diversity exists (possibly generated through increased recombination and/or mutation rates). Immune system genes naturally fall into this category, since greater diversity reduces the chance that a single pathogen might sweep through the population (Little and Parham 1999; Trachtenberg et al. 2003). For other genes, especially those involved in fundamental biological processes that evolve very slowly, such as DNA repair (Modrich and Lahue 1996) or DNA packaging (Pehrson and Fuji 1998), allelic diversity could even be a disadvantage, since it might disrupt finely tuned processes. This observation suggests an evolutionary justification for the diversity in the extent of linkage disequilibrium in the genome—it is possible that the genome is organized to allow greater diversity in some genes and greater conservation in others depending on gene function, so as to provide the greatest possible advantage to the organism.

The scale of the data generated by the International HapMap Project leads us to select computationally efficient analysis methods that could be efficiently applied on a genome-wide scale. Coalescent-based approaches for estimating local recombination rates (Hudson 2001) and identifying recombination hotspots (Li and Stephens 2003; McVean et al. 2004) provide interesting, but more computationally intensive alternatives. Using the ENCODE data generated by the HapMap project, we compared recombination rate estimates (McVean et al. 2004) in regions we identified as “hotspots” for the decay of disequilibrium with estimates for the rest of the genome. The “hotspots” we identified exhibited recombination rates that were 10–20× higher than background levels. Overall, we expect that our results and conclusions reflect biological underpinnings and will be replicated using different analytical strategies.

Methods

Data set

All of our analyses are based on release 16c (June 2005) of the genotype data generated by the International HapMap Consortium (2003). Genotypes for all 22 autosomes and the X chromosome were downloaded from the HapMap Project Web site (http://hapmap.cshl.org/). We downloaded the nonredundant QC-filtered genotype set, which included genotypes for 1,105,003 markers in 30 CEPH trios from Utah (CEU sample, 120 independent founder chromosomes), 1,076,387 markers in 30 Yoruba trios from Ibadan, Nigeria (YRI sample, 120 independent founder chromosomes), and 1,087,321 markers in 45 unrelated Chinese individuals from Beijing and 44 unrelated Japanese individuals from Tokyo (CHB+JPT sample, 178 independent founder chromosomes).

Calculation of marker allele frequencies

Marker allele frequencies were estimated by maximum likelihood using a rapid implementation of the E-M algorithm that accommodates both family data and unrelated individuals (Abecasis and Wigginton 2005). The algorithm accommodates X chromosome data appropriately by modeling males as hemizygous. Within each sample, only markers with estimated minor allele frequencies ≥5% were retained for subsequent analyses, resulting in a total of 774,921 markers analyzed in the CEU sample, 814,615 markers analyzed in the YRI sample, and 702,895 markers analyzed in the CHB+JPT sample.

Calculation of pairwise disequilibrium coefficients

Haplotype frequencies for all pairs of SNPs separated by <1,000,000 bp were estimated by maximum likelihood using the same rapid implementation of the E-M algorithm for family data (Abecasis and Wigginton 2005). As usual, pairwise disequilibrium was summarized using the r² measure, which was calculated using estimated haplotype frequencies. In total, we calculated pairwise disequilibrium coefficients for 229,624,668 marker pairs in the CEU sample, 253,755,566 marker pairs in the YRI sample, and 191,677,546 marker pairs in the CHB+JPT sample.

Sliding window analyses of linkage disequilibrium

Within each population, we carried out sliding window analyses of the decay of linkage disequilibrium. These analyses were repeated with three different sliding window sizes (100,000, 500,000, and 1,000,000 bp). For each window size, we divided the genome into overlapping windows (50% overlap between consecutive windows) and estimated a curve describing the decay of r² within each window of the form E(r²_ij) = 1/(1 + R_ij) (Ohta and Kimura 1969). Within each window, we assumed that the population recombination rate R_ij between any two SNPs i and j, which is a function of the effective population size and the recombination rate between SNPs, was proportional to the base-pair distance d_ij between the pair of SNPs. Specifically, we used a least-squares approach to estimate a single parameter corresponding to the per base-pair population recombination rate (4Nρ) and defined R_ij =4Nρ * d_ij. In this simple model, the effective population size, N, and per base-pair recombination rate, ρ, are not estimated separately, but rather, their product is estimated as a single parameter.

Identification of hotspots for the breakdown of linkage disequilibrium

Recombination events can cluster within precisely localized recombination hotspots (Jeffreys et al. 2001), and regions of rapid breakdown of linkage disequilibrium can be used to localize these hotspots without direct measurement of recombination rates (McVean et al. 2004). To identify regions of rapid breakdown of linkage disequilibrium, we systematically evaluated intervals defined by pairs of consecutive markers separated by <10,000 bp. For each interval, we considered the two flanking and five equally spaced flanking markers spanning 40 kb on either side of the interval (for a total of 12 markers) and calculated the maximum spanning r² coefficient by considering all 36 pairings of flanking markers. Intervals without six genotyped markers within the flanking 40 kb on either side were deemed to be inadequately covered and were excluded from this analysis. Intervals were grouped in 100-bp bins with other intervals of similar size (e.g., intervals of 9900–10,000 in one bin, intervals of 9800–9900 bp in another bin, etc.). Intervals that were adequately covered were classified as regions of rapid breakdown of linkage disequilibrium, and therefore, potential recombination hotspots whenever the maximum spanning r² statistic was in the bottom 2% of statistics for that bin.

Comparison with fine-scale recombination rate estimates

Fine-scale recombination rate estimates for the ENCODE regions were calculated by Gil McVean and Colin Freeman (Oxford University) using the reversible-jump Markov chain Monte Carlo method (McVean et al. 2004). Brief details of their analysis follow. The MCMC approach explores the posterior distribution of fine-scale recombination rate profiles, sampling the distribution of both the number and location of change-points in fine-scale recombination rates, and is implemented in the package LDhat. A block-penalty of 5 was used (calibrated by simulation and comparison to data from sperm-typing studies). Each region was analyzed as a single run with 10,000,000 iterations, sampling every 5000^th iteration and discarding the first third of all samples as burn-in. Estimates were generated separately from each of the four ENCODE resequencing populations and then combined to give a single figure. Differences between populations did not appear to be significant.

Analysis of sequence features

For the genomic features, binned counts were made from tracks available in the UCSC Genome Browser or from tables in the UCSC Table Browser (Kent et al. 2002; Karolchik et al. 2004), or were based directly on the reference sequence for the July 2003 human assembly (NCBI Build 34, UCSC hg16). Bins were defined along the full length of each chromosome including gaps with widths of 100, 500, or 1000 kb and overlap of 50% between consecutive bins. The featureBits program (publicly available in the UCSC source tree) was used to uniquely count each position in the bin that is covered in the given track/table; positions that are covered by multiple elements were counted only once.

The locations of genes, exons, introns, and UTRs were obtained from the knownGenes table at the UCSC Table Browser (http://genome.ucsc.edu/cgi-bin/hgTables). When there was evidence for alternative splicing, we used a broad definition for exons and other genic features. For example, a base was considered protein coding if it was covered by a coding-sequence (CDS) exon for at least one transcript. The gene counts were derived from a featureBits reduction of this same table; the strict counts are the sum of the fraction of each gene that is found in the bin, while the loose gene counts are the number of partial or total gene overlaps for each gene in the bin. Assignments of individual bases to repeats are from featureBits reductions of the rmsk table (originally generated using the RepeatMasker program, http://www.repeatmasker.org) either whole or subsets by the repClass field. Similarly, gaps with and without additional padding are from the gap table and filtered by type. CpG islands were retrieved from the cpgIsland table, transcription factor binding sites are from the tfbsCons table, transcribed fragments are from the affyTransfrags table, genomic duplications are from the genomicSuperDups table, and conserved elements are from the phastConsElements table in the hg17 assembly and lifted to hg16 before featureBits reduction (Siepel et al. 2005). The conserved noncoding sequences (cns table) are a subset of phastCons elements with known coding sequences removed (in this case, all coding sequences from NCBI refSeq genes, UCSC knownGenes, and ENSEMBL genes). GC content was calculated with the hgGc-Percent program on the hg16 assembly. Identity with other species is the number of nucleotides that align identically between the human and mouse (mm3) or rat (rn3) genomes in a multiz alignment (Blanchette et al. 2004).

Estimates of sequence polymorphism

Estimates of sequence polymorphism, or the per base-pair nucleotide diversity, were calculated using a previously described algorithm (Sachidanandam et al. 2001) by Jim Mullikin (NHGRI) for 5-kb windows throughout the genome. The algorithm (Sachidanandam et al. 2001) aligns publicly available sequence traces to the human genome sequence and uses the proportion of heterozygous bases in regions of high-quality sequence to estimate sequence polymorphism. The quantity π represents the likelihood that a single nucleotide will be heterozygous when compared between two randomly sampled chromosomes. This quantity is generally small, and for ease of comparison, in all instances where π is tabulated, we have multiplied it by 10,000.

Comparison of linkage disequilibrium and sequence features within sliding windows

We correlated linkage disequilibrium, sequence polymorphism, number of genes, and the number of bases assigned to each genomic feature in two ways. First, we calculated the Spearman rank correlation coefficient between linkage disequilibrium and each of the other characters. Second, we sorted all bins according to the estimated degree of linkage disequilibrium within the bin and separated bins into four quartiles (0%–25% of all bins according to estimated disequilibrium, 25%–50% of all bins, etc.). Then, we calculated the summary distribution of each feature for each group of bins.

Comparison of linkage disequilibrium and sequence features within hotspots

To compare the sequence composition of intervals identified as regions where linkage disequilibrium broke down rapidly with the sequence of other genomic intervals we evaluated, we first “standardized” summary descriptions for all intervals to obtain the proportion of bases in the interval assigned to each feature. We then used a simple t-test (with unequal variances) to compare the average sequence composition of hotspots and other intervals. For ease of presentation, the proportion of bases assigned to each feature was multiplied by 10,000 for presentation in Tables 5 and 6.

Analysis of gene ontology data

To examine the relationship between gene categories and linkage disequilibrium, classification terms at a depth of four levels from the origin of the “Biological Function” hierarchy were selected from the Gene Ontology (GO) controlled vocabulary (Ashburner et al. 2000; Harris et al. 2004). From each term, all matching genes in the GO database (seqdblite, June 2005 release) were selected. The seqdblite database includes all GO assignments except those that are based only on “inferred from electronic annotation”, which is less reliable (Harris et al. 2004). The SWISSPROT IDs assigned to each gene were matched to UCSC known genes, and the transcription start and stop position were determined against the July 2003 human genome assembly (NCBI build 34; UCSC hg16).

After averaging fitted disequilibrium coefficients across populations, windows in the genome were organized into four quartiles as follows: a quartile with the 25% highest disequilibrium coefficients, a quartile with the 25% smallest disequilibrium coefficients, and two intermediate quartiles. Genes were classified as being in a region of strong disequilibrium if they overlapped a window in the top quartile of the genome. Genes were classified as being in a region of weak disequilibrium if they overlapped a window in the bottom quartile of the genome. Genes were left unclassified if they did not overlap a window in the two extreme quartiles or if they overlapped windows in both quartiles.

Multivariate analysis

In order to build a parsimonious model for the relationship between linkage disequilibrium and genomic sequence features, we used the forward-selection model building approach. First, we used quantile normalization to transform observed linkage disequilibrium values and the number of bases associated with each feature within a particular genomic window into a normally distributed z-score. Specifically, we calculated a rank for each observed statistic and then replaced the statistic with the value Φ^–1 (rank/no. of windows), where Φ^–1 denotes the inverse of the standard normal distribution. Quantile normalization ensures that our analysis is robust to outliers and should not induce any artificial (i.e., nonbiological) correlations.

For model selection, we first evaluated all regression models with the extent of linkage disequilibrium as the dependent variable, including a single predictor as an independent variable. We then selected the predictor that resulted in the best model fit (smallest residual sum-of-squares) into the model. In a second round, we evaluated all models, including the predictor selected in the first round and one additional predictor. In the third round, we evaluated models with three predictors, including the two predictors from the second round, and so on.

Acknowledgments

We thank the International Hapmap Consortium for making a rich, high-quality data set publicly available, Jim Mullikin (NHGRI) for providing estimates of sequence polymorphism throughout the genome, and Gil McVean and Colin Freeman (University of Oxford) for providing fine-scale recombination rate maps of the encode regions, and Jim Kent and the rest of the UCSC Genome Browser staff for analysis tools and database support. We also thank many members of the HapMap analysis committee for discussion and comments on earlier versions of this work. G.R.A. and H.M.M. were funded in part by grant HG02651 from the National Human Genome Research Institute. A.V.S. was funded through a grant (P.I. Lincoln Stein, Cold Spring Harbor Laboratory) from the SNP Consortium, Ltd., supplemented by additional funding from the National Institutes of Health. D.J.T. was supported by National Human Genome Research Institute grants IPH41HG02371 and HG02238 to David Haussler and Jim Kent (University of California, Santa Cruz).

[Supplemental material is available at www.genome.org. The following individuals kindly provided reagents, samples, or unpublished information as indicated in the paper: J. Mullikin, G. McVean, and C. Freeman.]

Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.4421405. Freely available online through the Genome Research Immediate Open Access option.

References

Abecasis, G.R. and Wigginton, J.E. 2005. Handling Marker-Marker disequilibrium: Pedigree analysis with clustered markers. Am. J. Hum. Genet. (in press). [DOI] [PMC free article] [PubMed]
Abecasis, G.R., Ghosh, D., and Nichols, T.E. 2005. Linkage disequilibrium: Ancient history drives the new genetics. Hum. Hered. 59: 118–124. [DOI] [PubMed] [Google Scholar]
Ashburner, M., Ball, C.A., Blake, J.A., Botstein, D., Butler, H., Cherry, J.M., Davis, A.P., Dolinski, K., Dwight, S.S., Eppig, J.T., et al. 2000. Gene Ontology: Tool for the unification of biology. The Gene Ontology Consortium. Nat. Genet. 25: 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
Begun, D.J. and Aquadro, C.F. 1992. Levels of naturally occurring DNA polymorphism correlate with recombination rates in D. melanogaster. Nature 356: 519–520. [DOI] [PubMed] [Google Scholar]
Blanchette, M., Kent, W.J., Riemer, C., Elnitski, L., Smit, A.F., Roskin, K.M., Baertsch, R., Rosenbloom, K., Clawson, H., Green, E.D., et al. 2004. Aligning multiple genomic sequences with the threaded blockset aligner. Genome Res. 14: 708–715. [DOI] [PMC free article] [PubMed] [Google Scholar]
Broman, K.W., Murray, J.C., Sheffield, V.C., White, R.L., and Weber, J.L. 1998. Comprehensive human genetic maps: Individual and sex-specific variation in recombination. Am. J. Hum. Genet. 63: 861–869. [DOI] [PMC free article] [PubMed] [Google Scholar]
Cardon, L.R and Abecasis, G.R. 2003. Using haplotype blocks to map human complex trait loci. Trends Genet. 19: 135–140. [DOI] [PubMed] [Google Scholar]
Dawson, E., Abecasis, G.R., Bumpstead, S., Chen., Y., Hunt, S., Beare, D.M., Pabial, J., Dibling, T., Tinsley, E., Kirby, S., et al. 2002. A first-generation linkage disequilibrium map of human chromosome 22. Nature 418: 544–548. [DOI] [PubMed] [Google Scholar]
Deininger, P.L. and Batzer, M.A. 2002. Mammalian retroelements. Genome Res. 12: 1455–1465. [DOI] [PubMed] [Google Scholar]
Edwards, A.O., Ritter III, R., Abel, K.J., Manning, A., Panhuysen, C., and Farrer, L.A. 2005. Complement factor H polymorphism and age-related macular degeneration. Science 308: 421–424. [DOI] [PubMed] [Google Scholar]
Eisenbarth, I., Vogel, G., Krone, W., Vogel, W., and Assum, G. 2000. An isochore transition in the NF1 gene region coincides with a switch in the extent of linkage disequilibrium. Am. J. Hum. Genet. 67: 873–880. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fullerton, S.M., Bernardo Carvalho, A., and Clark, A.G. 2001. Local rates of recombination are positively correlated with GC content in the human genome. Mol. Biol. Evol. 18: 1139–1142. [DOI] [PubMed] [Google Scholar]
Gabriel, S.B., Schaffner, S.F., Nguyen, H., Moore, J.M., Roy, J., Blumenstiel, B., Higgins, J., DeFelice, M., Lochner, A., Faggart, M., et al. 2002. The structure of haplotype blocks in the human genome. Science 296: 2225–2229. [DOI] [PubMed] [Google Scholar]
Gibbs, R.A., Weinstock, G.M., Metzker, M.L., Muzny, D.M., Sodergren, E.J., Scherer, S., Scott, G., Steffen, D., Worley, K.C., Burch, P.E., et al. 2004. Genome sequence of the Brown Norway rat yields insights into mammalian evolution. Nature 428: 493–521. [DOI] [PubMed] [Google Scholar]
Haines, J.L., Hauser, M.A., Schmidt, S., Scott, W.K., Olson, L.M., Gallins, P., Spencer, K.L., Kwan, S.Y., Noureddine, M., Gilbert, J.R., et al. 2005. Complement factor H variant increases the risk of age-related macular degeneration. Science 308: 419–421. [DOI] [PubMed] [Google Scholar]
Harris, M.A., Clark, J., Ireland, A., Lomax, J., Ashburner, M., Foulger, R., Eilbeck, K., Lewis, S., Marshall, B., Mungall, C., et al. 2004. The Gene Ontology (GO) database and informatics resource. Nucleic Acids Res. 32: D258–D261. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hill, W.G. and Robertson, A. 1966. The effect of linkage on limits to artificial selection. Genet. Res. 8: 269–294. [PubMed] [Google Scholar]
Hinds, D.A., Stuve, L.L., Nilsen, G.B., Halperin, E., Eskin, E., Ballinger, D.G., Frazer, K.A., and Cox, D.R. 2005. Whole-genome patterns of common DNA variation in three human populations. Science 307: 1072–1079. [DOI] [PubMed] [Google Scholar]
Hirschhorn, J.N. and Daly, M.J. 2005. Genome-wide association studies for common diseases and complex traits. Nat. Rev. Genetics 6: 95–108. [DOI] [PubMed] [Google Scholar]
Huang, S.W., Friedman, R., Yu, N., Yu, A., and Li, W.H. 2005. How strong is the mutagenicity of recombination in mammals? Mol. Biol. Evol. 22: 426–431. [DOI] [PubMed] [Google Scholar]
Hudson, R.R. 1990. Gene genealogies and the coalescent process. In: Oxford surveys in evolutionary biology (eds. D. Futuyma and J. Antonovics). Oxford University Press, New York.
Hudson, R.R. 2001. Two-locus sampling distributions and their application. Genetics 159: 1805–1817. [DOI] [PMC free article] [PubMed] [Google Scholar]
The International HapMap Consortium. 2003. The International HapMap Project. Nature 426: 789–796. [DOI] [PubMed] [Google Scholar]
Jeffreys, A.J., Kauppi, L., and Neumann, R. 2001. Intensely punctate meiotic recombination in the class II region of the major histocompatibility complex. Nat. Genet. 29: 217–222. [DOI] [PubMed] [Google Scholar]
Karolchik, D., Hinrichs, A.S., Furey, T.S., Roskin, K.M., Sugnet, C.W., Haussler, D., and Kent, W.J. 2004. The UCSC Table Browser data retrieval tool. Nucleic Acids Res. 32: D493–D496. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ke, X., Durrant, C., Morris, A.P., Hunt, S., Bentley, D.R., Deloukas, P., and Cardon, L.R. 2004. Efficiency and consistency of haplotype tagging of dense SNP maps in multiple samples. Hum. Mol. Genet. 13: 2557–2565. [DOI] [PubMed] [Google Scholar]
Kent, W.J., Sugnet, C.W., Furey, T.S., Roskin, K.M., Pringle, T.H., Zahler, A.M., and Haussler, D. 2002. The human genome browser at UCSC. Genome Res. 12: 996–1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
Klein, R.J., Zeiss, C., Chew, E.Y., Tsai, J.Y., Sackler, R.S., Haynes, C., Henning, A.K., Sangiovanni, J.P., Mane, S.M., Mayne, S.T., et al. 2005. Complement factor H polymorphism in age-related macular degeneration. Science 308: 385–389. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kong, A., Gudbjartsson, D.F., Sainz, J., Jonsdottir, G.M., Gudjonsson, S.A., Richardsson, B., Sigurdardottir, S., Barnard, J., Hallbeck, B., Masson, G., et al. 2002. A high-resolution recombination map of the human genome. Nat. Genet. 31: 241–247. [DOI] [PubMed] [Google Scholar]
Kruglyak, L. 1999. Prospects for whole genome linkage disequilibrium mapping of common disease genes. Nat. Genet. 22: 139–144. [DOI] [PubMed] [Google Scholar]
Li, N. and Stephens, M. 2003. Modeling linkage disequilibrium and identifying recombination hotspots using single-nucleotide polymorphism data. Genetics 165: 2213–2233. [DOI] [PMC free article] [PubMed] [Google Scholar]
Little, A.M. and Parham, P. 1999. Polymorphism and evolution of HLA class I and II genes and molecules. Rev. Immunogenet. 1: 105–123. [PubMed] [Google Scholar]
Liu, N., Sawyer, S.L., Mukherjee, N., Pakstis, A.J., Kidd, J.R., Kidd, K.K., Brookes, A.J., and Zhao, H. 2004. Haplotype block structures show significant variation among populations. Genet. Epidemiol. 27: 385–400. [DOI] [PubMed] [Google Scholar]
Lupski, J.R. 1998. Genomic disorders: Structural features of the genome can lead to DNA rearrangements and human disease traits. Trends Genet. 14: 417–422. [DOI] [PubMed] [Google Scholar]
McVean, G.A., Myers, S.R., Hunt, S., Deloukas, P., Bentley, D.R., and Donnelly, P. 2004. The fine-scale structure of recombination rate variation in the human genome. Science 304: 581–584. [DOI] [PubMed] [Google Scholar]
Modrich, P. and Lahue, R. 1996. Mismatch repair in replication fidelity, genetic recombination, and cancer biology. Annu. Rev. Biochem. 65: 101–133. [DOI] [PubMed] [Google Scholar]
Nachman, M.W., Bauer, V.L., Crowell, S.L., and Aquadro, C.F. 1998. DNA variability and recombination rates at X-linked loci in humans. Genetics 150: 1133–1141. [DOI] [PMC free article] [PubMed] [Google Scholar]
Nei, M. and Li, W.H. 1973. Linkage disequilibrium in subdivided populations. Genetics 75: 213–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
Nordborg, M. and Tavare, S. 2005. Linkage disequilibrium: What history has to tell us. Trends Genet. 18: 83–90. [DOI] [PubMed] [Google Scholar]
Ohta, T. and Kimura, M. 1969. Linkage disequilibrium due to random genetic drift. Genet. Res. 13: 47–55. [Google Scholar]
Pehrson, J.R. and Fuji, R.N. 1998. Evolutionary conservation of histone macroH2A subtypes and domains. Nucleic Acids Res. 26: 2837–2842. [DOI] [PMC free article] [PubMed] [Google Scholar]
Prak, E.T. and Kazazian Jr., H.H. 2000. Mobile elements and the human genome. Nat. Rev. Genet. 1: 134–144. [DOI] [PubMed] [Google Scholar]
Sachidanandam, R., Weissman, D., Schmidt, S.C., Kakol, J.M., Stein, L.D., Marth, G., Sherry, S., Mullikin, J.C., Mortimore, B.J., Willey, D.L., et al. 2001. A map of human genome sequence variation containing 1.42 million single nucleotide polymorphisms. Nature 409: 928–933. [DOI] [PubMed] [Google Scholar]
Schaffner, S.F. 2004. The X chromosome in population genetics. Nat. Rev. Genet. 5: 43–51. [DOI] [PubMed] [Google Scholar]
Siepel, A., Bejerano, G., Pedersen, J.S., Hinrichs, A., Hou, M., Rosenbloom, K., Clawson, H., Spieth, J., Hillier, L.W., Richards, S., et al. 2005. Evolutionarily conserved elements in vertebrate, insect, worm, and yeast genomes. Genome Res. 15: 1034–1050. [DOI] [PMC free article] [PubMed] [Google Scholar]
Tishkoff, S.A., Dietzsch, E., Speed, W., Pakstis, A.J., Kidd, J.R., Cheung, K., Bonne-Tamir, B., Santachiara-Benerecetti, A.S., Moral, P., and Krings, M. 1996. Global patterns of linkage disequilibrium at the CD4 locus and modern human origins. Science 271: 1380–1387. [DOI] [PubMed] [Google Scholar]
Trachtenberg, E., Korber, B., Sollars, C., Kepler, T.B., Hraber, P.T., Hayes, E., Funkhouser, R., Fugate, M., Theiler, J., Hsu, Y.S., et al. 2003. Advantage of rare HLA supertype in HIV disease progression. Nat. Med. 9: 928–935. [DOI] [PubMed] [Google Scholar]
Waterston, R.H., Lindblad-Toh, K., Birney, E., Rogers, J., Abril, J.F., Agarwal, P., Agarwala, R., Ainscough, R., Alexandersson, M., An, P., et al. 2002. Initial sequencing and comparative analysis of the mouse genome. Nature 420: 520–562. [DOI] [PubMed] [Google Scholar]
Weissenbach, J., Gyapay, G., Dib, C., Vignal, A., Morissette, J., Millasseau, P., Vaysseix, G., and Lathrop, M. 1992. A second-generation linkage map of the human genome. Nature 359: 794–801. [DOI] [PubMed] [Google Scholar]
Yu, A., Zhao, C., Fan, Y., Jang, W., Mungall, A.J., Deloukas, P., Olsen, A., Doggett, N.A., Ghebranious, N., Broman, K.W., et al. 2001. Comparison of human genetic and sequence-based physical maps. Nature 409: 951–953. [DOI] [PubMed] [Google Scholar]
Zareparsi, S., Branham, K.E., Li, M., Shah, S., Klein, R.J., Ott, J., Hoh, J., Abecasis, G.R., and Swaroop, A. 2005. Strong association of the Y402H variant in complement factor H at 1q32 with susceptibility to age-related macular degeneration. Am. J. Hum. Genet. 77: 149–153. [DOI] [PMC free article] [PubMed] [Google Scholar]

Web site references

http://genome.ucsc.edu/cgi-bin/hgTables; UCSC Table Browser.
http://hapmap.cshl.org/; HapMap Project Web site. [DOI] [PMC free article] [PubMed]
http://www.repeatmasker.org; RepeatMasker, A.F.A. Smit and P. Green, unpubl.

[ref1] Abecasis, G.R. and Wigginton, J.E. 2005. Handling Marker-Marker disequilibrium: Pedigree analysis with clustered markers. Am. J. Hum. Genet. (in press). [DOI] [PMC free article] [PubMed]

[ref2] Abecasis, G.R., Ghosh, D., and Nichols, T.E. 2005. Linkage disequilibrium: Ancient history drives the new genetics. Hum. Hered. 59: 118–124. [DOI] [PubMed] [Google Scholar]

[ref3] Ashburner, M., Ball, C.A., Blake, J.A., Botstein, D., Butler, H., Cherry, J.M., Davis, A.P., Dolinski, K., Dwight, S.S., Eppig, J.T., et al. 2000. Gene Ontology: Tool for the unification of biology. The Gene Ontology Consortium. Nat. Genet. 25: 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref4] Begun, D.J. and Aquadro, C.F. 1992. Levels of naturally occurring DNA polymorphism correlate with recombination rates in D. melanogaster. Nature 356: 519–520. [DOI] [PubMed] [Google Scholar]

[ref5] Blanchette, M., Kent, W.J., Riemer, C., Elnitski, L., Smit, A.F., Roskin, K.M., Baertsch, R., Rosenbloom, K., Clawson, H., Green, E.D., et al. 2004. Aligning multiple genomic sequences with the threaded blockset aligner. Genome Res. 14: 708–715. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref6] Broman, K.W., Murray, J.C., Sheffield, V.C., White, R.L., and Weber, J.L. 1998. Comprehensive human genetic maps: Individual and sex-specific variation in recombination. Am. J. Hum. Genet. 63: 861–869. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref7] Cardon, L.R and Abecasis, G.R. 2003. Using haplotype blocks to map human complex trait loci. Trends Genet. 19: 135–140. [DOI] [PubMed] [Google Scholar]

[ref8] Dawson, E., Abecasis, G.R., Bumpstead, S., Chen., Y., Hunt, S., Beare, D.M., Pabial, J., Dibling, T., Tinsley, E., Kirby, S., et al. 2002. A first-generation linkage disequilibrium map of human chromosome 22. Nature 418: 544–548. [DOI] [PubMed] [Google Scholar]

[ref9] Deininger, P.L. and Batzer, M.A. 2002. Mammalian retroelements. Genome Res. 12: 1455–1465. [DOI] [PubMed] [Google Scholar]

[ref10] Edwards, A.O., Ritter III, R., Abel, K.J., Manning, A., Panhuysen, C., and Farrer, L.A. 2005. Complement factor H polymorphism and age-related macular degeneration. Science 308: 421–424. [DOI] [PubMed] [Google Scholar]

[ref11] Eisenbarth, I., Vogel, G., Krone, W., Vogel, W., and Assum, G. 2000. An isochore transition in the NF1 gene region coincides with a switch in the extent of linkage disequilibrium. Am. J. Hum. Genet. 67: 873–880. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref12] Fullerton, S.M., Bernardo Carvalho, A., and Clark, A.G. 2001. Local rates of recombination are positively correlated with GC content in the human genome. Mol. Biol. Evol. 18: 1139–1142. [DOI] [PubMed] [Google Scholar]

[ref13] Gabriel, S.B., Schaffner, S.F., Nguyen, H., Moore, J.M., Roy, J., Blumenstiel, B., Higgins, J., DeFelice, M., Lochner, A., Faggart, M., et al. 2002. The structure of haplotype blocks in the human genome. Science 296: 2225–2229. [DOI] [PubMed] [Google Scholar]

[ref14] Gibbs, R.A., Weinstock, G.M., Metzker, M.L., Muzny, D.M., Sodergren, E.J., Scherer, S., Scott, G., Steffen, D., Worley, K.C., Burch, P.E., et al. 2004. Genome sequence of the Brown Norway rat yields insights into mammalian evolution. Nature 428: 493–521. [DOI] [PubMed] [Google Scholar]

[ref15] Haines, J.L., Hauser, M.A., Schmidt, S., Scott, W.K., Olson, L.M., Gallins, P., Spencer, K.L., Kwan, S.Y., Noureddine, M., Gilbert, J.R., et al. 2005. Complement factor H variant increases the risk of age-related macular degeneration. Science 308: 419–421. [DOI] [PubMed] [Google Scholar]

[ref16] Harris, M.A., Clark, J., Ireland, A., Lomax, J., Ashburner, M., Foulger, R., Eilbeck, K., Lewis, S., Marshall, B., Mungall, C., et al. 2004. The Gene Ontology (GO) database and informatics resource. Nucleic Acids Res. 32: D258–D261. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref17] Hill, W.G. and Robertson, A. 1966. The effect of linkage on limits to artificial selection. Genet. Res. 8: 269–294. [PubMed] [Google Scholar]

[ref18] Hinds, D.A., Stuve, L.L., Nilsen, G.B., Halperin, E., Eskin, E., Ballinger, D.G., Frazer, K.A., and Cox, D.R. 2005. Whole-genome patterns of common DNA variation in three human populations. Science 307: 1072–1079. [DOI] [PubMed] [Google Scholar]

[ref19] Hirschhorn, J.N. and Daly, M.J. 2005. Genome-wide association studies for common diseases and complex traits. Nat. Rev. Genetics 6: 95–108. [DOI] [PubMed] [Google Scholar]

[ref20] Huang, S.W., Friedman, R., Yu, N., Yu, A., and Li, W.H. 2005. How strong is the mutagenicity of recombination in mammals? Mol. Biol. Evol. 22: 426–431. [DOI] [PubMed] [Google Scholar]

[ref21] Hudson, R.R. 1990. Gene genealogies and the coalescent process. In: Oxford surveys in evolutionary biology (eds. D. Futuyma and J. Antonovics). Oxford University Press, New York.

[ref22] Hudson, R.R. 2001. Two-locus sampling distributions and their application. Genetics 159: 1805–1817. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref23] The International HapMap Consortium. 2003. The International HapMap Project. Nature 426: 789–796. [DOI] [PubMed] [Google Scholar]

[ref24] Jeffreys, A.J., Kauppi, L., and Neumann, R. 2001. Intensely punctate meiotic recombination in the class II region of the major histocompatibility complex. Nat. Genet. 29: 217–222. [DOI] [PubMed] [Google Scholar]

[ref25] Karolchik, D., Hinrichs, A.S., Furey, T.S., Roskin, K.M., Sugnet, C.W., Haussler, D., and Kent, W.J. 2004. The UCSC Table Browser data retrieval tool. Nucleic Acids Res. 32: D493–D496. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref26] Ke, X., Durrant, C., Morris, A.P., Hunt, S., Bentley, D.R., Deloukas, P., and Cardon, L.R. 2004. Efficiency and consistency of haplotype tagging of dense SNP maps in multiple samples. Hum. Mol. Genet. 13: 2557–2565. [DOI] [PubMed] [Google Scholar]

[ref27] Kent, W.J., Sugnet, C.W., Furey, T.S., Roskin, K.M., Pringle, T.H., Zahler, A.M., and Haussler, D. 2002. The human genome browser at UCSC. Genome Res. 12: 996–1006. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref28] Klein, R.J., Zeiss, C., Chew, E.Y., Tsai, J.Y., Sackler, R.S., Haynes, C., Henning, A.K., Sangiovanni, J.P., Mane, S.M., Mayne, S.T., et al. 2005. Complement factor H polymorphism in age-related macular degeneration. Science 308: 385–389. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref29] Kong, A., Gudbjartsson, D.F., Sainz, J., Jonsdottir, G.M., Gudjonsson, S.A., Richardsson, B., Sigurdardottir, S., Barnard, J., Hallbeck, B., Masson, G., et al. 2002. A high-resolution recombination map of the human genome. Nat. Genet. 31: 241–247. [DOI] [PubMed] [Google Scholar]

[ref30] Kruglyak, L. 1999. Prospects for whole genome linkage disequilibrium mapping of common disease genes. Nat. Genet. 22: 139–144. [DOI] [PubMed] [Google Scholar]

[ref31] Li, N. and Stephens, M. 2003. Modeling linkage disequilibrium and identifying recombination hotspots using single-nucleotide polymorphism data. Genetics 165: 2213–2233. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref32] Little, A.M. and Parham, P. 1999. Polymorphism and evolution of HLA class I and II genes and molecules. Rev. Immunogenet. 1: 105–123. [PubMed] [Google Scholar]

[ref33] Liu, N., Sawyer, S.L., Mukherjee, N., Pakstis, A.J., Kidd, J.R., Kidd, K.K., Brookes, A.J., and Zhao, H. 2004. Haplotype block structures show significant variation among populations. Genet. Epidemiol. 27: 385–400. [DOI] [PubMed] [Google Scholar]

[ref34] Lupski, J.R. 1998. Genomic disorders: Structural features of the genome can lead to DNA rearrangements and human disease traits. Trends Genet. 14: 417–422. [DOI] [PubMed] [Google Scholar]

[ref35] McVean, G.A., Myers, S.R., Hunt, S., Deloukas, P., Bentley, D.R., and Donnelly, P. 2004. The fine-scale structure of recombination rate variation in the human genome. Science 304: 581–584. [DOI] [PubMed] [Google Scholar]

[ref36] Modrich, P. and Lahue, R. 1996. Mismatch repair in replication fidelity, genetic recombination, and cancer biology. Annu. Rev. Biochem. 65: 101–133. [DOI] [PubMed] [Google Scholar]

[ref37] Nachman, M.W., Bauer, V.L., Crowell, S.L., and Aquadro, C.F. 1998. DNA variability and recombination rates at X-linked loci in humans. Genetics 150: 1133–1141. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref38] Nei, M. and Li, W.H. 1973. Linkage disequilibrium in subdivided populations. Genetics 75: 213–219. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref39] Nordborg, M. and Tavare, S. 2005. Linkage disequilibrium: What history has to tell us. Trends Genet. 18: 83–90. [DOI] [PubMed] [Google Scholar]

[ref40] Ohta, T. and Kimura, M. 1969. Linkage disequilibrium due to random genetic drift. Genet. Res. 13: 47–55. [Google Scholar]

[ref41] Pehrson, J.R. and Fuji, R.N. 1998. Evolutionary conservation of histone macroH2A subtypes and domains. Nucleic Acids Res. 26: 2837–2842. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref42] Prak, E.T. and Kazazian Jr., H.H. 2000. Mobile elements and the human genome. Nat. Rev. Genet. 1: 134–144. [DOI] [PubMed] [Google Scholar]

[ref43] Sachidanandam, R., Weissman, D., Schmidt, S.C., Kakol, J.M., Stein, L.D., Marth, G., Sherry, S., Mullikin, J.C., Mortimore, B.J., Willey, D.L., et al. 2001. A map of human genome sequence variation containing 1.42 million single nucleotide polymorphisms. Nature 409: 928–933. [DOI] [PubMed] [Google Scholar]

[ref44] Schaffner, S.F. 2004. The X chromosome in population genetics. Nat. Rev. Genet. 5: 43–51. [DOI] [PubMed] [Google Scholar]

[ref45] Siepel, A., Bejerano, G., Pedersen, J.S., Hinrichs, A., Hou, M., Rosenbloom, K., Clawson, H., Spieth, J., Hillier, L.W., Richards, S., et al. 2005. Evolutionarily conserved elements in vertebrate, insect, worm, and yeast genomes. Genome Res. 15: 1034–1050. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref46] Tishkoff, S.A., Dietzsch, E., Speed, W., Pakstis, A.J., Kidd, J.R., Cheung, K., Bonne-Tamir, B., Santachiara-Benerecetti, A.S., Moral, P., and Krings, M. 1996. Global patterns of linkage disequilibrium at the CD4 locus and modern human origins. Science 271: 1380–1387. [DOI] [PubMed] [Google Scholar]

[ref47] Trachtenberg, E., Korber, B., Sollars, C., Kepler, T.B., Hraber, P.T., Hayes, E., Funkhouser, R., Fugate, M., Theiler, J., Hsu, Y.S., et al. 2003. Advantage of rare HLA supertype in HIV disease progression. Nat. Med. 9: 928–935. [DOI] [PubMed] [Google Scholar]

[ref48] Waterston, R.H., Lindblad-Toh, K., Birney, E., Rogers, J., Abril, J.F., Agarwal, P., Agarwala, R., Ainscough, R., Alexandersson, M., An, P., et al. 2002. Initial sequencing and comparative analysis of the mouse genome. Nature 420: 520–562. [DOI] [PubMed] [Google Scholar]

[ref49] Weissenbach, J., Gyapay, G., Dib, C., Vignal, A., Morissette, J., Millasseau, P., Vaysseix, G., and Lathrop, M. 1992. A second-generation linkage map of the human genome. Nature 359: 794–801. [DOI] [PubMed] [Google Scholar]

[ref50] Yu, A., Zhao, C., Fan, Y., Jang, W., Mungall, A.J., Deloukas, P., Olsen, A., Doggett, N.A., Ghebranious, N., Broman, K.W., et al. 2001. Comparison of human genetic and sequence-based physical maps. Nature 409: 951–953. [DOI] [PubMed] [Google Scholar]

[ref51] Zareparsi, S., Branham, K.E., Li, M., Shah, S., Klein, R.J., Ott, J., Hoh, J., Abecasis, G.R., and Swaroop, A. 2005. Strong association of the Y402H variant in complement factor H at 1q32 with susceptibility to age-related macular degeneration. Am. J. Hum. Genet. 77: 149–153. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Sequence features in regions of weak and strong linkage disequilibrium

Albert V Smith

Daryl J Thomas

Heather M Munro

Gonçalo R Abecasis

Abstract

Results

Genotype data

Variation in linkage disequilibrium in the genome

Figure 1.

Figure 2.

Figure 3.

Figure 4.

Correlation of linkage disequilibrium with sequence features

Table 1.

Table 2.

Base composition in regions of high and low linkage disequilibrium

Table 3.

Table 4.

Gene categorization in regions of high and low linkage disequilibrium

Table 5.

Hotspots for the breakdown of linkage disequilibrium

Sequence features of recombination hotspots

Table 6.

Table 7.

Multivariate analysis

Table 8.

Figure 5.

Discussion

Methods

Data set

Calculation of marker allele frequencies

Calculation of pairwise disequilibrium coefficients

Sliding window analyses of linkage disequilibrium

Identification of hotspots for the breakdown of linkage disequilibrium

Comparison with fine-scale recombination rate estimates

Analysis of sequence features

Estimates of sequence polymorphism

Comparison of linkage disequilibrium and sequence features within sliding windows

Comparison of linkage disequilibrium and sequence features within hotspots

Analysis of gene ontology data

Multivariate analysis

Acknowledgments

References

Web site references

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases