Large-scale recombination rate patterns are conserved among human populations

Abstract

In humans, most recombination events occur in a small fraction of the genome. These hotspots of recombination show considerable variation in intensity and/or location across species and, potentially, across human populations. On a larger scale, the patterns of recombination rates have been mostly investigated in individuals of European ancestry, and it remains unknown whether the results obtained can be directly applied to other human populations. Here, we investigate this question using genome-wide polymorphism data. We show that population recombination rates recapitulate a large part of the genetic map information, regardless of the population considered. We also show that the ratio of the population recombination rate estimate of two populations is overall constant along the chromosomes. These two observations support the hypothesis that large-scale recombination patterns are conserved across human populations. Local deviations from the overall pattern of conservation of the recombination rates can be used to select candidate regions with large polymorphic inversions or under local selection.

Recombination events do not occur evenly across the genome: Small regions of the chromosomes (1–2 kb long) have a recombination rate (i.e., the average number of recombination events per generation per unit of length) 10-fold to 100-fold higher than surrounding regions. Recent studies have yielded increasing evidence that these recombination hotspots are frequent in the human genome and are responsible for a large fraction of the overall recombination events (Crawford et al. 2004; McVean et al. 2004). More than 50% of all recombination seems to occur in less than 10% of the genome. At least some of these recombination hotspots differ in locations and/or intensity between species (Ptak et al. 2004a, 2005; Winckler et al. 2005) as well as, to some extent, between human populations (Crawford et al. 2004). Recently, Jeffreys and colleagues have compared the recombination rate obtained from sperm typing with the footprints of historical recombination events in the linkage disequilibrium patterns for a 200-kb region, and their results support the possibility of rapid evolution of hotspots (Jeffreys et al. 2005). These observations suggest that small-scale recombination rates can vary considerably in intensity, location, and over time. On the other hand, if we consider a much larger scale, results from the Icelandic population show that the overall number of recombination events can vary among individuals (Kong et al. 2004). Genetic maps generated in different mammalian species show large variations in the overall length of the map and therefore in the species recombination rate (the physical map being of roughly constant size) (Rogers et al. 2000). This suggests that large-scale recombination rates can also vary, which raises the question whether they differ among human populations. We currently do not have much information on large-scale recombination rates in populations of non-European ancestry, as the most detailed human genetic maps have been developed using either CEPH families (Broman et al. 1998) or large Icelandic pedigrees (Kong et al. 2002, 2004). Inferences of recombination rates from linkage maps established in different populations have been shown to be technically difficult and prone to artifacts (Jorgenson et al. 2005). Alternatively, one could try to estimate large-scale recombination rates by analyzing the effect of recombination on diversity patterns using linkage disequilibrium (later referred to as LD). However, this approach does not easily allow testing whether recombination rates differ between populations, as population history, through differences in the effective population size, is a strong confounding factor of LD measurements (Pritchard and Przeworski 2001).

While still not enabling quantitative comparisons (see Jorgenson et al. 2005 for the results of such analyses), we describe here two methods, based on LD patterns, that take into account the effect of demography to investigate qualitative population differences in recombination rates. Analyses of large-scale recombination rate pattern differences (i.e., the variation of the recombination rates along the chromosomes) among three human populations using genome-wide diversity data produced by Perlegen Sciences Inc. (Hinds et al. 2005) show that, over the entire genome, the recombination rate patterns are highly conserved.

Results and Discussion

Comparable estimates of ρ in different populations

Variation in the length of the genealogy along the chromosomes can result in apparent differences in the recombination rate: A longer genealogy would allow more opportunities for recombination (and mutation). Non-African populations show evidence of bottlenecks in their history (see, e.g., Harpending and Rogers 2000; Akey et al. 2004), and these drastic reductions in population size can increase stochastic differences in the length of the genealogy along the chromosomes according to whether the lineages coalesce before or after the bottleneck (Galtier et al. 2000; Wall et al. 2002). This effect can potentially introduce differences in the population recombination rate pattern between populations of African and non-African origin. However, we note that the value of the standard deviation of 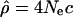(i.e., the estimate of population recombination rate) relative to its mean is similar, or slightly greater, in African-Americans relative to Americans of non-African ancestry (Table 1). Thus, the effect of bottlenecks on the genealogy is likely averaged over the 1-Mb scale we consider here to estimate ρ and therefore has less influence on our results.

Table 1.

Summary statistics

	ρ		Pearson's r
	Mean	SD	r2	99% CI
European-American	0.000192	0.000132	0.5087	[0.4733-0.5431]
Han Chinese	0.000200	0.000138	0.4986	[0.4624-0.5329]
African-American	0.000405	0.000278	0.4964	[0.4610-0.5314]

Average value of and chromosomal position

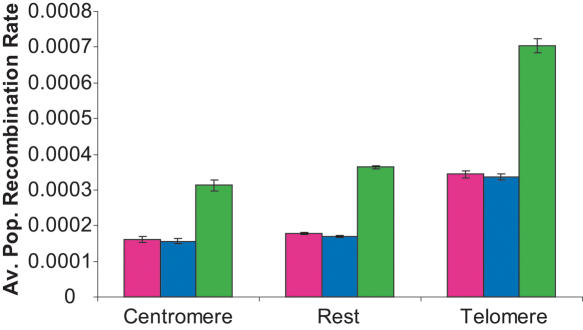
Recently Jorgenson and colleagues found shorter genetic distances in the telomeric regions of Asian individuals relative to individuals of African or European origin (Jorgenson et al. 2005). They suggested that this variation is unlikely due to a technical artifact but might represent a biologically based mechanism. In order to test their observation, and to determine whether the variation of recombination rates along the chromosomes differs between populations, we divided the genome into three broad categories: centromeric regions, telomeric regions, and the rest of the genome (see Methods for details). We calculated the average for each population and each category. The results are presented in Figure 1. We found that, for all populations, telomeric regions have higher population recombination rates than the rest of the genome (Student's t-test, p 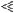0.001), while centromeric regions tend to have slightly lower recombination rate estimates (Student's t-test, p_HanChin. = 0.019, p_Eur.-Amer. = 0.058, p_Afr.-Amer. < 0.001). These results confirmed previous observations based on analyses of genetic maps (see, e.g., Broman et al. 1998; The International Human Genome Sequencing Consortium 2001). We tested specifically whether the population recombination rates in the telomeric regions of Han Chinese were significantly lower than in the two other populations by an analysis of partial regression. To take into account the quantitative difference in population recombination rates between populations (due to differences in N_e), we used the value of 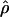in the centromeric and “rest of the genome” regions to normalize 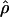in the telomeric region (Cohen et al. 2003). The adjusted mean of the logarithm of 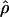for the telomeric regions in Han Chinese was slightly lower than the adjusted mean in European-Americans but not statistically different from it (adjusted means of log ρ in telomeric region: HanChin. = –3.455, Eur.-Amer. = –3.461, Afr.-Amer. = –3.201, p_{HanChin./Eur.-Amer.} = 0.813, p_{HanChin./Afr.-Amer.} < 0.001). Thus, we could not reproduce the observation from Jorgenson et al. (2005) that individuals of Asian ancestry present comparatively lower recombination rates in telomeric regions. It is, however, possible that this difference is due to an overlapping but not identical definition of the telomeric regions: We defined as telomeric the 10 Mb at the end of each chromosomal arm, while Jorgenson et al. (2005) considered the interval between the two most telomeric markers in their genotyping set.

Figure 1.

Average value of 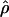in each population for, respectively, telomeric regions, centromeric regions, and the rest of the genome. The mean values of the European-American population are in blue, of the Han Chinese in pink, and of the African-Americans in green. The bars represent two standard errors from the mean.

Correlation between 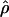and c_map

In order to test more precisely whether the patterns of recombination rates differ along the genome among populations, we compared for each 1-Mb window the recombination rate estimate obtained from the DeCode map (c_map) (Kong et al. 2002) with the population recombination rate 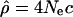obtained from genotype data. The slope of the regression line between these two estimates of recombination rate will be proportional to N_e and therefore likely differs for different populations. However, if large-scale recombination rate patterns differ among populations, the strength of the correlation (i.e., Pearson's r) should be higher for Americans of European ancestry than it is in the other populations since the DeCode map is based on the analysis of a European population. In other words, if the recombination rate patterns have changed, c_map should be a better predictor of ρ for the European-Americans than it is for the African-Americans or the Han Chinese from the Los Angeles area.

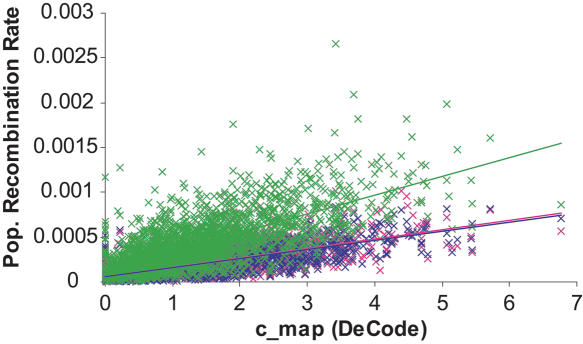
Figure 2 displays 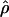versus c_map for 2609 windows of 1 Mb in three populations. As expected, the slope of the regression is different in African-Americans compared to European-Americans or individuals of Asian ancestry: For the same value of c_map, ρ estimated in African-Americans is roughly twice as large as it is in the other populations. Interestingly, the Pearson's r-values obtained for the different populations are very similar despite these slope differences (Table 1). The 99% confidence intervals show large overlaps between the values obtained in the different populations (Table 1). Thus, we find no support for a stronger correlation between 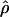and the DeCode c_map in European-Americans than it is in the other populations. One possible concern is that the European individuals used in the Perlegen data set and the DeCode map come from two different populations (respectively, European-Americans and Icelandic). If the recombination rate patterns differ as much between Icelandic and European-American individuals as they do between European-Americans and, respectively, Han Chinese and African-Americans, the correlation strengths between the DeCode c_map and 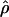in different populations would also be similar. However, the same analysis performed using the Marshfield map (Broman et al. 1998), based on European-American individuals, yields, qualitatively, a very similar result (Supplemental Fig. S1). Thus, the comparison of recombination rate estimates obtained from LD data and large pedigrees supports a scenario of large-scale recombination rate pattern conservation between human populations.

Figure 2.

Plot of the recombination rate estimates for 2609 windows of the human genome. Each point represents a 1-Mb window displayed according to the value of the DeCode recombination rate c_map (on the x-axis) and to the population recombination rate 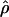calculated using 23 unrelated individuals from the Perlegen data set (on the y-axis). The estimates for the Han Chinese population are in pink, for the African-Americans in green, and for the European-Americans in blue. The straight lines are the regression lines obtained for each population.

One possible pitfall of our analysis is that human populations share most of their history and thus the similarities in 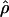could simply be due to excess signal of old common recombination events, while we miss recent differences in the recombination rate patterns. However, it is worth noting here that the values of r² are strikingly large (roughly 50% of the variation of the ρ estimates can be explained by c_map). This is an indication that the recombination rate patterns at the 1-Mb scale do not change drastically with time, as one measurement based on recombination events occurring in a few generations (i.e., the genetic map) is a good predictor of another estimate based on recombination events that occurred on a much deeper time scale (i.e., LD). This result is supported by findings of previous studies on small-scale recombination rates that show high correlation between LD estimates and results from sperm typing (Wall et al. 2003; Ptak et al. 2004a; but see also Jeffreys et al. 2005). We therefore feel confident that the estimate of ρ recapitulates most of the information about recombination rates.

Ratio of ρ between populations

Another method to compare recombination rate differences among populations using polymorphism data is to look at the variation of the ratio of ρ for two populations along the chromosomes. If the recombination rate c is identical in the two populations, the ratio 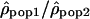is then proportional to N_e(pop1)/N_e(pop2). Therefore, if the recombination rate patterns are conserved, one expects this ratio along the chromosomes to be constant. In contrast, if the recombination rate patterns differ between populations 1 and 2, 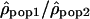will be equal to N_e(pop1)c₁/N_e(pop2)c₂, with the ratio c₁/c₂ varying along the genome.

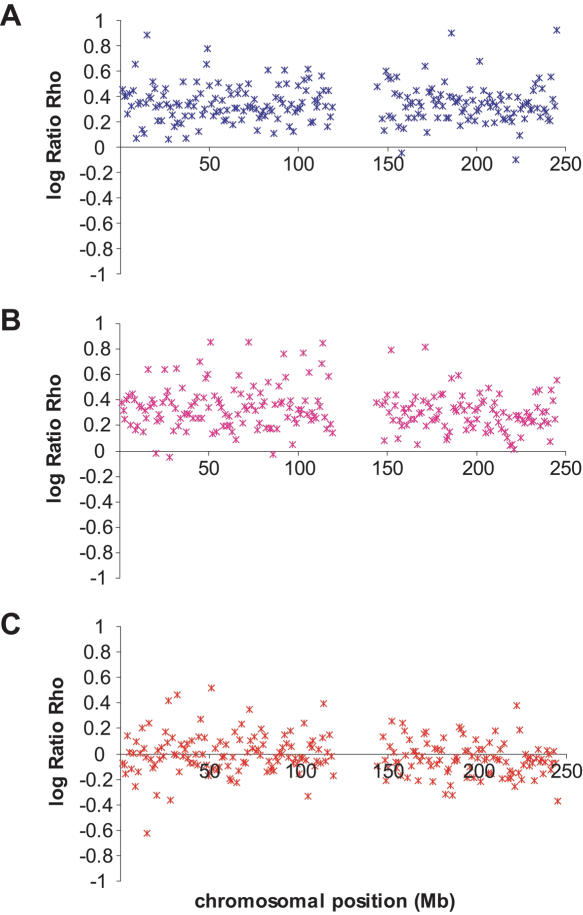
The variation of the log ratios 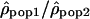along Chromosome 1 is displayed in Figure 3 (see Supplemental Figs. S2–S22 for Chromosomes 2 to 22). The ratios 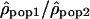seem globally constant along the chromosomes, and this graphical observation is supported by autocorrelation analyses that detect weak correlations, significant in two out of the three comparisons, but with autocorrelation coefficients r very close to zero (lag = 1, n = 2556, r_{HanChin.–Afr.-Amer.} = 0.062, p_{HanChin.–Afr.-Amer.} = 0.001, r_{Eur.-Amer.–Afr.-Amer.} = 0.057, p_{Eur.-Amer.–Afr.-Amer.} = 0.003, r_{HanChin.–Eur.-Amer.} = 0.031, p_{HanChin.–Eur.-Amer.} = 0.105). These findings suggest that the recombination rate patterns among human populations are similar, in agreement with the results of our correlation analyses.

Figure 3.

Variation of the log₁₀ ratio 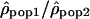along Chromosome 1. Each point of the figure represents one window of 1 Mb displayed according to its position on the chromosome (x-axis) and the value of the log ratios . (A) The log ratios 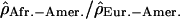are shown in blue; (B) the log ratios 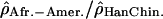are shown in pink; and (C) the log ratios 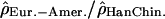are shown in red. See also Supplemental Figures S2 to S22 online for the variation along Chromosomes 2 to 22.

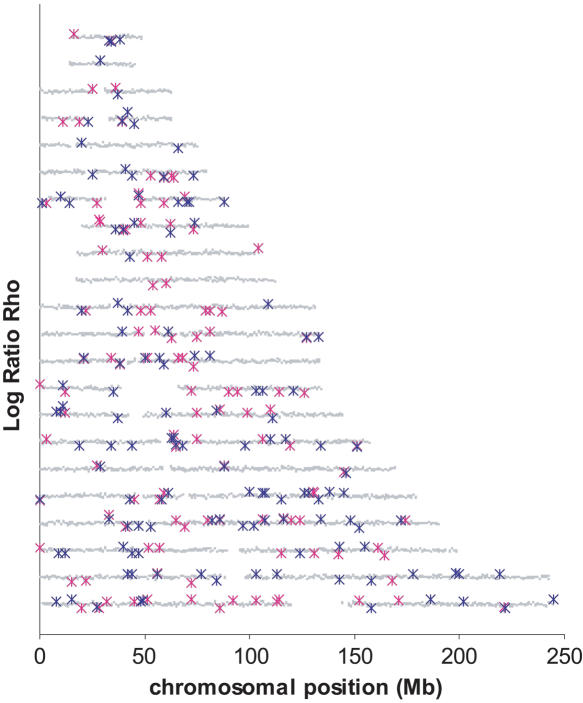
We then investigated whether the 5% most extreme values of 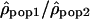were concentrated in some particular portions of the chromosomes. Figure 4 shows the distribution of these “extreme” ratios on the genome for the comparisons between African-Americans and either European-Americans or Han Chinese (see Supplemental Fig. S23 for a blowup of Chromosomes 1 to 5 and Supplemental Fig. S24 for the comparison between European-Americans and Han Chinese). We found no significant differences in the proportion of extreme values per chromosome compared to a uniform distribution according to the chromosome length (χ² test, df = 21, 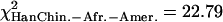, p_{HanChin.–Afr.-Amer.} > 0.25, 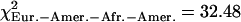, p_{Eur.-Amer.–Afr.-Amer.} > 0.05, 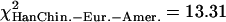, p_{HanChin.–Eur.-Amer.} > 0.5).

Figure 4.

Position of the windows with the 5% most extreme log ratios 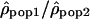. The chromosomes are organized according to their number from 1 (lowest y-axis coordinate) to 22 (on top). Each gray point represents the value of the log ratio 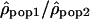for one 1-Mb window and is displayed according to its position on the chromosome (on the x-axis). The 5% most extreme log ratios 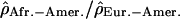are shown in blue and 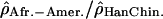in pink. See also Supplemental Figure S23 for a blowup of Chromosomes 1 to 5 and Supplemental Figure S24 for the 5% most extreme log ratios .

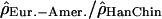If one compares the distribution of extreme windows between centromeric regions, telomeric regions, and the rest of the chromosomes to a uniform distribution along the genome (Supplemental Fig. S25), the difference is marginally significant (χ² test, df = 2, 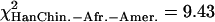, p_{HanChin.–Afr.-Amer.} = 0.009, 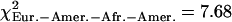, p_{Eur.-Amer.–Afr.-Amer.} = 0.022, 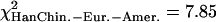, p_{HanChin.–Eur.-Amer.} = 0.020). This finding could represent some slight biological differences between populations, or possibly, a false positive of our statistical tests.

Local variation of recombination rates between populations

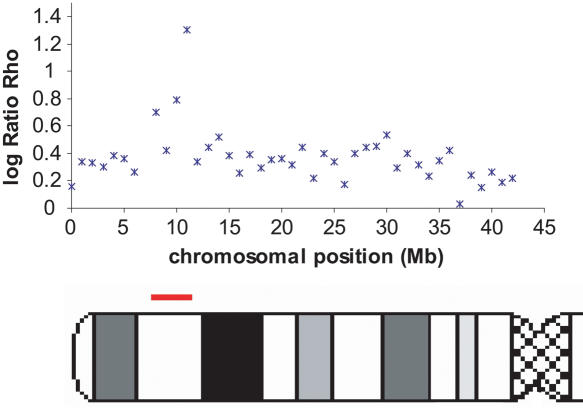
Finally, we tried to evaluate whether some of these most extreme ratios of recombination rate between two populations could represent biological outliers. We showed that for most of the genome the recombination patterns are very similar across populations, which allows us to investigate unusual local deviations from this overall picture. Local positive selection could lead to such apparent discrepancies of population recombination rates by increasing or decreasing the effective population size (i.e., N_e) of one of the populations relative to the other. Polymorphic chromosomal inversions of several megabases could lead to lower recombination rates (caused by a restriction of crossovers in heterozygotes) and a larger extent of LD (caused by the “admixture” of inverted and noninverted chromosomes) and thus, to major population differences if the frequency of these rearrangements differs in the two populations considered. In order to filter out false positives, we chose to analyze only regions containing, within 3 Mb, at least two extreme values of 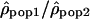in the same tail of the distribution. We identified a total of 22 regions, six displaying an extreme ratio in the African-American/Han Chinese comparison, seven in the African-American/European-American comparison, six for the European-American/Han Chinese comparison, one identified both in European-American/Han Chinese and African-American/European-American comparisons, and two for which both comparisons European-American/Han Chinese and African-American/Han Chinese yield extreme values. These regions are shown in the Supplemental material (Supplemental Table T1). Interestingly, the region with the most extreme ratios in this list coincides perfectly with a well-described polymorphic inversion on Chromosome 8p23 (Fig. 5). This inversion is present frequently in individuals of European ancestry but not in individuals of African ancestry (Giglio et al. 2001; Sugawara et al. 2003). Our results are consistent with the expectation of lower population recombination rates in European-Americans compared to the African-Americans. While looking at a much broader scale, Jorgenson and colleagues also proposed this inversion to be responsible for differences in the linkage map lengths of different ethnic groups (Jorgenson et al. 2005).

Figure 5.

Variation of the log ratios 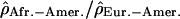along the chromosomal arm 8p. The position of the polymorphic inversion at 8p23 is shown by the red bar on the chromosome picture.

Validation using an independent data set

Given the emergence of an independent data set provided by the International HapMap Consortium (The International HapMap Consortium 2003), we tested whether a data set composed of 45 (as opposed to 23) individuals would give different results. We estimated the population recombination rate ρ using the same approach (Hudson 2001) for 281 windows of Chromosome 2 and Chromosome 4p (produced at the McGill University and Genome Quebec Innovation Center). The means of the population rate estimates obtained in the two data sets for the European-American and Han Chinese individuals were very similar (for the European-Americans, 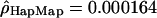and 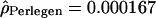; and for the Han Chinese, 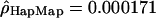and 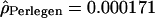). We did not detect any differences in the variances of the estimates between the Perlegen and HapMap data sets (F test, df = 280, p_HanChin. = 0.226, p_Eur.-Amer. = 0.288). The distribution of the population recombination rates per window across these chromosomes was also highly correlated between the two data sets (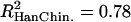, 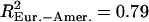) (see also Supplemental Fig. S26). This shows that, at the scale considered for our analysis, a sample of 46 chromosomes yields estimates of the population recombination rate similar to a sample of 90 chromosomes (i.e., we could not detect any difference in accuracy). This is also supported by studies of recombination rates on a smaller scale using the same sample size (Crawford et al. 2004; Ptak et al. 2004b) that find that the population recombination rate estimated from these data allow identification, or confirmation, of hotspots as well as potential population differences. We replicated all analyses previously performed with the HapMap data for Chromosomes 2 and 4p and obtained qualitatively very similar results. The only notable difference consists of significantly higher population recombination rates, on average, for the population of African ancestry in the Perlegen data set than in the HapMap (data not shown). This difference may reflect the more diverse geographic origins of the African-Americans compared to the Yoruba individuals analyzed by the HapMap project, who all come from the same locality, Ibadan, in Nigeria.

Conclusions

While small-scale recombination rates seem to be highly dynamic in time and in space and may possibly vary among human populations, we find that large-scale recombination patterns are highly conserved across human populations. One possible explanation is that the exact position and intensity of recombination hotspots can vary among humans but that the overall frequency of hotspots over a larger scale is maintained. Inter-individual differences in the number of recombination events per meiosis is well documented (for review, see, e.g., Laurie and Hulten 1985; Yu et al. 1996; Broman et al. 1998; Kong et al. 2002; Lynn et al. 2004), and it has been suggested that these differences may have a genetic basis. Our results indicate that these individual differences are likely averaged when populations (or population gene-alogies) are considered. However, our findings do not contradict the hypothesis that genetic polymorphism underlies the individual recombination rate differences, since these allelic differences are unlikely to show extreme differentiation between populations unless the selection regime differs for different populations. Given the overall conservation of recombination rates among human populations, the observation that humans have a genetic map length that is larger than most other mammals (Rogers et al. 2000) still remains to be explained. This apparent difference in recombination pattern is also supported by recent studies of hotspots in chimpanzees (Ptak et al. 2004a, 2005; Winckler et al. 2005). A large-scale recombination map in chimpanzees would be valuable to test whether the recombination patterns did change drastically in the human lineage. Additionally, our result suggests that the genetic maps built using European populations can effectively be used to make inferences in other populations. These results also imply that large regions under local positive selection, which would lead to apparent differences in the recombination rates estimated from polymorphism, are rare in humans. The few local deviations from the overall picture of conservation of recombination rates among populations can be used to investigate further potential polymorphic chromosomal rearrangements or large regions under positive selection in one population.

Methods

We divided the human genome into 1-Mb nonoverlapping windows and retrieved for each window the genotypes for individuals from the three populations analyzed by Perlegen Sciences Inc. (Hinds et al. 2005): European-Americans (Utah residents with ancestry from northern and western Europe), African-Americans, and Han Chinese (from the Los Angeles area). These SNPs were chosen to be approximately evenly distributed across the human genome with an average of one SNP per 1.8 kb (for a total of 1,586,383 SNPs). In order to have identical sample size in all populations, we only considered 23 individuals from the European-American and Han Chinese populations. To eliminate biases observed when information-poor windows are used in the analysis, we excluded from our analyses all windows containing <100 polymorphic markers in one (or more) population (i.e., the windows are identical in all populations, but the SNPs considered within a window can be slightly different). We estimated the population recombination rate 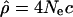from the genotypes using the composite likelihood method proposed by Hudson (2001). This method offers several key advantages for our purpose over traditional measurements of LD, such as r² or |D′|: (1) it is less sensitive to ascertainment bias in the choice of SNPs (Evans and Cardon 2005); (2) it is less sensitive to allele frequencies; and (3) it allows direct comparison of different regions (Pritchard and Przeworski 2001). Overall, we analyzed 2613 nonoverlapping windows of 1 Mb covering the 22 autosomal chromosomes.

We retrieved the DeCode recombination rate estimate (Kong et al. 2002) for 2609 windows from the UCSC Genome Browser using the appropriate freeze (hg16). We compared, for each of these windows, the DeCode recombination rate (later referred to as c_map) to the population recombination rate ρ_cl (i.e., the composite likelihood estimate of ρ) estimated from genotype data and performed a linear regression analysis for each of the three populations. We estimated the 99% confidence interval for r² obtained in the three regression analyses by transforming Pearson's r into Fischer's z. We also performed the same analysis using the Marshfield recombination rates (Broman et al. 1998) obtained for 1741 windows.

To test whether we could confirm the observation of Jorgenson et al. (2005) that individuals of Asian ancestry had a lower recombination rate in telomeric regions than individuals of European or African ancestry, we divided the 2613 windows for which we calculated an estimate of the population recombination rate into three categories: those belonging to telomeric regions (the 10 Mb closer to the chromosomal arm end) and those belonging to centromeric regions (the 10 Mb on each side of the centromere), and grouped the other windows into a “rest of the genome” category. We excluded from this analysis three windows that fall into both centromeric and telomeric categories (on Chromosome 18 between positions 7,000,000 and 9,999,999). For each population, we calculated the mean and standard errors of 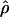of the windows in each category. We also averaged per population, the estimates of telomeric, centromeric, and “rest of the genome” for each chromosome and tested in a partial regression (Cohen et al. 2003) whether the adjusted means of the telomeric regions were lower in Han Chinese than they were in the other populations given the difference in means in centromeric and “rest of the genome” regions. For this analysis, we log-transformed the means of the population recombination rate per region per chromosome to meet the assumption of normality in the partial regression.

We analyzed the ratio 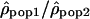by dividing, for each window, the estimate of ρ in one population by the estimate of ρ in another population. We used the logarithm of the ratios to give identical weight to both populations and validate the assumption of normality. To estimate whether the variation of the ratios along the chromosomes differs from a uniform distribution, we calculated the autocorrelation between the ratios 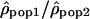of adjacent windows. The autocorrelation of the ratio 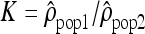in window i with window (i + 1) (i.e., lag of one) is given by (Box et al. 1994):

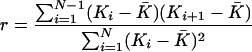where N is the total number of consecutive windows (N = 2556). For all three ratio series, we investigated the distribution along the genome of the 5% most extreme ratios (i.e., the 2.5% lowest and 2.5% highest values). We tested whether some chromosomes were significantly richer or poorer in these extreme ratios than expected under a uniform distribution across the genome using a χ² test. We also investigated how the 5% most extreme windows were distributed with regard to their chromosomal position. For this purpose, we divided the windows into telomeric region, centromeric region, and the rest of the genome (using the criteria mentioned above) and evaluated with a χ² test whether the distribution of the extreme ratios into these categories was significantly different from a uniform distribution along the chromosomes. Finally, we tested whether windows with an extreme ratio of 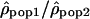clustered in some parts of the genome by screening for regions with at least two such extreme ratios within 3 Mb, where all the extreme ratios had to be either in the 2.5% highest or in the 2.5% lowest end of the distribution.

To estimate the influence of the sampling scheme, we compared this data set with the data produced by the HapMap project (The International HapMap Consortium 2003) for individuals from four populations: CEPH (Utah residents with ancestry from northern and western Europe), Yoruba (from Ibadan, Nigeria), Han Chinese (from Beijing, China), and Japanese (from Tokyo, Japan). We used genotypes produced at McGill University and Genome Quebec Innovation Center that cover the entire Chromosome 2 and the short arm of Chromosome 4 (for a total of 281 nonoverlapping windows of 1 Mb). At the time of the analysis, the HapMap data consisted of approximately one SNP every 4 kb (Release #15, February 2005). To have identical sample size in all populations, we only considered 45 of the 60 unrelated individuals for the CEPH and Yoruba populations. Most of the SNPs of two data sets are different, and the choice of the SNPs followed different strategies for both projects (Hinds et al. 2005). Most of the European individuals are common in these two data sets, while the individuals from the other populations are different. We compared the mean of the population recombination rates for the European-Americans and Han Chinese in the two data sets and tested whether the variance in the estimates differs with an F test. All analyses performed using genome-wide information from Perlegen were replicated using the HapMap genotypes of the individuals from the four populations for Chromosomes 2 and 4p.