Abstract
The dynamics of biological processes depend on the structure and flexibility of the interacting molecules. In particular, the conformational diversity of DNA allows for large deformations upon binding. Drug–DNA interactions are of high pharmaceutical interest since the mode of action of anticancer, antiviral, antibacterial and other drugs is directly associated with their binding to DNA. A reliable prediction of drug–DNA binding at the atomic level by molecular docking methods provides the basis for the design of new drug compounds. Here, we propose a novel Monte Carlo (MC) algorithm for drug–DNA docking that accounts for the molecular flexibility of both constituents and samples the docking geometry without any prior binding-site selection. The binding of the antimalarial drug methylene blue at the DNA minor groove with a preference of binding to AT-rich over GC-rich base sequences is obtained in MC simulations in accordance with experimental data. In addition, the transition between two drug–DNA-binding modes, intercalation and minor-groove binding, has been achieved in dependence on the DNA base sequence. The reliable ab initio prediction of drug–DNA binding achieved by our new MC docking algorithm is an important step towards a realistic description of the structure and dynamics of molecular recognition in biological systems.
INTRODUCTION
Ligand binding to macromolecules plays a key role in biology and medicine as steering mechanism in biological processes. More specifically, the binding of drugs to proteins and DNA has been of great interest in recent years leading to a large body of structural studies using both experimental and theoretical methods. Owing to the central role of DNA in replication and transcription, DNA has been a major target for antibiotic, anticancer and antiviral drugs (1). The effects of nucleic acid binding drugs are known for various diseases such as cancer, malaria, AIDS and other viral, bacterial and fungal infections (2). The majority of DNA drugs are aromatic compounds of low molecular weight often carrying positive charges (3). The different modes of drug binding to DNA include intercalation between adjacent base pairs, intrusion into the minor groove and into the major groove. Intercalation and minor-groove binding are the predominant DNA-binding modes of small ligands (2–4). Sequence specificity of drug–DNA binding is limited owing to the restricted size of drugs but is generally higher for minor-groove binders than for intercalators (2,3).
Atomic-resolution structures of drug–DNA complexes have been reported by X-ray crystallography and NMR spectroscopy (4–8). Most of the DNA intercalating drugs show preferences to bind sequences of alternating purine and pyrimidine bases and GC-rich sequences (2,6). Intercalation requires a major deformation owing to the formation of a binding cavity (3,4), in contrast to minor-groove binding that does not require major conformational changes of the DNA (3). The majority of DNA-binding drugs binds at the minor groove of B-DNA and show a higher affinity for AT-rich sequences (4,7,9). The minor groove of sequences with alternating A and T bases is generally narrow allowing favorable van der Waals contacts between the drug and the DNA (4,8) in contrast to GC-rich sequences where bulky amino groups of guanine bases at the minor groove affect the groove geometry (2,7). The advancement in understanding sequence-specific drug–DNA recognition allows for designing improved new drugs (8). The DNA major groove offers more specific contacts for establishing hydrogen bonds with the drug but van der Waals contacts are less favorable owing to groove dimensions (2). Also, the major groove is often occupied by proteins whose biological activity can be affected by minor-groove binding drugs (2). Drug–DNA binding is in most cases non-covalent although covalent bonds may be formed with reactive ligands (3,4).
Studies on the prediction of interaction modes between biological molecules have been always a major driving force in the development of molecular modeling algorithms. Studies on drug–DNA binding were performed in order to elucidate the energetic origins of the binding in terms of intermolecular forces and induced conformational changes and to develop new drug design strategies (10–13). Thermodynamic studies have analyzed drug binding to DNA in terms of free energy as the interplay between unfavorable deformations and entropy losses on one hand and favorable hydrophobic, electrostatic and van der Waals contributions on the other (11–14). Molecular modeling studies of drug–DNA interactions have been limited owing to the complexity of such systems. Therefore, binding-site predictions are often biased by a prior ligand positioning relative to the target molecule (15). Molecular dynamics (MD) simulations of drug–DNA complexes were reported for timescales ≤10 ns providing information on the flexibility of the structure of the complex within a single energy minimum (14,16). A sufficient sampling of the conformational space including transitions between different energy minima requires longer time scales that are not reachable in state-of-the-art MD simulations (15). In contrast to contemporary methods, a novel Monte Carlo (MC) approach for nucleic acids has been successful in sampling the structure and flexibility of papillomavirus E2-DNA-binding sites providing new insights into the origins of intrinsic DNA bending (17,18).
Molecular docking is a computational method for predicting ligand–receptor binding when both the binding site and binding mode are unknown (19). Docking studies were focused mainly on protein-related systems and have been restricted until recently to rigid molecules of either one or both constituents of the complex (19–22). Recent developments include partial flexibility in the docking process (23), either directly by applying certain degrees of freedom such as side chain rotations (24–27) or by docking an ensemble of conformations of the target molecules (28–32). In addition, previous docking approaches for small ligands were biased by prior binding-site definitions (20,22,27,28). The number of docking studies that involve DNA is very small and in these studies DNA was treated as a rigid molecule although nucleic acids are in general much more flexible than proteins (33–36). Limited conformational flexibility of DNA was included by modifying specific structural parameters such as overall winding and bending (37). Several studies applied MC methods for either rigid body moves of the DNA and protein components in the docking process (33,34,37) or post-docking energy minimizations (38). Docking algorithms are based on reduced atom representations (30,33), all-atom force fields (34,37) or knowledge-based potentials for specific ligand–DNA interactions (39).
This study presents a new docking algorithm that combines full flexibility of both the DNA and the ligand with an all-atom force field. The proposed algorithm is an ab initio docking method without any bias in the binding-site sampling. Both the moves of the drug and the DNA target relative to each other and the internal flexibility of the two molecules are defined by MC variables. The docking method is based on the assumption of fixed bond lengths (17). We have chosen to demonstrate the method of flexible MC docking to methylene blue (MB)–DNA binding because the binding mode in this system depends on the DNA base sequence and not on the propensity of the drug to act as a minor-groove binder or an intercalator. The structural information on MB binding to DNA is based on spectroscopic data suggesting that MB binds preferentially at the minor groove of DNA with alternating AT bases and intercalates into DNA of the analogous alternating GC sequence (40) in accordance with energy minimization studies (41–43). Owing to the sequence dependence of MB–DNA binding, this system is appropriate for the assessment of a novel ab initio docking method because the choice of the drug doesn't imply any prior binding-geometry definition. MB has drug-like structural properties including cationic charge and an extended aromatic system. Also, MB has only four rotatable methyl groups as internal degrees of freedom. MB is a phenothiazinium dye whose photosensitizing and antimalarial activity accounts for its pharmacological importance (44,45). Our flexible ab initio docking of MB to DNA and the MC sampling of MB–DNA-binding sites and binding modes provide new insights into the sequence dependence of drug–DNA binding.
MATERIALS AND METHODS
The flexible drug–DNA docking and conformational sampling of drug–DNA binding are based on a new MC approach developed for DNA (46,47). Based on the constant bond length approximation, the MC algorithm combines collective with internal variable moves. Each nucleotide is described by rigid-body translations and rotations (six collective variables) complemented by variations of the sugar phase and amplitude, the glycosidic angle, two endocyclic torsion and one endocyclic bond angle of the DNA backbone (six internal variables). This set of 12 variables per nucleotide, complemented by rotations of the thymine methyl groups, ensures local MC moves but results in DNA strand breaks. The DNA backbone is closed after each chain breakage by an analytical method defined in the torsion and bond angle space (47). Thus, all endocyclic torsion and bond angles are varied either as independent MC or dependent closure variables. Explicit sodium ions electro-neutralize the polyanionic system and their Cartesian coordinates are used to define MC moves of the counter ions. Energy calculations are based on the Cornell et al. (48) AMBER force field. In addition, an implicit solvent description (49,50) is used and a force field artifact in favor of non-canonical backbone conformation has been corrected (46). The MC algorithm for nucleic acids has been shown to result in fast equilibration and efficient conformational sampling (17).
Herein, we propose a new MC algorithm for ab initio drug docking to DNA. The entirety of MC variables for nucleic acids and counter ions, whose modifications comprise one MC cycle, includes rigid-body translations and rotations of the ligand relative to the DNA and additional internal variables describing the internal flexibility of the specific drug. A ligand-based reference axes system has been defined (41), and the MB molecule is translated and rotated relative to the DNA global helix axis and a central reference nucleotide (six collective variables). As shown in Figure 1, MB is a planar heterocyclic molecule that contains four rotatable methyl groups representing its flexibility within the approximation of fixed bond lengths and a rigid aromatic system (four internal variables). Thus, 10 MC variables have been added for the entirely flexible treatment of MB–DNA complexes in MC simulations. In view of the cationic charge of MB, the number of counter ions was adjusted to ensure electro-neutrality. The drug and the counter ions move freely within a cylinder around the DNA helix of a radius of 100 Å from the global helix axis and a height of twice the DNA length. Both drug and ions are reflected from the cylinder's inner surface if they cross the cylinder borders.
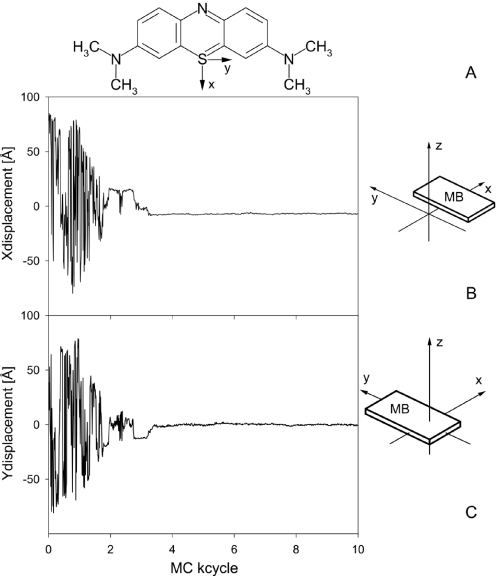
Figure 1.
MB and its position throughout the docking process. The drug-based axis system is depicted in the chemical structure of MB (A). The structural parameters X-displacement (B) and Y-displacement (C) of MB are shown as a function of MC cycles during the initial 10 MC kcycles for the docking trial with the lowest total energy on average. The translational parameters are calculated based on the position of the drug-based axis system with respect to the DNA global helix-axis system (41).
The MC docking simulations were performed with MB initially placed at the periphery of the DNA surrounding cylinder. For statistical reasons, MC simulations were started from 20 different initial configurations with MB at distances of 30–100 Å from the central DNA base pairs. The docking target used is a DNA dodecamer of the sequence 5′-GCGCGCATATAT-3′. The combination of two hexamers of different sequences of alternating bases, referred to as GC-tract and AT-tract, enables docking simulations that search for base sequence preferences in addition to establishing the binding mode. The purine–pyrimidine alternating sequences have been chosen because the available spectroscopic data were reported for such DNA targets (40). The MC docking simulations comprise 500 MC kcycles each providing only a rough sampling of binding sites rather than full equilibration.
In order to obtain a comprehensive sampling of binding sites and binding modes, MC simulations were started from previously reported conformations of MB bound to DNA (41,43). To explore base sequence effects on drug–DNA binding, MC simulations were performed on MB binding to DNA dodecamers with alternating AT or alternating GC base sequences. These MC simulations of MB–DNA complexes were performed with 2000 MC kcycles in order to achieve full equilibration. Thus, two aspects of drug–DNA recognition namely docking and binding-mode sampling are combined in this study.
RESULTS AND DISCUSSION
Flexible ab initio MB–DNA docking
Docking simulations were started from 20 different configurations with MB off the center of the DNA target by either a radial distance of 90 Å on average (85% of the trials) or an axial distance of 34 Å on average (15%). The docking of MB to DNA was achieved in all docking trials with a stable MB–DNA binding established within the initial 3–26 MC kcycles, as stated in Table 1. The docking process is illustrated for the energetically best-rated prediction by the following: (i) in terms of X-displacement and Y-displacement of MB (Figure 1), (ii) by MC snapshots throughout the docking process and initial binding-site sampling (Figure 2) and (iii) in terms of Rise of MB and total energy of the MB–DNA complex including sodium counter ions (Figure 3). The translational parameters X-displacement, Y-displacement and Rise of MB are calculated as defined in Ref. (41) based on the drug-based axis system (Figure 1). For reasons of clarity, it should be emphasized that MC trajectories contain ensembles and do not reflect any timescale of dynamic processes.
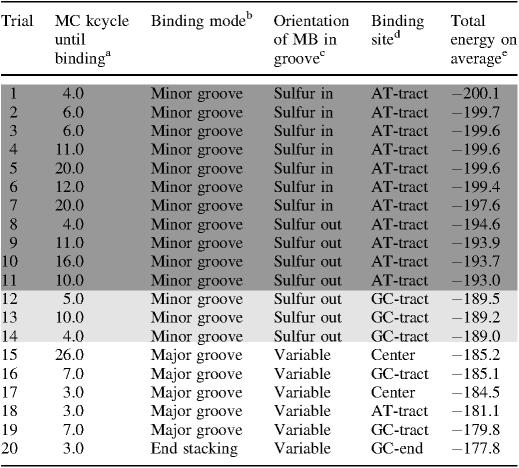
Table 1.
Binding modes and sites achieved by the docking in MC simulations
The number of MC cycles for establishing MB–DNA bindinga is given for the 20 MC docking trials starting from different positions and orientations of MB relative to the DNA, complemented by the resulting binding modeb with a specification of the orientation of MBc (Sulfur in: Sulfur points into the groove; Sulfur out: Sulfur points outside the groove; Variable: the orientation is variable), and the final DNA-binding site of MBd. The docking trials are ordered by the average of the total energy (in kcal/mol)e calculated on the basis of every 10th snapshot conformation from 50 to the 500 MC kcycles, hence after MB binding to DNA was achieved.
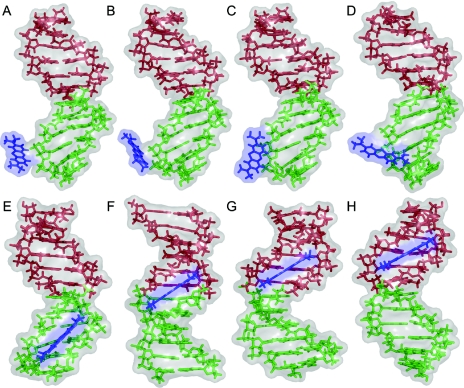
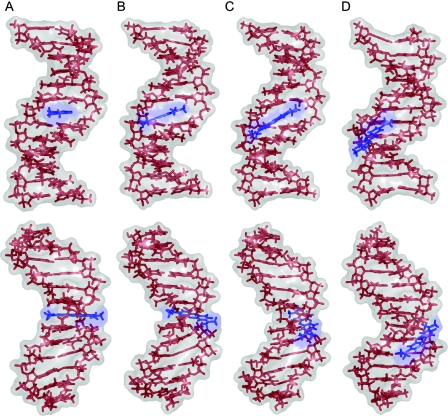
Figure 2.
MC snapshot conformations of MB–DNA docking and binding-site transitions. The docking process is illustrated for the docking trial with the lowest total energy on average. The upper panel shows MC snapshots after 196 MC cycles (A) 223 MC cycles (B) 262 MC cycles (C) and 280 MC cycles (D). The lower panel shows MC snapshots after 342 MC cycles (E), 1780 MC cycles (F) 7070 MC cycles (G) and 8740 MC cycles (H). The views are varied by rotations around the DNA helix axis in order to face the drug-binding site. MB is shown in blue and the two DNA tracts with different alternating base sequences in green (GC-tract) and red (AT-tract). Note that although the view is rotated there are no major deformations of the DNA target upon minor-groove binding.
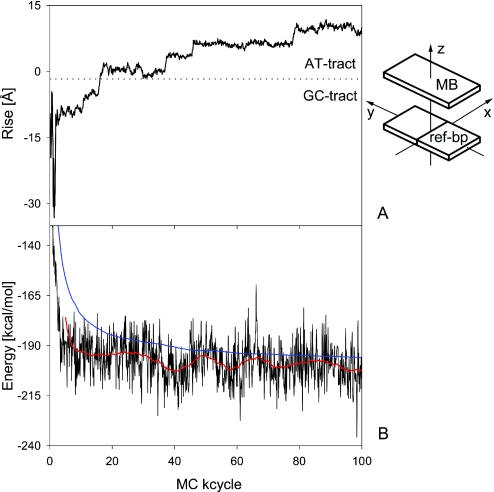
Figure 3.
Drug position and total energy throughout the docking and migration of MB. The structural parameter Rise of MB (A) and the total energy of the system (B), consisting of MB, the DNA target and counter ions, are shown as a function of MC cycles during the initial 100 MC kcycles for the docking trial with the lowest total energy on average. The Rise of MB is calculated based on the position of the drug-based axis system with respect to the plane of the central 6:C–G base pair (41) and illustrates the migration of MB along the minor groove from the GC-tract (bp 1–6, negative Rise of MB) to the AT-tract (bp 7–12, positive Rise of MB). The total energy values of every 100th MC snapshot (in black) are complemented by their smoothed course (in red) and accumulated averages proving an efficient equilibration (in blue).
The number of 9.4 MC kcycles that was required on average to establish an MB–DNA complex corresponds to ∼100 min CPU time of a Linux-operated 2.7 GHz processor. Thus, considering the full flexibility of both partner molecules throughout the docking process, the new MC algorithm proves to be a highly efficient docking method. Beside the efficiency, another crucial requirement for successful docking is the reliability of the binding prediction. Docking into an intercalation cavity has not been achieved so far by contemporary methods and is not likely to occur without the use of constraints forcing cavity opening throughout the docking process. Our simulations of MB binding at the surface of a flexible DNA are performed without the application of any constraints. In addition, the target-dodecamer is composed of two hexamers differing in their base sequence. Therefore, the docking includes the prediction of sequence preferences of MB–DNA binding.
Of the 20 docking trials 14 (70%) result in minor-groove binding whereas 5 of the trials (25%) predict major-groove binding, and only 1 (5%) of them indicates that MB is bound by stacking interactions to the end base pair of the GC-tract. The different docking predictions are listed in Table 1 rated on the basis of the total average energy after binding and preliminary equilibration was achieved (MC trajectory from 50 to 500 MC kcycles). Remarkably, the 14 of the docking trials (70%) predicting minor-groove binding are energetically best rated. In 11 of the minor-groove binding predictions (78%), MB binds to the AT-tract of the DNA target and in the remaining 3 (22%) to the GC-tract. A significant drop in the total energy of 3.5 kcal/mol between docking trials #11 (highest energy for AT-tract binding) and #12 (lowest energy for GC-tract binding) demonstrates that MB binding in the minor groove of AT-rich sequences is most favorable. MB is inserted into the minor groove in two different orientations with its central sulfur atom either making van der Waals contacts with the floor of the groove or directed outwards the groove. In the latter orientation, MB's central nitrogen atom is inserted into the groove allowing for favorable hydrogen bonding with the DNA. Interestingly, of the two orientations of MB within the minor groove the one with the sulfur atom pointing into the groove is energetically in favor (by 3 kcal/mol). The two orientations of MB are uniformly distributed among the docking trials that predict minor-groove binding. However, the less favored orientation of MB for binding at the minor groove of the AT-tract (sulfur atom directed outwards) is the only one shown by minor-groove binding of MB to the GC-tract.
In four of the AT-tract binding predictions, MB was bound initially to the GC-tract but migrated throughout the simulation towards the AT-tract. This migration is illustrated for the top docking trial (#1 in Table 1) by MC snapshot conformations (Figure 2) and by the transition from a negative Rise of MB (i.e. bound to the GC-tract) to a positive Rise (i.e. bound to the AT-tract) with respect to the reference base pair 6:C–G in the center of the DNA target (Figure 3). MB binds to DNA in docking trial #1 within <5 MC kcycles as illustrated by translational parameters of MB (Figure 1). MB approaches the DNA backbone in an orientation that does not enable a stable binding (Figure 2A). Following a re-orientation of the drug the interaction becomes more favorable (Figure 2B). This is followed by enhanced contact surface between the drug and the DNA phosphodiester backbone that allows for favorable van der Waals interactions as well as electrostatic attraction between the cationic drug and polyanionic DNA phosphate groups (Figure 2C). Starting from this stabilized binding, MB intrudes the DNA minor groove first partly with one of its edges (Figure 2D) and then as a whole (Figure 2E). Thus, major re-orientation of MB induced by the interplay of attractive and repulsive interactions were needed to achieve MB binding at the minor groove.
In docking trial #1, MB binds initially at the minor groove of the GC-tract (Figure 2E) and migrates via the junction between the two hexamer tracts (Figure 2F) towards the AT-tract (Figures 2G) finally reaching the center of the AT-tract (Figure 2H). This migration from the GC- to the AT-tract minor groove requires 50 MC kcycles reflected by the Rise of MB (Figure 3), a parameter that describes the drug translation along the DNA helix axis. The initial MB binding to the GC-tract (MB Rise of −9.2 Å averaged over the first 15 MC kcycles) changes via distinct transition sites to the AT-tract (MB Rise of +9.9 Å averaged over the last 20 MC kcycles of the shown period). The MB Rise shows a much smaller SD of ±0.7 Å between 80 and 100 MC kcycles in comparison with ±5.0 Å during the initial 15 MC kcycles indicating the stabilization of MB binding at the AT-tract minor groove.
The migration of MB from the GC- to the AT-tract demonstrates an efficient binding-site sampling within a relatively small number of MC simulation cycles. Notably, in all the docking trials where MB moved from the GC- to the AT-tract, the sulfur atom pointed towards the groove's interior. In contrast, the GC-tract binding predictions were characterized by the opposite orientation of MB. The bulky amino groups of the guanine bases hinder the migration of MB along the minor groove. In addition, if MB acts as a hydrogen-bond acceptor via its central nitrogen atom interacting with guanine amino groups, this hydrogen bond further hampers transition between minor-groove binding sites. Such interactions stabilize the minor-groove binding of MB to the GC-tract in docking trials #12–14 (Table 1) although migration towards the AT-tract is probable to occur in longer MC simulations.
Major-groove binding is predicted by only four of the docking trials (25%). The difference in total average energy between the least-favorable minor-groove binding and the most favorable major-groove binding prediction is 3.8 kcal/mol. The major-groove binding complexes are characterized by highly variable positions and orientations of the ligand relative to the target-DNA. MB ‘travels’ and ‘turns’ within the wide major groove showing intermediate configurations that are stabilized by non-specific van der Waals contacts between MB and the DNA. In addition, MB makes excursions from the center of the major groove towards the polyanionic phosphodiester backbone where the electrostatic interaction with the cationic drug contributes to binding.
A single docking trial (5%) results in stacking of MB at the GC-end base pair associated with a rise of 2 kcal/mol in the average energy compared with major-groove binding. It should be noted that MB binding by end stacking is due to the use of a DNA target of a finite length, making this configuration somewhat artificial but yet an appropriate model-dependent binding site. Transitions from end stacking to minor-groove binding in two docking trials (#4 and #8), both from AT-end stacking, occurred within the initial docking period as given in Table 1. In case of docking trial #11, the transition from a long-lasting GC-end stacking to minor-groove binding occurred only after 143 MC kcycles. The unfavorable stacking persistence is reflected by the lower average energy. However, end stacking can be considered as intercalation-like binding owing to similar stacking interactions. Thus, the higher stability of GC-end over AT-end stacking refers to the preference of MB to bind GC-rich sequences by intercalation (40,41).
The strong preference of minor-groove over major-groove binding (70%) obtained by the docking simulations is in agreement with available spectroscopic data (40). This result is remarkable because the insertion of MB into the narrow minor groove is by far more complex than its insertion into the spacious major groove. Electrostatic attraction is the major driving force for the docking of MB onto DNA. Following this attraction, MB can easily penetrate into the major groove in any orientation whereas penetration into the minor groove requires a specific orientation of MB approximately parallel to the DNA backbone. The prediction of MB binding at the narrow minor groove is possible because the MC docking algorithm enables re-orientations of the drug molecule following specific interactions at the DNA surface.
The MC docking does not predict intercalation for two reasons: (i) the formation of an intercalation cavity is associated with high-energy barriers involving base unstacking, DNA untwisting and transitions to non-canonical backbone conformations; (ii) the insertion of the drug into the cavity and the formation of the intercalation pocket must occur simultaneously. Spectroscopic data and theoretical studies have shown that MB minor-groove binding is the favored binding mode in the case of DNA with alternating AT base sequence whereas intercalation is favored for DNA with sequences of alternating GC bases (40,41,43). The preference of minor-groove binding drugs for AT-rich sequences is ascribed to favorable hydrophobic and van der Waals interactions (13,14), which is in accordance with experimental data for MB and other DNA drugs (4,7,9). Since an atomic-resolution structure of MB bound to DNA is not yet available, there is no experimental evidence regarding the orientation of MB when it is bound at the minor groove. According to two criteria, prediction statistics and energy ranking, MC docking of MB to DNA results in both energetically favorable binding mode and binding site.
MB–DNA-binding mode transition
We performed MC simulations (2000 MC kcycles) of MB binding to DNA dodecamers with sequences of alternating AT or alternating GC bases. The starting configurations of the MC simulations presented here were obtained previously by energy minimization studies in conjunction with a continuum treatment of solvent effects (41,43). MB is initially intercalated in gauche orientation at the central TpA base pair of the dodecamer with alternating AT sequence (43). Gauche intercalation describes the rotation of MB by ∼140° around the DNA helix axis with respect to the parallel orientation where the long axis of MB is parallel to those of the flanking base pairs (41). MB is initially intercalated in parallel orientation at the central CpG base pair of the dodecamer with alternating GC sequence resulting in dyad symmetry of the complex as the long axis of MB coincides with the dyad axis of the DNA (41).
MC snapshot conformations illustrating the transition from MB intercalation to minor-groove binding are shown in Figure 4. The intercalation although being energetically less favorable local-minimum structure (Figure 4A) persists throughout 1100 MC kcycles, taking 7–8 days CPU time of a Linux-operated 2.7 GHz processor. During this period, the structure is getting prepared for the drug release by reversing non-canonical α/γ torsion-angle flips of the DNA backbone. Several transitions between (−gauche, +gauche) and (trans, trans) conformations of the (α, γ) torsion angles at the intercalation cavity occur in both directions without binding-mode implications. The repeated reversal of the α/γ-flip in the first strand towards canonical backbone conformations after 975 MC kcycles is the essential step that increases the helix winding at the intercalation site and hence hampers the stabilizing stacking interactions of the drug with its adjacent base pairs. Following this, the drug vacates the intercalation cavity after 1100.2 MC kcycles within only 1 MC kcycle (Figure 4B and C). The closure of the intercalation cavity occurs immediately within the following 5 MC kcycles. However, the binding-mode transition is completed only after 1125.7 MC kcycles (Figure 4D) when the α/γ-flip of the second strand is replaced by canonical backbone conformations. Thus, the binding-mode transition occurs throughout 25.5 MC kcycles, for which 4–5 h CPU time are required.
Figure 4.
MC snapshot conformations of the MB–DNA-binding-mode transition. The transition from MB intercalation (A) to minor-groove binding (D) is illustrated in two different orientations: a view into the central minor groove (upper panel) and a view perpendicular to that direction (lower panel). MC snapshots show the intercalation before the transition after 1100.2 MC kcycles (A), intermediate states after 1100.8 MC kcycles (B) and 1101.3 MC kcycles (C), and the resulting minor-groove binding after 1125.7 MC kcycles when the backbone has taken up canonical conformations (D). MB is shown in blue and the DNA with alternating AT base sequence in red.
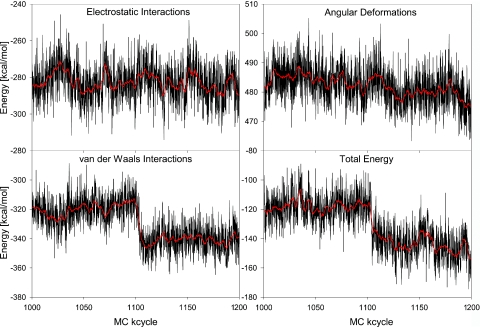
The energetics of the binding-mode transition is shown in Figure 5 for the trajectory between 1000 and 1200 MC kcycles. Here, the total energy is decomposed into the three components: electrostatic, van der Waals and angular deformation energy. The spontaneous drop in the total energy upon the binding-mode transition is caused by favorable van der Waals interactions as a result of MB minor-groove binding. In contrast to the van der Waals energy, there is no significant variation in the electrostatic energy. The angular deformation energy becomes more favorable after MB migrates to the minor groove owing to transitions from non-canonical backbone conformations associated with drug intercalation to canonical ones. In comparison with the spontaneous drop in the van der Waals energy, the angular deformation energy decreases in a slower rate along the MC trajectory. However, a drop in the deformation energy marks the reversal to canonical backbone conformations of the second DNA strand after 1125.7 MC kcycles.
Figure 5.
Energy variation upon the MB–DNA-binding-mode transition. The energy components and total energy are shown as a function of MC cycles for the part of the trajectory between 1000 and 1200 MC kcycles that includes the transition from MB intercalation to minor-groove binding. The binding-mode transition occurs shortly after 1100 MC kcycles. MC snapshot values of every 100th MC cycle (in black) are complemented by their smoothed course over the MC trajectory (in red).
The energy profiles in Figure 5 clearly identify van der Waals interactions as the major driving force that induces the transition from MB intercalation to minor-groove binding. A detailed trajectory analysis rationalizes the relatively long trajectory required for this transition as follows. The reversal of one of the α/γ-flips reduces the relative stability of the intercalation cavity. Also, in a conformational excursion shortly before the binding-mode transition, a minor-groove narrowing of the DNA region that eventually absorbs the drug occurs after 1025 MC kcycles. This groove narrowing is associated with an inter-strand stacking of adenine bases that results in a channel-shaped minor groove into which the drug penetrates after leaving the intercalation site. Figure 5 illustrates that this transition state is characterized by more favorable van der Waals interactions and higher electrostatic repulsion owing to shorter inter-strand backbone distances. Favorable interactions of the drug with the walls of the DNA minor groove assist in completing the binding-mode transition.
The conformational MC ensemble has been divided into two sub-ensembles that represent the initial intercalation and the final minor-groove binding. Rough conformational equilibration is usually reached within 250 MC kcycles from the start of the MC simulation as shown for DNA (17). After the binding-mode transition, 150 MC kcycles are considered as rough re-equilibration period. Thus, the MC sub-ensemble between 250 and 1000 MC kcycles characterizes intercalation (Phase I), and the MC sub-ensemble between 1250 and 2000 MC kcycles represents minor-groove binding (Phase II). The average structural and energetic characteristics of the two sub-ensembles comprised of equal numbers of MC snapshot structures are given in Table 2.
Table 2.
Structural and energetic comparison of intercalation and minor-groove binding
| Phase Ia | Phase IIa | Differenced | |
|---|---|---|---|
| Structural parametersb | |||
| Rise (Å) | 7.0 ± 0.4 | 3.4 ± 0.3 | |
| Roll (degrees) | −13.6 ± 6.8 | 2.9 ± 7.6 | |
| Helix Twist (degrees) | 26.7 ± 6.9 | 37.8 ± 4.5 | |
| Sugar phases (degrees) | 74.4 ± 48.9/93.2 ± 48.8 | 145.8 ± 19.0/145.7 ± 20.0 | |
| Energy terms (kcal/mol)c | |||
| Total energy | −117.8 | −146.7 | −28.9 |
| Electrostatic interactions | −282.3 | −283.7 | −1.4 |
| DNA–DNA | −203.7 | −201.4 | 2.3 |
| DNA–MB | −12.0 | −12.0 | 0.0 |
| DNA–ions | −95.8 | −101.5 | −5.7 |
| MB–ions | 4.1 | 4.1 | 0.0 |
| MB–MB | 1.7 | 1.7 | 0.0 |
| Ions–ions | 23.4 | 25.4 | 2.0 |
| Van der Waals interactions | −321.4 | −343.2 | −21.8 |
| DNA–DNA | −284.4 | −308.0 | −23.6 |
| DNA–MB | −43.7 | −41.5 | 2.2 |
| DNA–ions | −1.0 | −1.4 | −0.4 |
| MB–ions | −0.1 | −0.1 | 0.0 |
| MB–MB | 7.8 | 7.8 | 0.0 |
| Ions–ions | 0.0 | 0.0 | 0.0 |
| Angular deformations | 485.9 | 480.2 | −5.7 |
Intercalation of MB between adjacent base pairs in Phase I (250–1000 MC kcycles) and MB–DNA minor-groove binding in Phase II (1250–2000 MC kcycles)a are compared on the basis of structural parameters at the central base pair stepb, as defined by CURVES (51,52), and the energy decomposition for the complete system drug–DNA–ionsc. The given structural parameters and energy values are MC ensemble averages of every 10th snapshot conformation within the respective part of the trajectory. Rise, Roll, Helix Twist and the sugar phase values given along with their SDs refer to the central TpA intercalation site. The total energy is composed of electrostatic, van der Waals and angular deformation energy contributions. The further decomposition of the pairwise interactions is given for different components of the system whereas the deformation energy applies to DNA torsion and bond angles. The energy differences between Phase I and Phase IId illustrate the energetic variation upon the binding-mode transition.
The average structural parameters of the central base pair step of the DNA target in Phase I are characteristic of the intercalation geometry as follows. The large Rise of 7.0 Å is due to the stacking interactions of MB with two adjacent base pairs at the intercalation site. The low Helix Twist of 26.7° characterizes local helix unwinding and the sugar moieties show O1′-endo puckering modes, both were shown to be associated with intercalation. In contrast to Phase I, the structural parameters in Phase II (Rise of 3.4 Å, Helix Twist of 37.8°) are typical of canonical B-DNA since minor-groove binding does not require major DNA deformations. The C2′-endo sugar puckers are also typical of B-DNA, unlike the corresponding values at the intercalation site which are non-symmetrical owing to long-living α/γ-flips. SDs of the structural parameters are given in Table 2, indicating a higher flexibility of the sugar puckering at the intercalation site in comparison with sugar moieties in B-DNA environment.
The stabilization of the corresponding binding modes of the conformational ensembles in Phase I and Phase II is compared in terms of the various energy components given in Table 2. Here, we do not analyze the actual transition as shown in Figure 3 but compare the reasonably equilibrated MC sub-ensembles of the two different binding modes. Minor-groove binding is favored over intercalation by 28.9 kcal/mol. This is contributed mainly by van der Waals interactions (21.8 kcal/mol) with DNA–DNA interactions (23.6 kcal/mol) dominating the overall van der Waals effect. In contrast, van der Waals interactions between MB and the DNA are more favorable for intercalation than for minor-groove binding by 2.2 kcal/mol owing to stacking interactions. Second among the energetic contributions stands the angular deformation energy, which is less favorable for intercalation by 5.7 kcal/mol owing to non-canonical backbone conformations associated with backbone elongation at the intercalation cavity.
The difference in electrostatic energy is also in favor of minor-groove binding over intercalation although to a smaller extent (1.5 kcal/mol). However, the DNA–DNA electrostatics favors intercalation by 2.3 kcal/mol since the anionic charges are more dispersed owing to the helix lengthening. Counter-ion effects overcompensate the DNA–DNA repulsion through a more effective ion aggregation at the DNA surface. This variation in ion–DNA interaction results from ion repulsion by the cationic drug in the grooves. Thus, MB competes with the counter ions for DNA-binding sites. Figure 2 shows that the intercalated MB affects both grooves. However, the drug molecule does not interfere with ion aggregation in the major groove in the case of minor-groove binding. Yet, the electrostatic effects are relatively minor, and it should be recalled that our algorithm uses a simplified implicit solvent description. Despite these approximations, the MC sampling causes a transition from intercalation to minor-groove binding and yields the energetically favorable binding mode in agreement with spectroscopic and previous theoretical studies of MB–DNA binding (40,43).
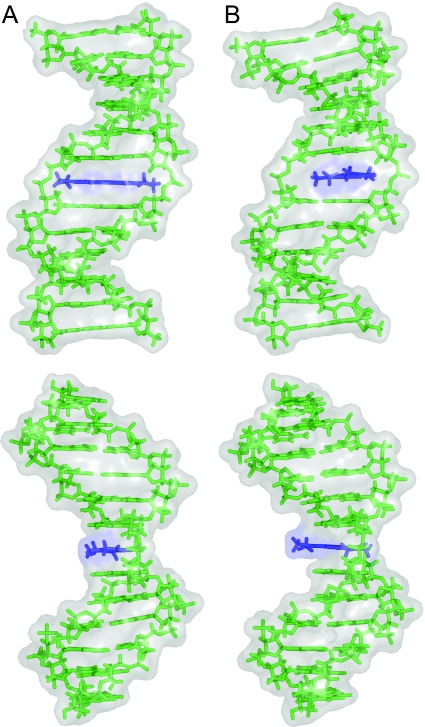
For reasons of comparison, MC simulations of MB binding by intercalation to a DNA dodecamer with a sequence of alternating GC bases were performed with the same protocol. Here, the binding mode does not alter along the MC trajectory of 2000 MC kcycles. The data confirm the stability of MB binding by intercalation to GC-rich sequences (40,41) although the stacking geometry varies by rotation of the MB plane around the DNA helix axis as shown in Figure 6. The symmetric intercalation with MB's long axis parallel to the neighboring base pairs represents the predominant intercalation geometry during the whole MC simulation. Structural parameters of MB as defined in Ref. (41) characterize intercalation modes using the drug-based axis system shown in Figure 1. In the MC snapshot shown in Figure 6A, MB is displaced towards the DNA major groove (positive X-displacement of 0.6 Å) and intercalated in parallel orientation (Helix Twist of 0.0°). Frequent conformational excursions vary the intercalation mode and hence the drug–DNA stacking geometry. To reach the orientation shown in Figure 6B, MB ‘turns’ around the DNA helix axis (Helix Twist of 50.0°), which allows for a deeper intrusion of MB into the intercalation cavity towards the minor groove (negative X-displacement of −1.8 Å). Despite the rotational flexibility of MB within the intercalation pocket, MB returns to the most stable symmetric intercalation.
Figure 6.
MC snapshot conformations of MB–DNA intercalation. The stacking geometry variation is illustrated by views into the central minor groove (upper panel) and views perpendicular to that direction (lower panel). MB is intercalated into the central CpG base pair step with a Helix Twist of 0.0° after 631 MC kcycles (A) and undergoes a conformational excursion reaching its maximal Helix Twist of 50.0° after 632.38 MC kcycles (B). The Helix Twist of MB is calculated based on the orientation of the drug-based axis system with respect to the central 6:C–G base pair (41). MB is shown in blue and the DNA with alternating GC base sequence in green.
Hence, the new MC approach samples the flexibility of the MB–DNA-binding geometry in dependence on the specific environment. Transitions between alternative binding sites and binding modes are assisted by internal MC variables of the binding partners. In particular, rotatable methyl groups of the drug and thymine bases act in a ‘gear-wheel’-like manner with van der Waals ‘cogs’. Interestingly, MB intercalated into DNA shows a different binding behavior in dependence on the base sequence. When bound to an AT-rich DNA sequence, the drug undergoes a transition from intercalation to minor-groove binding. When bound to a GC-rich DNA sequence, the drug persists to intercalate throughout the 2000 MC kcycles. Both results are in accordance with previously reported experimental data (40) and theoretical binding studies (41,43). Thus, our new MC algorithm demonstrates the sequence dependence of MB–DNA-binding modes.
SUMMARY AND CONCLUSIONS
The new MC algorithm for flexible drug–DNA docking has proven to be both efficient and reliable. The ab initio docking of MB to DNA can be accomplished fast within 100 min CPU time. In 70% of the energetically best rated binding predictions, the MC docking results in the energetically favorable binding mode that is MB minor-groove binding to DNA. Moreover, the AT-tract as the preferred minor-groove binding site is predicted by 78% of the corresponding docking trials. Both the drug and the DNA target are totally flexible and no constraints are applied during the simulations. The MC simulations sample the interactions of MB with the minor groove as demonstrated by the migration between different binding sites.
In addition, our all-atom MC simulations have achieved the transition between two interaction modes of the drug–DNA complex, intercalation between base pairs and minor-groove binding. The change in the binding mode has been analyzed in terms of structural and energetic aspects showing that van der Waals interactions are the driving force for this conversion. DNA deformations upon intercalation, such as cavity opening, helix unwinding and non-canonical conformations of the sugar-phosphate backbone, converge to structural parameters of B-DNA, which are characteristic of minor-groove binding. The migration between alternative binding sites and the transition between binding modes in reasonable simulation periods is achieved owing to the flexibility of the binding partners. Moreover, the transition between binding modes depends on the DNA base sequence. In accordance with experimental data, MB intercalation changes into minor-groove binding for AT-rich DNA but is stable for GC-rich DNA. Hence, the effect of the base sequence on drug–DNA-binding modes becomes a realistic object of molecular modeling in drug design studies in particular, and for understanding molecular recognition in biological processes in general.
Acknowledgments
The authors acknowledge Dr Miriam Eisenstein and Malka Kitayner from the Weizmann Institute of Science for valuable comments on the manuscript. R.R. acknowledges for funding the Minerva Foundation (Max Planck Society for the Advancement of Science) and the Kimmelman Center for Biomolecular Structure and Assembly (Weizmann Institute of Science). Z.S. acknowledges support from the Israel Science Foundation, the Minerva Foundation, and holds the Helena Rubinstein professorial chair in Structural Biology. Funding to pay the Open Access publication charges for this article was provided by the Kimmelman Center for Biomolecular Structure and Assembly.
Conflict of interest statement. None declared.
REFERENCES
- 1.Hurley L.H., Boyd F.L. DNA as a target for drug action. Trends Pharmacol. Sci. 1988;9:402–407. doi: 10.1016/0165-6147(88)90067-3. [DOI] [PubMed] [Google Scholar]
- 2.Bischoff G., Hoffmann S. DNA-binding of drugs used in medicinal therapies. Curr. Med. Chem. 2002;9:312–348. doi: 10.2174/0929867023371085. [DOI] [PubMed] [Google Scholar]
- 3.Han X., Gao X. Sequence specific recognition of ligand–DNA complexes studied by NMR. Curr. Med. Chem. 2001;8:551–581. doi: 10.2174/0929867003373337. [DOI] [PubMed] [Google Scholar]
- 4.Neidle S., Nunn C.M. Crystal structures of nucleic acids and their drug complexes. Nature Prod. Rep. 1998;15:1–15. doi: 10.1039/a815001y. [DOI] [PubMed] [Google Scholar]
- 5.Geierstanger B.H., Wemmer D.E. Complexes of the minor groove of DNA. Annu. Rev. Biophys. Biomol. Struct. 1995;24:463–493. doi: 10.1146/annurev.bb.24.060195.002335. [DOI] [PubMed] [Google Scholar]
- 6.Lisgarten J.N., Coll M., Portugal J., Wright C.W., Aymami J. The antimalarial and cytotoxic drug cryptolepine intercalates into DNA at cytosine–cytosine sites. Nature Struct. Biol. 2002;9:57–60. doi: 10.1038/nsb729. [DOI] [PubMed] [Google Scholar]
- 7.Neidle S. DNA minor-groove recognition by small molecules. Nature Prod. Rep. 2001;18:291–309. doi: 10.1039/a705982e. [DOI] [PubMed] [Google Scholar]
- 8.Wemmer D.E. Designed sequence-specific minor groove ligands. Annu. Rev. Biophys. Biomol. Struct. 2000;29:439–461. doi: 10.1146/annurev.biophys.29.1.439. [DOI] [PubMed] [Google Scholar]
- 9.Ren J., Chaires J.B. Sequence and structural selectivity of nucleic acid binding ligands. Biochemistry. 1999;38:16067–16075. doi: 10.1021/bi992070s. [DOI] [PubMed] [Google Scholar]
- 10.Chaires J.B. Drug–DNA interactions. Curr. Opin. Struct. Biol. 1998;8:314–320. doi: 10.1016/s0959-440x(98)80064-x. [DOI] [PubMed] [Google Scholar]
- 11.Chaires J.B. Energetics of drug–DNA interactions. Biopolymers. 1997;44:201–215. doi: 10.1002/(SICI)1097-0282(1997)44:3<201::AID-BIP2>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
- 12.Haq I., Ladbury J. Drug–DNA recognition: energetics and implications for design. J. Mol. Recognit. 2000;13:188–197. doi: 10.1002/1099-1352(200007/08)13:4<188::AID-JMR503>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
- 13.Haq I. Thermodynamics of drug–DNA interactions. Arch. Biochem. Biophys. 2002;403:1–15. doi: 10.1016/S0003-9861(02)00202-3. [DOI] [PubMed] [Google Scholar]
- 14.Shaikh S.A., Ahmed S.R., Jayaram B. A molecular thermodynamic view of DNA–drug interactions: a case study of 25 minor-groove binders. Arch. Biochem. Biophys. 2004;429:81–99. doi: 10.1016/j.abb.2004.05.019. [DOI] [PubMed] [Google Scholar]
- 15.Trent J.O. Molecular modeling of drug–DNA complexes: an update. Methods Enzymol. 2001;340:290–326. doi: 10.1016/s0076-6879(01)40428-9. [DOI] [PubMed] [Google Scholar]
- 16.Harris S.A., Gavathiotis E., Searle M.S., Orozco M., Laughton C.A. Cooperativity in drug–DNA recognition: a molecular dynamics study. J. Am. Chem. Soc. 2001;123:12658–12663. doi: 10.1021/ja016233n. [DOI] [PubMed] [Google Scholar]
- 17.Rohs R., Sklenar H., Shakked Z. Structural and energetic origins of sequence-dependent DNA bending: Monte Carlo simulations of papillomavirus E2-DNA binding sites. Structure. 2005;13:1499–1509. doi: 10.1016/j.str.2005.07.005. [DOI] [PubMed] [Google Scholar]
- 18.Siggers T., Silkov A., Honig B. Bending in the right direction. Structure. 2005;13:1400–1401. doi: 10.1016/j.str.2005.09.002. [DOI] [PubMed] [Google Scholar]
- 19.Halperin I., Ma B., Wolfson H., Nussinov R. Principles of docking: an overview of search algorithms and a guide to scoring functions. Proteins. 2002;47:409–443. doi: 10.1002/prot.10115. [DOI] [PubMed] [Google Scholar]
- 20.Ewing T.J., Makino S., Skillman A.G., Kuntz I.D. DOCK 4.0: search strategies for automated molecular docking of flexible molecule databases. J. Comput. Aided Mol. Des. 2001;15:411–428. doi: 10.1023/a:1011115820450. [DOI] [PubMed] [Google Scholar]
- 21.Eisenstein M., Katchalski-Katzir E. On proteins, grids, correlations, and docking. C. R. Biol. 2004;327:409–420. doi: 10.1016/j.crvi.2004.03.006. [DOI] [PubMed] [Google Scholar]
- 22.Lee K., Czaplewski C., Kim S.Y., Lee J. An efficient molecular docking using conformational space annealing. J. Comput. Chem. 2005;26:78–87. doi: 10.1002/jcc.20147. [DOI] [PubMed] [Google Scholar]
- 23.Eisenstein M. Introducing a 4th dimension to protein-protein docking. Structure. 2004;12:2095–2096. doi: 10.1016/j.str.2004.11.001. [DOI] [PubMed] [Google Scholar]
- 24.Mangoni M., Roccatano D., Di Nola A. Docking of flexible ligands to flexible receptors in solution by molecular dynamics simulation. Proteins. 1999;35:153–162. doi: 10.1002/(sici)1097-0134(19990501)35:2<153::aid-prot2>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- 25.Kimura S.R., Brower R.C., Vajda S., Camacho C.J. Dynamical view of the positions of key side chains in protein–protein recognition. Biophys. J. 2001;80:635–642. doi: 10.1016/S0006-3495(01)76044-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fernandez-Recio J., Totrov M., Abagyan R. ICM-DISCO docking by global energy optimization with fully flexible side-chains. Proteins. 2003;52:113–117. doi: 10.1002/prot.10383. [DOI] [PubMed] [Google Scholar]
- 27.Tatsumi R., Fukunishi Y., Nakamura H. A hybrid method of molecular dynamics and harmonic dynamics for docking of flexible ligand to flexible receptor. J. Comput. Chem. 2004;25:1995–2005. doi: 10.1002/jcc.20133. [DOI] [PubMed] [Google Scholar]
- 28.Claussen H., Buning C., Rarey M., Lengauer T. FlexE: efficient molecular docking considering protein structure variations. J. Mol. Biol. 2001;308:377–395. doi: 10.1006/jmbi.2001.4551. [DOI] [PubMed] [Google Scholar]
- 29.Gray J.J., Moughon S., Wang C., Schueler-Furman O., Kuhlman B., Rohl C.A., Baker D. Protein–protein docking with simultaneous optimization of rigid-body displacement and side-chain conformations. J. Mol. Biol. 2003;331:281–299. doi: 10.1016/s0022-2836(03)00670-3. [DOI] [PubMed] [Google Scholar]
- 30.Zacharias M. Protein–protein docking with a reduced protein model accounting for side-chain flexibility. Protein Sci. 2003;12:1271–1282. doi: 10.1110/ps.0239303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Grunberg R., Leckner J., Nilges M. Complementarity of structure ensembles in protein–protein binding. Structure. 2004;12:2125–2136. doi: 10.1016/j.str.2004.09.014. [DOI] [PubMed] [Google Scholar]
- 32.Smith G.R., Sternberg M.J., Bates P.A. The relationship between the flexibility of proteins and their conformational states on forming protein–protein complexes with an application to protein–protein docking. J. Mol. Biol. 2005;347:1077–1101. doi: 10.1016/j.jmb.2005.01.058. [DOI] [PubMed] [Google Scholar]
- 33.Knegtel R.M., Antoon J., Rullmann C., Boelens R., Kaptein R. MONTY: a Monte Carlo approach to protein–DNA recognition. J. Mol. Biol. 1994;235:318–324. doi: 10.1016/s0022-2836(05)80035-x. [DOI] [PubMed] [Google Scholar]
- 34.Bastard K., Thureau A., Lavery R., Prevost C. Docking macromolecules with flexible segments. J. Comput. Chem. 2003;24:1910–1920. doi: 10.1002/jcc.10329. [DOI] [PubMed] [Google Scholar]
- 35.Adesokan A.A., Roberts V.A., Lee K.W., Lins R.D., Briggs J.M. Prediction of HIV-1 integrase/viral DNA interactions in the catalytic domain by fast molecular docking. J. Med. Chem. 2004;47:821–828. doi: 10.1021/jm0301890. [DOI] [PubMed] [Google Scholar]
- 36.Roberts V.A., Case D.A., Tsui V. Predicting interactions of winged-helix transcription factors with DNA. Proteins. 2004;57:172–187. doi: 10.1002/prot.20193. [DOI] [PubMed] [Google Scholar]
- 37.Knegtel R.M., Boelens R., Kaptein R. Monte Carlo docking of protein–DNA complexes: incorporation of DNA flexibility and experimental data. Protein Eng. 1994;7:761–767. doi: 10.1093/protein/7.6.761. [DOI] [PubMed] [Google Scholar]
- 38.Caflisch A., Niederer P., Anliker M. Monte Carlo docking of oligopeptides to proteins. Proteins. 1992;13:223–230. doi: 10.1002/prot.340130305. [DOI] [PubMed] [Google Scholar]
- 39.Ge W., Schneider B., Olson W.K. Knowledge-based elastic potentials for docking drugs or proteins with nucleic acids. Biophys. J. 2005;88:1166–1190. doi: 10.1529/biophysj.104.043612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tuite E., Norden B. Sequence-specific interactions of methylene-blue with polynucleotides and DNA—a spectroscopic study. J. Am. Chem. Soc. 1994;116:7548–7556. [Google Scholar]
- 41.Rohs R., Sklenar H., Lavery R., Roder B. Methylene blue binding to DNA with alternating GC base sequence: a modeling study. J. Am. Chem. Soc. 2000;122:2860–2866. [Google Scholar]
- 42.Rohs R., Sklenar H. Methylene blue binding to DNA with alternating GC base sequence: continuum treatment of salt effects. Indian J. Biochem. Biophys. 2001;38:1–6. [PubMed] [Google Scholar]
- 43.Rohs R., Sklenar H. Methylene blue binding to DNA with alternating AT base sequence: minor groove binding is favored over intercalation. J. Biomol. Struct. Dyn. 2004;21:699–711. doi: 10.1080/07391102.2004.10506960. [DOI] [PubMed] [Google Scholar]
- 44.Tuite E.M., Kelly J.M. Photochemical interactions of methylene blue and analogues with DNA and other biological substrates. J. Photochem. Photobiol. B. 1993;21:103–124. doi: 10.1016/1011-1344(93)80173-7. [DOI] [PubMed] [Google Scholar]
- 45.Wainwright M., Amaral L. The phenothiazinium chromophore and the evolution of antimalarial drugs. Trop. Med. Int. Health. 2005;10:501–511. doi: 10.1111/j.1365-3156.2005.01417.x. [DOI] [PubMed] [Google Scholar]
- 46.Rohs R. 2002. Simulation of structure formation and ligand binding of nucleic acids in the space of collective and internal variables. PhD Thesis, Freie Universität Berlin, Germany. http://www.diss.fu-berlin.de/2003/3/ [Google Scholar]
- 47.Sklenar H., Wüstner D., Rohs R. Using internal and collective variables in Monte Carlo simulations of nucleic acid structures: chain breakage/closure algorithm and associated Jacobians. J. Comput. Chem. 2006;27:309–315. doi: 10.1002/jcc.20345. [DOI] [PubMed] [Google Scholar]
- 48.Cornell W.D., Cieplak P., Bayly C.I., Gould I.R., Merz K.M., Ferguson D.M., Spellmeyer D.C., Fox T., Caldwell J.W., Kollman P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1996;117:5179–5197. [Google Scholar]
- 49.Lavery R., Sklenar H., Zakrzewska K., Pullman B. The flexibility of the nucleic-acids: (II). The calculation of internal energy and applications to mononucleotide repeat DNA. J. Biomol. Struct. Dyn. 1986;3:989–1014. doi: 10.1080/07391102.1986.10508478. [DOI] [PubMed] [Google Scholar]
- 50.Rohs R., Etchebest C., Lavery R. Unraveling proteins: a molecular mechanics study. Biophys. J. 1999;76:2760–2768. doi: 10.1016/S0006-3495(99)77429-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lavery R., Sklenar H. Defining the structure of irregular nucleic acids: conventions and principles. J. Biomol. Struct. Dyn. 1989;6:655–667. doi: 10.1080/07391102.1989.10507728. [DOI] [PubMed] [Google Scholar]
- 52.Lavery R., Sklenar H. The definition of generalized helicoidal parameters and of axis curvature for irregular nucleic acids. J. Biomol. Struct. Dyn. 1988;6:63–91. doi: 10.1080/07391102.1988.10506483. [DOI] [PubMed] [Google Scholar]