Tautomeric selectivity of the excited-state lifetime of guanine/cytosine base pairs: The role of electron-driven proton-transfer processes

Abstract

The UV spectra of three different conformers of the guanine/cytosine base pair were recorded recently with UV-IR double-resonance techniques in a supersonic jet [Abo-Riziq, A., Grace, L., Nir, E., Kabelac, M., Hobza, P. & de Vries, M. S. (2005) Proc. Natl. Acad. Sci. USA 102, 20–23]. The spectra provide evidence for a very efficient excited-state deactivation mechanism that is specific for the Watson–Crick structure and may be essential for the photostability of DNA. Here we report results of ab initio electronic-structure calculations for the excited electronic states of the three lowest-energy conformers of the guanine/cytosine base pair. The calculations reveal that electron-driven interbase proton-transfer processes play an important role in the photochemistry of these systems. The exceptionally short lifetime of the UV-absorbing states of the Watson–Crick conformer is tentatively explained by the existence of a barrierless reaction path that connects the spectroscopic ¹π π * excited state with the electronic ground state via two electronic curve crossings. For the non-Watson–Crick structures, the photochemically reactive state is located at higher energies, resulting in a barrier for proton transfer and, thus, a longer lifetime of the UV-absorbing ¹π π * state. The computational results support the conjecture that the photochemistry of hydrogen bonds plays a decisive role for the photostability of the molecular encoding of the genetic information in isolated DNA base pairs.

The genetic information of all prokaryotes and eukaryotes is molecularly encoded in the DNA. Considering the wealth of heterocyclic chemistry, it is amazing that only four bases [adenine (A), cytosine (C), guanine (G), and thymine (T)] and only two base pairs (AT and GC) provide the hardware of the genetic code. Moreover, each of the AT and GC dimers can exist in many different hydrogen-bonded structures in the gas phase (1–4). Nevertheless, only a single conformer of AT and GC, the Watson–Crick (WC) structure, is used for the encoding of the genetic information in DNA. These facts suggest that not only the DNA bases but also the WC base pairs must have very specific properties that have lead to their selection at an early stage of the evolution of life.

It was reported recently in this journal that there exists an astonishing selectivity in the photochemistry of GC base-pair structures in the gas phase. The WC form of GC∥ has been shown to exhibit a strongly broadened UV-absorption spectrum, in stark contrast to two other low-energy conformers of the GC dimer, which exhibit sharp UV spectra (5). The unusually large line width of the UV spectrum, together with the very low intensity of the resonance-enhanced multiphoton ionization signal, indicate an extremely short lifetime of the optically absorbing ¹π π * state of the WC form of GC, which is at least 2 orders of magnitude shorter than those of other conformers of GC or other base pairs such as GG (5). It has been concluded that a particularly efficient excited-state deactivation process must exist in the WC conformer of GC. This rapid excited-state deactivation may be essential for the quenching of destructive photochemical reactions, endowing this particular molecular structure with a unique degree of photostability (5).

A similar observation was reported recently for a simple mimetic model of DNA base pairs, the 2-aminopyridine dimer (6). Femtosecond time-resolved mass spectroscopy of 2-aminopyridine clusters has revealed a significant shortening of the excited-state lifetime of the hydrogen-bonded dimer. Ab initio calculations of reaction pathways and potential-energy profiles have provided a mechanistic explanation of the enhanced excited-state deactivation of the dimer: a dark ¹π π * excited state of charge-transfer (CT) character, which is strongly stabilized by the transfer of a proton, connects the UV-absorbing state with the electronic ground state via two conical intersections (6, 7). The latter can provide the mechanism for ultrafast internal conversion to the electronic ground state (8). The existence of a related ultrafast excited-state quenching mechanism has also been predicted for the WC structure of GC (9).

In the present work, we have extended the earlier calculations (9) for the WC form of GC to include the two other conformers, for which UV spectra have been recorded (1–3). The computational results support the explanation of the pronounced photochemical selectivity in GC base-pair structures in terms of the relative energetic location of a photoreactive CT state.

Methods

The ground-state equilibrium geometries of three conformers of the GC hydrogen-bonded dimer (the WC form A as well as dimers B and C, in the notation used in ref. 5) have been optimized with the CC2 method, which is a simplified (and thus computationally less expensive) variant of coupled-cluster theory with single and double excitations from the reference configuration (10, 11). Planarity (C_s symmetry) of the dimers has been imposed as a constraint in the geometry optimization. The actual equilibrium geometries of hydrogen-bonded GC dimers are slightly nonplanar because of the inherent pyramidization of the amino groups. However, the lowering of the ground-state energy caused by out-of-plane deformation is very small [e.g., 0.28 kcal/mol (1 kcal = 4.18 kJ) for the WC form (9)]. Because planarity of the nuclear framework greatly simplifies the excited-state electronic-structure calculations, we consider here the planar systems.

The same method (CC2) was used for the optimization of the minimum geometry of the lowest CT state, which involves excitation from the highest occupied molecular orbital of guanine to the lowest unoccupied orbital of cytosine.

Given the geometry of the reactant (the ground-state equilibrium geometry) and the geometry of the product (the equilibrium geometry of the CT state), the linear-synchronous-transit reaction path connecting these geometries has been constructed. In this approach, all internal coordinates (bond lengths and bond angles) are varied in a proportional manner from the reactant to the product. Single-point energy calculations of the low-lying ¹π π * and ¹nπ * excited states as well as the ground state have been performed along this reaction path with the CC2 method.

In addition, the minimum-energy path for the proton-transfer reaction in the lowest locally excited spectroscopic state [this is the ¹π π *(L_b) state of guanine, in the notation used by Platt (12)] has been determined by excited-state geometry optimization with the CC2 method using the NH distance of the azine group as the driving coordinate. We have followed the reaction path until the energy of the locally excited state collapses to the CT-state energy in the geometry-optimization process, which indicates that the barrier associated with the (avoided) crossing of the ¹π π *(G) potential-energy function with that of the reactive CT state has been reached.

The standard SV(P) split-valence double-ζ Gaussian basis set with polarization functions on heavy atoms (13) was used in the CC2 calculations, making use of the resolution-of-the-identity approximation for the evaluation of electron-repulsion integrals (14). All calculations were carried out by using the turbomole program suite (15).

Equilibrium geometries of the electronic ground state (S₀) and the CT state of the tautomers A, B, and C of the guanine/cytosine dimer are reported in the supporting information, which is published on the PNAS web site.

Results and Discussion

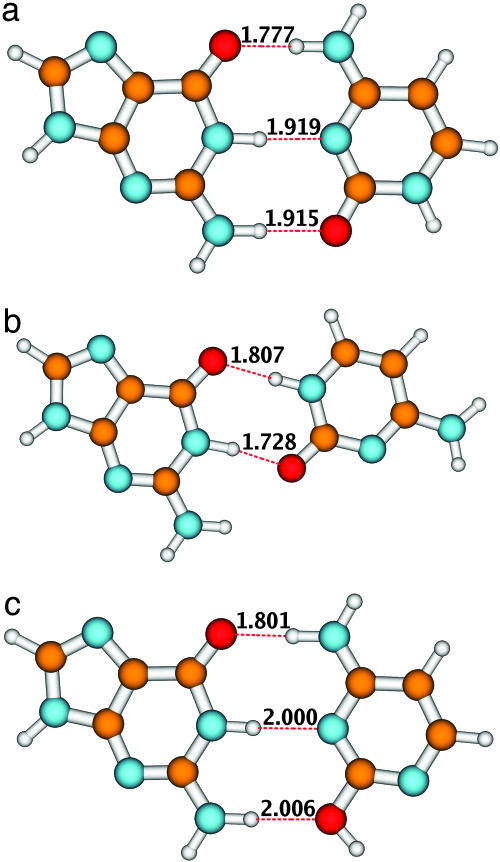
The ground-state geometry of the WC form of the GC base pair (A) and the two energetically lowest non-WC forms (B and C) is shown in Fig. 1. The equilibrium geometries of these systems are similar to those determined in ref. 16 (M. Kabelac and P. Hobza, personal communication) with second-order Møller–Plesset perturbation theory (MP2). Therefore, only the most important geometry parameters (the hydrogen-bond lengths) are specified in Fig. 1. In accordance with the MP2 results of ref. 16 (M. Kabelac and P. Hobza, personal communication), the WC structure is found to represent the most stable form of the GC dimer. The next most stable isomer (form B) is higher in energy by 3.7 × 10^–18 J (5.3 kcal/mol) at the CC2 level. Form C, in which cytosine is in the “rare” enol form, is higher in energy by 7.7 × 10^–18 J (11.0 kcal/mol) than the WC form. All three GC dimers are bonded by fairly strong hydrogen bonds, as indicated by the corresponding bond lengths (see Fig. 1).

Fig. 1.

Equilibrium structures of the ground state of the three conformers of the GC dimer. The numbers denote bond lengths in angstroms.

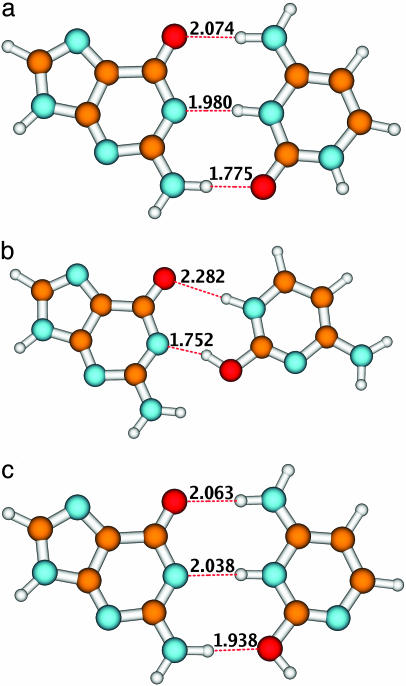
As has been shown previously for the WC form of the GC base pair, the guanine-to-cytosine ¹π π * CT state plays a decisive role in the photophysics of this system (9). When populated, it leads to the spontaneous transfer of a proton from guanine to cytosine. This proton transfer neutralizes the electronic-charge separation and results in the formation of a less polar biradical structure (9). In principle, the number of biradical structures that can be formed is equal to the number of hydrogen bonds in the system, because along each hydrogen bond a proton can follow the electron. The fact that the lowest CT state is of guanine-to-cytosine character for all three dimers (the proton thus has to be transferred from guanine to cytosine) limits the number of possible biradical structures to two for the WC and C forms and to one for the B form. The calculations have shown that the global minimum of the CT energy surface corresponds to the transfer of the azine hydrogen atom of G. The geometries of these hydrogen-transferred biradical structures are shown in Fig. 2.

Fig. 2.

Equilibrium structures of the ¹π π * CT state after transfer of the proton for the three conformers of the GC dimer. The numbers denote bond lengths in angstroms.

Fig. 2 reveals that these structures are bonded, similar to the parent systems, by fairly strong hydrogen bonds. In the WC dimer, the upper (keto-amino) hydrogen bond of the biradical is elongated, whereas the lower (amino-keto) hydrogen bond is considerably shorter than that in the ground state. The shortening of the hydrogen bond is less pronounced in structure C, in which the amino group of guanine is bonded to the enol group of cytosine. In the CT state of dimer B, the keto-azine hydrogen bond is strongly elongated (compare Figs. 1 and 2).

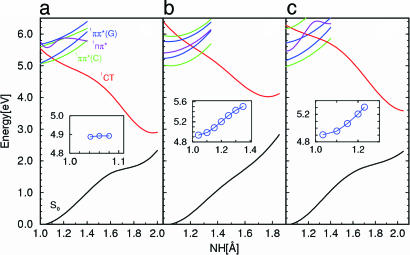
The potential energies of the ground state and the lowest excited singlet states of the three conformers of the GC dimer are shown in Fig. 3 as functions of the linear-synchronous-transit reaction path. The abscissa in Fig. 3 is the NH-bond length of the H-bonded azine group of guanine, which is the proton-donating group in all three dimers (compare Figs. 1 and 2). Fig. 3 is intended to give a qualitative overview. To obtain quantitative information on curve crossings and reaction barriers, minimum-energy reaction paths have to be considered (see below). The potential-energy function of the lowest ¹nπ * state is included in Fig. 3 for completeness, although this state does not play a role in the ensuing discussion.

Fig. 3.

Potential-energy functions of the S₀ state, the locally excited ¹π π * states of guanine (blue) and cytosine (green), the lowest ¹nπ * state (violet), and the ¹π π * CT state (red) of the WC conformer (a), the conformer B (b), and the conformer C (c) of the CG dimer. The potential-energy functions have been calculated along the linear-synchronous-transit proton-transfer reaction path from the S₀ minimum (Fig. 1) to the biradical minimum (Fig. 2). (Insets) Potential-energy function of the lowest excited singlet state (the locally excited ¹π π * state of guanine) calculated along the minimum-energy path for stretching of the NH bond of the azine group of guanine (the proton-transfer coordinate). The potential-energy functions shown in the insets provide estimates of the energy barriers for proton transfer.

The enormous stabilization of the ¹π π *CTstate(¹CT) by the transfer of the proton is eye-catching. This large energy gain results from the reneutralization of the CT state by the transfer of the proton (“the proton follows the electron”). Although the stabilization energy of the CT state is approximately the same in the three dimers, the WC form is distinguished by the considerably lower vertical excitation energy of the ¹π π *(CT) state. As a result, the lowest locally excited singlet states of the WC form are predissociated by the reactive CT state near the minima of their potential-energy surfaces, whereas for the B and C forms these curve crossings with the reactive CT state occur ≈1 eV above the minimum of the lowest locally excited ¹π π * state. Thus, in a qualitative sense, the potential-energy functions shown in Fig. 3 are consistent with the observation of sharp absorption spectra for the B and C conformers near the band origin. For the WC conformer, on the other hand, even the lowest vibronic levels of the locally excited state seem to be predissociated by the essentially repulsive potential-energy function of the CT state. Although Fig. 3 does not show explicit crossings of the CT and ground-state potential-energy functions, the S₀ and ¹CT energies approach each other so closely for R_NH = 2 Å that it is likely that a conical intersection of the multidimensional potential-energy surfaces can be found nearby. We remark that the CC2 method is not adequate for the investigation of the potential-energy surfaces in the immediate vicinity of the conical intersection. In ref. 9, the ¹CT–S₀ intersection of the WC tautomer has been characterized with state-averaged complete-active-space self-consistent-field (CASSCF) calculations as well as with second-order perturbation theory based on the CASSCF reference (CASPT2). It has been found that a moderate increase of the distance of the purine and pyrimidine rings leads to a crossing of the (diabatic) ¹CT and S₀ potential-energy functions. A detailed characterization of the multidimensional potential-energy surfaces at the conical intersection requires considerable additional computational effort.

Although the crossings of the potential-energy functions of the lowest vertically excited state [¹π π *(C), green] and the CT state (¹CT, red) in Fig. 3 provide a qualitative estimate of the energy required for proton transfer, these crossings are not the true energy barriers, because the potential-energy functions shown in Fig. 3 do not pertain to minimum-energy reaction paths. After excited-state geometry optimization, the ¹π π * state of guanine (blue) becomes the lowest excited singlet state for all three tautomers. The insets in Fig. 3 display the potential-energy profiles of the ¹π π *(G) state along the minimum-energy path for proton transfer on the S₁ surface of the three dimers. The energy of the ¹π π *(G) state can be optimized until the (avoided) crossing with the ¹π π *(CT) state is reached. When the NH-bond length of guanine is increased further, the energy collapses to the (repulsive) ¹CT energy. The potential-energy curves (Fig. 3 Insets) thus indicate the actual energy barriers for proton transfer on the S₁ surface of the dimers. It is seen that in conformers B and C, proton transfer is inhibited by a barrier of ≈10 kcal/mol in the ¹π π *(G) state (Fig. 3 b and c, Insets), whereas no such barrier exists in the ¹π π *(G) state of the WC conformer (Fig. 3 a, Inset). Consequently, the existence of relatively long-lived vibronic levels is expected for conformers B and C, whereas for the WC conformer a barrierless access to the ¹CT–S₀ conical intersection, and thus ultrafast radiationless decay to the electronic ground state, is predicted.

In summary, it has been shown that the WC form of the GC dimer is distinguished among the lowest-energy conformers of the GC hydrogen-bonded dimer by the low excitation energy of the guanine-to-cytosine ¹π π * CT state. In the WC conformer, the potential-energy functions of the lowest optically accessible excited states (the locally excited ¹π π * states of G and C) are crossed along the proton-transfer reaction path by the reactive potential-energy function of the CT state near their minima, resulting in complete predissociation of the locally excited electronic states. In the B and C conformers of the GC dimer, on the other hand, these curve crossings occur higher in energy. As a result, these conformers exhibit relatively long-lived vibronic levels and sharp UV-absorption spectra near the band origin.

Although the conical intersection of the ¹π π * CT state with the S₀ state has not yet been characterized in detail, the present results indicate characteristic differences among the three conformers also in this respect. The ¹CT–S₀ state crossing along the proton-transfer coordinate occurs at lower energy in the WC conformer than in the other two conformers, which indicates that the conical intersection of the S₁ and S₀ adiabatic potential-energy surfaces is more rapidly accessible in the WC conformer than in the other two low-energy conformers.

We thus have obtained ab initio-based evidence that the ultrafast radiationless deactivation of the UV-absorbing ¹π π * states is more efficient in the WC form than in other low-energy forms of the GC hydrogen-bonded dimer. This finding explains the spectacular differences in the UV-absorption spectra of different tautomers of the GC base pair (5). It seems plausible that the WC conformer of the GC base pair has been selected in early stages of biological evolution on account of its uniquely efficient excited-state deactivation, which enhances the photostability of this species.