Abstract
Adaptive radiation is defined as the evolution of ecological and phenotypic diversity within a rapidly multiplying lineage. When it occurs, adaptive radiation typically follows the colonization of a new environment or the establishment of a “key innovation,” which opens new ecological niches and/or new paths for evolution. Here, we take advantage of recent developments in speciation theory and modern computing power to build and explore a large-scale, stochastic, spatially explicit, individual-based model of adaptive radiation driven by adaptation to multidimensional ecological niches. We are able to model evolutionary dynamics of populations with hundreds of thousands of sexual diploid individuals over a time span of 100,000 generations assuming realistic mutation rates and allowing for genetic variation in a large number of both selected and neutral loci. Our results provide theoretical support and explanation for a number of empirical patterns including “area effect,” “overshooting effect,” and “least action effect,” as well as for the idea of a “porous genome.” Our findings suggest that the genetic architecture of traits involved in the most spectacular radiations might be rather simple. We show that a great majority of speciation events are concentrated early in the phylogeny. Our results emphasize the importance of ecological opportunity and genetic constraints in controlling the dynamics of adaptive radiation.
Keywords: ecological, modeling, speciation, diversification, parapatric
Adaptive radiation is not only often spectacular but also a remarkably complex process, which is affected by many different factors (genetical, ecological, developmental, environmental, etc.) interacting in interwoven nonlinear ways. Different, sometimes contradictory scenarios explaining adaptive radiation have been advanced (1–3). Which scenarios are more plausible and general is a highly controversial question. Because of the long time scale involved and the lack of precise data on its initial and intermediate stages, even identifying general patterns of adaptive radiation is very difficult (1, 2, 4–6). As a result, no clear discussion of general patterns of adaptive radiation exists in the literature. Whether the patterns identified in specific case studies apply to other systems is, in general, unknown.
Adaptive radiation can be viewed as an extension of the process of speciation (driven by ecological factors and subject to certain initial conditions) to larger temporal and spatial scales. Recent explosion in empirical work on speciation (7) has been accompanied by the emergence of a quantitative theory of speciation (8). In contrast, there have been almost no attempts to build genetically based models of large-scale evolutionary diversification. The few existing examples (8–10) are applicable only to asexual populations or do not treat explicitly spatially heterogeneous selection and ecological competition but concentrate on stochastic factors instead. However, diversifying selection is thought to be very important in adaptive radiations, and it has been shown that adaptive diversification in similar environments can overcome stochasticity and historical contingencies (11).
We build on a model of speciation by means of adaptation to a new ecological niche occurring simultaneously with the evolution of genetically based preferences for the niche (12, 13). Although this model was originally proposed as a model of nonallopatric speciation in the apple maggot fly Rhagoletis pomonella (14), it is applicable to other systems where individuals choose an ecological niche in which they mate and raise offspring. Besides its generality and simplicity, this model is known to provide one of the easiest ways to achieve nonallopatric speciation (8). Furthermore, it is the only mathematical model of nonallopatric speciation strongly supported by experimental work (15). We will use this model within the framework of parapatric speciation (7, 8, 16, 17) in which spatial heterogeneity in selection, isolation by distance, and migration into new patches all play crucial roles. Our goal is to help identify potential general patterns of adaptive radiation and evaluate their characteristic time scales.
We consider a scenario in which a few individuals of a sexual diploid species colonize a new environment (e.g., an island or a lake) in which a number of spatially structured empty ecological niches are available. For example, Anolis radiation on Caribbean islands is largely driven by adaptation to six ecological niches associated with different parts of vegetation (4). The founders have low fitness but still may seed a population that is able to survive throughout the environment at low densities because there are plenty of resources and there are no competitors. The founders have no particular preference for the ecological niches available in the new environment. However, as selection acts on the new genetic variation supplied by mutation, different lineages can get adapted to and simultaneously develop genetic preferences for different ecological niches. The process of ecological and phenotypic diversification driven by selection for local adaptation will be accompanied by the growth in the densities of emerging species.
Model
In our model, space is subdivided into a rectangular array of “patches,” each of which can support a population of a certain size. For example, one can think of different types of vegetation or soil or different parts of a lake environment. There are k environmental factors θi (i = 1, 2,..., k). Each of these factors can take only two discrete values, 0 and 1, corresponding to, say, sandy or rocky lake bottom, high or low light level, etc. Consequently, each patch belongs to one of 2k possible types (“ecological niches”). For example, habitat specialist niches into which Caribbean anoles have evolved are multidimensional, involving several distinct and independent aspects of morphology (18). Initially, ecological niches are assigned to patches randomly with equal probabilities.
Each individual has 2k additive characters controlled by different unlinked diallelic loci with equal effects: k “ecological characters,” xi, and k“preferences,” yi (i = 1,2,..., k). All characters are scaled to be between 0 and 1. The ith ecological character xi controls the fitness component wi associated with the ith environmental factor. Specifically, wi is a decreasing function of |xi – θi|. That is, each ecological character is subject to directional selection toward an extreme value (0 or 1). The overall fitness w is taken to be the product of the fitness components (i.e., w = w1w2... wk). Within each niche selection acts on viability and is density dependent. Note that a hybrid between two individuals adapted to the two alternative states of an environmental factor will have an intermediate phenotype and low fitness in both environments [as implied in the scenario of ecological speciation (2, 19, 20)].
The ith preference character yi controls preference component pi for the ith environmental factor. Specifically, pi is a decreasing function of |yi – θi|. That is, the closer yi is to θi, the stronger is the preference for the corresponding environmental state. The overall preference for an ecological niche characterized by environmental factors θ1, θ2,..., θk is taken to be the product of the individual preference components (i.e., p = p1p2... pk). The probability that an adult enters a patch to mate and raise offspring is proportional to its preference p for the ecological niche present in the patch. Empirical data show that genetic variation in habitat preference is common (21). Note that a hybrid between two individuals with strong preferences to the two alternative states of an environmental factor will have low preference for either environment [e.g., as experimentally demonstrated in species of maggot flies Rhagoletis where hybrids show reduced response to parental host-fruit odors (22)].
Each individual also has a number of multiallelic neutral loci subject to stepwise mutation (23). These loci are used to evaluate the levels of genetic divergence within and between species one would observe if using microsatellite markers.
With a small probability ε per generation, each patch goes extinct. When this extinction happens, all individuals present there die, and the “niche” assigned to this patch is chosen anew randomly. The later assumption is a simple way to have some turnover of ecological niches. For example, if a patch represents a tree of a certain host species, then when the tree dies its space can be occupied by a tree of a different host species.
Generations are discrete and nonoverlapping. The life cycle consists of viability selection, preferential dispersal of surviving adults among neighboring patches (including the patch of origin), and random mating among individuals within the patch and offspring production. For example, this life cycle is common in Diptera and Lepidoptera (13). We assume that genetic incompatibilities and sexual selection are absent; the only type of reproductive isolation possible is through differences in habitat preferences and selection against immigrants from divergent habitats (24). An example is provided by two sympatric species of phytophagous ladybird beetles reproductively isolated only by host-plant specificity (25). The assumption of random mating within patches implies that any costs of mate choice, which can easily prevent divergence and speciation (8, 26), are absent.
In our model, for each individual, there is a niche, say niche J, where it is most fit, and there is a niche, say niche I, for which it has the strongest preference. We interpret each individual for whom J = I as a member of species I. We will interpret all other individuals as “hybrids.” Because both fitness in a niche and preference for a niche are controlled genetically, our “species” also represent distinguishable genetic clusters that are reproductively isolated to a certain degree. The degree of reproductive isolation gets progressively amplified as a by-product of ecological adaptation and strengthening of preferences.
Methods
Here we provide some additional details on the model and simulations.
Density-Dependent Viability Selection. Fitness component wi is given by a Gaussian function, wi = exp[–(xi – θi)2/(2σ2)], where σ is a parameter measuring the strength of selection. The overall fitness w= w1... wk controls a carrying capacity, K = K0w, associated with the phenotype, where K0 is the maximum carrying capacity. The probability that an individual survives to the age of reproduction is given by the Beverton–Holt model (27): 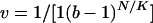 , where b > 0 is the average number of offspring per female, andKN is the number of juveniles in the patch.
, where b > 0 is the average number of offspring per female, andKN is the number of juveniles in the patch.
Habitat Preference. Preference component pi is given by a linear function of yi, pi = 1/2 ± ai(yi – 1/2), where 0 ≤ ai ≤ 1 is a parameter measuring the maximum possible preference and the sign is “+” for θi = 1 and “–” for θi = 0. If ai = 0, no preference can evolve, whereas if ai = 1, the strongest possible preference, i.e., pi = 1, can evolve.
Dispersal. Each adult migrates to one of the eight neighboring patches or returns back to its native patch with probabilities proportional to its preferences for the corresponding ecological niches. For patches at a boundary, the number of patches available for emigration is reduced according to the number of neighboring patches.
Mating. Mating pairs are formed in the following way. Each adult is chosen once as a “female.” For each female, a “male” is chosen randomly among remaining adults. Each mating results in a number of offspring drawn from a Poisson distribution with parameter b. Under this mating scheme the variance effective population size (28) of the juveniles is equal to Ne = (4N – 2)/(2 + 3/4), where N is the number of juveniles. Recombination is free. Mutation occurs with a small probability.
Initial Conditions. Kinit adults populate a single patch in the upper left corner of the system. All individuals are identical homozygotes with all traits exactly at 1/2. There is no genetic variation in the neutral loci either.
Parameter Values. We varied system size (8 × 8, 16 × 16, 32 × 32), number of loci per each trait (L = 4, 8, 16), and the local extinction rate (ε = 0, 0.0025, 0.01, 0.04). The following parameters did not change: number of traits, k = 3; number of founders, Kinit = 10; maximum carrying capacity, K0 = 500, σ = 0.356 (which corresponds to the fitness of the generalists being 0.05 of the maximum possible value); average number of offspring, b = 4; maximum strength of preference, ai = 0.99; number of “microsatellite” loci, M = 8; and mutation probability, μ = 10–5 for the loci controlling ecological and preference traits and μn = 10–3 for the microsatellite loci. Fifty runs were done for each parameter combination. Simulations ran for 100,000 generations or until global extinction.
Population Genetic Structure at Neutral Loci. To estimate the levels of spatial structuring in neutral loci we used the analysis of molecular variance (AMOVA) framework (29, 30). Specifically, let yspi represents the ith haplotype in the pth patch of the sth species. Using a linear model, yspi = y + αs + βsp + γspi, where y is the vector of expected allelic states. The effects α, β, and γ stand for the species, the patch, and the individual, respectively, and are assumed random, additive, and independent, with associated variance components 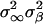 , and
, and 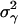 . Let the total variance be
. Let the total variance be 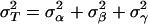 . The relevant intraclass correlations are
. The relevant intraclass correlations are 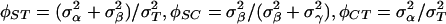 . Genetic distances between pairs of haplotypes, which are the crucial component of the AMOVA framework, were computed by using two different approaches. In the first approach, the genetic distance was defined as the Hamming distance so that each locus contributed 0 (if the alleles are identical) or 1 (if alleles are different). The corresponding estimates of the intraclass correlations are labeled as FST, FSC, and FCT. In the second approach, each locus contributed the value equal to the square of mutational steps separating the two alleles taking into account the stepwise mutation model (30). The corresponding estimates of the intraclass correlations are labeled as RST, RSC, and RCT.
. Genetic distances between pairs of haplotypes, which are the crucial component of the AMOVA framework, were computed by using two different approaches. In the first approach, the genetic distance was defined as the Hamming distance so that each locus contributed 0 (if the alleles are identical) or 1 (if alleles are different). The corresponding estimates of the intraclass correlations are labeled as FST, FSC, and FCT. In the second approach, each locus contributed the value equal to the square of mutational steps separating the two alleles taking into account the stepwise mutation model (30). The corresponding estimates of the intraclass correlations are labeled as RST, RSC, and RCT.
Numerical Results and Biological Interpretations
For parameter combinations used in our numerical simulations, adaptive radiation into a number of ecological niches often follows the colonization of a new environment. Fig. 1 illustrates some states reached by the system with k = 3 (and, thus, 8 possible ecological niches) after 100,000 generations of evolution with no local extinction. In the four cases shown, two, four, four, and eight species have emerged. (A representative gallery of graphical results is provided in the supporting information, which is published on the PNAS web site.) In the cases shown, a large number of local populations are close to the carrying capacity. However, in some patches populations are very small. These populations are “sink populations” (31) that cannot adapt to the conditions they experience because of the deleterious effect of migration of locally maladapted genotypes. Generally, in the course of the simulations, ecological traits evolve faster, approach their optimum trait values closer, and maintain less genetic variation at (stochastic) equilibrium than the preference traits.
Fig. 1.
Examples of the system state after 100,000 generations with three environmental factors and no local extinction. Each square represents a patch. The color of the square defines the ecological niche assigned to the patch. Each local population is represented by a circle. The radius of the circle is proportional to the population size (the maximum radius corresponds to a population at carrying capacity). The color of the circle defines the niche preferred by the majority of individuals. Matching of the color of the corresponding square and circle (observed in most cases) means that the majority of individuals in the patch have preference for the ecological conditions they experience. There are 8 × 8 systems with 2 species (A) and 4 species (B) and 16 × 16 systems with 4 (C) and 8(D) species. Each of the six traits is controlled by L = 4 loci.
Success of Colonization. Table 1 illustrates the effects of some parameters on the probability of successful colonization. We differentiate between the short-term establishment (STE), i.e., survival for the first 500 generations, and the long-term establishment (LTE), i.e., survival for the first 100,000 generations. Overall, the probability of STE decreases with the system size (P < 0.001) and the local extinction rate (P = 0.0555); the effect of the number of loci and of the interaction of different factors are statistically insignificant. LTE was never observed in 8 × 8 systems, whereas STE guaranteed LTE in 32 × 32 systems. In systems of intermediate size (i.e., 16 × 16) local extinction actually promoted LTE. For example, with L = 8, LTE was observed only 5 times with ε = 0.01 but 22 times with ε = 0.04. This unexpected observation is explained by the fact that local extinction, besides decreasing the population size, increases the turnover of niches and, thus, allows the species to spread through larger areas, which in turn increases its chance of survival.
Table 1. Number of times the population has survived to generations 500 and 100,000 out of 50 runs.
| System size
|
||||
|---|---|---|---|---|
| L | ε | 8 × 8 | 16 × 16 | 32 × 32 |
| 4 | 0.0025 | 19 (0) | 32 (32) | 30 (30) |
| 4 | 0.01 | 15 (0) | 28 (18) | 29 (29) |
| 4 | 0.04 | 15 (0) | 30 (13) | 17 (17) |
| 8 | 0.0025 | 25 (0) | 22 (22) | 25 (25) |
| 8 | 0.01 | 18 (0) | 27 (5) | 29 (29) |
| 8 | 0.04 | 18 (0) | 23 (22) | 23 (23) |
| 16 | 0.0025 | 27 (0) | 29 (28) | 31 (31) |
| 16 | 0.01 | 17 (0) | 35 (22) | 33 (33) |
| 16 | 0.04 | 21 (0) | 19 (19) | 30 (30) |
Number of times the population has survived to generation 500 and to generation 100,000 (in parentheses) out of the 50 runs done as a function of the system size, the number of loci per trait L, and the local extinction rate ε.
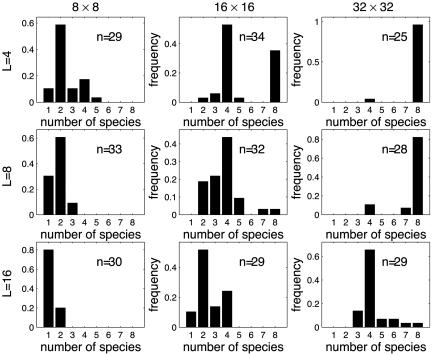
“Area Effect.” In Anolis lizards, empty ecological niches get filled only on islands of sufficiently large area (4). This area effect in the case of no local extinction is illustrated in Fig. 2. The figure clearly shows that larger areas allow for more intensive diversification. In our simulations, eight ecological niches are always available. However, in systems of smaller size, not all niches are filled. The area effect has the following explanation. First, larger areas can support larger population sizes, which in turn results in more advantageous mutants on which diversifying selection can act. Second and more importantly, in larger areas new locally advantageous genes may become better protected by distance from the diluting effect of locally deleterious genes, which otherwise can easily prevent adaptation to a new niche (32). Isolation by distance allows new advantageous combinations of genes to accumulate in large numbers promoting further adaptations to new ecological niches. Similar effects are observed when local extinction is allowed (data not shown). In this case, the area effect is augmented by a higher persistence of large populations in the presence of local extinction.
Fig. 2.
The distribution of the number of species observed after 100,000 generations with no local extinction in systems of different size and with different number of loci per trait, L. The numbers of runs, n, resulting in successful colonization (out of 50 runs) are marked.
Effect of the Number of Loci. Fig. 2 also shows that increasing the number of loci underlying the traits decreases diversification. This effect happens because a larger number of loci implies weaker selection per each individual locus and a stronger overall effect of recombination in destroying coadapted gene complexes.
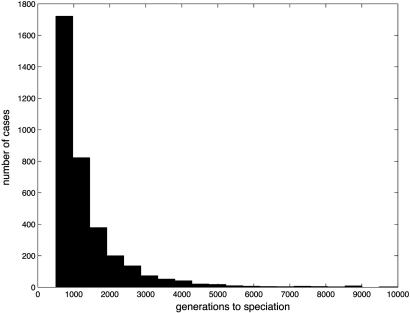
Timing of Speciation. Typically, if more than one species emerges, there is a burst of speciation soon after colonization rather than a more or less continuous process of speciation (see Fig. 3). Similar behavior has been observed in a number of other models (8). The explanation can be given in terms of ecological opportunity and genetic constraints (33). Initially, the former is much larger (because there are more empty niches, local densities are low, and competition is weaker), whereas the latter is much smaller (because the founders are not specialized) than later in the radiation. As a consequence, in our simulations >98% of speciation events occurred within the first 10,000 generations.
Fig. 3.
The distribution of the time to speciation. There were only 23 cases when speciation occurred between generations 10,000 and 20,000, and there were 43 cases when speciation occurred after 20,000 generations (out of 3,587 cases). The time of speciation was defined as the generation when the number of adults in a species reached 100 for the first time.
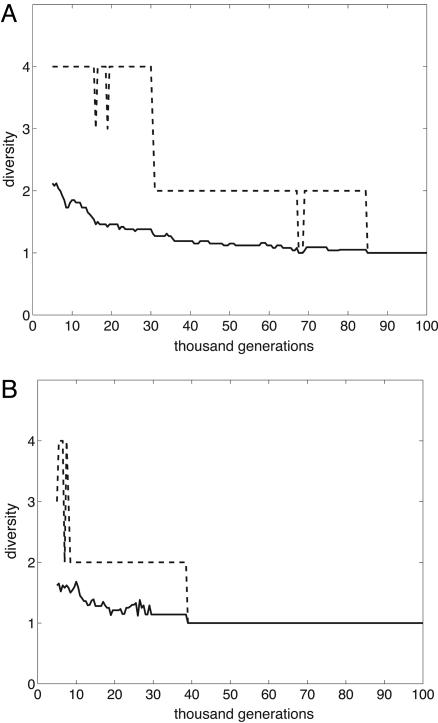
“Overshooting Effect.” In some adaptive radiations, the diversity (i.e., the number of species) peaks early in the radiation. For example, the number of species of spiny-legged Tetragnatha spiders on younger Hawaii islands is larger than on the older ones (6). Our simulations provide some support for the generality of this overshooting effect. For example, all runs corresponding to 8 × 8 systems resulted in eventual extinction. However in some of these runs up to three species were observed at some point in time. Another illustration is given in Fig. 4, which shows a decline in the average species diversity and maximum species diversity observed in some runs in 16 × 16 systems. An explanation of the overshooting effect can be given in terms of the differences between the rates of species extinction and origination. Whereas the former is more or less constant in time (excluding the first few thousand generations), the latter decreases in time because of the effects of ecological opportunity and genetic constraints as discussed above. Note that the overshooting effect was system-size specific: it was not observed in 32 × 32 systems. The reason, most likely, is that in larger systems a longer period is needed for a decline in diversity to become apparent.
Fig. 4.
Examples of the dynamics of average (solid line) and maximum (dashed line) diversity in 16 × 16 systems with L = 8 loci. The first 5,000 generations are excluded. Only the runs not resulting in global extinction are used. Two different local extinction rates are ε = 0.0025 (A) and ε = 0.01 (B).
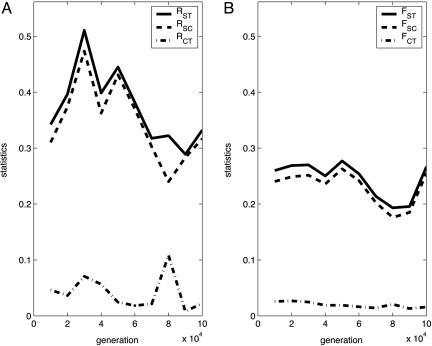
Hybridization and Neutral Gene Flow. In our simulations, species can stably maintain their divergence in a large number of selected loci for very long periods of time despite substantial hybridization and gene flow that removes differentiation in neutral markers. The level of hybridization has been characterized by the proportion of individuals that are not hybrids and by a statistic, Cramer's V (34), measuring the strength of association between the optimum and the most preferred niches. Both are typically high but never very close to 1. Another illustration is given in Fig. 5, which shows that the level of divergence in neutral microsatellite loci between populations from different species is comparable with that between populations from the same species. This phenomenon is observed in spite of the fact that the species have significantly diverged in 96 selected loci. Similar observations are often made in natural populations. For example, blue butterfly species Lycaeides idas and Lycaeides melissa utilize different hosts and have diverged significantly in morphology, yet show no differentiation in neutral markers (35).
Fig. 5.
The dynamics of the measures characterizing the spatial structuring of the system. RST and FST are the correlations of random pair of haplotypes within patches, relative to that of random pairs of haplotypes drawn from the whole system. RSC and FSC are the correlations of random pair of haplotypes within patches, relative to that of random pairs of haplotypes drawn from the group of patches (i.e., species). RCT and FCT are the correlations of random pairs of haplotypes within a group of patches (i.e., species), relative to that of random pairs of haplotypes drawn from the whole system. Shown is run no. 15 done in a 32 × 32 system with L = 16 and extinction rate ε = 0.0025. In this run, two species emerged within the first 10,000 generations. Five adults were sampled from each deme. (A) Stepwise mutation model. (B) Hamming distance model. The fact that RCT and FCT are small implies that the divergence between populations of different species is comparable with that between populations from the same species.
“Least Action Effect.” In our simulations, if speciation occurs after the initial burst, it usually involves a change in a single pair of characters. This observation provides theoretical support for a prediction that shifts to radically different hosts will be much less common than shifts to similar hosts (36). That is, if a host shift happens, it proceeds, metaphorically speaking, in the direction of least action. A related observation is that when some niches are not filled, the existing species differ in the minimum number of characteristics (one or two). These effects are explained by the fact that the deleterious effects of immigration of locally disadvantageous genes on the possibility of accumulation of locally advantageous genes become stronger with genetic difference between immigrating and resident genotypes.
Discussion
Here, we have built an explicit-genetic model of adaptive radiation driven by selection for adaptation to discrete multivariate ecological niches. We have shown that strong ecologically based spatially heterogeneous selection coupled with limited migration and genetically based habitat choice can indeed result in rapid phenotypic and ecological diversification and the emergence of multiple species.
In our model, ecological traits evolve faster, approach their optimum trait values closer, and maintain less genetic variation at (stochastic) equilibrium than the preference traits. Our results provide strong theoretical support and an explanation for the area effect (4), i.e., the observation that ecological niches are filled only on islands and in lakes of sufficiently large area. This effect mainly occurs because in larger areas emerging advantageous genes are better protected by distance from the diluting effect of locally deleterious genes. Geographic structure of species is fundamental to other important macroevolutionary patterns such as long-term stasis (37). Our results also provide support, clarification, and explanation for the overshooting effect (6), i.e., the observation that species diversity declines after reaching a peak early in the radiation. The overshooting effect is explained by the decline in the species origination rate in the face of approximately constant extinction rate. We show that the great majority of speciation events occur soon after colonization of a new environment. This effect happens because, initially, both ecological opportunity is larger and genetic constraints are less strict than later on. The fact that “bottom-heavy” phylogenies are the rule rather than the exception questions the validity of statistical methods used for evaluating the rates of speciation and estimating phylogenies that explicitly or implicitly assume that speciation events are distributed uniformly in time. Our model suggests that local extinction can promote global establishment of the species in a new environment. We show that diversification is most extensive when the phenotypic traits are controlled by few loci. This finding suggests that the genetic architecture of traits underlying the most spectacular adaptive radiations might be rather simple. In our model, “host shifts” typically proceed in the direction of least action, i.e., involve a small number of traits, which supports a similar argument made long ago (36). We show that species can stably maintain their divergence in a large number of selected loci for very long, effectively infinite, periods of time despite substantial hybridization and gene flow that removes differentiation in neutral markers. This observation strongly supports the idea that genomes can be rather “porous” (14, 38).
Most of the patterns discussed here have been identified previously in specific biological systems. However the generality of these patterns cannot be assured on the basis of single cases that currently are known. The fact that we were able to reproduce these macroevolutionary patterns starting with microevolutionary processes of mutation, random drift, migration, recombination, and selection, strongly supports the generality of these patterns. We expect that these patterns will be observed in most adaptive radiations.
Besides apparently being able to capture the essence of adaptive radiation qualitatively, the model studied here allows to make some quantitative conclusions. By using biologically realistic mutation rates and assuming no initial genetic variation (see ref. 26 on the importance of these model components), we showed that 10,000 generations can be sufficient for the emergence of up to 8 ecologically differentiated species (or even 16 species in a limited number of simulations performed with k = 4). Many more species can potentially emerge in a comparable time if the dimensionality k of the niche is higher and the spatial dimension is larger than that used here.
Because of the computing-power limitations we varied only a limited number of parameters. Here we briefly discuss the expected effects of changing other parameters and assumptions. Some of these expectations are supported by limited simulations. Weaker selection will result in the formation of a single “hybrid swarm” with no distinguishable genetic clusters. Reduced probability of leaving the patch will make divergence slower (because selection against immigrants from diverged habitats will be less effective). Assuming nonequal allelic effects will constrain divergence and result in fewer species (because the loci with smaller effects will be less responsive to selection and, thus, will diverge to a smaller degree). If migration occurs before rather than after selection, the likelihood of speciation will significantly increase. Allowing for selfing will greatly increase the likelihood of adaptive radiation by increasing the persistence of local populations. Linkage will result in differential genetic divergence across parts of genome with genes closely linked to selected loci being more differentiated than loosely linked genes. As a result, diverged genes will tend to form clusters (8, 38, 39). Allowing for other forms of reproductive isolation (e.g., genetic incompatibilities or genetically based mate choice) to evolve is not expected to change dramatically the patterns discussed above because they will evolve at much slower rates than ecological traits and habitat preferences (8).
More empirical data are needed to evaluate the generality and relevance of the patterns identified here and test the predictions made.
Supplementary Material
Acknowledgments
We thank J. H. Williams, J. A. Fordyce, and reviewers for comments and M. D. Vose for help with numerical implementations. This work was supported by grants from the National Institutes of Health and the National Science Foundation. The simulations were performed on the Frodo cluster of the Scalable Intracampus Research Grid (SInRG), University of Tennessee, Knoxville.
Author contributions: S.G. designed research, performed research, analyzed data, and wrote the paper; and A.V. wrote simulation code.
Conflict of interest statement: No conflicts declared.
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Simpson, G. G. (1953) The Major Features of Evolution (Columbia Univ. Press, New York).
- 2.Schluter, D. (2000) The Ecology of Adaptive Radiation (Oxford Univ. Press, Oxford).
- 3.Mayr, E. (1963) Animal Species and Evolution (Belknap, Cambridge, MA).
- 4.Losos, J. B. (1998) in Evolution on Islands, ed. Grant, P. (Oxford Univ. Press, Oxford), pp. 210–224.
- 5.Salzburger, W. & Meyer, A. (2004) Naturwissenschaften 91, 277–290. [DOI] [PubMed] [Google Scholar]
- 6.Gillespie, R. (2004) Science 303, 356–359. [DOI] [PubMed] [Google Scholar]
- 7.Coyne, J. & Orr, H. A. (2004) Speciation (Sinauer, Sunderland, MA).
- 8.Gavrilets, S. (2004) Fitness Landscapes and the Origin of Species (Princeton Univ. Press, Princeton).
- 9.Chow, S. S., Wilke, C. O., Ofria, C., Lenski, R. E. & Adami, C. (2004) Science 305, 84–86. [DOI] [PubMed] [Google Scholar]
- 10.Hubbell, S. P. (2001) The Unified Neutral Theory of Biodiversity and Biogeography (Princeton Univ. Press, Princeton).
- 11.Losos, J. B., Jackman, T. R., Larson, A., deq Ueiroz, K. & Rodriguez-Schettino, L. (1998) Science 279, 2115–2118. [DOI] [PubMed] [Google Scholar]
- 12.Diehl, S. R. & Bush, G. L. (1989) in Speciation and Its Consequences, eds. Otte, D. & Endler, J. A. (Sinauer, Sunderland, MA), pp. 345–365.
- 13.Fry, J. D. (2003) Evolution 57, 1735–1746. [DOI] [PubMed] [Google Scholar]
- 14.Feder, J. L. (1998) in Endless Forms: Species and Speciation, eds. Howard, D. J. & Berlocher, S. H. (Oxford Univ. Press, New York), pp. 130–144.
- 15.Rice, W. R. & Salt, G. (1990) Evolution 44, 1140–1152. [DOI] [PubMed] [Google Scholar]
- 16.Endler, J. A. (1977) Geographic Variation, Speciation and Clines (Princeton Univ. Press, Princeton). [PubMed]
- 17.Gavrilets, S. (2003) Evolution 57, 2197–2215. [DOI] [PubMed] [Google Scholar]
- 18.Harmon, L. J., Kolbe, J. J., Cheverud, J. M. & Losos, J. B. (2005) Evolution 59, 409–421. [PubMed] [Google Scholar]
- 19.Rundle, H. D. & Nosil, P. (2005) Ecol. Lett. 8, 336–352. [Google Scholar]
- 20.Forister, M. L. (2005) Evolution 59, 1149–1155. [PubMed] [Google Scholar]
- 21.Jaenike, J. & Holt, R. D. (1991) Am. Naturalist 137, S67–S90. [Google Scholar]
- 22.Linn, C. E., Dambroski, H. R., Feder, J. L., Berlocher, S. H., Nojima, S. & Roelofs, W. L. (2004) Proc. Natl. Acad. Sci. USA 101, 17753–17758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ohta, T. & Kimura, M. (1973) Genet. Res. 22, 201–204. [DOI] [PubMed] [Google Scholar]
- 24.Nosil, P., Vines, T. H. & Funk, D. J. (2005) Evolution 59, 705–719. [PubMed] [Google Scholar]
- 25.Katakura, H., Shioi, M. & Kira, Y. (1989) Evolution 43, 1045–1053. [DOI] [PubMed] [Google Scholar]
- 26.Gavrilets, S. (2005) Evolution 59, 696–699. [Google Scholar]
- 27.Kot, M. (2001) Elements of Mathematical Ecology (Cambridge Univ. Press, Cambridge, U.K.).
- 28.Crow, J. F. & Kimura, M. (1970) An Introduction to Population Genetic Theory (Harper & Row, New York).
- 29.Excoffier, L., Smouse, P. & Quattro, J. (1992) Genetics 131, 479–491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Excoffier, L. (2001) in Handbook of Statistical Genetics, eds. Balding, D. J., Bishop, M. & Cannings, C. (Wiley, New York), pp. 271–307.
- 31.Holt, R. D. (1997) Evol. Ecol. 11, 723–731. [Google Scholar]
- 32.Riechert, S. E. (1993) Behav. Ecol. Sociobiol. 32, 355–363. [Google Scholar]
- 33.Erwin, D. H., Valentine, J. W. & Sepkoski, J. J. (1987) Evolution 41, 1177–1186. [PubMed] [Google Scholar]
- 34.Bishop, Y. M. M., Feinberg, S. E. & Holland, P. W. (1975) Discrete Multivariate Analysis: Theory and Practice (MIT Press, Cambridge, MA).
- 35.Nice, C. C., Fordyce, J. A., Shapiro, A. M. & French-Constant, R. (2002) Ecol. Entomol. 27, 702–712. [Google Scholar]
- 36.Bush, G. (1969) Evolution 23, 237–251. [DOI] [PubMed] [Google Scholar]
- 37.Eldredge, N., Thompson, J. N., Brakefield, P. M., Gavrilets, S., Jablonski, D., Jackson, J. B. C., Lenski, R. E., Lieberman, B. S., McPeek, M. A. & Miller, W., III (2005) Paleobiology 31, 133–145. [Google Scholar]
- 38.Wu, C.-I. (2001) J. Evol. Biol. 14, 851–865. [Google Scholar]
- 39.Emelianov, I., Marec, F. & Mallet, J. (2004) Proc. R. Soc. London Ser. B 271, 97–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.