Iron spin transition in Earth's mantle

Abstract

High-pressure Mössbauer spectroscopy on several compositions across the (Mg,Fe)O magnesiowüstite solid solution confirms that ferrous iron (Fe²⁺) undergoes a high-spin to low-spin transition at pressures and for compositions relevant to the bulk of the Earth's mantle. High-resolution x-ray diffraction measurements document a volume change of 4–5% across the pressure-induced spin transition, which is thus expected to cause seismological anomalies in the lower mantle. The spin transition can lead to dissociation of Fe-bearing phases such as magnesiowüstite, and it reveals an unexpected richness in mineral properties and phase equilibria for the Earth's deep interior.

W. S. Fyfe proposed 45 years ago that the effect of high pressure deep inside the Earth's mantle may be to collapse the atomic orbitals of iron from the high-spin to the low-spin state (1). This transition would represent a major change in chemical-bonding character for one of the Earth's most important elements (Fig. 1), with predictions suggesting as much as a 45% collapse in the ionic volume of ferrous iron in silicates and oxides (2). Elastic moduli, thermal conductivity, electrical transport, and other physical and chemical properties of Fe-bearing minerals could thus be dramatically altered at depth due to the spin transition. Consequently, there has been much interest in the high- to low-spin transition (3), and high-pressure studies of the past decade have demonstrated that it can indeed take place in oxides similar to those thought to be present in the deep mantle (4–10).

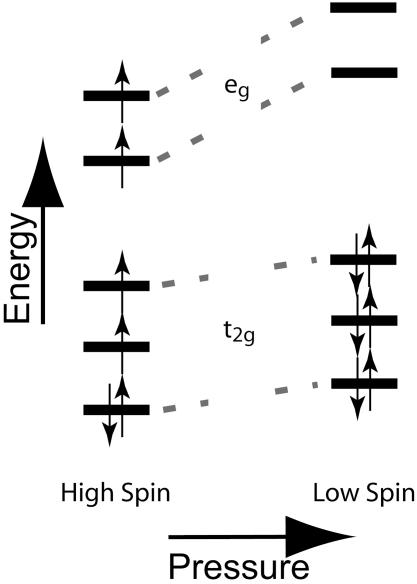
Fig. 1.

Distribution of electrons among 3d orbitals for 6-fold coordinated Fe²⁺ in high-spin (left) and low-spin (right) configurations. The electronic structure of the ion consists of six 3d electrons around an argon core [1s² 2s² 2p⁶ 3s² p⁶], with the e_g orbitals pointing toward and the t_2g orbitals pointing between the first-neighbor oxygen ions. Hund's rule, predicting that the high-spin state is favored because spin-pairing costs energy, applies at low pressure and results in the ferrous ion having a magnetic moment caused by the presence of unpaired spins. With increasing pressure, the energies of all of the orbitals rise, but they rise more rapidly for the e_g than for the t_2g because the former experience more extensive overlap with the nearest-neighbor oxygen electrons than do the t_2g orbitals. Therefore, the low-spin configuration that is diamagnetic (all electrons being spin-paired, therefore no magnetic moment) becomes energetically favored with pressure. The energies of the two orbital types are reversed for tetrahedral (4-fold), cubic (8-fold), or dodecahedral (12-fold) coordination, with e levels lower than t levels, such that a magnetic moment is present for both high- and low-spin configurations in these cases (3).

In the present study, we investigate the high- to low-spin transition across the (Mg,Fe)O magnesiowüstite solid solution (see Supporting Text I, which is published as supporting information on the PNAS web site). This oxide is believed to comprise up to ≈30 molar percent of the lower mantle, and is thus the second-most abundant mineral phase of the Earth's rocky interior after (Mg,Fe)SiO₃ perovskite (11, 12).

Materials and Methods

Three sample materials, of composition (Mg_0.8Fe_0.2)O, (Mg_0.5Fe_0.5)O, and (Mg_0.2Fe_0.8)O, were prepared by reaction of ⁵⁷Fe-enriched Fe-oxalate with MgO in a reduced atmosphere (to avoid the presence of Fe³⁺). The Fe³⁺ content was in all cases below the detection limit of Mössbauer spectroscopy, hence below 1% of the total Fe. For each Mössbauer experiment, the sample was loaded together with several ruby chips (for pressure determination) in a 100-μm diameter sample chamber drilled in a Re foil indented to 25-μm thickness. The sample assemblages were compressed between 200-μm diamond culets by using a modified piston-cylinder diamond-anvil cell. Mössbauer spectra were collected by using a 10-mCi ⁵⁷Co(Rh) point source (1 Ci = 37 GBq).

Powder samples of (Mg_0.8Fe_0.2)O, from the same batch as used for Mössbauer spectroscopy, were mixed with (Mg_0.1Fe_0.9)O (from the material studied in ref. 13) in a 1:3 volume ratio for our x-ray diffraction experiments. Two different series of experiments were performed, using Ar or a methanol:ethanol:water mixture (16:3:1 volume ratio) as a pressure-transmitting medium. Ruby chips were loaded together with the sample powder, and pressure for each run was determined by the ruby-fluorescence shift (14) measured on four to six ruby grains. The sample chamber was created by drilling a 200-μm diameter hole in Re or stainless-steel foils preindented to a thickness of 30 μm, and the samples were compressed between 300-μm or 350-μm culets with membrane or screw-driven piston-cylinder diamond-anvil cells. To reduce pressure gradients across the sample, we warmed the cell up to 450 K after each pressure increment in most of the experiments. The maximum variation in pressure measured across the sample chamber was 6 GPa at 57.4 GPa (see Fig. 4).

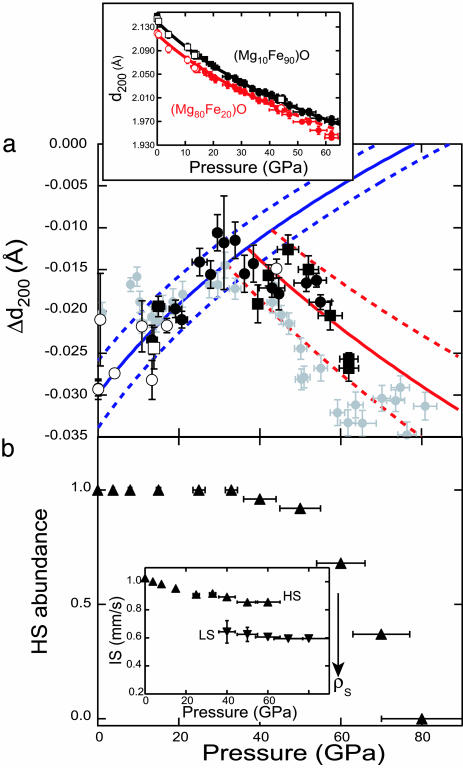
Fig. 4.

Structural effect of spin transition. (a) Difference in d-spacing for the 200 diffraction lines (Δd₂₀₀) of Mg_0.8Fe_0.2O – Mg_0.1Fe_0.9O magnesiowüstite compositions, measured as a function of pressure at 300 K. Circles indicate experiments with an alcohol mixture as a pressure medium, and squares refer to experiments for which Ar was the pressure medium; filled symbols are for data collected on compression, and open symbols are for data collected on decompression. The blue curve (with estimated 1σ uncertainty shown as a dashed line) is obtained by fitting Δd₂₀₀ measured at pressures below 35 GPa to a linear dependence of normalized pressure on the Eulerian strain (12, 14). The red line (with 1σ envelope) is for the finite-strain fit of the observed Δd₂₀₀ at pressures above 35 GPa. For comparison, the Δd₂₀₀ calculated from the measurements in ref. 8 on (Mg_0.83Fe_0.17)O are shown in gray (these were not used to constrain the blue and red curves and error envelopes, but they show good agreement with our results within mutual uncertainties). (Inset) The absolute d-spacings for the 200 lines of the two compositions. The d-spacings approach each other with increasing pressure up to the spin transition at 35 GPa and then diverge (i.e., appearance of the low-spin state softens the equation of state of the x = 0.80 composition). (b) Abundance of Fe in the low-spin state, as determined from high-pressure Mössbauer spectra collected from Mg_0.8Fe_0.2O at 6 K. (Inset) The measured isomer shift (IS) for both low- and high-spin Fe components. Note that the x-ray emission measurements (8) exhibit spectra intermediate between those of high-spin (HS) and low-spin (LS) states at pressures of 54–67 GPa for an x = 0.83 sample, in good agreement (within mutual uncertainties of abundances and pressures) with our results. The isomer shift is proportional to the s-electron density at the nucleus (ρ_S), and the large difference observed between the two spin states agrees with the expectation that the radius of the Fe²⁺ ion decreases significantly across the spin transition.

Synchrotron x-ray powder diffraction was performed at beamline 12.2.2 of the Advanced Light Source of the Lawrence Berkeley National Laboratory, at beamline 13-ID-D of the GeoSoilEnviro-Consortium for advanced Radiation Sources (GSECARS), and at beamline 16-ID-B of the High-Pressure Collaborative Access Team (HP-CAT) at the Advanced Photon Source of the Argonne National Laboratory. X-ray diffraction patterns were collected with a Mar345 image-plate or Bruker SMART 2000 charge-coupled device using monochromatic radiation of 0.4959 Å, 0.3344 Å, or 0.4325 Å wavelength (at the Advanced Light Source and the two beamlines at the Advanced Photon Source, respectively). Nonhydrostatic stresses and peak broadening reduced the resolution of the 200 lattice-plane d-spacing from 0.2% to 0.3% across the span of our pressure range.

Results and Discussion

We collected ⁵⁷Fe Mössbauer spectra as a function of pressure (0–120 GPa) and temperature (6–300 K) on three (Mg_xFe_1–x)O magnesiowüstite samples with x = 0.2, 0.5, and 0.8. This nuclear spectroscopy involves absorption of 14.4-keV electromagnetic radiation by energy levels of the ⁵⁷Fe nucleus that are shifted and split in response to variations in charge density, electric field gradients, and magnetic-spin interactions of the Fe electron orbitals. The Mössbauer spectrum therefore acts as a fingerprint for the spin state of the iron atoms and their magnetic interactions throughout the crystalline structure. The Néel transition from paramagnetic to antiferromagnetic states [from disordered to oppositely ordered Fe²⁺ spins, induced by decreasing temperature (at constant pressure) or increasing pressure (at constant temperature)] is readily determined from the 6-fold magnetic hyperfine splitting of the absorption peak (Fig. 2). The magnitude of the magnetic moment at the Fe site is measured from the hyperfine splitting observed in the spectra, and this can be seen to decrease as one approaches the Néel transition in the antiferromagnetic state (i.e., with increasing temperature or decreasing pressure). Thus, the site magnetization can serve as a probe for the transition from the high-spin (magnetic) to the low-spin (nonmagnetic) state of Fe²⁺ compounds (15, 16). Indeed, we found that a new absorption line with no magnetic hyperfine splitting appears in Mössbauer spectra of FeO compressed above 90 GPa at 300 K (4) and grows with increasing pressure at the expense of the magnetically split lines corresponding to the antiferromagnetic state.

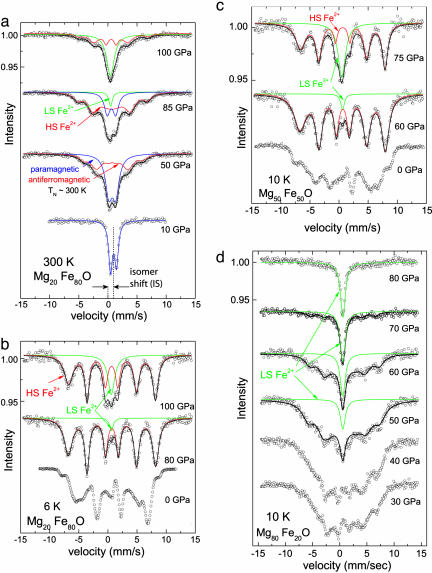
Fig. 2.

Mössbauer absorption spectra as a function of pressure for (Mg_xFe_1–x)O magnesiowüstites having Mg content x = 0.20 at 300 K (a) and 6 K (b) and for x = 0.50 (c) and x = 0.80 (d) at 10 K. Antiferromagnetic ordering (hyperfine splitting) appears by 50 GPa in a and is already present at zero pressure in b, c, and d, whereas the unsplit absorption feature characteristic of the nonmagnetic (low-spin) state emerges at pressures of 40–50 GPa in a and b, 60 GPa in c, and 80 GPa in d. This is but an illustrative selection of spectra that lead to the transition pressures and temperatures (and uncertainties) quoted in Table 1. Our current sampling of pressures and temperatures (both increasing and decreasing) nevertheless does not allow us to reliably determine the slope (dP/dT) of the high-spin to low-spin Fe transition boundary.

Our new results document the same behavior for (Mg_xFe_1–x)O compositions with x ranging from 0.2 to 0.8. At a constant temperature, increasing pressure causes the appearance first of the antiferromagnetic state (magnetically split spectral lines) and then, on further compression, of a new spectral line exhibiting no magnetic splitting (Fig. 2). The data clearly show that the hyperfine splitting increases with pressure for magnesiowüstite in the antiferromagnetic state. Hence, at yet higher pressures, at which antiferromagnetic coupling ought to be stronger, we cannot attribute the appearance of an unsplit, paramagnetic absorption line to the Néel transition but must instead explain it by the appearance of a nonmagnetic, diamagnetic state of Fe²⁺. This signal is therefore characteristic of the high-spin to low-spin transition in (Mg_xFe_1–x)O. The transition is completed over a pressure interval that depends on the chemical composition of the solid solution, with the sample exhibiting coexistence of high-spin and low-spin states over a finite pressure range in good accord with published x-ray emission spectra (refs. 5, 6, and 8; see Supporting Text II).

The pressure at which we observe the first evidence of the spin transition decreases remarkably with increasing Mg content across the (Mg,Fe)O solid solution, varying from 90 GPa in the case of FeO to 40 GPa for (Mg_0.8Fe_0.2)O (Table 1; Fig. 3). The effect of composition on the spin-transition pressure can be understood as being attributable to the (Mg_xFe_1–x)O molar volume decrease with decreasing iron content (increasing x) (17). That is, the effect of Mg enrichment is to put the Fe site under increased local pressure (mean stress), thereby reducing the additional compression required to access the low-spin state. We did not resolve an effect of temperature on the transition pressure, but there is good agreement between the onset and completion of the spin transition we observe in (Mg,Fe)O by Mössbauer spectroscopy with the range of pressures characterized by x-ray emission spectra intermediate between those of high-spin and low-spin state for similar magnesiowüstite compositions (6, 8).

Table 1. Néel temperature (T_N) at zero pressure and spin-transition pressure onset (P_HS→LS) for (Mg,Fe)O magnesowüstite based on Mössbauer spectra.

Composition	TN at 0 GPa, K	PHS→LS, GPa
Mg0.8Fe0.2O	25	40 (±10)
Mg0.5Fe0.5O	80	60 (±10)
Mg0.2Fe0.8O	140	80 (±10)
Fe0.97O	190	90 (±5)

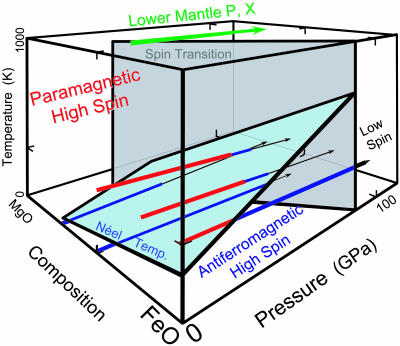
Fig. 3.

Summary of high-pressure ⁵⁷Fe Mössbauer spectroscopy results, at 6–300 K, on (Mg,Fe)O magnesiowüstite, which along with silicate perovskite is thought to make up the bulk of the Earth's lower mantle (>60% of the planetary interior on a molar basis; refs. 7 and 8). At high pressures and low temperatures, magnesiowüstite is antiferromagnetic (blue lines), with a site-magnetization that increases under pressure. A new signal indicative of a nonmagnetic (diamagnetic, black lines) site appears abruptly at pressures above 30–90 GPa, depending on composition, and is interpreted as the onset of the high- to low-spin transition (gray surface). For mantle compositions, with bulk Mg/(Mg+Fe) ratio as high as x = 0.9, the spin transition occurs at pressures as low as 30–40 GPa, corresponding to the shallowest part of the lower mantle. This figure illustrates only a subset of pressure–temperature paths explored for various compositions (Table 1), with spectra also being collected as a function of temperature at constant (high) pressure (see also ref. 4). We have not determined the Néel (light blue surface) and spin transitions for compositions with higher Mg content than x = 0.8; the former presumably exhibits a critical line beyond which antiferromagnetic ordering is impossible because of the low concentration of Fe, whereas the spin transition would be expected to take place even for trace-impurity levels of ferrous iron in MgO.

Assuming negligible temperature dependence upon the crystal field, we expect that the spin transition in magnesiowüstite takes place over a broad range of pressures, from the lowermost mantle (at depths >2,100 km) for pure FeO up to the shallowest part of the lower mantle (<1,000 km depth) for nearly pure MgO (Table 1). As the bulk composition of the mantle is thought to have a molar ratio of x = Mg/(Mg + Fe) close to 0.7–0.9 (e.g., ref. 11), this means that Fe is in the low-spin state for magnesiowüstites throughout most of the Earth's lower mantle (Fig. 3).

High-resolution x-ray powder diffraction patterns (see Materials and Methods), obtained from mixtures of two different magnesiowüstite compositions, (Mg_0.8Fe_0.2)O and (Mg_0.1Fe_0.9)O, yield tight constraints on the volume change through the spin transition. We have examined the pressure dependence of the 200 diffraction line (18), which is unaffected by the rhombohedral or monoclinic distortion of the NaCl structure that takes place at 18 GPa in (Mg_0.1Fe_0.9)O (19–23), and find that the compression curves of the x = 0.1 and the x = 0.8 composition approach each other as pressure is increased toward 35 GPa (Fig. 4a). Because data were simultaneously collected from both samples on decompression as well as compression, and also with different pressure media, we can compare the effect of composition on the equations of state of magnesiowüstites with greater accuracy than has previously been possible.

Starting at ≈35 GPa, we observe an increase in the separation between the 200 reflections of the two compositions. We interpret this as being attributable to the spin transition decreasing the volume of (Mg_0.8Fe_0.2)O relative to (Mg_0.1Fe_0.9)O, which does not undergo this transition until 85 GPa. Fits to our Mössbauer spectra document the fraction of Fe in the low-spin state as increasing from 0% to ≈50% between 40 and 60 GPa for Mg_0.8Fe_0.2O (Fig. 4b), and from the x-ray data we estimate a relative contraction in lattice parameter of 1.0 (±0.2) percent over the same pressure range (Fig. 4a). The results indicate a volume change of 4.6 (±0.7) percent across the high-spin to low-spin transition in Mg_0.8Fe_0.2O (i.e., a 1.6 ± 0.2% change in lattice parameter for complete conversion to low-spin Fe) (24), in good agreement with independent x-ray diffraction results obtained on (Mg_0.75Fe_0.25)O (8) (Fig. 4).

The volume change we obtain for the spin transition is comparable to the ≈3–7% density changes associated with the olivine → spinel, ilmenite → perovskite, or spinel → perovskite + oxide transitions responsible for the seismic-velocity discontinuities defining the top of the transition zone at 410-km depth and the top of the lower mantle at 660-km depth. Taking into account possible complications from nonstoichiometry (17) (see Supporting Text III), we do not have enough information to determine how the volume change across the spin transition varies with composition. It may be that the ≈3–4% density change observed for FeO at high pressures, either across a shock-induced transformation (18) or across the transformation to the inverse-NiAs structure (19, 21), is linked to the high- to low-spin transition, but the overlapping roles of structural and electronic transitions is not well understood. In any case, the present results do show a substantial change in density associated with the spin transition for bulk compositions having Mg/Fe ratios pertinent to the Earth's mantle.

These results may help explain a variety of apparent anomalies or inconsistencies that have appeared in the literature. In particular, (Mg,Fe)O magnesiowüstite must now be considered a ternary, not a binary, system at high pressures, with components MgO, ^HSFeO (high-spin FeO), and ^LSFeO (low-spin FeO) (ref. 17; see Supporting Text IV). Therefore, it is reasonable that under certain high-temperature annealing conditions, magnesiowüstite might be found to decompose into two separate phases at high pressures (25, 26), whereas under different conditions no such decomposition is seen (refs. 19 and 21; cf. ref. 24).

We note that the change with pressure in the partitioning of iron between (Mg,Fe)SiO₃ perovskite and (Mg,Fe)O magnesiowüstite [with iron favoring the oxide by nearly an order of magnitude below 40 GPa, whereas it shows more equivocal preference at high pressures (27–29)] appears to correlate with the pressure at which the high- to low-spin transition sets in. The profound change in bonding character due to the spin transition, and the influence of site coordination on the 3d energy levels of ferrous iron (Fig. 1), make it plausible that iron partitioning would exhibit significant changes with pressure in the mantle. Our new results, together with other recent findings (8–10), strongly suggest that the phase behavior, chemical bonding, and physical properties of (Mg,Fe)O and other Fe-bearing minerals are thus far richer at conditions of the Earth's deep interior than has previously been recognized.