Comparison of human lumbar facet joint capsule strains during simulated high-velocity, low-amplitude spinal manipulation versus physiological motions

Abstract

BACKGROUND CONTEXT

Spinal manipulation (SM) is a n effective treatment for low back pain (LBP), and it has been theorized that SM induces a beneficial neurophysiological effect by stimulating mechanically sensitive neurons in the lumbar facet joint capsule (FJC).

PURPOSE

The purpose of this study was to determine whether human lumbar FJC strains during simulated SM were different from those that occur during physiological motions.

STUDY DESIGN/SETTING

Lumbar FJC strains were measured in human cadaveric spine specimens during physiological motions and simulated SM in a laboratory setting.

METHODS

Specimens were tested during displacement-controlled physiological motions of flexion, extension, lateral bending, and axial rotations. SM was simulated using combinations of manipulation site (L₃, L₄, and L₅), impulse speed (5, 20, and 50 mm/s), and pre-torque magnitude (applied at T₁₂ to simulate patient position; 0, 5, 10 Nm). FJC strains and vertebral motions (using six degrees of freedom) were measured during both loading protocols.

RESULTS

During SM, the applied loads were within the range measured during SM in vivo. Vertebral translations occurred primarily in the direction of the applied load, and were similar in magnitude regardless of manipulation site. Vertebral rotations and FJC strain magnitudes during SM were within the range that occurred during physiological motions. At a given FJC, manipulations delivered distally induced capsule strains similar in magnitude to those that occurred when the manipulation was applied proximally.

CONCLUSIONS

FJC strain magnitudes during SM were within the physiological range, suggesting that SM is biomechanically safe. Successful treatment of patients with LBP using SM may not require precise segmental specificity, because the strain magnitudes at a given FJC during SM do not depend upon manipulation site.

Introduction

In a recent national survey on patterns and perceptions of care [1], more people afflicted with back pain sought conventional therapy (such as physical therapy) versus chiropractic care (37% vs. 20%, respectively). However, patients who sought chiropractic therapy were more often satisfied with the treatment (61% vs. 37% seeking conventional therapy). This is concurrent with recent meta-analyses of randomized clinical trials that indicated that spinal manipulation (SM) was an effective treatment for low back pain (LBP), with rare incidence of serious adverse effects [2,3]. However, S M has evolved empirically and little is known about the physiological mechanisms by which it is effective [4].

The biomechanics of high-velocity, low-amplitude (HVLA) SM have been studied in vivo [4,5]. A patient is positioned side-lying with varying degrees of pelvic rotation. The practitioner administers a preload force on a single vertebral process (eg, lumbar mamillary process) to rotate the vertebra near the limits of its active range of motion. Then, an impulse load is applied such that the resultant displacement does not exceed the passive range of motion of the joint [4]. The preload force transmitted through the trunk approximates 100 N, and the transmitted force during the impulse, which is maintained for approximately 200 ms, ranges from 50 to 400 N [5–8]. Vertebral motions during SM are relatively small (rotations: 1–2.5° [9]; translations: .25–1.62 mm [10]) as demonstrated by in vivo studies [9,10] and predictive modeling [11]. Although these studies provide useful information about the biomechanics of SM, the kinematics of the lumbar vertebrae using six degrees of freedom (DoF) during SM have never been quantified.

The vertebral motions that develop during SM load the facet joint capsule (FJC). The application of a HVLA SM in the L₃–L₅ region can result in “gapping” of the L_3–4, L_4–5, or L₅-S₁ facet joints [12]. The audible “crack” that often accompanies HVLA SM is believed to originate from a rapid distention of the facet joint surfaces causing cavitation within the synovial fluid [13]. Both phenomena imply that the FJC undergoes deformation (strain) during SM, though this has never been observed nor quantified.

The FJC is innervated with mechanoreceptors and mechano-nociceptors [14,15], and FJC strains (or stresses) during SM may be sufficient to stimulate these neurons. Mechanoreceptors innervating paraspinal tissues in cats responded in a graded fashion to the direction of an innocuous load applied to a lumbar vertebra [16]. Simulated SM can either increase or decrease the discharge of neurons innervating paraspinal tissues [17]. Large strains during SM may stimulate FJC mechano-nociceptors. Alternatively, high FJC strain rates could provide a novel stimulus for FJC mechanoreceptors [18].

It has been theorized that HVLA SM induces a beneficial neurophysiological effect by stimulating the mechano-sensitive neurons of the FJC [19]. The mechanical force delivered during SM or the biomechanical changes caused by SM may alter the inflow of sensory information from neurons innervating the paraspinal tissues to the central nervous system. These changes may reduce central sensitization, a phenomenon where the receptive fields of central neurons are increased and innocuous stimuli gain access to pain pathways [19]. Similarly, the pain-relieving effects of SM may also be the result of changes in neural plasticity, where afferent input resulting from SM could alter nociceptive circuits [20].

The purpose of the current study was to measure FJC plane strains during physiological motions and simulated SM. It was hypothesized that simulated SM would result in FJC strain magnitudes within the range that occurs during physiological motions, which would indicate that SM was a “biomechanically safe” procedure. It was also hypothesized that FJC strain magnitudes would be independent of manipulation site, which would indicate that the effects of SM may also occur distal to the manipulation site. Preliminary data have been presented in abstract [21] and thesis form [22].

Methods

Preparation of specimens

Intact human lumbar spine specimens (n=7; mean age: 64.3 years ±4.2 SD; range: 60–73; sex: 6 males, 1 female) were shipped frozen from the National Disease Research Interchange (Philadelphia, PA). Specimens (T₁₂ - sacrum) were unembalmed and procured within 24 hours postmortem from donors without history of spine pathology. All specimens were X-rayed (anterior-posterior and lateral views) to verify that they did not exhibit any gross pathology or substantial scoliosis (ie, >9°). Before testing, the spines were dissected free of all superficial soft tissue (including insertions of multifidi muscles) to expose the FJC. As was done in prior studies [23,24], the spinous processes were removed to facilitate the imaging of markers attached to FJC surfaces for plane strain measurements. Specimens were oriented such that the L₃ and L₄ end plates were horizontal to the testing surface, and were potted at the sacrum using a quick-setting epoxy (Bondo; Bondo Corporation, Atlanta, GA). Throughout testing, specimens were kept moist by periodic spraying with phosphate-buffered saline (PBS, pH=7.4) and by wrapping them in PBS-soaked gauze.

Physiological motions

The spines were tested during physiological motions of extension, flexion, left lateral bending, and right lateral bending using methods previously described in detail [23,24]. Briefly, the sacrum was rigidly fixed to the testing surface, and the T₁₂ vertebral body was connected to a rod via a rigid U-shaped coupling with a pin through the middle of the vertebral body, allowing a single degree of freedom (Fig. 1a). The coupling was in series with a force transducer (Model XLS1-150; Load Cell Central, Monroeton, PA) (range ±660 N, resolution .07 N) mounted to a linear actuator (Model ME3528-406C; Galil, Inc., Rocklin, CA) by a low friction universal joint. As the spine was actuated, loads were applied without inducing a moment at the point of application. For all four motion types, a trial consisted of 10 cycles to 40 mm displacement (at T₁₂) at 1 0 mm/s. The magnitude of global spine displacement was selected from the prior study [23] as that which was largest in magnitude while producing moments at L5-S1 below a predetermined limit of 10 Nm (a threshold beyond which can produce load–displacement relationships suggestive of damage to soft tissues of the spine [25]).

Fig. 1.

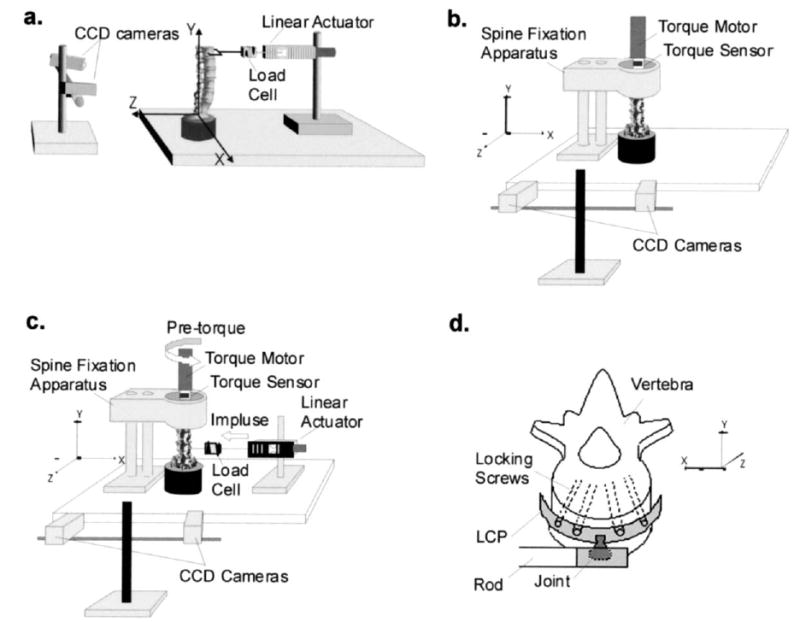
Schematics of the experimental setups. For all testing protocols, vertebral kinematics and facet joint capsule strains were measured by optically tracking infrared reflective markers using the two charge coupled device (CCD) cameras. The orientation axes of the system are shown for each view. (a) Specimens were tested during physiological motions of extension, flexion, and lateral bending using a displacement-controlled linear actuator motor. A load cell was in series with the motor to measure the applied load. (b) Spine specimens were tested during physiological motions of axial rotations using a torque motor, which was in series with a torque sensor to measure the applied torque. (c) Spine specimens were tested during simulated spinal manipulation (SM) using both the torque motor and linear actuator motor. The torque motor was used to apply a pre-torque to the specimen to simulate patient position, and a custom-built spine fixation apparatus was used to hold the specimen in place during mechanical testing. During SM simulations, the linear actuator motor was used to deliver the impulse load to L₃, L₄, and L₅. The direction of the pre-torque and the manipulation are shown. (d) During simulated SM, the linear actuator motor was attached to the anterior aspect of the vertebral body of interest using a Synthes Small Fragment Locking Compression Plate (LCP). The LCP was attached to a joint (allowing 30° of rotation), which was connected to the linear actuator via a rod.

After specimens were tested during motions of extension, flexion, and lateral bending, the spine specimens were prepared for testing during physiological motions of left and right axial rotation (Fig. 1b). Specimens were potted at T₁₂ using the same quick-setting epoxy used to pot the sacrum. Once the sacrum was locked to the testing surface, an aluminum plate (12 cm diameter, .6 cm thick) was secured to the epoxy at T₁₂ using at least three self-tapping machine screws. The plate had a ¾″, 3-cm-high, 6-point bolt soldered to its surface, and the bolt was connected to a ¾″ socket that was in series with a torque transducer (Model TTD400; Futek, Irvine,CA) and atorque motor (Model ME2130-198B; Galil, Inc., Rocklin, CA). Mechanical testing consisted of 15 cycles to 20° left and right axial rotation (at T₁₂) at 6°/s. The magnitude of displacement was determined in preliminary studies [22] as the largest displacements that reliably produced torque measurements below the predetermined threshold of 10 Nm [25].

Impulse loading

Preconditioning procedure

The lumbar spine is a viscoelastic structure, though its elastic properties have been studied more extensively [26]. In order to produce more reliable load-displacement curves, specimens were preconditioned before impulse loading. A 10 Nm torque was applied to T₁₂ and held for 10 seconds, then released, and the angle of rotation was recorded. An intertrial interval of 3 minutes was used to allow the specimen to return to the physiological state [23,24]. The procedure was repeated until the angular displacement was the same for three consecutive torque applications (±.1°). A torque of 10 Nm was chosen for the preconditioning procedure to ensure that the pre-torque magnitudes used to simulate patient positioning (5 and 10 Nm) would be within the pseudo-elastic range and that the specimen would not relax under the constant pre-torque during mechanical testing (see below).

Mechanical testing

After preconditioning, the sacrum remained locked to the testing surface and the torque motor was used to apply a pre-torque (0, 5, or 10 Nm about the +Y-axis) to the specimen at T₁₂ (Fig. 1c). The purpose of the pre-torque was to simulate different degrees of patient positioning, typical of in vivo lumbar SM [4]. The 0 N m pre-torque simulated a side-lying patient, and the 5 and 10 Nm pre-torques simulated increasing degrees of pelvic rotation, respectively. After the pre-torque was applied, the superior portion of the specimen was locked into the spine fixation apparatus. Then, the linear actuator was attached to the anterior aspect of the L₃ vertebral body using a Synthes Small Fragment Locking Compression Plate (Synthes, USA, Paoli, PA) (LCP, Fig. 1d). The LCP was connected to a swivel-head joint (which allowed 30° rotation), and the joint was attached to a threaded rod in series with the force transducer and the linear actuator. The spine was actuated at L₃ by applying an impulse load parallel to the X-axis, creating simultaneously translation and rotation of the vertebrae.

SM simulations consisted of a pre-load phase (to simulate positioning of the joint near the limits of its range of motion) and a peak impulse (to simulate the impulse force administered) [5–8]; the entire simulation consisted of 7 mm total displacement (Fig. 2). During the preload phase, the actuator was displaced 2/3 the total displacement (4.66 mm) at 10 mm/s and held for 500 ms. Then, the peak impulse was applied by displacing the remaining 1/3 of the total displacement (2.33 mm) at 5, 20, or 50 mm/s, after which the actuator was returned to its initial position. The speed and displacement magnitudes were determined in preliminary studies [22] as those that were the best combination to achieve load magnitudes (50–400 N) and impulse durations (~200 ms) within the range that occur during SM in vivo [8], while considering the strength of the coupling to the vertebral body and the limits of the actuator motor.

Fig. 2.

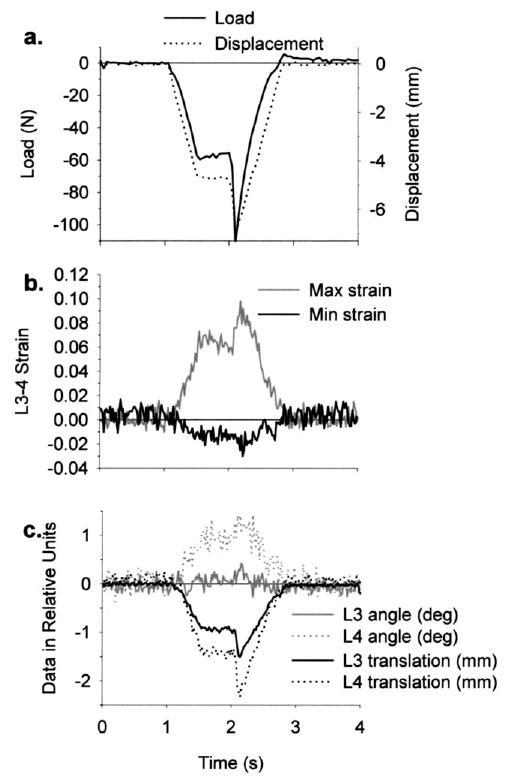
Representative data from a simulation of spinal manipulation applied to the anterior aspect of L₄, which simultaneously produced rotation (+Y-axis) and translation (−X-axis) of the vertebrae (see Fig. 1 for orientation axes). (a) A single trial consisted of 7 mm total displacement, which was comprised of a preload (maintained for 500 ms) and peak impulse. In the trial shown, the impulse was delivered at 50 mm/s. (b) Facet joint capsule maximum (max) and minimum (min) principal strains (left L_3–4 capsule strains shown) were typically opposite in sign. (c) Vertebral kinematics (Y-axis rotations and X-axis translations of L₃ and L₄ are shown) were measured using six degrees of freedom, and the dominant vertebral motions occurred in the direction of the applied manipulation. Load–time, strain–time and vertebral motion–time relationships closely resembled displacement–time relationships.

The six DoF kinematics of the vertebrae (L₃, L₄, and L₅) were optically measured, using a commercial kinematic system (Model 50; Qualisys, Inc., Gothenburg, Sweden), by imaging at 50 Hz (using two charge coupled-device cameras) the displacements of sets of three noncollinear markers fixed to the transverse processes (TP) of the vertebrae. Using the same cameras, the three-dimensional (3D) displacements of markers attached to the FJC were tracked for subsequent plane strain calculations. The impulse was applied to L₃ using all combinations of pre-torque and speed while imaging markers attached to the L_3-4 through L₅-S₁ FJCs and the L₃, L₄, and L₅ TPs on the right side of the spine. Next, the LCP was moved to the anterior aspect of the L₄ vertebra and the protocol repeated, then the procedure was repeated again at the L₅ vertebra. The right FJCs were then covered with PBS-soaked gauze and the left FJCs and TPs were imaged while applying the impulse to L₅, L₄, and finally to L₃. The FJC plane strains (L_3–4 through L₅-S₁) and vertebral motions (6 DoF, L₃ through L₅) at peak impulse were determined, both relative to the neutral and pre-torqued positions of the spine.

Data analysis and statistics

Vertebral kinematics

Using the method of Soderkvist and Wedin [27], vertebral angles and translations, relative to the vertical neutral or pre-torquedposition of the spine, werecomputed using the 3D displacements of the markers attached to the TPs. Because the vertebrae were treated as rigid bodies, the vertebral angles and translations for a given combination of pre-torque, manipulation site, and speed were taken as the mean respective value measured while tracking the right and left sides of the spine. Motions for each degree of freedom were computed relative to both the neutral and pre-torqued position of the spine (to determine the amount of motion that occurred during the pre-torque application and during application of the impulse, respectively). The magnitudes of the total vertebral translations were computed by taking the square root of the sum of the squared displacements along the X-, Y-, and Z-axes for that vertebra.

Plane strain calculations

FJC plane strains were measured using methods previously described in detail [23,24]. Briefly, capsule plane strains (Lagrangian large strain formulation) were measured by optically tracking the displacements of infrared reflective markers (1 mm radius) glued to capsule surfaces. Capsule markers were typically placed as 3 × 3 arrays forming four quadrilaterals, from which plane (ɛ_xx, ɛ_yy, ɛ_xy) and principal strains (E1 and E2, defined as the principal strains whose directions were closest to the X-axis and Y-axis, respectively) were calculated for each quadrilateral element relative to the vertical neutral or pre-torqued position of the spine. As has been done in studies of FJC strains in the cervical [28] and lumbar [23,24] spines, E1 and E2 were organized as either “maximum” (positive) or “minimum” (negative) principal strains (hereafter denoted as ${\widehat{E}}_1$ and ${\widehat{E}}_2$, respectively) regardless of their respective absolute magnitudes. Mean FJC ${\widehat{E}}_1$ and ${\widehat{E}}_2$ were computed as the mean of the respective values from the quadrilateral elements.

During physiological motions of extension, flexion, and lateral bending, strain data for the FJCs on both the right and left sides of the spine were computed for the first three specimens. Preliminary analyses indicated that there were no significant differences between the strains on the right and left FJCs (Mann-Whitney rank sum test, p>.05) (SigmaStat Version 2.03; SPSS, Inc., Chicago, IL), so for the remaining spines, strain data were collected for the left FJCs only. Strain data from the right and left sides of the first three spines during flexion and extension were averaged. Similarly, strains during lateral bending were organized as tensile bending (left bending on the right FJCs and right bending on the left FJCs) and compressive bending (right bending on the right FJCs and left bending on the left FJCs) and then averaged. Because of the mirror symmetry observed during lateral bending in these preliminary analyses, as well as in prior studies [23], strain data on the left FJCs only were collected during axial rotations. During simulated SM, strain data on both sides of the spine were collected as described above. Total FJC strain during a given combination of pre-torque magnitude, speed, and manipulation site was computed as the sum of the strain that occurred during the pre-torque application and the strain at peak impulse.

Statistics

Mean loads during simulated SM were reported for the preload and the total (ie, peak) load. Moments during the preload and at peak impulse of the simulated SM were calculated as the products of the respective load magnitudes and the moment arms. The moment arm was measured, using digital calipers (.01 mm resolution) (Model 14-648-17; Control Company, Friendswood, TX), as the perpendicular distance between the point load application (ie, at the joint on the coupling) to the estimated center of rotation of the manipulated vertebra [29,30]. All statistical analyses were performed using SigmaStat (SigmaStat Version 2.03; SPSS, Inc., Chicago, IL). Significant differences in preload and peak impulse load and moment were calculated using a three-factor analysis of variance (ANOVA, factors: manipulation site, speed, and pre-torque magnitude; α = .05) with post hoc Tukey tests (α = .05). Preliminary analyses demonstrated that there were no significant differences in FJC strains or vertebral kinematics across impulse speed, so for each combination of manipulation site and pre-torque magnitude the mean respective value was determined. A two-factor repeated measures analysis of variance (RM-ANOVA) with post hoc Tukey tests (α = .05) was used to detect significant differences in total FJC strain, vertebral translation, and vertebral rotation across manipulation site and pre-torque magnitude.

Results

Spine specimens

No gross pathologies of the spine specimens were evident by visual inspection or on plain film X-rays. Capsules were visually inspected at low power magnification (6×) and were found to be intact, exhibiting characteristic gross normal appearance including white color and a predominantly medial to lateral orientation of collagen fibrils [31]. One spine specimen was potted at the sacrum such that it was difficult to attach the LCP to the anterior aspect of L₅, so for this spine the manipulations were applied to L₃ and L₄ only. Because repeated measures statistical tests were used, this specimen was omitted from the analysis of the FJC strain and vertebral kinematics data (ie, it was used in the analyses of load and moment data only).

Load and moment

Loads during simulated SM (Fig. 3) were within the range measured in vivo [5–8]. Mean load magnitudes during the preload phase ranged from 61 to 152 N, whereas mean total load magnitudes ranged from 86 to 230 N. Load magnitudes during the preload and total (ie, peak) load magnitudes varied significantly with manipulation site (ANOVA, p<.001), where loads at a given vertebra were significantly larger than those that occurred at the more superior vertebrae in both cases (Tukey, p<.05). Preload and total load magnitudes varied significantly with pre-torque magnitude (ANOVA, p<.001), and both preload and total load magnitudes were significantly larger with 5 N m and 10 Nm pre-torque versus 0 N m pre-torque (Tukey, p<.05). Impulse speed did not have a significant effect on preload or total load magnitude (ANOVA, p>.07). There were no significant interactions among manipulation site, pre-torque magnitude, and impulse speed (ANOVA, p>.61).

Fig. 3.

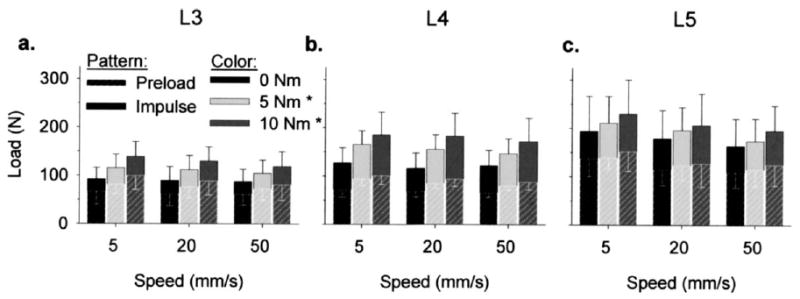
Load magnitudes during simulated manipulations of the lumbar spines (n=7) were site-specific (manipulation sites: (a) L₃, (b) L₄, (c) L₅). Both preload and total load magnitudes at L₄ and L₅ were significantly larger than those that occurred at the respective more superior vertebrae (3-way ANOVA, p<.001). Preload and total load magnitudes did not vary significantly with speed (ANOVA, p=.075). ^*Both preload and total load magnitudes were larger with 5 Nm and 10 Nm pre-torque versus 0 Nm pre-torque (3-way ANOVA, p<.001).

Mean moment during the preload ranged from 3.9 to 8.1 Nm, whereas the mean moments at peak impulse ranged from 5.2 to 11.5 Nm (Fig. 4). The applied moments during the preload phase and at peak impulse varied significantly with manipulation site (ANOVA, p<.001); the moments at L₄ and L₅ were significantly larger than those that occurred at L₃ (Tukey, p<.05). Preload and total moment magnitudes varied significantly with pre-torque magnitude (ANOVA, p<.02), with larger moments occurring with 10 Nm pre-torque versus 0 Nm pre-torque (Tukey, p<.05). There were no significant differences in moment across impulse speeds (ANOVA, p>.2), nor were there any significant interactions among manipulation site, pre-torque magnitude, or impulse speed (ANOVA, p>.92).

Fig. 4.

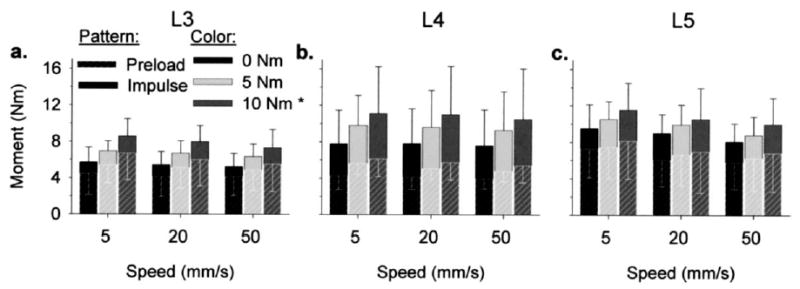
Preload and total moment magnitudes during simulated manipulations of the lumbar spines (n=7) were site-specific (manipulation sites: (a) L₃, (b) L₄, (c) L₅). L₄ and L₅ moments (both preload and total) were significantly larger than L₃ moments (3-way ANOVA, p<.001). Preload and total moment magnitudes did not vary significantly with speed (ANOVA, p>.07). ^*Both preload and total moment magnitudes were larger with 10 Nm pre-torque versus 0 Nm pre-torque (3-way ANOVA, p<.001).

Vertebral translation

L₃, L₄, and L₅ vertebral translations occurred predominantly in the direction of the applied impulse (−X-axis; Fig. 5). Translations along the other two axes were relatively small in absolute magnitude and were more variable than those along the dominant axis. Vertebral translations along a given axis and the total vertebral translations did not vary significantly with pre-torque magnitude or manipulation site (ANOVA, p>.05), and there were no significant interactions between pre-torque magnitude and manipulation site (ANOVA, p>.10).

Fig. 5.

Vertebral translation (trans) magnitudes during simulated manipulations of lumbar spines (n=6) were not site-specific. Compared with the translations along the Y- and Z-axes, translations were larger in absolute magnitude along the X-axis (the direction of the applied impulse). Total vertebral translations were computed as the vector sum of the translations that occurred along the three axes. Total vertebral translations and the translations that occurred along a given axis were of similar magnitude, regardless of whether the manipulation was applied locally or distally (ANOVA, p>.05). Vertebral translations also did not vary with pre-torque magnitude (ANOVA, p>.05).

Vertebral rotation

L₃, L₄, and L₅ vertebral rotations during SM (Fig. 6) were within the range that occurred during physiological motions (Table 1). L₃, L₄, and L₅ vertebral rotations were relatively small about the X-axis (Fig. 6). L_3, L₄, and L₅ X-axis rotations did not vary significantly with pre-torque magnitude (ANOVA, p>.3) or manipulation site (ANOVA, p>.25). There were no significant interactions between manipulation site and pre-torque magnitude at L₃, L₄, or L₅ (ANOVA, p>.80).

Fig. 6.

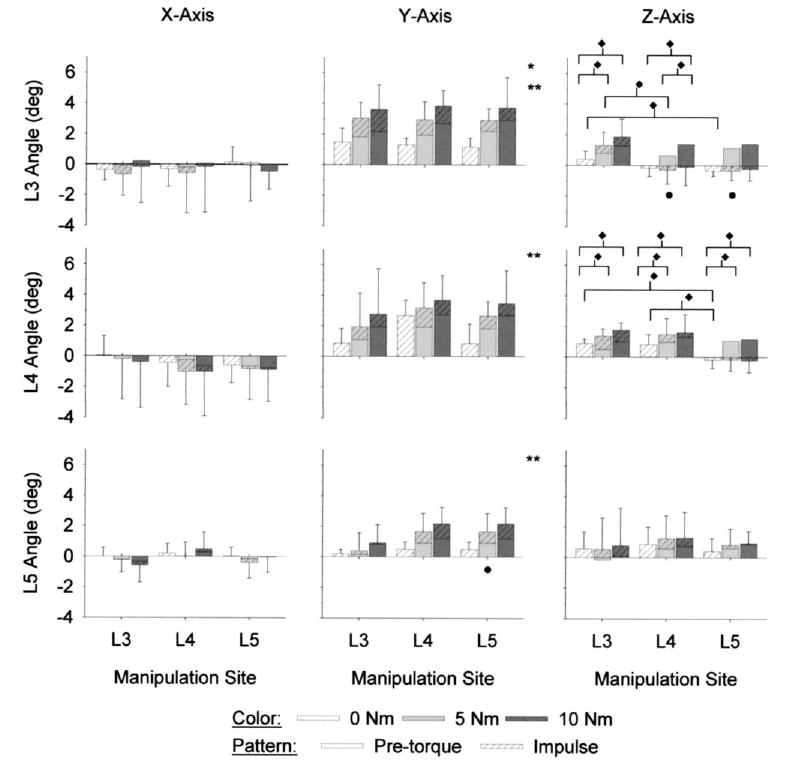
Site-specific lumbar spine manipulations (n=6) induced vertebral rotations both locally and distally. X-axis rotations (see Fig. 1 for orientation axes) were relatively small in absolute magnitude and were highly variable. At a given vertebra, and for a given combination of manipulation site and pre-torque magnitude, rotations were typically largest in absolute magnitude about the Y-axis, which was the direction of the applied pre-torque and impulse load. Z-axis rotations were relatively small; at L₃ and L₄ the magnitude and direction of Z-axis rotations were dependent upon pre-torque magnitude and manipulation site. ^*5 Nm pre-torque significantly larger than 0 Nm pre-torque (ANOVA, p<.015). ^**10 Nm pre-torque significantly larger than 0 Nm pre-torque (ANOVA, p<.015). ^ Significantly different versus L₃ manipulation site (ANOVA, p<.03). ♦ Significant interactions between pre-torque and manipulation site (ANOVA, p<.035).

Table 1.

Mean vertebral rotations (in degrees) of the lower lumbar vertebrae during physiological motions^*

	X axis			Y axis			Z axis
Motion	L3	L4	L5	L3	L4	L5	L3	L4	L5
E	7.8 (4.2)	6.0 (3.1)	3.4 (1.7)	3.2 (2.8)	0.9 (1.1)	−0.2 (0.8)	3.1 (3.1)	1.6 (2.9)	0.5 (0.8)
F	−10.5 (3.8)	−6.6 (3.2)	−2.1 (3.1)	−2.1 (2.8)	−1.4 (1.9)	0.1 (1.1)	−0.9 (1.7)	−1.0 (1.5)	−0.8 (1.2)
LB	−4.2 (3.6)	−0.7 (1.8)	−0.4 (1.3)	1.0 (3.5)	0.0 (2.0)	−0.4 (1.3)	10.9 (1.6)	7.7 (1.0)	3.5 (1.0)
RB	0.8 (4.2)	1.0 (2.1)	0.0 (1.1)	0.4 (4.1)	0.2 (3.9)	0.5 (0.7)	−10.5 (2.8)	−7.0 (2.4)	−3.8 (1.1)
LA	0.9 (1.5)	−0.4 (3.8)	0.3 (0.5)	2.0 (2.7)	2.1 (2.2)	0.7 (1.3)	1.1 (2.2)	1.2 (1.6)	0.9 (0.9)
RA	−0.5 (1.7)	0.4 (3.3)	0.0 (0.3)	−1.7 (2.8)	−1.2 (1.5)	−0.7 (1.4)	−1.2 (1.3)	−1.4 (0.8)	−1.0 (0.8)

^*Standard deviations shown in parentheses. Motions were as follows: E = extension; F=flexion; LB=left lateral bending; RB=right lateral bending; LA=left axial rotation; RA=right axial rotation.

For a given combination of pre-torque magnitude and manipulation site, Y-axis vertebral rotations were typically largest in absolute magnitude compared with those that occurred about the other two axes (Fig. 6). Y-axis rotations at L₃, L₄, and L₅ varied significantly with pre-torque magnitude (ANOVA, p<.01). L₃ Y-axis rotations were significantly larger with 5 Nm and 10 Nm pre-torque versus 0 Nm pre-torque (Tukey, p<.05). At L₄ and L₅, Y-axis rotations were significantly larger with 10 Nm pre-torque versus 0 Nm pre-torque (Tukey, p<.05).

Y-axis rotations at L₃ did not vary significantly with manipulation site (ANOVA, p=.922). L₄ Y-axis rotations also did not vary significantly with manipulation site (ANOVA, p=.213), although at a given pre-torque the mean rotations appeared larger when the manipulation was applied to L₄. At L₅, Y-axis rotations varied significantly with manipulation site (ANOVA, p=.021), and were larger in magnitude when the manipulation was applied at L₅ versus at L₃ (Tukey, p<.05). There were no significant interactions between manipulation site and pre-torque magnitude at L₃, L₄, or L₅ (ANOVA, p>.17).

Although smaller in absolute magnitude, vertebral rotations about the Z-axis demonstrated more significant trends than did those about the Y-axis (Fig. 6). L₃ and L₄ Z-axis rotations varied significantly with pre-torque magnitude (ANOVA, p<.001); Z-axis rotations with 5 N m and 10 Nm pre-torque were significantly larger than those with 0 N m pre-torque (Tukey, p<.05). L₅ Z-axis rotations were not significantly affected by pre-torque magnitude (ANOVA, p=.148). L₃ Z-axis rotations varied significantly with manipulation site (ANOVA, p=.027), with larger angles occurring when the manipulation was applied at L₃ versus at L₄ or L₅ (Tukey, p<.05). Manipulation site did not have a significant effect on L₄ or L₅ Z-axis rotations (ANOVA, p>.06).

Although there were no significant interactions between pre-torque magnitude and manipulation site in L₅ Z-axis rotations (ANOVA, p=.820), L₃ and L₄ Z-axis rotations exhibited significant interactions (ANOVA, p<.03). At L₃, Z-axis rotations with 0 N m pre-torque were significantly different when the manipulation was applied to L₃ versus at L₅ (Tukey, p<.05); although the absolute magnitudes of the angles were similar, they were opposite in sign (and hence direction). With 5 N m pre-torque, L ₃ Z-axis rotations were significantly larger when the manipulation was applied to L₃ versus at L₄ (Tukey, p<.05). When the manipulation was applied at L₄, L₃ Z-axis rotations were significantly larger with 10 Nm pre-torque versus 5 Nm and 0 Nm pre-torque (Tukey, p<.05). When the manipulation was applied at L₃ and L₅, the L₃ Z-axis rotations were significantly larger with 5 N m and 10 Nm pre-torque versus 0 N m pre-torque (Tukey, p<.05).

L₄ Z-axis rotations exhibited significant interactions at 0 Nm pre-torque and at all three manipulation sites (ANOVA, p=.01). With 0 Nm pre-torque, L₄ Z-axis rotations were significantly larger when the manipulation was applied at L₄ and L₃ versus L₅ (Tukey, p<.05). At all three manipulation sites, L₄ Z-axis rotations were significantly larger with 5 N m and 10 Nm pre-torque versus 0 N m pre-torque (Tukey, p<.05).

Facet joint capsule plane strains

${\widehat{E}}_1$ strains (maximum). Mean ${\widehat{E}}_1$ FJC plane strains during simulated SM on the left and right sides of the spine were similar in magnitude (Fig. 7). On the left side of the spine, L_3-4 ${\widehat{E}}_1$ strains varied significantly with pre-torque magnitude (ANOVA, p=.002), where ${\widehat{E}}_1$ FJC strains were larger with 5 Nm and 10 Nm pre-torque versus 0 N m pre-torque (Tukey, p<.05). ${\widehat{E}}_1$ strains in the left L_4–5 and L₅-S₁ FJCs also varied significantly with pre-torque magnitude (ANOVA, p<.03), where larger strain magnitudes occurred with 10 Nm pre-torque versus 0 N m pre-torque (Tukey, p<.05). There were no significant differences in ${\widehat{E}}_1$ strain magnitudes with pre-torque magnitude on the right side of the spine (ANOVA, p>.05).

Fig. 7.

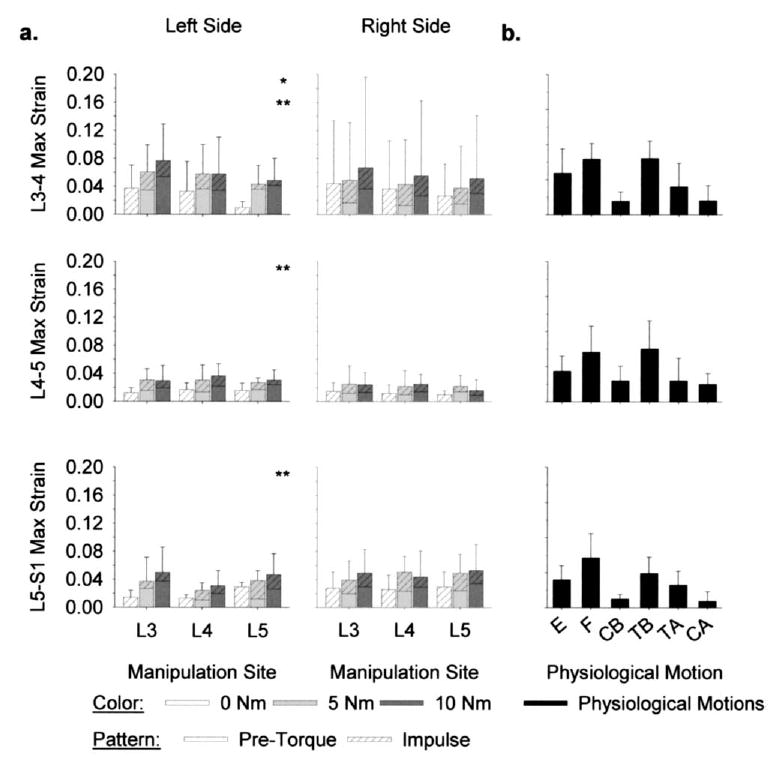
Facet joint capsule (FJC) maximum (max) principal strains ( ${\widehat{E}}_1$, n=6) (a) during simulated spinal manipulation (SM) were within the range that occurred (b) during physiological motions of extension (E), flexion (F), lateral bending (CB=compressive bend; TB=tensile bend), and axial rotations (TA=tensile axial; CA=compressive axial). During SM, FJC strains on both sides of the spine were induced regardless of whether the manipulation was applied distally or locally (ANOVA, p>.13). On the left side of the spine, FJC strain magnitudes were larger with 5 Nm (^*) and 10 Nm (^**) pre-torque versus 0 Nm pre-torque (ANOVA, p<.03).

On both sides of the spine, simulated SM induced ${\widehat{E}}_1$ FJC strains distally (Fig. 7). There were no significant differences in mean ${\widehat{E}}_1$ strain magnitudes with manipulation site at L_3–4, L_4–5, or L₅-S₁ (ANOVA, p>.12). There were also no significant interactions between pre-torque magnitude and manipulation site at any of the FJCs (ANOVA, p>.28).

Mean ${\widehat{E}}_1$ strains during simulated SM were well within the range that occurred during physiological motions (Fig. 7). The largest mean ${\widehat{E}}_1$ strains occurred during physiological motions of lateral bending (L_3–4 and L_4–5 FJCs) and flexion (L₅-S₁ FJC). Mean ${\widehat{E}}_1$ strains during simulated SM were well within the 95% confidence intervals of the largest mean ${\widehat{E}}_1$ strains during physiological motions at L_3–4, L_4–5, and L₅-S₁ (upper limit: 10.4%, 11.3%, and 11.5% strain, respectively).

${\widehat{E}}_2$ strains (minimum). Mean ${\widehat{E}}_2$ strains on the left L_3–4, L_4–5, and L₅-S₁ FJCs did not vary significantly with pre-torque magnitude (ANOVA, p>.19). On the right side of the spine, mean ${\widehat{E}}_2$ strains at L_3–4 varied significantly with pre-torque magnitude (ANOVA, p=.043), where L_3–4 ${\widehat{E}}_2$ strains were larger in absolute magnitude with 10 Nm pre-torque versus 0 Nm pre-torque (Tukey, p<.05). At the L_4–5 and L₅-S₁ FJCs on the right side of the spine, ${\widehat{E}}_2$ strains were not significantly affected by pre-torque magnitude (ANOVA, p>.09).

On both sides of the spine, FJC ${\widehat{E}}_2$ strains were induced distal to the applied manipulation (Fig. 8). Applying the manipulation distally did not significantly increase or decrease FJC mean ${\widehat{E}}_2$ strain magnitudes (ANOVA, p>.14). There were no significant interactions between pre-torque magnitude and manipulation site at L_3–4, L_4–5, or L₅-S₁ (ANOVA, p>.10).

Fig. 8.

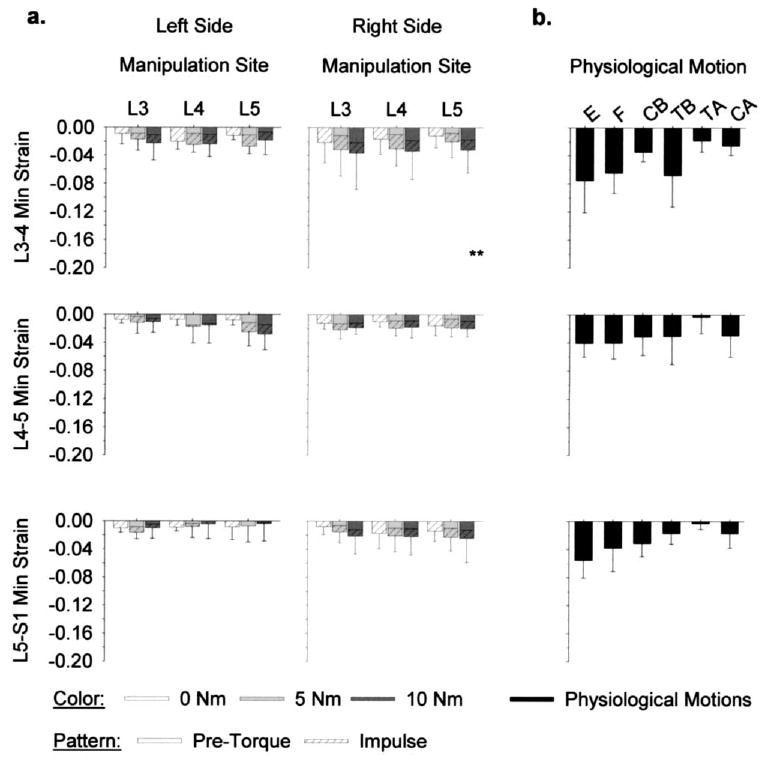
Facet joint capsule (FJC) minimum (min) principal strains ( ${\widehat{E}}_2$, n=6) (a) during simulated spinal manipulation were within the range that occurred (b) during physiological motions of extension (E), flexion (F), lateral bending (CB=compressive bend; TB=tensile bend), and axial rotations (TA=tensile axial; CA=compressive axial). During SM, FJC strains on both sides of the spine were induced, regardless of whether the manipulation was applied distally or locally (ANOVA, p>.14). ^**10 Nm pre-torque significantly larger than 0 Nm pre-torque (ANOVA, p<.05).

Mean ${\widehat{E}}_2$ strains during simulated SM were well within the range that occurred during physiological motions (Fig. 8). At all three joint levels, mean ${\widehat{E}}_2$ strains were largest in absolute magnitude during physiological motions of extension. During simulated SM, mean ${\widehat{E}}_2$ strains were always within the 95% confidence interval of ${\widehat{E}}_2$ strains during extension (upper limit: −11.8%, −6.4%, and −7.7% at L_3–4, L_4–5, and L₅-S₁, respectively).

Discussion

This is the first report of simulated SM in human cadaveric spine specimens while simultaneously measuring lumbar FJC plane strains and vertebral kinematics using six DoF. Loads and vertebral motions during simulated SM were similar in magnitude to those reported for in vivo SM [4,8,32]. S M FJC principal strains were within the range that occurred during physiological motions, implying that SM is biomechanically safe and provides an innocuous mechanical stimulus for FJC mechanically sensitive neurons. FJC strains were induced distal to the manipulation site, indicating that the theorized neurophysiological effects of SM elicited by FJC neuron firing [19] may be initiated distally as well.

Load and moment

The simulated SMs in this study applied forces within the range of in vivo SM [8]. However, the mean applied moments during the preload phase and at peak impulse were substantially smaller in magnitude (3.9–8.1 Nm and 5.2–11.5 Nm, respectively) than those predicted for in vivo SM (30–50 Nm and 100–150 Nm, respectively) [8]. Studies in the thoracic spine suggest that a large percentage of the force applied during SM is transmitted to the soft tissues (which were absent in this study) and not to the manipulated segment, because of an increase in contact area associated with an increase in applied force [33]. If this is also the case in the lumbar spine, then forces developed in this study probably exceeded those that would be transmitted in vivo to the manipulated segment. In part, the difference between the measured and predicted moments may be because in this study the sacrum was fixed to the testing apparatus whereas during in-vivo HVLA SM, the pelvis can be further rotated. Regardless, the forces generated in this study were sufficient to achieve relative vertebral movements similar in magnitude to those that have been estimated to occur during in vivo HVLA-SM [8].

Vertebral motion

This is the first report describing lumbar vertebral motions during simulated SM using all six possible DoF. Others have measured thoracic 2D intervertebral motions in two orthogonal planes during cadaver SM and reported similar ranges of translation and rotations as measured in the current study [34–36]. Assessment of vertebral motions using all six DoF using a similar technique would require imaging three bone pins, or perhaps three noncollinear points on two bone pins, using two cameras positioned at a smaller angle (ideally at 45°).

Tracking the motion of the vertebrae in 3D overcame limitations associated with other methods for determining vertebral motions. Though imaging modalities such as magnetic resonance imaging [12,30] or X-ray [9] are less invasive, the frequency of data acquisition is low compared with the rate at which the loads are applied during HVLA-SM, and they provide information in 2D only. While the results of the current study show that the translations during SM occur primarily along a single axis, tracking vertebral motions in 3D eliminates errors resulting from motion out of plane. More importantly, in the current study substantial vertebral rotations occurred about two axes; this information would have been missed if only 2D measurements were taken. The use of accelerometers has allowed for the determination of vertebral translation, by twice integrating the acceleration-time profile, about all three axes during in vivo [37,38] and cadaver SM [39]. Although data acquisition rate can be increased substantially compared with magnetic resonance imaging or X-ray, the accelerometers used in the prior studies did not differentiate between linear and angular accelerations. Any rotation of the accelerometer off of its primary axis decreases the sensitivity of the measurement. Gal et al. [34] determined that accelerometers significantly overestimated absolute vertebral translations and significantly underestimated relative vertebral translations compared with those measured using bone pins. The method used in the current study was sufficient to discriminate between translation and rotation, and the data acquisition rate was sufficient to identify the magnitude of motion at peak impulse.

Intervertebral motions during spinal mobilization (ie, low velocity low amplitude, and no impulse loading) [9,40,41] were similar in magnitude to those in the current study. However, vertebral translations during spinal mobilization tended to be much larger (range: 8.8–11.5 mm compared with only 0–2.3 mm in the current study) [9]. This difference may have partially been the result of the much longer durations of the applied loads (3 minutes in Lee and Evans [9]), which allowed the viscoelastic structures of the spine to “creep”. Additionally, the prior studies measured vertebral displacements during spinal mobilizations using transducers applied to the surface of the skin overlying the spinous processes. The large vertebral translations measured could have been the result of compression of the skin and subcutaneous fat overlying the mobilized segment, which could be as large as 10 mm [40,42].

Vertebral motions during HVLA SM have been studied in the thoracic spine [35]. The absolute translations of the thoracic vertebrae were larger than those observed in the current study (3–12 mm vs. 0–2.3 mm, respectively), whereas intervertebral rotations were slightly smaller (.2–1.8° vs. .2–2.2°, respectively). In the prior study, a PA load (which would be along the Z-axis in the current study) was applied to the right transverse process of a thoracic vertebra. The difference in translation magnitudes may have been due both to the difference in load direction, as well as the morphological differences between the lumbar and thoracic spines (and hence relative stiffness).

In the current study, site-specific manipulations resulted in systemic biomechanical responses in the lumbar spine. Vertebral translations were similar in magnitude, regardless of whether the manipulation was applied distally or locally. This was in contrast to an in vivo study by Nathan and Keller [10], where L_3–4 translations in a patient free of spine pathology increased nearly linearly as the load was applied closer to the joint (manipulations applied to T₁₁ through L₃). It is difficult to compare these results with those of the current study, because the prior study was limited to a single normal patient. Vertebral displacements probably would have decreased in the current study as well if the manipulations were applied more distally. In contrast to the vertebral translations, the magnitude of vertebral rotation in the current study depended upon whether the manipulation was applied locally or distally, particularly the Z-axis rotations. These results concur with those of Powers et al. [41], where manipulation site had a significant effect on both the magnitude and direction of rotation.

FJC strains

The FJC strain magnitudes were at the high end of the range that occurred during physiological motions. Because human FJCs are innervated with low threshold mechano-receptors and mechano-nociceptors [43], it suggests that the FJC could contribute to the theorized beneficial neuro-physiological effect of SM [19]. In cat knee joint capsules, stretch-activated mechanoreceptors (Group II or Ruffini) had relatively low thresholds (~1–5 kPa) [44]. As the modulus of elasticity of human FJC is roughly 3 MPa [45], this threshold would be exceeded at even 1% strain of FJC. To the extent that human FJC afferents are similar to cat knee joint capsule afferents, it suggests that human low threshold capsule afferents would be stimulated during physiological motions or SM. The magnitude of the FJC strains developed during SM in the current study provides biomechanical evidence that supports the theory for the FJC’s involvement in the beneficial neurophysiological effects of SM.

FJC strains during simulated SM did not exceed those that occurred during physiological motions in human lumbar (see current study and [23]) and cervical [28] FJCs, so it is also likely that SM is a procedure that is biomechanically safe and provides a stimulus that is sub-threshold for FJC mechano-nociceptors. Although FJC strain magnitudes during SM were similar to those that occurred during physiological motions, the high strain rates that occurred during SM could provide a novel mechanical stimulus for capsule mechanoreceptors. Mechanoreceptors innervating rabbit lumbar FJC and paraspinal muscles responded to joint loading and loading rate, suggesting that these afferents could function as “velocity detectors” [18]. The high strain rates that occur during SM could provide a nonphysiological (yet, biomechanically safe) stimulus for human FJC afferents.

Although the paraspinal tissues overlying the FJCs were removed in order to measure FJC strains, the strain magnitudes in the current study were probably similar in magnitude to those that occur in vivo. Paraspinal static muscle tone and reflex contractions stiffen the spine, which could potentially decrease intervertebral motions during in vivo SM, and hence decrease FJC strains. Conversely, contraction of multifidus muscles, which have insertions on the FJC surface, could generate strain independent of those resulting from intervertebral motion itself [24]. However, the muscle reflex response during in vivo HVLA SM is delayed by 50–200 ms after the application of the thrust [46], and the peak strains measured in the current study occurred at peak displacement. Hence, it is likely that the FJC strain magnitudes in this study were reasonable estimates of the FJC strains that occur during SM in vivo.

Despite the fact that vertebral rotations varied significantly in magnitude or direction with manipulation site, FJC strain magnitudes were similar regardless of where the manipulation was applied. This implies that segmental specificity may not be as important as previously postulated in the efficacy of SM [47,48]. Patients with neck pain who received SM had the same beneficial results regardless of whether the SM was targeted at a specific involved motion segment or performed generally to the cervical spine [49]. During in vivo lumbar SM, cavitation phenomena (ie, the audible “crack”) occurred in distal lumbar facet joints as frequently as in targeted joints [50]. Hence, the benefits of SM may not arise solely from the events that occur local to the manipulated facet joint.

There are several methodological factors to consider when interpreting the results of this study. First, the cadaver spines were obtained from an older population; lumbar spines from younger subjects tend to be more flexible and the FJC strain magnitudes for a given joint moment are larger (unpublished observations). Second, although every effort was taken to keep the specimens moist using PBS-soaked gauze and by misting the specimens with PBS, the FJCs were exposed directly to air for significant periods of time. Third, the tissues overlying the FJCs, as well as the spinous processes and its associated ligaments, were removed to enable viewing of FJC markers. Because the protocol was run under displacement control, this would not have affected the measurement of FJC strains or vertebral motions, but removal of these supporting structures could have resulted in smaller loads than develop in vivo. Because the vertebral motions in the current study were similar in magnitude to those that occur during SM in vivo [34–36], and as the magnitudes of intervertebral motion and FJC strain are related [23], it is likely that the FJC strains measured in the current study were similar to those that occur in vivo.

In conclusion, site-specific SM resulted in systemic biomechanical responses of the lumbar vertebrae. FJC strain magnitudes were at the high end of the range that occurred during physiological motions; hence SM is likely a biomechanically safe procedure and sufficient to stimulate low threshold capsule mechanoreceptors. The high strain rates that occur during SM may provide a “nonphysiological” stimulus that affects a pattern of mechanoreceptor firing, which may contribute to the theorized beneficial neurophysiological effect of SM. FJC strain magnitudes at the manipulated joint did not differ significantly from those that occurred when the manipulation was applied distally, suggesting that successful treatment of patients with LBP using SM may not require precise lumbar segmental specificity. Clinical and neurophysiological studies should be conducted to determine the efficacy of targeted manipulation in the lumbar spine.