The ligand-sensitive gate of a potassium channel lies close to the selectivity filter

Abstract

Potassium channels selectively conduct K⁺ ions across cell membranes and have key roles in cell excitability. Their opening and closing can be spontaneous or controlled by membrane voltage or ligand binding. We used Ba²⁺ as a probe to determine the location of the ligand-sensitive gate in an inwardly rectifying K⁺ channel (Kir6.2). To a K⁺ channel, Ba²⁺ and K⁺ are of similar sizes, but Ba²⁺ blocks the pore by binding within the selectivity filter. We found that internal Ba²⁺ could still access its binding site when the channel was shut, which indicates that the ligand-sensitive gate lies above the Ba²⁺-block site, and thus within or above the selectivity filter. This is in marked contrast to the voltage-dependent gate of K_V channels, which is located at the intracellular mouth of the pore.

Introduction

Ion channels are intrinsic membrane proteins that act as gated pores to regulate the movement of ions across cell membranes. Their opening and closing (gating) is central to their function and is regulated by membrane voltage, mechanical force or ligand binding (Hille, 2001). Potassium channels are one of the largest groups of ion channels, and have pivotal roles in the function of many cell types. Mutations in K⁺-channel genes, many of which impair gating, result in diseases such as epilepsy, deafness, cardiac disorders and impaired insulin secretion (Ashcroft, 2000).

The crystal structure of the bacterial K⁺ channel KcsA has provided a paradigm for the pore of K⁺ channels (Doyle et al., 1998; Zhou et al., 2001). Each of the four subunits of KcsA has two transmembrane helices, which form an inverted teepee (Fig. 1A). The helix-bundle crossing region defines the inner entrance of the pore and is proposed to serve as an intracellular gate to the channel (Fig. 1B, b; Doyle et al., 1998; Liu et al., 2001; Perozo et al., 1999). Support for this idea comes from the fact that the crystal structure of the bacterial K⁺ channel MthK, imaged in the open state, reveals a widening of the pore at the helix-bundle crossing region (Jiang et al., 2002). Functional studies indicate that the activation gate of the voltage-dependent K⁺ (K_V) channel Shaker is also located at the bundle crossing (Del Camino et al., 2000; Del Camino & Yellen, 2001). Access of the small cations Cd⁺ and Ag⁺ (and by inference K⁺) to the internal cavity is regulated by this gate (Del Camino & Yellen, 2001).

Figure 1.

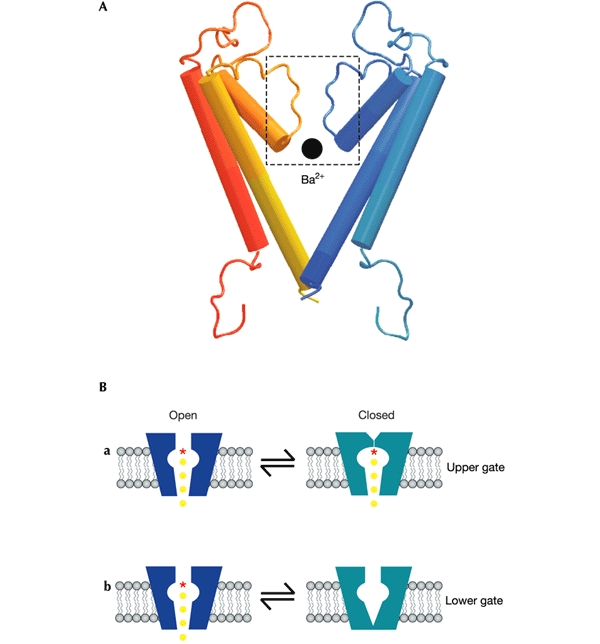
Putative locations of K⁺ channel gates. (A) Homology model of two of the four subunits of Kir6.2, generated by using the sequence alignment of Capener et al. (2000) and the crystallographic coordinates of KcsA (Doyle et al., 1998). A Ba²⁺ ion is shown to scale at the entrance to the selectivity filter. (B) Schematic models showing two possible locations for the gate(s) of K⁺ channels; at the selectivity filter (a) or at the helix-bundle crossing (b).

However, evidence is accumulating that the selectivity filter of K⁺ channels might also act as a gate (Fig. 1A, B, a). At low K⁺, the selectivity filter of KcsA is occluded by the rotation of Gly 77 into the permeation path (Zhou et al., 2001) and spin-labelling studies suggest that small conformational changes take place at the selectivity filter during gating (Perozo et al., 1999). The ability of permeant ions to influence K_V channel gating (Armstrong et al., 1982) is also most readily explained by an effect on the selectivity filter. This has led to the suggestion that the selectivity filter of K_V channels might contribute to intrinsic gating, even if it does not serve as the voltagesensitive gate. In the case of cyclic-nucleotide-gated channels, a recent study suggests that the ligand-sensitive gate lies above the helix-bundle crossing and thus, by default, might reside within the selectivity filter (Flynn & Zagotta, 2001). The location of the ligandsensitive gate of the inwardly rectifying K⁺ (Kir) channels is unknown. Here, by studying block by internal Ba²⁺, we provide direct evidence that the ligand-sensitive gate of the Kir channel Kir6.2 is not located at the helix-bundle crossing but lies within, or above, the selectivity filter.

Results

Like KcsA, Kir6.2 has two transmembrane helices, linked by a pore loop, and cytoplasmic amino and carboxy termini (Fig. 1A). Four pore-forming Kir6.2 subunits associate with four regulatory SUR subunits to form the ATPsensitive K⁺ channel, and binding of ATP to the cytosolic domains of Kir6.2 results in channel closure (Ashcroft & Gribble, 1999). In the absence of ATP, K_ATP channels exhibit spontaneous bursts of openings, separated by long closed intervals (Trapp et al., 1998). ATP decreases the frequency and duration of the bursts and increases the duration and frequency of the long closed times. Mutations in the helix-bundle crossing region dramatically increase the burst duration, but do not alter the duration of the long closed times (Trapp et al., 1998). This suggests that the helix-bundle crossing does not serve as the ligandsensitive gate.

We exploited the fact that Ba²⁺ binds within the selectivity filter of K⁺ channels (Neyton & Miller, 1988a,b; Jiang & MacKinnon, 2000) to determine the location of the gate closed by ATP. If the helix-bundle crossing serves as the ligandsensitive gate, then ATP should slow the rate and reduce the affinity of the internal Ba²⁺ block. In contrast, if the gate lies above the Ba²⁺-binding site, the Ba²⁺ block should be largely unaffected by the presence of the nucleotide.

Fig. 2A shows that Kir6.2/SUR1 currents were unaffected by the presence of intracellular Ba²⁺ at −40 mV, but that the cation induced a rapid time- and voltage-dependent block of outward currents on depolarization. Increasing ATP to 15 μM, which decreased Kir6.2/SUR1 currents by ∼70% (Fig. 2C), produced a small but significant acceleration of block by Ba²⁺ (Fig. 2B, D). This effect is the opposite of that expected if the access of Ba²⁺ to its binding site is impaired when the channel is shut by ATP, and implies that the gate lies above the Ba²⁺-binding site. Ba²⁺ did not alter the half-maximal inhibitory concentration (IC₅₀) for ATP inhibition (6 ± 2 μM (n = 6) compared with 6 μM in the absence of Ba²⁺ (Gribble et al., 1998)), which argues against an electrostatic (gating-independent) effect of ATP on Ba²⁺ binding.

Figure 2.

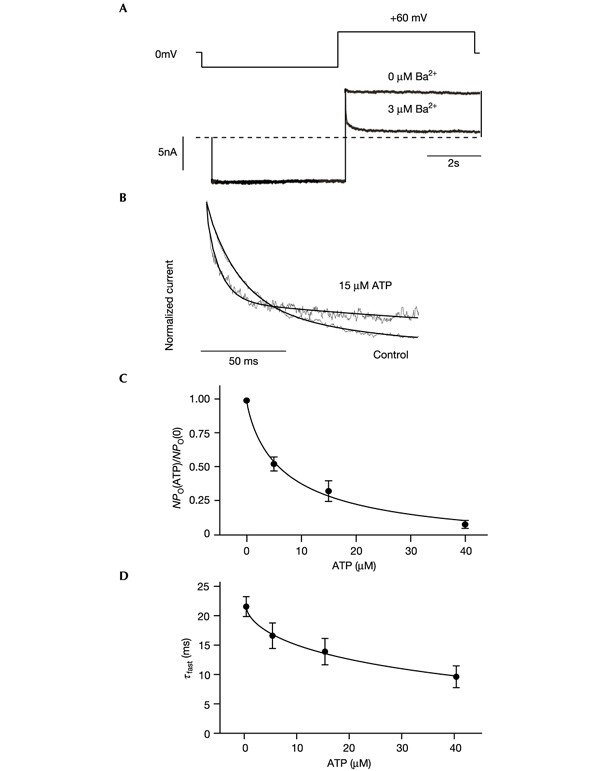
Modulation of Ba⁺ block by ATP indicates that the gate does not lie at the helix-bundle crossing. (A) Macroscopic Kir6.2/SUR1 currents (below, dotted line indicates 0 pA) recorded in response to the voltage protocol shown above. Ba²⁺ (3 μM free) was present in the intracellular solution throughout and produced a rapid block of outward currents on depolarization. (B) Time course of block of Kir6.2/SUR1 currents by 3 μM free Ba²⁺ in the absence and subsequently the presence of 15 μM ATP (grey lines), normalized to peak current amplitude. The time course of block was best fitted (solid lines) by the sum of two exponential curves: control (n = 6), τ_f = 23.5 ± 3.0 ms (A_f = 0.65 ± 0.03) and τ_s = 289 ± 26 ms (A_s = 0.35 ± 0.03). In 15 μM ATP (n = 6), τ_f = 13.9 ± 2.2 ms (A_f = 0.56 ± 0.09) and τ_s = 176 ± 22 ms (A_s = 0.44 ± 0.09). The extent of block by Ba²⁺ was decreased from 0.84 ± 0.02 in control solution to 0.72 ± 0.03 in the presence of ATP (n = 6). (C) ATP dependence of normalized current amplitude at +60 mV (n = 6). The current in the presence of Ba²⁺ (I_Ba) is expressed as a fraction of the mean of that in the control solution before and after Ba²⁺ application (I₀). The line is drawn to I_Ba/I₀ = 1/(1 + ([ATP]/IC₅₀)^h) (equation 1), where IC₅₀ = 6.0 ± 1.5 μM and h = 0.86 ± 0.11. (D) ATP dependence of the time constant of Ba²⁺ block (τ_f) at +60 mV (n = 6).

To explain how ATP accelerates block by Ba²⁺, we simulated the block of macroscopic currents, using rate constants obtained from single-channel recordings (Fig. 3A). Regardless of the free parameters used to fit the kinetic model, these simulations show that if Ba²⁺ binds only to the open state (that is, above the gate), a decrease in channel open probability (P_o) reduces the rate and extent of block (Fig. 3B, C). Because this is not observed experimentally, the gate closed by ATP cannot lie below the Ba²⁺-binding site. The simulations also confirm that if Ba²⁺ binds equally well to both open and closed states (that is, below the gate), there is no change in the rate or extent of block with P_o (Fig. 3D, E). Experimentally, Ba²⁺ block was accelerated and decreased in its extent when the ATP concentration was increased (Fig. 2B). This effect can be simulated if Ba²⁺ binds below the gate and if, in the closed state, the off-rate is faster and the on-rate is increased by ATP (Fig. 3F). Thus, our results indicate that Ba²⁺ binds below the gate closed by ATP, and further suggest that Ba²⁺ binding is destabilized when the channel closes.

Figure 3.

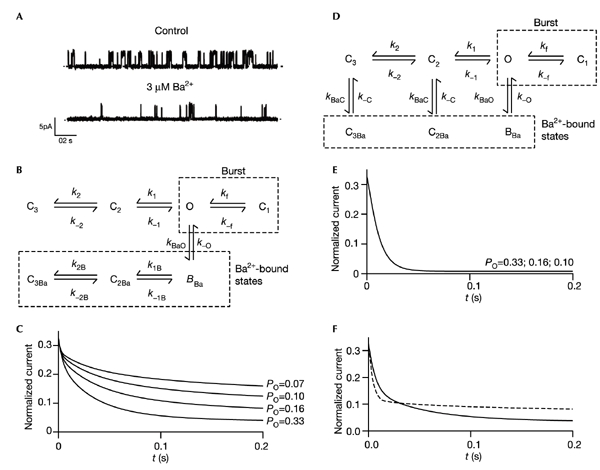
Simulations of block of macroscopic currents by Ba²⁺, based on single-channel data. (A) Single Kir6.2/SUR1 currents recorded at +60 mV from an inside-out patch in the absence (above) or presence (below) of 3 μM free Ba²⁺. Ba²⁺ decreased the mean open time from 6.1 ± 1.3 ms to 3.9 ± 0.6 ms, decreased the duration of the bursts of openings from 10.0 ± 2.8 ms to 5.1 ± 0.4 ms, and induced an additional long closed time with a duration of 310 ± 97 s (n = 3). The estimated rate constants for Ba²⁺ block, calculated from the open and closed time durations, were 82 ± 13 s⁻¹ for τ_on and 3.2 ± 0.3 s⁻¹ for τ_off. The fact that transitions to the long closed states C₂ and C₃ contribute significantly to intrinsic gating (Fig. 3B), and that the corresponding rate constants are of similar magnitude to those of Ba²⁺ block, accounts for the multi-exponential time course of block of macroscopic currents (Bernasconi, 1976). We did not analyse the effect of ATP on Ba²⁺ block at the single-channel level because ATP introduces additional closed states. (B, D) Kinetic schemes of K_ATP channel gating used in the simulations C (B) and E, F (D), respectively: (B) Ba²⁺ does not enter the channel in the closed state; (D) Ba²⁺ can enter the channel in both open and closed states. O, open state; C₁, intraburst closed state; C₂, C₃, long interburst closed states. B_Ba, C_2Ba,C_3Ba, Ba²⁺ blocked states. The following parameters were calculated from the single-channel data: k₁ = 130 s⁻¹, k₋₁ = 79 s⁻¹, k₂ = 5 s⁻¹, k₋₂ = 16 s⁻¹, k_BaO = 80 s⁻¹, k_−O = 3 s⁻¹. The contributions of the transitions between B_Ba, C_2Ba and C_3Ba to P_o turn out to be minimal, and were omitted for simplicity. (C, E, F) Simulated time course of Ba²⁺ block at +60 mV for different values of P_o, assuming that ATP primarily affects the rate constants k₁ and k₂, and does so in an approximately equal manner (Trapp et al., 1998; Fan & Makielski, 1999). Reduced P_o values were simulated by increasing both k₁ and k₂ twofold (P₀ = 0.16), threefold (P₀ = 0.10) or fourfold (P₀ = 0.07). (C) Ba²⁺ binds only to the open state. k_1B = k₁/50; k_2B = k₂/50. No simulations were able to reproduce the experimental data. Varying k_1B, k_2B, k⁻¹B or k−2B (independently or simultaneously) with respect to their equivalent rates in the absence of Ba²⁺ principally affected the slow component of block (τ_s). In the absence of ATP, the data were most closely fitted by models in which the contributions of transitions between B_Ba, C_2Ba and C_3Ba to P_o were minimal. (E) Ba²⁺ binds equally to all states (k_BaO = k_BaC, k_−O = k_−C). (F) Ba²⁺ binds to all states but, in the closed state, the off-rate is faster (k_−C = 50k_−O) and ATP increases the on-rate. Solid line, ATP-free, P₀ = 0.33, k_BaC = k_BaO; dashed line, plus ATP, P₀ = 0.1, k_BaC = 3k_BaO.

We tested the effect of increasing P_o on Ba²⁺ block by using a mutant channel (Kir6.2-C166S/SUR1) that exhibits a markedly enhanced P_o (0.85; Trapp et al., 1998). If access to the Ba²⁺-binding site is prevented when the channel is closed, the C166S mutation is predicted to accelerate the time course and increase the extent of Ba²⁺ block. However, no change in the rate of block by 3 μM Ba²⁺ was observed (τ = 22.6 ± 0.9 ms and τ_f = 23.5 ± 3.0 ms for mutant (n = 6) and wild-type (n = 6) channels, respectively). Thus, these data provide additional support for the view that the gate lies above the Ba²⁺-binding site.

Crystallographic studies of KcsA suggest that Ba²⁺ binds at the inner end of the selectivity filter, to the backbone of Val 76 and the side-chain of Thr 75 (Zhou et al., 2001). The equivalent residues in Kir6.2 are Thr 130 and Ile 131 (Fig. 4A; Capener et al., 2000). Mutation of Thr 130 to valine in Kir6.2 did not result in functional channels, but mutation of Val 129 to threonine caused a marked decrease in Ba²⁺ affinity: the IC₅₀ was 12 ± 0.2 μM (n = 5) compared with 0.8 ± 0.04 μM (n = 5) for the wild-type channel (Fig. 4B). The maximum extent of block was 82 ± 1% (n = 5), indicating that Ba²⁺ might act as a partial blocker of V129T currents (Fig. 4B, C). These results confirm the Ba²⁺-binding site of Kir6.2 lies within (or above) the selectivity filter, and indicate that the V129T mutation might modify the binding site allosterically. Studies on other Kir channels have also implicated this region in Ba²⁺ block (Lu et al., 2001; Alagem et al., 2001; Zhou et al., 1996).

Figure 4.

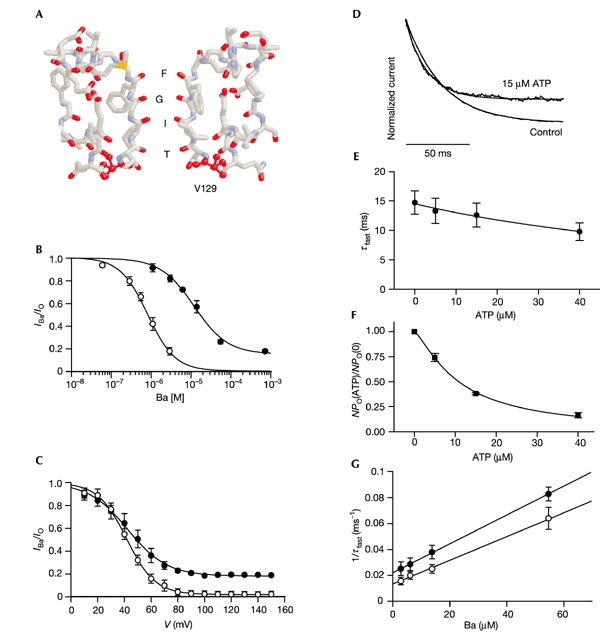
Block of the V129T mutant by Ba²⁺. (A) Homology model of the selectivity filter of Kir6.2, based on that of KcsA. (B) Relationship between [Ba²⁺]_i and macroscopic Kir6.2/SUR1 (open circles, n = 5) or Kir6.2-V129T/SUR1 (filled circles, n = 5) currents at +60 mV, obtained using the voltage protocol shown in Fig. 2A. Steadystate currents were obtained by fitting two (Kir6.2/SUR1) or one (Kir6.2-V129T/SUR1) exponential(s) to the time course of the current decay. The line is drawn to I_Ba/I_O = a + (1 − a)/(1 + ([Ba²⁺]/IC₅₀)^h), where I_Ba and I_O are the steady-state currents in the presence and absence of Ba²⁺, [Ba²⁺]_i is the free Ba²⁺ concentration, IC₅₀ is the [Ba²⁺]_i at which the inhibition is half-maximal, a is the fraction of unblocked current, and h is the Hill coefficient. The best fit to the wild-type data was obtained with IC₅₀ = 0.87 μM, h = 1.2, a = 0. For V129T, IC₅₀ = 12 μM, h = 1.0 and a = 0.15. There was no marked difference in the ATP sensitivity of wild-type and mutant channels: IC₅₀ = 6.0 ± 1.5 μM (n = 3) for wild-type and 10.8 ± 0.5 μM (n = 5) for V129T channels. (C) Voltage dependence of steady-state block by 3 μM free Ba²⁺ for Kir6.2/SUR1 (open circles; n = 5) or Kir6.2-V129T/SUR1 (filled circles; n = 5) channels. The patch was held at the given voltage and then exposed to Ba²⁺. The lines are the best fit to I_Ba/I_O = a + (1 − a)/(1 + [Ba²⁺]/K_d), where K_d = k_off/k_on; k_on and k_off are the on- and off-rates of the Ba²⁺ block, respectively. Each rate constant is given by k = exp(−zδFV/2RT), thus: I_Ba/I_O = a + (1 − a)/{1 + [Ba²⁺]/K_d (V = 0)exp(−zδFV/RT)}. The best fit to the wild-type data was obtained with δ = 1.12, a = 0; the best fit to the V129T data was obtained with δ = 0.85, a = 0.182. (D) Time course of Ba²⁺ (55 μM free) block of Kir6.2-V129T/SUR1 currents in the absence or presence of 15 μM ATP. The extent of block by Ba²⁺ was reduced from 0.66 ± 0.06 in control solution to 0.6 ± 0.06 in the presence of ATP (n = 5). (E) ATP dependence of time constants of block by Ba²⁺ at +60 mV (n = 5). (F) ATP dependence of normalized current amplitude at +60 mV (n = 5). The line is drawn to equation 1 (Fig. 2C) with IC₅₀ = 10.8 ± 0.5 μM and h = 1.31 ± 0.06. (G) Reciprocal time constants for Ba²⁺ block of Kir6.2-V129T/SUR1 (n = 5) at +60 mV in the absence (open circles) or presence (filled circles) of 15 μM ATP, as a function of [Ba²⁺]_i. The line is drawn to 1/τ_fast = k_off + k_on[Ba²⁺]_i. The values for k_off and k_on are given in the text.

Block of V129T channels by Ba²⁺ was well fitted by a single-exponential curve (τ = 14.7 ± 2.0 ms at 55 μM free Ba²⁺; n = 5) that became faster with ATP (Fig. 4D–F). This allowed us to measure τ as a function of [Ba²⁺]_i and to calculate the effective on-rate and off-rate constants of block (Fig. 4G). The on-rate constant was little changed by the absence or presence of 15 μM ATP, being (9.3 ± 0.7) × 10⁵ M⁻¹ s⁻¹ and (11.1 ± 0.1) × 10⁵ M⁻¹ s⁻¹ (n = 5), respectively. In contrast, the off-rate constant increased with ATP concentration, being 13 ± 5 s⁻¹ in the absence of ATP and 22 ± 0.1 s⁻¹ in the presence of 15 μM ATP (n = 5). These values predict a K_d of 14 μM Ba²⁺ in the absence of ATP, which is in good agreement with that found for steadystate block (Fig. 4B). Thus, changes in off-rate seem largely to account for the reduced extent of Ba²⁺ block found for V127T channels with increasing [ATP]_i. This indicates that ATP modifies the Ba²⁺-binding site, destabilizing cation binding.

Discussion

Our results suggest that intracellular Ba²⁺ is still able to access its binding site when the K_ATP channel is closed by ATP, because the rate of block is not slowed when ATP is increased. Thus, the ATP-dependent gate must be located above the Ba²⁺-block site. Because Ba²⁺ binds at the inner end of the selectivity filter (probably near Thr 130), this puts the ligand-sensitive gate within (or above) the selectivity filter. Because there is no obvious place higher up, we favour the idea that the gate lies within the selectivity filter (pore loop) itself, but our data are also consistent with the idea that the gate lies above the filter. Whichever is correct, the helix-bundle crossing region at the internal mouth of the pore cannot serve as a gate for Ba²⁺. Because Ba²⁺ is almost the same size as K⁺ (crystal radii 2.7 and 2.66 Å, respectively), K⁺ must also be able to enter the pore when the channel is shut by ATP.

There is some evidence that the binding site for Ba²⁺ is modified when the channel is closed, because Ba²⁺ block is accelerated and decreased in amplitude when ATP is present. One possibility is that a conformational change consequent on channel closure accelerates the off-rate of Ba²⁺ into the internal cavity. This might be more likely if the gate and the Ba²⁺-binding site are located close together. Although our data place the gate for K⁺ ions at or above the selectivity filter, they do not exclude the possibility that large conformational changes take place at the helix-bundle crossing region during gating of Kir6.2, nor that this region might serve as a gate for large molecules (such as thiol reagents).

ATP inhibits, and phosphatidylinositol (4,5)-biphosphate (PtdInsP₂) stimulates, K_ATP channel activity by altering the frequency of the long closed times (Trapp et al., 1998; Fan & Makielski, 1999). Thus, both agents probably modulate the same gate. Taken together, our data are consistent with the idea that this ligand-operated gate is not at the helix-bundle crossing region but resides within, or above, the selectivity filter (Fig. 1Ba). Thus, binding of ATP (or PtdInsP₂) to the cytosolic domains of Kir6.2 must cause a conformational change that is propagated, through the transmembrane domains, up to the pore loop region. Gating of K_ATP channels, and possibly also other members of the inwardly rectifying K⁺ channel family, must therefore operate differently from that of K_V channels (Del Camino & Yellen, 2001).

Speculation

How might the selectivity filter serve as a gate for K⁺? One possibility is that the permeation path becomes physically occluded by one or more amino acids. An alternative idea is that electrostatic changes gate K⁺ flux through the pore, an effect that need not necessarily be associated with large changes in protein structure. A key question is whether the ligand-dependent gating discussed here, and the intrinsic fast closings within bursts of openings (Proks et al., 2001), operate on the same or different gates.

Methods

Xenopus laevis oocytes were injected with ∼2 ng of SUR1 (GenBank accession number L40624) and ∼0.1 ng of wild-type or mutant Kir6.2 (GenBank D50581) messenger RNAs (Trapp et al., 1998). Currents were measured 1–4 d later in excised inside-out patches, at 18–24 °C, using an Axopatch 200B patch-clamp amplifier. Macroscopic currents were filtered at 2 kHz and digitized at 5 kHz. Single-channel currents were measured at +60 mV, digitized at 20 kHz and filtered at 5 kHz; their kinetics was analysed as described by Trapp et al. (1998). The external (pipette) and internal (bath) solutions contained (in mM): 107 KCl, 10 EGTA, 10 HEPES (adjusted to pH 7.2 with KOH). BaCl₂ (in mM, given in parentheses) was added to the internal solution to give free concentrations (in μM) of 0.056 (0.01), 0.3 (0.05), 0.56 (0.1), 1.14 (0.2), 2.94 (0.5), 6.2 (1), 13.9 (2) and 55 (5). Free [Ba²⁺]_i was calculated with the binding constants of Martell & Smith (1974). Concentrations in the text refer to free Ba²⁺ concentrations. Data are given as means ± s.e.m.

Ba²⁺ block of macroscopic currents was simulated with ModelMaker (Cherwell Scientific Publishing, Oxford). Rate constants for channel gating in the absence of Ba²⁺ or ATP were calculated from kinetic parameters measured in single-channel studies, using a conventional model of K_ATP channel gating (Fig. 3B, D; Gillis et al., 1989). It was assumed that channel closure does not alter the mobility of ions in the parts of the pore that remain freely accessible to the bath solution.