Placing confidence limits on the molecular age of the human–chimpanzee divergence

Abstract

Molecular clocks have been used to date the divergence of humans and chimpanzees for nearly four decades. Nonetheless, this date and its confidence interval remain to be firmly established. In an effort to generate a genomic view of the human–chimpanzee divergence, we have analyzed 167 nuclear protein-coding genes and built a reliable confidence interval around the calculated time by applying a multifactor bootstrap-resampling approach. Bayesian and maximum likelihood analyses of neutral DNA substitutions show that the human–chimpanzee divergence is close to 20% of the ape–Old World monkey (OWM) divergence. Therefore, the generally accepted range of 23.8–35 millions of years ago for the ape–OWM divergence yields a range of 4.98–7.02 millions of years ago for human–chimpanzee divergence. Thus, the older time estimates for the human–chimpanzee divergence, from molecular and paleontological studies, are unlikely to be correct. For a given the ape–OWM divergence time, the 95% confidence interval of the human–chimpanzee divergence ranges from –12% to 19% of the estimated time. Computer simulations suggest that the 95% confidence intervals obtained by using a multifactor bootstrap-resampling approach contain the true value with >95% probability, whether deviations from the molecular clock are random or correlated among lineages. Analyses revealed that the use of amino acid sequence differences is not optimal for dating human–chimpanzee divergence and that the inclusion of additional genes is unlikely to narrow the confidence interval significantly. We conclude that tests of hypotheses about the timing of human–chimpanzee divergence demand more precise fossil-based calibrations.

Determining the age of the most recent common ancestor of humans and their closest African ape relatives has been the subject of scientific inquiry for over a century. This age is important for assessing the evolutionary rate of morphological and molecular changes in humans, assigning key fossils in hominoid phylogeny, and estimating when the common ancestor of all humans lived. The paleontological approach has been hampered by the paucity of fossils of some lineages. The first chimpanzee fossil, for example, was only just reported in 2005 (1). As recently as the mid-1960s (2), the African apes were considered to be distant relatives of the human lineage, but subsequent molecular phylogenetic analyses have shown that the chimpanzee and human are sister species and have led to a revision of the age of their divergence (3–13). Currently, the earliest unequivocal upright hominids at 4.2 millions of years ago (Ma) provide the minimum age for human–chimpanzee divergence (14), and some recently proposed early hominids dated between 5 and slightly more than 6 Ma are thought to provide an estimate close to the actual species divergence (15–19). However, a divergence time of 12.5 Ma for humans and chimpanzees has been entertained recently as well (20), and so the fossil record and its interpretation give a range of 4.2–12.5 Ma.

To employ molecular data to test alternative hypotheses derived from the fossil record, we require credible confidence intervals (C.I.s) of the molecular age of human and chimpanzee divergence. However, studies using molecular data have yielded disparate values as well (3–13 Ma), because of differences in the number of genes used, types of substitutions (synonymous, noncoding, and nonsynonymous) analyzed, calibration points used, and statistical methods used (3–13). Furthermore, current estimates of C.I.s of molecular divergence times fail to consider a comprehensive set of factors contributing to variance, such as a limited number of genes (gene sampling error), a limited number of sites for each gene (variance contributed by sequence divergence-estimation procedures), rate differences among lineages, and inherent uncertainty in the time used for calibrating lineage-specific and relaxed molecular clocks (21, 22). These factors point to the need to use a large number of genes and a closely positioned calibration point to reduce the statistical variance of the estimated time and increase our power in testing alternative fossil-based hypotheses.

Therefore, we have assembled a data set containing the largest number of nuclear genes available to estimate the timing of human–chimpanzee divergence in reference to the ape–Old World monkey (OWM) divergence. To build credible C.I.s, we have developed a multifactor bootstrap-resampling (MBR) approach that can incorporate the variances mentioned above. Furthermore, we have conducted computer simulations under random and correlated deviations from a constant-rate model to examine the statistical validity of C.I.s generated by the MBR approach when using a large number of genes for a few species to date very recent speciation events. This evaluation is particularly important for the analysis of closely related species, because tests of rate constancy are often powerless in rejecting genes in which different lineages evolve at different rates (5, 23). In the following, we have also compared results obtained by using different types of point substitutions in the same set of protein-coding genes, including amino acid sequence differences, nucleotide substitutions at the second and third codon positions, and neutral substitutions at 4-fold-degenerate sites (with and without hypermutable CpG positions).

Materials and Methods

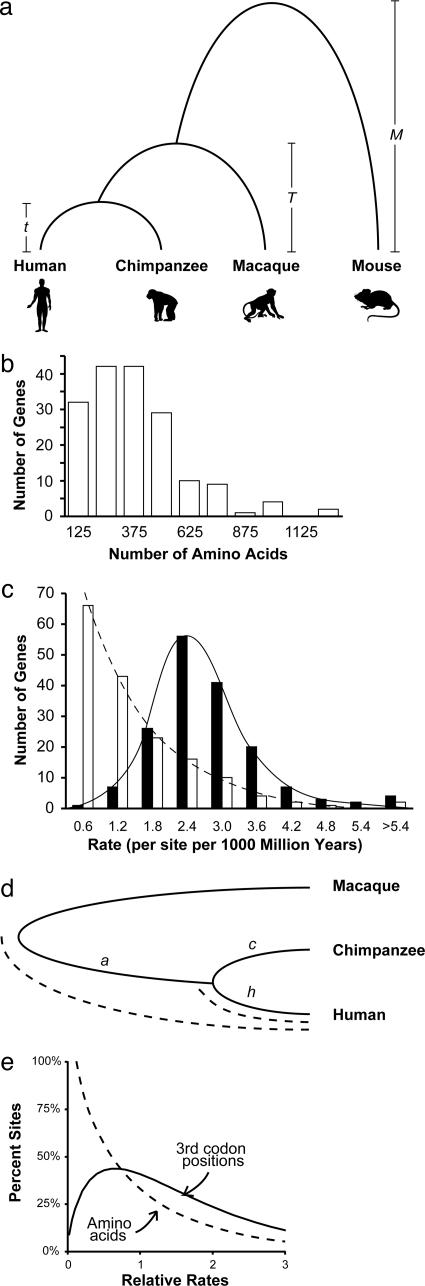
Data Collection. To maximize the number of useable genes and employ a close primate calibration species for estimating human–chimpanzee divergence time, we assembled 167 orthologous protein sequence sets for human (Homo sapiens), chimpanzee (Pan troglodytes), macaque (Macaca mulatta), and mouse (Mus musculus), considering their phylogenetic relationships (Fig. 1a) (for details see Data Collection in Supporting Text, which is published as supporting information on the PNAS web site). Observed distributions of protein lengths (Fig. 1b) and rates (Fig. 1c, open bars) show considerable variation, as expected. The protein sequence alignments were used as guides (for codon boundaries) to generate coding DNA sequence alignments and evolutionary rates at the third codon positions (Fig. 1c, solid bars). We identified all third codon positions that were 4-fold-degenerate in all species for each gene for analysis as well. Because CpG dinucleotides mutate 7–10 times faster than other dinucleotides, 4-fold-degenerate sites were separated into those that were involved in CpG dinucleotides and those that were not (24, 25).

Fig. 1.

Characteristics of the data. (a) Phylogenetic relationships of human, chimpanzee, macaque, and mouse. (b) Histogram showing the length distribution of proteins used. (c) Distributions of the average evolutionary rates of amino acids (open bars) and third codon positions (solid bars) for 167 protein-coding genes analyzed in this study. Evolutionary rates were estimated assuming a 90 Ma date for primate–rodent divergence (5, 22, 46). (d) Schematic showing how lineage-specific molecular clocks were used to estimate the human–chimpanzee divergence time by using the ML distances between species pairs. The human–chimpanzee divergence time is given by the fraction ([h + c]/2)/(a + [h + c]/2) of the time assumed for ape–OWM divergence. (e) Distribution of evolutionary rates among sites for amino acids (dashed curve; shape parameter = 0.83) and third codon positions (solid curve; shape parameter = 1.65) obtained in ML analyses of concatenated sequences (53,008 codons) of 167 protein-coding genes. In each case, modeling the rate variation among sites by using a gamma distribution produced a significantly better fit (P < 0.005).

Estimation of Divergence Times Using Local Clocks. We used a lineage-specific method with maximum likelihood (ML) estimates of sequence divergence generated by using paml 3.14 (26) and the Bayesian timing method implemented in the multidivtime software (21). For the ML method (referred to as the ML-distance approach), we concatenated all sequences into a supergene, estimated branch lengths in the four-species tree using paml 3.14, and inferred divergence times in a lineage-specific manner (Fig. 1d). To estimate evolutionary distances in paml 3.14, a general time reversible (GTR) model with a gamma (Γ) distribution describing the rate variation among sites (GTR+Γ) was used for DNA sequences and a Jones–Taylor–Thornton (JTT)+Γ model with a discrete gamma distribution (with five rate categories) was used for the amino acid sequences. In the Bayesian analysis, we used the same supergene described above, with a F84+Γ model for DNA and a JTT+Γ model for amino acid sequences, based on the most sophisticated models available in multidivtime software (21).

Estimation of C.I.s. Although the ML-distance and Bayesian methods provide C.I.s and standard errors for estimated times, they do not simultaneously incorporate the variances introduced by the estimation of genetic distances from individual genes, sampling error due to the use of a limited number of genes, rate variation among evolutionary lineages (in ML-distance), and the distribution of uncertainty in calibration times. To do this, we developed a MBR approach for generating C.I.s in which these variances can be explicitly incorporated when one uses ML, Bayesian, or other methods as estimators of time. We chose a bootstrap, rather than an analytical, approach because it is less dependent on specific assumptions about the distribution of the data, and analytical formulations are often too cumbersome to incorporate phylogenetic correlations (27). The algorithm for this process and its properties are given in Supporting Text. We also conducted computer simulations to evaluate the statistical accuracy of the MBR method in generating an appropriate C.I. when used in conjunction with the ML-distance and Bayesian methods for a large number of genes and for only four species (see Supporting Text).

Results and Discussion

We first used the ML-distance method in which a lineage-specific molecular clock is applied to estimate the human– chimpanzee divergence time (see Fig. 1 and Materials and Methods). This method requires a priori knowledge of at least one species divergence time to calibrate the local molecular clock. We took a conservative approach and used a minimum date of 23.8 Ma (boundary of the Oligocene and Miocene) for the ape–OWM divergence (28) (see Supporting Text). We focused on the minimum time of divergence because the inference of the true (mean) time of divergence of any two lineages requires a more robust fossil record for calibration than is generally available for most groups of organisms, and especially these primates. Most past molecular clock studies have also estimated minimum divergence times for this reason (29). In recent years, many methods have been developed that attempt to estimate mean times of divergence by specifying both minimum and maximum calibration points. However, whereas most minimum calibrations are robust, this is not true for maximum calibrations or the implicit assumption about the probability density assumed for fossil calibration uncertainty (29). It is difficult to provide convincing evidence that a phylogenetic divergence event did not occur earlier than a particular point in time. Errors in assignment of maximum constraints, whether too young or too old, will potentially bias the mean time estimate.

Analysis of Third Codon Positions. A likelihood ratio analysis of third codon positions from 167 genes (53,008 codons) indicated significant rate variation among sites (Fig. 1e), so we used a GTR+Γ model in all further analyses. Using a 23.8 Ma minimum date for ape–OWM divergence, we obtained an ML-distance estimate of 4.74 Ma, which is older than the age of 4.2 Ma for the earliest unequivocal postcranial evidence of upright hominids (14) but younger than some recently proposed early hominids dated from between 5 and ≈6 Ma (15–19).

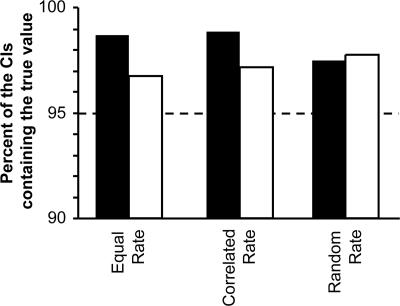
However, the absolute dates derived above depend directly on the time used to calibrate the molecular clock, and it is important to focus on the size of the C.I. relative to the estimate, rather than on the point estimate of time alone. Using the MBR approach, we obtain a 95% C.I. of 3.88–5.65 Ma for the minimum date. This C.I. spans –18% to +19% of the estimated time. Our computer simulations under equal, random, and correlated models of rate evolution show that the 95% C.I. generated by MBR indeed contains the true value ≥95% of the time when all third positions are resampled, regardless of gene boundaries (Fig. 2).

Fig. 2.

The percent of simulation replicates in which the 95% C.I. generated by the MBR method includes the simulated true value using the ML-distance (filled bars) and Bayesian approaches (open bars). (See Supporting Text for a description of the rate-variation models and how the data were parameterized.) We simulated 1,000 167-gene equivalent data sets under each rate-variation regime and conducted MBR analyses to obtain C.I.s for the ML-distance (GTR+Γ) and Bayesian (F84+Γ) approaches. The results show that 95% C.I.s contain the true value more often than required, particularly for the ML-distance method. This finding shows that modeling-rate variation among lineages (as in the Bayesian method) should lead to narrower C.I.s when the underlying model for correlated evolutionary rates among lineages is satisfied (constant and correlated rate cases), as compared with the ML-distance approach, in which rate variation is incorporated into the C.I. instead of being modeled. Interestingly but not unexpectedly, Bayesian and ML methods perform similarly when the assumptions of the Bayesian model are not satisfied (random rate-variation case). This finding is consistent with a study showing that a Bayesian approach with lognormal rate-variation model does not accommodate uncorrelated rate variation (47).

Of all third codon positions, the 4-fold-degenerate sites are expected to be under the least amount of natural selection. We divided these sites into those that were involved in CpG dinucleotides and those that were not, because the 4-fold-degenerate sites involved in CpG dinucleotide configurations mutate much faster (24, 25). Analysis of 19,311 non-CpG 4-fold-degenerate sites produced an estimate of 4.75 Ma, which is almost identical to that given by third codon positions, but the 95% C.I. was wider (–25% to +31%). Because the data set size (in terms of the number of sites) was the largest for the third codon positions, we considered only third codon positions in all further DNA sequence analyses.

Analysis of Nonsynonymous Substitutions. Unexpectedly, ML-distance analyses of amino acids and second codon positions yielded estimates of human–chimpanzee divergence that were >40% larger than those obtained from the third codon positions and 4-fold-degenerate sites. In fact, neither the estimate obtained using amino acids (6.80 Ma), nor the third-position estimate (4.74 Ma) fell within the 95% confidence limit of the other (4.78–8.86 Ma and 3.88–5.65 Ma for amino acids and third positions, respectively). This finding is surprising because both DNA and protein substitutions are expected to provide concordant results, especially when using a large number of protein-coding genes.

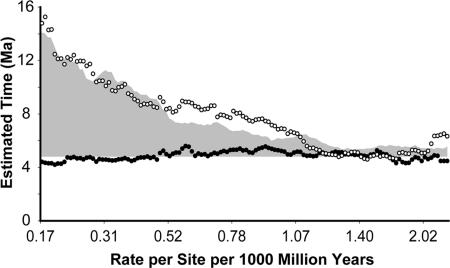
A cursory examination of the time estimates based on the rate of amino acid substitutions revealed a tendency toward larger estimates for very slowly evolving proteins. The 40 most slowly evolving proteins (based on evolutionary divergence of human and mouse proteins) provide an estimate more than three times higher than the 40 fastest evolving proteins. In contrast, the third codon position estimates are similar whether obtained from genes corresponding to proteins evolving with low, medium, or fast rates and coincide with the estimates obtained from fast-evolving proteins (Fig. 3). These patterns suggest a disproportionate inflation of sequence divergence for closely related species as compared with distantly related species, an effect that would be the greatest for the most slowly evolving proteins. The skewed inflation of sequence divergence estimates for closely related sequences may be attributed to sequencing errors, presence of ancestral polymorphisms (30), persistence of slightly deleterious polymorphisms (31, 32), and masking of deleterious mutations in heterozygotes (33). Although these factors affect all amino acids and third codon positions, the most slowly evolving sequences (e.g., highly conserved proteins) are affected the most relative to their rate and the time of sequence divergence.

Fig. 3.

Dependence of human–chimpanzee divergence time estimate on the rate of amino acid sequence evolution when using amino acids (open symbols) and third codon positions (solid symbols). Each value represents the time estimate obtained from an analysis of 40 concatenated proteins and is plotted at the median amino acid distance between human and mouse for that set of proteins. Proteins were sorted in ascending order based on the human–mouse amino acid sequence divergence, and ML-distance analyses were performed on amino acids (JTT+Γ) and third codon positions (GTR+Γ) on sets of 40 proteins in a sliding window that shifted by one protein at a time. The gray region shows the additional time obtained in computer simulations when sequencing errors and within-species polymorphisms contributed three amino acid sequence changes per 1,000 aa, and ML-distance analyses were conducted on the resulting amino acid sequence alignment following the procedure described above. The human–chimpanzee divergence times estimated are minimum times because a 23.8 Ma date for ape–OWM divergence was assumed (see text); however, the shape of the distribution remains unchanged irrespective of the clock-calibration time used. Similar results were obtained when using the Bayesian methods (results not plotted).

Our computer simulations showed that if the cumulative effect of nonneutral polymorphism due to factors described above produced, at an average, three differences per 1,000 aa, then an overestimation pattern similar to the magnitude and trend observed for the real data would be obtained (Fig. 3, gray area). Furey et al. (34) have already reported sequencing error rates of 0.5 bp per 1,000 nucleotides for human GenBank data, which translates to one error per 1,000 aa (because >75% of base pair errors in three codon positions result in an error at the amino acid sequence level). Although genomic sequences have a lower error rate, within-species comparisons in humans indicate a 1 in 1,000 bp difference at the genome level between individuals (35). This variation contributes nonfixed differences between species and affects the estimate of human–chimpanzee divergence in the same way as the sequencing errors. Sequencing error rate for available chimpanzee sequences is higher than that for humans (4 times versus 10 times coverage; see Ensembl, www.ensembl.org), and chimpanzees are known to have a much higher within-population polymorphism (33), both of which would lead to an overestimation in the present case.

In addition to the above factors, the fixation of lineage-specific amino acid substitutions due to positive selection (36) may also make the use of amino acid sequences problematic. However, it is unlikely to be the major contributing factor in the present case, because none of the slowest-evolving proteins in our data set were found to be involved in host defense, immunity, or olfaction (36, 37). On the other hand, the most rapidly evolving proteins, which show estimates similar to those obtained from the third codon positions, contain a large proportion of genes known to be candidates for positive selection (which show nonsynonymous to synonymous substitution ratios of >0.5). In any event, because of the observed artifact mentioned above, we do not further consider the estimates based on amino acid sequence analysis.

Bayesian Inference of the Minimum Time for Human–Chimpanzee Divergence. The relative rate analysis shows that human third codon positions are 17% more divergent than those of chimpanzee and that the 4-fold-degenerate non-CpG sites are evolving ≈20% more slowly in hominoids than in OWM. Both of these rate differences are insignificant [P > 0.05 in Tajima's test (23)] and are in agreement with those reported elsewhere (33). The difference between hominoids and OWM is similar in magnitude to that reported in an analysis of large data sets by Yi et al. (38) and Kumar and Subramanian (39). It is one-half of that reported by Steiper et al. (40), whose estimates of relative rates depend on fossil-based divergence times for within-hominoid and within-cercopithecoid species, although an outgroup was not used in their analyses.

In any case, the observation of any rate differences in the hominoid–OWM comparison means that the ancestral human–chimpanzee lineage may not be evolving at the same rate as those leading to humans and chimpanzees, violating the assumptions made in the ML-distance approach. Therefore, we applied Bayesian analysis as implemented in multidivtime (21) that models rate variation among lineages to generate a better estimate of human–chimpanzee divergence. We used 23.8 Ma for the ape–OWM divergence time as the root-to-tip mean (RTTM = 23.8) in the multidivtime Bayesian analyses to make results directly comparable to the ML-distance method (see Supporting Text for parameters used for Bayesian analysis). This produced an estimate of 4.98 Ma for the third codon positions and of 5.17 for the 4-fold-degenerate non-CpG sites. These estimates are marginally higher than those for the ML-distance estimates, but the discrepancy becomes smaller when we compare the ratio of the times of the target (human–chimpanzee) and calibration (ape–OWM) divergence events. Even though we provide an explicit time (RTTM) for the ape–OWM split, multidivtime infers time estimates for both human–chimpanzee and ape–OWM divergences. These estimates give consistent ratios of 0.21 (4.98/24.00) and 0.21 (5.17/24.37) for the third codon positions and the 4-fold-degenerate non-CpG sites, respectively. In the ML-distance method, the time ratio is 0.20 for the third codon positions (4.74/23.8) and also 0.20 (4.75/23.8) for the 4-fold-degenerate non-CpG sites. Therefore, the time ratios for the Bayesian estimates are only 5% higher than are those obtained using the ML approach. Bayesian methods also produced a narrower 95% C.I. (–12% to +19%) as compared with the C.I. (–18% to +19%) of the ML-distance approach for the third codon position data. Our computer simulations confirmed that the MBR C.I.s contain the true value with a frequency of >95% in the Bayesian approach as well (Fig. 2). Because the C.I.s generated using the MBR approach with the Bayesian analysis are smaller, we use them below.

Comparison with Previous Studies. Our minimum estimates of 4.74 and 4.98 Ma from ML-distance and Bayesian methods, respectively, based on the minimum 23.8 Ma date for ape–OWM divergence, are smaller than many previous molecular time estimates. There are three primary reasons for this difference. First, many studies have presented (and sometimes preferred) the higher divergence times estimated by using the protein sequences or by using all three codon positions (e.g., refs. 5 and 10). However, as shown above, the inclusion of slowly evolving amino acid sequences (or first and second codon positions) is likely to bias time estimates for the human–chimpanzee divergence. This pattern is also seen in the Bayesian analysis of amino acid sequences, which produces an ≈60% larger time estimate as compared with the third codon positions, with a 95% C.I. that does not overlap with that obtained from the analysis of third codon positions.

Second, different studies have used vastly different divergence times (20–35 Ma) for the ape–OWM split to calibrate molecular clocks. A comparison of the estimated and assumed time ratios resolves this discrepancy. For example, our ratios from 0.21 to 0.20 are consistent with the 0.21 value reported in analyses conducted by using >150,000 bp of noncoding data by Stieper et al. (40), 97 protein-coding genes by Wildman et al. (9), and complete mitochondrial DNA by Schrago et al. (ref. 41; see also ref. 7). Therefore, in the absence of a firmly established calibration date, it is better to consider all results as ratios of human–chimpanzee to ape–OWM divergence times.

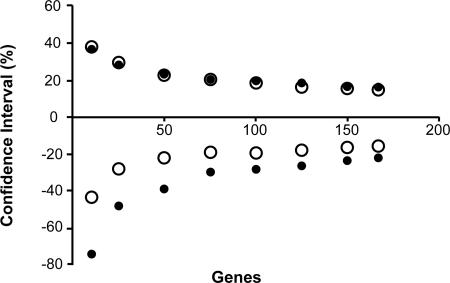
Third, most previous studies were based on the analysis of fewer genes. In those cases, the true C.I. accounting for the variance from gene sampling, multiple-hit correction, and evolutionary rate differences among species is expected to be rather large. This effect is evident from the lower and upper limits of the 95% C.I.s obtained by using smaller random subsets of 167 genes (Fig. 4). When the number of genes is <10 (e.g., ref. 5), the 95% C.I. is nearly as large as the time estimate itself. The C.I. declines to ≈50% if 50 genes are used (e.g., refs. 7 and 10). With the use of 100 or more genes, uncertainties contributed by rate variation among lineages become predominant, and the C.I. width declines only slowly. Thus, little is to be gained by adding data from more genes, but using more species may help narrow the 95% C.I. width in the future.

Fig. 4.

The relationship of the lower and upper limits of the 95% C.I.s (as a percentage of the estimated time) with the number of genes analyzed by using the ML-distance approach (filled circles) and the Bayesian analysis (open circles). Each point is an average based on computed C.I.s of 10 random subsets of genes. The dashed line illustrates the trend of the Bayesian interval. Similar results were obtained by using the data generated by computer simulation based on the evolutionary parameters of the third positions in different genes.

Incorporating Multiple Fossil Bounds in the Bayesian Inference. Bayesian methods allow more fossil constraints to be used in species divergence time estimation, such as a minimum constraint of 4.2 Ma (14) for the human–chimpanzee divergence. After adding this constraint and keeping RTTM = 23.8, we found that the human–chimpanzee divergence time increased by 53%. However, the ratio of estimated times for ape–OWM and human–chimpanzee divergences was 0.21, which is the same ratio obtained without placing the minimum bound on the human–chimpanzee divergence. Setting RTTM (time for the common ancestor of human, chimpanzee, and macaque) to 35 Ma in the Bayesian analyses again produced the same time ratio (0.21), even though the estimate of human–chimpanzee time became even larger.

To determine which estimates are likely to be correct, we conducted analyses with and without the human–chimpanzee constraint of 4.2 Ma for the simulated data under equal, random, and correlated evolutionary rate variation. [In the random rate case, the rate at each branch is randomly selected from a uniform distribution of rates so as to introduce a ±40% random noise in evolutionary rate independently for each gene. In the correlated rate, the assignment of lineage-specific rate uses a stationary lognormal distribution in which the rates vary from branch to branch as a random walk for a given gene, so that rates drift up or down along the branches of any lineage (42, 43). See Supporting Text.] In all cases, time ratios were recovered with high accuracy, but the absolute times estimated were strongly dependent on the calibration constraints used in the Bayesian analyses, as observed in the analysis of the real data.

At this stage, it is important to revisit the distinction between estimating minimum and true times of species divergence (see discussions in ref. 29). Clearly, the exclusive use of minimum calibration times, derived from the fossil record, will produce only minimum time estimates of the target divergence and its C.I., irrespective of the sophistication of the methods used (29). Focusing on minimum time estimates provides at least two advantages. For one, asserting a minimum time constitutes a definite, falsifiable statement, namely that a divergence occurred before some specified date. Alternatively, we could specify upper and lower bounds on calibration times (44) in an effort to estimate “true” divergence time, but doing so would require the incorporation of invariably subjective specifications of calibration time uncertainty. The results of our application of Bayesian methodologies to real and simulated data, discussed above, indicate that the absolute times of human–chimpanzee divergence inferred by using a four-species construct are strongly affected by the upper and lower bounds used, but these methods are successful in correctly estimating ratios of time estimates for different nodes in the phylogeny.

In fact, the estimated C.I.s from Bayesian analyses are unlikely to be around the “true” divergence time, unless a probability distribution around the range of times inferred from the fossil record can be assigned (29). For example, if we have established minimum and maximum values for calibration time but have reason to believe from fossil evidence that the true divergence time is closer to the former than the latter, then the time distribution may be triangular or lognormal (29). In other cases, the best we can do is to associate a standard deviation with the calibration time and, if necessary, assume a normal or uniform distribution. In some instances we may have evidence pointing toward a certain shape of distribution, in which case the MBR method can be used to explicitly specify this distribution. For example, if we assume a linearly declining probability distribution with 23.8 Ma as minimum (and most probable) estimate of ape–OWM and 35 Ma as its maximum, we obtain a 95% C.I. of 4.17–7.13 Ma. In this case, the C.I., rather than the actual date, should be reported because the ad hoc form of distribution used strongly determines the central value of the time estimated rather than any biological knowledge.

Conclusions

Even when mean or true times of divergence between species are difficult to estimate with molecular clocks, because of uncertainties in fossil calibrations, minimum and relative times of divergence can still be obtained. Here we have shown that the divergence of chimpanzees and humans is such a case, because of the current lack of robust calibration points. Our genome-scale analyses show that the minimum time of that divergence was very close to one-fifth of the ape–OWM divergence, with a 95% C.I. from –12% to +19% of that time. This result can be used to test hypotheses that arise in the literature. For example, if claims of late Miocene (≈6 Ma) fossil hominids (15–17) are correct, then the ape–OWM divergence occurred at least 24–25 Ma or earlier based on the 95% C.I. (Table 1). This date extends the age of that latter divergence only slightly from the accepted 23.8 Ma. Conversely, if fossils of hominoids or OWM were discovered and dated to 27 Ma, this would imply a minimum time of divergence of between 4.9 and 6.6 Ma for chimpanzees and humans. Because large gaps in the fossil record are not implied in either case, they would be compatible with current understanding of the primate fossil record. In contrast, the recent suggestion that some ape-like fossil teeth from Africa might be from the African ape clade and that the human–chimpanzee divergence time might be even older than 12.5 Ma (20) seems to be extremely unlikely. This inference is because extrapolation of the upper 95% confidence limit from Table 1, using this date, implies a minimum ape–OWM divergence time of ≈55 Ma, >30 million years earlier than supported by current fossil evidence. Similarly old molecular clock dates (13.5 Ma, based on mitochondrial DNA and using nonprimate calibration points) for the human–chimpanzee divergence (12, 45) present the same problem. By enabling tests such as these, new fossil discoveries and better radiometric dating of existing fossils provide the best prospects for improved understanding of the timing of events in hominid evolution.

Table 1. Confidence limits on the human–chimpanzee divergence time for different calibration times for ape–OWM divergence.

	Human—chimpanzee divergence, Ma
Ape—OWM calibration,* Ma	Time	95% C.I.†
23.8	4.98	4.38-5.94
25.0	5.22	4.55-6.20
27.0	5.54	4.89-6.60
29.0	5.96	5.20-6.98
31.0	6.33	5.55-7.39
33.0	6.67	5.85-7.78
35.0	7.02	6.13-8.37

^*Ingroup RTTM used in the Bayesian analyses of the third codon positions under a F84+Γ model in the MULTIDIVTIME software (21).

^†The 95% C.I.s were obtained from 1,000 replicates of the MBR procedure described in the text.