A Relative-Entropy Algorithm for Genomic Fingerprinting Captures Host-Phage Similarities

Abstract

The degeneracy of codons allows a multitude of possible sequences to code for the same protein. Hidden within the particular choice of sequence for each organism are over 100 previously undiscovered biologically significant, short oligonucleotides (length, 2 to 7 nucleotides). We present an information-theoretic algorithm that finds these novel signals. Applying this algorithm to the 209 sequenced bacterial genomes in the NCBI database, we determine a set of oligonucleotides for each bacterium which uniquely characterizes the organism. Some of these signals have known biological functions, like restriction enzyme binding sites, but most are new. An accompanying scoring algorithm is introduced that accurately (92%) places sequences of 100 kb with their correct species among the choice of hundreds. This algorithm also does far better than previous methods at relating phage genomes to their bacterial hosts, suggesting that the lists of oligonucleotides are “genomic fingerprints” that encode information about the effects of the cellular environment on DNA sequence. Our approach provides a novel basis for phylogeny and is potentially ideally suited for classifying the short DNA fragments obtained by environmental shotgun sequencing. The methods developed here can be readily extended to other problems in bioinformatics.

Genome analysis has uncovered many sequence differences among organisms. Both mononucleotide and dinucleotide content, as well as codon usage, vary widely among genomes (6). The size of even small bacterial genomes is statistically sufficient to determine a substantially richer set of sequence-based features describing each organism. However, many of these features have remained elusive, in the coding regions in particular, due to complicated constraints. Each (protein-coding) gene encodes a particular protein, which constrains its possible nucleotide sequence. Because the genetic code is degenerate, this constraint still allows for an enormous number of possible DNA sequences for each gene. Also, the overall codon usage in each gene is known to have strong biological consequences, possibly determined by isoaccepting tRNA abundances (5). In order to isolate new features within the coding regions, these constraints must be factored out.

To solve this problem, we create a background genome that shares exactly the above-described constraints with the real genome but is otherwise random (4). The background genome encodes all the same proteins, and the codon usage is precisely matched for each gene. The hidden features for which we are searching are contained in the differences between the background genome and the real genome. The problem is reduced to extracting these differences.

We have incorporated information theory into an algorithm to systematically compute the over- and underrepresented strings of nucleotides (words) in the real genome compared to those of the background (see Materials and Methods for details). A major difficulty in finding these words is that they are not independent. For example, if the word ACGT is underrepresented, then ACGTA will also be underrepresented, as well as ACG, etc. The assumption is that only one of these words has biological significance, while the others are “along for the ride.” This problem extends to all words. As the set of words of a given length is finite and so are genomes, the frequency of any one word affects the frequency of all others. We devised an iterative algorithm which uses an information theory measure to select the word contributing the most to the difference between the real and background genomes. At each step, we added this word to a list and then factored out its effects by rescaling the background genome. In this way, we obtained a list of words, each of which is likely to have biological significance, that contribute independently to the difference between the real and background genomes. The size of the genome determines the length of words that we have statistical power to resolve. For a typical bacterium such as Escherichia coli, we can conservatively include lengths of up to 7 nucleotides. The amino acid order and codon usage by gene are held fixed, so the features that our algorithm uncovers are complementary to mononucleotide content and codon usage. For typical bacteria, the algorithm finds 100 to 200 sequences between 2 and 7 nucleotides in length (Table 1). These previously hidden signals contain a wealth of biological information.

TABLE 1.

E. coli word list

Sequence no.	Sequence	Over- or underrepresented		Sequence no.	Sequence	Over- or underrepresented
1	GGCC	−		51	CACCA	+
2	TAG	−		52	GGTACC	−
3	GCTGG	+		53	TTCG	−
4	TTGGA	−		54	TGGG	−
5	CCC	−		55	GAGACC	−
6	GGCGCC	−		56	GATCG	−
7	GTCC	−		57	CCCTG	−
8	GCCGGC	−		58	CTGGCTG	+
9	GGCG	+		59	CTGGCA	+
10	GAGG	−		60	AAAAAAA	−
11	CCAAG	−		61	TGGCCT	+
12	GGGT	−		62	GGAG	−
13	TTGCC	+		63	GAGCTC	−
14	CTAG	−		64	CTCGAC	+
15	GCCAG	+		65	CAGCAA	+
16	CTGCAG	−		66	AGAC	−
17	AAGAG	+		67	TCCAA	−
18	ACTGG	+		68	TATGAT	−
19	GAAC	−		69	TATA	−
20	GTGT	−		70	GGAC	−
21	TTGG	−		71	TGGCCA	−
22	TCAAG	−		72	TTCCTCG	+
23	CGCTG	+		73	CTGTC	−
24	CGGTA	+		74	TGTG	−
25	CACGTG	−		75	TCTGA	−
26	CCGCGG	−		76	CAGAT	−
27	GGCTC	−		77	CGTG	−
28	CATG	−		78	CAAG	−
29	CAGCTG	−		79	CTGCTGG	−
30	TCGGA	−		80	TTTTTT	−
31	CGGCCG	−		81	TCGCA	−
32	AATT	−		82	TATCG	+
33	TTGCT	+		83	TGCGA	−
34	CGAG	−		84	CTGGGGC	+
35	GGGGG	−		85	TGAAG	+
36	TCGTG	−		86	GTCTGG	+
37	CTGAG	−		87	GTCGAT	+
38	GACC	−		88	GCATGC	−
39	CTTG	−		89	GAAT	−
40	GGTCTC	−		90	GTTGA	+
41	CCTGGA	−		91	CAGTAA	+
42	CTCC	−		92	GAGCC	−
43	GCGGA	−		93	ACGCT	+
44	TCAGG	+		94	CAGCGA	+
45	AGCGCT	−		95	TCCGA	−
46	TGGTG	+		96	CTGGAAG	+
47	TCGTA	−		97	TCTTA	−
48	CGCC	+		98	CTCAGA	−
49	CGGCA	+		99	TTGACA	−
50	TTCCCG	+		100	CCATGG	−

MATERIALS AND METHODS

Relative-entropy algorithm.

To discover the words that are the most significantly over- and underrepresented in the coding regions of a genome, we first created a randomized background genome that we used for comparison with the real genome. This was accomplished by randomly permuting the codons corresponding to each amino acid within every gene (4). A new coding sequence was created which had the same amino acid content and codon usage per gene as the actual genome but was otherwise random. We then counted the number of occurrences for each word, w, of length 2 to 7 in this randomized genome. (Our choice of 7 as the maximum-length word to consider was dictated by the total length of the coding sequence in the genome of interest. The average number of occurrences of each word should be >>0 in order for our algorithm to be robust.) The procedure to generate random genomes was repeated 30 times, at which point the standard deviation in number of occurrences converged for the words. We then computed the average N_B(w) background count of each word w. We chose, for reasons that will be clarified below, to determine N_B(w) by considering only words of length 7 and generating the counts for smaller-length words by counting substrings. We let L(w) equal the length of the word w and 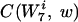equal the number of times the string w is contained in the string 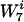of length 7. As an example, if w is AAC and 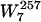is AACAAAC, then L(w) equals 3 and 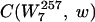equals 2.

N_B(W₇ⁱ) = 1/30 × (the sum of the number counts of W₇ⁱ in all 30 background genomes).

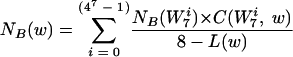(1)

Likewise, we let N_R(w) equal the count of w in the real genome. In what follows, we worked with frequencies (or equivalently probabilities) rather than counts, so we formed the frequencies for each word with the formulas P_B(w) = N_B(w)/L and P_R(w) = N_R(w)/L, where L is the overall length of our coding sequence.

The two frequency distributions P_B and P_R were the starting point for the word search algorithm. This algorithm consists of two steps that were iterated in turn. In the first step, the word that most significantly separates the real from the background distribution was selected, based on a measure of significance to be described below. In the second step, the background probability distribution was rescaled to factor out the difference due to the word found in step 1. These two steps were repeated a fixed number of times or until the background distribution was sufficiently close to the real one.

The Kullback-Leibler distance between the real and background probability distributions is given by

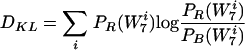(2)

Then, we wanted to find a figure of merit that measures the extent to which any word w, of length 2 to 7, contributes to D_KL. A natural measure is given by

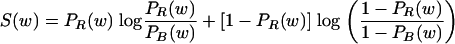(3)

This can also be thought of as a Kullback-Leibler distance between two probability distributions, namely, the coarse-grained real and background distributions where we know only if a given word is or is not w (12). In the first step of the iteration, we chose a word w of length 2 to 7 which maximizes the significance measure S(w).

The next step was to rescale the background distribution in a minimal way, such that the contribution of w became identical in both the real and background distributions. For the rescaling to be minimal, the ratios of frequencies of words 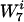of length 7 that contain w the same number of times should not change. That is, we wanted to rescale all words 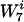with the same 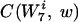by an equal factor. Therefore, we needed to work with an appropriate coarse graining of the detailed probability distributions. Our distribution for the background was defined as the set of words 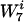of length 7, with the probabilities 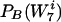. We partitioned this set of 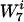into disjoint subsets where each element of a given subset contained the word w an equal number of times. These sets are

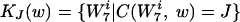(4)

with J = {0,…, 6} and

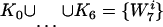(5)

We wanted to rescale these disjoint subsets K_J(w) such that the probabilities of being in a given subset in the real and background distributions were equal.

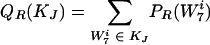(6)

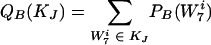(7)

These are well-defined probability distributions because they are grouped elements from the old probability distribution (and their probabilities are added). A rescaling that factors out the contribution of w while conserving probability is given by

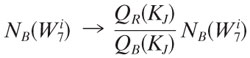(8)

where W₇ⁱ ∈ K_J, for all i. Note that with this rescaled distribution, the figure of merit for w is now S^rescaled(w) = 0, so the contribution of w to D_KL has been removed. We then repeated step 1 to find the next word, w′, etc.

It is not hard to see in this iterative algorithm that the background distribution 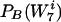converges to the real distribution, 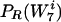. This is because D_KL is monotonically decreasing (see below). It is well known that D_KL is nonnegative and is 0 if and only if the two distributions are identical. The algorithm will not halt before convergence is achieved, since the equation S(w) = 0 for all w also implies that the real and background distributions are identical. Finally, D_KL cannot converge to a positive value, since one could then find a word that would reduce it below that value.

For applications, we had to decide when the iterations were no longer contributing statistically significant words to the list. This cutoff is the point where it becomes likely that chance fluctuations would create the most significant remaining word, appropriately corrected for multiple hypotheses [the set of all words of length L(w)]. The cutoff occurs when the selected word w satisfies

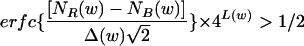(9)

where Δ(w) is the standard deviation of the background count for w. For applications in this paper, we stopped after 100 iterations, which is substantially below the cutoff.

Proof that D_KL decreases monotonically with rescaling.

Given two probability distributions {p_j} and {q_j}, with j ∈ S and S the set of possible outcomes, the Kullback-Leibler distance is

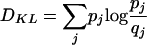(10)

This is nonnegative and zero only if the distributions are identical.

Consider a disjoint partition of S, into r sets, S₁… S_r, i.e.,

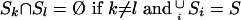(11)

Next, define the coarse-grain probabilities,

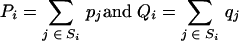(12)

Assume that Q_i is >0 for all i. We note that both P_i and Q_i are themselves probability distributions.

Define the rescaled distribution,

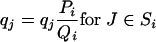(13)

The new Kullback-Leibler distance is

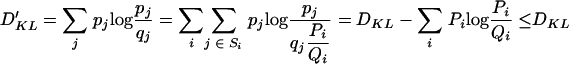(14)

with equality only if P_i equals Q_i for all i.

Scoring algorithm.

To score a coding sequence S of length s with respect to a genome G of length g, we first generated a word list for G as described above, with the following modification: words were added to the list only if they would be significant for a sequence of length s. This significance was determined by rescaling the counts and the standard deviations for each word to the scale s. We multiplied the counts of each word in the background genome and the real genome by s/g, which gives the expected counts, N_b and N_r, for the sequence S. The standard deviation was rescaled by 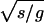, giving Δ^s. If the word satisfied the equation |N_r − N_b| > 3 × Δ^s, then it was included on the list; otherwise, it was skipped. Because s is much less than g, this standard was substantially more strict than the multiple-hypothesis corrected cutoff described above. The rest of the iterative procedure, including rescaling the background distribution, was the same as that described above. This new list L formed the scoring template with the number of words X. To get the score, we formed the background B of the sequence S by the same Monte Carlo shuffling procedure as that described above. We then implemented the following iterative algorithm: at each step, we took a word W from the ordered list L. We then compared the counts of that word in the sequence S and the background B, adding 1 to our score only if the direction of the bias for W between S and B was the same as that for W between the genome G and its background, that is, only if W was overrepresented in both G and S compared to their respective backgrounds or was underrepresented in both. We then rescaled B in the manner described above to factor out the effects of W and proceeded to the next step. Going through the entire list L, we got a number Y out of X possible words for which there was agreement between the genome and the sequence. The final score was 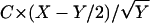, with C as a constant. For every short sequence, scoring was done for all 164 bacterial species in the NCBI database (http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?db=Genome), which includes 253 chromosomes.

Metric for phylogenetic tree.

The metric utilized 50-kb slices and the scoring method described above. The distance between two genomes, A and B, was calculated in three steps. First, all of the 50-kb slices of genome A were scored against the full genome B, and then the scores were averaged. The same process was repeated for the 50-kb slices of genome B scored against genome A. Second, the two averages were symmetrized. Lastly, the symmetrized score was subtracted from the maximum possible score. This distance has most of the properties of a metric-symmetric, positive definite zero only if A equals B, although it does not obey the triangle inequality. We used nearest-neighbor clustering and employed the PHYLIP software package to output the tree (3).

RESULTS

Although the word lists were generated from entire bacterial genomes, they correspond to features of DNA sequence which are homogeneous throughout the genomes. We confirmed this in two separate ways. First, using E. coli as an example, we divided the genome in half and ran the algorithm on the two halves independently. The resulting lists were the same up to statistical fluctuations. For lists of 100 words, the top 80 words were on both lists. The process was repeated multiple times with different divisions, and the results were similar.

For our second check that under- and overrepresentation of the words are local features of the genome, we created an elementary algorithm to score sequences of coding DNA based on the word lists from each genome. This algorithm takes as its inputs a coding DNA sequence and a list of words and assigns that sequence a score based on the under- and overrepresentation of the words in the sequence (see Materials and Methods). The 253 bacterial chromosomes greater than 100 kb in length in the NCBI database were broken up into 50-kb and 100-kb slices. These sequences were scored separately against all 164 species. Ninety-two percent of the 100-kb slices scored highest with their own species. Using 50-kb sequences, 86% scored best with their own species. This confirms that the words correspond to features that are homogeneous throughout each bacterial genome. Neither GC content nor codon usage has this property of homogeneity; both vary substantially within single genomes. Additionally, this outcome suggests that the scoring procedure based on these hidden words is a useful classifier of sequences. For instance, the sequences attained from microbes in the Sargasso Sea described by Venter et al. (9) can be compared with known bacteria without requiring homologous genes. (The best known bacterial genome classifier is an oligonucleotide approach developed by Karlin and Cardon [6]. Even with our naïve first version of the scoring algorithm, the results for 50 kb and 100 kb were slightly better than those with the most-comprehensive oligonucleotide approach, which involves comparing frequencies of oligonucleotides with lengths up to 4. Our scoring was substantially better than that of the dinucleotide approach applied by Venter et al. [9].)

Our approach is also well suited for studying the relationship between viruses and their hosts. Since virus DNA is copied and expressed inside a host, one might expect that viruses and their hosts share some evolutionary pressures. However, mononucleotide contents and codon usages differ dramatically between host and phage. Some information has been gained from oligonucleotide comparisons, but our scoring system described in Materials and Methods is more than 60% better. Out of the set of sequenced DNA phages on the NCBI website, 185 phages have known primary hosts. Many of the phages are known or suspected to have multiple host species within the same genus. For this reason, we considered host targets at the genus level. The 164 species divide into 108 different genera. For our algorithm, the correct host genus scored highest for 93 of the 185 phages, and 131 phages had the correct host in the top three scores (Table 2). For comparison, the best oligonucleotide scoring system has 58 of 185 correct host genera. Both codon usage and mononucleotide content are poor predictors of phage hosts.

TABLE 2.

Scoring of phage host predictions

Phage type	% of phages with:
	Top score	Top three scores
All	50	71
dsDNA	58	82
Lytic	45	59
Temperate dsDNA	70	93

By restricting our analysis to double-stranded DNA (dsDNA) phages, which comprise the large majority of known phages, our host predictions improved significantly. Removing the 35 single-stranded DNA phages improved the scoring to 87/150 or 58% for the top score and 123/150 or 82% for the top three scores. The phages can be further stratified into temperate and lytic (1). For temperate dsDNA phages, which still constitute the majority of sequenced phages, our prediction for hosts was excellent (93% in the top three, with 70% with the top score). Lytic phages did not score as well, although still better than 50% in the top three, suggesting that their DNA is not subject to the same evolutionary pressures as those of the host cell.

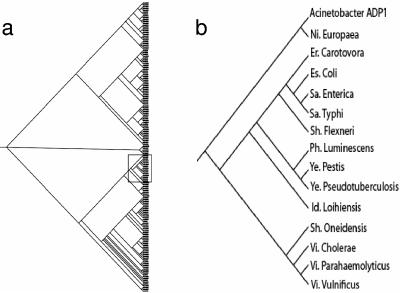
We adapted our scoring algorithm to form a distance between genomes (see Materials and Methods). Applying hierarchal clustering to a matrix of distances of the set of 164 bacterial species, we created a phylogenetic tree (Fig. 1a). The tree captures most of the standard bacterial taxonomy. For an example, see Fig. 1b, which shows that the Enterobacteria are grouped in the same clade. This suggests that the properties encoded by the word lists are conserved evolutionarily. Since the distance is based on a whole-genome property, we avoided some of the common pitfalls in making phylogenetic trees, like lateral gene transfer. Also, this method allowed the addition of new species in the tree without requiring any homologous genes or even a large amount of sequenced genomes.

FIG. 1.

(a) Phylogenetic tree for the 164 bacterial species found in the NCBI database. A rectangle encloses the enterobacterial clade. (b) A blowup of the enterobacterial clade of the tree. Results for Acinetobacter strain ADP1, Nitrosomonas europaea, Erwinia carotovora, Escherichia coli, Salmonella enterica, Salmonella enterica serovar Typhi, Shigella flexneri, Photorhabdus luminescens, Yersinia pestis, Yersinia pseudotuberculosis, Idiomarina loihiensis, Shigella oneidensis, Vibrio cholerae, Vibrio parahaemolyticus, and Vibrio vulnificus are shown. The only enterobacterium missing from this group is Buchnera aphidicola.

DISCUSSION

We have introduced an algorithm that finds over 100 new signals in the coding regions of each bacterial genome. The set of applications presented includes the use of these signals (words) as a classifier and a genomic connection between phages and their hosts, as well as the creation of a phylogenetic tree. These are only a subset of the potential applications for the algorithm. Some possible uses for eukaryotes include splice site detection, mRNA degradation or stabilization signals, tissue specificity, and host-virus relationships. Real exons have overrepresented signals, such as exon splicing enhancers (2). Our algorithm can determine a comprehensive list of over- and underrepresented sequences in real exons, which could be used to separate real exons from confounding intronic sequences. For mRNA stability, a few groups have measured the decay rates for large numbers of mRNAs in a variety of organisms, including humans (8, 11). The range of half-lives spans 2 orders of magnitude, but the signals or structures that determine this difference in stability are unknown. If our algorithm is applied to a set of the 1,000 most rapidly decaying mRNAs and the 1,000 most stable mRNAs, the differences in the two lists should provide a set of important signals. For tissue specificity, it has been shown in the last couple of years that genes primarily expressed in different tissues have distinct properties; their codon usages and GC contents are different (7, 10). We should be able to find additional signals that distinguish tissues. These signals have the potential to provide information about the host tissue for viruses. Unlike codon usage and mononucleotide content, which are not shared by phages and bacterial hosts (or by human viruses and their host tissues), our algorithm is an excellent predictor of viral hosts.

This algorithm can also be used to help find transcription factor binding sites. From the DPInteract database (http://arep.med.harvard.edu/dpinteract/), we extracted the set of known binding sites for the 13 transcription factors that had 15 or more binding sites listed for E. coli. The binding sites determined a set of weight matrices that score the binding motifs. By running the weight matrices over the real E. coli genome and comparing them with the background E. coli genome, we found that 12 of the 13 motifs were significantly (4 standard deviations) underrepresented in the coding region. This procedure can be used as a filter to decide whether a motif is real, which is of immediate utility, as the commonly used motif finders pick out excess signals that are not real transcription factor binding motifs.

For wider use of these signals, we hope to develop a background model that fairly represents true coding regions. Many bioinformatics problems require searching for a longer motif or sequence by comparing it with a random background. These problems have proved difficult because there is no procedure to generate a background model that includes all of the biases in real genomes. Our algorithm determines all of the short global biases. Creating a background model that respects these biases will allow a variety of difficult bioinformatics problems to become tractable.