Structural changes involved in protein binding correlate with intrinsic motions of proteins in the unbound state

Abstract

Protein–protein binding usually involves structural changes that may extend beyond the rearrangements on a local scale, and cannot be explained by a classical lock-and-key mechanism. Several models have been advanced to explain the flexible binding of proteins such as the induced fit mechanism where the ligand is postulated to induce a conformational change at the interaction site upon binding, or the preexisting equilibrium hypothesis that assumes that protein samples an ensemble of conformations at equilibrium conditions and that the ligand binds selectively to an active conformation. We explored the equilibrium motions of proteins that exhibit relatively large (nonlocal) conformational changes upon protein binding using the Gaussian network model and the anisotropic network model of protein dynamics. For four complexes, LIR-1/HLA-A2, Actin/DNase I, CDK2/cyclin, and CDK6/p16^INK4a, the motions calculated for the monomer exhibiting the largest conformational change, in its unbound (free) form, correlate with the experimentally observed structural changes upon binding. This study emphasizes the preexisting equilibrium/conformational selection as a mechanism for protein–protein interaction and lends support the concept that proteins, in their native conformation, are predisposed to undergo conformational fluctuations that are relevant to, or even required for, their biological functions.

Protein–protein interactions underlie the execution and control of cellular activities. Understanding the mechanisms by which protein recognition and interactions occur is a major task both for experimental and computational biology. Several models have been suggested to describe the mechanisms of interactions of proteins, starting from the “lock-and-key” model proposed by Emil Fisher (1). While this model insightfully emphasizes the importance of shape complementarity between the two structures, the proteins in their bound form exhibit structural changes with respect to their unbound form. The conformational changes associated with protein–protein interactions vary from local changes in side chains rotameric states to global changes in structure such as collective domain movements (2, 3). The “induced fit” model (4) has been introduced to account for this type of plasticity of proteins, as opposed to rigid-docking inherent in the lock-and-key model. The induced fit model suggests that substrate binding induces a change in the 3D structure of its receptor. A geometric fit is thus ensured only after the structural rearrangements of the proteins induced by their recognition/interaction.

Betts and Sternberg (5) analyzed the conformational changes that accompany binding for a set 39 complexes, predominantly enzyme inhibitors; this set of complexes show minor to moderate conformational change. They concluded that (at least for enzyme inhibitors) protein–protein recognition occurs by the mechanism of induced fit. However, many complexes undergo conformational changes substantially larger than those explored in this study (2, 3). Bosshard (6) noted that “induced fit is possible only if the match between the interacting sites is strong enough to provide the initial complex enough strength and longevity so that induced fit takes place within a reasonable time.” Thus, the mechanism of association of the complexes that undergo large structural changes cannot be explained by the induced fit model alone.

In recent years, the “preexisting equilibrium/conformational selection” model emerged as an alternative for induced fit (7, 8) based on of the funnel-like free energy landscape concept of protein folding theories (9, 10). This concept, implicit in the well known Monod–Wyman–Changeux (MWC) model introduced for describing hemoglobin allostery four decades ago (11), postulates that the native state of a protein may not be defined by a single conformation but rather by an ensemble of closely related conformations (or substates) that coexist in equilibrium; the most suitable conformer(s) among these will bind the substrate, shifting the equilibrium toward complex formation. The energy landscape near the native state contains several minima corresponding to these substates. The more flexible the protein, the lower the barrier between the substates, and the larger the ensemble of acceptable near native conformations. The observed structural changes in some cases are beyond local side chains rearrangements near the binding site but rather entire domain movements.

Several experimental studies support the validity of preexisting equilibrium as a mechanism for protein–protein interactions. Kinetic studies done by Berger et al. (12) and Foote and Milstein (13) exemplify the preexisting equilibrium mechanism for antigen–antibody complexes. For example, of the two isomeric conformations detected by x-ray crystallography for the SPE7 antibody (14), only one possesses a promiscuous, low-affinity binding site for haptens, which result in a high-affinity complex further stabilized by induced fit. Preexisting equilibrium may not explain antibody–antigen complex selection, exclusively.

Here, we study the mechanism of interaction of four protein–protein pairs that exhibit substantial conformational changes upon complexation: LIR (leukocyte Ig-like receptor)/HLA-A2 (15), actin/DNase I (16), cyclin-dependent kinase 2 (CDK2)/cyclin (17), and CDK6/p16^INK4A (INK4) (18). The collective dynamics of the proteins are explored, using the Gaussian network model (GNM) (19, 20) and the anisotropic network model (ANM) (21, 22) of protein dynamics. We show that the structural changes observed in the complex relative to the structure of the same protein in the unbound form correlate with the intrinsic fluctuations of the unbound protein near its equilibrium state. In some cases, the equilibrium dynamics per se (i.e., conformations accessed via collective fluctuations near the native state) can fully account for the observed structural changes; in others, the intrinsic conformational preferences appear to be complemented by additional rearrangements triggered by the interaction with the substrate, suggesting that the final stabilized forms result from the combination of accessible substates and their further rearrangements induced upon substrate recognition.

Methods

GNM. In the GNM, each residue is represented by a single node positioned at its C^α atom (19). Nodes within a cutoff distance of r_c ≤ 7 Å are connected by springs of force constant γ, which leads to Gaussian fluctuations in the node positions and inter-residue distances. The topology of the network of N nodes (residues) is fully defined by the Kirchhoff matrix Γ, the elements of which are

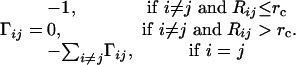[1]

We are primarily interested in determining the mean-square fluctuations of a particular residue i or the cross-correlations, 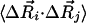, between residue fluctuations. The statistical mechanical average over all fluctuations leads to (19, 23, 24)

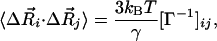[2]

where [Γ^–1]_ij denotes the ijth element of the inverse of Γ. The mean-square fluctuation is simply found by replacing j by i in Eq 2.

Mode Analysis. The motions along different GNM modes are found by eigenvalue decomposition Γ = U Λ U^–1, where U is the orthogonal matrix of eigenvectors u_k of Γ, and Λ is the diagonal matrix of the eigenvalues (λ_k), 1 ≤ k ≤ N. The eigenvalues represent the frequencies of the N–1 nonzero GNM modes and are organized in ascending order such that λ₁ ≤ λ₂ ≤ ··· ≤ λ_N–1 and λ_N = 0. The ith element (u_k)_i of the kth eigenvector describes the fluctuation (deformation) of residue i from its equilibrium position along the kth principal coordinate. The mean-square fluctuation of residue i can be rewritten as a weighted sum of the square fluctuations driven by all modes as

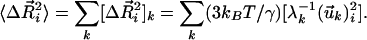[3]

GNM enables us to predict the relative sizes of motions accessed by different modes, not their directions, the GNM fluctuations being isotropic by definition. The directions of collective motions are characterized by the ANM.

ANM. The ANM (21, 22) is equivalent to a normal mode analysis where the Hessian H is based on a harmonic potential of the form

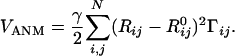[4]

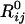and R_ij are the original (native state) and deformed (by ANM modes) distances between residues i and j. A relatively large cutoff value (r_c = 12 Å) is adopted in the ANM to ensure the coherence of the network. Eigenvalue decomposition of H yields 3N–6 eigenvectors 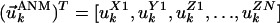, the components of which describe the motions of the N residues in the X, Y, and Z directions according to the kth mode. The components of 3N-dimensional vector 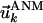are conveniently organized into N superelements of size 3 × 1, designated as 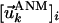, corresponding to a given residue each. Mapping ANM modes to GNM ones is done by comparing the square of the fluctuations 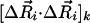between the resulting modes in the two models.

Construction of ANM-Predicted Deformed Structures. In as much as the fluctuations are symmetric with respect to the equilibrium positions of residues 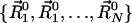, two sets of deformed structures are obtained for each mode k as

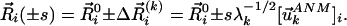[5]

Here, s is a parameter that scales the size of the deformation. Theoretically, s is equal to (k_BT/γ)^1/2; however, in the absence of quantitative information on γ, it is left as a variable to optimally match the absolute displacements observed between the unbound and bound forms while the relative displacements are not affected. Here, we used s =–15, 25, 15, and –30 for the respective proteins listed in the data set. If the obtained structure contained distorted bond lengths/angles, it was further subjected to a short energy minimization by using the moe package (Chemical Computing Group, Montreal) with the AMBER94 force field (25) and a tolerance of 1.0 kcal/mol.

Data Set. The following Protein Data Bank (26) entries were used for the unbound/bound forms: LIR-1, 1G0X (27)/1P7Q (15); Actin, 1J6Z (28)/1ATN (16); CDK2, 1HCL (29)/1FIN (17); and CDK6, 1HCL (29)/1BI7 (18). No unbound structure of CDK6 is available. The unbound structure of CDK2 was used instead for modeling the unliganded structure of CDK6 as suggested in refs. 18 and 30.

Results

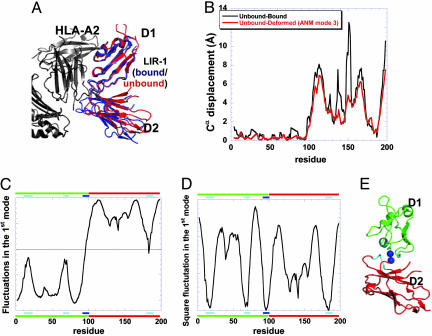
LIR1/HLA-A2. The LIR family of proteins comprises a set of immunoreceptors expressed on the surface of lymphoid and myeloid cells (31, 32). LIR-1 is a receptor for a broad range of MHC class I molecules (33) and transmits an inhibitory signal upon activation. The structure of the ligand-binding domain of LIR-1 has been solved in the unbound (free, unliganded) form (27) as well as in the complex with MHC class I molecule HLA-A2 (15). Comparison of the unbound and bound forms of LIR-1 shows a change in the D1–D2 interdomain angle from ≈85° in the unbound form to 100° in the bound form (15) (Fig. 1A).

Fig. 1.

LIR-1 structure and dynamics and comparison with LIR-1/HLA-A2 complex. (A) Comparison of the structures of LIR-1 in the unbound (red) and bound (blue) conformations. The bound form refers to the complex formed with HLA-A2 (black). The domains 1 (D1; residues 4–96) of the two LIR-1 structures are superimposed. The angle between the domains D1 and D2 of LIR-1 is observed to open up by 10–16° in the complex (15). (B) Difference in C^α positions between unbound and bound LIR-1 (black curve), and between unbound and its deformed form driven by ANM mode 3 (red curve). The close similarity between the two curves suggests that the structural change between the bound and unbound forms of LIR-1 is ensured by the fluctuations of the protein along this particular mode of motion, which are already favored/accessible before substrate recognition and binding. (C) Displacements along the first principal mode predicted by the GNM, showing that the motions of the domains D1 and D2 are anticorrelated motion. The inversion in the direction of fluctuations occurs at residues V95 and T96 (global hinge center). (D) Square fluctuations of residues in GNM mode 1. Three local minima (cyan bar) are observed, in addition to the global minimum at hinge region (blue bar), which cluster in the interface between the two domains, as illustrated in E. The ribbon diagram in E is colored by the domains and hinge regions indicated by the bars in D. The ribbon diagrams in all figures were drawn by using pymol (44).

GNM analysis (see Methods) of LIR-1 dynamics reveals that the D1 and D2 domains of the receptor in the unbound form are subject to anticorrelated (concerted but opposite direction) fluctuations in the most cooperative (first) global mode of motion at equilibrium conditions. The D1 domain tends to move in the negative direction along the mode axis, whereas the D2 domain moves in the opposite direction (Fig. 1C), and vice versa. The direction of motion is inverted between residues V95 and T96; these residues serve as the hinge region between the two domains. The most mobile and most constrained regions of the structure in this global mode are identified from the maxima and minima, respectively, in the square fluctuations (Fig. 1D). The curve represents the normalized distribution of square fluctuations in the first mode, also referred to as the global fluctuation profile. It contains one global minimum corresponding to the hinge region (blue bar along the upper abscissa) and three local minima (cyan bars). These minima, although not contiguous along the sequence, map to structural regions clustered in space, in close proximity to the hinge residues. The corresponding structural elements can be seen in Fig. 1E, colored in accord with the bars in Fig. 1D.

The GNM analysis thus enables us to identify the hinge center and structural elements that participate in, or closely interact with, the hinge region, the relative mobility of each residue in the most cooperative (global) fluctuations of the protein, and the types of correlations between domain motions. To assess the absolute directions of the domain motions, a complementary calculation (ANM) was performed (see Methods). ANM mode 3 computed for the unbound LIR-1 is found to be equivalent to the GNM global mode (see Methods). Strikingly, this mode exhibits a high correlation with the experimentally observed structural changes of LIR-1 between the bound and unbound forms. To quantify this correlation, the D1 domains (residues 4–96) of the unbound and bound structures of LIR-1 were superimposed and the difference in the C^α atom positions between the two forms were calculated (Fig. 1B, black curve). On average, the D2 domain moves by 4.8 Å. The deformed structure of LIR-1 was then independently calculated by adding the ANM predicted (mode 3) fluctuations to each residue of the unbound structure (see Methods). The C^α displacements were measured as above between the unbound and its deformed form (Fig. 1B, red curve), which yielded a correlation coefficient of 0.89 with the experimental data. The high similarity between the two curves indicates that this mode explains well the conformational change occurring between the bound and unbound forms of LIR-1. It is conceivable that not only this mode operates to confer the observed structure in the complex. The differences between the two curves, especially near K135–C144 and Q147–S154, point to additional local rearrangements, of the type of induced fit, that assist in stabilizing the bound form. Yet, these results clearly demonstrate that the unbound conformation of LIR-1 has an intrinsic tendency to reconfigure into the bound conformation. Therefore, the likely mechanism for interaction between LIR-1 and HLA-A2 is that LIR-1 fluctuates between the unbound and bound conformation (in addition to other conformations that are being sampled) and HLA-A2 selectively binds the deformed conformation that is observed in the complex.

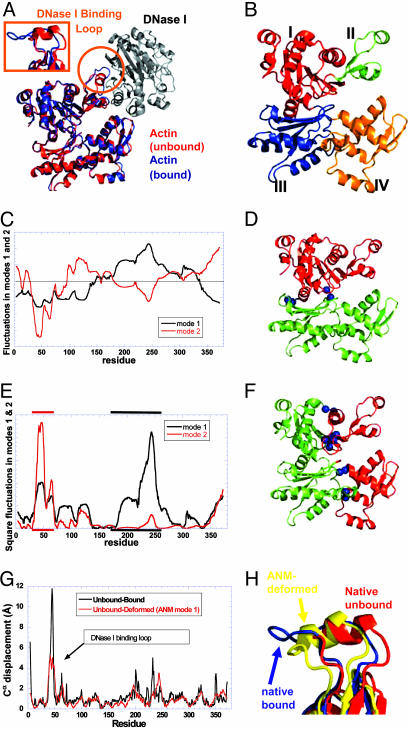
Actin/DNase I. Actin is the major component of the thin filaments in muscle cells and of the cytoskeleton in non-muscle cells. It takes part in many biological functions such as muscle contraction, lamellopodia extrusion, cell locomotion endocytosis, intracellular trafficking, and cell division (34, 35). This multitude of biological activity is mediated by interaction with actin-binding proteins (36). The actin structure was solved in the unbound state (28) and in complex with DNase I (16) (Fig. 2A). It is composed of four subdomains (Fig. 2B): subdomain I (residues 1–32, 70–144, and 338–372), subdomain II (residues 33–69), subdomain III (residues 145–180 and 270–337), and subdomain IV (residues 181–269) (16). Actin subdomain II forms the major interaction with DNase I. The DNase I-binding loop (residues H40–G48) within subdomain II is folded into an α helix in the unbound conformation; in the bound conformation, it becomes a β-turn and is hydrogen-bonded as an additional strand to the β-sheet in DNase I (Fig. 2A).

Fig. 2.

Actin structure and dynamics and comparison with the actin/DNase I complex. (A) The actin/DNase I complex is colored blue (actin) and black (DNase I); the structure of actin in the unbound state is shown in red. The DNase I-binding loop of actin (circled in orange, enlarged in Inset) changes its conformation from a helix to a β-turn upon complexation. (B) Actin is composed of four subdomains: I (residues 1–32, 70–144, and 338–372), II (33–69), III (145–180 and 270–337), and IV (181–269) (16). (C) Motions along GNM modes 1 and 2 as a function of residue index, computed for actin in the unbound form, the corresponding ribbon diagrams (D and F) colored according to the correlations revealed in C, and the associated square fluctuations in residue positions (E). In mode 1, subdomains I and II (red in D) undergo en bloc fluctuations opposite in direction to those of subdomains III and IV (green in D), the residues R147–T148 and A331–P332 serving as hinge regions (shown as blue beads). In the second mode, subdomains I and III move in opposite direction with respect to subdomains II and IV (E); residues 12–13, 17–18, 29–30, 95–96, 181–182, and 259–260 lie at the interface between these pairs of domains. (G) Comparison between experimentally observed (black curve) and theoretically predicted (red curve) displacements in C^α atoms between the unbound and bound forms of actin. Experimental data result from the comparison of two known structures (see Data Set). Theoretical results are obtained by deforming the unbound structure along the ANM mode 1 (see Methods). Whereas the overall deformation pattern is closely captured by this mode, the predicted displacement (5 Å) at the DNase I-binding loop falls short of the experimentally observed one (11 Å). (H) Conformation of the DNase binding loop in the unbound (red), ANM-deformed (yellow), and bound (blue) conformations.

The equilibrium dynamics of the unbound actin explored by using the GNM yielded the fluctuation profiles illustrated in Fig. 2 C–F. The residue displacements along the first (black curve) and the second (red curve) GNM mode axes are shown in Fig. 2C. The associated color-coded ribbon diagrams are shown in Fig. 2 D (first mode) and F (second mode), which reveal the different pairs of domains (red and green) subject to anticorrelated movements in the two modes and the corresponding hinge residues (blue beads). In the first principal mode, subdomains I and II move in the negative direction, whereas subdomains III and IV move in the positive direction, and vice versa. Residues R147–T148 and A331–P332 serve as hinges. In the second principal mode, subdomains I and III exhibit anticorrelated motions with respect to subdomains II and IV, and residues N12–G13, V17–K18, A29–V30, R95–V96, A181–G182, and E259–T260 lie at the interface between these two regions, thus serving as hinge sites for the second global mode. Finally, Fig. 2E display the fluctuation profiles (square movements) driven by the two modes, subdomain IV is distinguished by its high mobility in mode 1 (indicated by the black bar along the upper abscissa). The second mode, on the other hand, imparts a high mobility in subdomain II (red bar) and, in particular, in the DNase I-binding loop.

The potential mechanism of reconfiguration of actin upon binding DNase I has been examined with the ANM. The first ANM mode is found to correspond to the second GNM mode upon comparison of the square fluctuation profiles induced by these modes. This same mode also shows the highest correlation, among all accessible modes, with the experimentally observed structural change of actin DNase I-binding loop (correlation coefficient of 0.62) between its bound and unbound forms. To make a quantitative assessment of the level of agreement between the predicted deformed structure of actin and the one observed upon binding DNase I, we performed an analysis similar to the one presented above for LIR-1/HLA-A2 complex (Fig. 2G), i.e., we first evaluated the displacements in the C^α atoms between the unbound and bound forms experimentally characterized, after optimal superimposition of the two forms (black curve). The same calculation was then repeated for the theoretically predicted (by ANM mode 1) deformed structure and the unbound form (red curve). The agreement between the two curves is noteworthy (correlation coefficient of 0.65) given the simplicity of the model. The structure assumed by actin in the DNase I-bound form is almost entirely driven/facilitated by, or consistent with, the preexisting (in the unbound form) global fluctuations of actin. Precisely, the ANM mode 1 of actin in the free form plays a dominant role in making accessible its reconfigured form observed in the complex.

While the overall reconfiguration of the unbound form predicted by ANM mode 1 closely matches the experimentally observed change in structure between the bound and unbound forms of actin (Fig. 2G), it is worth noting that there are some minor differences between the two sets of data. In particular, the DNase I-binding loop of actin is computed to move toward its unbound conformation, by a displacement of ≈5 Å using ANM. However, this displacement is small compared with that experimentally observed (12 Å) upon complex formation. Fig. 2H displays the conformation of the DNase I-binding loop in the unbound actin (red), deformed structure sampled by ANM mode 1 (yellow), and the experimentally known bound conformation (blue). It can easily be seen that the loop does move toward the unbound conformation, but it remains helical and does not adopt the extended β-turn structure, i.e., the loop possesses the intrinsic tendency to move toward the bound conformation; however, further changes in structure, mainly the helix unwinding and the β-turn formation, probably result from direct interaction with DNase I. In other words, the unbound form is predisposed to alter its structure as functionally needed for binding or accommodating the substrate, but the final stabilization of the complex involves further rearrangements on a local scale, presumably induced only after binding (or directly interacting with) the substrate.

CDK/Cyclin and CDK/p16^INK4a. CDKs are Ser/Thr kinases that play a central role in coordinating eukaryotic cell cycle. Their activation requires binding of cyclin subunits and phosphorylation, while their inhibition is achieved by binding of inhibitors such as Cip and INK4 subunits. Both activation and inhibition mechanisms involve conformational changes in and around their catalytic cleft, implying that flexibility plays a central role in their function (for a review, see ref. 37). CDK2 structure has been solved in the free state (29, 30), as well as in complexes such as CDK2/cyclin A (17) and CDK2/KAP (38). The conformations of CDK2 in the complexes with cyclin A or KAP show close similarities; therefore, the former is considered for further analysis. We also analyzed another complex, CDK6/p16^INK4a (18), formed by another member (CDK6) of the same family of kinases. No unbound structure of CDK6 is available. Given the high level of sequence similarity between CDK2 and CDK6 (50% sequence identity), which implies that the two kinases have similar structures (18, 30), we used the unbound structure of CDK2 for modeling the unliganded structure of CDK6.

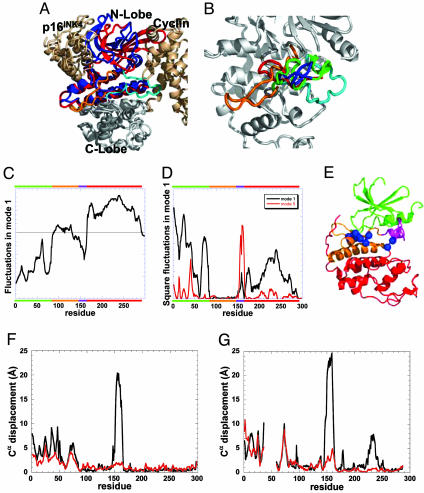
Cyclin and p16^INK4a bind to opposite sites of the kinase (Fig. 3A). Upon complex formation, the N-lobe (residues 1–86) of CDK2/6 adopts a distinct conformation in the two cases, which in addition, differs from the unbound conformation, whereas the structure of the C-lobe (residues 166–298) in the two complexes is closely superimposable. Substantial structural rearrangements also occur at the activation loop of CDK, as illustrated in Fig. 3B.

Fig. 3.

CDK structure and dynamics and comparison with complexes CDK2/cyclin A and CDK6/INK4. (A) Structure of CDK2/6 in complex with INK4 and cyclin A. The C-lobe of the CDKs in the two complexes are optimally superimposed to visualize the structural changes in the N-lobe (blue in the complex with cyclin and red in the complex with INK4), and in activation loops (cyan and orange, respectively). (B) Closer view of the activation loop in the unbound state of CDK (green), INK4-bound state (orange), and cyclin-bound state (cyan); in addition, the deformed conformation of the activation loop along the two fluctuating directions of the ANM mode 19 are shown in red and blue. (C–E) GNM dynamics of unbound CDK2. The motions along the first GNM mode are shown in C, and corresponding square fluctuations are shown in D (black curve). The N-lobe (residues 1–96; green bar along the upper abscissa) and the C-lobe (residues 166–298; red bar) move in opposite directions. Three sets of residues, L87–F90, P130–Q131, and V164–T165, lie at the interface between these anticorrelated regions. D also shows the square fluctuations induced in GNM mode five (red curve), which induces in the activation loop (residues 148–163, purple bar) motions comparable with those of the C-lobe in the first mode. (E) Ribbon diagram of CDK2 color coded according to the bars in D; hinge residues are shown as blue spheres. (F and G) Comparison of the experimentally observed change in C^α positions (difference between bound and unbound forms after optimal superimposition of the C-lobe; black curve) with the ANM-predicted deformations (red curve), shown for the complexes with cyclin (F) and p16^INK4a (G). The αC region is missing in the CDK6 structure, resulting in the observed gap between residues 37–58. The similarity between the two curves in both panels indicates that CDK has the intrinsic tendency to undergo lobe movements to facilitate substrate binding, unlike the activation loop.

A GNM/ANM analysis was conducted for unbound CDK2 similarly to those presented for unbound LIR1 and actin, so as to assess its potential reconfigurations that would facilitate/accommodate substrate binding. The GNM mode analysis (Fig. 3 C–E) reveals anticorrelated movements between the N- and the C-lobes in the first mode, and points to three stretches of residues, L87–F90, P130–Q131, and V164–T165, acting as hinges at the interfacial region between the two lobes. Fig. 3 C and D displays the relative displacements of residues along this global mode, and the corresponding square fluctuations, respectively (black curves). Fig. 3D also shows the square displacements driven by the fifth mode (red curve), which ensures the mobility of the activation loop of the protein. The two mode curves in Fig. 3D are normalized (divided by their eigenvalues) to permit a comparative assessment of relative mobilities of residues in the two modes. In the first mode, the N-lobe (green bar on the upper abscissa) and the C-lobe (red bar) enjoy relatively high mobility, whereas the intermediate residues 91–147 (orange bar) are practically immobile. The activation loop fluctuations driven by the fifth mode (residues 148–163, purple bar) are comparable with those of the C-lobe in the first mode. Fig. 3E shows the ribbon diagram of unbound CDK2 colored by the bars in Fig. 3D.

ANM calculations performed for CDK2 identified ANM mode 2 to be equivalent to GNM mode 1, and correlate (correlation coefficient of 0.64) with the displacements undergone by CDK2 upon complexation with cyclin, except for the activation loop (see Fig. 3F). Likewise, the ANM mode 3 shows the highest correlation (coefficient of 0.57) with the observed structural difference between CDK2 in the unbound state and CDK6 in the complex with p16^INK4a (Fig. 3G). The C^α coordinates in the large loop between the helices αG and αH (residues 225–238) of unbound CDK2 depart from their counterpart in CDK6 (residues 241–252) by 6–8 Å, which cannot be accounted for by the ANM predicted deformation (in addition to the activation loop displacements that fall short of those deduced from the comparison of the two known structures). We note that this region is poorly determined in the CDK6/p16^INK4a complex, and the reported B-factor at these residues in the complex with p16^INK4a is ≈100 Ų (as opposed to ≈20 Ų for CDK6/cyclin A). Finally, ANM mode 19 is identified to be equivalent to GNM mode 5 and describes the motion of the activation loop. Fig. 3B shows the conformation of the activation loop in the experimentally determined unbound state of CDK2 (green), INK4-bound state (orange), and cyclin-bound state (cyan); in addition, the predicted deformed conformation along the two directions of fluctuations favored by of the ANM mode 19 are shown in red and blue. The loop apparently tends to fluctuate toward the bound conformations; however, its flexibility is limited and cannot deploy the full reconfiguration observed in the complexes. These results are consistent with the above GNM results (Fig. 3D), which show that the mobility of the activation loop is comparable with that of the N-lobe and does not surpass it. The results imply that the N-lobe has an intrinsic ability to move toward the bound conformations, whereas the activation loop does not have the same ability. We conjecture that unbound CDK fluctuate between conformations in which the relative orientation of the N-lobe and the C-lobe varies. Cyclin (or p16^INK4a) binds to a conformation that closely resembles the bound orientation of the two lobes and stabilizes it, and only then is the activation loop rearranged to assume its bound orientation. It is not surprising to find that the CDKs that regulate cell cycle under tight control do not posses an intrinsic ability to fluctuate all of the way to a conformation that will closely resemble the active one; rather, they need the interaction with an activator (i.e., cyclin) to achieve such functional changes in structure.

Discussion

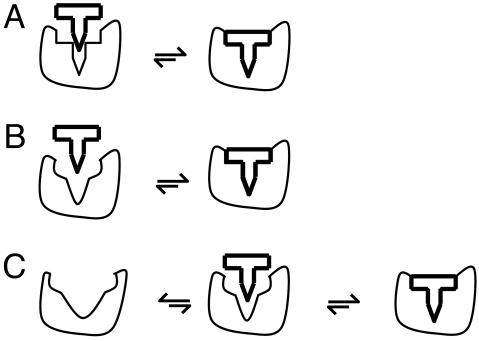
The above four examples demonstrate that significant conformational changes associated with protein–protein interactions correlate with the intrinsic motions of the proteins in the unbound state. The association mechanism of these complexes cannot be explained by using either the lock-and-key model (Fig. 4A) or the induced fit model (Fig. 4B). Because of the substantial structural difference between the bound and unbound forms of the examined proteins, it is unlikely that a formation of a transient complex between the unbound conformations and its substrate will be stable enough to allow for the necessary conformational changes to take place (6), unless the proteins are already predisposed to undergo these changes in structure, or even sample these structures as accessible microstate within an ensemble of conformers that define the native (macro) state under native state conditions.

Fig. 4.

Models for protein–protein interactions. (A) Lock-and-key mechanism. (B) Induced Fit. (C) Preexisting equilibrium followed by induced fit.

LIR-1/HLA-A2 complex is an example where a high correlation is found between the experimentally observed structural differences (between unbound and bound LIR-1) and the theoretically (ANM) predicted conformational fluctuations. Therefore, it is likely that LIR-1 in the free state samples a conformation that closely resembles its bound form and that the predisposition of this conformer facilitates its recognition and interaction with HLA-A2. Actin/DNase I, CDK2/cyclin, and CDK6/p16^INK4a are examples where the observed structural differences correlate with the ANM predicted motions, but some further rearrangements, specially on a local scale near the binding loops, are required that are presumably achieved only after substrate binding. These results suggest that the preexisting equilibrium and induced fit are not two mutually exclusive processes, but rather that both mechanisms likely play a part. The question is to assess the extent of each mechanism. Essentially, the formation of a complex perturbs the free energy landscape experienced by the protein, shifting the equilibrium from the original minimum to a new position in favor of the bound form (7).

This work is in agreement with several experimental data that suggest the role of a preexisting equilibrium in selecting/facilitating complex formation. This mechanism is consistent with the Monod–Wyman–Changeux (MWC) model, as opposed to the sequential induced fit mechanism (39, 40). Kinetic measurements of antigen–antibody formation (12, 13), as well as recent combined crystallographic and kinetic analysis by James et al. (14), support the preexisting equilibrium mechanism for a number of antigen–antibody complexes.

The current work, together with recent experimental (39, 41) and computational (42, 43) observations, invites attention to the fundamental concept that proteins possess intrinsic, structure-encoded abilities to undergo collective motions that are functional. In other words, (i) each protein has a unique fluctuation dynamics at equilibrium conditions, fully defined by its 3D structure, and (ii) this fluctuation dynamics is relevant to, or required for, function. The rationale is that proteins evolved to have equilibrium (native) structures and associated conformational fluctuations that are required to effectively achieve their functions.