Abstract
Evolution should have played important roles in determining folding mechanisms and structures of proteins. In this article we discuss how the folding mechanisms had been affected by the early stage of evolution through which the uniqueness of structure had developed. Although the process of such early-time evolution has remained a mystery, a plausible scenario is that the evolution of proteins toward the ordered structures was guided by functional selection pressure as demonstrated in vitro and in silico. We examine the in silico functional selection of sequences and show that there is a significant correlation between two different processes toward the unique 3D structure, the evolutionary development of structure through sequence selection, and the folding process of the resultant sequence. This finding could be rephrased as protein folding recapitulates the emergence of topology in the molecular evolution. The correlation suggests a guideline for engineering foldable proteins.
Keywords: functional selection, molecular evolution, superfunnel, folding mechanism, energy landscape
Ernst Haeckel's statement that ontogeny recapitulates phylogeny, or the embryonic developmental process is a repeat of the evolutionary process, has been a subject of intense intellectual argument since the 19th century (1). Although his claim has been regarded as incorrect in its literal sense, comparison of the developmental process and the evolutionary history has been productive as witnessed in the recent advancement in evolutionary developmental biology or “evo-devo.” The early stages of development are typically conserved among the evolutionarily related species, whereas the later stages tend to differ (2–4). Such a correlation between the developmental and evolutionary processes should be based on the bottom-up features of these structure formation processes, which are typical in natural organisms but are rare in artifacts. Both processes share the feature that the cumulative effects of small modifications in the local rules within each cell and between cells progressively brings about the intricate balance among the local rules found within the present-day organisms.
Here, we should point out that such local and cumulative features of the structural organization are not limited to embryonic development but are ubiquitous in cellular and molecular biological structural formation processes. In this article, we take protein folding as an example of such a biological structure formation process. Proteins fold to unique native structures according to the evolutionarily designed interactions among amino acid residues. Again, both the folding process and the evolutionary changes of sequences are cumulative processes of local changes, and thus we may be able to expect the correlation between these processes. The intrinsic relationships between the evolutionary history and the folding mechanisms have been suggested by the similarities and differences among folding mechanisms of multiple proteins (5–9). Amino acid sequence is conserved at the position of the folding core common to globins (6), differences in the folding mechanism are correlated to the evolutionary diversification in lysozymes and α-lactalbumins (7), and conserved folding mechanisms were found among proteins having similar native conformations (8, 9). However, these studies compared the group of present-day proteins sharing common topology and did not directly analyze the evolutionary structural formation process itself.
As it has been well recognized that the folding ability toward unique 3D structures is not an inherent property of polypeptides but has been developed through the evolutionary selection of less-ordered structures (10, 11), the evolutionary process before folding ability was established may have affected the folding mechanisms of the resultant foldable sequence. Such early-time evolution of proteins has remained largely a mystery. Recent in vitro experiments, however, suggested a plausible scenario that polypeptides may have evolved to be foldable to unique structures through the selection under functional requirements. Although in many cases the functional requirement imposes selection pressure on local structures at the functional sites, in vitro experiments have shown that the ability to fold to unique global structures can be established through functional selection (12). Functional polypeptides have been selected from random sequence libraries by using mRNA-display (13) and phage-display techniques (14, 15), and a sequence foldable to a structure that resembles the zinc-binding motif has evolved through the selection for ATP binding (16, 17). Besides, we have previously shown, using computer simulation, that functional selection suffices to make a random sequence with disordered structure evolve into sequences foldable to unique structure (18, 19). We take advantage here of having a system by which the evolutionary structural formation can be monitored both directly and quantitatively; we investigate the effect of molecular evolution on the folding mechanisms by closely examining the computer simulation of the functional selection of simplified model polypeptides.
Methods
Simulated Functional Selection. We assume that having a proper steric configuration at the active site is a necessary condition for polypeptides to be functional. The functionality thus defined can be evaluated rapidly for a simplified computer model of polypeptides (20). Amino acid residues in the polypeptide are represented by beads of β-carbons making up a 47-residue polypeptide. At each generation of the functional selection, the folding process is simulated by using the Brownian dynamics method. Starting from a stretched conformation, final structures from the 95,001st to 100,000th step are sampled for each of 50 individual folding runs. The fitness of the polypeptide under the selective pressure is evaluated by the degree of convergence of the active-site configuration (DCAC), defined as the reciprocal of the average deviation of positions of four active-site residues from those of the reference active-site residues of a model functional protein:
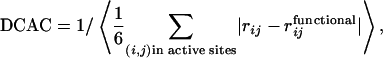 |
[1] |
where rij is the distance between β-carbons of the active-site residues and 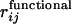 is that in the model functional protein for which we have used the engrailed homeodomain [Protein Data Bank (PDB) ID code 1enh], a DNA binding protein. Here, residues 39, 40, 41, and 43, which are highly conserved in engrailed homeodomains of different species, are chosen as the constituents of the active site. The angle brackets represent the average over 5,000 × 50 structures. Evolution is modeled here as successive trials of point mutation on a polypeptide sequence. At the ith generation of the selection, a mutant sequence mut(i) is obtained by mutating the original sequence seq(i) at a random position. From the folding simulation using mut(i), the DCAC for mut(i) is calculated. Sequence selection is biased toward the increase in fitness in a way that allows some fluctuations with the decrease of fitness to an extent determined by a control parameter
is that in the model functional protein for which we have used the engrailed homeodomain [Protein Data Bank (PDB) ID code 1enh], a DNA binding protein. Here, residues 39, 40, 41, and 43, which are highly conserved in engrailed homeodomains of different species, are chosen as the constituents of the active site. The angle brackets represent the average over 5,000 × 50 structures. Evolution is modeled here as successive trials of point mutation on a polypeptide sequence. At the ith generation of the selection, a mutant sequence mut(i) is obtained by mutating the original sequence seq(i) at a random position. From the folding simulation using mut(i), the DCAC for mut(i) is calculated. Sequence selection is biased toward the increase in fitness in a way that allows some fluctuations with the decrease of fitness to an extent determined by a control parameter 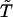 . If the DCAC is increased by the mutation, mut(i) is passed to the next generation as seq(i + 1). If the DCAC is decreased by the mutation, mut(i) is selected with the probability
. If the DCAC is increased by the mutation, mut(i) is passed to the next generation as seq(i + 1). If the DCAC is decreased by the mutation, mut(i) is selected with the probability 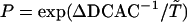 , where ΔDCAC–1 = (DCACseq(i))–1 – (DCACmut(i))–1 and
, where ΔDCAC–1 = (DCACseq(i))–1 – (DCACmut(i))–1 and 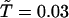 , and seq(i) is selected with the probability 1 – P. Starting with a random sequence, this procedure was repeated up to the 200th generation for each evolutionary selection run.
, and seq(i) is selected with the probability 1 – P. Starting with a random sequence, this procedure was repeated up to the 200th generation for each evolutionary selection run.
Brownian Dynamics Simulation. The chain connecting beads of β-carbons is subjected to three kinds of forces: the force derived from the empirical potential, the weak attractive force between hydrophobic and other residues, and the random force corresponding to the thermal noise. The empirical potential, which depends on 20 amino acid species and the distance along the chain, was derived to represent the distribution of spatial distance between β-carbons in a library of protein structures (20). The library consisted of 75 mutually dissimilar structures in the PDB. See Appendix for more details. Starting from a stretched conformation, the method can reproduce native conformations of small helical proteins such as engrailed homeodomain (PDB ID code 1enh) and calcium-binding protein (PDB ID code 5icb). It should be noticed that engrailed homeodomain is not included in the library, so that there is no specific bias toward the structure of engrailed homeodomain in the potential.
Results and Discussion
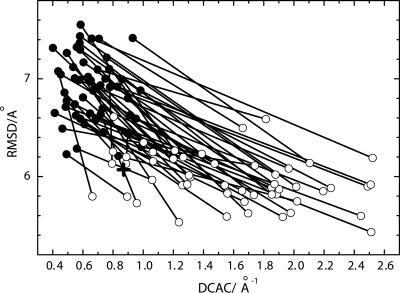
Among 50 runs of the functional selection we performed, 31 selection runs generated the functional sequences as shown in Fig. 1 in the sense that the stability of the configuration at the active site has reached a level comparable to that in the simulated small natural proteins. As reported previously (18, 19), these functional sequences assume unique global conformations. Thus, the selection of sequences for the chain to have a stable local configuration at the active site, which is a necessary requirement for the peptide to be functional, is sufficient to bring about stable global conformations. The folded structures that resulted from the independent selection runs were generally dissimilar to each other in their global structures even though they have the same local active-site configuration.
Fig. 1.
Changes in DCAC and rms distance (RMSD) through 50 independent runs of the functional selection. For each selection run, a filled circle for the initial random sequence and an open circle for the resulted sequence with the smallest RMSD in 200 generations are connected by a line. RMSD is averaged over all of the (50 × 49)/2 pairs of final structures of 50 folding trajectories for the sequence at each generation. The cross shows the averaged RMSD and DCAC of the model functional protein (PDB ID code 1enh) calculated from 50 independent folding simulations using the same model of folding.
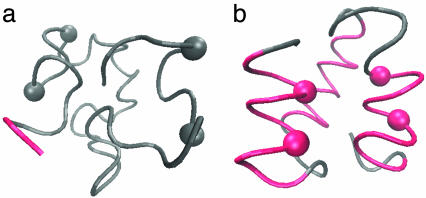
Fig. 2a is an example of structural development throughout the progress of the simulated functional selection. In the beginning of the selection run (Fig. 2a Top, the 95th generation), multiple folding simulations of the sequence did not result in any definite structure and the polypeptide stayed in a random coil state. In the middle of the selection run (Fig. 2a Middle, the 126th generation), the active site tends to form a helix and a few long-range interactions involving the active site are now found. At the later generations (Fig. 2a Bottom, the 172nd generation), the selected sequence adopts a definite compact conformation that has stable helices.
Fig. 2.
Emergence of a definite structure through the functional selection and the folding of the evolved sequence. Four active-site residues are represented by balls and formed helical structures are colored red. (a) Examples of structures at the 95th, 126th, and 172nd generations in the functional selection. These structures were sampled from the last 5,000 steps of folding simulations at each generation. (b) The structures sampled at the 23,400th, 44,000th, and 99,990th steps along a folding trajectory of the evolved sequence.
Fig. 2b shows the conformation change observed in a folding simulation of the evolved sequence in Fig. 2a, which resembles the evolutionary process in Fig. 2a. To quantify this similarity, we characterize the time of formation of interresidue contacts in the folding simulation of the evolved sequence as follows. For each evolved sequence, we performed 50 independent folding simulations with different realizations of random thermal fluctuation in the Brownian dynamics calculation and monitored the interresidue pair distances. For each folding trajectory, “native contacts” are defined to be those residue pairs for which the interresidue distance averaged over the last 10,000 steps is closer than a cut-off (see Appendix) in >33 folding trajectories of 50 trajectories simulated. Each native contact is regarded to have become “fixed” at the first step after which it remains formed until the last step of the folding trajectory. The number of fixed native contacts, Qfold, normalized so that Qfold equals unity when all native contacts are fixed, is a monotonously increasing function of time steps and thus serves as a measure of time. We represent the Qfold at which a contact between the ith and jth residues becomes fixed as 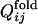 for each folding trajectory. For a pair of contacts ij and kl, the difference in the Qfold of the contact fixation is defined as
for each folding trajectory. For a pair of contacts ij and kl, the difference in the Qfold of the contact fixation is defined as 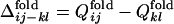 .
.
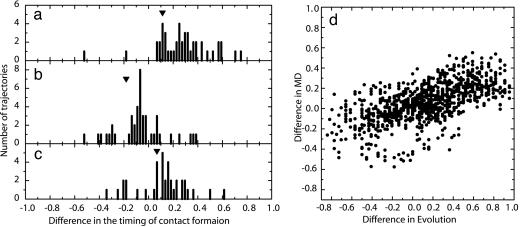
Fig. 3 shows the distribution of 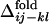 for several contact pairs, observed in 50 folding trajectories for the evolved sequence in Fig. 2b.
for several contact pairs, observed in 50 folding trajectories for the evolved sequence in Fig. 2b. 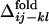 tends to deviate from zero for several reasons. First, the contacts near the active-site residues are fixed earlier than the other contacts (Fig. 3a), which is consistent with the observation that the functionally important residues are often involved in folding cores (8, 21, 22). Second, the short-range contacts are fixed earlier than the long-range contacts (Fig. 3b). Third, even if both contacts are long-range and involve active-site residues, the contact between two helices is formed earlier than the contact between a helix and a surrounding loop, suggesting that the contacts between helices are important for global stabilization (Fig. 3c). In summary, the folding process of the evolved sequence is not completely random but the ordering of contact fixation has occurred concordantly with the emergence of the global structure. The distributions obtained from other selected sequences have shown similar results.
tends to deviate from zero for several reasons. First, the contacts near the active-site residues are fixed earlier than the other contacts (Fig. 3a), which is consistent with the observation that the functionally important residues are often involved in folding cores (8, 21, 22). Second, the short-range contacts are fixed earlier than the long-range contacts (Fig. 3b). Third, even if both contacts are long-range and involve active-site residues, the contact between two helices is formed earlier than the contact between a helix and a surrounding loop, suggesting that the contacts between helices are important for global stabilization (Fig. 3c). In summary, the folding process of the evolved sequence is not completely random but the ordering of contact fixation has occurred concordantly with the emergence of the global structure. The distributions obtained from other selected sequences have shown similar results.
Fig. 3.
Distributions of 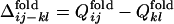 obtained from the 50 folding trajectories of the resultant sequence. (a–c)
obtained from the 50 folding trajectories of the resultant sequence. (a–c) 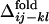 for i, j = 18, 22 and k, l = 40, 43 (a), for i, j = 18, 22 and k, l = 22, 40 (b), and for i, j = 6, 40 and k, l = 22, 40 (c). The corresponding
for i, j = 18, 22 and k, l = 40, 43 (a), for i, j = 18, 22 and k, l = 22, 40 (b), and for i, j = 6, 40 and k, l = 22, 40 (c). The corresponding 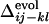 s are shown by inverted triangles;
s are shown by inverted triangles; 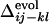 = 0.11, –0.18, and 0.068, in a, b, and c, respectively. (d) Comparison between
= 0.11, –0.18, and 0.068, in a, b, and c, respectively. (d) Comparison between 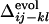 and the averaged
and the averaged 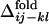 for all of the pairs of contacts ij and kl in the evolved structures, where average is taken for
for all of the pairs of contacts ij and kl in the evolved structures, where average is taken for 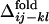 over 50 folding trajectories.
over 50 folding trajectories.
We next compare the development of the definite structure in the evolutionary selection run and the folding process of the resultant sequence in terms of the contact fixation. The time of the contact fixation in the course of the evolutionary selection run can be quantified in a similar manner. The native contact is regarded to become fixed at the first generation after which it remains formed until the last generation. The number of fixed native contacts, Qevol, normalized so that Qevol equals unity at the last generation, is a monotonously increasing function of generation. The generation at which a contact between the ith and jth residues becomes fixed can therefore be represented by the value of Qevol at that generation, i.e., 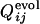 . In Fig. 3 a–c,
. In Fig. 3 a–c, 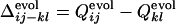 are designated by ▾ to compare them with the corresponding distributions of
are designated by ▾ to compare them with the corresponding distributions of 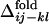 . In Fig. 3d, the averaged
. In Fig. 3d, the averaged 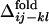 is compared with
is compared with 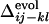 for all of the pairs of contacts, where we can find a noticeable correlation between
for all of the pairs of contacts, where we can find a noticeable correlation between 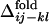 and
and 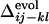 (correlation coefficients are 0.62 with P < 0.0001). This result shows that the statistical tendency in the order of the contact fixation in the folding process is correlated to the corresponding order of the contact fixation in the evolutionary selection.
(correlation coefficients are 0.62 with P < 0.0001). This result shows that the statistical tendency in the order of the contact fixation in the folding process is correlated to the corresponding order of the contact fixation in the evolutionary selection.
As the correlation obtained above is somewhat obscured by the probabilistic nature of folding, we introduce another parameter describing a degree of early fixation of contacts in folding processes, 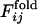 , which is less sensitive to fluctuations over different folding trajectories than
, which is less sensitive to fluctuations over different folding trajectories than 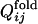 .
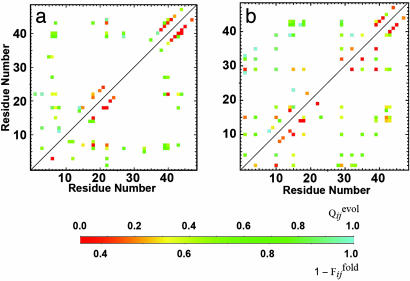
. 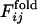 is defined to be the fraction of the number of trajectories in which the contact between the ith and jth residues is already fixed when Qfold = 0.5. In Fig. 4a,
is defined to be the fraction of the number of trajectories in which the contact between the ith and jth residues is already fixed when Qfold = 0.5. In Fig. 4a, 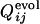 and
and 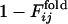 are displayed in the upper left and lower right, respectively, which clearly shows the similarity in the order of the appearance of fixed contacts (the correlation coefficient is 0.72 with P < 0.001). The early fixed region includes the active-site residues (residues 39, 40, 41 and 43) and those neighboring the active site in the final conformation (residues 20, 21 and 23). In Fig. 4b,
are displayed in the upper left and lower right, respectively, which clearly shows the similarity in the order of the appearance of fixed contacts (the correlation coefficient is 0.72 with P < 0.001). The early fixed region includes the active-site residues (residues 39, 40, 41 and 43) and those neighboring the active site in the final conformation (residues 20, 21 and 23). In Fig. 4b, 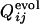 and
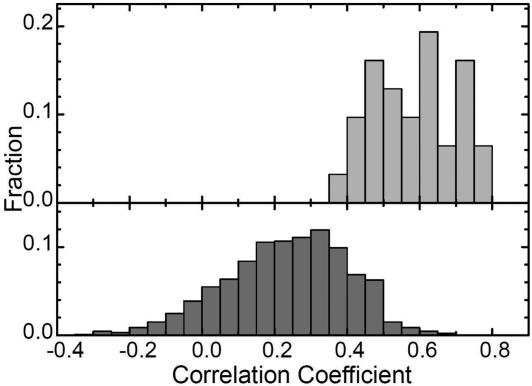
and 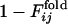 for the other selection run are shown (the correlation coefficient is 0.62 with P < 0.001). In this case, the early fixed region also includes the residues important for the global structure stabilization (residues 29 and 30), as well as the residues in the active site and those neighboring the active site. The correlation coefficients for 15 of 31 successful selection runs were >0.6. The significance of the correlation is apparent when the distribution of the correlation coefficients between
for the other selection run are shown (the correlation coefficient is 0.62 with P < 0.001). In this case, the early fixed region also includes the residues important for the global structure stabilization (residues 29 and 30), as well as the residues in the active site and those neighboring the active site. The correlation coefficients for 15 of 31 successful selection runs were >0.6. The significance of the correlation is apparent when the distribution of the correlation coefficients between 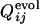 of the selection run and
of the selection run and 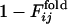 of the folding run using the resultant sequence (Fig. 5 Upper) is compared with the cross-correlation coefficients between
of the folding run using the resultant sequence (Fig. 5 Upper) is compared with the cross-correlation coefficients between 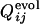 of the selection run and
of the selection run and 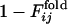 of the folding run using the sequences resultant from the other selection runs (Fig. 5 Lower).
of the folding run using the sequences resultant from the other selection runs (Fig. 5 Lower).
Fig. 4.
Comparison between 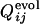 , the normalized number of fixed native contacts at the generation that the contact between the ith and jth residues is fixed in the evolutionary simulation (the upper left triangle) and
, the normalized number of fixed native contacts at the generation that the contact between the ith and jth residues is fixed in the evolutionary simulation (the upper left triangle) and 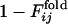 , where the
, where the 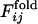 is the fraction of the number of folding simulations in which the contact between ith and jth residues is fixed at Qfold = 0.5 of the final sequence (the lower right triangle). The color from red to blue corresponds to
is the fraction of the number of folding simulations in which the contact between ith and jth residues is fixed at Qfold = 0.5 of the final sequence (the lower right triangle). The color from red to blue corresponds to 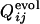 and
and 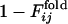 from 0 to 1.(a) Comparison between
from 0 to 1.(a) Comparison between 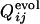 and
and 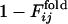 for the same selection run as used in Figs. 2 and 3. (b) Comparison between
for the same selection run as used in Figs. 2 and 3. (b) Comparison between 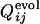 and
and 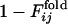 for the selection run through which the three-helix structure was developed.
for the selection run through which the three-helix structure was developed.
Fig. 5.
Distributions of correlation coefficients between 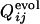 and
and 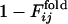 . (Upper) The distribution of correlation coefficients between
. (Upper) The distribution of correlation coefficients between 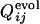 and the corresponding
and the corresponding 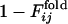 for 31 selection runs that resulted in the defined structure formation. (Lower) The distribution of 31 × 30 cross-correlation coefficients between
for 31 selection runs that resulted in the defined structure formation. (Lower) The distribution of 31 × 30 cross-correlation coefficients between 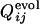 for selection runs and
for selection runs and 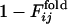 for formation of the same contact sets in the folding runs of the sequences resulting from the other selection runs.
for formation of the same contact sets in the folding runs of the sequences resulting from the other selection runs.
To investigate whether the correlation between two processes depends on the close positioning of active-site residues along the sequence, we have also performed the selection runs with another set of active-site residues spatially localized within the native structure of the same protein (PDB ID code 1enh), which were arbitrarily chosen so that they are well separated along the sequence. An example of the evolutionary structural development is shown in Fig. 6, in which the random structure at the early generation (Fig. 6a) developed into the helix bundle structure (Fig. 6b) when the configuration formed by residues 4, 8, 35, and 39 was used for the fitness calculation. In this example, the functional and foldable sequences were generated in 22 of 50 selection runs examined. The correlation coefficient between 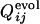 and
and  were >0.6 for 7 of those 22 runs. Thus the correlation between two processes seems to be independent on the active-site position along the sequence.
were >0.6 for 7 of those 22 runs. Thus the correlation between two processes seems to be independent on the active-site position along the sequence.
Fig. 6.
An example of structural development in the functional selection when the residues distant along the sequence were assumed to form the spatially localized active-site configuration. The structure formed among residues 4, 8, 35, and 39 in PDB ID code 1enh was used as the model functional configuration to evaluate DCAC in Eq. 1.(a) A structure at the first generation. (b) The structure at the 197th generation. Four active-site residues are represented by balls, and helical structures are colored red.
The parallelism between evolution and folding observed here could be interpreted as follows: As the evolutionary selection proceeds from the sequence with random structure, unique structure gradually develops in a contact-by-contact manner, where fixation of a new contact depends on the contacts fixed earlier. Hierarchy in the unique global structure of the evolved sequence preserves this interdependence of the contact fixation, and therefore the contacts fixed earlier in the evolution promotes the fixation of the other contacts also in the course of the folding of the evolved sequence. This picture is consistent with the observation that the folding mechanism is primarily determined by the topology of native structure of proteins (23, 24). In addition, the energetic stabilization should affect the mechanism of the structure development in both the evolution and folding in a coupled manner. Because contacts fixed earlier in the evolution have a greater chance of being energetically stabilized by mutational design of local interactions, those contacts tend to be fixed earlier also in the folding of the resultant sequence.
From the lattice model simulations, it has been proposed that the sequences with thermodynamically stable structures are often robust against mutations (25) and that the native-state stability is gradually decreased as more mutations are introduced to the prototype sequence of the neutral net, which is a feature called the superfunnel (26). In those studies, however, all of the structures, except for the native structure, were classified to be in the denatured state irrespective of how many native contacts they have, and the discussion was restricted to the neutral net of sequences with which the native structure remains stable. In contrast, the parallelism observed here offers an alternative view of superfunnel in which the native contacts are gradually formed both in the sequence evolution and the folding process, thus making the two structure formation processes correlated to each other. Mutational robustness of natural proteins should also be understood as a natural consequence of this parallelism.
The present results offer a theoretical background for designing artificial proteins by using functional selection. Assuming the symmetry between the sequence space and the structure space, rapidly foldable sequences are expected to be found within relatively few generations, whereas slowly foldable sequences can take more generations. Therefore the most easily found functional sequences will usually be rapidly foldable sequences, which should be why the functional selection can generate foldable sequences in vitro (15, 16). Likewise, the strategy to design the folding core (27) or use stable proteins as scaffolds at the early stage of directed evolution (28) followed by the later design of less stable peripheries should be consistent with the parallelism between natural evolutionary sequence design and the folding process. It would be also interesting to pursue the possibility to design a desirable folding intermediate through the guided selection course toward the structure at intermediate generations.
Although it is not clear now what exact roles functional selection has played in the natural evolution of proteins, we may be able to guess possible scenarios. Especially the recent identification of the ubiquity of intrinsically disordered proteins (29, 30) raises the possibility that the protein structures at the time of gene duplication and speciation were not so rigid as has usually been considered normal for the existing natural proteins. Coevolution of function and structure under slightly different selection pressures acting on a protein family with such disordered structures would lead to the examples of the present-day proteins with similar native structures but with partially different folding cores (7, 31–33). It should be also noted that the frequent involvement of the functionally important site in folding cores (8, 21, 22) can be interpreted as a natural consequence of the functional selection in which the structure around the functional site is early developed in the evolutionary history.
Our finding can be rephrased as protein folding recapitulates the emergence of topology in molecular evolution, which is a molecular counterpart of Haeckel's statement. Critical and quantitative comparison between the structural formation process and the evolutionary history may also be applicable to other biological complex structures at molecular (34, 35) and cellular levels, which should lead to the deeper insights into the biological processes.
Acknowledgments
This work was supported by grants from the Ministry of Education, Culture, Sports, Science, and Technology, Japan, grants from the Japan Society for Promotion of Science, and grants for the 21st century Centers of Excellence program for Frontiers of Computational Science. T.P.T. was supported by a Japan Society for the Promotion of Science Research Fellowship for Young Scientists.
Appendix
Potentials for Folding Simulations. The polypeptide is represented by a chain of connected beads of β-carbons (20). The interaction potential among residues is expressed by the sum of two-body potentials,
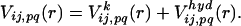 |
[2] |
The first term of the right side of Eq. 2 is the empirical potential constructed from a library of 75 structures selected from table 2 of ref. 36. When the spatial distance between the ith and jth residues is r and their amino acid types are p and q, the empirical potential for this residue pair, 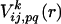 is
is
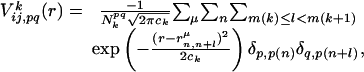 |
[3] |
where k represents the class of the distance along the sequence that satisfies m(k) ≤ |i – j| < m(k + 1) with m(k) = k for 1 ≤ k ≤ 10, m(11) = 11, m(12) = 13, m(13) = 16, m(14) = 20, m(15) = 25, m(16) = 31, m(17) = 41, m(18) = 61, m(19) = 101, and m(20) = 151. p(n) and p(n + l) are amino acid types of the nth and n + lth residues of the μth structure in the library and 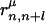 is the spatial distance between those residues. δp,p(n) = 1 when p = p(n) and δp,p(n) = 0, otherwise.
is the spatial distance between those residues. δp,p(n) = 1 when p = p(n) and δp,p(n) = 0, otherwise. 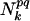 is the number of pairs found in the library satisfying δp,p(n) = 1 and δq,p(n+l) = 1 at the same time. The sum of the Gaussian functions with means
is the number of pairs found in the library satisfying δp,p(n) = 1 and δq,p(n+l) = 1 at the same time. The sum of the Gaussian functions with means 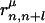 and a standard deviation ck = 0.5k Å reflects the spatial distributions of residue pairs in the library. The hydrophobic interaction, which is a weak attraction between hydrophobic and other residues, is
and a standard deviation ck = 0.5k Å reflects the spatial distributions of residue pairs in the library. The hydrophobic interaction, which is a weak attraction between hydrophobic and other residues, is
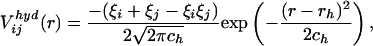 |
[4] |
where ξi = 1 when p(i) = Ala, Val, Leu, Ile, Met, Phe, Trp, or Pro and ξi = 0, otherwise. ch = 7.0 Å and rh = 6.0 Å were used.
Definition of Fixed Native Contacts. The native contacts for each evolved sequence are defined to be pairs of amino acid residues for which distances, averaged over the last 10,000 steps in each folding trajectory, are closer than cut-off distances in >65% of folding trajectories. Cut-off distances are 6.5 Å for residue pairs separated along the backbone by three to five residues, 12.0 Å for residue pairs separated by more than nine residues, and the values for residue pairs separated by six to eight residues are obtained by interpolation using the polynomial. In the evolutionary run, the native contact is regarded to become fixed at the generation after which it remains formed until the last generation. In obtaining Qfold or 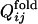 , distances as functions of time are smoothed beforehand to remove subtle fluctuations by averaging over time steps [t – 5,000, t + 5,000].
, distances as functions of time are smoothed beforehand to remove subtle fluctuations by averaging over time steps [t – 5,000, t + 5,000].
Author contributions: T.P.T., T.Y., and M.S. designed research; C.N. performed research; C.N. and M.S. contributed new analytic tools; C.N., T.P.T., T.Y., and M.S. analyzed data; and C.N., T.P.T., and M.S. wrote the paper.
Conflict of interest statement: No conflicts declared.
Abbreviations: DCAC, degree of convergence of the active-site configuration; PDB, Protein Data Bank; RMSD, rms distance.
References
- 1.Haeckel, E. (1896) The Evolution of Man: A Popular Exposition of the Principal Points of Human Ontogeny and Phylogeny (Appleton, New York).
- 2.Pennisi, E. & Roush, W. (1997) Science 277, 34–37. [DOI] [PubMed] [Google Scholar]
- 3.Holland, P. W. H. (1999) Nature 402, C41–C44. [DOI] [PubMed] [Google Scholar]
- 4.Arthur, W. (2002) Nature 415, 757–764. [DOI] [PubMed] [Google Scholar]
- 5.Gunasekaran, K., Eyles, S. J., Hagler, A. T. & Gierasch, L. M. (2001) Curr. Opin. Struct. Biol. 11, 83–93. [DOI] [PubMed] [Google Scholar]
- 6.Ptitsyn, O. B. & Ting, K.-L. H. (1999) J. Mol. Biol. 291, 671–682. [DOI] [PubMed] [Google Scholar]
- 7.McKenzie, H. A. & White, F. H., Jr. (1991) Adv. Protein Chem. 41, 173–315. [DOI] [PubMed] [Google Scholar]
- 8.Mirny, L. A. & Shakhnovich, E. I. (1999) J. Mol. Biol. 291, 177–196. [DOI] [PubMed] [Google Scholar]
- 9.Plaxco, K. W., Larson, S., Ruczinski, I., Riddle, D., Thayer, E. C., Buchwitz, B., Davidson, A. R. & Baker, D. (2000) J. Mol. Biol. 298, 303–312. [DOI] [PubMed] [Google Scholar]
- 10.Onuchic, J. N., Luthey-Schulten, Z. & Wolynes, P. G. (1997) Annu. Rev. Phys. Chem. 48, 545–600. [DOI] [PubMed] [Google Scholar]
- 11.Mirny, L. & Shakhnovich, E. (2001) Annu. Rev. Biophys. Biomol. Struct. 30, 361–396. [DOI] [PubMed] [Google Scholar]
- 12.James, L. C. & Tawfik, D. S. (2003) Trends Biochem. Sci. 28, 361–368. [DOI] [PubMed] [Google Scholar]
- 13.Keefe, A. D. & Szostak, J. W. (2001) Nature 410, 715–718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yamauchi, A., Nakashima, T., Tokuriki, N., Hosokawa, M., Nogami, H., Arioka, S., Urabe, I. & Yomo, T. (2002) Protein Eng. 15, 619–626. [DOI] [PubMed] [Google Scholar]
- 15.Hayashi, Y., Sakata, H., Makino, Y., Urabe, I. & Yomo, T. (2003) J. Mol. Evol. 56, 162–168. [DOI] [PubMed] [Google Scholar]
- 16.Surdo, P. L., Walsh, M. A. & Sollazzo, M. (2004) Nat. Struct. Mol. Biol. 11, 382–383. [DOI] [PubMed] [Google Scholar]
- 17.Krishna, S. S. & Grishin, N. V. (2004) Structure 12, 1125–1127. [DOI] [PubMed] [Google Scholar]
- 18.Yomo, T., Saito, S. & Sasai, M. (1999) Nat. Struct. Biol. 6, 743–746. [DOI] [PubMed] [Google Scholar]
- 19.Sasaki, T. N. & Sasai, M. (2002) J. Biol. Phys. 28, 483–492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sasai, M. (1995) Proc. Natl. Acad. Sci. USA 92, 8438–8442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Barzilai, A., Kumar, S., Wolfson, H. & Nussinov, R. (2004) Proteins 56, 635–64921. [DOI] [PubMed] [Google Scholar]
- 22.Saito, S., Sasai, M. & Yomo, T. (1997) Proc. Natl. Acad. Sci. USA 94, 11324–11328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Baker, D. (2000) Nature 405, 39–42. [DOI] [PubMed] [Google Scholar]
- 24.Onuchic, J. N. & Wolynes, P. G. (2004) Curr. Opin. Struct. Biol. 14, 70–75. [DOI] [PubMed] [Google Scholar]
- 25.Li, H., Helling, R., Tang, C. & Wingreen, N. (1996) Science 273, 666–669. [DOI] [PubMed] [Google Scholar]
- 26.Bornberg-Bauer, E. & Chan, H. S. (1999) Proc. Natl. Acad. Sci. USA 96, 10689–10694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chin, J. W. & Schepartz, A. (2001) J. Am. Chem. Soc. 123, 2929–2930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Petrounia, I. P. & Arnold, F. H. (2000) Curr. Opin. Biotechnol. 11, 325–330. [DOI] [PubMed] [Google Scholar]
- 29.Wright, P. E. & Dyson, H. J. (1999) J. Mol. Biol. 293, 321–331. [DOI] [PubMed] [Google Scholar]
- 30.Dunker, A. K., Lawson, J. D., Brown, C. J., Williams, R. M., Romero, P., Oh, J. S., Oldfield, C. J., Campen, A. M., Ratliff, C. M., Hipps, K. W., et al. (2001) J. Mol. Graphics Model. 19, 26–59. [DOI] [PubMed] [Google Scholar]
- 31.Nishimura, C., Prytulla, S., Dyson, H. J. & Wright, P. E. (2000) Nat. Struct. Biol. 7, 679–686. [DOI] [PubMed] [Google Scholar]
- 32.Friel, C. T., Capaldi, A. P. & Radford, S. E. (2003) J. Mol. Biol. 326, 293–305. [DOI] [PubMed] [Google Scholar]
- 33.Hamill, S. J., Steward, A. & Clarke, J. (2000) J. Mol. Biol. 297, 165–178. [DOI] [PubMed] [Google Scholar]
- 34.Wright, M. C. & Joyce, G. F. (1997) Science 276, 614–617. [DOI] [PubMed] [Google Scholar]
- 35.Fontana, W. (2002) BioEssays 24, 1164–1177. [DOI] [PubMed] [Google Scholar]
- 36.Hendlich, M., Lackner, P., Weitckus, S., Floeckner, H., Froschauer, R., Gottsbacher, K., Casari, G. & Sippl, M. J. (1990) J. Mol. Biol. 216, 167–180. [DOI] [PubMed] [Google Scholar]