Modeling the spatiotemporal cortical activity associated with the line-motion illusion in primary visual cortex

Abstract

Our large-scale computational model of the primary visual cortex that incorporates orientation-specific, long-range couplings with slow NMDA conductances operates in a fluctuating dynamic state of intermittent desuppression (IDS), which captures the behavior of coherent spontaneous cortical activity, as revealed by in vivo optical imaging based on voltage-sensitive dyes. Here, we address the functional significance of the IDS cortical operating points by investigating our model cortex response to the Hikosaka line-motion illusion (LMI) stimulus—a cue of a quickly flashed stationary square followed a few milliseconds later by a stationary bar. As revealed by voltage-sensitive dye imaging, there is an intriguing similarity between the cortical spatiotemporal activity in response to (i) the Hikosaka LMI stimulus and (ii) a small moving square. This similarity is believed to be associated with the preattentive illusory motion perception. Our numerical cortex produces similar spatiotemporal patterns in response to the two stimuli above, which are both in very good agreement with experimental results. The essential network mechanisms underpinning the LMI phenomenon in our model are (i) the spatiotemporal structure of the LMI input as sculpted by the lateral geniculate nucleus, (ii) a priming effect of the long-range NMDA-type cortical coupling, and (iii) the NMDA conductance–voltage correlation manifested in the IDS state. This mechanism in our model cortex, in turn, suggests a physiological underpinning for the LMI-associated patterns in the visual cortex of anaesthetized cat.

Although it is an age-old wisdom, our perception of the world is clearly a partial reflection of our own state of mind. Recent advances in large-scale and multimode experimental methods in neuroscience, such as in vivo optical imaging based on voltage-sensitive dyes (VSD), have produced highly resolved, beautiful spatiotemporal images of intrinsic cortical states, and they have afforded us a glimpse, however fleeting, into the inner workings of the brain. Armed with the plethora of data accumulated over the last few decades about the primary visual cortex (V1), it is now possible to begin to address fundamental questions, such as how incoming visual information might be affected by intrinsic cortical states, leading to perception or illusory perception.

The intrinsic spontaneous ongoing spatiotemporal activity of V1 as revealed by VSD imaging exhibits intricate coherent behavior, not that of unstructured homogeneous noise (1–3). Cortical regions separated by up to 4 mm can exhibit correlated patterns, which are observed to drift with the characteristic time scale ≈80 ms. Intriguingly, these fluctuating spontaneous patterns often resemble patterns of cortical activity that are evoked by certain visual stimulation, with the spontaneous firing rate of individual neurons highest when within a wandering cortical state that resembles a state evoked by optimal stimuli for those neurons.

These spatiotemporal activity patterns can be viewed as high-dimensional projections of the full network dynamics, and they carry information that may not be discernable by analyzing very low-dimensional projections of the full dynamics via only a few individual neurons within the same system. Dynamic functional information about the cortex can be encoded in spatiotemporal patterns of cortical activity. For instance, spatiotemporal cortical activity can reveal oscillations, correlations, or distinct spiking patterns in specific neuronal ensembles over large spatial distances. Spatiotemporal activity recordings can capture the collective behavior of neuronal ensembles and potentially discriminate between competing theoretical cortical mechanisms, a discrimination that may not be possible when measuring only a single neuron within a large system.

Previous theoretical work has attempted to characterize the spontaneous background state, a “cortical operating point,” as an attractor of a dynamical system: a long-time state adopted in the absence of stimulus. For example, the “marginal state attractor” (4) only allows for a single low-dimensional mode to be active in the cortex at any given time, with the external input merely pushing the cortex into a specific one of these marginal (broken-symmetry) states. Similar low-dimensional attractors have been invoked to model the highly excited cortical behavior implied by visual hallucinations (5, 6). These low-dimensional attractors strongly restrict the possible modes of the model cortex. However, experimental observations show that different spatial regions of V1 can simultaneously sustain competing patterns over long time scales (≈80 ms) (1–3).

In contrast, our previous work (7) reveals how the cortex may operate in a more general type of cortical operating point, one which is intrinsically stochastic and allows for coherent spatiotemporal fluctuations. Our model cortex, with orientation-specific, long-range (LR) lateral connections§ containing a slow (NMDA-type) excitatory component, countered by strong local cortical inhibition, achieves a fluctuating dynamic regime of intermittent desuppression (IDS) (7) with physiologically reasonable correlations between conductance, voltage, and realistic spontaneous firing rates (≲5 spikes per s). This IDS state is in an intermittent cycle: (i) the eventual decay of cortical inhibition permits a few spontaneous excitatory firing events that, via LR lateral connections, enhance the NMDA conductances of orientation domains with similar orientation preference within ≈1 mm; (ii) a cascade of successive firing events further recruits neighboring iso-orientation domains across ≈4 mm and establishes conductance and voltage patterns that are often very similar to the patterns of activity evoked by oriented gratings; and (iii) the subsequent rise in cortical inhibition suppresses any further recruitment, and the pattern slowly drifts or decays over the time scale of the NMDA conductance (≈80 ms), leaving the inhibition to decay naturally. In our simulations, the phenomena associated with the structured patterns of this IDS state capture the behavior of ongoing spontaneous activity as observed in experiment (7).

A natural conceptual question arises: What are the functional implications of the IDS cortical operating point? Does this characterization of spontaneous V1 dynamics facilitate our understanding of how V1 responds to stimuli? A particularly fascinating visual stimulus is the Hikosaka line-motion illusion (LMI) stimulus paradigm.¶ As revealed by VSD imaging (13), there is an intriguing similarity between the V1 spatiotemporal activity in response to (i) a small square that drifts linearly across visual space and (ii) the Hikosaka LMI stimulus (12). This preattentive visual illusion (14) is fascinating because it suggests that our comprehension is linked to a mechanism in the early stages of the visual pathway that cannot discriminate disparate stimuli (13). Can our IDS state be invoked to account for this spatiotemporal similarity in our model V1 cortex?

To model evoked spatiotemporal activity over an extended cortical area (≈25 mm²), we construct a large-scale numerical model for a patch of V1 as well as its feedforward lateral geniculate nucleus (LGN) input, with physiologically reasonable parameters. For such work in computational neuroscience, computational scale-up is an urgent issue. Because the IDS dynamics exhibit intrinsic correlated fluctuations that cannot easily be captured by a coarse-grained formalism such as mean firing-rate representation (15), our computational scale-up is accomplished through an algorithmic approach, instead of statistical coarse-grained formalisms. We develop and implement a fast adaptive algorithm (16) to simulate a coupled system of ≈10⁶ cortical point neurons. In terms of theoretical understanding, large-scale computational models allow us to confront the issue of realizability of simple, idealized mechanisms within a realistic network. In this study of LMI-associated spatiotemporal patterns, we note that our use of an idealized V1 model without higher-order feedback is consistent with the suggestion that the spatiotemporal activity in early visual areas is a cortical correlate of the bottom-up mechanisms underlying the preattentive LMI (13). As we will show below, our numerical cortex produces spatiotemporal patterns in response to the LMI stimulus that are very similar to those observed experimentally, and the IDS operating point plays a critical functional role in this response. The essential ingredients of the detailed network mechanisms underpinning the LMI phenomenon in our model cortex are (i) the LGN-sculpted spatiotemporal structure of the LMI input, (ii) a priming effect of the LR NMDA-type cortical coupling, and (iii) the NMDA conductance–voltage correlation manifested in the IDS state. This mechanism in our model cortex, in turn, suggests a physiological underpinning for the LMI-associated patterns in the visual cortex of anaesthetized cat (13).

Finally, as these studies illustrate, the technological advances in modern experimentation that permit the observation of spatiotemporal cortical activity patterns, and the technological advances in modern computation that permit the large-scale simulation of these spatiotemporal patterns, allow for complementary experimental and theoretical studies that were beyond reach just a decade ago.

Methods

The Model. For details, see Supporting Text, which is published as supporting information on the PNAS web site. We model an ≈6 mm × 4 mm patch of V1 cortex by constructing a two-dimensional lattice of ≈10⁶ model point neurons (with label i). Because visual angles subtended by stimuli in our study are sufficiently small, retinotopic effects are ignored. Each neuron has a cortical position x_i corresponding to its location in the model cortex. There are 80% excitatory neurons and 20% inhibitory neurons. Half of the neurons receive direct LGN input, whereas the other half do not. Every neuron also has a preferred orientation θ_i(x_i), which is laid out in predetermined pinwheels (see Fig. 1A) (8, 9). We note that our network is an effective or “lumped” model of V1 because we do not include the detailed laminar structure of V1 (7).

Fig. 1.

Cortical architecture and spontaneous activity. (A) A lattice of ≈10⁶ neurons distributed in 12 × 8 = 96 orientation hypercolumns spanning an ≈6mm × 4 mm patch of cortical space. The color labels the preferred orientation of a neuron at the corresponding location. A neuron in the black dot receives local isotropic excitation (inhibition) from randomly, sparsely coupled neurons inside the local range indicated by the small pink (cyan) circle and LR orientation-specific excitation from other neurons inside the yellow-rimmed domains of similar orientation preference. The typical lateral extent of the LR connections is shown by the yellow ellipse. The white box Φ is a typical subregion used for quantifying spontaneous activity. (B) The similarity index ρ(θ, t). (C) The firing rate m(θ, t) of all excitatory neurons in Φ that prefer orientation θ over the same cortical period as in B. (D) The cross-correlation 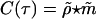. (E) The autocorrelation of m(θ, t).

The dynamics of the ith neuron's membrane potential V_i is governed by a single compartment, conductance-based, exponential integrate-and-fire equation (17, 18). Every neuron is locally isotropically sparsely connected to ≈400 nearby neurons, within ≈250 μm (19), at random. In our model, there are slow (≈80 ms) NMDA (20–27) in addition to fast (≈3 ms) AMPA excitatory conductances in the orientation-specific LR connections, which project to both excitatory and inhibitory neurons (10, 28–30). The LR spatial coupling kernel has spatial scale σ^LR = 1,500 μm with eccentricity 1∼2 (11, 31) with a random distribution of the major axes and connects neurons in different pinwheels with similar preferred orientations.

In our simulation, cortical activity is quantified by the slaving voltage , where , and are its leakage, AMPA, NMDA, and GABA conductances, respectively, and V^L, V^E, and V ^I are the leak, excitatory, and inhibitory reversal potentials, respectively. We use V^S(x, t) to represent (32) the subthreshold dendritic potentials associated with the VSD optical signal in the superficial layers of the cortex (3, 33).

Our model cortex is driven by background noise and a model LGN (mLGN) (for details, see Supporting Text). Both the background spike times and the mLGN spike times are independently sampled from Poisson processes. The background rate is spatiotemporally uniform (i.e., homogeneous background), and the mLGN rates are given by a linear spatiotemporal convolution of the visual stimulus. Because of the random distribution of preferred phase (34), our mLGN has the same spatially averaged mean of feedforward input rate to any small cortical area. A strong visual stimulus will induce a large modulation in input rate from the mLGN, which will cause more firing.

The network architecture is illustrated in Fig. 1 A. Fig. 2 displays the stimulus paradigms for the moving square and LMI, as well as the corresponding mLGN output rate in our model.

Fig. 2.

mLGN-sculpted cortical input for the drifting-square and LMI stimulus paradigms. (A) Typical mLGN time kernel, with a fast rise and a slow decay. (B) Typical mLGN spatial Gabor kernels for various orientations with a particular spatial phase and spatial frequency. (C) Visual stimulus of a square of size 1.5° × 1.5° moving at ≈32° per s. (D) Spatiotemporal distribution of the mLGN output firing rate determined by convolving the moving-square input in C with the time kernel of A and the Gabor function indicated by the square in B.(E) LMI stimulus. First, a stationary square is displayed for 48 ms, then a blank screen is shown for 10 ms, and then a stationary bar of size 6° × 1.5° is displayed. (F) Spatiotemporal distribution of mLGN output firing rate obtained by convolving the LMI input with the mLGN time kernel and the Gabor function (note that the mLGN output is simply a linear function of the input, and there is no progressive rightward growth of activity). These stimuli closely resemble what is used in experiment (13). Frame times are shown at right, with increment Δ = 9.6 ms throughout the text, which corresponds to the frame rate used in the VSD imaging experiment (13).

The Dynamic Regime: IDS. Our model cortex with a strong NMDA-type LR coupling, countered by a strong inhibition, can give rise to a strongly fluctuating dynamics with the IDS cycle (as described in the Introduction), generating spontaneous, coherent, ongoing spatiotemporal activity patterns as in real cortex (7). In our simulations, we observe a correlation between the spatial patterns of V^S(x, t), NMDA conductance g^N(x, t), and the firing rate m(x, t), with moderate rate, only when our numerical cortex is in an IDS state. Furthermore, the IDS state seems to be the only cortical operating point in which subthreshold activity is also correlated with low (2–10 spikes per s) spontaneous firing rates as well as with moderate (10–60 spikes per s) evoked firing rates. It turns out that these correlations play a significant role in our modeling in this work. Therefore, we operate our numerical cortex in an IDS regime by setting appropriate local excitatory, inhibitory, and LR excitatory cortico–cortical coupling strengths. Our model is thus strongly constrained, left with only few parameters to tune. In what follows, we use the term “model cortex” (denoted as mC) to refer to our numerical cortex with this specific class of parameters.

As described in ref. 7, the spontaneous activity patterns of the mC can be quantified (1, 2) by the similarity index ρ(θ, t) obtained by spatially correlating the instantaneous unevoked voltage profile V^S(x, t) recorded in a ≈4-mm² subregion (Φ in Fig. 1A) of our mC with the preferred cortical state V^S_P (x, θ). The V^S_P (x, θ_d) is the spike-triggered average of the evoked activity profiles V^S(x, T_sp, θ_d) obtained by stimulating our mC with a high-contrast drifting grating of orientation θ_d, where T_sp is a spike time of a neuron with the orientation preference θ_d (1, 7). As reported before (7) and recapitulated in Fig. 1B, in our mC, the spontaneous voltage profile sometimes resembles one of the preferred cortical states, and the pattern drifts with time scale ≈80 ms.

Here, we further discuss the causal relationship between spatial patterns and spiking events in the IDS regime. We measure the firing rate m(θ, t) of neurons in the recorded subregion that prefer orientation θ, as shown in Fig. 1C, and the time-correlation between ρ(θ, t) and m(θ, t), i.e.,

where , are normalized versions of ρ, m with 0 mean and variance 1. For the spontaneous dynamic regime of our mC, each intermittent recruitment event is precipitated by a few spikes that quickly (≤5 ms) generate a cascade of activity and create a spatial NMDA pattern that accentuates a particular orientation. Once such a pattern is established, it in turn induces more spiking events within ≈10 ms. Therefore, even though most spontaneous activity patterns are induced by a few significant spikes, the majority of spikes in the system are simply caused by a spatial pattern of activity that has been just established. This causality is reflected in the cross-correlation C(τ) as shown in Fig. 1D, which exhibits a peak at τ ≈ –10 ms, indicating that the firing rate is a strong signifier of the cortical state observed milliseconds earlier. We further note that the autocorrelation of m(θ, t), as shown in Fig. 1E, indicates that there are roughly two time scales, ≲10 ms, as associated with recruitment, and ≈80 ms, which is related to the slow decay (≈80 ms) of a pattern.

Results

To calibrate the strength of our mLGN, we use the experimentally observed V1 response to a flashed stationary square via real-time VSD-based optical imaging, as reproduced in Fig. 3B from ref. 13, and choose the LGN input strength so that the flashed-square input (Fig. 3A) generates a physiologically reasonable activity pattern within the mC as shown in Fig. 3C. Just as in the real cortex (13), the quickly flashed square (lasting from 0–48 ms) gives rise to a delayed surge of cortical activity, the onset of which is ≈50 ms after the square is initially presented, and then eventually decays (after another ≈130 ms). We note that, for each of our simulations, we present stimulus only after the spontaneous activity in the mC has reached a statistically steady state.

Fig. 3.

Activity patterns of our mC vs. experiment (13). (A–C) Flashed-stationary-square stimulus. Visual input (A), the VSD imaging of cat visual cortex (B), and the V^S profile of mC (C) are shown. (D–F) Stationary-bar stimulus. Visual input (D), the VSD imaging of cat visual cortex (E), and the V^S profile of mC (F) are shown. (G–J) Moving-square stimulus. Visual input (G), the VSD imaging of cat visual cortex (H), the V^S profile of mC (I), and the NMDA gn profile of mC (J) are shown. Note the strong correlation between V^S and gn.(K–N) LMI stimulus. Visual input (K), the VSD imaging of cat visual cortex (L), the V^S profile of mC (M), and the NMDA gn profile of mC (N) are shown. Note that mC activity profiles (M and N) show progressively growing activity from 8Δ to 11Δ even though the visual input (K) and the mLGN output (Fig. 2F) do not. B, E, H, and L have the same scales for activity corresponding to the upper color bar. [Reproduced with permission from ref. 13 (Copyright 2004, Macmillian Publishers Ltd.).] C, F, I, J, M, and N are obtained by averaging five trials with the same activity scales as indicated by the lower color bar (with numerical values for V^S and gn × 10²). See Fig. 2 for stimulus sizes. The time for each frame is shown at left, with increment Δ = 9.6 ms.

Our mC is presented with various other stimuli similar to those used in experiment: a stationary bar, a drifting square, and the LMI stimulus (Fig. 3 D, G, and K, respectively). The resulting spatiotemporal activity profiles are displayed in Fig. 3 F, I, and M. By juxtaposing frames corresponding to the same time, it is easy to see that these results are in very good agreement with the experimental observations, as reproduced in Fig. 3 E, H, and L. As can be seen clearly in Fig. 3 D–F, a stationary bar also produces a delayed surge of cortical activity, the onset of which is ≈50 ms after the bar is presented, and then it eventually decays (after another ≈130 ms). As shown in Fig. 3 G–I, the moving-square stimulus induces activity near the cortical area corresponding to the square's initial position after a similar initial delay (≈50 ms). This activity grows progressively rightward to fill out the cortical area corresponding to the square's path, and then it eventually decays. Fig. 3J reveals the NMDA g^N-signature of the mC, and it can be clearly seen that the voltage activity V^S is highly correlated with the NMDA conductance. As noted before, this nontrivial correlation is observed only in an IDS regime and plays a critical role in the LMI spatiotemporal dynamics (see Discussion). Finally, in Fig. 3 K–N, we illustrate the spatiotemporal dynamics under the LMI stimulus paradigm—a quickly flashed (lasting from 0–48 ms) stationary square followed (10 ms later) by a stationary bar. As can be seen in Fig. 3 M and N, the V^S and g^N activity of the mC initially manifests near the cortical area corresponding to the square and grows steadily rightward to fill out the area corresponding to the bar. This activity has the same time course and spatial spread as in the real cortex (Fig. 3L). Just as in the real cortex (13), this activity is strikingly similar to the spatiotemporal pattern generated by the moving square (see Fig. 3 I–J); this similarity is believed to be associated with the illusory line-motion perception (13). We note that this rightward growth of activity begins ≈77 ms after the square is flashed, which is well before the time t ≈ 100 ms when the cortex would exhibit a significant response to the presentation of the bar alone (see frame 11Δ in Fig. 3F). It is important to note that this growth cannot simply be attributed to feedforward input from the mLGN, as clearly seen by comparing Fig. 3M and 2F. As will be explained in Discussion, the cortico–cortical interactions underlie the growth in activity from 77 to 116 ms. Incidentally, we note that the peak firing rate of excitatory neurons in our mC under the above stimuli is below 60 spikes per s, which is consistent with the experimental measurement (13).

To investigate the cue-contrast dependence of this “LMI phenomenon,” i.e., the progressive spread of cortical activity induced by the LMI stimulus, we stimulate our mC with many different versions of the LMI stimulus paradigm. Following the experiment in ref. 13, each version of the LMI stimulus is identical to the original one, as shown in Fig. 3K, except for the contrast of the initial square cue (the subsequent bar is at the same contrast for all versions of the stimulus). For each stimulus, we record the thresholded activity. Fig. 4 summarizes the measurement of the resulting “wavefront” position as a function of time. For cue contrast below 0.04, there is little to no discernible wavefront. For contrasts between 0.05 and 0.10, we observe that the wave starts earlier for higher contrast and the wave speed is ≈0.1 m/s, which is consistent with the experimentally reported activity spread speed in V1 (13, 35, 36). These observations agree well with the VSD imaging experiment (figure 4e in ref. 13).

Fig. 4.

Effect of cue contrast on onset and propagation of mC activity under LMI stimulus paradigm. The average horizontal coordinate of the activity front obtained by thresholding gn or V^S profiles is plotted against the times of measurement. Note the delay of the growing activity for lower contrast cues and the independence of activity growing speed on the cue contrast.

Discussion

The cortical activity induced by the LMI stimulus (as seen in Fig. 3 L and M) is clearly not a linear spatiotemporal convolution of the LMI stimulus itself (e.g., Fig. 2F). In experiment, it is difficult to pinpoint the origin of this nonlinear phenomenon, which might have multiple sources in the real cortex, including feedback from higher levels. However, in our simulation, the LMI phenomenon arises as a consequence of the recurrent cortico–cortical interactions within our mC, which has no structured feedback. This result suggests that the minimal cortical architecture captured in our V1 model could be the primary cause of the experimentally observed LMI phenomenon.

It turns out that the key ingredients of the mechanism underlying the LMI phenomenon in our mC are (i) the mLGN-sculpted spatiotemporal profile of the LMI input, (ii) the cue-induced facilitative effect of the LR NMDA-type cortical connections, and (iii) the g^N–V correlation in spatial patterns in the IDS state. Fig. 5 illustrates the mechanism in detail.

Fig. 5.

Network mechanism underlying the LMI phenomenon. Column 1 shows visual input to mLGN. Column 2 shows spatial modulation in mLGN firing rate input to mC. Column 3 shows spatiotemporal distribution of firing rate in mC. Column 4 shows NMDA conductance profile in mC. Column 5 shows the voltage activity profile in mC. The cortical spatial scale in columns 2–5 is the same as in Fig. 3N. The red patches correspond to the activity of a numerical cortex with weak LR cortical connections. The red and purple arrows indicate causal relationships of activity in this LGN-dominated numerical cortex, which is driven predominantly by the feedforward mLGN input. The green patches and green arrows correspond to the additional activity and the causal relationships induced by strong LR lateral cortical couplings of NMDA-type in our recurrent mC. (See text for details.)

First, we consider the effect of the LMI stimulus on a numerical cortex with very weak LR lateral cortical connectivity and comparatively strong input strength from the mLGN. For this hypothetical LGN-dominated cortex, we would observe spatial patterns of mLGN input modulation, firing rate, and voltage like those indicated by the red patches in Fig. 5. (The meaning of the green patterns and the fourth column of Fig. 5 will be discussed in the next paragraph.) The initial flashed square (at 0 ms) causes a transient increase in the spatial modulation in the input rate from the mLGN, as indicated by the red arrow a in Fig. 5. This input modulation from the mLGN immediately impinges on the left area of this numerical cortex (see red arrow b in Fig. 5) and slowly builds up enough excitatory cortical conductance, after ≈50 ms, to cause firing (see purple arrow b in Fig. 5). In this LGN-dominated case, the cortical firing gives rise to a weak voltage signature in the left area of the mC (see red arrow c in Fig. 5) that will decay when the mLGN input dies away. Later, when the bar is shown (at 58 ms), the mLGN causes a transient increase in the spatial modulation of input rate throughout the left to right areas of the numerical cortex (see red arrow d in Fig. 5). As this slowly building input rate modulation impinges on the mC (red and purple arrows e in Fig. 5), there is essentially no difference between the middle and right areas of this mLGN-dominated cortex; both are equally stimulated over the ≈50-ms interval starting from the onset of the bar. Afterward, the mLGN causes cortical firing simultaneously throughout the left to right areas of the feedforward numerical cortex (see the end of arrow e in Fig. 5). As before, the voltage signature is weakly correlated with the firing rate profile, which is essentially a time-delayed version of the input from the mLGN. This LGN-dominated cortex behaves essentially linearly, and the LMI phenomenon is not observed.

Now we turn to our mC, which has relatively strong LR cortical couplings of NMDA-type. In this case, we observe the set of activity patterns indicated by the combination of red and green patches in Fig. 5. (Note that the green color here does not label inhibition. It indicates additional activities induced via LR lateral cortical interaction.) Initially the mC has a response similar to the LGN-dominated numerical cortex discussed earlier. The flashed square causes an increase in the input modulation from the mLGN (as indicated by red arrow a in Fig. 5), which eventually builds up enough excitatory cortical conductance to cause cortical recruitment (red and purple arrows b in Fig. 5). From here on, the mC response differs from the response of the LGN-dominated numerical cortex. Because of strong LR cortical couplings, the few cortical spikes triggered by the mLGN in the left area of the mC increase the NMDA conductance of neurons in the nearby cortical area spanned by the LR connection spatial scale (green arrow A in Fig. 5). The NMDA time scale τ^N = 80 ms is sufficiently long so that this g^N persists in the area (green arrow C in Fig. 5) after the mLGN input modulation has decayed. Because of the g^N–V correlation in the IDS state (as indicated by green arrow B in Fig. 5), the voltage signature also persists for many tens of milliseconds. Now, when the mLGN starts to respond to the bar (red arrows d and e in Fig. 5), the activity in the middle of the mC is already different from the right area of the mC. Specifically, because of the spatial decay of the LR coupling kernel, the middle of the mC has a higher NMDA conductance and subthreshold voltage, and, on average, the neurons in the middle of the mC are closer to firing than the neurons in the right area of the mC.∥ Thus the input modulation from the mLGN due to the bar, which steadily builds excitatory conductance throughout the cortex, causes cortical recruitment in the middle of the mC before any recruitment occurs in the right area of the mC (see green arrow D in Fig. 5). Note that, in order for this mechanism to work, it is important that the square cue only “primes” the middle of the mC, i.e., the cue-induced NMDA conductance should not cause too much firing in the middle of the mC but only facilitate the recruitment of future spiking events. This sequence of events (recruitment → NMDA → subthreshold voltage → primed mC → facilitation of nearby recruitment) continues under the influence of the bar, and the activity profile grows rightward across the mC.**

It is important to note that this wave of activity is not a result of physical synaptic transmission times or axonal–dendritic conduction speeds (we investigated both of these effects in our simulations, via a delay between the time of a spike and the onset of its postsynaptic conductance, and found that they did not alter our network mechanisms). Rather, the initial recruitment caused by the square establishes a spatial NMDA distribution that has higher conductance in the middle of the mC than in the right area of the mC, as a consequence of the spatial decay of the LR coupling kernel. This spatial distribution is then converted to a temporal profile by the slowly increasing input rate modulation from the mLGN caused by the bar. In effect, the cue induces a transient cortical operating point (i.e., the middle area of the mC is primed) from which the cortex responds to the bar. In this sense, the network itself underlies the origin of the wavelike activity.

The NMDA-facilitated priming mechanism, as described in Fig. 5, also offers insight into the effects of the cue contrast on the onset and propagation of the wavelike activity profiles observed both in experiment (13) and in our simulations, as shown in Fig. 4 (as mentioned above, the contrast for the bar remains fixed while different contrasts of the square cue are compared). Because high-contrast stimulus causes more initial firing events than low-contrast stimulus does, a high-contrast square cue causes more recruitment in the left area of the mC and increases the subthreshold voltage (via the LR NMDA-type connections) in the middle of the mC more than a low-contrast square cue would. Thus, a high-contrast cue in the LMI stimulus brings the middle of the mC closer to firing than a low-contrast cue does. Therefore, it takes less time for the bar-induced mLGN input to cause recruitment in the middle of the mC, and hence the activity growth starts earlier in the high-contrast case than in the low-contrast case. After the middle of the mC recruits and the activity growth begins, there is essentially no difference between low and high cue contrast because the contrast of the bar flashed later is the same for different versions of the LMI stimulus.

To further validate the NMDA-facilitated priming mechanism, we present the LMI stimulus paradigm to other numerical cortices with different dynamical properties. Clearly, because of the limited duration of the priming effect, if the delay between the cue and the bar is too long, then there will be no LMI phenomenon. In addition, if we artificially shorten (lengthen) the rise time scale of the mLGN time kernel, then the recruitment occurs earlier (later). Accordingly, the wave of the growing activity onsets earlier (later) (data not shown).

First, we verify the LGN-dominated picture described above by tuning the numerical cortex to a homogeneous operating point (7, 37). This cortex shares all of the parameters of the mC except for the LR strengths S^LR, which are sufficiently weak so that the IDS behavior is destroyed. Hence, no g^N–V correlation is present. Thus, the cortical firing events in the left area of the weak numerical cortex no longer affect nearby cortical regions via LR couplings (the effect indicated by green arrows A and B in Fig. 5 no longer exists). From our mechanism, we expect that, if this weak numerical cortex is presented with the LMI stimulus, mLGN driven behavior should be obtained, as confirmed in Fig. 6A. Note that by moving away from the IDS cortical operating point, the NMDA conductance profile is indeed no longer correlated with the voltage, as seen in Fig. 6B.

Fig. 6.

Activity patterns for other numerical cortices under LMI stimulus. (A and B) Model cortex with very weak LR connections. The activity profile is essentially the LGN-dominated case (see the red patches in Fig. 5). The voltage (A) is not correlated with the NMDA profile (B). (C and D) Model cortex with almost all AMPA-type LR connections (i.e., Λ≈ 0). The activity profile of voltage (C) and NMDA (D) is again similar to the LGN-dominated case. (E and F) The standard mC, except that the gn values are flipped at 68 ms. This flip results in the right area of the mC being primed and hence firing before the middle of the mC. The activity of voltage (E) and NMDA (F) grows from right to left instead of from left to right. (G and H) The standard mC, except that the NMDA release is blocked in the left area of the mC. The square cue can no longer prime the middle of the mC, and the activity profile of voltage (G) and NMDA (H) in the right area of the mC looks similar to those when the bar is flashed alone (Fig. 3F). (I and J) Numerical cortex with very strong local inhibition. The right area of the strongly inhibited cortex recruits before the middle area, which is under suppression induced by the square cue. (K and L) The standard mC stimulated by a slowly growing bar (instead of a moving square), which grows from the left at speed of ≈16° per s. The spatial patterns of voltage (K) and NMDA (L) exhibit a slower growing rate than those under our standard LMI stimulus. (M and N) The spatial patterns of voltage (M) and NMDA (N) under our standard LMI stimulus for the standard mC are displayed for comparison. See Fig. 2 for stimulus sizes. The spatial scales for each cortical frame are the same as in Fig. 3N. All spatial patterns are obtained by averaging five trials with activity scales indicated by the color bar (with numerical values for V^S and gn × 10²).

We also study possible LGN-dominated behavior by constructing a model cortex without NMDA-type LR connections. We use the same parameters as the mC except for the parameter Λ, which is set to be nearly zero, where Λ models the percentage of NMDA receptors in these lateral connections (see Supporting Text). In this case, again, the cortical operating point moves away from the IDS, and the NMDA profile is uncorrelated with the voltage (Fig. 6D). Even though the cortical firing events caused by the flashed square increase the voltage in the left area of the numerical cortex, the LR conductance is AMPA-type and decays rapidly. The short-lived AMPA-facilitated priming effect in the middle of the cortex should not affect the response to the bar (the effect indicated by green arrow C in Fig. 5 no longer persists). As a consequence, the LMI stimulus is expected not to produce a wave of cortical activity, as confirmed in Fig. 6C. We suggest that these LGN-dominated regimes might be accessible in real cortex via pharmacological manipulation to rebalance the LGN input and cortico–cortical LR interactions.

To highlight the significance of the persistent spatial NMDA conductance profile in the priming mechanism, we perform the following “tailored-priming” experiment. The parameters from the mC are fixed, and the LMI stimulus is presented as usual, but at the 68 ms time point, the value of the NMDA conductance of each neuron is forcefully exchanged with the corresponding value at the horizontally reflected cortical point. Right after the flip, the NMDA conductance profile should have larger values at the right of the mC than in the middle of the mC. Contrary to the original scenario (Fig. 3M), this flip would result in the right area of the mC being primed instead of the middle of the mC. Thus, from our mechanism, we would expect that the onset of the bar first initiates firing in the right area of the mC, and that the activity would grow gradually from right to left, which is indeed confirmed in Fig. 6 E and F. We can also flip the GABA and/or AMPA conductances at various times, but the balance of the network is quickly restored within ≈10 ms, and the priming mechanism is not affected, thus the resulting activity profile is almost indistinguishable from Fig. 6 M and N afterward (data not shown).

We perform the following numerical simulation, which may be realizable pharmacologically in experiment. We again use the parameters from the mC but block the NMDA-type release in the cortical area corresponding to the flashed square within the left area of the mC. In this case, the LR connections should no longer increase the subthreshold voltage of nearby neurons. Thus, the middle of the mC would not be primed when the bar appears. As a consequence, we expect that the phenomenon of growing activity should not be observed, and the voltage signature outside of the blocked region should look essentially similar to that of the bar alone, as verified in Fig. 6 G and H by comparison with Fig. 3 E and F.

We emphasize that not every numerical cortex in the IDS regime produces the same type of growing spatiotemporal activity under the LMI stimulus. In our mechanism, it is crucial for the cue to be of a facilitative priming effect. If the flashed square does not give rise to a sufficient increase in NMDA conductance in the middle of the mC, those neurons will not be more likely to fire by the time the bar is presented and, thus, will recruit at the same time as the neurons in the right area of the mC. On the other hand, if the flashed square increases the activity too strongly in the middle of the mC, then the middle of the mC becomes saturated as a result of the cue, rather than primed. For example, if the LR connections are too strong, then a single recruitment event induced by the cue does not merely increase the NMDA conductance of nearby regions but also causes a substantial amount of cortical firing in the middle of the cortex. If the local inhibition is also very strong, then this increase in cortical firing can strongly suppress nearby cortical regions, making further recruitment events less likely and actually “antipriming” the neighboring regions (the effect indicated by green arrow D in Fig. 5 no longer exists). Hence, the onset of the bar can cause firing in the right area of the numerical cortex at the same time as it would if the bar were presented alone, and the middle of the numerical cortex may activate later due to the inhibitory suppression. To verify this effect, we design a numerical cortex with very strong LR NMDA lateral and local inhibitory connections, which also adopts IDS-like behavior in the spontaneous state. Fig. 6 I and J confirm the antipriming scenario in this strongly inhibitory numerical cortex, where the middle of the cortex activates later than the right area in response to the bar.

Note that an LMI stimulus paradigm gives rise to a sensation of a particular speed (12). As revealed experimentally (13), a growing bar also generates a progressive growth of spatiotemporal activity similar to that under the LMI stimulus, and the growth rate of the spatial pattern is slower when the growing speed of the bar is slower. This observation also is reproduced in our mC. Fig. 6 K and L shows that, under the stimulus of a bar growing at speed ≈16° per s, the resulting spatiotemporal activity pattern has a slower growth rate than the patterns observed under our standard LMI stimulus (i.e., 48-ms cue and a stationary bar after a 10-ms delay), as shown in Fig. 6 M and N, which closely resemble the spatiotemporal pattern under a drifting square moving at ≈32° per s, as seen previously by comparing Fig. 3 M with I.

Based on our mechanism, it is easy to predict which stimuli could result in a motion illusion, and we can come up with many alternatives to the square cue and subsequent rectangular bar of the LMI paradigm. Note that, in our mechanism, the only requirement for growing cortical activity is that the “bar” be visually proximal to the “cue.” More specifically, the cue that primes the mC can be anything that creates an NMDA conductance profile with a spatial gradient. The subsequent bar can be anything that takes advantage of this gradient and causes recruitment in one cortical area before another. Fig. 7 A–D displays several possible cues (Upper) and bars (Lower), which illustrate that our mechanism does not require sharp, straight edges (Fig. 7 A, C, and D), high contrast (Fig. 7 A, C, and D), spatial connectivity of the visual stimulus (Fig. 7 B and C), or the cue being a subset of the bar figure (Fig. 7 A and B). Each variation on the LMI stimulus can be constructed by flashing the cue for 40 ms or so and then steadily displaying the corresponding bar (see Movie 1, which is published as supporting information on the PNAS web site). Fig. 7 E–H illustrates a numerical experiment in which we present a variant on the LMI stimulus to our mC. The growing activity profile in the mC is similar to that evoked by a continuously growing visual stimulus (Fig. 7 I–L). Clearly, our predictions cannot extend to very large stimuli, or stimuli with multiple cues one after another, because such stimuli may involve retinotopy, attention, or other physiological complications (14, 38).

Fig. 7.

Predicted variants of the LMI stimulus. (A–D) Various different cues (Upper) and bars (Lower) that we predict will create illusory motion phenomenon. (E–H) Stimulus using only the cue and a long, curved blob in a manner similar to the LMI stimulus. The visual input. The cue of size ≈1.5° × 1.5° and the blob width ≈1.5° and horizontal span ≈6° (E), its mLGN output (F), and its spatiotemporal activity patterns of voltage (G) and NMDA (H) in the mC are shown. The mC activity profile grows outwards from the cue and fills out the cortical area corresponding to the blob (note that our cue here is on the right). (I–L) Growing blob stimulus (I), its mLGN output (J), and its spatiotemporal activity patterns of voltage (K) and NMDA (L) in the mC. The spatial scales for each cortical frame are the same as in Fig. 3N. All spatial patterns are obtained by averaging five trials with the same activity scales as in Fig. 6.

We emphasize that our results are robust to model parameters as well as the individual neuronal model used. We can achieve the LMI phenomenon with the same mechanisms, by retuning the cortical parameters, even if we use linear or quadratic integrate-and-fire point neurons; add other neuronal phenomenon such as synaptic depression or axonal delay times; or change the cortical architecture slightly, for example, (i) with the eccentricity of our LR elliptic coupling kernel, ranging from 1∼2 and with any orientation of the ellipse, (ii) with local excitatory or inhibitory interaction length scales, ranging from 100 μm to 300 μm, or (iii) with the NMDA percentage Λ ranging from 5% to 100% and, most importantly, with the NMDA decay time ranging from τ^N = 40 ms to τ^N = 80 ms.

Finally, this work suggests a functional role for the priming mechanism, namely, a role in the general cortical processing for temporal ordering and the spatiotemporal binding of two stimuli closely related in space and time.